Vibrations in Leaking Spherical Valves with Annular Seal †
Abstract
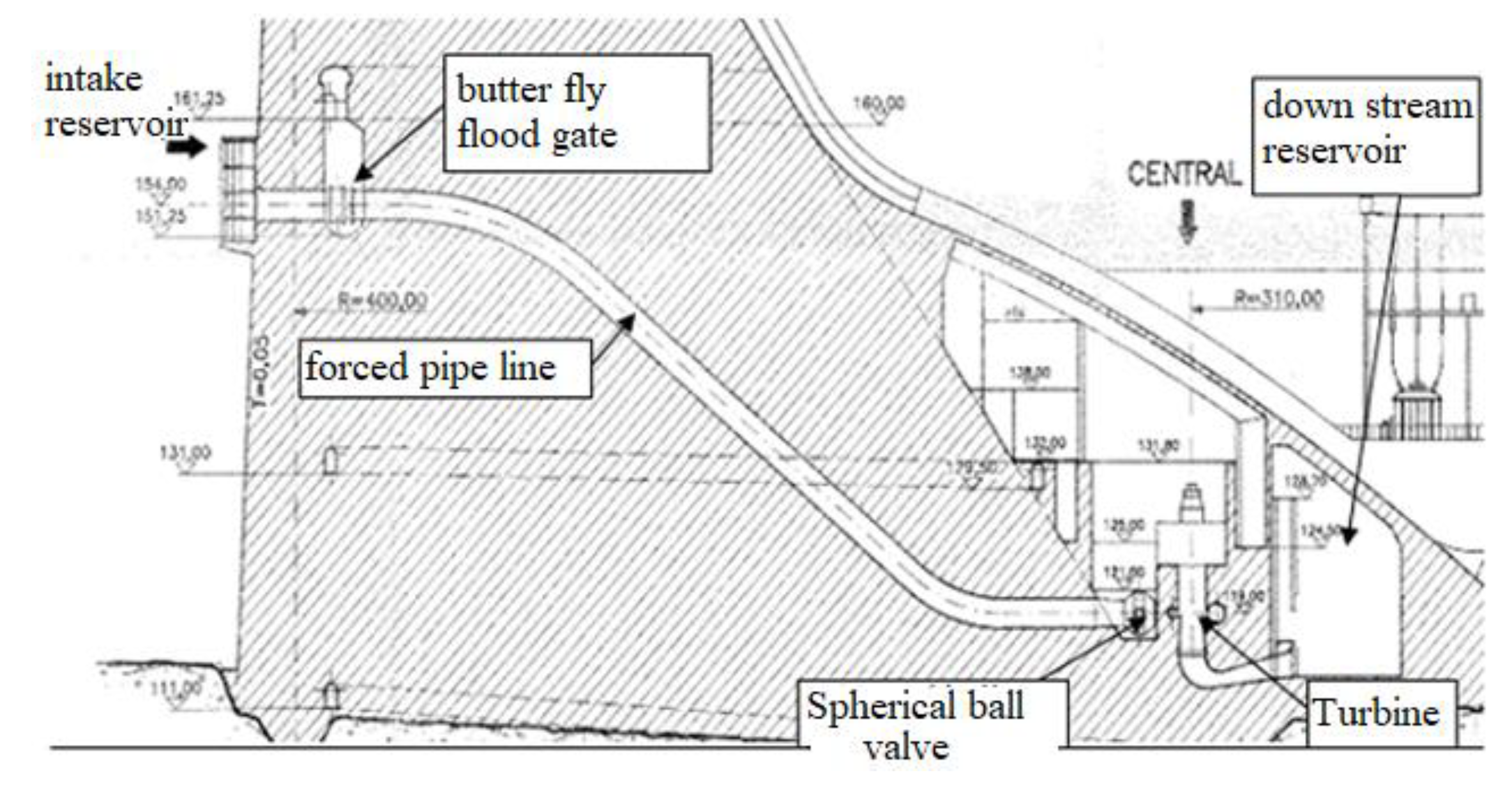
:1. Introduction
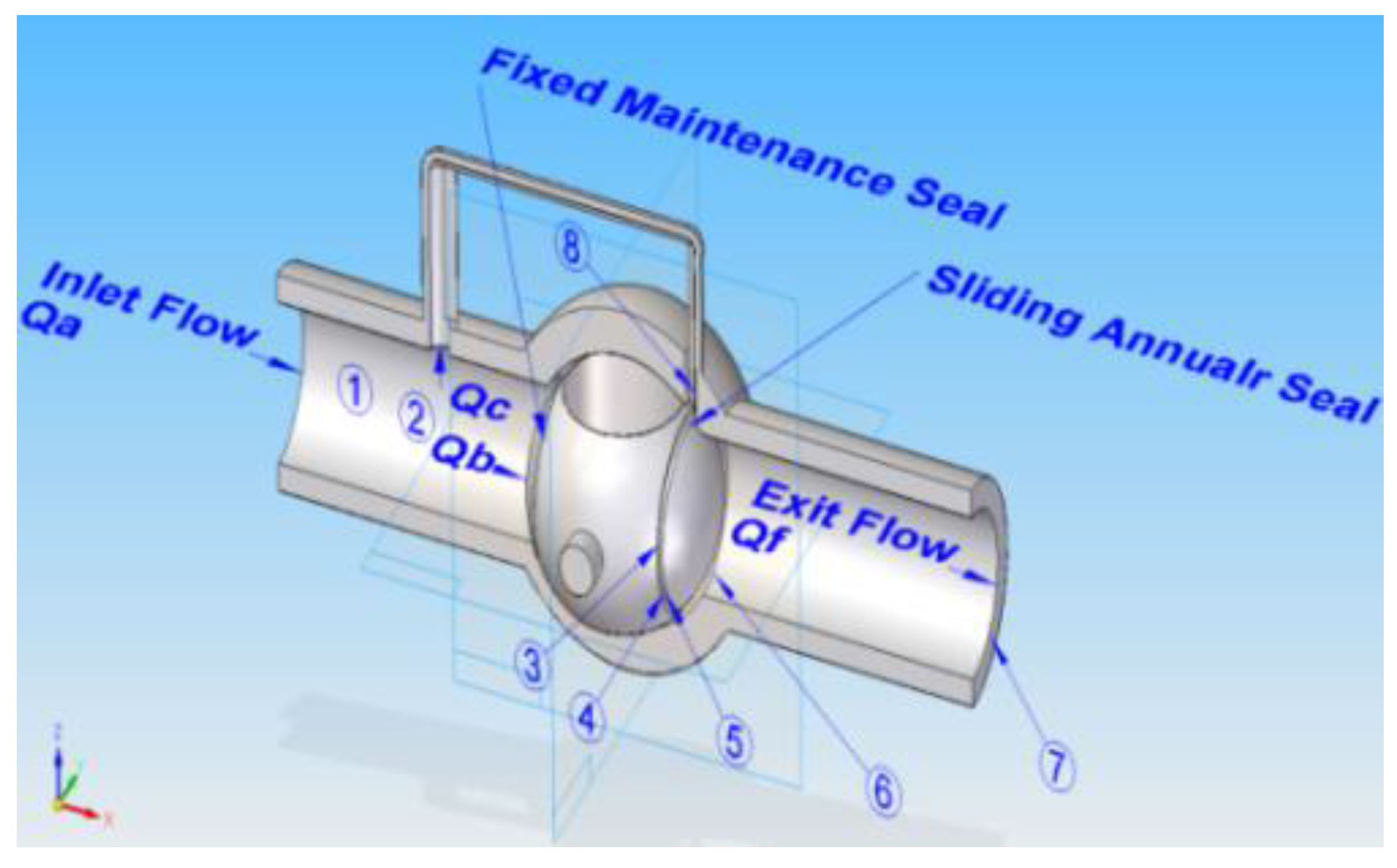
2. Seal Specifications
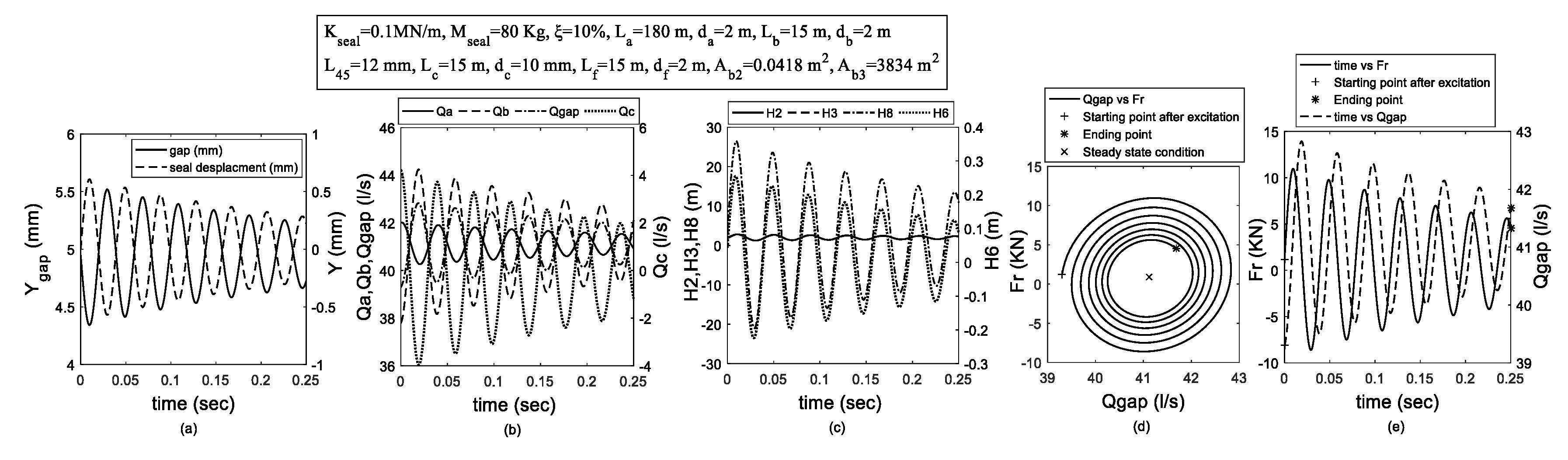
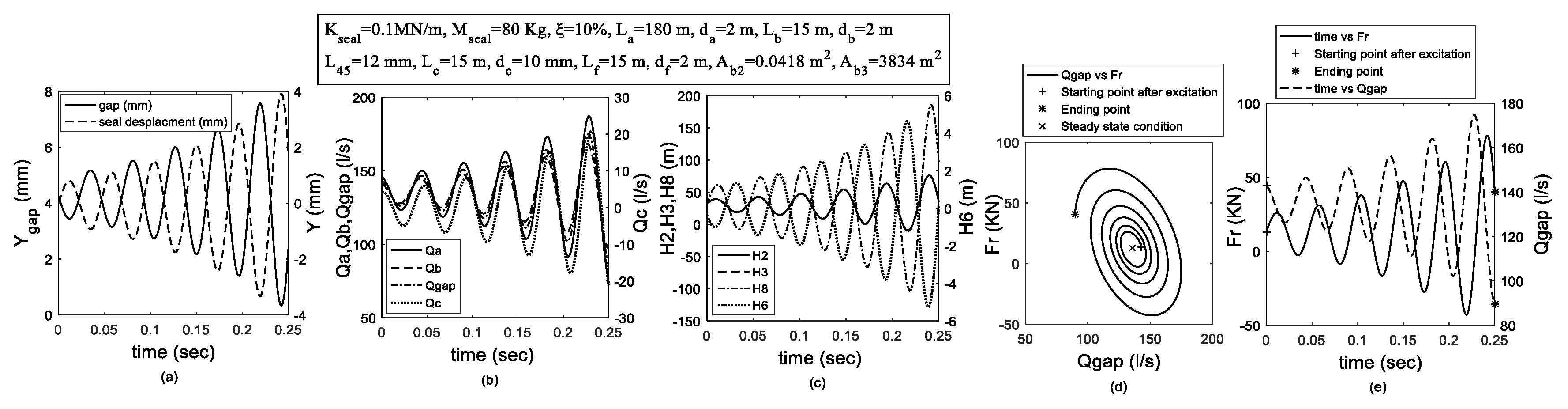
3. Theoretical Model and Procedure
4. Results
5. Conclusions
Acknowledgments
References
- Available online: http://www.saltosdelnavia.com/en/salime-hydropower-plant_57936.html (accessed on 15 June 2018).
- Budyans, R.G.; Nisbett, J.K.; Shigley, J.E. Shigley’s Mechanical Engineering Design, 9th ed; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Raw, S.S. Mechanical Vibration, 6th ed; Pearson: Harlow, UK, 2017. [Google Scholar]
- Rockwell, E.N.D. Flow-Induced Vibrations-an Engineering Guide; Editorial A. A. Balkema: Rotterdam, The Netherlands, 1994. [Google Scholar]
- Cimbala, J.M.; Cengel, Y.A. Fluid Mechanics Fundamentals and Applications, 2nd ed.; McGraw-Hill: New York, NY, USA, 2010. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Awad, H.; Parrondo, J.; González, V. Vibrations in Leaking Spherical Valves with Annular Seal. Proceedings 2018, 2, 1444. https://doi.org/10.3390/proceedings2231444
Awad H, Parrondo J, González V. Vibrations in Leaking Spherical Valves with Annular Seal. Proceedings. 2018; 2(23):1444. https://doi.org/10.3390/proceedings2231444
Chicago/Turabian StyleAwad, Hesham, Jorge Parrondo, and Víctor González. 2018. "Vibrations in Leaking Spherical Valves with Annular Seal" Proceedings 2, no. 23: 1444. https://doi.org/10.3390/proceedings2231444
APA StyleAwad, H., Parrondo, J., & González, V. (2018). Vibrations in Leaking Spherical Valves with Annular Seal. Proceedings, 2(23), 1444. https://doi.org/10.3390/proceedings2231444




