NPSH Experimental Data for Two Centrifugal Pumps ^†

Abstract

Cavitation consists in a local mass and heat transfer phenomenon, which involves the formation and collapse of vapor cavities. For industrial applications, the interest is focused on Fluid Machinery, increasing the difficulties due to the complex geometrical arrangements and working conditions. Within such frame, the work on cavitation for centrifugal pumps has been a matter of study in the last decades. The main conclusion of the present study is to show the NPSH curves for two available geometries with different impeller diameters and, then, a comparison is done. The results open the test case to possible numerical implementation and future analysis.

1. Introduction

Cavitation is the process of vapour bubble formation in low-pressure flow regions and it is an undesirable phenomenon in pumps. Cavitation induces pressure fluctuations and uneven load distributions [1], thereby seriously reducing the efficiency of pumps and affecting their operational stability. Microjets and impact forces due to collapsed cavities can erode the surface of flow passage components and damage the impeller blades. Cavitations can significantly reduce the service life of pumps. Therefore, pump cavitation, as a main cause of pump damage, should be avoided. But moreover, cavitation inherently involves a possible energy loss with all the associated drawbacks.

The effects of cavitation, despite being a non-stationary phenomenon, are usually grouped into a design parameter that allows to be on the side of safety and thus to avoid the appearance of it. The so-called NPSH, or Net Positive Suction Head, is usually defined for pumps, that is, positive net height in the suction constitutes a measure of the energy (or height, because it is an incompressible flow) available at the suction of the pump above the energy (height) that would result in the appearance of cavitation. The definition of the NPSH is done with the equation that relates the proximity of the local pressure to the vapor pressure of the liquid, which in a practical basis leads to (1):

$$NPSH=\frac{P_I-P_v}{\rho g}+\frac{1}{2g}{V}_I^2+C$$

(1)

In this Equation (1), the static and dynamic pressure (with an additional experimental constant) are compared to the vapor pressure to determine the NPSH or, in other words, the cavitation margin [2]. Typical parabolic-shape curves are expected for that calculation. In the case of the available circuit, and given that the measured pressure is practically at the inlet of the pump, the previous expression (1) is used and a value for C = 0.5 m is added, typical from the bibliography. It is intended to obtain the curve of the so-called 3% fall, thus indicating a loss of performance of that percentage in the height of elevation.

Once the two NPSH curves (one for each model of pump) are obtained experimentally, it is tried to deduce a valuable information that could be used to define the state against cavitation, in spite of the realistic estimations that can be calculated nowadays with CFD codes.

2. Experimental Set-Up

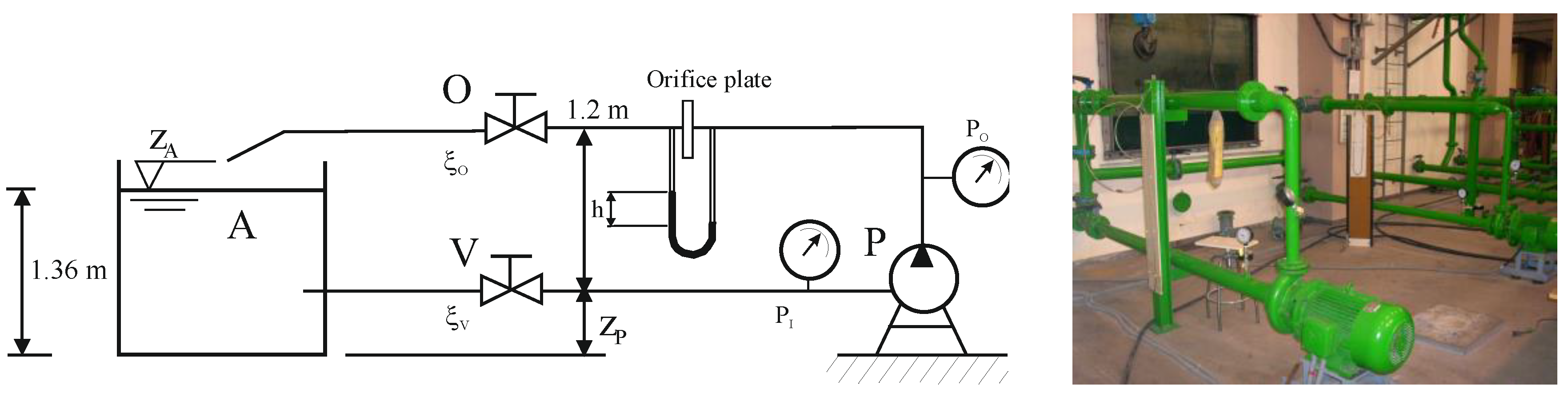
A test bench for the experimental study is available at the Área de Mecánica de Fluidos in Gijón (Spain), as shown in Figure 1. The previous experience of the authors in the study of the dynamic pressure field on a centrifugal pump [1] allowed a consequent step into the cavitation research. The set-up consists of two centrifugal pumps installed in a system similar to the one sketched in Figure 1 (left hand side). For each pump (P), the system includes a tank A (opened to the atmosphere), an inlet pipe with a valve V (that will be used in the cavitation tests), two manometers to obtain inlet and outlet pressure (P_I and P_O, respectively), an orifice plate to measure the flow rate and a valve O, placed downstream of the pump, to change the working conditions. Both pumps were tested at a rotating speed n = 2930 rpm.

Fluid variables were captured in a steady basis using the available devices in the test bench. Particularly, the measurement of the flow rate in the experiments was made using the indirect measurement of the pressure drop in the orifice plate, which had been previously calibrated, as shown in Figure 1 (left hand side sketch). The inlet and outlet pressures were obtained with the two manometers placed in the inlet and outlet of the pump, respectively (they are clearly seen in Figure 1, right hand side picture).

This set-up has been widely used and studied in previous works by the research team (among others, [1]) and available data on the orifice plate calibration and on the uncertainty for the different variables is considered. Particularly, manometer show an uncertainty that influences the head in a value always lower than 3.8%, the NPSH in a 4.1%, while the flow rate measurement, with the orifice plate, promotes an uncertainty for the flow rate below 1.7%, all within a 95% confidence level.

Firstly, a series of tests are done in order to obtain the pumps performance curves. Secondly, a more specific tests are carried out to experimentally define the cavitation performance of both pumps.

3. Experimental Results

Following the classical procedure for pump testing, the two available pumps, with a maximum delivery power (according to manufacturer) of 15 kW and 30 kW, have been tested in the described set-up. A full description of the two pumps is done in the frame of a steady flow analysis.

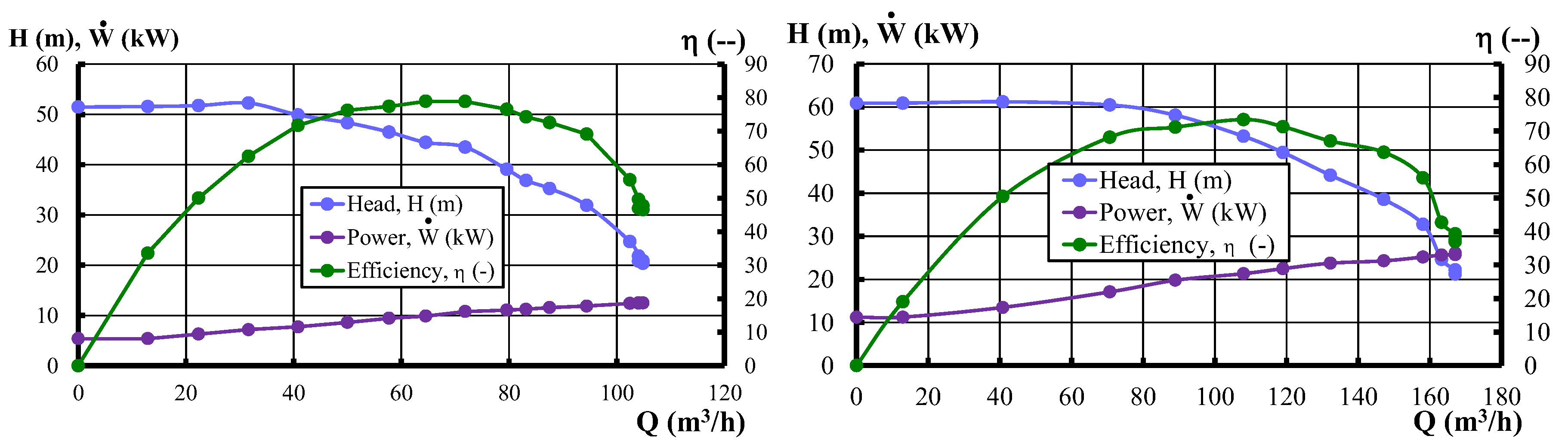
As can be observed, Figure 2 shows the performance curves for the two pumps. The head, power and efficiency of both pumps can be analyzed, as a function of the flow rate or working point, by changing the value of ξ_O. Some conclusions that can be deduced from the two graphs are the following:

• Classical head vs. flow rate curves were obtained for both pumps. The low flow rate part of the pumps is almost horizontal, with a classical parabolic decrease from a certain point. The last horizontal point lies around 32 m³/h for the 15 kW pump (Figure 2, left) and around 70 m³/h for the 30 kW unit (Figure 2, right). The curves are plotted in blue in Figure 2.
• Power vs. flow rate curves have been obtained by placing an electrical meter at the motor connection. This means that some motor power loss is being attributed to the pump hydraulic efficiency, but this is a quite widespread practical approach in pump industry. Purple curves in Figure 2.
• Efficiency vs. flow rate curves show the classical shape, with a maximum or nominal flow rate at Q_N = 64.54 m³/h for the 15 kW pump and at Q_N = 108.00 m³/h for the 30 kW one. Green curves in Figure 2.

So, globally speaking, the expected trends for centrifugal pumps have been retrieved, similar to what can be found in textbooks. As the next step, and keeping the steady flow hypothesis, a series of cavitation measurements were done. The experimental procedure to obtain the cavitation is established in five steps:

• The pump is put to work at a certain operating point. Pressure loss in the orifice plate and power can be measured, as in the case of the performance curves determination.
• The pressure at the suction of the pump was progressively reduced, using the valve located in that position. This is equivalent to increase the value ξ_V (lower valve in right hand side of Figure 1).
• The valve continues to close in the suction until there is a fall of around 3% in the performance curve or cavitation noise starts being heard. Although the different intermediate values are collected, only three points are considered to be representative, as it will be explain in what follows.
• The value of the pressure measured by the vacuum gauge at the suction is recorded as final value.
• The NPSH is calculated from such value, according to Equation (1).

After following the before mentioned procedure, Figure 3 shows the change in the NPSH for one of the tested pumps. Curves of head vs. NPSH are plotted for two flow rates (low flow rate at the left hand side of Figure 3 and high flow rate at the right of Figure 3). As mentioned, only three values are shown to clearly find the pressure drop when approaching the point of incipient cavitation.

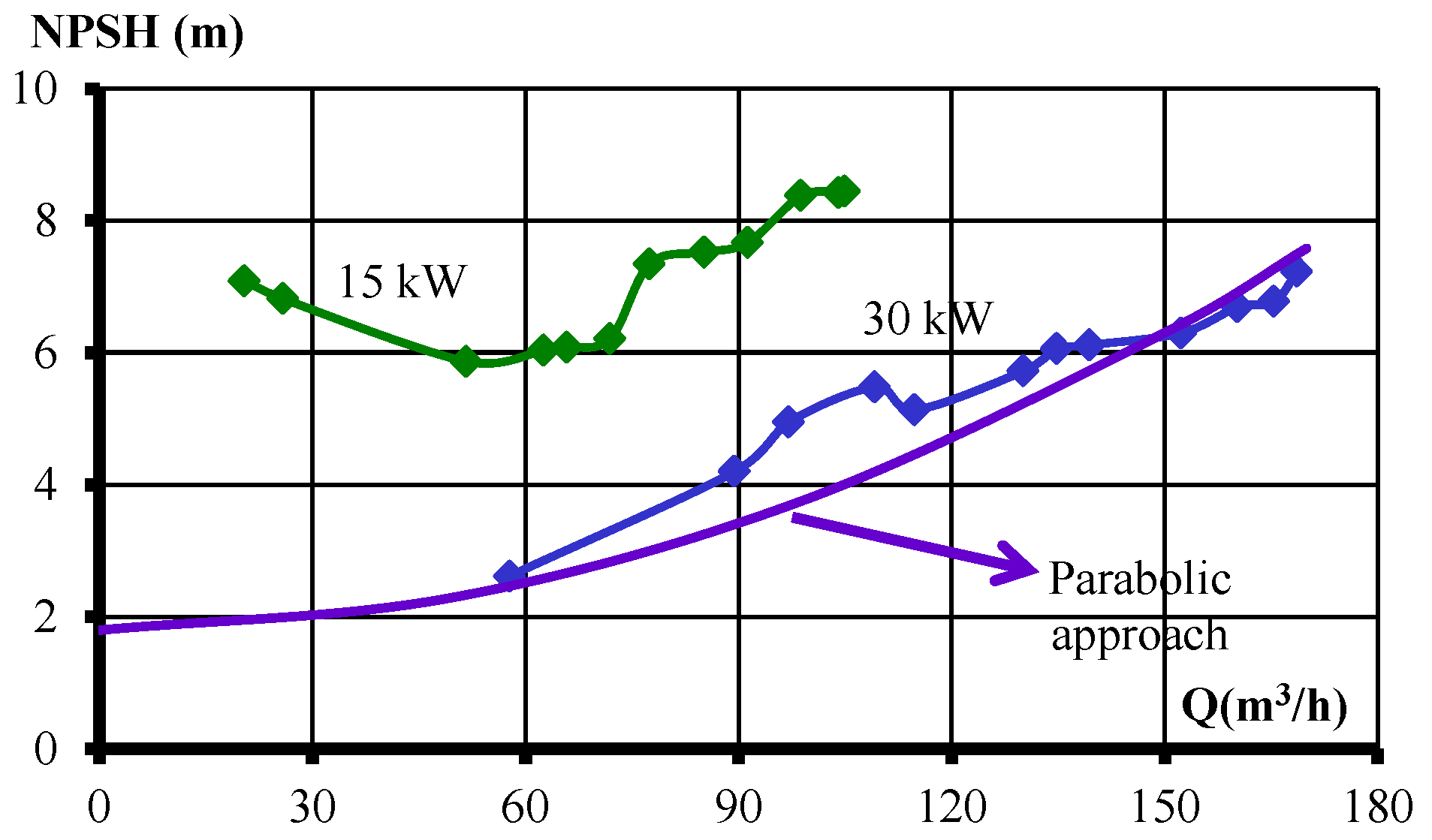
Finally, and after grouping all the available measurements from the cavitation tests for the two pumps and the different working conditions (or flow rate ranges), NPSH curves as a function of the flow rate could be plotted. Figure 4 shows the comparison between NPSH curves for both centrifugal pumps. These curves show a different trend for each pump. Thus, for the 15 kW pump, a “V” shaped curved is retrieved, while for the 30 kW pump a continuously increasing curve was found.

An additional trend curve has been plotted in Figure 4 to see how the adjustment of these lines is. Using a minimum square type of approximation, the following parabolic equation was found, valid for the 30 kW pump:

$$NPSH=0.8+2\times {10}^{-4}{Q}^2$$

(2)

With this curve, the similarity laws could be applied to obtain the possible cavitation performance at another rotating speed in a quicker way than using the individual data.

4. Conclusions

An experimental campaign has been taken up, in the frame of a doctoral study, for two centrifugal pumps. The well-known head, power, efficiency and NPSH curves as a function of the flow rate have been obtained in order to define the static flow conditions of the two pumps.

Apart from the more widespread values, namely head, power and efficiency, the main conclusion of the study shown here is the experimental measurement of the NPSH curves for two available geometries, with different impeller diameters and, as a final step, a comparison that has been done. The results open the test case to possible numerical implementations and future analysis, following for instance [3].

The whole set of steady curves for the two pumps are therefore obtained and differences could be observed. Globally speaking, the expected trends have been experimentally found, although particular values are of great interest for the forthcoming research.