Investigation of Thermodynamic Properties of the Slurry of the Molding Process Beryllium Ceramics ^†

Abstract

Obtaining of ceramic fabrications by hot molding from dispersion materials with anomalous physical properties, such as BeO is particularly complicated. In this case, the difficulties of obtaining of quality products were caused firstly by thermal properties of beryllium oxide, in particular, its unique thermal conductivity. Results of experiments and calculations of the mathematical model of the motion and heat exchange of the slurry mass in the annular cavity are presented. The results of experiments and calculations show the process of molding of the slurry in the annular cavity.

1. Introduction

The development of new areas of science and directions of technology advances increased requirements to the level of properties and to the quality of ceramic fabrications, are increasingly becoming more popular products of complex configuration from new non-metallic materials (high thermal conductivity, oxygen-free, superconducting, etc.). Technology of hot casting under pressure [1,2] remains the basis for the obtaining long-length, multi-channel, complex shaped ceramic fabrications from non-plastic powders, in spite of the using of isostatic pressing. The results of experimental researches and the generalization them by calculations of mathematical model of process molding of the thermoplastic slurry beryllium oxide are presented in this paper.

2. Experimental Data of Rheological Properties of the Thermoplastic Slurry

The thermoplastic slurry (highly-viscous suspension) represents a two-phase disperse system, where the solid minerals phase—beryllium oxide powder, liquid phase—organic binder [3]. The organic coupler consists of three components: paraffin, beeswax and the oleic acid in the proportion 82%:15%:3%.

Investigation of thermo physical properties of the thermoplastic slurry depending on the temperature, the heat at the phase transition is the main problem, in that they largely determine the technological and operational characteristics of beryllium ceramics.

3. Discussion of Optimization Calculations Data

The parameters have changed in the optimization calculations: casting speed, cooling conditions and the design of the cooling circuit. At the inlet of the cylindrical part of the annular cavity the temperature of the slurry is constant and equal $80℃$, which corresponded to the industrial casting conditions.

The release of heat of crystallization during the phase transition of the slurry from the viscous-plastic state to the solid-plastic takes into account in numerical calculations. The coaxial cavity consists of two concentric cylinders with radii of 6 and 10 mm, respectively, which makes it possible to obtain a ceramic product in the form as a tube. The cooling contour of the cavity is divided into 3 parts. Temperature of the cooling water in the first part is $t_1=80℃$, in the second part - $t_2=59℃$, in the third part -$t_3=20℃$.

3.1. Changing the Speed at $U_0=$10 mm/min and $U_0=$20 mm/min

The Temperature of the Slurry at the Inlet of the Channel Is Constant across the Cross-Section

The profile of the longitudinal component of the velocity attains the shape of shear flow of the fluid near the inlet section due to high viscosity of the thermoplastic slurry (Figure 1). Wall temperature in the first cooling contour is $t_1=80 ℃$ and temperature field changes from $t=80 ℃$ to $t=64.5 ℃$ in this zone (Figure 1). Temperature isolines (isotherms) show the regions of the constant temperature and internal structure of the slurry mass which is in liquid state. Wall temperature is $t_2=59 ℃$ in the second cooling contour. Sharp reduction of the wall temperature generates intensity growth of the slurry cooling, it also leads to the change of the rheological and thermo-physical properties of the slurry. Heat pick-up growth results in reduction of the temperature field in the second cooling contour (Figure 1). There is a transition zone in the beginning of the second contour, where temperature field is variable and expresses the transition of the slurry from the liquid state into the viscous-plastic state. The slurry temperature changes from $t=80 ℃$ to $t=59 ℃$ and defines upper boundary of the zone with constant temperature $t_2=59 ℃$. Wall temperature in the third cooling contour is $t_3=20 ℃$., which leads to the further cooling of the slurry mass and temperature reduction from $t=59 ℃$ to $t=45 ℃$ in the transition zone. According to the experimental data, change in aggregate state takes place at temperature $t_f=55 ℃$. In energy equation heat release during aggregate state change occurs due to solidification of the viscous-plastic slurry.

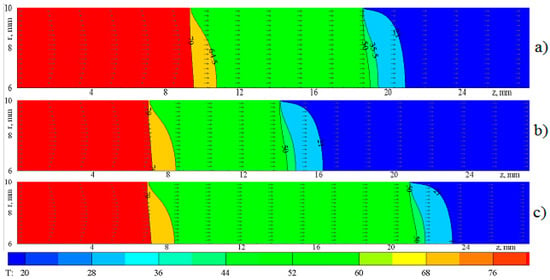
Figure 1. Distributions of the temperature over the annular cavity length at different ratio of the length of the cooling circuits at $U_0=10 mm/min$, (a) L₁ = L₃ = 9.4 mm, L₂ = 9.2 mm; (b) L₁ = L₂ = 7 mm, L₃ = 14 mm; (c) L₁ = L₃ = 7 mm, L₂ = 14 mm.

Increase of Molding Velocity $u_0=20 mm/min$ by Twice, while the other Parameters Stay the Same, Has an Impact on the Structural Change of the Slurry (Figure 2).

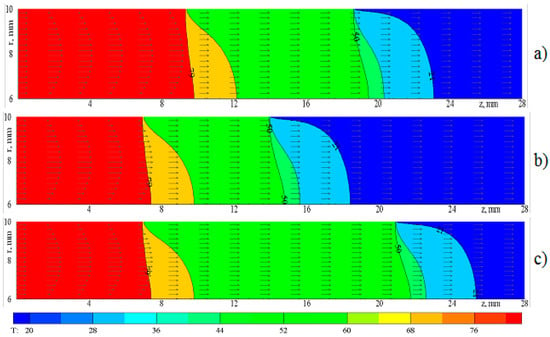
Figure 2. Distributions of the temperature over the annular cavity length at different ratio of the length of the cooling circuits at $u_0=20 mm/min$, (a) L₁ = L₃ = 9.4 mm, L₂ = 9.2 mm; (b) L₁ = L₂ = 7 mm, L₃ = 14 mm; (c) L₁ = L₃ = 7 mm, L₂ = 14.

3.2. Figures

The total cavity length amounts to $l=28 mm$, the lengths of the first, second, and third sections are $l_1=9.4, l_2=9.2, l_3=9,4$ (Figure 1a and Figure 2a); $l_1=7, l_2=7, l_3=14$ (Figure 1b and Figure 2b); $l_1=7, l_2=14, l_3=7$ (Figure 1c and Figure 2c).

3.3. Formatting of Mathematical Components

The Shvedov-Bingham rheological model was used to describe the rheological property, the relation between the shear stress $\tau$ and shear rate $\frac{\partial u}{\partial r}$ of the thermoplastic slurry:

$$\tau ={\tau }_0+\mu \frac{\partial u}{\partial r}$$

(1)

where $\tau$ is the shear stress, ${\tau }_0$ is the yield strength, $\mu$ is the plastic viscosity coefficient. The ultrasonic effect (USE) influences the rheological properties of the slurry. The plastic viscosity coefficient $\mu \left(Pa·s\right)$ and the yield strength ${\tau }_0\left(Pa\right)$ of the slurry depend on temperature $T$, and the experimental data at the relative mass fraction of the binder $\omega =0.1$ prior the USE are described by the empirical dependencies

$$\begin{gathered} \mu =5.5+6.2exp\left(-\frac{T-334}{6}\right), \\ {\tau }_0=19+11.41exp\left(-\left(T-340\right)/5.47\right) \end{gathered}$$

(2)

after the USE:

$$\begin{gathered} \mu =2.5·{10}^{14}exp\left(-0.09068 T\right), \\ {\tau }_0=5.93·{10}^{8}exp\left(-0.04968T\right) \end{gathered}$$

(3)

The slurry density is determined by the concentration of the beryllium powder and the binder:

$$\rho =\frac{{\rho }_{BeO}·{\rho }_{bin}}{\left(\left(1-\omega \right){\rho }_{bin}+\omega ·{\rho }_{BeO}\right)}\times {10}^3$$

(4)

where ${\rho }_{BeO}$ is the beryllium density, ${\rho }_{bin}$ is the coupler density, $\omega$ is the relative mass fraction of the coupler in the fractions of unity.

The coupler density is temperature-dependent and is determined by the empirical formula

$${\rho }_{bin}=0.8485+0.0755·\cos \left(0.0571·T-16.736\right)$$

The beryllium density is ${\rho }_{BeO}=3.02 g/c{m}^3$. The coupler density in temperature range from 348 to 318$℃$ varies within the limits ${\rho }_{bin}=0.784-0.8845g/c{m}^3$, and at the solidification, the thermoplastic slurry density increases from 2.3498 to 2.4327 $g/c{m}^3$ for $\omega =0.1$. As the experimental data of [3] show, the USE does practically not affect the slurry thermal conductivity and heat capacity, they depend on temperature in the form

$$\lambda =7.1exp\left(-0.01T+2.73\right), \frac{W}{m·K}$$

(5)

$$c_p=1000exp\left(0.00345T-0.94\right), \frac{J}{kg·K}$$

(6)