Abstract
Given the diversity of meanings nowadays, creativity and mathematical creativity are difficult to define. However, it is crucial to do so, whether in society, in education or in mathematics education. Creativity is not valued as an integral part of the classroom context of mathematics or in Teacher practice, possibly due to the constant changes of Portuguese curricular. In this sense, it is necessary to promote the development of creativity as an integral part of the pedagogical practice of each teacher. The teacher’s role is fundamental to allow students opportunities to use the didactical resources, such as the mathematical tasks. In the 21st century, creativity and mathematical creativity have become important in Portuguese curricula through the implementation of the Students Profile in the end of compulsory schooling. This profile appeals to the development of creativity regarding of values, competences and guiding Principles, in order to mobilize schools and society for a better education. It is desirable that a young person, after leaving compulsory schooling, becomes a citizen capable of thinking critically, autonomously and creatively. Thus, in order to look for creative teaching approaches and strategies for the mathematical contents, it was decided to question students on the alluded concepts. This research took place in the academic year 2017/2018, with 14 participants aged between 15 and 21 years old (mean ages M = 17.36 and DP = 1.82) of two classes from one group of Portuguese state schools. The methodology was qualitative and interpretative, using a multiple case study design, one in a 10th grade class and another in a 12th. In data processing related to the analysis of the written documents, content analysis was used, and examples that represent each category were presented. The results achieved indicated, for these participants, that conceptions of creativity and mathematical creativity were not divergent in the two cases. In fact, the participants associated creativity with the category of Create something new and different and mathematical creativity with the category of Innovation.
1. Introduction
Given to the diversity of meanings up, up to today, of creativity and mathematical creativity are difficult to define. However it is crucial, this development whether in society, in teaching or in mathematics teaching. Creativity and Creativity Mathematical is not are valued as an integral part of the classroom context of mathematics and in practices of teachers, possibly due to the constant changes of Portuguese curricula. In this sense, it is necessary to potential the creativity and creativity mathematical as an integral part of the pedagogical practice of each teacher. The teachers’ role is essential to allow students to use the didactical resources, such as the mathematical tasks for this development and create enriching contexts. Specifically, in the educational context, the development of creativity is crucial according to Van Harpen and Sriraman [1], just right as creativity motivates the student for learning and, impacts school success. In the 21st century, creativity and mathematical creativity have recently become important Portuguese’s curricula through the implementation of the new Student Profile the exit of Mandatory Schooling of Ministry of Education binding Portuguese [2]. This profile appeals to the development of creativity in the Values, Competences and Guiding Principles, in order to mobilize the school and the society for a better education. It is wanted that the young person, after leaving mandatory schooling, become a citizen capable of thinking critically, autonomously and creative. In this sense and in order to research for creative teaching approaches and strategies for the mathematical contents, it was decided to question before students on the alluded conceptions. That why, it is important for teachers to know their students ‘conceptions of the concept of creativity and mathematical creativity, because which have a primordial role in delineating strategies and teaching methodologies that promote students’ creative thinking. It is vital that teachers of Mathematics at their professional practice promote creativity by innovating in their teaching methods and strategies so as to encourage students to one significant learning.
The teachers to become concerned with their professional practices on the basis of creative of mathematics teaching Henriksen and Mishra [3]. In investigation of Nakano [4] involving teachers, in the study of the conception creativity, was considered as being the capacity to create something new. In this way, it becomes pertinent that teachers provide creative classroom environments, inserted in learning contexts that encourage the autonomy and the active participation of students Yelós [5]. For to promote the knowledge, skills and attitudes of new Profile of students the exit education binding Portuguese ME [2]. The Creativity emerges in the part of the Vision of the educational action that intends that young people leaving compulsory education, was able citizen think creatively. Still in this Profile, in the part of the values, the intention is the promotion of the creativity and the practice of a school culture, with emphasis of the: (...) innovation, (...), creative thinking, and discovery of new solutions and applications.
In the studies carried out by Leikin and Pitta-Pantazi [6] about to the importance of a creative classroom environment, the authors’ emphasized, as primordial aspects, the selection of tasks, interactive classes, and the accomplishment of collaborative work among peers, among others, which are likely to contribute to creative teaching. In relation to the understanding of the concept of mathematical creativity, Feinstein [7] one investigation in different contexts and with different participants, that mathematical creativity is associated with the creation of ideas and the innovation. In another investigation about the development of mathematical creativity, the author Leikin [8] considers that it is related to the Innovation (novelty or originality).
2. Experimental
The methodology used was of a qualitative and interpretive nature and the case study. This case is multiple, compose of two cases, Case I and Case II (10th and 12th grades). This investigation took place in academic year 2017/2018, with total 15 participants of Vocational Education in secondary (67% of masculine gender and 33% of feminine gender) with ages between 15 and 21 years old (mean ages M = 17.36 and standard deviation DP = 1.82) of two classrooms from one grouping of schools public Portuguese. The data collection instrument was based on the questionnaire survey, applied in a Mathematics class. In the processing of the data we opted for the content analysis of the participants’ answers two a questions of the questionnaire and to the formulation of categories of analysis. As for the interpretative nature of the methodology, this was based on the perspective of Erickson [9]: of class as an organized means for learning; of teaching as an aspect of the learning environment, and the perspectives and meanings of the students. The case study was used because of the one pointed out by Stake [10], intending the understanding of a particular case. So the cases are in line with the characteristics of a case study: to explore, to describe, explain and evaluate. The method of data analysis focused on the content analysis of the participants’ responses of survey questionnaire Bardin [11] and of formulation of recursively defined categories of analysis, in view of the objective that was proposed Sampieiri, Colado and Lucio [12]. For Esteves [13] the categories of analysis are: “[...] the operation through which data are classified and reduced after they have been identified as pertinent in order to reconfigure responses to the objectives of the study, becoming categories” p. 109. A. The construction of the categories of analysis was done after having classified and reduced the number of responses and the identification of different phrases or phrases that could integrate the intended objective Cohen, Manion and Morrison, [14]. It should be noted that these categories were in accordance with the principles of Bardin [11]: homogeneity, completeness, exclusivity, objectivity and pertinence.
3. Results
For results obtained in questions 7 and question 8 of the questionnaire survey: What is creativity for you? and what is mathematical creativity for you? the categories of analysis constituted for the first question was: category one—Create something new and different and category two—Others. In this category one, were also included answers about expressions: creating things, inventing things, thinking about innovating, new (originality) and different ideas. In category two, Participants’ responses, with no specific meaning or by little explicitness, as expressions of form: capacity for great universal value and being creative. For the second question, three categories of analysis were developed: category three—Class environment, category four—Innovation and category two—Others. In category four participants’ answers were presented, involving expressions of the genre: originality, own ideas (unusual ideas), have mathematical ideas, classes different from usual and invent (new) exercises. In category two, Participants’ responses, with no specific meaning or by little explicitness, as expressions of form: motivation and intelligence.
The results achieved by Table 1 and Table 2, for this group of participants, indicate that conceptions of creativity and mathematical creativity were not divergent we in the two cases. In fact, the participants of Case I and II, have associated creativity to the category of Create something new and different, and mathematical creativity was associated the category Innovation. One participant did not respond to question 8 by Table 2.

Table 1.
Conceptions of creativity.

Table 2.
Conceptions of mathematical creativity.
Analyzing the results of Table 1 and Table 2, the concepts of creativity in I and I cases were very similar, with 56% and 83%, respectively of respondents responding according to category 1—Create something new and different. In the conception of mathematical creativity, this group of participating students have another conception of the term, although in both cases the term was very similar, where 71.3% and 67% respectively responded in the category four—Innovation. These results are in agreement with the studies of Feinstein [7] and Leikin [8] that consider mathematical creativity as being Innovation. Finally, to illustrate these results, three figures, named by Figure 1, Figure 2 and Figure 3, are presented, which represent four written responses given by the students participating in each of the cases and their respective conceptions. The student’s participants are called AP 2, AP 10, AP 7 and AP 9, because they are the categories of analysis that we think are the most representative. It is not intended to generalize the results, but the selection of resolutions (responses) in an intentional.

Figure 1.
Response given by the participant (AP 2) of Case I about conception creativity.
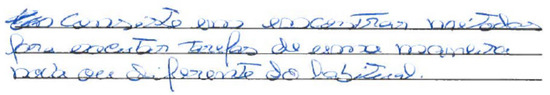
Figure 2.
Response given by the participant (AP 10) of Case II about conception creativity.

Figure 3.
Response given by the participant (AP 7) of Case I about conception creativity mathematical.
The previous answer “For me creativity is the ability to create, produce or invent new things” (AP 2), refers to the use of creating, inventing or producing something new, which presupposes teaching based on the development of creativity through novelty Nakano [4] and ME [2].
The previous figure says: “It consists of finding methods to perform tasks in a new or different way that usual” (AP 10) representative of the category of analysis Create something new and different, focused novelty and in environment of the classroom by task itself for creativity in Henriksen and Mishra [3], Yelós [5] and Leikin and Pitta-Pantazi [6].
The Figure 3 descoded “It is to have several useful ideas in mathematics” (AP 9) about the analysis category Innovation. It turns out that mathematical creativity ware associated with the emergence of mathematical ideas and deduce the presence of innovation through efficacy (useful) and quality according to the studies of Feinstein [7] and Leikin [8].
The Figure 4 translated “For me mathematical creativity is to invent exercises within the classroom” (AP 9) about the analysis category Innovation, it turns out that creativity mathematical was allied to invention of exercise according to the category description Innovation Leikin [8].

Figure 4.
Response given by the participant (AP 9) of Case II about conception creativity mathematical.
4. Conclusions
After analyzing the conceptions of the participants in the three case studies, on the concept of creativity and creativity mathematical, as the main final considerations is to highlight the similarity of conceptions of Case I and case II about the same conception. These results are in line with studies carried out investigations of Nakano [4] about conception of creativity and of Leikin [8] with secondary school students, the conception of creativity was assumed to be innovation. The main contributions of the present research are the contribution to the development of studies on the conceptions of the terms creativity and mathematical creativity in Portuguese secondary school students of professional courses, for possible methodological approaches to teaching mathematical contents in the curricular programs of agreement with the new profile of the Portuguese student and also in the changes in the educational practices of the teachers in face of the results obtained by this group of participating students. Thus, it was also intended to contribute to the awareness of the educational community for the development of creativity and more specifically the mathematical creativity in the educational context, and the use of creativity in the teaching practices of Mathematics teachers. As a future recommendation, the call for the development of additional research in this area, in order to understand if the other participants of these years of study have the same conceptions or if there are significant differences.
References
- Van Harpen, X.; Sriraman, B. Creativity and mathematical problema posing. An analysis of higth school students´ mathematical problem posing in China and USA, Educ. Stud. Math. 2013, 82, 201. [Google Scholar]
- Ministério da Educação, M. Perfil dos Alunos à Saída da Escolaridade Obrigatória; Ministério da Educação: Lisboa, Portugal, 2017. [Google Scholar]
- Mishra, P.; Henriksen, D. Revisited and remixed: Creative variations and twisting knobs. TechTrends 2014, 58, 20–23. [Google Scholar] [CrossRef]
- Nakano, T.C. Programas de treinamento em criatividade: Conhecendo as práticas e resultados. Psicologia Escolar e Educacional 2011, 15, 311–322. [Google Scholar] [CrossRef]
- Yélos, P. La problemática de la capacitacion de docentes en ejercicio: Uma alternativa de solucion. Linhas Críticas 2002, 8, 289–307. [Google Scholar] [CrossRef]
- Leikin, R.; Pitta-Pantazi, D. Creativity and mathematics education: The state of the art. Math. Educ. 2013, 45, 159–166. [Google Scholar] [CrossRef]
- Feinstein, J. The Nature of Creative Development; Stanford Business Books: Los Angeles, CA, USA, 2006. [Google Scholar]
- Leikin, R. Creativity in Mathematics and the Education of Gifted Students; Sense Publishers: Rotterdam, The Netherlands, 2009. [Google Scholar]
- Erickson, F. Handbook of Research on Teaching; Macmillan: New York, NY, USA, 1986. [Google Scholar]
- Stake, R. The Art of Case Study Research; Sage Publications: Los Angeles, CA, USA, 1995. [Google Scholar]
- Bardin, L. Análise de Conteúdo; Edições 70: Lisboa, Portugal, 1979. [Google Scholar]
- Sampieiri, R.H.; Collado, C.F. Metodologia de Pesquisa, 3rd ed.; McGraw-Hill: São Paulo, Brazil, 2003. [Google Scholar]
- Esteves, M. Fazer Investigação: Contributos para a Elaboração de Dissertações e Teses; Porto Editora: Porto, Portugal, 2006. [Google Scholar]
- Cohen, L.; Manion, L.; Morrisson, K. Research Methods in Education, 6th ed.; Routledge: London, UK, 2009. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).