Real-time Recognition of Interleaved Activities Based on Ensemble Classifier of Long Short-Term Memory with Fuzzy Temporal Windows ^†

Abstract

In this paper, we present a methodology for Real-Time Activity Recognition of Interleaved Activities based on Fuzzy Logic and Recurrent Neural Networks. Firstly, we propose a representation of binary-sensor activations based on multiple Fuzzy Temporal Windows. Secondly, an ensemble of activity-based classifiers for balanced training and selection of relevant sensors is proposed. Each classifier is configured as a Long Short-Term Memory with self-reliant detection of interleaved activities. The proposed approach was evaluated using well-known interleaved binary-sensor datasets comprised of activities of daily living.

1. Introduction

Globally, the population demographics are gradually shifting from younger to older age groups meaning elderly care is becoming unsustainable [1]. In order to relieve some workload from carers, whilst encouraging older adults to remain independent at home, assistive systems have been developed [2]. Some of these systems are capable of identifying simple to complex human activities, as well as the context in which they occur, from sensor data; this is currently a core aspect of smart assistive technologies [3]. Activity recognition assists with identifying the tasks being carried out and can determine whether the occupant has any difficulties with completing tasks or daily activities [4]. When tasks and scenarios become more complex, they are referred to as interleaved activities [5].

In this paper, we address the real-time recognition of interleaved activities. Real time refers to the recognition of activities while they are taking place; new sensor events are recorded, whilst streaming, without including explicit information on the evaluations labelled time interval [6]. In this way, the methodology presented in this work faces two key problems: (i) learning from activities which are developed in any order, interweaving and performing tasks in parallel if desired [7]; and (ii) recognizing activities in real time, without including explicit information on the future sensor events [8].

Activity recognition is the process of retrieving high level knowledge about activities and occurrences taking place in an environment such as a smart home; whilst also learning about the behaviour of those present in the environment [9].

Real-time activity recognition is a challenging area of smart home technology [8]. The main difficulty with real-time activity recognition approaches is the ability to correctly define the size of the temporal window to allow effective recognition of activities [6,10]. The main concern of including a single sliding window is that the more sensor events from the past are included, the more noise the data representation includes on the model [11]. In this work, the use of multiple temporal windows and fuzzy aggregation methods are proposed to enable the long and middle-term evaluation of sensors.

Furthermore, daily activity datasets suffer from a severe class imbalance problem [12,13], which are presented when their classes are not equally represented [14]. We balance the training dataset for each activity classifier in order to solve the imbalance problem within datasets.

In the context of interleaved activities, a scarce number of approaches face this complex problem. In [15] authors proposed a multi-layer model for activity recognition, using RFID technology and appliance signatures to identify errors related to cognitive decline from daily activities. Focusing on morning routine activities, they carried out activity recognition in real time through RFID based localization and through the use of electrical sensors. It was found that using multiple sensors increased the accuracy of recognition, however, interleaved activities were not considered. In [16], authors addressed this challenge using a data set collected from an elderly person living alone by means of an event-driven approach [6]. It was found that although they were able to effectively distinguish concurrent activities, more event factors could have been used for better accuracy in results, as only the timing and the sensor were taken in to account when the location could have been added.

In [17], authors present an approach through ontological and probabilistic reasoning, which requires a relevant knowledge engineering effort to define a comprehensive ontology of activities, home environment, and sensor events. This work does not include real-time evaluation presenting a results based on sensor events of 81%.

In this work, we face to novelty challenge of the real-time recognition of interleaved activities, which present a hard problem due to: (i) the evaluation in real-time while the activities are being developed without including future information of sensors; and (ii) the concurrence and disorder of activities performed by the participants.

The remainder of the paper is structured as follows: the Section 2 details an overview of the methodology proposed. In Section 3, we highlight the experiments performed, of which are discussed in Section 4. Finally, the Conclusions and Ongoing Works are presented in Section 5, providing a critique of the study overall and proposing plans for future work.

2. Methodology

In this section, we detail the proposed methodology for recognizing interleaved human activities in real-time, using an ensemble classifier of Long Short-Term Memory, with Fuzzy Temporal Windows. It is based on a previous methodology for sequential learning of activity recognition [18]. This work is based around the following: (i) the concurrent activation in a parallel way of the ensemble of activity-based classifiers to provide a suitable interleaved response; and (ii) the computing of relevant sensors, which are filtered for improving the learning capabilities.

In summary, the proposed methodology for real-time recognition of interleaved activities is focused on three key points:

• A fuzzy temporal representation of long-term and short-term activations, which define temporal sequences.
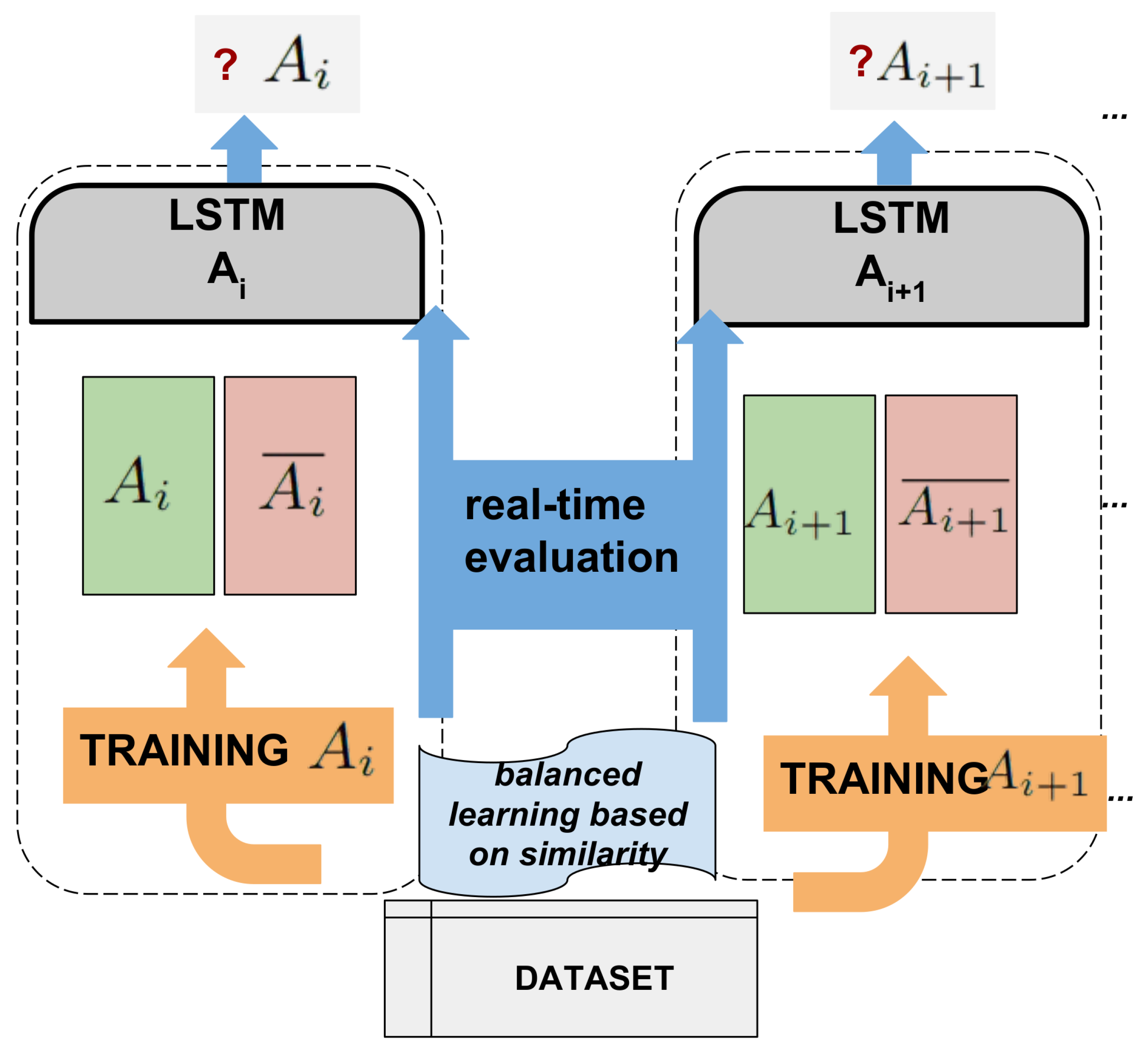
• An ensemble of of activity-based classifiers, which are defined by the suitable sequence classifier: Long Short-Term Memories (LSTM) [19].
• Balanced learning for each activity-based classifier, to avoid the imbalance problem that suffers daily activity datasets [12,13]. It is optimized by the similarity relation between activities which: (i) determines the adequate samples within the training dataset, based on the similarity with activity to learn; and (ii) filters the relevant sensors to take into account in the learning process.

In Figure 1, we show the scheme of the methodology proposed.

2.1. Representation of Binary Sensors and Activities

A set of binary sensors is represented by $S=\{S_1,\dots ,S_{\left|S\right|}\}$ and a set of daily activities is represented by $A=\{A_1,\dots ,A_{\left|A\right|}\}$, where $\left|S\right|$ and $\left|A\right|$ are the number of sensors and daily activities respectively. They are described by a set of binary activations within a set of ranges of time, which are defined by a starting and ending point of time by Equation (1):

$$\begin{array}{c}{S}_i=\{S_{i_0},\dots ,S_{|S_i|}\},S_{i_j}=\{S_{i_j}^0,S_{i_j}^{+}\}\\ A_i=\{A_{i_0},\dots ,A_{|A_i|}\},A_{i_j}=\{A_{i_j}^0,A_{i_j}^{+}\}\end{array}$$

(1)

where (i) $|S_i|$, $|A_i|$ is the total number of activations for a given binary sensor $S_i$ and daily activity respectively; and (ii) $S_{i_j}^0$,$S_{i_j}^{+}$ is the starting and ending point of a given time of activation.

2.2. Segmentation of Dataset in Time-Slots

We generated a segmented timeline defined by time-slots (also known as time-steps), which indicate the activation of activities and sensors for a given in a time interval of fixed duration $\Delta t$. The range for evaluating each time-slot $t_i$ is defined by a sliding window between $[t_i,t_i+\Delta t]$.

For each time-slot and a given sensor we determine its activation based on if it has been activated within it:

$$\begin{array}{c}S(t_i,s)=\left\{\begin{array}{cc}1\hfill & \exists [S_{s_j}^0,S_{s_j}^{+}]\cap [t_i,t_i+\Delta t]\forall S_{s_j}\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.\end{array}$$

(2)

In a similar way, for define the activation of an activity a in a time-slot $t_i$,:

$$\begin{array}{c}S(t_i,a)=\left\{\begin{array}{cc}1\hfill & \exists [A_{i_j}^0,A_{i_j}^{+}]\cap [t_i,t_i+\Delta t]\forall A_{i_j}\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.\end{array}$$

(3)

Each sensor or activity is represented as a set of activation by ordered time-slots $S\left(s\right)=\{S(t_0,s),\dots ,S(t_n,s)\}$. For sake of simplicity, we call extensively $t^{+}$ to a time-slot $t_i$ in the timeline T.

2.3. Sensor Features Defined by Fuzzy Temporal Windows

In this Section, a binary-sensor representation approach based on fuzzy temporal windows (FTWs) is detailed. FTWs are therefore described from a given current time $t^{*}$ to a past point of time $t_i$ as a function of the temporal distance $\Delta t_i^{*}=t^{*}-t_i,t^{*}>t_i$ [20]. For that, a given FTW $T_k$ relates the sensor activation $S(s,t_i)$ in a current time $t^{*}$ to a fuzzy set $T_k(\Delta t_i^{*})$, which is characterized by a membership function ${\mu }_{\widetilde{T_k}}(\Delta t_i^{*}=t^{*}-t_i)$. For a given FTW, we can write $T_k(\Delta t_i^{*})$ instead of ${\mu }_{\widetilde{T_k}}(\Delta t_i^{*})$.

Firstly, for a given FTW $T_k$ and the current time $t^{*}$, each past sensor activation $S{t}_i,s$ is weighted by calculating the degree of time-activation within the fuzzy temporal window $T_k$ according to Equation (4).

$$T_k(s,t^{*},t_i)=S(t_i,s)\cap T_k(\Delta t_i^{*}),t_i<=t^{*}$$

(4)

Secondly, the degrees of time-activation are aggregated using the t-norm operator in order to obtain a single activation degree of both fuzzy sets $S\left(s\right)\cap T_k$ by Equation (5).

$$T_k(s,t^{*})=S\left(s\right)\cup T_k(\Delta t^{*})=\bigcup _{\overline{t_i}\in T}S(t_i,s)\cap T_k(\Delta t_i^{*}),t_i<=t^{*}$$

(5)

We propose using the maximal and minimal operators as t-norms, which are recommended for representing binary sensors [21].

$$\begin{array}{c}{T}_k(s,t^{*})=S\left(s\right)\cup T_k(\Delta t^{*})=max(min(S(t_i,s),T_k(\Delta t_i^{*})),\forall t_i\in T,t_i<=t^{*}\end{array}$$

(6)

2.4. Sequence Features of FTW

The representation of sensor activation based on FTWs is used to define a sequence for the purposes of classification. It has been proposed that FTWs of incremental temporal sizes are defined, to collect the long-term to the short-term temporal activations.

Each TFW $T_k$ is described by a trapezoidal function based on the time interval from a previous time $t_i$ to the current time $t^{*}$: $T_k(\Delta t_i^{*})[l_1,l_2,l_3,l_4]$ is described by a fuzzy set characterized by a membership function whose shape corresponds to a trapezoidal function. The well-known trapezoidal membership functions are defined by a lower limit $l_1$, an upper limit $l_4$, a lower support limit $l_2$, and an upper support limit $l_3$ (refer to Equation (7)):

$$TS\left(x\right)[l_1,l_2,l_3,l_4]=\left\{\begin{array}{cc}0\hfill & x\le l_1\hfill \\ (x-l_1)/(l_2-l_1)\hfill & l_1<x<l_2\hfill \\ 1\hfill & l_2\le x\le l_3\hfill \\ (l_4-x)/(l_4-l_3)\hfill & l_3<x<l_4\hfill \\ 0\hfill & l_4\le x\hfill \end{array}\right.$$

(7)

To generate FTWs in a simple manner, we propose to define them from a set of incremental ordered times of evaluation $L=\{L_1,\dots ,L_{\left|L\right|}\},L_{i-1}<L_i$, which the limits of the trapezoidal functions are calculated regarding to the index of the temporal window $T_k$.

$$T_k=T_k(\Delta t_i^{*})[L_k,L_{k-1},L_{k-2},L_{k-3}]$$

(8)

In order to define the FTWs, we purpose incremental FTWs straightforwardly defined by the Fibonacci sequence [22] $L=\{1,2,3,5,8,\dots \}·\Delta t$, whose example is shown in Figure 2.

So, L generates a feature vector: (i) which is composed of components the $T_k(s,t^{+})$ for each time-slot in the timeline $t^{+}$ and a given sensor s; and (ii) whose size is equal to the number of TFWs times the number of sensors $\left|T\right|\times \left|S\right|$:

$$T(s,t^{+})=\{T_0(s,t^{+})\to \dots \to T_k(s,t^{+})\to \dots \to T_{\left|T\right|}(s,t^{+})\}$$

(9)

2.5. Ensemble of Classifiers for Activities

Each LSTM activity-based classifier is focused on learning a given activity $A_i$ by means of a balanced training dataset. Therefore, each classifier learns two class problems: the target activity $A_i$ and not-being the target activity $\overline{A_i}$, which represents other classes and idle class.

For each time-slot $t^{+}$ and a given classifier $A_i$ the target class $O\left(t^{+}\right)$ is defined by:

$$O\left(t^{*}\right)=\left\{\begin{array}{cc}1\hfill & S(A_i,t^{+})==1\hfill \\ 0\hfill & S(A_i,t^{+})\ne 1\hfill \end{array}\right.$$

(10)

So, $O\left(t^{+}\right)$ represents the target class to learn by each classifier, whose activation can be concurrent with several activities $\exists A_i,A_j,t^{+}:S(A_i,t^{+})=S(A_j,t^{+})=1,A_j\ne A_i$.

The feature vector for this time-slot $t^{+}$ is formed by the sequence of aggregated activation degrees $T_k(s,t^{+})$ from the FTWs $T_k$ for each sensor s for a given time-slot $t^{+}$, as we described in Section 2.4.

Once the learning process is complete, the activation of the target activity $A_i$ is presented when the prediction for the target activity $p_{A_i}$ overcomes the prediction of not-being the target activity $p_{\overline{A_i}}$. We note several classifiers within the ensemble which can (and must) be activated in same time-slot $t^{+}$.

2.5.1. Balancing Learning With Similarity Relation Between Activities and Filtering of Relevant Sensors

In this section, we describe how to build ad-hoc balanced training for each activity-based classifier from the similarity relation between other activities and filter the relevant sensors while the learning process.

Based on a given activity $A_i$ and other activity $A_j$, we define a similarity relation $R_a$ as a function $R_a:A_i\times A_j\to [0,1]$, which determines the similarity degree between both activities.

To compute the similarity, we calculate a similarity relation $R_s:A_i\times S_j\to [0,1]$ between activities and sensors using the relative frequency of sensor activation within each activity:

$$\begin{array}{c}{R}_s(A_i,S_j)=\frac{|S_j\cap A_i|}{{\sum }_{S_k}^S|S_j\cap A_i|}\end{array}$$

(11)

where $|S_j\cap A_i|$ represents the number of time-slots activated when the sensor $S_j$ is activated together with the activity $A_i$. This measure is also called Mutual Information [6].

First, the similarity $R_s(A_i,S_j)$ is used to compute the relevant sensors $S_j^{+}$ for a given activity $A_i$ based on a relevance factor $s_{\alpha }$:

$$\begin{array}{c}{S}_j^{+}:R_s(A_i,S_j)>s_{\alpha }\end{array}$$

(12)

Secondly, we evaluate the similarity relation between activities $R_a$ aggregating the similarity relation between their sensors:

$$\begin{array}{c}{R}_a(A_i,A_j)={\displaystyle \sum _{S_k}^S}{R}_a(A_i,S_k)\times R_a(A_j,S_k),A_i\ne A_j\end{array}$$

(13)

Thirdly, we propose to build a balanced-activity training dataset, which contains a weight or percentage of samples for each activity $A_i$ based on the similarity relation:

• $w_{A_i}$, defines a fixed percentage of samples corresponding to the activity to learn.
• $w_{A_0}$, defines a fixed percentage of samples corresponding to any activity (Idle).
• $w_{\overline{A_i}}$, configures a dynamic percentage from the all other activities in the balanced-activity training dataset $w_{A_i}+w_{A_0}+w_{\overline{A_i}}=1$, which is calculated by weighting the normalized similarity degree with the percentage from the other activities:

  $$\begin{array}{c}{w}_{A_j}=w_{\overline{A_i}}\times \widetilde{R_a}(A_i,A_j)\end{array}$$

  (14)

In order to re-sample the time-slots for each balanced-activity training dataset, a straightforward random process is included to select a random time-slots rejecting or accepting based on the percentages of activities $w_{A_i}$.

3. Experimental Setup

In this Section, the experiments performed on the proposed methodology is evaluated using the interleaved dataset [7], which provides data from 20 participants who performed eight activities in any order, interweaving and performing tasks in parallel if desired. Up to three activities can be performed concurrently by the participant. We note the complexity of learning in this extreme problem.

The activities developed were (1) Filling a medication dispenser; (2) Watching a DVD; (3) Watering plants; (4) Answering the phone; (5) Preparing a birthday card; (6) Preparing soup; (7) Cleaning; and (8) Choosing an outfit. 41 sensors, including motion, item and water sensors, describe the activities within WSU smart apartment testbed.

The methodology proposed in this work uses following parameters:

• Number of FTWs=$\left|T\right|=10$.
• Incremental FTWs defined by the Fibonacci sequence [22] $L=\{720,540,360,180,60,30,8,5,3,2,1\}·\Delta t$.
• For balancing training dataset for each activity:

  −

  Number of training samples = 5000.

  −

  Percentage of samples from target activity $w_{A_i}=0.4$.

  −

  Percentage of idle activity $w_{A_0}=0.1$.

  −

  Percentage of samples corresponding to the non-target activity $w_{\overline{A_i}}=0.6$.

• For each LSTM activity-based classifier: learning rate = 0.003, number of neurons = 64, number of layers = 3.

We evaluated three different time intervals of fixed duration $\Delta t$ to define the time-slots $\Delta t=\{30\mathrm{s},60\mathrm{s},90\mathrm{s}\}$ and three different values for the relevance factor; to identify the selected sensors for learning in each activity $s_{\alpha }=\{0\%,3\%,6\%\}$. For this, two metrics are introduced:

• F1-coverage (F1-sc), which provides an insight into the balance between precision ($precision=\frac{TP}{TP+FP}$), and recall ($recall=\frac{TP}{TP+FN}$) from predicted and ground truth time-slots. Although well-known in activity recognition [23], we note a key issue from this metric on time interval analysis: the false positives of an activity, far from any time interval activation, are equally computed to false positives closer to end of activities. Which is common in the end of activities more so than in interleaved activities.
• F1-interval-intersection (F1-ii), evaluates the time intervals of each activity based on: (i) the precision of predicted time intervals; which intersects to a ground truth time interval; (ii) the recall of the ground truth time intervals; which intersects with a predicted time interval.

For evaluation purposes we have developed a leave-one-participant cross-validation, where for each participant, the test is composed by the activities performed by the given participant and training is composed by the activities performed by other participants.

4. Results

In this section we describe the results of F1-sc and F1-ii from the interleaved dataset [7].

Table 1. Global results.

	$\mathbf{\Delta }\mathit{t}$	F1-ii			F1-sc
		${\mathit{s}}_{\mathit{\alpha }}=\mathbf{0}\%$	${\mathit{s}}_{\mathit{\alpha }}=\mathbf{3}\%$	${\mathit{s}}_{\mathit{\alpha }}=\mathbf{6}\%$	${\mathit{s}}_{\mathit{\alpha }}=\mathbf{0}\%$	${\mathit{s}}_{\mathit{\alpha }}=\mathbf{3}\%$	${\mathit{s}}_{\mathit{\alpha }}=\mathbf{6}\%$
0 slot margin	30s	84.54	80.75	79.13	70.95	70.78	66.98
	60s	85.96	85.87	86.35	73.03	73.89	72.52
	90s	81.50	87.60	90.47	68.52	75.99	75.48
1 slot margin	30s	88.30	85.46	87.34	73.97	72.91	69.56
	60s	88.09	89.26	91.05	74.31	77.16	74.77
	90s	84.23	91.96	95.61	70.86	77.94	77.58

describes the metrics for the duration of time-slots $\Delta t=\{30\mathrm{s},60\mathrm{s},90\mathrm{s}\}$ and the the relevance factor $s_{\alpha }=\{0\%,3\%,6\%\}$ for each configuration of values. Due to the recognition of the activities being frequently adjacent to the ground truth of the activity, included also is: (i) a strict comparison without error margin 0-time-slot, and (ii) a time-slot margin, comparing the prediction and ground truth; which evaluates as correct if both match in the adjacent time-slot. Finally, in

Table 2. Detailed values of metric F1-ii for each activity, duration of time-slot $\Delta t$ and relevance factor $s_{\alpha }$.

	$\mathbf{\Delta }\mathit{t}$ = 30 s			$\mathbf{\Delta }\mathit{t}$ = 60 s			$\mathbf{\Delta }\mathit{t}$ = 90 s
${\mathit{A}}_{\mathit{i}}$	${\mathit{s}}_{\mathit{\alpha }}=\mathbf{0}\%$	${\mathit{s}}_{\mathit{\alpha }}=\mathbf{3}\%$	${\mathit{s}}_{\mathit{\alpha }}=\mathbf{6}\%$	${\mathit{s}}_{\mathit{\alpha }}=\mathbf{0}\%$	${\mathit{s}}_{\mathit{\alpha }}=\mathbf{3}\%$	${\mathit{s}}_{\mathit{\alpha }}=\mathbf{6}\%$	${\mathit{s}}_{\mathit{\alpha }}=\mathbf{0}\%$	${\mathit{s}}_{\mathit{\alpha }}=\mathbf{3}\%$	${\mathit{s}}_{\mathit{\alpha }}=\mathbf{6}\%$
t1	90.06	86.17	92.83	91.16	94.87	98.29	91.19	92.43	100.00
t2	91.35	84.26	90.40	85.69	87.37	90.41	85.61	93.39	93.37
t3	82.58	85.05	88.95	86.21	90.87	90.23	78.29	93.74	91.04
t4	82.00	71.05	71.67	81.28	77.74	75.65	75.65	86.04	86.72
t5	91.78	89.07	89.92	95.08	95.85	95.07	87.07	91.84	96.58
t6	88.91	92.32	83.02	90.84	96.27	95.62	90.18	93.93	100.00
t7	93.30	85.91	89.26	85.28	87.64	89.50	85.15	90.36	98.15
t8	86.45	89.83	92.72	89.19	83.44	93.59	80.68	94.00	98.99
t9	88.30	85.46	87.34	88.09	89.26	91.05	84.23	91.96	95.61

and

Table 3. Detailed values of metric F1-sc for each activity, duration of time-slot $\Delta t$ and relevance factor $s_{\alpha }$.

	$\mathbf{\Delta }\mathit{t}$ = 30 s			$\mathbf{\Delta }\mathit{t}$ = 60 s			$\mathbf{\Delta }\mathit{t}$ = 90 s
${\mathit{A}}_{\mathit{i}}$	${\mathit{s}}_{\mathit{\alpha }}=\mathbf{0}\%$	${\mathit{s}}_{\mathit{\alpha }}=\mathbf{3}\%$	${\mathit{s}}_{\mathit{\alpha }}=\mathbf{6}\%$	${\mathit{s}}_{\mathit{\alpha }}=\mathbf{0}\%$	${\mathit{s}}_{\mathit{\alpha }}=\mathbf{3}\%$	${\mathit{s}}_{\mathit{\alpha }}=\mathbf{6}\%$	${\mathit{s}}_{\mathit{\alpha }}=\mathbf{0}\%$	${\mathit{s}}_{\mathit{\alpha }}=\mathbf{3}\%$	${\mathit{s}}_{\mathit{\alpha }}=\mathbf{6}\%$
t1	81.50	76.64	77.82	80.87	84.60	80.94	75.17	81.12	81.40
t2	76.74	67.88	64.55	73.99	75.72	74.56	75.85	76.89	72.87
t3	65.43	68.03	66.28	67.85	77.21	70.75	68.94	80.11	79.23
t4	63.07	50.49	50.20	60.47	61.56	46.15	58.42	61.73	46.15
t5	85.96	88.73	85.97	85.51	86.01	84.23	76.99	86.90	87.48
t6	70.67	75.63	58.03	75.28	80.41	74.60	67.11	73.99	76.96
t7	77.40	72.31	68.66	75.49	75.84	76.55	76.21	75.67	83.51
t8	70.99	83.56	84.94	75.03	75.93	90.39	68.15	87.13	92.99
t9	73.97	72.91	69.56	74.31	77.16	74.77	70.86	77.94	77.58

we detail the values of metrics for each activity and the best configuration of the relevance factor $s_{\alpha }$.

4.1. Discussion

From the results previously described, the suitable performance for the challenging problem presented in the interleaved dataset [7] is highlighted. The evaluation based on leave-one-participant cross-validation presents a hard comparative, due to each participant having the opportunity to carry out activities in any order, thus introducing unseen and unlearned habits within the activity learning process.

It is noted that the relevant detection of activity intervals, is presented by F1-ii) close or up to $90\%$ for the three duration of time-slots $\Delta t=\{30\mathrm{s},60\mathrm{s},90\mathrm{s}\}$. Patently, a higher aggregation of time-slots with duration $\Delta t=90\mathrm{s}$ increases the performance, but at the cost of reducing the evaluation time, which present three times less responses than $\Delta t=30\mathrm{s}$. For same reason, the difference in error margin between 0-time-slot and 1-time-slot is more relevant with $\Delta t=90\mathrm{s}$.

Furthermore, the use of a relevance factor $s_{\alpha }$, which identifies and selects the key sensors for each activity while learning, has increased the accuracy rate. In higher duration of time-slots $\Delta t=\{90\mathrm{s},60\mathrm{s}\}$ the filtering by the relevance factor is noteworthy due to a greater number of sensors being activated concurrently in the same time-slots. It increases the noise in the feature representation of sensors, but a filtering of relevant sensors aims to reduce the conflicting activations in time-slots.

In [17] the approach presents results based on sensor events without real-time capabilities of $81\%$, where the classification was evaluated only when a change in a sensor was detected. Due to this, our work is based on the evaluation of time-slots in the further timeline; a direct evaluation is not possible. The coverage of time-slots F1-sc presents an excellent prediction in real-time close to $75\%$, which is remarkable due to any external information and modelling being required previously, as well as, the requirements of evaluating in real-time each time-slot without introducing future information of sensor.

5. Conclusions and Ongoing Works

The use of fuzzy temporal representation on binary sensors, learned by an ensemble of Long Short-Term Memory, have been demonstrated as an encouraging methodology to recognize interleaved activities in real-time. The use of multiple FTWs enables a flexible temporal evaluation in interleaved activities, whose duration is strongly variant. Moreover, the Fibonacci sequence represents a suitable shape of incremental FTWs to avoid the hard selection in temporal segmentation.

The results show an encouraging real-time recognition of activity intervals, which represent the intersection of recognition intervals in the ground truth interval, as f1-ii$=90\%$. The coverage of predicted time-slots in real-time within the activity intervals is f1-sc$=75\%$.

In ongoing works, we will translate the proposed methodology in multi-occupancy and interleaved activities represented by recent devices, such as, wearable and vision sensors, which provide a challenging problem to be solved. To evaluate these non-binary sensors in long and middle-term, it will be necessary to extract several temporal features from signals including a filter to remove those non-relevant. For that, the performance of human defined features versus deep learning approaches will be also compared.