Computationally Efficient Bootstrap Expressions for Bandwidth Selection in Nonparametric Curve Estimation ^†

Abstract

Bootstrap methods are used for bandwidth selection in: (1) nonparametric kernel density estimation with dependent data (smoothed stationary bootstrap and smoothed moving blocks bootstrap), and (2) nonparametric kernel hazard rate estimation (smoothed bootstrap). In these contexts, four new bandwidth parameter selectors are proposed based on closed bootstrap expressions of the MISE of the kernel density estimator (case 1) and two approximations of the kernel hazard rate estimation (case 2). These expressions turn out to be very useful since Monte Carlo approximation is no longer needed. Finally, these smoothing parameter selectors are empirically compared with the already existing ones via a simulation study.

1. Introduction

This work deals with the well known problem of data-driven choice of smoothing parameters in nonparametric density and hazard rate estimation (see [1,2,3,4]). Our aim is also to propose new bootstrap procedures for nonparametric density estimation considering dependent data. On the other hand, hazard rate estimation is considered and two bootstrap bandwidth selectors based on some approximation of the kernel hazard rate estimator are proposed.

2. Nonparametric Density Estimation

Let us consider a random sample, $(X_1,\dots ,X_n)$, coming from a population with density f and the kernel density estimator (see [5,6]), which strongly depends on a bandwidth selector, h. In fact, its choice is really important since it regulates the degree of smoothing applied to the data.

In this context, the smoothed stationary bootstrap (SSB) resampling plan has been proposed (see the Appendix for a detailed description of the algorithm and [7]), as well as a bandwidth selector, namely $h_{SSB}^{*}$. It is the result of minimizing the SSB version of the MISE. A closed expression for the bootstrap MISE is also obtained by [7]. On the other hand, smoothed moving blocks bootstrap (SMBB) has been proposed (see the Appendix for a complete description of the method), as well as a bandwidth selector, $h_{SMBB}^{*}$, which is the minimizer in h of the closed expression for the $MIS{E}_{SMBB}^{*}$ (see [8] for a deeper insight on the topic). It is worth mentioning that the exact expressions for the $MIS{E}_{SSB}^{*}\left(h\right)$ and $MIS{E}_{SMBB}^{*}\left(h\right)$ are really useful since Monte Carlo approximation is no longer necessary.

3. Nonparametric Hazard Rate Estimation

Let us consider $(X_1,X_2,\dots ,X_n)$, a simple random sample coming from a population with continuous density f and cumulative distribution function F. Consider, additionally, the nonparametric hazard rate estimator (see [3,4]), the kernel density estimator ${\widehat{f}}_h$ and the kernel distribution estimator ${\widehat{F}}_h$. In order to establish a bootstrap bandwidth selector for the hazard rate estimator, two approximations of the hazard rate estimator are considered. The two hazard rate approximated versions are given by:

$$\begin{array}{ccc}\hfill {\tilde{r}}_{h,1}\left(x\right)& =& {\displaystyle \frac{{\widehat{f}}_h\left(x\right)}{1-F\left(x\right)}}.\hfill \\ \hfill {\tilde{r}}_{h,2}\left(x\right)& =& {\displaystyle \frac{1}{1-F\left(x\right)}}{\widehat{f}}_h\left(x\right)+{\displaystyle \frac{f\left(x\right)}{{(1-F\left(x\right))}^2}}{\widehat{F}}_h\left(x\right)-{\displaystyle \frac{f\left(x\right)}{{(1-F\left(x\right))}^2}}+r\left(x\right).\hfill \end{array}$$

Closed-form expressions of the MISE of ${\tilde{r}}_{h,1}$ and ${\tilde{r}}_{h,2}$, as well as their bootstrap versions can be found in [9]. Moreover, two bootstrap bandwidth selectors, namely $h_{BOOT1}$ and $h_{BOOT2}$, are defined as the minimizers of ${MISE}_{{\tilde{r}}_{h,1},w}^{*}\left(h\right)$ and ${MISE}_{{\tilde{r}}_{h,2},w}^{*}\left(h\right)$, respectively (see [9] for a deeper insight on the approach). It is worth mentioning that Monte Carlo approximation is not required.

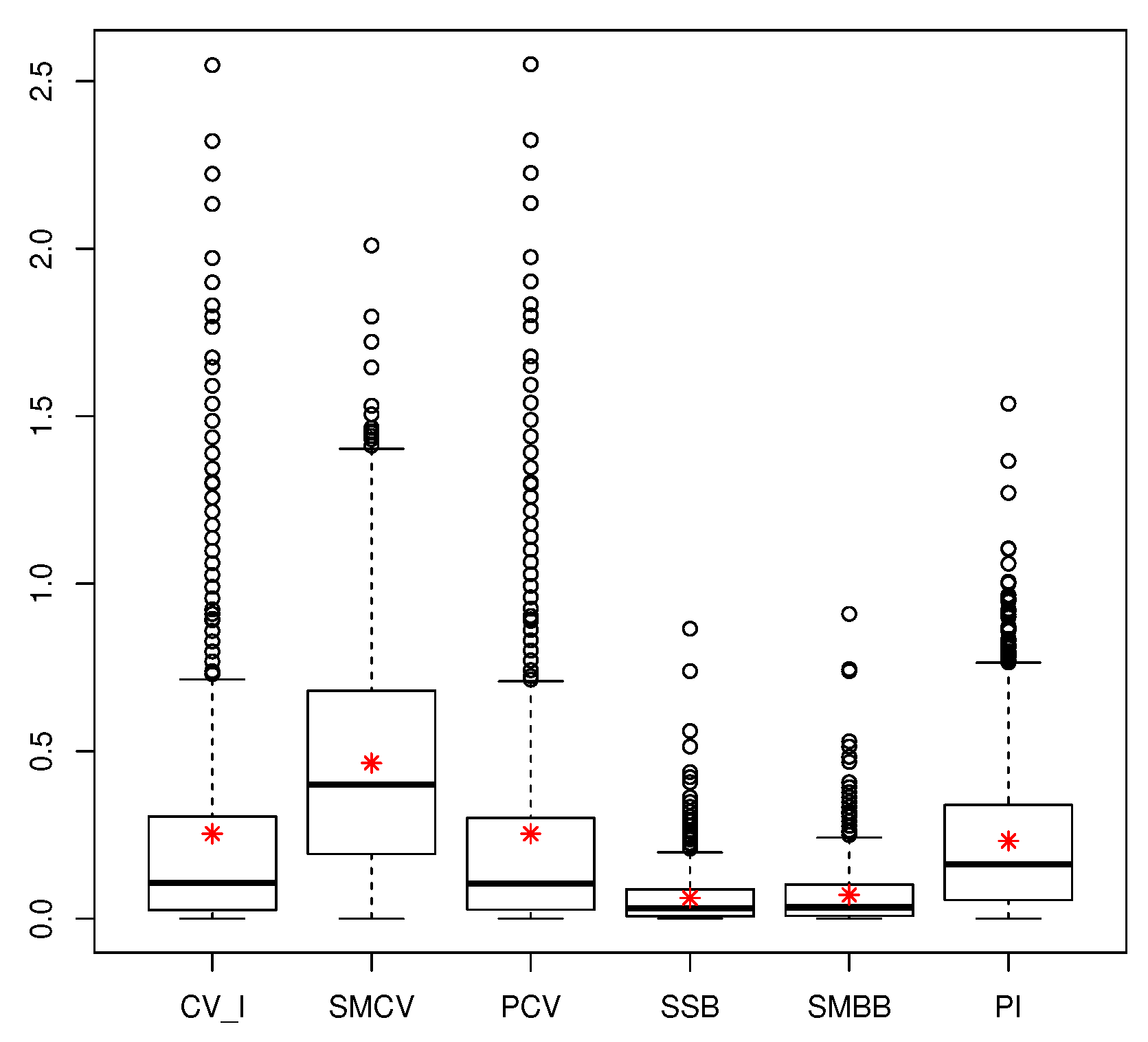
4. Simulation Results

A simulation study is now carried out in order to check the good empirical behaviour of the new smoothing parameter selectors in both contexts. These are the models considered:

• Density estimation: An AR(1) model given by $X_t=-0.6X_{t-1}+0.8a_t$, where $a_t\stackrel{d}{=}N(0,1)$.
• Hazard rate estimation: A Gumbel model such that $f\left(x\right)=e^{-x}{e}^{-e^{-x}},\forall x\ge 0$.

5. Discussion

Figure 1 shows that $h_{SSB}^{*}$ and $h_{SMBB}^{*}$ display a similar performance, actually the best one. According to

Table 1. Mean and median of $ISE\left(\widehat{h}\right)$, $n=100$, where $\widehat{h}=h_{CV}$ (third column), $h_{DO}$ (fourth column), $h_{BOOT1}$ (fifth column), $h_{BOOT2}$ (sixth column) and $h_{GCM}^{*}$ (seventh column).

		CV	DO	BOOT1	BOOT2	GCM
Gumbel model	Mean	$0.1656$	$0.01651$	$0.02914$	$0.02882$	$0.03595$
	Median	$0.15527$	$0.01037$	$0.012844$	$0.01282$	$0.01739$

, $h_{BOOT1}$ and $h_{BOOT2}$ display the overall best performance.