Generating Models for Model Predictive Control in Buildings ^†

Abstract

There are strong policy drivers for the promotion of energy efficiency in buildings. In the literature, Model Predictive Control (MPC) is seen as a promising solution to deal with the energy management problem in buildings. Model identification is the primary task involved in the design of MPC control and defining the good level of complexity for the thermal dynamic model is a critical question. This paper focuses on the development of reliable models that can be used to support the deployment of (Distributive (Di)) MPC application.

1. Introduction

It is well accepted that energy consumption in buildings accounts for more than 40% of the total primary energy resources throughout the world [1]. Therefore it is an essential to enact strategies for energy conservation and energy management in buildings [2,3]. A promising solution for BEMS [4] is Model Predictive Control (MPC) that is able to deal with various objectives at the same time, under constraints. For instance, both comfort and energy can be considered taking into account occupancy schedule, weather forecast, etc. MPC is a model-based control technique: it requires a dynamical discrete-time model of the building under control to predict the behavior in building zones. Although system modelling and parameter identification are mature scientific domains, their application to real buildings is still laboursome, time consuming and error prone [5]. This paper focuses on the development of reliable models that can be used to support the deployment of (Distributive (Di)) MPC applications.

2. Problem Statement

Consider a multizone building with thermal and comfort coupling between zones, actuators and outdoor conditions such as that depicted in Figure 1. We denote $u_i\left(k\right)$ as the manipulated variable, $w_i\left(k\right)$ as the exogenous ones and $v_i\left(k\right)$ the coupling effects. The modelling problem can be stated as follow: define the function $F\left(k,x_i,u_i,w_i,v_i\right)$, which represents the zone behavior and is accurate, modular and suitable for DiMPC, with respect to the highly coupled interactions.

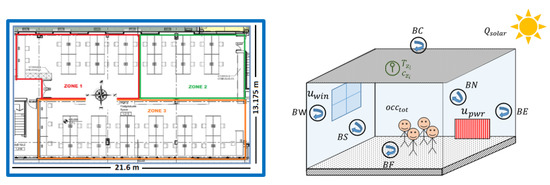
Figure 1. Building with multiple zones (left); zone representation with regulated, manipulated and exogenous variables (right).

3. Method

The measured data is represented by the tuple $(z_i,u_i,w_i)$ given by:

$$\begin{array}{cccc}\hfill z_i\left(k\right)& ={\left[T_{z_i}\left(k\right),c_{z_i}\left(k\right)\right]}^{⊺},\hfill & \hfill u_i\left(k\right)& ={\left[u_{win}\left(k\right),u_{pwr}\left(k\right)\right]}^{⊺},\hfill \end{array}$$

(1)

$$\begin{array}{cccc}\hfill w_i\left(k\right)& ={\left[n_{occ}\left(k\right),Q_{solar}\left(k\right)\right]}^{⊺}\hfill & \hfill v_i\left(k\right)& ={\left[T_{bnd}\left(k\right),C_{bnd}\left(k\right)\right]}^{⊺}\hfill \end{array}$$

(2)

where $n_{occ}$ is the number of occupants, $Q_{sol}$ the solar radiation, $T_{bnd}$ and $C_{bnd}$ the temperature and CO2 concentration at the boundaries. Assuming this tuple can be measured for N time samples, it is possible to apply identification techniques to seek a data-driven models. Here, we propose to represent the discrete-time thermal zone behavior by a Brunowski state-space form. The matrices are naturally sparse, which eases the identification process in finding solutions:

$$\begin{array}{cccccc}\hfill A& =\left[\begin{array}{cccccc}0& 1& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\\ a_{11}& a_{12}& a_{13}& a_{14}& a_{15}& a_{16}\\ 0& 0& 0& 0& 1& 0\\ a_{21}& a_{22}& a_{23}& a_{24}& a_{25}& a_{26}\\ a_{31}& a_{32}& a_{33}& a_{34}& a_{35}& a_{36}\end{array}\right],\hfill & \hfill B& =\left[\begin{array}{cc}{b}_{11}& b_{12}\\ b_{21}& b_{22}\\ b_{31}& b_{32}\\ b_{41}& b_{42}\\ b_{51}& b_{52}\\ b_{61}& b_{62}\end{array}\right],\hfill & \hfill C& =\left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 1& 0& 1\end{array}\right]\hfill \end{array}$$

(3)

Denote $\theta =\left[a_{ij},b_{ij},x_0\in {\mathbb{R}}^{n_x},\beta \in {\mathbb{R}}^{n_y}\right]$ the vector of parameters to identify with $\beta$ and $x_0$ representing an unknown offset and initial state. This vector is computed by resolving the following least-square problem:

$${\theta }^{*}=arg\underset{\theta \in D}{min}\sum _{k=1}^N{\left[y_i(k,\theta )-z_i\left(k\right)\right]}^2$$

(4)

subject to the parametrized model:

$$G\left(k,\theta \right)=\left\{\begin{array}{cc}\hfill x_i(k+1)& =A\left(\theta \right)x_i\left(k\right)+B_u\left(\theta \right)u_i\left(k\right)+B_w\left(\theta \right)w_i\left(k\right)+B_v\left(\theta \right)v_i\left(k\right),\hfill \\ \hfill y_i\left(k\right)& =C{x}_i\left(k\right)+\beta \left(\theta \right)\hfill \end{array}\right.$$

(5)

The zone model is given by:

$$F\left(k,x_i,u_i,w_i,v_i\right)=G\left(k,{\theta }^{*}\right)$$

(6)

The quality of the model is evaluated using the following specific index with $N_p$ the prediction horizon:

$${ϵ}_p\left(t\right)=\sum _{k=t}^{t+N_p}\Vert {{\displaystyle \frac{y_t\left(k\right)-z_t\left(k\right)}{z_t\left(k\right)}}}^2\Vert$$

(7)

4. Experimental Results

The case study is the Nimbus building in Cork Institute of Technology (CIT). It has been instrumented using TOPAs platform (see details in [6,7]). We focus on an open-space subdivided in three zones. The thermal and comfort behaviors are modelled using data captured in winter. Figure 2 shows their ${ϵ}_p$ index. Models are validated if total of occurences above ${ϵ}_p=20\%$ are less than below. For $N_p=2$, both thermal and CO2 models are validated; for $N_p=5$ only the thermal ones is accurate enough for predictive usage.

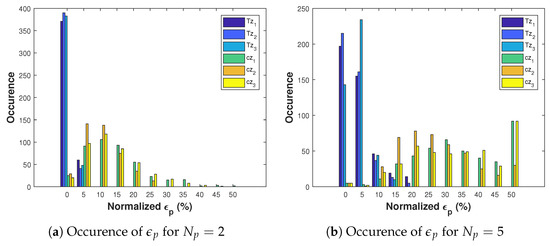
Figure 2. Validation of the modelling for the case-study.

The reliability of the models in real conditions is evaluated by running a DiMPC controller. The reference temperature is $T_{ref}=22{}^{\circ }\mathrm{C}$ and the comfort bounds is chosen as $[18{}^{\circ }\mathrm{C};26{}^{\circ }\mathrm{C}]$. In Figure 3, we compare the effect of the DiMPC control algorithm against baseline on zone temperatures. Thanks to the proposed modelling procedure, the DiMPC was able to demonstrate energy saving and improved thermal comfort. The same controller is applied during the summer (Figure 4). Weather conditions are warmer, the heating system have been shut down and the windows are the main actuators in this scenario. The temperature remains within the comfort bounds.

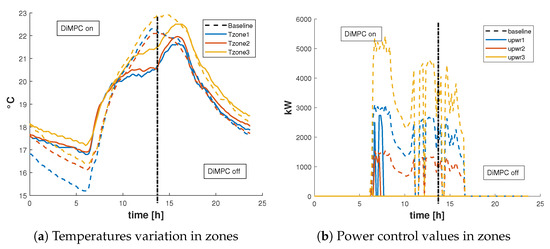
Figure 3. Comparison between DiMPC (plain lines) and baseline (dash line) control algorithms during winter: DiMPC is enabled during 14 h then disabled.

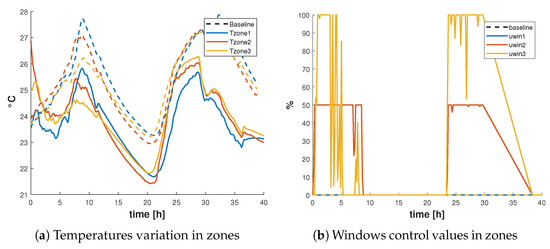
Figure 4. Comparison between DiMPC (plain lines) and baseline (dash line) control algorithms during summer: DiMPC is enabled during 40 h.

5. Conclusions

This paper has presented an initial analysis of a modeling approach to accurately develop (Di)MPC technology for evalution in real buildings. The solution has been evaluated in a real use case, showing the benifits of DiMPC for energy and comfort management. The approach is generic, in such a way that it is applicable for different types of buildings and building zones.