Sensing Characteristics of Smart Microsensor Systems for Measuring Relative Humidity in Pressurized Air †
Abstract
:1. Introduction
2. Measurement of Relative Humidity in Pressurized Air
3. Materials and Methods
3.1. Sensors Under Test
3.2. Measurement Set-Up
3.3. Measurement Sequence
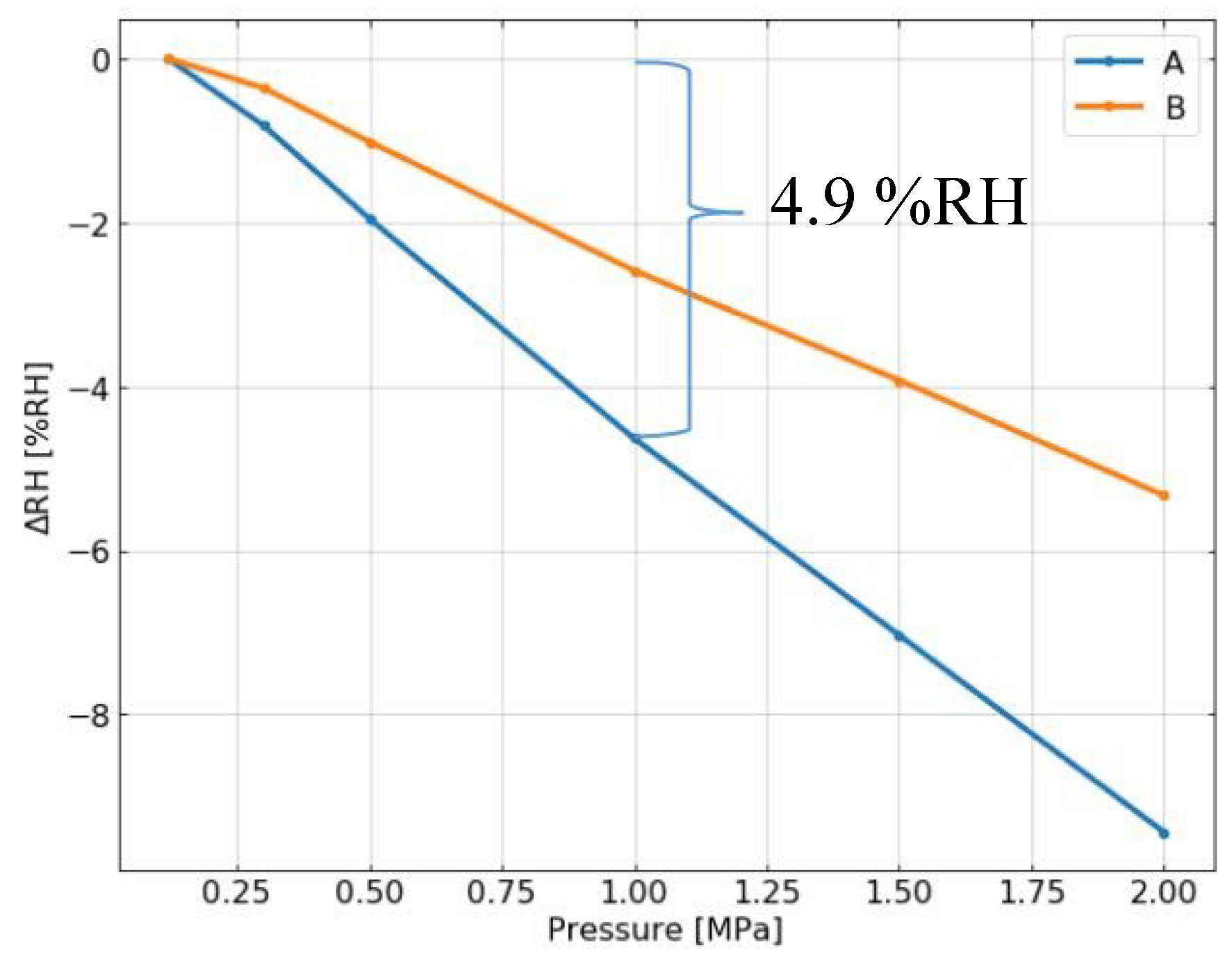
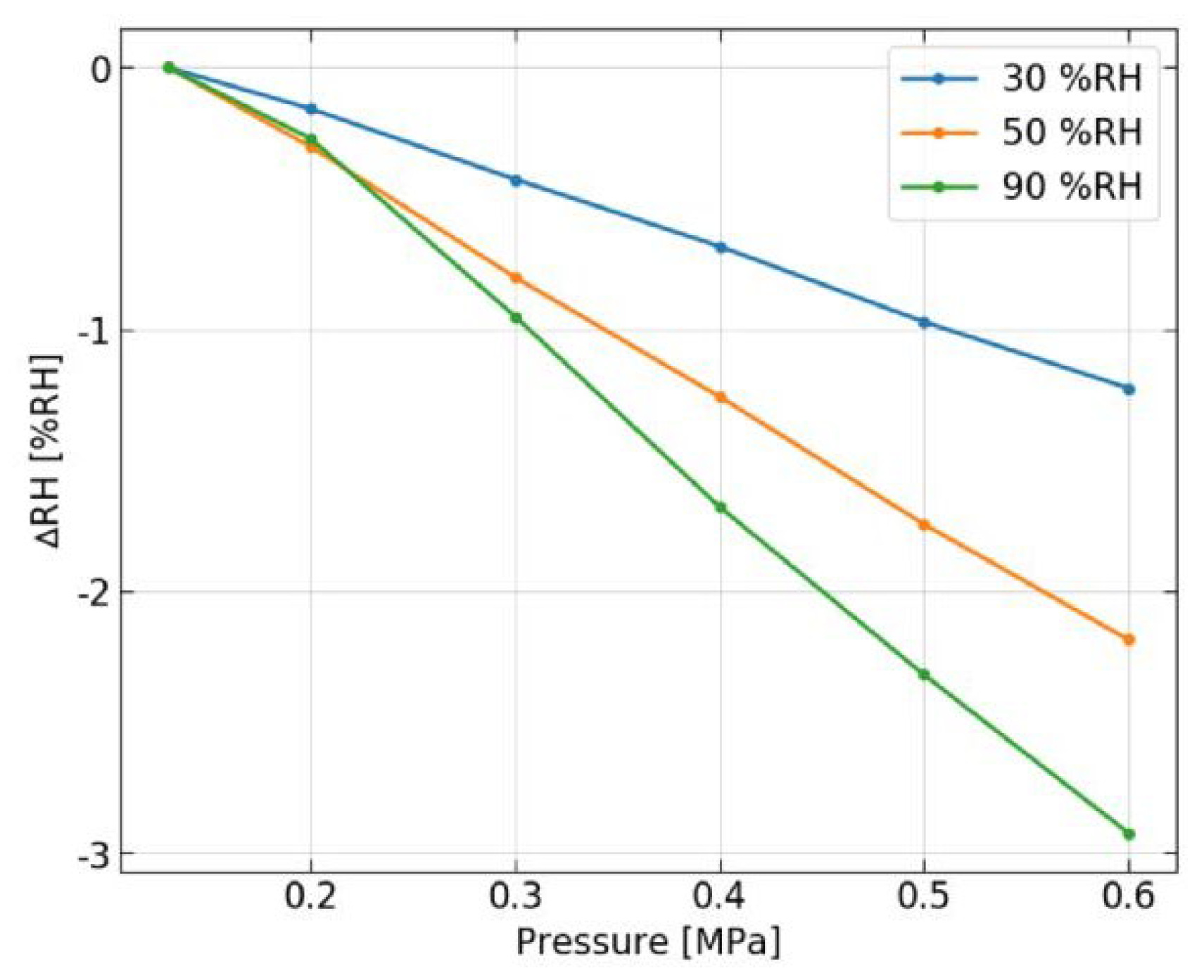
4. Results and Discussion
5. Conclusions and Outlook
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Greenspan, L. Functional Equations for the Enhancement Factors for CO2-Free Moist Air. J. Res. Natl. Bur. Stand. A 1975, 80A, 41–44. [Google Scholar] [CrossRef] [PubMed]
- Hardy, B. ITS-90 formulations for vapor pressure, frostpoint temperature, dewpoint temperature, and enhancement factors in the range −100 to +100 C. In Proceedings of the Third International Symposium on Humidity & Moisture, Teddington, London, UK, 6–8 April 1998; Volume 1, pp. 206–213. [Google Scholar]
- Stevens, M.; Bell, S.A.; Carroll, P.; Mortimer, S. Towards a standard for multi-gas and multi-pressure humidity calibrations. In Proceedings of the TEMPMEKO & ISHM 2010, Portoroz, Slovenia, 31 May–4 June 2010; Volume A, p. 311. [Google Scholar]
- Sensirion SHT 31. Available online: https://www.sensirion.com/en/environmental-sensors/humidity-sensors/digital-humidity-sensors-for-various-applications/ (accessed on 21 June 2018).

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weller, F.; Keller, D.; Wettstein, S.; Graf, M. Sensing Characteristics of Smart Microsensor Systems for Measuring Relative Humidity in Pressurized Air. Proceedings 2018, 2, 871. https://doi.org/10.3390/proceedings2130871
Weller F, Keller D, Wettstein S, Graf M. Sensing Characteristics of Smart Microsensor Systems for Measuring Relative Humidity in Pressurized Air. Proceedings. 2018; 2(13):871. https://doi.org/10.3390/proceedings2130871
Chicago/Turabian StyleWeller, Fabian, Dino Keller, Sascha Wettstein, and Markus Graf. 2018. "Sensing Characteristics of Smart Microsensor Systems for Measuring Relative Humidity in Pressurized Air" Proceedings 2, no. 13: 871. https://doi.org/10.3390/proceedings2130871
APA StyleWeller, F., Keller, D., Wettstein, S., & Graf, M. (2018). Sensing Characteristics of Smart Microsensor Systems for Measuring Relative Humidity in Pressurized Air. Proceedings, 2(13), 871. https://doi.org/10.3390/proceedings2130871



