Investigation of a Nonlinear Vibrational Energy Harvester in the Stochastic Resonance Regime †
Abstract
:1. Introduction
2. The Nonlinear Harvester and the Experimental Setup

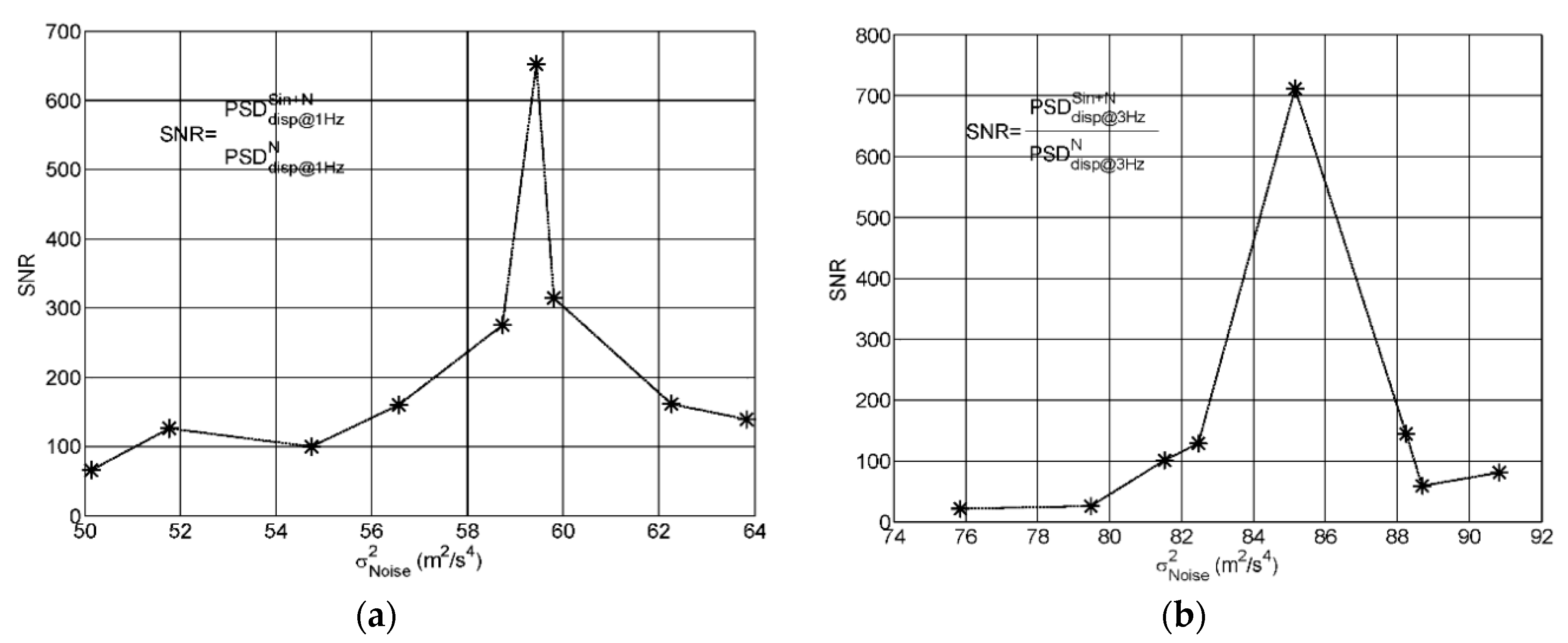
3. Experimental Results
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Roundy, S.; Wright, P.; Rabaey, J. A study of low level vibrations as a power source for wireless sensor nodes. Comput. Commun. 2003, 26, 1131–1144. [Google Scholar] [CrossRef]
- Harne, R.L.; Wang, K.W. A review of the recent research on vibration energy harvesting via bistable systems. Smart Mater. Struct. 2013, 22, 023001. [Google Scholar] [CrossRef]
- Baglio, B.A.S.; Bulsara, A.R.; Marletta, V. A bistable buckled beam based approach for vibrational energy harvesting. Sens. Actuators A Phys. 2013, 211, 153–161. [Google Scholar]
- Zhang, J.; Zhang, J.; Shu, C.; Fang, Z. Enhanced piezoelectric wind energy harvesting based on a buckled beam. Appl. Phys. Lett. 2017, 110, 183903. [Google Scholar] [CrossRef]
- Andò, B.; Baglio, S.; Bulsara, A.R.; Marletta, V.; Pistorio, A. Investigation of a Nonlinear Energy Harvester. IEEE Trans. Instrum. Meas. 2017, 66, 1067–1075. [Google Scholar] [CrossRef]
- Andò, B.; Baglio, S.; Bulsara, A.R.; Marletta, V.; Ferrari, V.; Ferrari, M. A Low-Cost Snap-Through Buckling Inkjet Printed Device for Vibrational Energy Harvesting. IEEE Sens. J. 2015, 15, 3209–3220. [Google Scholar] [CrossRef]
- Andò, B.; Baglio, S.; Bulsara, A.R.; Marletta, V.; Pistorio, A. Experimental and Theoretichal Investigation of a Nonlinear Vibrational Energy Harvester, Procedia Engineering. In Proceedings of the 29th European Conference on Solid-State Transducers, EUROSENSORS 2015, Freiburg, Germany, 6–9 September 2015; Volume 120, pp. 1024–1027. [Google Scholar]
- Andò, B.; Baglio, S.; Bulsara, A.R.; Marletta, V.; Pistorio, A. Performance Investigation of a Nonlinear Energy Harvester with Random Vibrations and Sub-Threshold Deterministic Signals. IEEE Trans. Instrum. Meas. 2017, 66, 992–1001. [Google Scholar] [CrossRef]
- Andò, B.; Baglio, S.; Marletta, V.; Bulsara, A.R. A Wireless Sensor Node Powered by NonLinear Energy Harvester. In Proceedings of the 13th IEEE Sensors Conference, Valencia, Spain, 2–5 November 2014; pp. 1583–1586. [Google Scholar]
- Andò, B.; Baglio, S.; Marletta, V.; Pistorio, A.; Bulsara, A.R. A Nonlinear Energy Harvesting with Asymmetry Compensation. Proceedings 2017, 1, 581. [Google Scholar] [CrossRef]
- Andò, B.; Baglio, S.; Marletta, V.; Pistorio, A.; Bulsara, A.R. A Measurement Methodology for the Characterization of a Compensated Nonlinear Energy Harvester for Vertical Operation, accepted for publication on IEEE Trans. Instrum. Meas. 2018. [CrossRef]
- Bulsara, A.R.; Gammaitoni, L. Tuning in to Noise. Physics Today 1996, 49, 39. [Google Scholar] [CrossRef]
- Data Sheet Article S-10-04-N. Available online: Https://www.supermagnete.it/eng/data_sheet_S-10-04-N.pdf (accessed on 18 July 2018).
| Frequency of the Subthreshold Input, (Hz) | STB Beam Threshold, ath_max (m/s2) | Subthreshold Input, asub_max (m/s2) | STD of the Noise, σopt, (m/s2) | Electrical Power, Pe, (μW) |
|---|---|---|---|---|
| 1 | 19.71 | 12.81 | 7.65 | 60 |
| 3 | 22.49 | 14.01 | 9.23 | 150 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andò, B.; Baglio, S.; Bulsara, A.R.; Marletta, V. Investigation of a Nonlinear Vibrational Energy Harvester in the Stochastic Resonance Regime. Proceedings 2018, 2, 1092. https://doi.org/10.3390/proceedings2131092
Andò B, Baglio S, Bulsara AR, Marletta V. Investigation of a Nonlinear Vibrational Energy Harvester in the Stochastic Resonance Regime. Proceedings. 2018; 2(13):1092. https://doi.org/10.3390/proceedings2131092
Chicago/Turabian StyleAndò, Bruno, Salvatore Baglio, Adi R. Bulsara, and Vincenzo Marletta. 2018. "Investigation of a Nonlinear Vibrational Energy Harvester in the Stochastic Resonance Regime" Proceedings 2, no. 13: 1092. https://doi.org/10.3390/proceedings2131092
APA StyleAndò, B., Baglio, S., Bulsara, A. R., & Marletta, V. (2018). Investigation of a Nonlinear Vibrational Energy Harvester in the Stochastic Resonance Regime. Proceedings, 2(13), 1092. https://doi.org/10.3390/proceedings2131092






