Investigation of the Relationship between Three- and One-Dimensional Infiltration Using a Mini Disc Infiltrometer †
Abstract
:1. Introduction
2. Materials and Methods
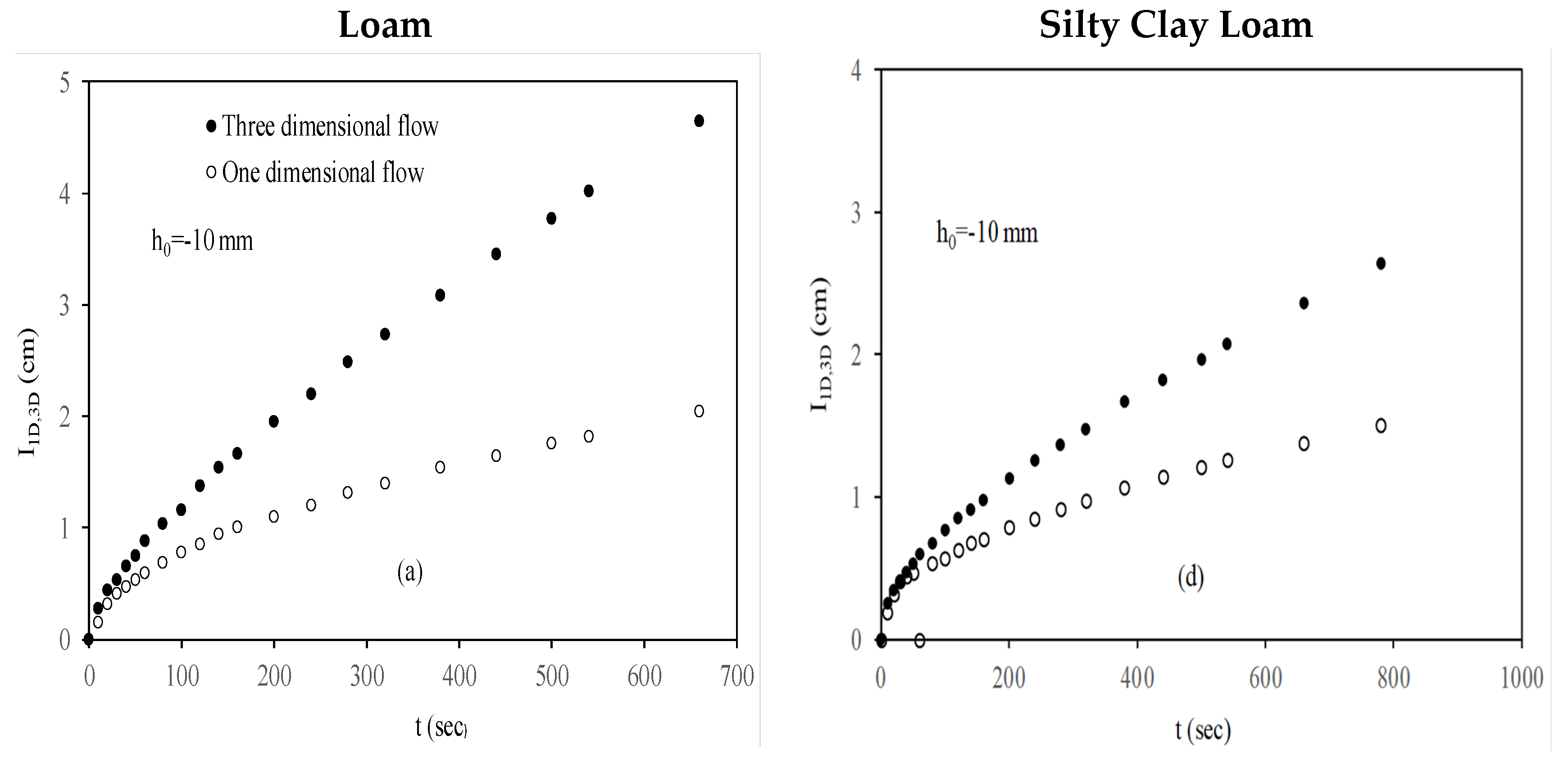
3. Results and Discussion
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Smettem, K.R.J.; Parlange, J.-Y.; Ross, P. J.; Haverkamp, R. Three-dimensional analysis of infiltration from the disc infiltrometer: 1. A capillary-based theory. Water Resour. Res. 1994, 30, 2925–2929. [Google Scholar] [CrossRef]
- Smettem, K.R.J.; Clothier, B.E. Measuring unsaturated sorptivity and hydraulic conductivity using multiple disc permeameters. J. Soil Sci. 1989, 40, 563–568. [Google Scholar] [CrossRef]
- Warrick, A.W. Models for disc infiltrometers. Water Resour. Res. 1992, 28, 1319–1327. [Google Scholar] [CrossRef]
- Haverkamp, R.; Ross, P.J.; Smettem, K.R.J.; Parlange, J.-Y. Three dimensional analysis of infiltration from disc infiltrometer 2. Physically-based infiltration equation. Water Resour. Res. 1994, 30, 2931–2935. [Google Scholar] [CrossRef]
- Vandervaere, J.P.; Vauclin, M.; Elrick, D.E. Transient flow from tension infiltrometers: I. The two parameter equation. Soil Sci. Soc. Am. J. 2000, 64, 1263–1272. [Google Scholar] [CrossRef]
- Smettem, K.R.J. Characterization of water entry into a soil with a contrasting textural class: Spatial variability of infiltration parameters and influence of macroporosity. Soil Sci. 1987, 144, 167–174. [Google Scholar] [CrossRef]
- Mohanty, B.P.; Ankeny, M.D.; Horton, R.; Kanwar, R.S. Spatial analysis of hydraulic conductivity measured using disc infiltrometers. Water Resour. Res. 1994, 30, 2489–2498. [Google Scholar] [CrossRef]
- Shouse, P.J.; Mohanty, B.P. Scaling of near-saturated hydraulic conductivity measured using disc infiltrometers. Water Resour. Res. 1998, 34, 1195–1205. [Google Scholar] [CrossRef]
- Clothier, B.E.; White, I. Measurement of sorptivity and soil water diffusivity in the field. Soil Sci. Soc. Am. J. 1981, 45, 241–245. [Google Scholar] [CrossRef]
- Ankeny, M.D.; Ahmed, Μ.; Kaspar, T.C.; Horton, R. Simple field method for determining unsaturated hydraulic conductivity. Soil Sci. Soc. Am. J. 1991, 55, 467–470. [Google Scholar] [CrossRef]
- Reynolds, W.D.; Elrick, E.D. Determination of hydraulic conductivity using a tension infiltrometer. Soil Sci. Soc. Am. J. 1991, 55, 633–639. [Google Scholar] [CrossRef]
- Zhang, R. Infiltration models for the disc infiltrometer. Soil Sci. Soc. Am. J. 1997, 61, 1597–1603. [Google Scholar] [CrossRef]
- Vandervaere, J.P.; Vauclin, M.; Elrick, D.E. Transient flow from tension infiltrometers: II. Four Methods to Determine Sorptivity and Conductivity. Soil Sci. Soc. Am. J. 2000, 64, 1272–1284. [Google Scholar] [CrossRef]
- Latorre, B.; Moret-Fernández, D.; Peña, C. Estimate of soil hydraulic properties from disc infiltrometer three-dimensional infiltration curve: Theoretical analysis and field applicability. Proced. Environ. Sci. 2013, 19, 580–589. [Google Scholar] [CrossRef]
- Wooding, R.A. Steady infiltration from shallow circular pond. Water Resour. Res. 1968, 4, 1259–1273. [Google Scholar] [CrossRef]
- Lazarovitch, N.; Ben Gal, A.; Simunek, J.; Shani, U. Uniqueness of soil parameters determined by a combined Wooding inverse approach. Soil Sci. Soc. Am. J. 2007, 71, 860–865. [Google Scholar] [CrossRef]
- Gardner, W.R. Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table. Soil Sci. 1958, 85, 228–232. [Google Scholar] [CrossRef]
- Vandervaere, J.P. The soil solution phase. In Methods of Soil Analysis: Part 4, Physical Methods; Dane, J.H., Topp, G.C., Eds.; SSSA, Inc.: Madison, WI, USA, 2002; pp. 889–894. [Google Scholar]
- Philip, J.R. The theory of infiltration: 4. Sorptivity and algebraic infiltration equations. Soil Sci. 1957, 84, 257–264. [Google Scholar] [CrossRef]
- Smiles, D.E.; Knight, J.H. A note on the use of the Philip infiltration equation. Aust. J. Soil Res. 1976, 14, 103–108. [Google Scholar] [CrossRef]
- Mini Disc Infiltrometer, User’s Manual; Decagon Devices Inc.: Pullman, DC, USA, 2007; 24p.
- Smettem, K.R.J.; Ross, P. J.; Haverkamp, R.; Parlange, J.-Y. Three-dimensional analysis of infiltration from the disc infiltrometer: 3. Parameter estimation using a double-disk tension infiltrometer. Water Resour. Res. 1995, 10, 2491–2495. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B. Estimation of sorptivity from disc-permeameter measurements. Geoderma 2000, 95, 305–324. [Google Scholar] [CrossRef]
- Vandervaere, J.P.; Peugeot, C.; Vauclin, M.; Angulo-Jaramillo, R.; Lebel, T. Estimating hydraulic conductivity of crusted soils using disc infiltrometers and minitensiometers. J. Hydrol. 1997, 188–189, 203–223. [Google Scholar] [CrossRef]
- Perroux, K.M.; White, I. Designs for disc permeameters. Soil Sci. Soc. Am. J. 1988, 52, 1205–1215. [Google Scholar] [CrossRef]



| Soil Type | Clay (%) | Silt (%) | Sand (%) | ρφ (g.cm−3) |
|---|---|---|---|---|
| L | 20.0 | 38 | 42.0 | 1.17 |
| SiCL | 36.5 | 52 | 11.5 | 1.23 |
| Soil Type | Pressure Head, h0 (mm) | Water Content, θ0 (cm3cm−3) | Soil Sorptivity, S0 (cm s−0.5) | R2 |
|---|---|---|---|---|
| L | −10 | 0.385 | 0.072 | 0.970 |
| −40 | 0.369 | 0.063 | 0.958 | |
| −70 | 0.362 | 0.058 | 0.986 | |
| SiCL | −10 | 0.464 | 0.061 | 0.990 |
| −30 | 0.446 | 0.046 | 0.990 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kargas, G.; Londra, P.; Anastasiou, K. Investigation of the Relationship between Three- and One-Dimensional Infiltration Using a Mini Disc Infiltrometer. Proceedings 2018, 2, 660. https://doi.org/10.3390/proceedings2110660
Kargas G, Londra P, Anastasiou K. Investigation of the Relationship between Three- and One-Dimensional Infiltration Using a Mini Disc Infiltrometer. Proceedings. 2018; 2(11):660. https://doi.org/10.3390/proceedings2110660
Chicago/Turabian StyleKargas, George, Paraskevi Londra, and Konstantinos Anastasiou. 2018. "Investigation of the Relationship between Three- and One-Dimensional Infiltration Using a Mini Disc Infiltrometer" Proceedings 2, no. 11: 660. https://doi.org/10.3390/proceedings2110660
APA StyleKargas, G., Londra, P., & Anastasiou, K. (2018). Investigation of the Relationship between Three- and One-Dimensional Infiltration Using a Mini Disc Infiltrometer. Proceedings, 2(11), 660. https://doi.org/10.3390/proceedings2110660







