Analysis of Monthly Rainfall Trend in Calabria (Southern Italy) through the Application of Statistical and Graphical Techniques †
Abstract
:1. Introduction
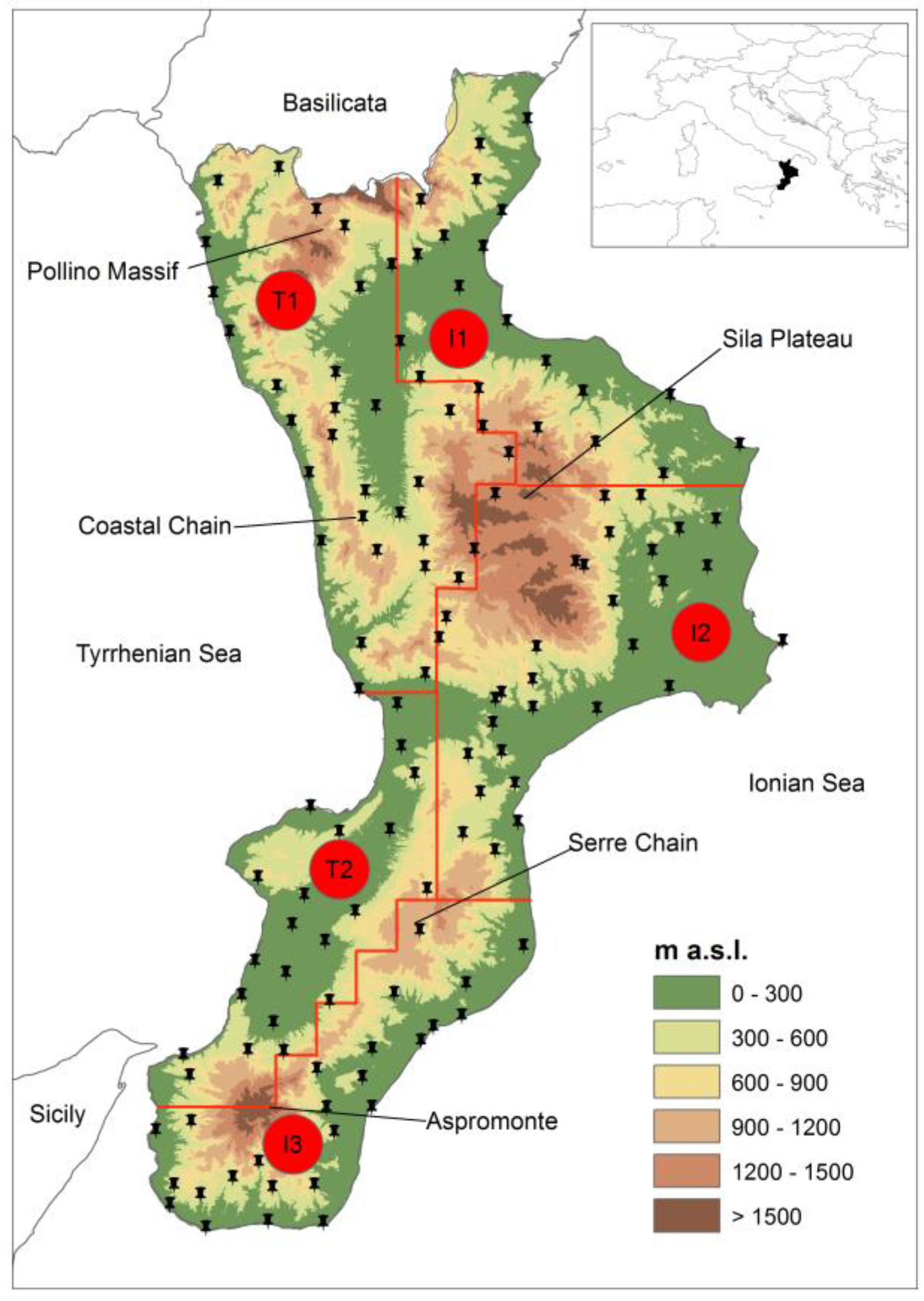
2. Study Area and Data
3. Methods
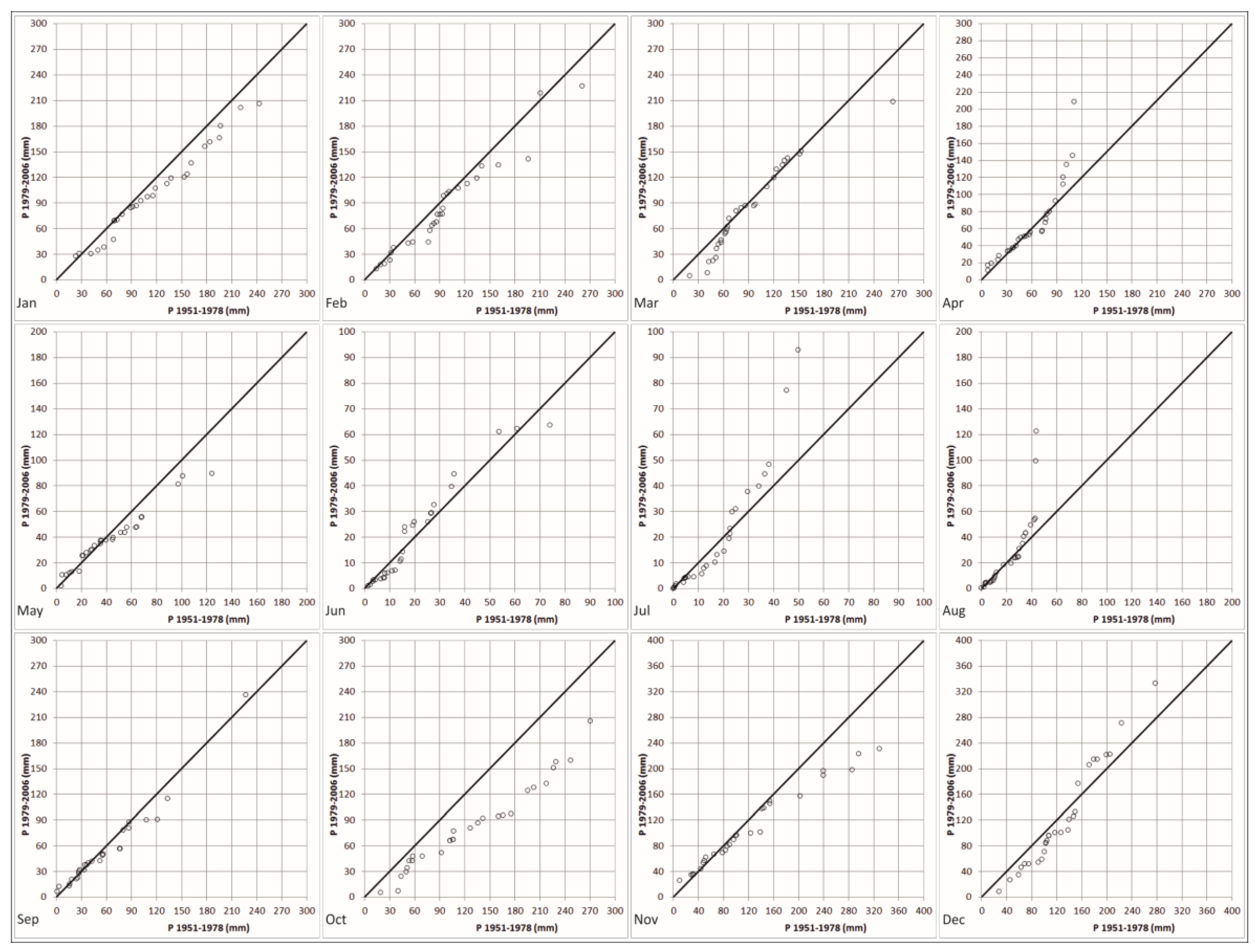
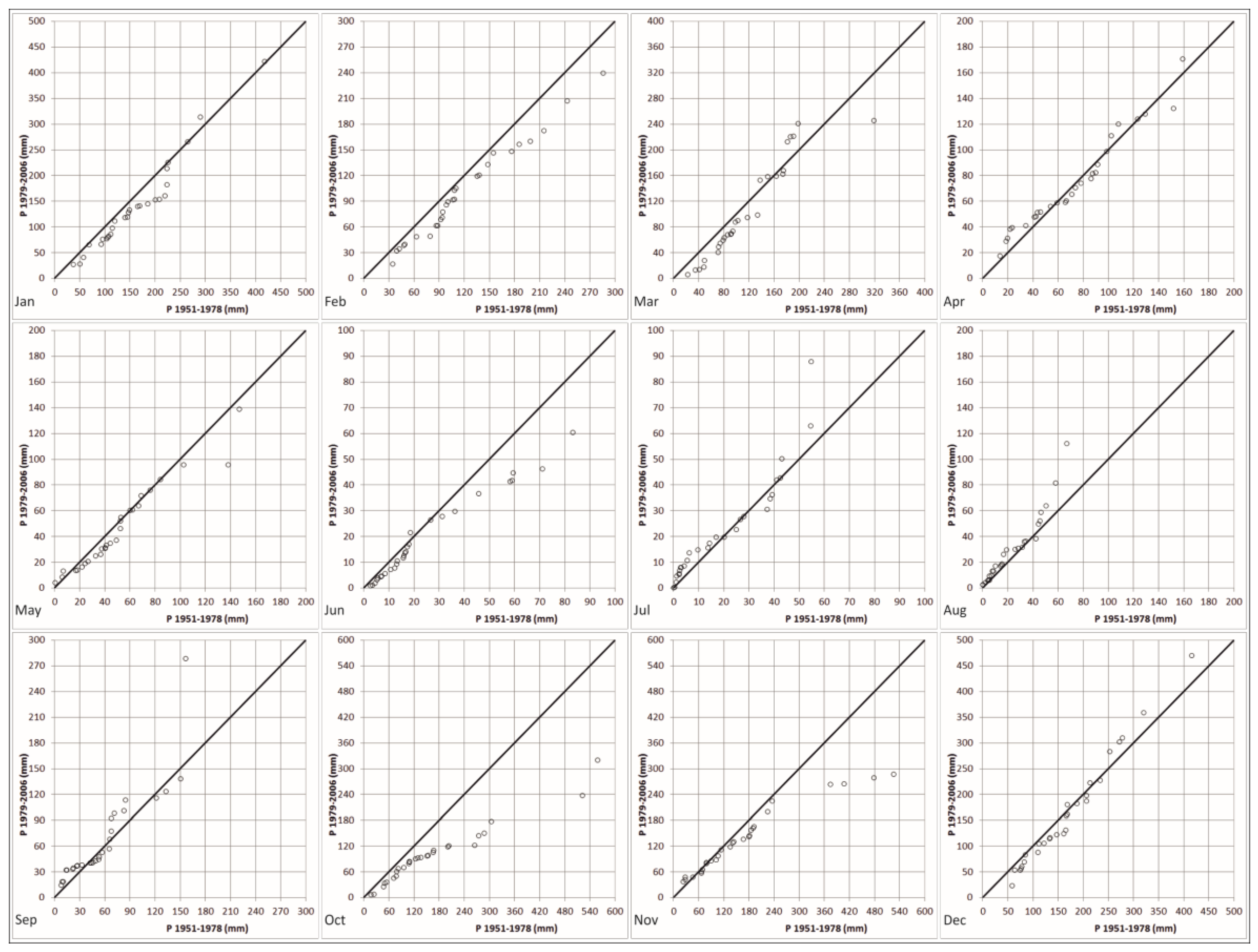
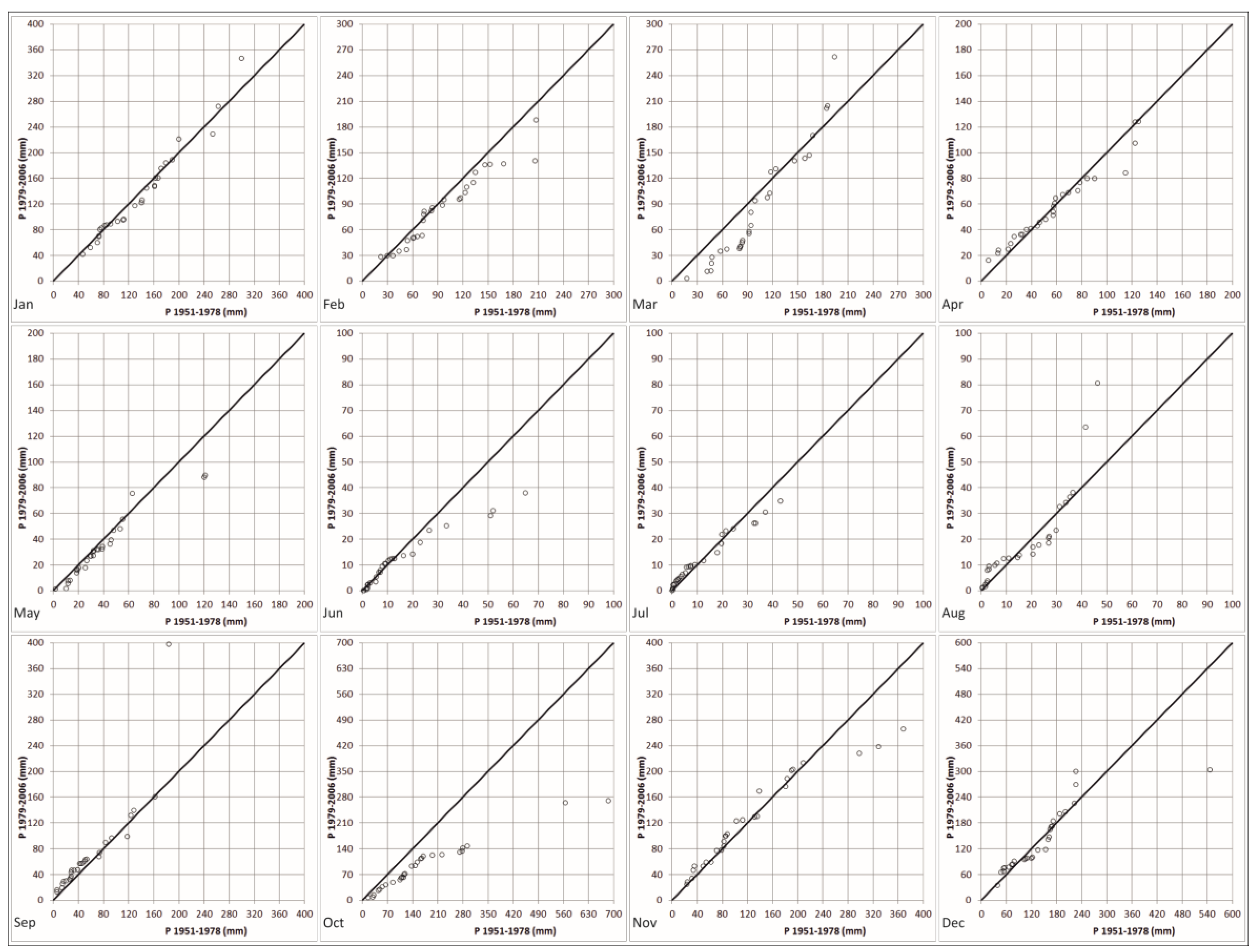
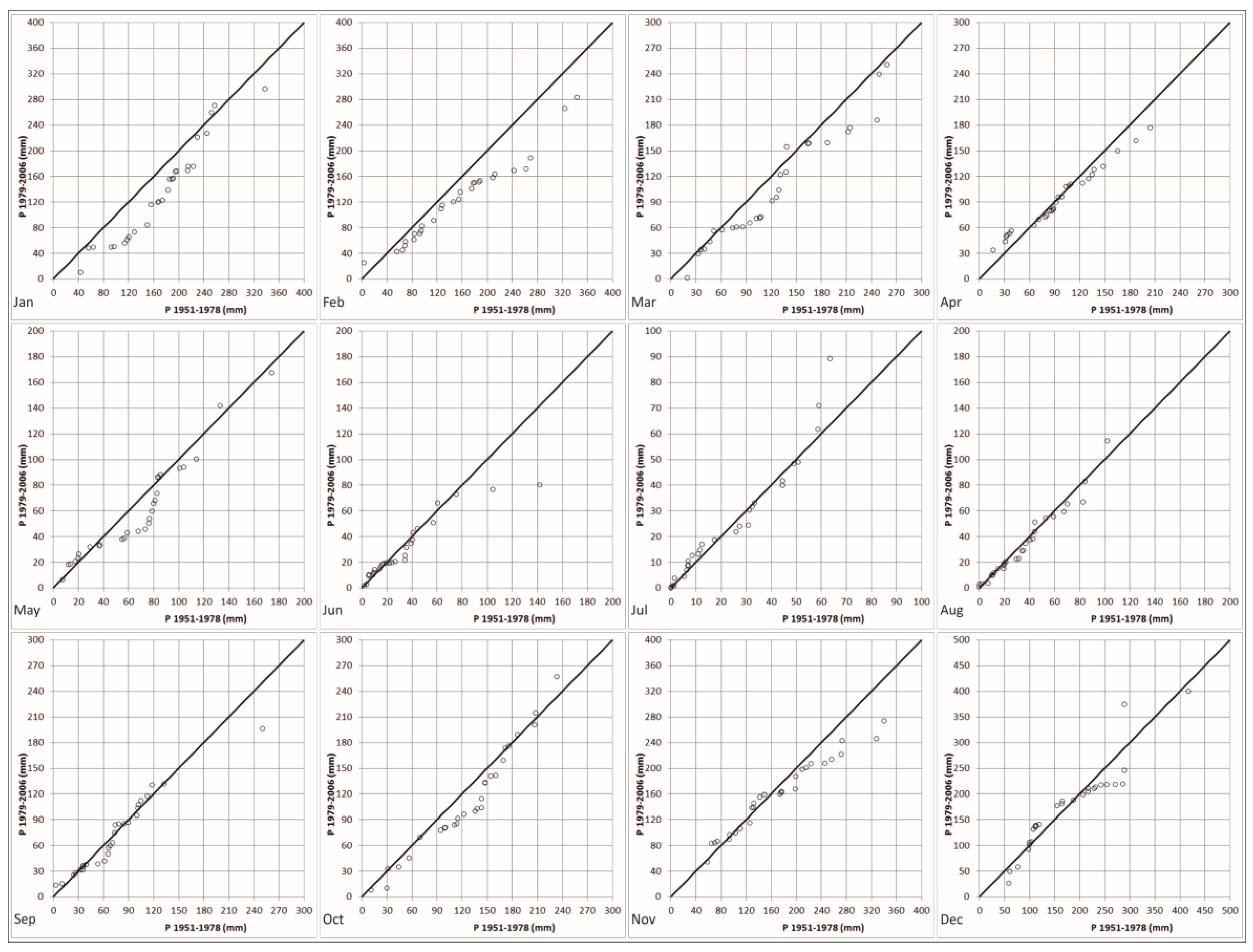
4. Results and Discussion
5. Conclusions
References
- IPCC. Summary for Policymakers; Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Ay, M.; Kisi, O. Investigation of trend analysis of monthly total precipitation by an innovative method. Theor. Appl. Climatol. 2015, 120, 617–629. [Google Scholar] [CrossRef]
- Del Rio, S.; Herrero, L.; Fraile, R.; Penas, A.P. Spatial distribution of recent rainfall trends in Spain (1961–2006). Int. J. Climatol. 2011, 31, 656–667. [Google Scholar]
- Caloiero, T. Analysis of rainfall trend in New Zealand. Environ. Earth Sci. 2015, 73, 6297–6310. [Google Scholar] [CrossRef]
- Longobardi, A.; Buttafuoco, G.; Caloiero, T.; Coscarelli, R. Spatial and temporal distribution of precipitation in a Mediterranean area (Southern Italy). Environ. Earth Sci. 2016, 75, 189. [Google Scholar] [CrossRef]
- Mehta, A.V.; Yang, S. Precipitation climatology over Mediterranean Basin from ten years of TRMM measurements. Adv. Geosci. 2008, 17, 87–91. [Google Scholar] [CrossRef]
- Reale. M.; Lionello, P. Synoptic climatology of winter intense precipitation events along the Mediterranean coasts. Nat. Hazards Earth Syst. Sci. 2013, 13, 1707–1722. [Google Scholar] [CrossRef]
- Lionello, P.; Giorgi, F. Winter precipitation and cyclones in the Mediterranean region: Future climate scenarios in a regional simulation. Adv. Geosci. 2007, 12, 153–158. [Google Scholar] [CrossRef]
- Brunetti, M.; Maugeri, M.; Monti, F.; Nanni, T. Temperature and precipitation variability in Italy in the last two centuries from homogenised instrumental time series. Int. J. Climatol. 2006, 26, 345–381. [Google Scholar] [CrossRef]
- Longobardi, A.; Villani, P. Trend analysis of annual and seasonal rainfall time series in the Mediterranean area. Int. J. Climatol. 2010, 30, 1538–1546. [Google Scholar] [CrossRef]
- Piccarreta, M.; Capolongo, D.; Boenzi, F. Trend analysis of precipitation and drought in Basilicata from 1923 to 2000 within a Southern Italy context. Int. J. Climatol. 2004, 24, 907–922. [Google Scholar] [CrossRef]
- Liuzzo, L.; Bono, E.; Sammartano, V.; Freni, G. Analysis of spatial and temporal rainfall trends in Sicily during the 1921–2012 period. Theor. Appl. Climatol. 2016, 126, 113–129. [Google Scholar] [CrossRef]
- Caloiero, T.; Buttafuoco, G.; Coscarelli, R.; Ferrari, E. Spatial and temporal characterization of climate at regional scale using homogeneous monthly precipitation and air temperature data: An application in Calabria (Southern Italy). Hydrol. Res. 2015, 46, 629–646. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Hafner Publishing Company: New York, NY, USA, 1962. [Google Scholar]
- Spearman, C. The proof and measurement of association between two things. Am. J. Psychol. 1904, 15, 72–101. [Google Scholar] [CrossRef]
- Şen, Z. An innovative trend analysis methodology. J. Hydrol. Eng. 2012, 17, 1042–1046. [Google Scholar] [CrossRef]
- Haktanir, T.; Citakoglu, H. Trend, independence, stationarity, and homogeneity tests on maximum rainfall series of standard durations recorded in Turkey. J. Hydrol. Eng. 2014, 19, 501–509. [Google Scholar] [CrossRef]
- Kisi, O.; Ay, M. Comparison of Mann–Kendall and innovative trend method for water quality parameters of the Kizilirmak River, Turkey. J. Hydrol. 2014, 513, 362–375. [Google Scholar] [CrossRef]
- Şen, Z. Trend identification simulation and application. J. Hydrol. Eng. 2014, 19, 635–642. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Ferrari, E.; Sirangelo, B. Analysis of Dry Spells in Southern Italy (Calabria). Water 2015, 7, 3009–3023. [Google Scholar] [CrossRef]
- Brunetti, M.; Caloiero, T.; Coscarelli, R.; Gullà, G.; Nanni, T.; Simolo, C. Precipitation variability and change in the Calabria region (Italy) from a high resolution daily dataset. Int. J. Climatol. 2012, 32, 57–73. [Google Scholar] [CrossRef]
- Brunetti, M.; Caloiero, T.; Coscarelli, R.; Gullà, G.; Nanni, T.; Simolo, C. Applicazione di test di omogeneità e tecniche di ricostruzione dei dati mancanti alle serie pluviometriche giornaliere calabresi per l’individuazione di aree omogenee e la stima dei trend. L’Acqua 2012, 2, 35–44. (In Italian) [Google Scholar]
- Coscarelli, R.; Caloiero, T. Analysis of daily and monthly rainfall concentration in Southern Italy (Calabria region). J. Hydrol. 2012, 416–417, 145–156. [Google Scholar] [CrossRef]
- Sirangelo, B.; Caloiero, T.; Coscarelli, R.; Ferrari, E. A stochastic model for the analysis of the temporal change of dry spells. Stoch. Environ. Res. Risk. Assess. 2015, 29, 143–155. [Google Scholar] [CrossRef]
- Sirangelo, B.; Caloiero, T.; Coscarelli, R.; Ferrari, E. Stochastic analysis of long dry spells in Calabria (Southern Italy). Theor. Appl. Climatol. 2017, 127, 711–724. [Google Scholar] [CrossRef]

| I1 | I2 | I3 | T1 | T2 | |
|---|---|---|---|---|---|
| mm/Decade | mm/Decade | mm/Decade | mm/Decade | mm/Decade | |
| Year | −33.8 *** | −53.2 *** | −41.5 ** | −45.8 *** | −30.9 ** |
| January | −6.9 * | −8.3 * | −2.9 | −14.8 ** | −9.9 *** |
| February | −4.0 | −7.0 | −3.6 | −13.0 ** | −5.3 |
| March | −5.8 * | −8.8 ** | −9.3 ** | −7.4 * | −7.6 * |
| April | 3.2 | 2.9 | 0.8 | 1.5 | 4.2 |
| May | −2.8 | −3.5 | −2.8 | −4.2 | −2.6 |
| June | 0.7 | −1.5 | −0.2 | −1.3 | −1.1 |
| July | 1.7 | 2.0 | 0.5 | 1.5 | 1.9 |
| August | 2.8 | 2.7 | 1.1 | 0.6 | 2.0 |
| September | 0.5 | 4.7 | 5.8 | 3.2 * | 3.7 |
| October | −15.2 *** | −24.1 ** | −28.6 ** | −5.5 | −16.4 ** |
| November | −10.4 * | −14.9 | −6.2 | −6.0 | −3.6 |
| December | 2.4 | 2.6 | 3.8 | −0.3 | 3.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caloiero, T.; Coscarelli, R.; Ferrari, E. Analysis of Monthly Rainfall Trend in Calabria (Southern Italy) through the Application of Statistical and Graphical Techniques. Proceedings 2018, 2, 629. https://doi.org/10.3390/proceedings2110629
Caloiero T, Coscarelli R, Ferrari E. Analysis of Monthly Rainfall Trend in Calabria (Southern Italy) through the Application of Statistical and Graphical Techniques. Proceedings. 2018; 2(11):629. https://doi.org/10.3390/proceedings2110629
Chicago/Turabian StyleCaloiero, Tommaso, Roberto Coscarelli, and Ennio Ferrari. 2018. "Analysis of Monthly Rainfall Trend in Calabria (Southern Italy) through the Application of Statistical and Graphical Techniques" Proceedings 2, no. 11: 629. https://doi.org/10.3390/proceedings2110629
APA StyleCaloiero, T., Coscarelli, R., & Ferrari, E. (2018). Analysis of Monthly Rainfall Trend in Calabria (Southern Italy) through the Application of Statistical and Graphical Techniques. Proceedings, 2(11), 629. https://doi.org/10.3390/proceedings2110629





