Improvement of Drainage Density Parameter Estimation within Erosion Potential Method ^†

Abstract

This paper analyses the possibilities to derive drainage density map, a parameter used within Erosion Potential Method (EPM, Gavrilović), for the Dubračina catchment study area in better detail and precision. EPM method is used for erosion assessment in the karstic areas characterized by torrential rivers. In this paper, three different methodologies were used to derive drainage density map each using different assumptions and allowing different spatial variability. The third case of drainage density map provides most realistic spatial variance of the drainage density parameter with lower values along the edges of the catchment and higher values concentrated along the river and tributary intersections.

1. Introduction

The one drainage basin attribute of the particular importance for this research is drainage density. Drainage density, $D_d$ is defined as the total length of channels per unit area [1] and it describes the spacing and distribution of the drainage ways in a catchment [2]. It can be said that the ratio that defines drainage density also represents the quantity of rivers in the catchment needed to drain the basin [3]. According to Marani et al. [4], drainage density, in practice, is defined by the statistical distribution and correlation structure of the lengths of un-channelled pathways [4].

This parameter is not constant in time, it evolves trough time as the drainage system in a catchment evolves [5]. This attribute of a drainage basin provides useful numerical measure of landscape dissection and runoff potential to hydrologists and geomorphologist. To measure drainage density is extremely difficult and it relies on a good topographic maps in a detailed scale [6,7]. As an alternative to drainage density, often a parameter potential drainage density is obtained from digital elevation data (DEM). The distinction between them is in the fact that the actual drainage density can be measured on site and it is based on the real drainage network map, while the potential one is derived from DEM and does not take into consideration the loss of surface runoff due to infiltration in the ground. For this reason, potential drainage density is always higher or equal to the actual drainage density in the analysed area [7].

During the last decades drainage density has been analysed in relation to many parameters among which in relation to soil erosion and soil erodibility [8] as well as sediment yield [9]. In 1945, Horton [1] defined un-channelled slope as a “belt of no erosion” with insufficient overland flow strength to induce erosion. Later on, Montgomery and Dietrich [10,11] as well as Dietrich et al. [12] confirmed his hypothesis. It is known that bare soils are much more erodible or prone to soil erosion. Catchments with such characteristics have higher drainage density and higher runoff production which leads to large flood peaks and volume [13]. Luoto [14] in his research highlighted the importance of soil erodibility and its effect on drainage density, and pointed relatively week effect of other parameters such as relief and bedrock geology on drainage density in comparison. Also, catchments with higher drainage density are prone to higher sediment yield values [15]. According to Tucker and Bras [16] a threshold for runoff erosion can influence landscape morphology and drainage density. Detachment-limited model was developed by Horward [17] where the controlling factors defining the relationship between drainage density and mean erosion rate are the dominant hillslope transport process and the presence or absence of a threshold for runoff erosion. Relation between drainage density and climatically driven erosional processes indicate drainage density as a catchment characteristics that can give an insight to signature processes and landscape history in the catchment. Analysis comparing erosion rates and drainage density can potentially be used to make conclusions about tectonic and geomorphic history [6].

Negative correlation between drainage density and slope angle are found in quickly eroding areas, while in areas prone to slow erosion processes the correlation between these two parameters is positive [17]. The relationship between slope angle and drainage density was found to be more directly related to the stages of channelization although previous research indicated its connection to dominant erosion types [18].

According to Gregory and Walling [9] review research, drainage density is often used: (i) in relation to catchment characteristics such as soil type or shape of the catchment; (ii) as an input or output of the drainage basin system and (iii) in relation to past and future conditions. This parameter has been recognized as one of the most important characteristics of natural terrain and a frequent topic in hydrology and geomorphology till today.

This paper analyses the possibilities to improve precision and obtain better output detail for Erosion Potential Method by deriving drainage density map with better detail and spatial variability. For this purpose three different methodologies are used to derive drainage density map on the case study Dubračina catchment, Croatia. The approaches use different assumptions and allow different spatial variability. First two approaches are commonly applied in Erosion Potential Method. The third approach is used in Erosion Potential Method for the first time and allows better detail and precision than the other two. The results are discussed and the differences in each drainage density map derived are compared.

2. Materials and Methods

When deriving drainage density (Equation (1)) for a catchment area, both perennial and intermittent rivers/tributaries need to be taken into consideration. If only perennial streams are included, drainage density value for the catchments with only intermittent streams would be equal to zero and in the flood event when both perennial and intermittent streams are active its values would be unrealistic [1]:

$$D_d=\frac{{{\displaystyle \sum }}_1^{n}L}{F},$$

(1)

where:

• L—Length of the waterway (km),
• n—Number of waterways,
• F—Contributing drainage area (km²).

The higher values of the drainage density indicate lower infiltration rates and higher surface flow velocity [19]. High drainage density is often related to high sediment yield transport trough river network, high flood peaks, steep hills, low suitability for agriculture.

Hydrogeological and geomorphological systems often have a heterogeneous characteristics that vary with scale from microstructures to continents [14]. Drainage network pattern is no exception, and consequently drainage density as well. The factors that influence drainage basin characteristics vary according to the scale of the input data (e.g., river network maps, digital elevation map, …).

According to Gregory and Walling [9] the usefulness of drainage density as model input parameter is limited by the method used to derive the drainage network and the maps and its scales representing catchment river network.

The conducted analysis described in this research is based upon research and gathered data from Dubračina Catchment area (Figure 1), situated in the Vinodol Valley in the County of Primorsko-Goranska, Croatia. The catchment area is 43.5 km². It has 12 torrential tributaries with approximant length of 41 km (

Table 1. Torrential tributaries length and sub-catchment area.

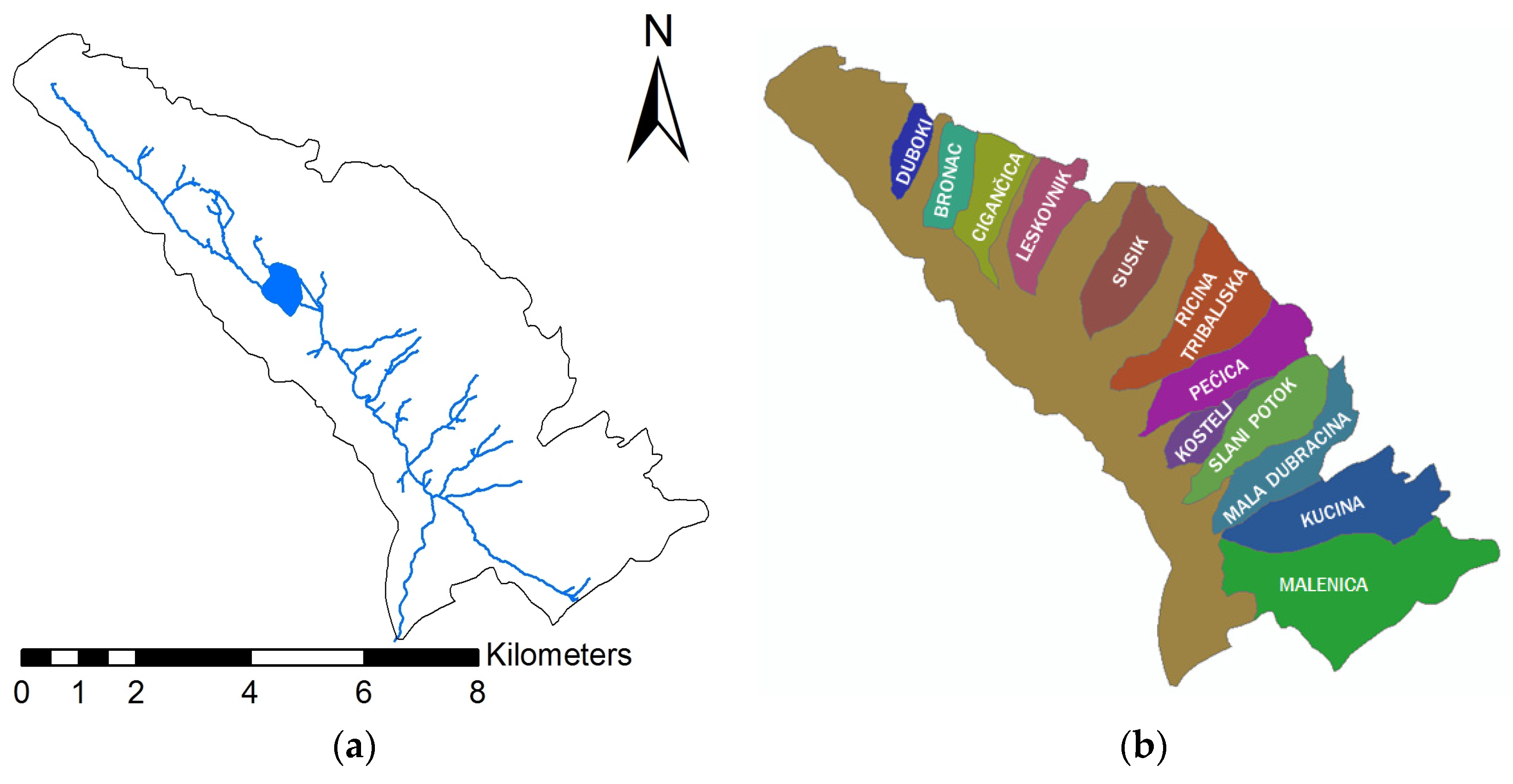
Tributary	Area (km2)	River Length (km)
Duboki	0.67	0.96
Bronac	0.99	1.62
Cigančica	1.49	3.03
Leskovnik	1.62	0.87
Susik	1.93	0.78
Ricina Tribaljska	2.74	1.71
Pećica	2.23	2.32
Kučina	0.82	1.04
Slani Potok	2.21	3.22
Mala Dubracina	2.09	3.00
Kucina	3.29	1.52
Malenica	5.54	4.00
Dubracina River		13.69
Small unnamed tributaries		3.23
Summarized	43.56	40.99

).

The catchment area is karstic area characterised by steep slopes, active sediment movement and Flysch. During the past it was affected by erosion processes, local landslides and flash floods. Today, 3 km² of its area is covered by excessive erosion and its most affected sub-catchments are Slani Potok and Mala Dubračina.

Drainage density for Dubračina catchment was derived three times using different assumptions and allowing different spatial variability.

In the first case scenario drainage density for Dubračina catchment is derived with assumption that the entire catchment is homogeneous with no spatial variance in its characteristics and as such in drainage density as well. For the calculation Equation (2) is used:

$$D_{d.I.Case}=\frac{l_p+l_a}{F},$$

(2)

where l_p is the length of the principal waterway, l_a is cumulated length of the secondary waterways and F is the catchment area.

The second case scenario takes into consideration sub-catchments variability. In this case, drainage density is calculated using the same equation (Equation (2)) for each sub-catchment separately.

In the third case scenario the drainage density was derived using the methodology proposed by Dobos and Daroussin [7]. They derived potential drainage density map using ARCGIS surrounding’s and the drainage network map derived from DEM (90 m resolution SRTM DEM). They first assigned the value one to each cell representing drainage lines. Upon that, the drainage density map is derived as a function of sums of all cell values that fall within a predefined shaped and sized neighbourhood (circle). The value for each pixel is then defined by moving the neighbourhood window and placing the desired pixel in the middle. Dobos and Daroussin [7] suggested the size and shape of the neighbourhood window to be variable for different case studies, depending on the current situation and user`s need, with a respect to minimum needed window size in order to get at least one drainage cell to avoid having empty neighbourhoods and zero value of drainage density. Opposite to that, too large windows lead to generalizing the $D_d$ map while smaller maintain the physiographic patterns.

For the Dubračina catchment square shape neighbour window with a size 1 × 1 km for a cell size of 1 × 1 m was used. The neighbour window with a size 1 × 1 km was chosen as to neutralize the value for area in the Equation (1) and thus drainage density for each cell is equivalent to the summation of all primary and secondary river lengths within the square window of 1 km². For Dubračina catchment the actual drainage density is calculated, based on the river network map with a scale size 1:25,000, obtained from Spatial Plan of Vinodol County [20], as opposite to the case presented by Dobos and Daroussin [7] where potential drainage density was calculated based on DEM derived river network.

The categorisation of drainage density parameter used in this research is based on proposed drainage density categorisation given by Ravi Shankar and Mohan [21] (

Table 2. Categorisation of drainage density given by Ravi Shankar and Mohan [21].

Category	Very Low	Low	Medium	High
$D_d$ (km/km2)	<1.0	1.0–2.0	2.0–3.5	>3.5

).

Derived drainage density was used later as input data in the Erosion Potential Method (

Table 3. Erosion Potential Method equations [22].

$W_a=T*P_a*\pi *\sqrt{Z^3}*F$	(3)	Wa—Total annual volume of detached soil (m3/year) T—Temperature coefficient (-) Pa—Average annual precipitation (mm) Z—Erosion coefficient (-) F—Study area (km2) T0—Average annual temperature (°C) Y—Soil erodibility coefficient (-) Xa—Soil protection coefficient (-) $\varphi$—Coefficient of type and extent of erosion (-) Ja—Average slope of the study area (%) ξ—Sediment delivery ratio (-) O—Perimeter of the study area (km) z—Mean difference in elevation of the study area (km) Dd—Drainage density (km/km2) lp—Length of the principal waterway (km) Gy—Actual sediment yield (m3/year)
$T=\sqrt{\frac{T_0}{10}+0.1}$	(4)
$Z=Y*X_a*\left(\varphi +\sqrt{J_a}\right)$	(5)
$\xi =\frac{\sqrt{O*z}}{\left(l_p+10\right)}*D_d$	(6)
$G_y=\xi *W_a$	(7)

) intended for the erosion intensity, sediment production assessment and transportation of sediment yield trough river network for the Dubračina catchment area.

3. Results and Discussion

The drainage density value (0.923 km/km²) obtained in the first case scenario corresponds to the very low drainage density class according to Ravi Shankar and Mohan’s [21] drainage density classification and is homogenous throughout the entire catchment.

For the second case scenario (Figure 2), using the same classification, five sub-catchments within the Dubračina catchment have very low (Sušik, Kučina, Leskovnik, Ričina and Malenica), another six low (Mužinići, Balasi, Mala Dubračina, Duboki, Slani Potok and Bronac) and only Bartolovac sub-catchments medium drainage density. It is know that low values of drainage density can indicate different things from higher infiltration rates and lower surface flow velocity to lower values of sediment yield transport through river network all of which do not necessarily relate to Slani potok and Mala Dubračina sub-catchments, two most severely affected sub-catchments by erosion processes. The approach used in second case scenario is the most often used, but both first and second case study approaches for deriving drainage density are continuously used in various case studies related to the application of the Erosion Potential method [23].

It can be seen from Figure 2 the difference in spatial variability and value ranges between the second and the third case scenario. Since, the first case represents homogenous drainage density for the entire catchment and today technological possibilities provide much more detailed and accurate maps, this case is disregarded from the future analysis shown in this paper. This map would in a need for an approximate and fast estimation of erosion sediment production, where most model parameters would be homogenous trough the catchment, be very useful and as such was applied many times on various catchment using Erosion Potential Method. Between the two other cases, the third case scenario provides the most spatially variant map and is the most complex one to derive. Besides mentioned, in case three the obtained drainage density map provides the most realistic spatial variance of this parameter, with lower drainage density values along the edges of the catchment and higher values concentrated along the river and tributary intersections where higher surface velocity, less infiltration rates and higher values for sediment yield transport are expected.

The question is how do these three different drainage density derivation approaches affect the results of Erosion Potential Method? The main model parameter dependent upon drainage density parameter is sediment delivery ratio ξ (Equation (6)). This parameter was calculated for all three case scenarios (Equation (8), Figure 3 and

Table 4. Sediment delivery ratio for the second case study.

Sub-Catchment	Sediment Delivery Ratio ξ
Sušik	0.0853
Kučina	0.1126
Leskovnik	0.1112
Ričina Tribaljska	0.1379
Malenica	0.1649
Pećica	0.2204
Kostelj	0.1903
Mala Dubračina	0.2886
Duboki	0.1909
Slani potok	0.2665
Bronac	0.2407
Cigančica	0.3291

) using different drainage maps (case 1–3):

$${\xi }_{Case1}=\frac{\sqrt{O*z}*\left(l_p+l_a\right)}{\left(l_p+10\right)*F}=0.2445,$$

(8)

The value ranges for the second and the third case scenario do not differ significantly but the spatial variation of the parameter is significantly different and it follows the variation pattern the same as drainage density. Since, the third case scenario provided the best spatial variability for drainage density parameter and its method was in previous research by Dobos and Daroussin [7] approved and defined as appropriate method for drainage density map derivation, the third case is chosen as the most appropriate input data for Erosion Potential Method application on Dubračina catchment.

4. Conclusions

The drainage density parameter was analysed and derived three times using different assumptions and allowing different spatial variability of the parameter. Until today, within the Erosion Potential Method drainage density parameter was calculated both as a unified value for the entire catchment or as one value for each sub-catchment, restricting its spatial variability and increasing its error. The third methodology used in this paper was proposed by Dabos and Daroussin [7] and the “actual” drainage density was calculated using the river map and not DEM derived river map as input data.

The Drainage density map, derived using the proposed methodology has provided a more realistic model input data with more detailed spatial variance of this parameter. Until today, there hasn’t been any research paper applying the Erosion Potential Method that uses this particular methodology for the derivation of drainage density and none uses drainage density map with spatial variability that is more than on sub-catchment level. For this reason, derived map for drainage density using this methodology is considered an enhancement to Erosion Potential Method accuracy and precision.