Abstract
Optimizing water distribution systems is an essential part of water resources allocation planning. It leads to challenging combinatorial optimization problems, for which meta-heuristics have been applied, notably genetic algorithms and ant colony optimization. The present paper introduces the application of the physarum algorithm, a recent biologically inspired algorithm, utilized hitherto for path finding problems in networks. Direct comparison is presented to ant colony optimization applied to a typical water supply system.
1. Introduction
The optimization of water distribution systems is a challenging complex problem and it has been treated so far by various methods, both conventional and meta-heuristic. The typical problem concerns sizing of the distribution system. A specific and common instance of the problem consists in the determination of the pipe diameters for the purpose of minimizing the total cost of materials. Due to the inherent difficulty of the problem, meta-heuristic methods are preferred in order to deal with the complexity and nonlinearities of both the objective function and the constraints. Genetic algorithms, harmony search, particle swarm optimization and ant colony optimization are among the methods employed and noted in the literature.
In this paper a recently developed algorithm inspired from the behavior of physarum polycephalum is applied. This algorithm was originally designed for the solution of network combinatorial optimization problems, such as the shortest path problem in an undirected graph. The biological basis of the algorithm is the observed ability of the single-cell organism physarum to detect shortest paths through a maze in order to reach food sources.
Regarding water distribution systems, no application of the physarum algorithm is noted in the literature. In the present paper, branched water distribution systems are optimized, in order to demonstrate the efficacy and efficiency of the proposed algorithm. A typical water supply system is optimized both by the physarum algorithm and by ant colony meta-heuristic. The latter entails certain similar concepts and a comparison is deemed to be appropriate. The comparison turns out to be in favor of the physarum algorithm. Application of the physarum algorithm to pressurized irrigation network has been presented in [1].
2. Problem Description
A branched water supply system is characterized by one or more reservoirs and a pipe system that conveys water to selected discharge locations. The pipe system extends in space without loops. Given the reservoir hydraulic head and the architecture of the water supply network, the required discharges the pressures at the junctions can be determined. It remains to choose the diameters so as to achieve an economic design under the proper restrictions.
Let
be the hydraulic head at the node j, where vj is the velocity and zj the elevation at the same node. If Hi denotes the corresponding quantity for node i which is connected to and upstream of node j, then
where hfij denotes the linear losses from i to j.
Finally, from Equation (1), the pressure at j can be approximated as
The linear losses along a pipe of length l, diameter d and with velocity v are given by
where f is a friction factor, given by a formula of Chen [2]:
where
where k is a roughness coefficient and Re the Reynolds number given by
where ν is the kinematic viscosity.
It is clear from Equations (1)–(5) that, given the pipe diameters of a branched water distribution system, successive heads and pressures can be determined at the ends of the conduits.
The optimization problem is then formulated as follows:
Select the pipe diameters for the conduits such that the total cost is minimized. The total cost equals
where li is the length of pipe i, ci the cost per unit length of the chosen pipe i. The cost ci is taken to be proportional to the unit weight of the chosen pipe.
The constraints imposed upon the possible solutions are:
Equation (6) implies a constraint on the diameter ranges, given that
Thus
The choice of the diameters is further restricted by the availability of specific commercial types of pipes.
As an example, a typical branched water supply system (BWSS) is shown in Figure 1, taken from the textbook of [3].

Figure 1.
Water supply system schematic.
It will be assumed that the required discharges for each conduit have been determined on the basis of the local water needs. These discharges, qi are shown in Table 1. The outgoing discharges can be read directly from Figure 1.

Table 1.
Discharges carried by the conduits.

Table 2.
Available commercial diameters.
By combining the diameter constraint (Equations (7) and (8)) with the data of the third column of Table 2 the allowable diameters for each pipe of the problem can be determined. As a result, the possible diameters for each one of the pipes are as shown in Table 3. The diameters are designated by the numbers of the first column of Table 2.

Table 3.
Possible diameters.
3. The Physarum Algorithm
The physarum polycephalum algorithm has been applied to the problem of finding shortest paths in undirected and directed networks [4]. The underlying biological prototype is based on the behavior of the physarum polycephalum, which is a amoeboid organism that develops a network of tubular elements in order to approach food sources. The shape of the network is suitably adjusted so as to extend in an optimal manner to the location(s) of the food sources. During this process the thickness of the tubes is suitably adjusted in order to accommodate the occurring variable flow through the nodes of the network. The tubes tend to grow in diameter as the flux grows, while they tend to disappear as the flux attenuates. Modeling of this behavior has given rise to the solution of the maze problem and to algorithms for finding shortest paths and Steiner trees in networks. The maze solving mechanism has been described in [5]. The derived mathematical model and algorithm for the shortest path and for the shortest tree in a given network is described in [6].
The mathematical problem for which the physarum algorithm was first employed, is formulated as follows [7]:
Let G = (V, E) be a graph, where V is the set of its vertices and E the set of its edges. One of the vertices is designated as the starting node and a number of other vertices are defined as terminal nodes. A cost is associated with each one of the edges. A connected subgraph of G, spanning all the terminal vertices is called a spanning tree. A minimal spanning tree is defined as the one of minimal cost, where the cost of the tree is the sum of the costs of its edges. If there is only one terminal node, then the problem is reduced to the shortest path problem from the start to the end node.
The physarum algorithm is based on a physical simulation model based on the hydraulics of Poiseuille flow. More specifically, if i and j are vertices of the graph, then the flux Qij through the tube connecting them is related to the pressures pi and pj at the ends of the tube as follows:
where Lij is the length and Dij the conductivity of the tube ij. The variable uij is defined as:
On the other hand, continuity imposes the following requirement on the set of the tubes converging on vertex j:
In the above Equation (1) stands for the start node and n for the end node, assuming that there is only one such vertex. The sign convention in the above summation assigns a positive sign to the incoming fluxes and a negative sign to the outgoing ones.
By combining the above Equations,
In case there are more than one terminal node, the above Equation is modified as follows:
where n1, n2, …nN are the terminal vertices.
The conductivities Dij follow an adaptation course according to the following differential Equation [4]:
where r is an attenuation coefficient and f(|Q|)=|Q|.
The above Equation is discretized as
The physarum algorithm is based on the above Equations and runs as follows:
Do
- Initialize
- Set
- Compute pi’s from Equation (11) or (12)
- Compute Qij’s from Equation (9)
- Compute ’s from Equation (13)
Until
Theoretical considerations related to convergence proofs can be found in [8]. Shortest path determination is noted through the conductivities Dij that finally dominate. These mark the sequence of the successive tubes that constitute the sought for shortest path. Specific examples are given, among others, in [6]. Applications in the formation of transport networks are noted in [9]. The next section shows how the physarum algorithm can be applied to the problem of minimizing the cost of a water distribution system, as formulated in the Section 2.
4. Application of the Physarum Algorithm to the Design of a Water Distribution System
The basic idea is to construct a virtual graph originating from the actual graph of the BWSS and to find paths of minimal length in the virtual graph. Every edge of the virtual graph is assigned a length equal to the cost of the actual pipe that it represents. Since there is generally more than one choice for each actual pipe, the virtual graph will consist of the same junctions as the actual one and of multiple alternative connections between these junctions, as in Figure 2, which depicts the virtual graph corresponding to the actual graph of Figure 1. The numbers on the graph of Figure 2 correspond to the numbers of the individual conduits of Figure 1. The alternative paths between connected nodes are clearly shown. They represent the possible diameters of Table 3.
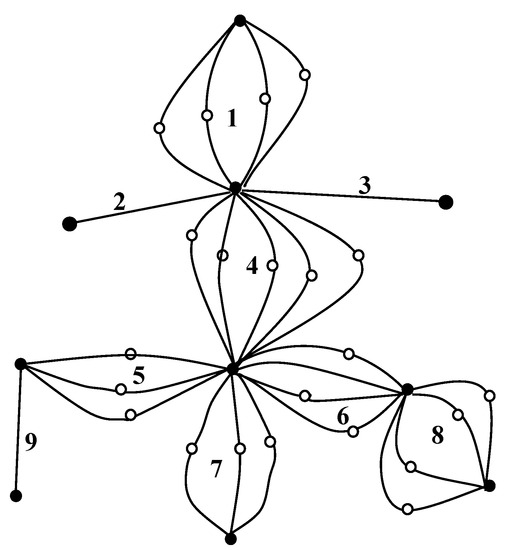
Figure 2.
Virtual graph of the BWSS.
The physarum algorithm will be applied to the virtual graph of Figure 2. Equation (12) will be employed in the implementation of the algorithm, since the graph includes more than one terminal node. Also, the application of Equations (10), (12) and (13) requires unique connections between the nodes. For that reason, additional fictitious nodes have been added, marked by white circles, as shown in Figure 2.
By running the physarum algorithm on the virtual graph of Figure 2, the optimal tree is determined and the sum of the lengths of its edges is obtained as a candidate for the optimal solution of the BWSS problem.
Regarding constraints, the one of the velocity range (Equations (7) and (8)) is automatically observed due to the existence of the alternative connections in the virtual graph. However, adjustments are still necessary in order to satisfy the pressures constraint of Inequality 6. Obviously, the pressures pi, i = 1, 2, …, n, where n is the number of the conduits, are functions of the set of selected diameters di, i = 1, 2, …, n, since they are determined from the linear losses and the successive heads by means of Equations (1)–(5). Therefore,
where d is the vector of the diameters d = (d1, d2, …, dn).
pi = pi(d),
A constraint function is defined as
gi(d) = 15 − pi(d), i = 1,2,..,n
Then the algorithm for the determination of the optimal diameters will runs as follows:
- Apply the physarum algorithm to the virtual graph.
- Obtain a preliminary diameters vector d
- Compute pi(d) and gi(d) for i = 1,2,..n through the hydraulic analysis (Equations (1)–(5))
- If gj(d) > 0, for some j, then the unit cost cj is adjusted as in step 5.
Otherwise exit the loop.
- 5.
- 6.
- The same adjustment is imposed on all pipes upstream of pipe j
- 7.
- The virtual lengths of the respective virtual edges are renewed
- 8.
- The physarum algorithm is applied and a new diameter vector d is obtained
- 9.
- Go to step 3
The coefficient λ of step 5 above, is a problem dependent adjustment or penalty parameter.
5. Results and Discussion
For purposes of comparison, the same BWSS was optimized by the ACO meta-heuristic. The latter involves the concept of alternative paths as the physarum algorithm. References to such ACO applications are [10,11,12]. In the ACO procedure, the pheromone paths that lead to pressures violating the constraint of Inequality (6) are penalized by an increased pheromone deposition. The same constraint is handled by the physarum algorithm by the coefficient λ of the previous section. The physarum algorithm gave an optimal value of 67,670 after three iterations of the algorithm of Section 4, while ACO with 10 ants and 5 iterations gave 78,930 for the objective function of the sample problem of this paper. More numerical experimentation is needed with larger and more complex water distribution systems, in order to establish the performance of the present competitive and promising algorithm.
Author Contributions
E.K. contributed the idea and presented an application of the physarum algorithm to irrigation systems. E.S. carried out the computational work. C.E. collaborated in technical water supply matters and in the writing of the text.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Koritsas, E. Optimization of Water Distribution Systems by Ant Colony Optimization and by the Physarum Algorithm. Postgraduate Thesis, Aristotle University of Thessaloniki, Thessaloniki, Greece, 2017. [Google Scholar]
- Zhang, X.; Wang, Q.; Adamatzky, A.; Chan, F.T.S.; Mahadevan, S.; Deng, Y. An Improved Physarum polycephalum Algorithm for the Shortest Path Problem. Sci. World J. 2014, 2014, 487069. [Google Scholar] [CrossRef]
- Nagaki, T.; Yamada, H.; Toth, A. Maze solving by an amoeboid organism. Nature 2000, 407, 470. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Chan, F.T.S.; Yang, H.; Deng, Y. An adaptive amoeba algorithm for shortest path tree computation in dynamic graphs. Inf. Sci. 2017, 405, 123–140. [Google Scholar] [CrossRef][Green Version]
- Liu, L.; Song, Y.; Zhang, H.; Ma, H.; Vasilakos, A. Physarum Optimization: A Biology-inspired Algorithm for the Steiner Tree Problem in Networks. IEEE Trans. Comput. 2015, 64. [Google Scholar] [CrossRef]
- Bonifaci, V. Physarum can compute shortest paths: A short proof. Inf. Process. Lett. 2013, 113, 4–7. [Google Scholar] [CrossRef]
- Tero, A.; Takagi, S.; Saigusa, T.; Ito, K.; Bebber, D.P.; Fricker, M.D.; Yumiki, K.; Kobayashi, R.; Nakagaki, T. Rules for Biologically Inspired Adaptive Network Design. Science 2010, 327, 439–442. [Google Scholar] [CrossRef] [PubMed]
- Pantokratoras, A. Urban Water Supply Systems (in Greek); Epikentro Publishers: Thessaloniki, Greece, 2015. [Google Scholar]
- Chen, N.H. An explicit equation for friction factor in pipe. Ind. Eng. Chem. Fundam. 1979, 18, 296–297. [Google Scholar] [CrossRef]
- Tu, Q.; Li, H.; Wang, X.K.; Chen, C. Ant Colony Optimization for the Design of Small-Scale Irrigation Systems. Water Resour. Manag. 2015, 29, 2323–2339. [Google Scholar] [CrossRef]
- Zecchina, A.C.; Simpson, A.R.; Maiera, H.R.; Leonarda, M.; Roberts, A.J.; Berrisford, M.J. Application of two ant colony optimisation algorithms to water distribution system optimisation. Math. Comput. Model. 2006, 44, 451–468. [Google Scholar] [CrossRef]
- Kanakis, P.; Papamichail, D.; Georgiou, P. Ant colony algorithm for optimization of pressurized irrigation networks. Hydrotechnika 2016, 24, 85–98. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).