Abstract
The failure of joints plays an important role in the overall performance of mains. One of the prevalent failure modes at polyvinyl chloride (PVC) joints is the rupture of pipe or joint, which may occur due to high angular deflection of the pipe with respect to the joint, caused by differential soil settlement. The present paper reports the construction and use of a finite element model to determine the maximum angular deflection of a variety of PVC joints in different loading situations. The resulting acceptable deflections vary between 3° and 8° per side, which differs significantly from installation guidelines. The results will support drinking water companies in substantiating the prioritization of maintenance and inspection.
1. Introduction
Being able to determine and predict the condition of the drinking water distribution network is crucial for optimal asset management. Failure of mains results from an interplay of, on the one hand, external and internal loads and, on the other hand, intrinsic material properties that determine the degradation- and failure mechanisms. In the Netherlands, PVC is the most applied pipe material. Its first application in Dutch mains was around 1950; currently more than half of the Dutch network (60,000 km) consists of PVC. Originally designed with a lifespan of 50 years in mind, around 10,000 km of the oldest pipes are now in operation past their life expectancy. This makes understanding the degradation and failure of PVC especially important.
As presented in a companion paper at this conference [1], KWR uses the computational tool Comsima (COMputation of Stresses In MAins) to simulate the condition of the distribution network. Comsima combines physical models of loading and degradation with Monte Carlo methods to translate a description of a main and its environment to an approximation of its physical state, including uncertainties. The physical state is compared to norms and design guidelines to obtain the main’s condition. One advantage of this approach is its modularity. Building blocks such as a new design standard, an additional loading mechanism or a more accurate description of a system parameter can be added later to expand the model and increase the accuracy of its results or its applicability.
This paper concerns recent work to gain more detailed knowledge of the loading that PVC push-fit joints can withstand. The failure of joints plays an important role in the overall performance of mains: the Dutch national failure database Ustore [2] shows that one third of all failures of PVC mains occur at the joints. One of the prevalent failure modes is pipe or joint rupture, which may occur due to high angular deflection of the pipe with respect to the joint, caused by differential soil settlement. Despite this significant contribution to mains failures, little is known about the maximum angular deflection that joints can withstand. Drinking water companies currently work with a maximum acceptable angular deflection of 3° per joint side, as recommended by the producers of PVC piping systems (e.g., [3]). However, this recommended value is based on the leak tightness test prescribed by international standards for PVC mains [4,5], and not on tests for mechanical strength. Moreover, the recommended value is a constant that is independent of joint design or loading situation, whereas it would be expected that different joints in different situations can withstand different angular deflections.
The goal of the present study was to use the finite element method (FEM) to construct a three dimensional model of the stresses in rigid PVC pipes and push-fit joints due to angular deflection. FEM is inherently well suited to quickly evaluate the combined effects of different loads on the complex geometries of the joints [6,7]. Because of this, the model could subsequently be used to study the maximum acceptable angular deflection in a wide variety of different situations defined by diameter, joint design and pipe insertion, whereas experiments would be too expensive and time consuming to effectively probe such dependencies. The results will serve as a new building block in Comsima that allows for a better evaluation of the effects of differential soil settlement on the performance of mains. The expanded model will therefore allow drinking water companies to translate their knowledge of the PVC network to a better a priori estimation of its condition. This will help them with substantiating the prioritization of maintenance and inspection.
2. Methods
2.1. Overview of the Modeled Systems
In total, 54 different system combinations of a PVC pipe inserted into a PVC push-fit joint were tested. Joints for 3 different pipe diameters (110, 200 and 315 mm) were tested for the designs of 2 different PVC producers. Of a third producer, one design was tested for diameters 110 and 200 mm, and a second design was tested for the diameter of 200 mm.
For each joint, a pipe of corresponding diameter with a pressure class of 0.75 MPa was chosen. The wall thickness of the pipes for each diameter are listed in Table 1. Systems were tested with the pipe fully inserted into the joint, 1 mm away from the bumper-ring in the center of the joint, and with incomplete insertion, halfway between the bumper ring and the rubber seal. The insertions as measured from the joint opening are listed in Table 1.

Table 1.
Some relevant dimensions of the different simulated systems.
Finally, each system was subjected to 3 different loading levels, corresponding to 3 combinations of water pressure (respectively 0.3, 0.4 or 0.5 MPa, corresponding to typical pressure levels in the Dutch drinking water distribution network) and soil loading (respectively 0.01, 0.015 or 0.02 MPa, corresponding to the typical soil types, water pressures and installation depths in the Netherlands).
2.2. Model Asumptions and Failure Criterion
The most important assumption of the model is that, when subjected to a too high angular deflection, joint and pipe will fail because the resulting stresses lead to cracking of the material. Cracks in PVC mains typically initiate around stress concentrators in the material on the μm–mm scale while the global stresses in the material are still well below the yield stress (~56 MPa [8,9]). Therefore, the FEM model will be used to calculated the global stress distribution in the system. As a result, the PVC can be described as a linear viscoelastic material, which is appropriate for PVC at stresses below the yield stress [10]. To determine ‘failure’, stresses in the system are compared to a stress threshold that corresponds to failure through crack growth within a given time.
The speed at which cracks grow and thus the time required for cracks to lead to failure depend on stress, temperature and the quality of the material. While the influence of material quality on crack growth depends on many factors that are difficult to quantify in practice, regulations for the quality of PVC mains relate the time to failure to the global stresses in pipes. These require a time to failure of at least 1 h at materials stresses of 42 MPa, 100 h at 35 MPa, and an extrapolated time to failure of a least 25 years at material stresses of 25 MPa [11]. In this study, an angular deflection was defined to be unacceptable when it causes stresses above 21 MPa, which may lead to failure before 100 years, based on further extrapolation of the regulations.
2.3. FEM Model
A FEM model of each system was constructed and run in COMSOL Multiphysics (COMSOL inc., Burlington, VT, USA) and its structural mechanics module.
The geometry of each system was constructed from blueprints that provided by the producers. This was done by copying one half of the schematized cross-section of the pipe and joint walls to a work plane. The work plane was then rotated around the longitudinal axis of the pipe for 180° (see Figure 1a). The geometry was meshed by dividing a wall cross-section into free quads and then applying the sweep operation to the meshed cross-section to mesh the geometry in the radial direction. The mesh size was reduced until solutions were mesh-invariant.

Figure 1.
(a) The simulated geometry was constructed by rotating the blueprint provided by the PVC producer 180° around the pipe axis. (b) Contact between pipe and coupling is modeled with a contact pair boundary condition. (c) The coupling is kept in place with a fixed constraint boundary condition. (d) Soil load is modeled as a force per area, in combination with a corresponding normal force on the opposite surfaces (not shown). (e) The half system is completed with a symmetry boundary condition. (f) The coupling’s rubber seal is modeled as a spring foundation boundary condition. (g) The water pressure is modeled as a force per area inside the pipe, and inside the part of the coupling behind the rubber seal. (h) An angular deflection, defined as ϕ = tan−1(Y/L) is imposed on the system by applying a prescribed movement Y to a point on the extremity of the pipe, a distance L away from the coupling’s opening.
The PVC of the joint and pipe was modeled as a linear elastic material (also see Section 2.2). Values for the relevant material properties were provided by the PVC producers: the elastic modulus E = 3000 MPa; the semi-stable elastic modulus after long term viscoelastic relaxation Elong = 1500 MPa; and the Poisson’s ratio v = 0.4. Because simulations concerned the long-term steady state only, no information on the timescales of stress relaxation were required.
Contact between pipe and joint was modeled by assigning a contact pair to the surfaces highlighted in Figure 1b. The joint is kept in place with a fixed constraint boundary condition, applied to the surface highlighted in Figure 1c. Symmetry was assumed on the bare cross-sections of the pipe and joint wall to complete the geometry, as shown in Figure 1e. The SBR sealing ring was modeled as a spring boundary condition with a Shore A hardness of 55 (E = 3 MPa), as shown in Figure 1f. A vertical force per area boundary condition was used to represent the soil load as shown in Figure 1d. Note that the soil does not work directly on the part of the pipe that is inserted in the joint. A second vertical force per area (not shown) is applied to the opposite surfaces to model the contact with the soil supporting the pipe. A third pressure boundary condition was used to model the internal water pressure, as shown in Figure 1g. Note that the water pressure works on both the inside and the outside of the pipe behind the sealing ring and only works on the part of the joint behind the sealing ring.
A prescribed displacement boundary condition with magnitude Y in vertical direction was applied to a central point on the extremity of the pipe opposite of the joint (blue dot, Figure 1h). This way, an angular deflection was induced in the system (Figure 1h). The magnitude of the resulting deflection ϕ was defined as ϕ = tan−1(Y/L), with L the length of the pipe outside of the joint.
The maximum acceptable angular deflection of a given system was determined by running a series of stationary simulations for gradually increasing angular deflection. The solution to each simulation served as the initial conditions for the next. To this end, Y was first increased from 0 mm tot 10 mm in steps of 1 mm and was subsequently increased with steps of 5 mm until stresses above the failure criterion occurred in a solution.
3. Results
Figure 2 shows the distribution of the von Mises stress in a typical system of joint and pipe for increasing angular deflection. When no significant angular deflection is present (left), the highest stresses occur in the pipe outside the coupling, due to the soil load and the water pressure. With increasing angular deflection, increasing stresses occur around the rubber seal and around those parts of pipe and coupling that are in contact. Stresses in the pipe are typically higher than those in the push-fit joint, as would be expected since the pipe wall is typically thinner than that of the joint.
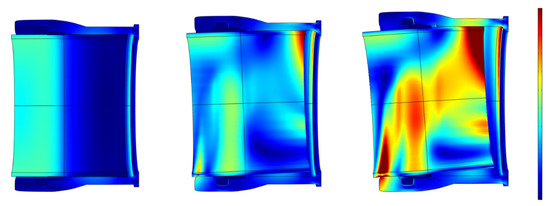
Figure 2.
The distribution of the von Mises stress for increasing angular deflection. The color scale represents stresses between 0 MPa (blue) and the failure criterion of 21 MPa (red).
Figure 3 shows typical curves of the maximum von Mises stress that occurs in a system as a function of the applied angular deflection. Roughly two regimes are visible. For the first few degrees, the stress is largely independent of the angular deflection. This regime marks the free rotation of the pipe within the joint’s chamber. A second regime of stress increasing linearly with deflection occurs once pipe and joint are in contact. Ultimately, this will lead to stresses higher than the failure criterion of 21 MPa. The deflection at which this occurs is defined as the maximum acceptable angular deflection (vertical dashed line).
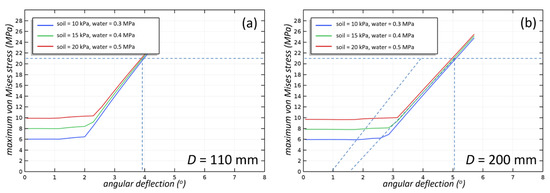
Figure 3.
Typical results. (a) The von Mises stress as a function of angular deflection in a simulated system of a pipe and a coupling of a given design. Differently colored curves represent different static loading conditions during simulations. The dashed horizontal line corresponds to the failure criterion of 21 MPa and the vertical line corresponds to the matching maximum acceptable angular deflection. (b) Analogous results of a system with the same coupling design, but scaled to a larger diameter. The diagonal lines guide a comparison between graphs.
During the regime of free movement, the maximum von Mises stresses occur in the pipe outside of the rubber seal (see Figure 2 on the left). These stresses are caused by the water pressure and the soil load, which is why the maximum stress in this regime is sensitive to the different loading situations, as represented by the differently colored curves. During the regime of contact, however, the maximum stresses are those that occur in the pipe due to deformation at the point of contact with the back of the joint. These stresses are largely independent of the loading situation, since this part of the pipe is surrounded by water and the soil load at this point is mostly carried by the joint. As a result, the maximum acceptable angular deflection of the push-fit joint is largely independent of the loading situation.
The results in Figure 3a,b correspond to push-fit joints from the same producer. The joints have the same general design, but are dimensioned to connect pipes of different diameters. The joint with the larger diameter has the larger maximum acceptable angular deflection. The results show two causes for this. Firstly, the initial regime of free rotation is longer for the larger diameter system, up to ~3° instead of ~2° for the smaller diameter system. Secondly, the stress in the larger diameter system increases with a smaller slope during the regime of contact, indicating that the deformation and the resulting stress are distributed more evenly in the larger system.
The resulting maximum acceptable angular deflections for all simulated system combinations of push-fit joint design, loading situation and pipe insertion are collected in Table 2. The data show that the maximum acceptable angular deflection increases with diameter and insertion. Differences up to 3° occur in equivalent designs of different producers in otherwise identical conditions. Overall, the maximum acceptable angular deflection varies between 2.9 and 8.4°.

Table 2.
Overview of the maximum acceptable angular deflections found for all simulated systems and loading conditions.
4. Discussion and Conclusions
4.1. Validation
The FEM model used in this study was based on several assumptions. Before the maximum acceptable angular deflections returned by the model can be relied on by the asset manager of a drinking water company, these assumptions should be validated. While the goal of the model is ultimately to remove the need for expensive experiments to evaluate angular deflection, several experiments will be required for validation. Efforts for experimental validation are currently underway.
The first thing to be verified is the assumption that joint failure due to angular deflection is caused by increasing stresses leading to cracking. To this end, the occurrence of other failure modes at deflections up to the maximum acceptable angular deflections determined by the model needs to be excluded. Especially the leak tightness of the rubber seal at higher deflections needs to be confirmed. If problems with the rubber seal turn out to play a role, the seal’s approximation as a spring foundation boundary condition needs to be replaced with a contact model geometry and an accompanying failure criterion.
Subsequently, it should be verified whether the timescale of failure at a given maximum acceptable angular deflection matches the timescale of 100 years assumed in the failure criterion. Several model assumptions may prove conservative in this respect. Modeling the PVC as a linear viscoelastic material may overestimate the stresses that actually occur, thereby underestimating the time to failure. Also, the failure criterion is based on the relation between stress and crack growth, but neglects the time required for crack initiation, which again leads to an underestimation of the time to failure. Validation of this aspect will require temperature accelerated failure experiments and corresponding adjustments of the FEM model for comparison. Should actual time scales of failure deviate for those assumed by the model, the model and failure criterion could be expanded with more sophisticated approximations for material deformation and crack growth, respectively.
4.2. Concluding Remarks
The FEM simulations indicate values between 3 and 8° for the maximum acceptable angular deflections of the push-fit joints tested in this study. That is a substantial variation as compared to the standard 3° based on leak tightness that is reported in the installation guidelines of the producers. Differences in angular deflection result from differences in design, diameter or insertion depth, whereas differences in the loading situation have a negligible effect. These results emphasize the need of a drinking water company’s asset manager for a situation specific method to judge angular deflections during the condition assessment of mains. Once validated, the FEM model can be a powerful tool for scanning the maximum acceptable angular deflection of many different push-fit joint geometries in a fast and cost effective way, which may then serve as input data for overarching condition assessment models such as Comsima.
Author Contributions
K.A.v.L. and B.W. conceived and designed the model. K.A.v.L. performed the experiments, analyzed the data and wrote the paper.
Funding
This study was funded by the drinking water companies PWN and Vitens within the context of the BTO collective research program of the Dutch drinking water sector, project number 401821-001.
Acknowledgments
The authors are grateful to PVC producers Dyka, Pipelife and Wavin for providing the blueprints of the studied joints.
Conflicts of Interest
The authors declare no conflict of interest. The funding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results. A user committee of experts working for the sponsors was consulted during the project to ensure applicability of the results to the drinking water practice.
References
- Wols, B.; Moerman, A.; Horst, P.; van Laarhoven, K. Prediction of pipe failure in drinking water distribution networks by Comsima. In Proceedings of the 3rd EWaS international conference on “Insights on the water-energy-food nexus”, Lefkada Island, Greece, 27–30 June 2018. [Google Scholar]
- Vreeburg, J.H.G.; Vloerbergh, I.N.; van Thienen, P.; de Bont, R. Shared failure data for strategic asset management. Water Sci. Technol. 2013, 13, 1154–1160. [Google Scholar] [CrossRef]
- Pipelife, P.V.C. Drukleidingen. Available online: http://www.pipelife.nl/nl/media/pdfs/Brochure_PVCdrukleidingen_A6.pdf (accessed on 29 January 2018).
- Arsenio, A.M. Lifetime Prediction of PVC Push-Fit Joints. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2013. [Google Scholar]
- ISO. 13783:1997 Plastics Piping Systems—Unplasticized PVC End-Load-Bearing Double-Socket Joints—Test Method for Leak Tightness and Strength while Subjected to Bending and Internal Pressure; ISO 13783:1997; International Organization for Standardization: Geneva, Switzerland, 1997. [Google Scholar]
- Balkaya, M.; Moore, I.D. Analysis of a gasketed PVC pipe-joint. In TRB 2009 Annual Meeting; CD-ROM; Transportation Research Board of the National Academies: Washinton, DC, USA, 2009. [Google Scholar]
- Zhao, Z. Effect of Temperature on the Relaxation of Polyvinyl Chloride Flanges. Master’s Thesis, University of Quebec, Quebec City, Montreal, Canada, 2017. [Google Scholar]
- Mark, J.E. Polymer Data Handbook; Oxford University Press: Oxford, UK, 1999; pp. 928–934. ISBN 9780195181012. [Google Scholar]
- Davis, P.; Burn, S.; Moglia, M.; Gould, S. A physical probabilistic model to predict failure rates in buried PVC pipelines. Reliab. Eng. Syst. Saf. 2007, 92, 1258–1266. [Google Scholar] [CrossRef]
- Povolo, F.; Schwartz, G.; Hermida, E.B. Stress relaxation of PVC below the yield point. J. Polym. Sci. Part B Polym. Phys. 1996, 34, 1257–1267. [Google Scholar] [CrossRef]
- BSI. Plastics Piping Systems for Water Supply and for Buried and above-Ground Drainage and Sewerage under Pressure—Unplasticized Poly (Vinyl Chloride) (PVCU); NEN-EN-ISO 1452-1:2009; BSI: Wolverhampton, UK, 2009. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).