Searches for Magnetic Monopoles: A Review ^†

Abstract

This report briefly reviews selected searches for magnetic monopoles. The theoretical motivation behind their existence is highlighted. The focus is on the results of the searches and the bounds set in cosmic and collider detectors, especially in the current experiments operating at the Large Hadron Collider: ATLAS and MoEDAL.

1. Theoretical Motivation

The main theoretical motivations behind the hypothetical existence of magnetic monopoles are the symmetrisation of the Maxwell’s equations and the explanation of the charge quantisation. Dirac [1] proved that magnetic monopoles could explain the discrete nature of the electric charge, leading to the Dirac Quantisation Condition (DQC),

$$\alpha g=\frac{N}{2}e,N=1,2,...,$$

(1)

where $\alpha =\frac{e^2}{4\pi {\epsilon }_0}=\frac{1}{137}$ is the fine structure constant, e is the electron charge, ${\epsilon }_0$ is the vacuum permittivity, and g is the monopole magnetic charge in units $\hslash =c=1$. This quantisation condition should be modified by a factor of three if quarks existed free in Nature. The monopole mass and spin are not determined and are free parameters of the theory. This attractive proposal has revived a number of experimental investigations since then, with some of them briefly highlighted in this conference report.

The existence of magnetic monopoles, characterised by their isolated magnetic charges similar to electrically-charged particles, has been assumed over the years in many theoretical proposals [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]. On the other hand, dyons, carrying both magnetic and electric charge, offer a more involved solution leading to the DQC, which depends on the underlying theoretical scenario. Some of the theoretical scenarios predicting the existence of magnetic monopoles are listed below; a more comprehensive review is given in Ref. [19].

• Dirac monopole In Dirac’s formulation [1,20], magnetic monopoles are assumed to be point-like particles with quantum mechanical conditions leading to Equation (1), establishing the discrete nature of their magnetic charge. In spite of monopoles formally symmetrising the Maxwell’s equations, a numerical asymmetry emerges in the DQC: the minimum value of the magnetic charge is much larger than the smallest electric charge. Indeed, a magnetic monopole with a single Dirac charge $g_{\mathrm{D}}$ has an equivalent electric charge of $137\beta e/2$. Hence, for a relativistic monopole, the energy loss is around $68.5^2\simeq 4700$ times that of a minimum-ionising particle.
• Monopoles in GUTs Since the Grand Unified Theory (GUT) of strong and electroweak interactions predicted the existence of magnetic monopoles [21,22], searches for magnetic monopoles, in particular of cosmic origin, have been intensified substantially. In 1974, ’t Hooft [2] and Polyakov [3] showed that a unified gauge theory where electromagnetism is embedded in a semi-simple gauge group, such as $SU\left(2\right)$, would necessitate the existence of the monopole as a soliton with spontaneous symmetry breaking. GUT monopoles are too massive to be produced at any future accelerator, having a mass of $\mathcal{O}\left({10}^{15}\mathrm{GeV}\right)$ [23].
• Electroweak monopole Cho and Maison postulated the electroweak monopole [17,18,24,25] as a generalisation of the Dirac monopole, representing a hybrid of Dirac and ’t Hooft–Polyakov monopoles that carries magnetic charge twice that of the Dirac monopole. The latter is due to the quotient group $SU\left(2\right)\otimes U_Y\left(1\right)/U_{\mathrm{em}}\left(1\right)$, where $U_{\mathrm{em}}\left(1\right)$, which is the (unbroken) group of electromagnetism instead of, e.g., the $SU\left(2\right)$ group in the Georgi–Glashow model. Recent estimates of the electroweak monopole mass [26] indicate that it is possibly accessible at the LHC.
• Global monopoles They have been proposed [27] as space-time (cosmological) defects allowing for the spontaneous breaking of internal global $SO\left(3\right)$ symmetries in non-gauged Georgi–Glashow models. These monopoles carry no magnetic charge, yet gravitational effects away from their centre are significant, leading to a deficit angle in the (non-Minkowski) space-time. Such an effect may modify the forward scattering amplitude of Standard Model (SM) background particles, creating ring-like angular regions with very large scattering amplitude [28,29]. Such peculiar scattering patterns of ordinary SM particles may indicate indirectly the presence of a neutral global monopole in collider detectors, where they may be pair-produced [27,30]. Moreover, a variant of the global monopole model, including axion fields and a real electromagnetic field, coupling only gravitationally to the scalar $SO\left(3\right)$ symmetry breaking sector, has been proposed [31,32,33], resulting in axions capable of inducing electromagnetic monopole solutions with a real magnetic charge.
• Monopolium The lack of experimental confirmation of monopoles in Dirac’s proposal [1,20,34] may be attributed to monopoles not being seen freely because they form a bound state called monopolium [35,36,37,38], confined by strong magnetic forces. Monopolium is a neutral state, hence it is difficult to detect directly at a collider detector; however, its decay into photons would give a rather clear signal in the ATLAS, CMS and CMS-TOTEM Precision Proton Spectrometer (CT-PPS) detectors [39,40,41,42,43].

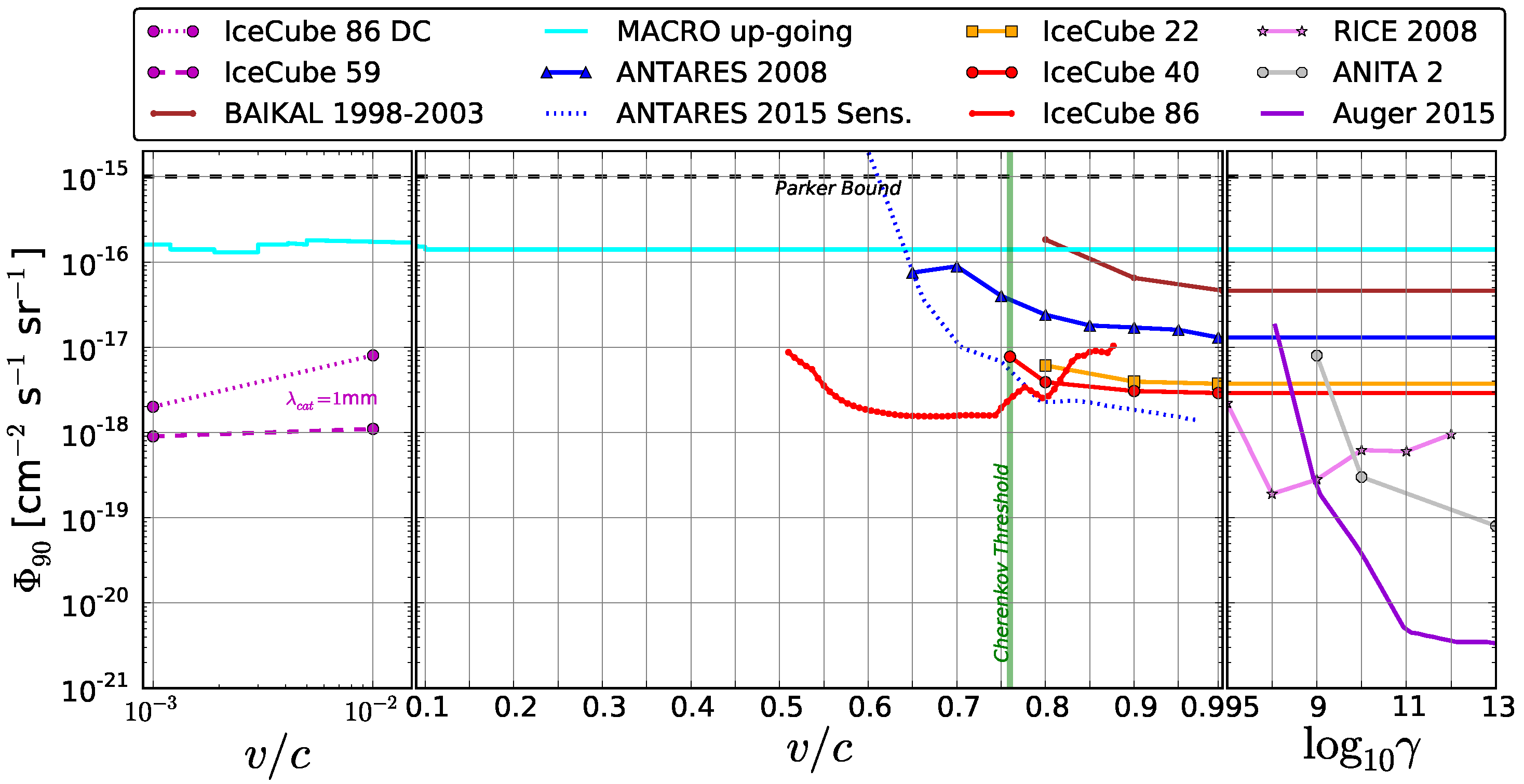
2. Searches for Cosmic Monopoles

Magnetic monopoles of cosmic origin are hypothesised to have been formed shortly after the Big Bang as topological defects arising when the Universe expanded and cooled. The existing galactic magnetic field $B\simeq 3\mathsf{\mu }\mathrm{G}$ would accelerate such monopoles, thus draining energy from the magnetic field, so its dissipation should not exceed its regeneration, should the galactic field be sustained. This requirement implies that an upper flux limit should be respected, the so-called Parker bound [44]

$$\Phi \lesssim {10}^{-15}{\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}{\mathrm{sr}}^{-1}.$$

(2)

Blas Cabrera and collaborators at Stanford University prepared an experiment with a four-turn, 5-cm-diameter loop, vertically oriented, connected to the superconducting input coil of a superconducting quantum interference device (SQUID) [45]. They observed a single candidate event during the 151 days of running of this experiment on 14 February 1982. If this candidate event is considered to be spurious, an upper limit of $6.1\times {10}^{-10}{\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}{\mathrm{sr}}^{-1}$ is derived, which is much larger than the Parker bound. Despite further improvements of the experimental setup to suppress possible background sources, this observation was not replicated. The best bound given by an induction detector on cosmic monopoles was obtained later by the same group: a 90% confidence limit (CL) on the monopole flux of $7.2\times {10}^{-10}{\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}{\mathrm{sr}}^{-1}$ [46].

Other direct cosmic searches have been performed on underground, surface and balloon-borne experiments targeting GUT monopoles in a mass range of $100÷{10}^4\mathrm{TeV}$ with a velocity spanning $\beta \sim {10}^{-4}÷1$. Up to now, there is no experimental evidence for cosmic magnetic monopoles—only bounds on their flux as a function of mass and velocity, summarised in Figure 7 of Ref. [47].

MACRO [48] was a large underground detector situated in the Gran Sasso laboratory. It has provided the best limits so far for GUT monopoles with a sensitivity that largely covers the velocity range, mostly thanks to the redundancy and complementarity of the various detector components it was comprising: liquid scintillation counters; limited streamer tubes; and nuclear track detectors (NTDs). However, due to its underground location, it was not sensitive to lower-energy monopoles, which are blocked by the Earth. MACRO set an upper limit on the monopole flux well below the Parker bound in almost all the $\beta$ range for GUT monopoles [49]. Limits were also set by an experiment at the Ohya stone quarries in Japan [50], featuring an array of CR-39 NTDs, while another experiment at Baksan [51] in Russia used liquid scintillation counters. Soudan 2 [52], in the United States, was a large, fine-grained tracking calorimeter composed of long drift tubes, and another tracking calorimeter, Kolar Gold Fields (KGF) [53], was deployed in India.

The SLIM detector, on the other hand, installed at high altitude in Bolivia at an altitute of $5400\mathrm{m}$, probed a region for intermediate-mass monopoles (${10}^5\lesssim M\lesssim {10}^{12}\mathrm{GeV}$), well below the GUT scale, which do not have enough energy to penetrate the entire atmosphere. The SLIM NTDs array covered an area $>400{\mathrm{m}}^2$ that, after four years of exposure, showed no signal of magnetic monopoles and set limits on cosmic monopole flux [54].

Relativistic monopoles can be sought by the emittance of Cherenkov radiation, when traveling through a homogeneous and transparent medium such as water or ice, which can be detected by arrays or strings of photomultiplier tubes. Neutrino telescopes such as Baikal [55], AMANDA [56], ANTARES [57,58] and IceCube [59,60] are sensitive to visible Cherenkov light emitted by a monopole with $\beta >0.75$ (direct Cherenkov). Additional light is produced by Cherenkov radiation from $\delta$-ray electrons along the monopole path for velocities down to $\beta =0.625$ (indirect Cherenkov). Furthermore luminescence may be induced by molecular excitation of the medium for monopole velocities of $\beta >0.01$. Results for relativistic monopoles from MACRO [49], ANTARES [58] and IceCube [60,61] are depicted in Figure 1 [62]. As is the case for neutrinos, a large background from cosmic muons inhibits searches for down-going candidates; up-going monopoles having traversed the Earth before reaching the detector are probed instead.

The flux of ultra-relativistic monopoles has been constrained by the Pierre Auger Observatory [65], which was sensitive to monopoles with Lorentz factor values $\gamma \sim {10}^9÷{10}^{12}$. Two other experiments exploited the radio-wave pulses from the interactions of a primary particle with ice to search for monopoles. The Radio Ice Cherenkov Experiment (RICE), consisting of radio antennas buried in the Antarctic ice, set a flux upper limit of ${10}^{-18}{\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}{\mathrm{sr}}^{-1}$ at 95% CL for intermediate-mass monopoles with ${10}^7<\gamma <{10}^{12}$ and a total energy of ${10}^{16}\mathrm{GeV}$ [63]. The ANITA-II balloon-borne radio interferometer, on the other hand, set a 90%-CL flux upper limit on the order of ${10}^{-19}{\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}{\mathrm{sr}}^{-1}$ for a Lorentz factor $\gamma >{10}^{10}$ at a total energy of ${10}^{16}\mathrm{GeV}$ [64].

3. Searches in Collider Experiments

Present and proposed future accelerators feature a centre-of-mass energy of $\mathcal{O}\left(10TeV\right)$, thus it is practically impossible to search for GUT monopoles in these machines. Nevertheless, searches have been carried out to detect direct or indirect signals of lower-mass monopoles. Searches have been performed at hadron–hadron, electron–positron and lepton–hadron experiments, mostly directly using scintillation counters, gas chambers and NTDs, taking advantage of the monopole high ionisation power [19,66,67]. Other analyses focus on exposed material for trapped monopoles or peculiar magnetic-charge trajectories. In addition, virtual-monopole processes enhancing production rates of certain final states have also been considered as indirect probes for monopoles.

3.1. Past Searches

Collider experiments typically express their results in terms of upper limits on a production cross section versus the monopole mass. To calculate these limits, an ansatz is used to model the kinematics of monopole–antimonopole pair production processes since perturbative field theory cannot be used to calculate the rate and kinematic properties of produced monopoles [68]. Limits therefore suffer from a degree of model-dependence, implying that a comparison between the results of different experiments can be problematic, in particular when this concerns excluded mass regions. This situation may be resolved if thermal production in heavy-ion collisions—that does not rely on perturbation theory—is considered [69,70]. Another recent proposal involves, for the cases of spin-½ and spin-1 monopoles, the introduction of a magnetic-moment term, which, together with the velocity-dependent coupling, allows for a perturbative treatment of the cross-section calculation [71,72,73]. Specifically, this may be possible if large values of the magnetic-moment parameter and slow-moving monopoles are considered.

At the Tevatron, the CDF [74] and E882 [75] experiments of Tevatron have performed searches for monopoles. The CDF experiment used a dedicated time-of-flight system while the E882 experiment employed the induction technique to search for stopped monopoles in discarded material exposed to $p\overline{p}$ collisions. Earlier searches at the Tevatron, such as at the D0 collision point [76], used NTDs and were based on comparatively modest amounts of integrated luminosity. Lower energy hadron–hadron experiments have employed a variety of search techniques including plastic track detectors at the CERN $\mathrm{Sp}\overline{\mathrm{p}}\mathrm{S}$ [77] and searches for trapped monopoles in a 300-GeV-proton beam dump [78].

The only LEP-2 search was made by OPAL [79] which quoted cross section limits for the production of monopoles with masses up to around 103 GeV. At LEP-1, searches were made with NTDs deployed around an interaction region, thus allowing high charges to be probed for masses up to ∼45 $\mathrm{GeV}$. Specifically, the L6-MODAL experiment [80] set limits for monopoles with charges in the range $0.9÷3.6g_{\mathrm{D}}$, whilst an earlier search by the MODAL experiment was sensitive to monopoles with charges as low as $0.1g_{\mathrm{D}}$ [81]. The deployment of NTDs around the beam interaction point was also used at earlier $e^{+}{e}^{-}$ colliders such as KEK by TRISTAN [82] and PETRA [83] at DESY. Searches at $e^{+}{e}^{-}$ facilities have also been made for particles following non-helical trajectories with the CLEO [84] and TASSO [85] detectors.

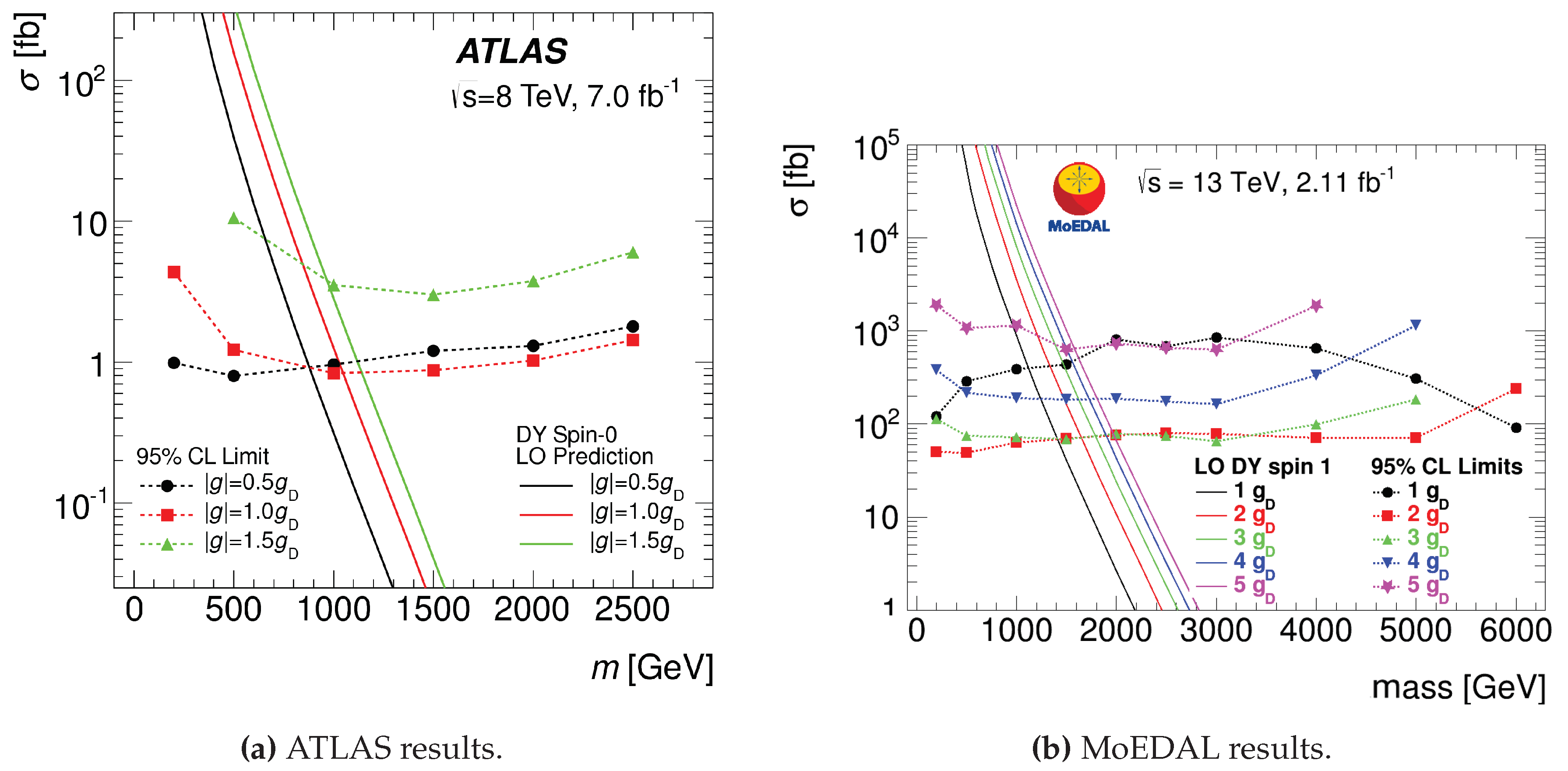
3.2. Searches for Monopoles in ATLAS

At the ATLAS experiment [86], searches for magnetic monopoles have been performed on 7-TeV [87] and on 8-TeV [88] data using the transition radiation tracker (TRT) [89,90] sensitivity to high-ionisation signals. The 8-TeV analysis relies on a dedicated trigger for highly-ionising particles, which makes use of the fraction of TRT hits passing a predefined high threshold, $f_{\mathrm{HT}}$. The discriminating particle characteristics used by this search are the energy dispersion in the electromagnetic calorimeter, w, and the $f_{\mathrm{HT}}$. The energy dispersion measures the fraction of the cluster energy contained in the most energetic cells of a cluster in each of the layers of the electromagnetic calorimeters.

Since no excess of data events was observed, the search is interpreted assuming the Drell–Yan (DY) production process with modified electromagnetic couplings as seen in Figure 2(a) [88]. The analysis is sensitive to magnetic charges of $0.5g_{\mathrm{D}}\le \left|g\right|\le 1.5g_{\mathrm{D}}$ and sets limits for spin-0 and spin-½ monopoles. The search excludes monopoles with a magnetic charge of 1$g_{\mathrm{D}}$ up to masses of 1340 GeV for a spin-½ hypothesis of the particle. In addition, a model independent cross section upper limit of 0.5 fb is set in fiducial regions where the selection efficiency is almost constant. This analysis has been updated recently by ATLAS with 13-TeV $pp$ collision data [91].

3.3. MoEDAL Experiment

MoEDAL (Monopole and Exotics Detector at the LHC) [93,94,95] is designed to search for manifestations of new physics through highly ionising particles in a manner complementary to ATLAS and CMS [96]. The main motivation for the MoEDAL experiment is to pursue the quest for magnetic monopoles at LHC energies [97]. Nonetheless, the detector is also designed to search for any massive, long-lived, slow-moving particles [98,99] with single or multiple electric charges arising in many scenarios of physics beyond the SM [97].

The MoEDAL detector [93,97] is deployed around the intersection region at Point 8 of the LHC in the LHCb experiment Vertex Locator cavern. It is a unique and largely passive LHC detector comprised of three main sub-detectors:

• Nuclear track detectors The main sub-detector system is made of a large array of CR-39, Makrofol^® and Lexan^TM NTD stacks surrounding the intersection area. The passage of an HI particle through the plastic detector is marked by an invisible damage zone along the trajectory. The damage zone is revealed as a cone-shaped etch-pit when the plastic detector is chemically etched. Then, the sheets of plastics are scanned looking for aligned etch pits in multiple sheets. The MoEDAL NTDs have a (low) threshold of $z/\beta \sim 5$, where z is the charge and $\beta =v/c$ the velocity of the incident particle. Another type of NTD installed is the Very High Charge Catcher ($z/\beta \sim 50$), consisting of two flexible low-mass stacks of Makrofol^®. It is the only NTD (partly) covering the forward region, being deployed in the LHCb acceptance between RICH1 and the Trigger Tracker.
• Magnetic trappers A unique feature of the MoEDAL detector is the use of paramagnetic magnetic monopole trappers (MMTs) to capture magnetically-charged HI particles. The aluminium absorbers of MMTs are subject to an analysis looking for magnetically charged particles at a remote SQUID magnetometer facility [100].
• TimePix radiation monitors The only non-passive MoEDAL sub-detector is an array of TimePix pixel devices distributed throughout the MoEDAL cavern, forming a real-time radiation monitoring system of beam-related backgrounds. The operation in time-over-threshold mode helps differentiating between various particles species from mixed radiation fields and measuring their energy deposition.

The high ionisation of slow-moving magnetic monopoles implies quite characteristic trajectories when such particles interact with the MoEDAL NTDs, which can be revealed during the etching process [93,97]. In addition, the high magnetic charge of a monopole (which is expected to be at least one Dirac charge $g_{\mathrm{D}}=68.5e$ (cf. (1)) implies a strong magnetic dipole moment, which in turn may result in a strong binding of the monopole with the aluminum nuclei of the MoEDAL MMTs. In such a case, the presence of a monopole trapped in an aluminium bar of an MMT would be detected through the existence of a persistent current, defined as the difference between the currents in the SQUID of a magnetometer before and after the passage of the bar through the sensing coil.

In the context of the MMT exposure during 2015–2016 of Run 2, no magnetic charge exceeding $0.5g_{\mathrm{D}}$ was detected in any of the exposed samples when passed through the ETH Zurich SQUID facility, allowing limits to be placed on monopole production. Model-independent cross-section limits have been obtained in fiducial regions of monopole energy and direction for $1g_{\mathrm{D}}\le \left|g\right|\le 6g_{\mathrm{D}}$ with the 8-TeV analysis [101]. The latest model-dependent cross-section limits are obtained for DY pair production of spin-1, spin-½ and spin-0 monopoles for $1g_{\mathrm{D}}\le \left|g\right|\le 5g_{\mathrm{D}}$ at 13 TeV [92], as shown in Figure 2b for spin-1. This analysis extended previously obtained bounds [102] and added new interpretations for a $\beta$-dependent coupling and for the first time for spin-1 monopoles. Monopole production via photon fusion has also been recently considered in MoEDAL monopole search analyses [103] following related phenomenological studies [71].

4. Conclusions and Outlook

The existence of magnetic monopoles should be confirmed experimentally and would modify our understanding of electrodynamics, rendering the Maxwell equation fully symmetric. The Dirac quantisation condition is a beautiful consequence of the existence of monopoles and therefore they represent an extremely appealing physical scenario. Various searches have been carried out utilising diverse detection techniques in both observational facilities and experiments in colliders.

Neutrino telescopes, such as ANTARES and IceCube currently, and KM3NeT and PINGU in the future, pursue the search for GUT monopoles in the cosmic front.

The CERN LHC, being the most powerful collider to-date, is the ideal machine to produce magnetic monopoles, if they exist. In particular, the MoEDAL experiment is specialising in the detection of magnetic monopoles and other highly ionising particles. MoEDAL has set the stringent bounds on high magnetic charges [103] and together with other LHC experiments, such as ATLAS [91] and possibly CMS, are going to continue probing the existence of light monopoles. Moreover, volumes exposed to LHC collisions, such as the Run-1 CMS beam pipe [104], will be scrutinised by SQUID for the presence of trapped monopoles. Another possibility to probe magnetic monopoles is given by their bound state, the monopolium, through their multiphoton final states [39,40,41,42] that can be tested in ATLAS and CMS.