The QCD Axion in Hot and Dense Matter †
Abstract
1. Introduction
2. NJL Model
3. Results and Discussions
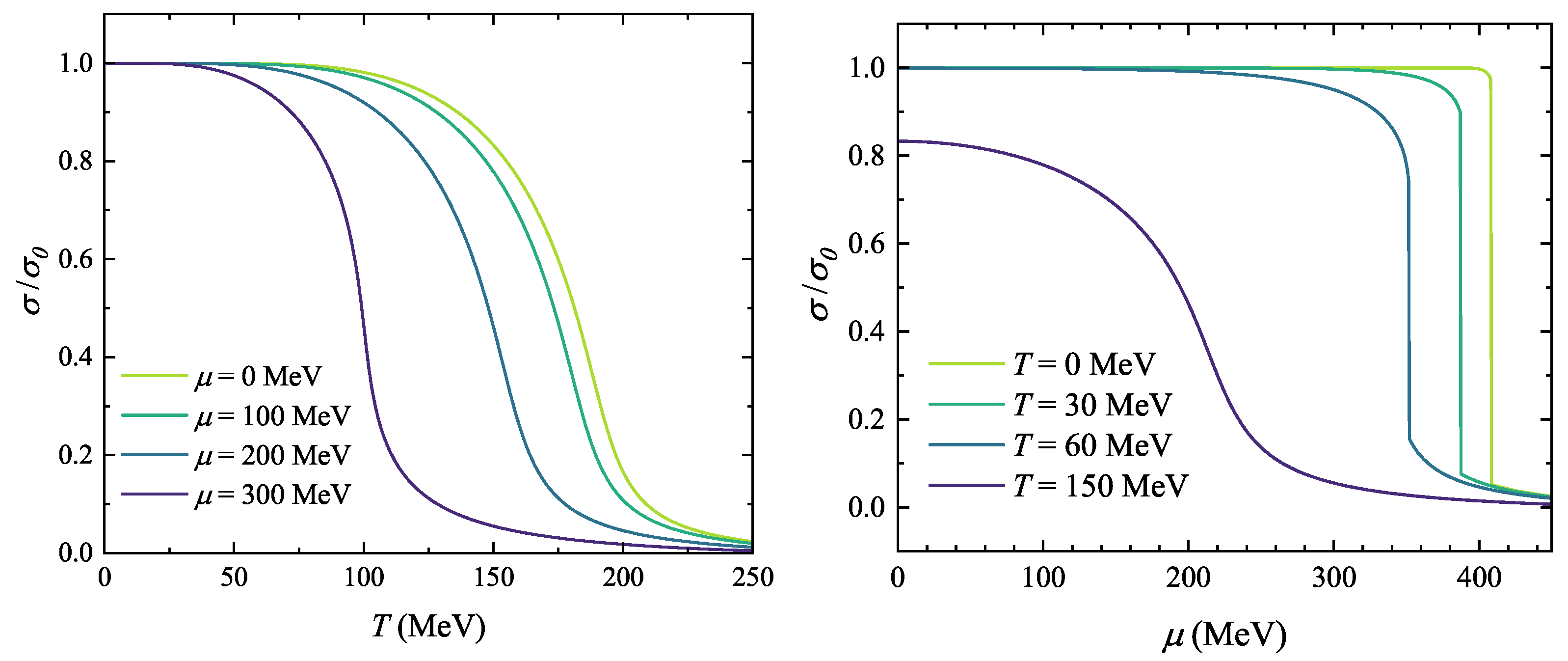
3.1. Chiral Condensate
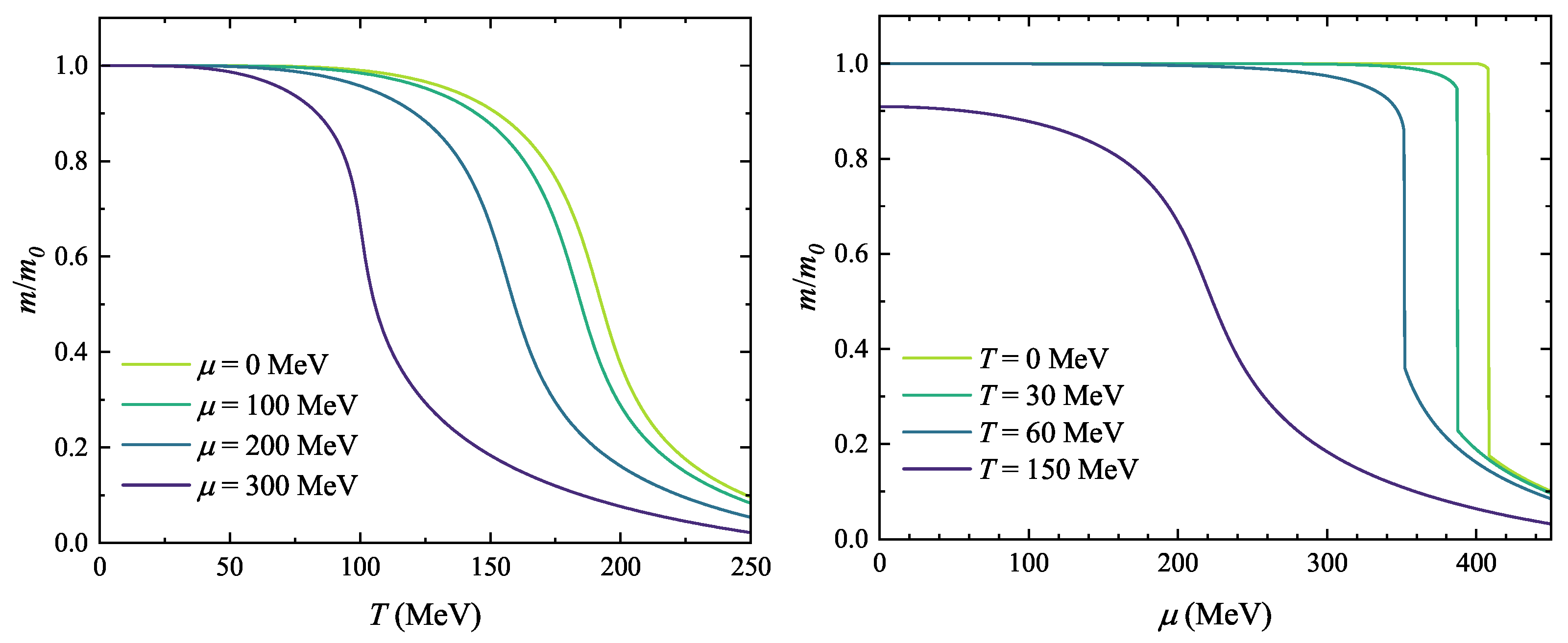
3.2. Axion Mass
3.3. Axion Self-Coupling Constant
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Weinberg, S. A New Light Boson? Phys. Rev. Lett. 1978, 40, 223–226. [Google Scholar] [CrossRef]
- Wilczek, F. Problem of Strong P and T Invariance in the Presence of Instantons. Phys. Rev. Lett. 1978, 40, 279–282. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H.R. CP Conservation in the Presence of Instantons. Phys. Rev. Lett. 1977, 38, 1440–1443. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H.R. Constraints Imposed by CP Conservation in the Presence of Instantons. Phys. Rev. D 1977, 16, 1791–1797. [Google Scholar] [CrossRef]
- Antel, C.; Battaglieri, M.; Beacham, J.; Boehm, C.; Buchmuller, O.; Calore, F.; Carenza, P.; Chauhan, B.; Clade, P.; Coloma, P.; et al. Feebly-Interacting Particles: FIPs 2022 Workshop Report. Eur. Phys. J. C 2023, 83, 1122. [Google Scholar] [CrossRef]
- Di Luzio, L.; Giannotti, M.; Nardi, E.; Visinelli, L. The Landscape of QCD Axion Models. Phys. Rep. 2020, 870, 1–117. [Google Scholar] [CrossRef]
- Lucente, G.; Carenza, P.; Fischer, T.; Giannotti, M.; Mirizzi, A. Heavy Axion-like Particles and Core-Collapse Supernovae: Constraints and Impact on the Explosion Mechanism. J. Cosmol. Astropart. Phys. 2020, 12, 008. [Google Scholar] [CrossRef]
- Lucente, G.; Mastrototaro, L.; Carenza, P.; Di Luzio, L.; Giannotti, M.; Mirizzi, A. Axion Signatures from Supernova Explosions through the Nucleon Electric-Dipole Portal. Phys. Rev. D 2022, 105, 123020. [Google Scholar] [CrossRef]
- Fischer, T.; Carenza, P.; Fore, B.; Giannotti, M.; Mirizzi, A.; Reddy, S. Observable Signatures of Enhanced Axion Emission from Protoneutron Stars. Phys. Rev. D 2021, 104, 103012. [Google Scholar] [CrossRef]
- Di Luzio, L.; Fiorentino, V.; Giannotti, M.; Mescia, F.; Nardi, E. Do Finite Density Effects Jeopardize Axion Nucleophobia in Supernovae? Phys. Rev. D 2025, 111, 015018. [Google Scholar] [CrossRef]
- Cavan-Piton, M.; Guadagnoli, D.; Oertel, M.; Seong, H.; Vittorio, L. Axion Emission from Strange Matter in Core-Collapse SNe. Phys. Rev. Lett. 2024, 133, 121002. [Google Scholar] [CrossRef] [PubMed]
- Choi, K.; Kim, H.J.; Seong, H.; Shin, C.S. Axion Emission from Supernova with Axion-Pion-Nucleon Contact Interaction. J. High Energy Phys. 2022, 2, 143. [Google Scholar] [CrossRef]
- Leinson, L.B. Axion Mass Limit from Observations of the Neutron Star in Cassiopeia A. J. Cosmol. Astropart. Phys. 2014, 08, 031. [Google Scholar] [CrossRef]
- Sedrakian, A. Axion Cooling of Neutron Stars. Phys. Rev. D 2016, 93, 065044. [Google Scholar] [CrossRef]
- Sedrakian, A. Axion Cooling of Neutron Stars. II. Beyond Hadronic Axions. Phys. Rev. D 2019, 99, 043011. [Google Scholar] [CrossRef]
- Buschmann, M.; Dessert, C.; Foster, J.W.; Long, A.J.; Safdi, B.R. Upper Limit on the QCD Axion Mass from Isolated Neutron Star Cooling. Phys. Rev. Lett. 2022, 128, 091102. [Google Scholar] [CrossRef]
- Buschmann, M.; Co, R.T.; Dessert, C.; Safdi, B.R. Axion Emission Can Explain a New Hard X-Ray Excess from Nearby Isolated Neutron Stars. Phys. Rev. Lett. 2021, 126, 021102. [Google Scholar] [CrossRef]
- Splittorff, K.; Verbaarschot, J.J.M. The QCD Sign Problem for Small Chemical Potential. Phys. Rev. D 2007, 75, 116003. [Google Scholar] [CrossRef]
- Xu, J.F.; Peng, G.X.; Lu, Z.Y.; Cui, S.S. Two-Flavor Quark Matter in the Perturbation Theory with Full Thermodynamic Consistency. Sci. China Phys. Mech. Astron. 2015, 58, 042001. [Google Scholar] [CrossRef]
- Buballa, M. NJL-model Analysis of Dense Quark Matter. Phys. Rep. 2005, 407, 205–376. [Google Scholar] [CrossRef]
- Volkov, M.K.; Radzhabov, A.E. The Nambu-Jona-Lasinio Model and Its Development. Phys. Uspekhi 2006, 49, 551–561. [Google Scholar] [CrossRef]
- Ayala, A.; Hernández, L.A.; Loewe, M.; Villavicencio, C. QCD Phase Diagram in a Magnetized Medium from the Chiral Symmetry Perspective: The Linear Sigma Model with Quarks and the Nambu–Jona-Lasinio Model Effective Descriptions. Eur. Phys. J. A 2021, 57, 234. [Google Scholar] [CrossRef]
- Lu, Z.Y.; Xia, C.J.; Ruggieri, M. Thermodynamics and Susceptibilities of Isospin Imbalanced QCD Matter. Eur. Phys. J. C 2020, 80, 46. [Google Scholar] [CrossRef]
- Lu, Q.; Chen, W.J.; Lu, Z.Y.; Xu, Y.; Li, X.Q. Equation of State and Thermodynamic Properties of Isospin Imbalanced Strongly Interacting Matter. Acta Phys. Sin. 2021, 70, 145101. (In Chinese) [Google Scholar] [CrossRef]
- Carignano, S.; Mammarella, A.; Mannarelli, M. Equation of State of Imbalanced Cold Matter from Chiral Perturbation Theory. Phys. Rev. D 2016, 93, 051503. [Google Scholar] [CrossRef]
- Detmold, W.; Orginos, K.; Shi, Z. Lattice QCD at Non-Zero Isospin Chemical Potential. Phys. Rev. D 2012, 86, 054507. [Google Scholar] [CrossRef]
- He, L.; Jin, M.; Zhuang, P. Pion Superfluidity and Meson Properties at Finite Isospin Density. Phys. Rev. D 2005, 71, 116001. [Google Scholar] [CrossRef]
- Kogut, J.B.; Sinclair, D.K. Lattice QCD at Finite Isospin Density at Zero and Finite Temperature. Phys. Rev. D 2002, 66, 034505. [Google Scholar] [CrossRef]
- Kogut, J.B.; Sinclair, D.K. The Finite Temperature Transition for 2-Flavor Lattice QCD at Finite Isospin Density. Phys. Rev. D 2004, 70, 094501. [Google Scholar] [CrossRef]
- Son, D.T.; Stephanov, M.A. QCD at Finite Isospin Density. Phys. Rev. Lett. 2001, 86, 592–595. [Google Scholar] [CrossRef]
- Lu, Z.Y.; Ruggieri, M. Effect of the Chiral Phase Transition on Axion Mass and Self-Coupling. Phys. Rev. D 2019, 100, 014013. [Google Scholar] [CrossRef]
- Murgana, F.; Comitini, G.; Ruggieri, M. Topological Susceptibility in the Superconductive Phases of Quantum Chromodynamics: A Dyson-Schwinger Perspective. Phys. Rev. D 2025, 111, 096008. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, W. Properties of the QCD Axion in Two-Flavor Color Superconductive Matter with Massive Quarks. Phys. Rev. D 2025, 111, 094043. [Google Scholar] [CrossRef]
- Carlomagno, J.P.; Gómez Dumm, D.; Scoccola, N.N. Topological Susceptibility and Axion Properties in the Presence of a Strong Magnetic Field within the Three-Flavor NJL Model. Phys. Rev. D 2025, 111, 074001. [Google Scholar] [CrossRef]
- Lopes, B.S.; Farias, R.L.S.; Dexheimer, V.; Bandyopadhyay, A.; Ramos, O.R. Axion Effects in the Stability of Hybrid Stars. Phys. Rev. D 2022, 106, L121301. [Google Scholar] [CrossRef]
- Kumar, D.; Mishra, H. CP Violation in Cold Dense Quark Matter and Axion Effects on the Non-Radial Oscillations of Neutron Stars. arXiv 2025. [Google Scholar] [CrossRef]
- Murgana, F.; Castillo, D.E.A.; Grunfeld, A.G.; Ruggieri, M. Topological Susceptibility and Axion Potential in Two-Flavor Superconductive Quark Matter. Phys. Rev. D 2024, 110, 014042. [Google Scholar] [CrossRef]
- Das, A.; Mishra, H.; Mohapatra, R.K. In Medium Properties of Axion within a Polyakov Loop Enhanced Nambu-Jona-Lasinio Model. Phys. Rev. D 2021, 103, 074003. [Google Scholar] [CrossRef]
- Horvatić, D.; Kekez, D.; Klabučar, D. Temperature Dependence of the Axion Mass in a Scenario Where the Restoration of Chiral Symmetry Drives the Restoration of the U_A(1) Symmetry. Universe 2019, 5, 208. [Google Scholar] [CrossRef]
- Liu, H.; Liu, Y.H.; Yang, Y.H.; Ju, M.; Wu, X.H.; Liu, H.M.; Chu, P.C. Axion Effects on Quark Matter and Quark-Matter Cores in Massive Hybrid Stars. Phys. Rev. D 2025, 111, L051501. [Google Scholar] [CrossRef]
- Chu, P.C.; Liu, H.; Liu, H.M.; Li, X.H.; Ju, M.; Wu, X.H.; Zhou, Y. Properties of Strange Quark Matter and a Quark Star with Axion Interactions within an SU(3) Nambu–Jona-Lasinio Model. Phys. Rev. D 2024, 110, 123031. [Google Scholar] [CrossRef]
- Bandyopadhyay, A.; Farias, R.L.S.; Lopes, B.S.; Ramos, R.O. Quantum Chromodynamics Axion in a Hot and Magnetized Medium. Phys. Rev. D 2019, 100, 076021. [Google Scholar] [CrossRef]
- Hooft, G.T. Computation of the Quantum Effects Due to a Four-Dimensional Pseudoparticle. Phys. Rev. D 1976, 14, 3432–3450. [Google Scholar] [CrossRef]
- Hooft, G.T. How Instantons Solve the U(1) Problem. Phys. Rep. 1986, 142, 357–387. [Google Scholar] [CrossRef]
- Zhang, B.; Castillo, D.E.A.; Grunfeld, A.G.; Ruggieri, M. Exploring the Axion Potential and Axion Walls in Dense Quark Matter. Phys. Rev. D 2023, 108, 054010. [Google Scholar] [CrossRef]
- Gong, H.F.; Lu, Q.; Lu, Z.Y.; Liu, L.M.; Chen, X.; Wang, S.P. QCD Topology and Axion Properties in an Isotropic Hot and Dense Medium. Eur. Phys. J. C 2024, 84, 1222. [Google Scholar] [CrossRef]
- Balkin, R.; Serra, J.; Springmann, K.; Weiler, A. The QCD Axion at Finite Density. J. High Energy Phys. 2020, 7, 221. [Google Scholar] [CrossRef]
- Sikivie, P.; Yang, Q. Bose-Einstein Condensation of Dark Matter Axions. Phys. Rev. Lett. 2009, 103, 111301. [Google Scholar] [CrossRef]
- Braaten, E.; Zhang, H. Colloquium: The Physics of Axion Stars. Rev. Mod. Phys. 2019, 91, 041002. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, H.-F.; Lu, Q.; Lu, Z.-Y. The QCD Axion in Hot and Dense Matter. Proceedings 2025, 123, 4. https://doi.org/10.3390/proceedings2025123004
Gong H-F, Lu Q, Lu Z-Y. The QCD Axion in Hot and Dense Matter. Proceedings. 2025; 123(1):4. https://doi.org/10.3390/proceedings2025123004
Chicago/Turabian StyleGong, Hong-Fang, Qi Lu, and Zhen-Yan Lu. 2025. "The QCD Axion in Hot and Dense Matter" Proceedings 123, no. 1: 4. https://doi.org/10.3390/proceedings2025123004
APA StyleGong, H.-F., Lu, Q., & Lu, Z.-Y. (2025). The QCD Axion in Hot and Dense Matter. Proceedings, 123(1), 4. https://doi.org/10.3390/proceedings2025123004





