Constraints on the Equation of State of Quark Stars from Compact Object Observations †
Abstract
1. Introduction
2. Revised Perturbative QCD Model
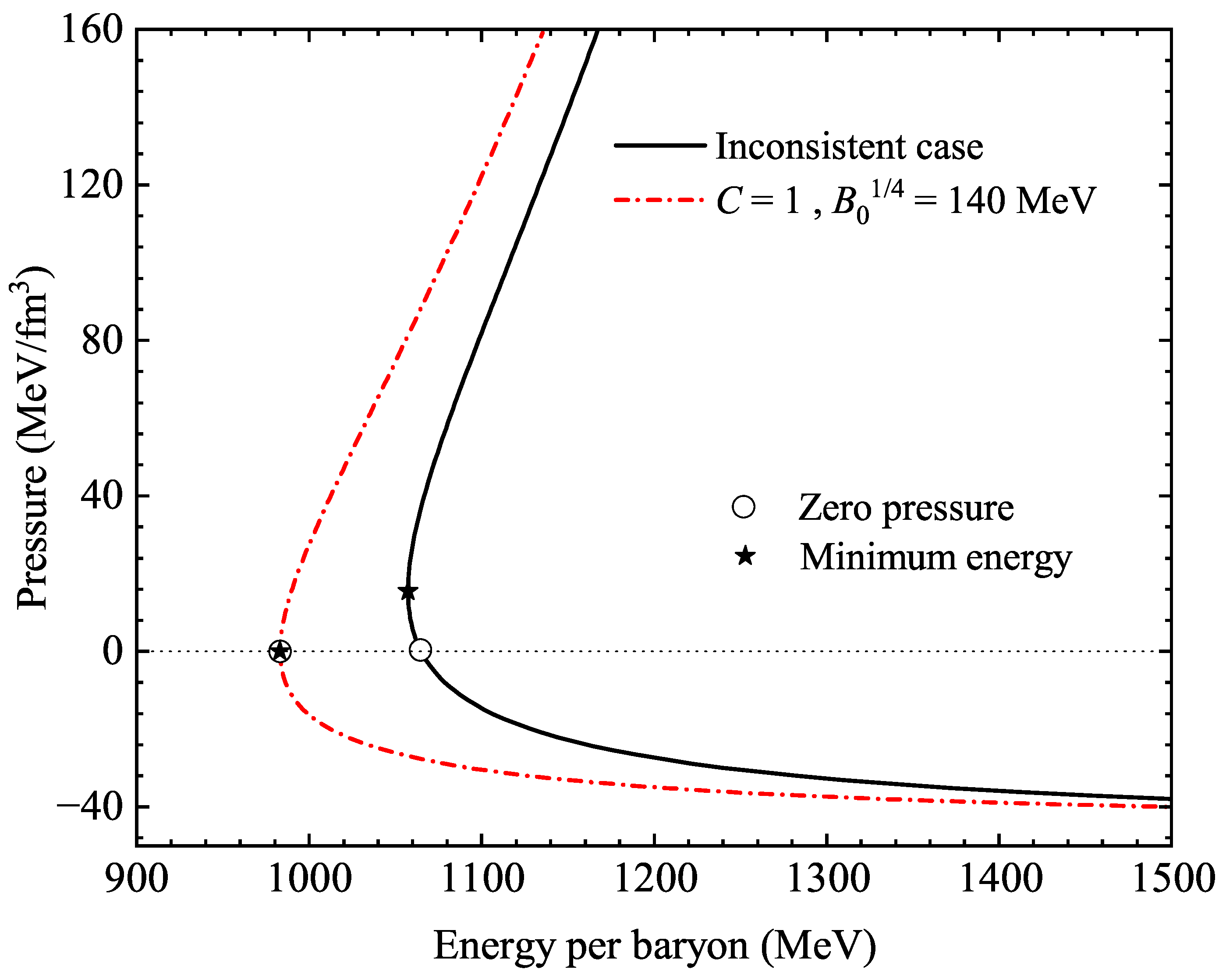
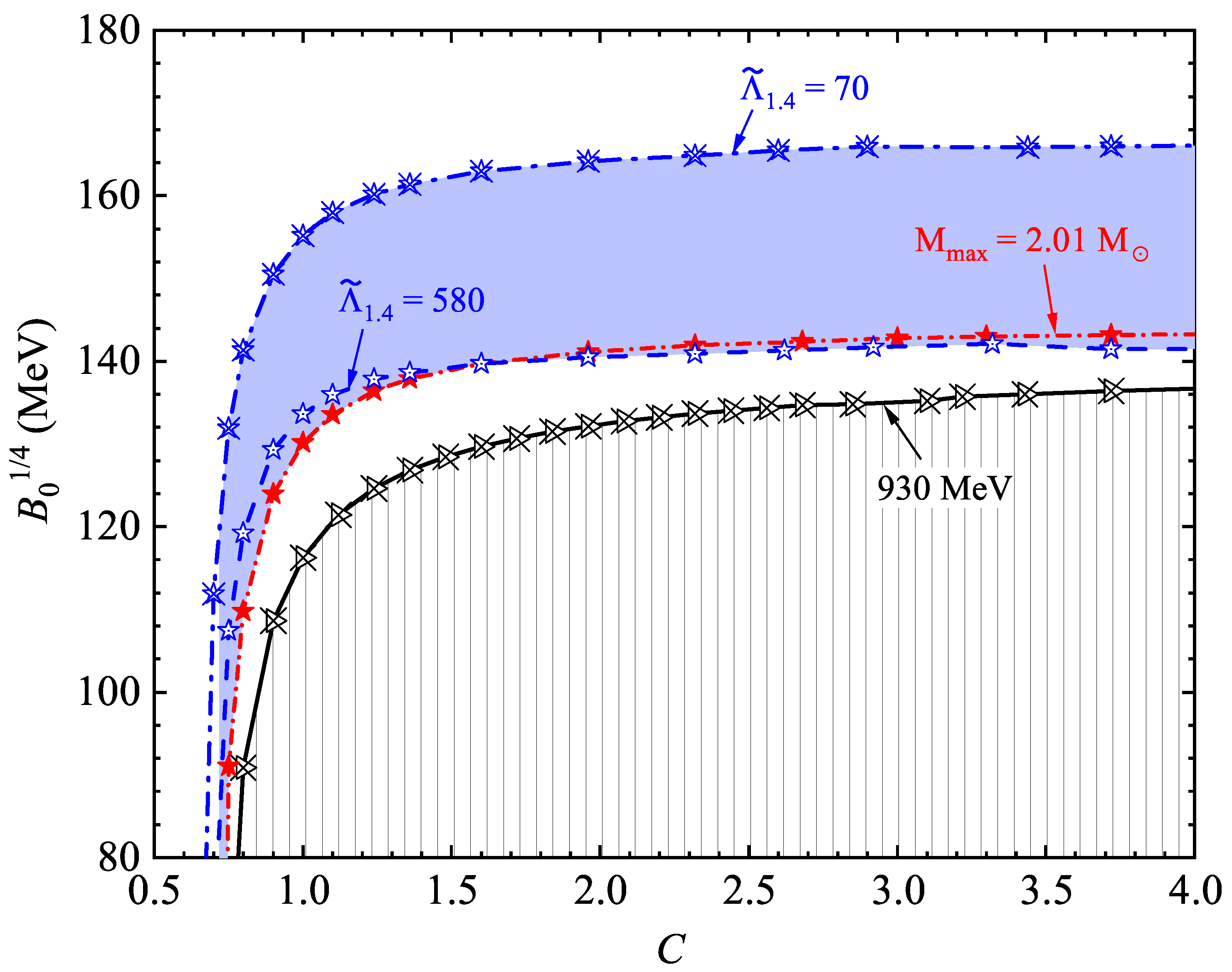
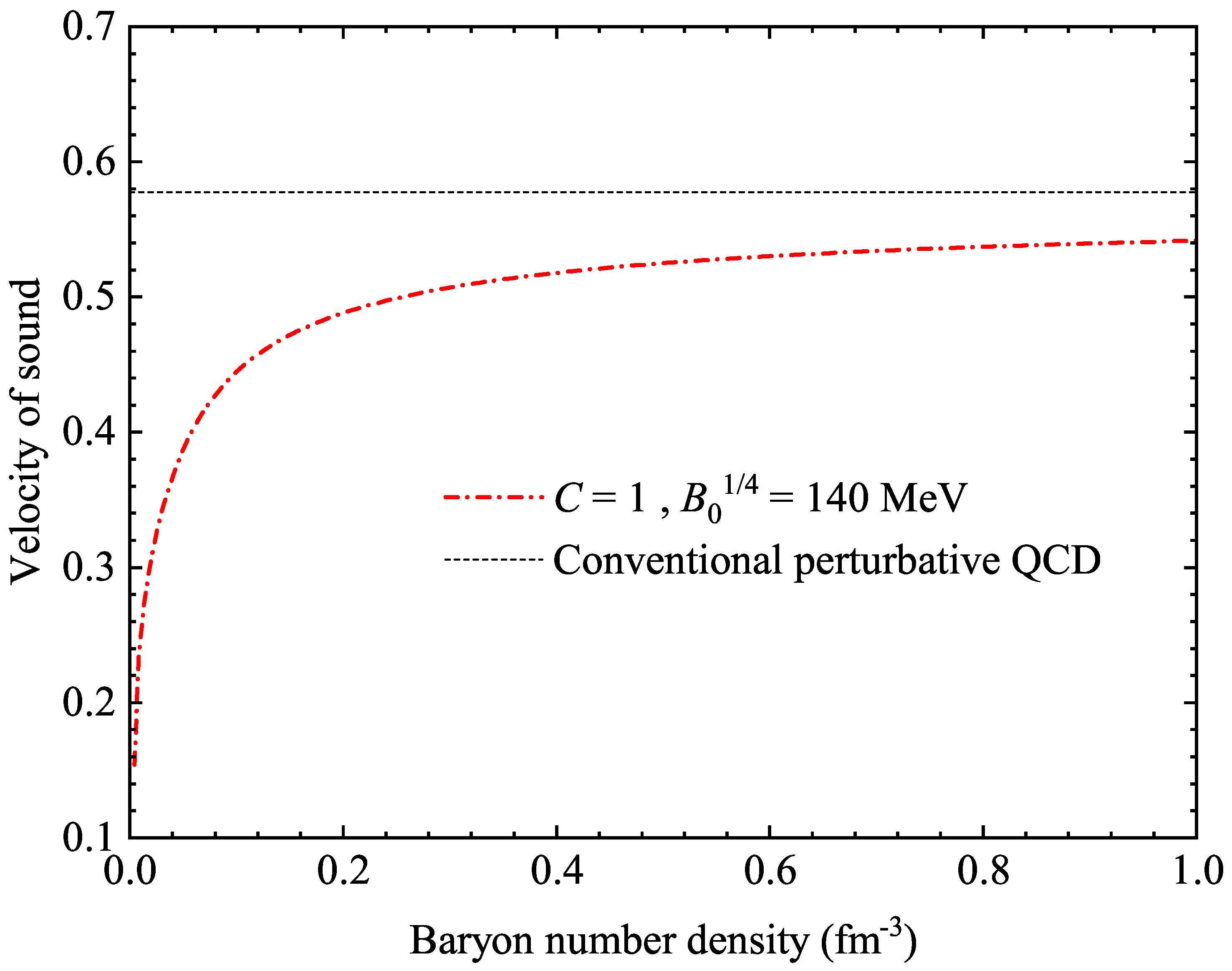
3. Numerical Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Banerjee, A.; Pradhan, A.; Sakalli, I.; Dixit, A. Properties of interacting quark star in light of Rastall gravity. Class. Quant. Grav. 2025, 42, 025008. [Google Scholar] [CrossRef]
- Tangphati, T.; Sakallı, İ.; Banerjee, A.; Pradhan, A. The effect of pressure anisotropy on quark stars structure in the Starobinsky model. Chin. Phys. C 2025, 49, 074111. [Google Scholar] [CrossRef]
- Oertel, M.; Hempel, M.; Klähn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar] [CrossRef]
- Baym, G.; Hatsuda, T.; Kojo, T.; Powell, P.D.; Song, Y.; Takatsuka, T. From hadrons to quarks in neutron stars: A review. Rept. Prog. Phys. 2018, 81, 056902. [Google Scholar] [CrossRef]
- Kurkela, A.; Romatschke, P.; Vuorinen, A. Cold Quark Matter. Phys. Rev. D 2010, 81, 105021. [Google Scholar] [CrossRef]
- Pretel, J.M.Z.; Tangphati, T.; Sakallı, İ.; Banerjee, A. White dwarfs in regularized 4D Einstein-Gauss-Bonnet gravity. Phys. Lett. B 2025, 866, 139581. [Google Scholar] [CrossRef]
- Pretel, J.M.Z.; Tangphati, T.; Banerjee, A.; Pradhan, A. Effects of anisotropic pressure on interacting quark star structure. Phys. Lett. B 2024, 848, 138375. [Google Scholar] [CrossRef]
- Tangphati, T.; Panotopoulos, G.; Banerjee, A.; Pradhan, A. Charged compact stars with color–flavor-locked strange quark matter in f(R,T) gravity. Chin. J. Phys. 2023, 82, 62–74. [Google Scholar] [CrossRef]
- Tangphati, T.; Karar, I.; Banerjee, A.; Pradhan, A. The mass–radius relation for quark stars in energy–momentum squared gravity. Annals Phys. 2022, 447, 169149. [Google Scholar] [CrossRef]
- Yuan, W.L.; Li, A.; Miao, Z.; Zuo, B.; Bai, Z. Interacting ud and uds quark matter at finite densities and quark stars. Phys. Rev. D 2022, 105, 123004. [Google Scholar] [CrossRef]
- Xia, C.J.; Maruyama, T.; Li, A.; Sun, B.Y.; Long, W.H.; Zhang, Y.X. Unified neutron star EOSs and neutron star structures in RMF models. Commun. Theor. Phys. 2022, 74, 095303. [Google Scholar] [CrossRef]
- Miao, Z.; Jiang, J.L.; Li, A.; Chen, L.W. Bayesian inference of strange star equation of state using the GW170817 and GW190425 data. Astrophys. J. Lett. 2021, 917, L22. [Google Scholar] [CrossRef]
- Chu, P.C.; Liu, H.; Liu, H.M.; Ju, M.; Wu, X.H.; Zhou, Y.; Li, X.H. Quark star matter within an extended quasiparticle model. Eur. Phys. J. C 2025, 85, 466. [Google Scholar] [CrossRef]
- Aarts, G.; Aichelin, J.; Allton, C.; Athenodorou, A.; Bachtis, D.; Bonanno, C.; Brambilla, N.; Bratkovskaya, E.; Bruno, M.; Caselle, M.; et al. Phase Transitions in Particle Physics: Results and Perspectives from Lattice Quantum Chromo-Dynamics. Prog. Part. Nucl. Phys. 2023, 133, 104070. [Google Scholar] [CrossRef]
- Wen, X.J.; Zhong, X.H.; Peng, G.X.; Shen, P.N.; Ning, P.Z. Thermodynamics with density and temperature dependent particle masses and properties of bulk strange quark matter and strangelets. Phys. Rev. C 2005, 72, 015204. [Google Scholar] [CrossRef]
- Chu, P.C.; Chen, L.W. Quark matter symmetry energy and quark stars. Astrophys. J. 2014, 780, 135. [Google Scholar] [CrossRef]
- Lu, Z.Y.; Peng, G.X.; Xu, J.F.; Zhang, S.P. Properties of quark matter in a new quasiparticle model with QCD running coupling. Sci. China Phys. Mech. Astron. 2016, 59, 662001. [Google Scholar] [CrossRef]
- Alba, P.; Alberico, W.; Bluhm, M.; Greco, V.; Ratti, C.; Ruggieri, M. Polyakov loop and gluon quasiparticles: A self-consistent approach to Yang-Mills thermodynamics. Nucl. Phys. A 2014, 934, 41–51. [Google Scholar] [CrossRef]
- Pal, S.; Chaudhuri, G. Medium effects in the MIT bag model for quark matter: Self-consistent thermodynamical treatment. Phys. Rev. D 2023, 108, 103028. [Google Scholar] [CrossRef]
- Carignano, S.; Mammarella, A.; Mannarelli, M. Equation of state of imbalanced cold matter from chiral perturbation theory. Phys. Rev. D 2016, 93, 051503. [Google Scholar] [CrossRef]
- Xu, J.F.; Peng, G.X.; Lu, Z.Y.; Cui, S.S. Two-flavor quark matter in the perturbation theory with full thermodynamic consistency. Sci. China Phys. Mech. Astron. 2015, 58, 042001. [Google Scholar] [CrossRef]
- Klahn, T.; Blaschke, D.; Typel, S.; van Dalen, E.N.E.; Faessler, A.; Fuchs, C.; Gaitanos, T.; Grigorian, H.; Ho, A.; Kolomeitsev, E.E.; et al. Constraints on the high-density nuclear equation of state from the phenomenology of compact stars and heavy-ion collisions. Phys. Rev. C 2006, 74, 035802. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Psaltis, D. Constraints on the equation of state of neutron star matter from observations of kilohertz QPOs. Nucl. Phys. B Proc. Suppl. 1998, 69, 123–128. [Google Scholar] [CrossRef]
- Yang, S.H.; Pi, C.M.; Zheng, X.P.; Weber, F. Confronting Strange Stars with Compact-Star Observations and New Physics. Universe 2023, 9, 202. [Google Scholar] [CrossRef]
- Xu, J.F.; Xia, C.J.; Lu, Z.Y.; Peng, G.X.; Zhao, Y.P. Symmetry energy of strange quark matter and tidal deformability of strange quark stars. Nucl. Sci. Tech. 2022, 33, 143. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, C.; Zhao, J.; Kiuchi, K.; Fujibayashi, S.; Zhou, E. Constraints of the maximum mass of quark stars based on postmerger evolutions. Phys. Rev. D 2024, 110, 103012. [Google Scholar] [CrossRef]
- Tangphati, T.; Sakallı, İ.; Banerjee, A.; Ali, A. Interacting quark star with pressure anisotropy and recent astrophysical observations. Chin. J. Phys. 2024, 91, 392–405. [Google Scholar] [CrossRef]
- Tangphati, T.; Karar, I.; Pradhan, A.; Banerjee, A. Constraints on the maximum mass of quark star and the GW 190814 event. Eur. Phys. J. C 2022, 82, 57. [Google Scholar] [CrossRef]
- Tangphati, T.; Banerjee, A.; Sakallı, İ.; Pradhan, A. Quark stars in Rastall gravity with recent astrophysical observations. Chin. J. Phys. 2024, 90, 422–433. [Google Scholar] [CrossRef]
- Banerjee, A.; Sakallı, İ.; Rayimbaev, J.; Ibragimov, I.; Muminov, S. Quark stars in energy–momentum squared gravity with recent astrophysical observations. Phys. Dark Univ. 2025, 48, 101866. [Google Scholar] [CrossRef]
- Banerjee, A.; Sakallı, İ.; Dayanandan, B.; Pradhan, A. Quark stars in f(R, T) gravity: Mass-to-radius profiles and observational data. Chin. Phys. C 2025, 49, 015102. [Google Scholar] [CrossRef]
- Tangphati, T.; Gogoi, D.J.; Pradhan, A.; Banerjee, A. Investigating stable quark stars in Rastall-Rainbow gravity and their compatibility with gravitational wave observations. JHEAp 2024, 42, 12–20. [Google Scholar] [CrossRef]
- Kumar, R.; Xia, C.-J.; Lu, Z.-Y.; Peng, G.-X. Theoretical and experimental constraints for the equation of state of dense and hot matter. Living Rev. Relativ. 2024, 27, 3. [Google Scholar] [CrossRef]
- Bogdanov, S.; Dittmann, A.J.; Ho, W.C.G.; Lamb, F.K.; Mahmoodifar, S.; Miller, M.C.; Morsink, S.M.; Riley, T.E.; Strohmayer, T.E.; Watts, A.L.; et al. Constraining the Neutron Star Mass-Radius Relation and Dense Matter Equation of State with NICER. III. Model Description and Verification of Parameter Estimation Codes. Astrophys. J. Lett. 2021, 914, L15. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. Lett. 2019, 887, L24. [Google Scholar] [CrossRef]
- Fonseca, E.; Cromartie, H.T.; Pennucci, T.T.; Ray, P.S.; Kirichenko, A.Y.; Ransom, S.M.; Demorest, P.B.; Stairs, I.H.; Arzoumanian, Z.; Guillemot, L.; et al. Refined Mass and Geometric Measurements of the High-mass PSR J0740+6620. Astrophys. J. Lett. 2021, 915, L12. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, X.; Adya, V.; et al. GW170817: Measurements of neutron star radii and equation of state. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef]
- Freedman, B.A.; McLerran, L.D. Fermions and Gauge Vector Mesons at Finite Temperature and Density. 3. The Ground State Energy of a Relativistic Quark Gas. Phys. Rev. D 1977, 16, 1169. [Google Scholar] [CrossRef]
- Xia, C.J.; Peng, G.X.; Chen, S.W.; Lu, Z.Y.; Xu, J.F. Thermodynamic consistency, quark mass scaling, and properties of strange matter. Phys. Rev. D 2014, 89, 105027. [Google Scholar] [CrossRef]
- Cao, Z.; Chen, L.W.; Chu, P.C.; Zhou, Y. GW190814: Circumstantial evidence for up-down quark star. Phys. Rev. D 2022, 106, 083007. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Kurkela, A.; Nättilä, J.; Vuorinen, A. Evidence for quark-matter cores in massive neutron stars. Nature Phys. 2020, 16, 907–910. [Google Scholar] [CrossRef]
- Holdom, B.; Ren, J.; Zhang, C. Quark matter may not be strange. Phys. Rev. Lett. 2018, 120, 222001. [Google Scholar] [CrossRef]
- Ma, Z.J.; Lu, Z.Y.; Xu, J.F.; Peng, G.X.; Fu, X.; Wang, J. Cold quark matter in a quasiparticle model: Thermodynamic consistency and stellar properties. Phys. Rev. D 2023, 108, 054017. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.-P.; Ma, Z.-J.; Xu, J.-F.; Lu, Z.-Y. Constraints on the Equation of State of Quark Stars from Compact Object Observations. Proceedings 2025, 123, 3. https://doi.org/10.3390/proceedings2025123003
Wang S-P, Ma Z-J, Xu J-F, Lu Z-Y. Constraints on the Equation of State of Quark Stars from Compact Object Observations. Proceedings. 2025; 123(1):3. https://doi.org/10.3390/proceedings2025123003
Chicago/Turabian StyleWang, Shu-Peng, Zhi-Jun Ma, Jian-Feng Xu, and Zhen-Yan Lu. 2025. "Constraints on the Equation of State of Quark Stars from Compact Object Observations" Proceedings 123, no. 1: 3. https://doi.org/10.3390/proceedings2025123003
APA StyleWang, S.-P., Ma, Z.-J., Xu, J.-F., & Lu, Z.-Y. (2025). Constraints on the Equation of State of Quark Stars from Compact Object Observations. Proceedings, 123(1), 3. https://doi.org/10.3390/proceedings2025123003




