Abstract
We discuss two quantum simulation schemes in which the coupling to an external bath may give rise to novel and interesting many-body physics. Namely, we first address the effect of local Markovian baths on the quantum annealing dynamics of an Ising-like chain: deviations from adiabaticity may display a nonmonotonic trend as a function of the annealing time, as a result of the competition between nonadiabatic effects and dissipative processes. Secondly, we provide a framework to induce persistent currents through the coupling with a structured reservoir which generates nonreciprocity, without the need of any applied gauge field.
1. Introduction
The recent spectacular advances in the field of quantum simulation have drastically enhanced our capability to control and monitor the dynamics of quantum many-body systems in a variety of physical implementation, including atomic and molecular optics, trapped ions, and cavity/circuit quantum electrodynamics [1]. In fact, it has been also possible to manipulate states of matter even in the presence of an external environment, e.g., by means of Rydberg atoms [2] or superconducting QED circuits [3]. The presence of a bath inevitably leads to a non-equilibrium process, where the coherent Hamiltonian dynamics may compete with the incoherent processes lead by the system-bath coupling.
Here, following the model proposed in Section 2, we address two peculiar situations that can be faced in up-to-date quantum simulation devices. We first concentrate, in Section 3, on the quantum annealing (QA) dynamics of a many-body system slowly driven across a phase transition, a typical situation of adiabatic quantum computation schemes, whose purpose is to identify the global minimum (ground state) of a given function over a set of many local minima [4,5]. The adiabatic unitary dynamics suggests that a slower annealing leads to a smaller density of defects generated when passing through the critical point [6], while the presence of an unstructured environment is likely to have an opposite effect [7]. The two competing effects might thus lead to interesting nonmonotonicities in the QA performance as a function of the annealing time [8,9,10].
Dissipation however is not necessarily detrimental: a constantly growing theoretical activity is now scrutinizing the possibility of engineering and probing system-bath couplings, in order to prepare and manipulate exotic many-body quantum states [11,12,13]. In Section 4 we focus on the generation of steady-state currents, using a general method to realize non-reciprocity by matching coherent and dissipative parts of the dynamics [14]. Persistent currents are one of the most attractive phenomena in mesoscopics; the versatility of cold-atom quantum simulators recently enabled to trap and control atomic currents in dissipation-free optical circuits through suitable gauge fields, with an unprecedented accuracy [15,16]. Nonetheless such currents profoundly differ from those obtained by reservoir engineering, since in the limit of large systems the former vanish, while the latter survive [17].
2. Model: A Driven-Dissipative Coupled-Cavity Array
To fix the ideas, we consider L coupled QED cavities in a one-dimensional (1D) ring geometry. This is the ideal platform where one can manipulate the various internal degrees of freedom and the coupling with ancillary systems. A unitary quadratic interaction between neighboring cavities can be implemented via standard quantum optical techniques. The resulting lattice Hamiltonian is
where describe the bosonic modes of each cavity (). The coupling to an external environment, typically Markovian, can be captured by a Lindblad master equation [18]:
where . Hereafter we adopt units of . The first term in the r.h.s. of Equation (2) describes the coherent evolution driven by Hamiltonian (1). The second term corresponds to the unavoidable coupling of each cavity to an independent bath (with strength ). We model this as a Lindblad jump operator , whose effect is to incoherently deplete the jth cavity [see the sketch in Figure 1a]. The third term accounts for an engineered two-site dissipation:
which can be obtained by coupling the two principal modes (j, ) with an auxiliary cavity mode (the bath) via a quadratic Hamiltonian [sketch in Figure 2a]. The two forms of dissipation may coexist, originating an interesting non-equilibrium behavior. For the sake of simplicity, we work in the photon blockade regime, where at most one excitation per cavity is admitted. Thus each bosonic mode is supposed to satisfy an hard-core constraint, and a cavity can be effectively regarded as a qubit.
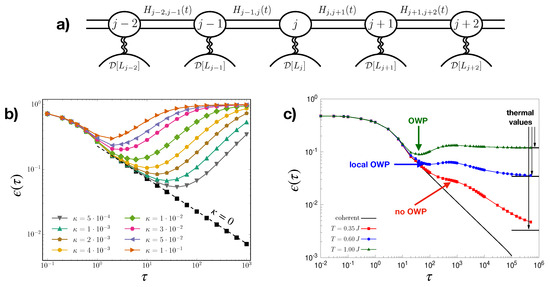
Figure 1.
(a) Setup for QA protocols. The various sites interact through time-varying Hamiltonian terms , and are locally coupled to independent reservoirs. (b,c) Excess energy as a function of the annealing time , for a quantum Ising chain locally coupled to: (b) a bath inducing incoherent decay mechanisms; (c) an Ohmic bath of quantum harmonic oscillators at different temperature T.
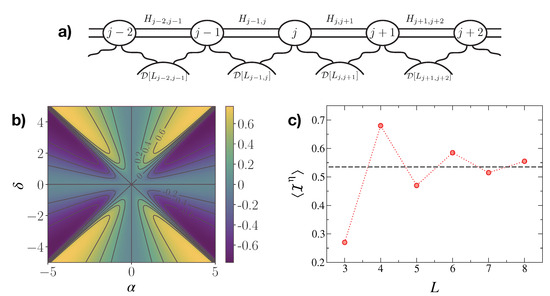
Figure 2.
(a) Setup to create persistent currents. The cavities interact unitarily via local Hamiltonian terms and dissipatively via engineered reservoirs induced by the dissipators . (b,c) Circulating current for a minimal scheme of non-local dissipation, as a function of: (b) the parameters (cluster mean-field data); (c) the system size L (exact diagonalization up to . Consistent results have been obtained with matrix product operators, enabling to reach much longer sizes [17]).
3. Quantum Annealing in the Presence of Dissipation
Setting the Hamiltonian couplings , in the hard-core limit one realizes the quantum Ising chain in a transverse field of strength , exhibiting a second-order phase transition at . We analyze the QA dynamics by tuning the field in time, according to a linear ramping:
where are spin- Pauli matrices for the jth qubit. We keep into account the unavoidable leakage of each cavity in terms of a decaying mechanism [Figure 1a]. The protocol (4) ensures that the system will cross the critical point and defects start to appear, irrespective of the time duration of the QA. We quantify adiabaticity loss through the excess energy , expressing the difference between the instantaneous energy and the ground-state energy of the instantaneous Hamiltonian.
In the absence of dissipation (), one finds a Kibble–Zurek (KZ) scaling of the excess energy with the QA speed , i.e., , which is obtained via knowledge of the Ising critical exponents associated with the corresponding transition at [6]. Such relation can be generalized to the case of initial thermal states, renormalizing the power-law scaling exponent [19,20]. On the other hand, a finite dissipation () may induce a competition between the generation of defects by means of KZ and incoherent driving. This typically manifests in a nonmonotonic behavior of the curves in Figure 1b, thus producing an optimal working point (OWP) that maximizes the QA performance [21]. The behavior of the OWP position with can be predicted by assuming independence between the two mechanisms: this is due to the choice of the bath, which is insensitive to the Hamiltonian details [9]. A more thorough modelization of dissipation, in terms of an independent Caldeira-Leggett Ohmic bath per cavity, gives rise to situations where the OWP may disappear [10,22], for low bath temperatures [see Figure 1c]. At intermediate temperatures, the curve for the excess energy in function of displays a local minimum at finite , but the actual global minimum is attained as a thermal plateau [10]. The additivity of the two above mentioned mechanisms breaks down as soon as the bath thermalization time is effectively shorter than the characteristic timescale for the system dynamics.
4. Persistent Currents Induced via Dissipation Engineering
A peculiar quantum state of matter can be stabilized through an engineered system-bath coupling, such as the two-site dissipation of Equation (3). This scheme is capable to exhibit directionality after suitably tuning the various system-bath couplings. Namely, considering two neighboring cavities, one can play with such that the equation of motion for the mode does not depend on , while that for depends on [14]. Scaling this mechanism all over the chain, a macroscopic current flow can be generated in the system [17]. For the sake of simplicity, let us take a minimal model where the Hamiltonian contains just a chemical potential , fixing the energy scale. As for the bath coupling, we only consider the non-local dissipation , dropping the local terms , and set , . The following Heisenberg equation of motion for the spin magnetization sets in:
The term , with , denotes a circulating non-conserved current. For (), the system is driven into a steady state which is completely aligned (anti-aligned) along the z axis. For the steady state is completely mixed, since the Lindblad operators create as many excitations as they annihilate. In all other cases, the imbalance between creation and annihilation of excitations generates a current. We scrutinized it through a self consistent cluster mean-field treatment [23,24], with clusters being made of two neighboring spins. Figure 2b shows that, when and are almost equal, the current takes large values, but it is also very sensitive to changes in the parameters: a small variation in them makes the current sharply change from positive () to negative () values. Using numerical techniques (exact diagonalization and matrix-product-operator simulations [25,26]), we scaled the chain length, observing indications of convergence of with L toward finite values [Figure 2c]. Reservoir-based currents are thus sensibly different from ordinary currents induced by gauge fields, the latter representing a boundary effect which vanishes in the thermodynamic limit. We also checked that these currents are robust against local unitary and dissipative imperfections, such as nearest-neighbor interaction terms in the Hamiltonian, of the form [17].
References
- Nature physics insight on quantum simulators. Nat. Phys. 2012, 8, No–4.
- Saffman, M.; Walker, T.G.; Mølmer, K. Quantum information with Rydberg atoms. Rev. Mod. Phys. 2010, 82, 2313. [Google Scholar] [CrossRef]
- Houck, A.A.; Türeci, H.E.; Koch, J. On-chip quantum simulation with superconducting circuits. Nat. Phys. 2012, 8, 292–299. [Google Scholar] [CrossRef]
- Farhi, E.; Goldstone, J.; Gutmann, S.; Lapan, J.; Lundgren, A.; Preda, D. A quantum adiabatic evolution algorithm applied to random instances of an NP-complete problem. Science 2001, 292, 472–475. [Google Scholar] [CrossRef]
- Santoro, G.E.; Martoňák, R.; Tosatti, E.; Car, R. Theory of Quantum Annealing of an Ising Spin Glass. Science 2002, 295, 2427–2430. [Google Scholar] [CrossRef]
- Dziarmaga, J. Dynamics of a quantum phase transition and relaxation to a steady state. Adv. Phys. 2010, 59, 1063–1089. [Google Scholar] [CrossRef]
- Fubini, A.; Falci, G.; Osterloh, A. Robustness of adiabatic passage trough a quantum phase transition. New J. Phys. 2007, 9, 134. [Google Scholar] [CrossRef]
- Patanè, D.; Silva, A.; Amico, L.; Fazio, R.; Santoro, G.E. Adiabatic dynamics in open quantum critical many-body systems. Phys. Rev. Lett. 2008, 101, 175701. [Google Scholar] [CrossRef]
- Keck, M.; Montangero, S.; Santoro, G.E.; Fazio, R.; Rossini, D. Dissipation in adiabatic quantum computers: lessons from an exactly solvable model. New J. Phys. 2017, 19, 113029. [Google Scholar] [CrossRef]
- Arceci, L.; Barbarino, S.; Rossini, D.; Santoro, G.E. Optimal working point in dissipative quantum annealing. Phys. Rev. B 2018, 98, 064307. [Google Scholar] [CrossRef]
- Diehl, S.; Micheli, A.; Kantian, A.; Kraus, B.; Büchler, H.P.; Zoller, P. Quantum States and Phases in Driven Open Quantum Systems with Cold Atoms. Nat. Phys. 2008, 4, 878. [Google Scholar] [CrossRef]
- Verstraete, F.; Wolf, M.M.; Cirac, J.I. Quantum computation, quantum state engineering, and quantum phase transitions driven by dissipation. Nat. Phys. 2009, 5, 633. [Google Scholar] [CrossRef]
- Bellomo, B.; De Pasquale, A.; Gualdi, G.; Marzolino, U. A tomographic approach to non-Markovian master equations. J. Phys. A: Math. Theor. 2010, 43, 395303. [Google Scholar] [CrossRef]
- Metelmann, A.; Clerk, A.A. Nonreciprocal photon transmission and amplification via reservoir engineering. Phys. Rev. X 2015, 5, 021025. [Google Scholar] [CrossRef]
- Ramanathan, A.; Wright, K.C.; Muniz, S.R.; Zelan, M.; Hill, W. T. , III; Lobb, C.J.; Helmerson, K.; Phillips, W.D.; Campbell, G.K. Superflow in a toroidal Bose-Einstein condensate: An atom circuit with a tunable weak link. Phys. Rev. Lett. 2011, 106, 130401. [Google Scholar] [CrossRef]
- Aghamalyan, D.; Cominotti, M.; Rizzi, M.; Rossini, D.; Hekking, F.; Minguzzi, A.; Kwek, L.-C.; Amico, L. Coherent superposition of current flows in an atomtronic quantum interference device. New J. Phys. 2015, 17, 045023. [Google Scholar] [CrossRef]
- Keck, M.; Rossini, D.; Fazio, R. Persistent currents by reservoir engineering. Phys. Rev. A 2018, 98, 053812. [Google Scholar] [CrossRef]
- Breuer, H.-P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: New York, NY, USA, 2002. [Google Scholar]
- De Grandi, C.; Gritsev, V.; Polkovnikov, A. Quench dynamics near a quantum critical point. Phys. Rev. B 2010, 81, 012303. [Google Scholar] [CrossRef]
- De Grandi, C.; Gritsev, V.; Polkovnikov, A. Quench dynamics near a quantum critical point: Application to the sine-Gordon model. Phys. Rev. B 2010, 81, 224301. [Google Scholar] [CrossRef]
- Dutta, A.; Rahmani, A.; Del Campo, A. Anti-Kibble-Zurek behavior in crossing the quantum critical point of a thermally isolated system driven by a noisy control field. Phys. Rev. Lett. 2016, 117, 080402. [Google Scholar] [CrossRef]
- Nalbach, P.; Vishveshwara, S.; Clerk, A.A. Quantum Kibble-Zurek physics in the presence of spatially correlated dissipation. Phys. Rev. B 2015, 92, 014306. [Google Scholar] [CrossRef]
- Tomadin, A.; Giovannetti, V.; Fazio, R.; Gerace, D.; Carusotto, I.; Türeci, H.E.; Imamoglu, A. Signatures of the superfluid-insulator phase transition in laser-driven dissipative nonlinear cavity arrays. Phys. Rev. A 2010, 81, 061801. [Google Scholar] [CrossRef]
- Jin, J.; Biella, A.; Viyuela, O.; Mazza, L.; Keeling, J.; Fazio, R.; Rossini, D. Cluster Mean-Field Approach to the Steady-State Phase Diagram of Dissipative Spin Systems. Phys. Rev. X 2016, 6, 031011. [Google Scholar] [CrossRef]
- Verstraete, F.; García-Ripoll, J.J.; Cirac, J.I. Matrix product density operators: simulation of finite-temperature and dissipative systems. Phys. Rev. Lett. 2004, 93, 207204. [Google Scholar] [CrossRef]
- Zwolak, M.; Vidal, G. Mixed-state dynamics in one-dimensional quantum lattice systems: A time-dependent superoperator renormalization algorithm. Phys. Rev. Lett. 2004, 93, 207205. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).