Abstract
Orbital angular momentum is a discrete degree of freedom that can access an infinite dimensional Hilbert space, thus enhancing the information capacity of a single optical beam. Continuous variables field quadratures allow achieving some quantum tasks in a more advantageous way with respect to the use of photon-number states. Here, we use a hybrid approach realizing bipartite continuous-variable Gaussian entangled state made up of two electromagnetic modes carrying orbital angular momentum. A q-plate is used for endowing a pair of entangled beams with such a degree of freedom. This quantum state is then completely characterized thanks to a novel design of a homodyne detector in which also the local oscillator is an orbital angular momentum-carrying beams so allowing the direct detection of vortex modes quadratures.
1. Introduction
Quantum entanglement, from simple bipartite systems up to complex multipartite ones, is a prominent resource in quantum information allowing to accomplish tasks not achievable with classical tools. In the context of Continuous Variable (CV) quantum optics, field quadratures are the encoding degrees of freedom (d.o.f) [1,2]. CV bipartite entangled states are efficiently produced by parametric down-conversion in Optical Parametric Oscillators (OPO) working below threshold [3,4,5,6]. Adopting a hybrid discrete-continuous variable approach can pave the way to multipartite entanglement. A possible implementation is to provide CV entangled modes with additional discrete d.o.f. Orbital Angular Momentum (OAM) represents, with no doubt, an easy to handle candidate. It characterizes a class of transverse optical modes that carry non-zero OAM so that many modes can co-propagate preserving their distinguishability. Unlike polarization, OAM is a discrete infinite-dimensional d.o.f. Beams carrying OAM are paraxial beams characterized by the presence of an azimuthal angle phase dependence . These beams have helical wavefronts and an optical vortex on the axis, i.e., a phase singularity in which the field vanishes. The integer number m represents the topological charge of the vortex and corresponds to the amount of OAM (in unit of ħ) carried by each photon in the beam. In ref. [7] we presented the generation of a Gaussian bipartite CV entangled state carrying OAM. There we endowed the Gaussian bipartite entangled state generated by a standard below-threshold type-II OPO with non-zero OAM. The CV entanglement, established between orthogonally polarized modes, is, then, imprinted between non-zero OAM modes by using a liquid crystal-based optical device commonly known as “q-Plate” (qP) [8]. Afterwards, the state is completely characterized by means of a reconfigurable Homodyne Detector (HD) capable of measuring quadratures relative to helical modes. In this way, we have provided a complete characterization of a multi-distinguishable polarization-OAM CV entangled state.
2. Results
Starting from a set of collected data we have reconstructed several two-helical-mode Covariance Matrices (CM) relative to bipartite entangled states. A typical experimental matrix is
which is in the so called standard form [9] where the diagonal elements contain the information on the average photon number of the single entangled mode, while the presence of non-vanishing terms in the off-diagonal blocks is a signature of entanglement between the two modes. This is proven by applying the Peres-Horodecki-Simon (PHS) [10,11,12] and the Duan Criteria [13]. Both inseparability criteria translate into inequalities written in terms of the CM’s elements ([14], [Equations (8) and (9)]). Applying those inequalities to the matrix in Equation (1) we obtain in both cases values that are by far over the bound. In the first case, the violation is 17 times its standard deviation, in the second case 8 times.
3. Materials and Methods
The starting point is the bipartite entangled Gaussian State (GS) generated by a type-II below-threshold OPO. In our experiment (sketched in Figure 1) the OPO works in frequency degeneration hence the two beams have the same frequency (@1064 nm) and emerge from the OPO as two Continuous Wave (CW) collinear cross-linearly-polarized beams each in a thermal state. Both the beams have a Gaussian transverse profile (TEM) so at this stage they do not carry OAM.
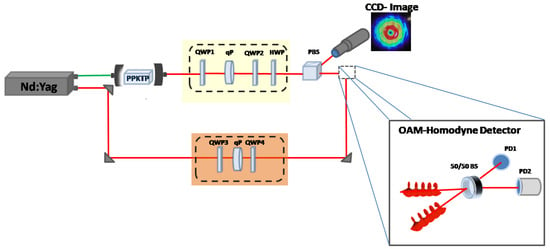
Figure 1.
Schematic of the experimental set-up. The second-harmonic output of a CW Nd:Yag laser, internally frequency doubled, is used as pump for an OPO based on a -cut PPKTP type-II crystal that generates a pair of frequency-degenerate orthogonally-polarized modes. The OPO threshold is mW and it is operated at of the threshold value. The yellow shadowed area including two quarter-wave plates (QWP1 and QWP2), a q-plate (qP) and a half-wave plate (HWP), represents the branch designed to manipulate the polarization and the OAM of the entangled beam. A similar set of optical components is employed along the LO branch to directly homodyne helical modes (dark orange shadow). The bottom-right inset shows an enlarged view of the homodyne detector.
The two beams are endowed with OAM thanks to a qP that couples polarization and OAM degrees of freedom. This device is essentially made up of a thin film of liquid crystals placed between two glass plates. It is birefringent, with a birefringence retardation that can be electrically tuned. Moreover it possesses a singular pattern of the optic axis with an integer or half-integer topological charge q. The optical action of such a device is described by the operator defined as follows:
denotes a beam with OAM m and polarization , with L (R) standing for left (right) circular polarization. From Equation (2) descends that a qP transforms the ingoing beam into two contributions, so acting as a beam-splitter in the OAM space. The first part is a beam essentially unmodified for what concerns both polarization and OAM. In the second, the polarization is flipped and the OAM is increased or decreased of depending on the initial polarization. The relative weights of the two contributions depend on the birefringence retardation . For an optimal tuning ( a single circularly polarized beam passing through the qP flips its polarization and acquires quanta of OAM. In our setup so that the two orthogonally polarized modes acquire OAM (). The qP is downstream of a quarter-wave plate (QWP1) aligned at that transforms the cross linear polarizations into cross circular ones. Then the two circular modes undergo the qP transformation:
The final modes are still co-propagating with opposite amounts of OAM . The distinguishability, that previously relied only on the polarization d.o.f., is now possible also by OAM.
In order to retrieve the experimental CM we adapted the single HD scheme presented in Ref. [15]. To this aim, besides homodyinig the two modes outing from the OPO, we also need to homodyne their following linear combinations
also carrying OAM. These four auxiliary modes can be easily obtained manipulating the two modes at the OPO output. More in detail, by rotating QWP1 so that its fast/slow axes coincide with , we have
By grouping modes with the same polarization it is easy to recognize the auxiliary modes c and d that have opposite circular polarizations and carry opposite amounts of OAM ()
In a similar way, by removing the first QWP1 so that the two modes enter the qP as linear combinations of circular polarizations
we obtain the opposite circularly polarized modes e and f carrying opposite OAM
A second quarter-wave plate (QWP2) transforms the orthogonal circular polarization back to orthogonal linear and eventually a half-wave plate (HWP) and a polarizing beam splitter (PBS) in front of the homodyne allows selecting which of the modes effectively reaches the detection stage. Homodyning these six modes requires a further effort with respect to standard homodyne detection involving modes with vanishing OAM. Homodyne detection relies indeed on the controlled interference, on a balanced BS, between the optical field under scrutiny and a strong coherent beam called Local Oscillator (LO). Hence, we have designed the LO so to easily switch between modes and . Thanks to this setup we have been able to homodyne these six modes routinely reaching a homodyne visibility of . This value of the visibility together with the cavity output coupling, the qP transmission, and all the other optical losses we estimate an overall collection efficiency of .
4. Conclusions
In conclusion, we have efficiently generated a bipartite continuous-variable entangled state endowed with non-zero OAM. Moreover we have performed its complete experimental characterization by measuring its full covariance matrix, using an OAM-reconfigurable single homodyne detection scheme. This experimental set-up has the potential to be generalized for generating multipartite quantum entangled states exploiting a hybrid discrete-continuous variable encoding.
References
- Grosshans, F.; Grangier, P. Continuous Variable Quantum Cryptography Using Coherent States. Phys. Rev. Lett. 2002, 88, 057902. [Google Scholar] [CrossRef] [PubMed]
- Grosshans, F.; van Assche, G.; Wenger, J.; Brouri, R.; Cerf, N.J.; Grangier, P. Quantum key distribution using gaussian-modulated coherent states. Nature 2003, 421, 238. [Google Scholar] [CrossRef]
- Ou, Z.Y.; Pereira, S.F.; Kimble, H.J.; Peng, K.C. Realization of the Einstein-Podolsky-Rosen paradox for continuous variables. Phys. Rev. Lett. 1992, 68, 3663. [Google Scholar] [CrossRef]
- Bowen, W.P.; Schnabel, R.; Lam, P.K.; Ralph, T.C. Experimental characterization of continuous-variable entanglement. Phys. Rev. A 2004, 69, 012304. [Google Scholar] [CrossRef]
- Laurat, J.; Keller, G.; Oliveira-Huguenin, J.A.; Fabre, C.; Coudreau, T.; Serafini, A.; Adesso, G.; Illuminati, F. Entanglement of two-mode Gaussian states: characterization and experimental production and manipulation. J. Opt. B 2005, 7, S577. [Google Scholar] [CrossRef]
- D’Auria, V.; Fornaro, S.; Porzio, A.; Solimeno, S.; Olivares, S.; Paris, M.G.A. ; Full Characterization of Gaussian Bipartite Entangled States by a Single Homodyne Detector. Phys. Rev. Lett. 2009, 102, 020502. [Google Scholar] [CrossRef] [PubMed]
- Pecoraro, A.; Cardano, F.; Marrucc, L.; Porzio, A. Continuous-variable entangled states of light carrying orbital angular momentum. Phys. Rev. A 2019, 100, 012321. [Google Scholar] [CrossRef]
- Marrucci, L.; Manzo, C.; Paparo, D. ; Optical Spin-to-Orbital Angular Momentum Conversion in Inhomogeneous Anisotropic Media. Phys. Rev. Lett. 2006, 96, 163905. [Google Scholar] [CrossRef] [PubMed]
- Olivares, S. Quantum optics in the phase space. Eur. Phys. J. Spec. Top. 2012, 203, 3. [Google Scholar] [CrossRef]
- Peres, A. Separability Criterion for Density Matrices. Phys. Rev. Lett. 1996, 77, 1413. [Google Scholar] [CrossRef] [PubMed]
- Horodecki, P. Separability criterion and inseparable mixed states with positive partial transposition. Phys. Lett. A 1997, 232, 333. [Google Scholar] [CrossRef]
- Simon, R. Peres-Horodecki Separability Criterion for Continuous Variable Systems. Phys. Rev. Lett. 2000, 84, 2726. [Google Scholar] [CrossRef] [PubMed]
- Duan, L.; Giedke, G.; Cirac, J.; Zoller, P. Inseparability Criterion for Continuous Variable Systems. Phys. Rev. Lett. 2000, 84, 2722. [Google Scholar] [CrossRef] [PubMed]
- Buono, D.; Nocerino, G.; Solimeno, S.; Porzio, A. Different operational meanings of continuous variable Gaussian entanglement criteria and Bell inequalities. Laser Phys. 2014, 24, 074008. [Google Scholar] [CrossRef]
- D’Auria, V.; Porzio, A.; Solimeno, S.; Olivares, S.; Paris, M.G.A. Characterization of bipartite states using a single homodyne detector. J. Opt. B Quantum Semiclass. Opt. 2005, 7, S750. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).