Testing a Best-Fit Hydrodynamical Model Using PCA †
Abstract
:1. Introduction
2. Materials and Methods
- TRENTo, a parametric wounded nucleon model for generation of initial conditions for hydrodynamics in HIC [5];
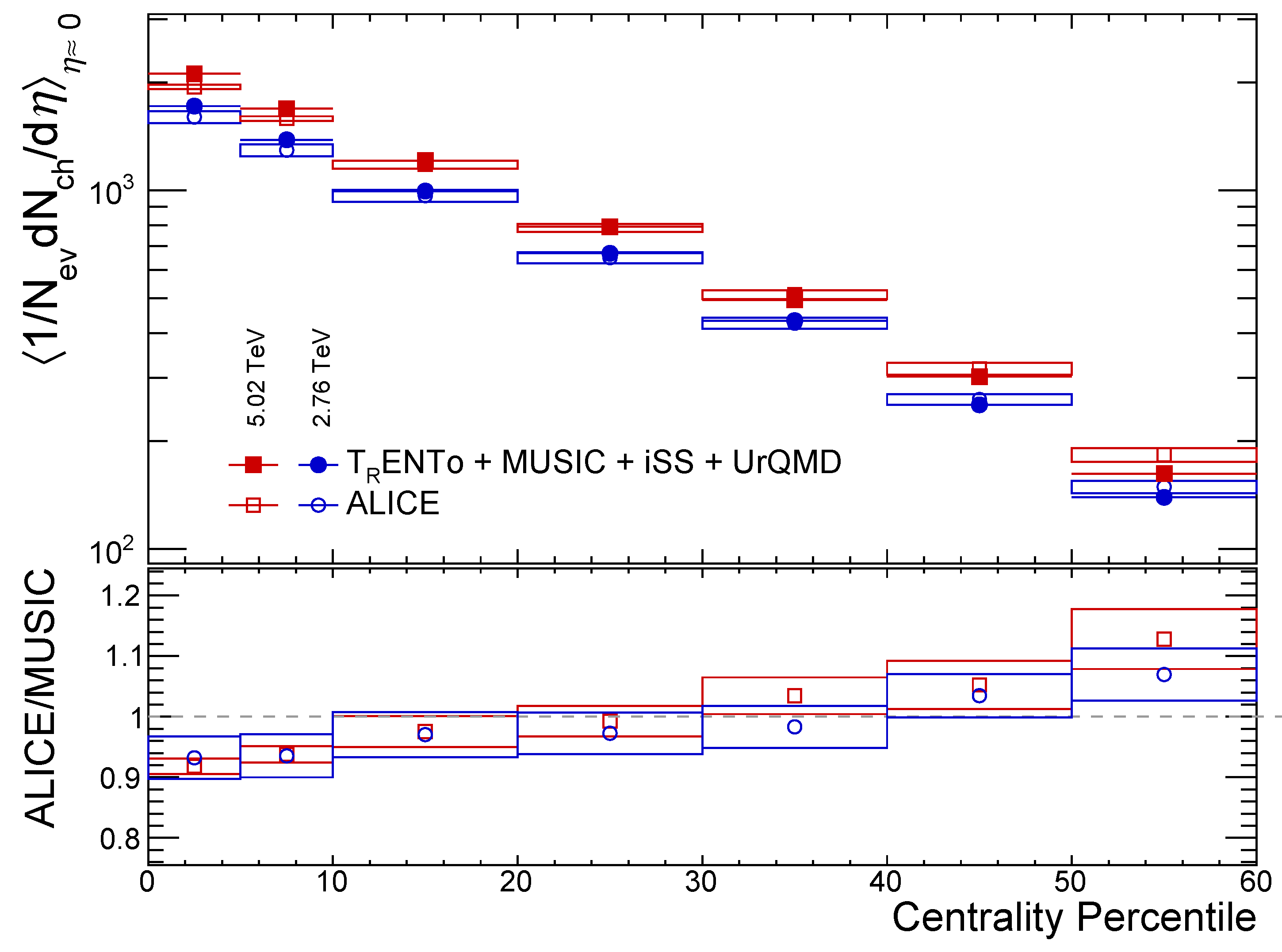
3. Results
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Heinz, U.; Snellings, R. Collective flow and viscosity in relativistic heavy-ion collisions. Ann. Rev. Nucl. Part. Sci. 2013, 63, 123–151. [Google Scholar] [CrossRef]
- Petersen, H.; Steinheimer, J.; Burau, G.; Bleicher, M.; Stöcker, H. Fully integrated transport approach to heavy ion reactions with an intermediate hydrodynamic stage. Phys. Rev. 2008, C78, 044901. [Google Scholar] [CrossRef]
- Bernhard, J.E.; Moreland, J.S.; Bass, S.A.; Liu, J.; Heinz, U. Applying Bayesian parameter estimation to relativistic heavy-ion collisions: simultaneous characterization of the initial state and quark-gluon plasma medium. Phys. Rev. 2016, C94, 024907. [Google Scholar] [CrossRef]
- Bernhard, J.E. Bayesian Parameter Estimation for Relativistic Heavy-Ion Collisions. Ph.D. Thesis, Duke University, Durham, The United States, 19 April 2018. [Google Scholar]
- Moreland, J.S.; Bernhard, J.E.; Bass, S.A. Alternative ansatz to wounded nucleon and binary collision scaling in high-energy nuclear collisions. Phys. Rev. 2015, C92, 011901. [Google Scholar]
- Bass, S.A.; Belkacem, M.; Bleicher, M.; Brandstetter, M.; Bravina, L.; Ernst, C.; Gerland, L.; Hofmann, M.; Hofmann, S.; Konopka, J.; et al. Microscopic Models for Ultrarelativistic Heavy Ion Collisions. Prog. Part. Nucl. Phys. 1998, 41, 255–369. [Google Scholar] [CrossRef]
- Bleicher, M.; Zabrodin, E.; Spieles, C.; Bass, S.A.; Ernst, C.; Soff, S.; Bravina, L.; Belkacem, M.; Weber, H.; Stöcker, H.; et al. Relativistic Hadron-Hadron Collisions in the Ultra-Relativistic Quantum Molecular Dynamics Model (UrQMD). J. Phys. 1999, G25, 1859–1896. [Google Scholar] [CrossRef]
- Bhalerao, Rajeev S. and Ollitrault, Jean-Yves and Pal, Subrata and Teaney, Derek. Principal Component Analysis of Event-by-Event Fluctuations. Phys. Rev. Lett. 2015, 114, 152301. [CrossRef] [PubMed]
- Schenke, B.; Jeon, S.; Gale, C. (3+1)D hydrodynamic simulation of relativistic heavy-ion collisions. Phys. Rev. 2010, C82, 014903. [Google Scholar] [CrossRef]
- Schenke, B.; Jeon, S.; Gale, C. Higher flow harmonics from (3+1)D event-by-event viscous hydrodynamics. Phys. Rev. 2012, C85, 024901. [Google Scholar]
- Aamodt K., Abrahantes Quintana A., Adamova D., Adare A., Aggarwal M., Aglieri Rinella G., Agocs A.G., Aguilar Salazar S., Ahammed Z., Ahmad N., Ahmad Masoodi A., et al (ALICE Collaboration). Centrality Dependence of the Charged-Particle Multiplicity Density at Midrapidity in Pb-Pb Collisions at = 2.76 TeV. Phys. Rev. Lett. 2011, 106, 032301. [CrossRef] [PubMed]
- Adam J. , Adamova D., Aggarwal M.M., Aglieri Rinella G., Agnello M., Agrawal N., Ahammed Z., Ahmad S., Ahn S.U., Aiola S., Akindinov A., et al (ALICE Collaboration). Anisotropic Flow of Charged Particles in Pb-Pb Collisions at = 5.02 TeV. Phys. Rev. Lett. 2016, 116, 222302. [CrossRef]
- Sirunyan A.M., Tumasyan A., Adam W., Ambrogi F., Asilar E., Bergauer T., Brandstetter J., Brondolin E., Dragicevic M., Erö J., Flechl M., et al (CMS Collaboration). Principal-component analysis of two-particle azimuthal correlations in PbPb and pPb collisions at CMS. Phys. Rev. 2017, C96, 064902.

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, T.N.d.; Chinellato, D.D.; Souza, R.D.d.; Hippert, M.; Luzum, M.; Noronha, J.; Takahashi, J. Testing a Best-Fit Hydrodynamical Model Using PCA. Proceedings 2019, 10, 5. https://doi.org/10.3390/proceedings2019010005
Silva TNd, Chinellato DD, Souza RDd, Hippert M, Luzum M, Noronha J, Takahashi J. Testing a Best-Fit Hydrodynamical Model Using PCA. Proceedings. 2019; 10(1):5. https://doi.org/10.3390/proceedings2019010005
Chicago/Turabian StyleSilva, Tiago Nunes da, David Dobrigkeit Chinellato, Rafael Derradi de Souza, Maurício Hippert, Matthew Luzum, Jorge Noronha, and Jun Takahashi. 2019. "Testing a Best-Fit Hydrodynamical Model Using PCA" Proceedings 10, no. 1: 5. https://doi.org/10.3390/proceedings2019010005
APA StyleSilva, T. N. d., Chinellato, D. D., Souza, R. D. d., Hippert, M., Luzum, M., Noronha, J., & Takahashi, J. (2019). Testing a Best-Fit Hydrodynamical Model Using PCA. Proceedings, 10(1), 5. https://doi.org/10.3390/proceedings2019010005




