1. Introduction
In high energy hadronic and nuclear collisions, a deconfined state of matter is created, where chiral symmetry is restored. The system expands and cools down, leading to the breaking of chiral symmetry. The possible consequence of the restoration and subsequent breaking of chiral symmetry is the formation of Disoriented Chiral Condensates (DCC) [
1,
2,
3,
4], the regions formed where the average chiral order parameter differs from its value in the vacuum. This can be explained by the Lagrangian of the linear sigma model [
2]. From the effective potential of the linear sigma model, it is clear that the region is in non-equilibrium. By radiating pions and kaons, the region equilibrates.
One can observe a distinct distribution of kaons produced by DCCs relative to generic (normal) production [
3,
6]. Under isospin symmetry, generic production yields an equal fraction of neutral and charged kaons. However, metastable DCC domains will favour the production of kaons with a particular isospin. If we consider SU(3) symmetry with massless quarks, the chiral order parameter can be described as
. Let us consider the probability distribution of the event wise ratio of the total number of neutral kaons to the total number of kaons produced in a single event. Let
be the fraction of neutral kaons over total kaons,
On general grounds, one expects because of isospin conservation in the strong interaction, that the production of all kaons species is equally probable. This mechanism leads to a binomial distribution of neutral kaon fraction peaked at one-half, i.e,
. If a DCC is formed, then the chiral field is misaligned with respect to the true vacuum direction. It realigns to the true vacuum direction, by radiating kaons. The probability distribution of the neutral kaon fraction taking into account the kaons from the DCC domain is very different from that of a generic case and was shown [
3,
6] to be of the form
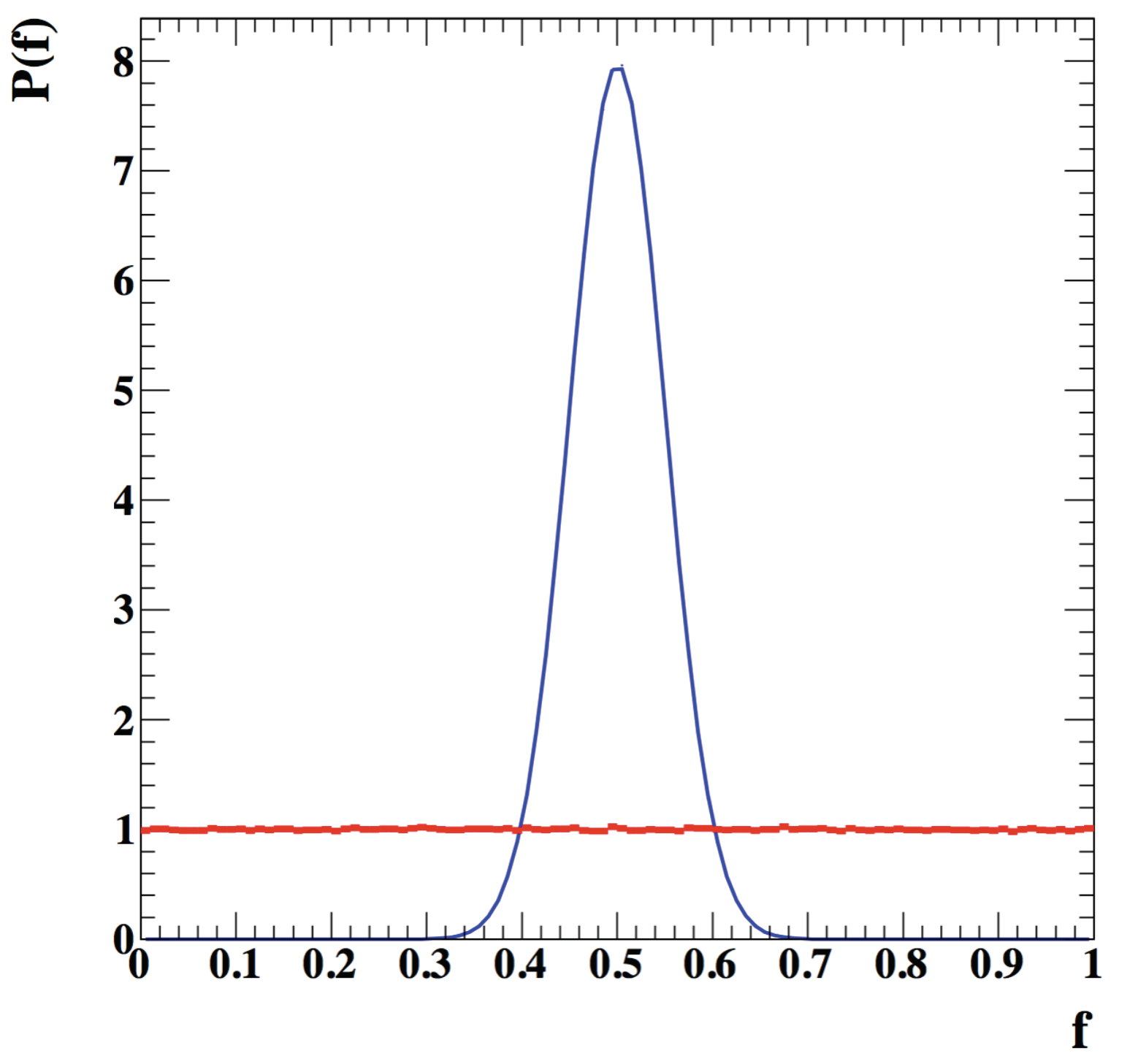
The distribution
for DCC (uniform) in
Figure 1 is completely different from that for a generic distribution (binomial). A significant departure from the value 0.5 for
can then provide the cleanest evidence for the formation of a DCC. Gavin and Kapusta [
7] proposed that the observable
[
8] can be used to study isospin fluctuations in the strangeness (kaon) sector by virtue of the central limit theorem. They also predicted if collision centrality is varied, isospin fluctuation can appear as a change in magnitude of dynamical isospin observable.
2. Fluctuation Observable:
The robust statistical observable
is useful for the study of fluctuations, because the identification techniques for charged and neutral kaons feature different efficiencies. Neutral kaons
and
are observed as
and
. We use the multiplicity of
as the neutral kaons as
is difficult to observe due to its long lifetime. These are detected by the decay
(69.2%BR). Evaluation of the correlation between
and
yield is obtained with a measurement of the relative isospin covariance
where
and
are the number of
and
respectively. We take
and
for kaons. This observable is robust against detection efficiency. The charged (
) and neutral variance (
) terms can be written as
To study isospin fluctuations in the kaon sector, the isospin observable can be defined as
The first two terms essentially measure the fluctuations of charged particle and neutral particle fluctuations. The third term measures the strength of charged-neutral kaon correlation. For purely statistical fluctuations, in the limit of very large multiplicity, these individual terms would become unity. However, for finite multiplicity, these terms can deviate from unity even if there are no dynamical fluctuations. So it is difficult to reach a conclusion based on the measurements of the individual terms. However, when all three terms are added to form
, by construction, the finite multiplicity statistical fluctuations are eliminated. Therefore,
becomes zero for purely statistical fluctuations and non-zero only in the presence of dynamical fluctuations or correlations [
9]. In this analysis we use
to study the hidden fluctuation among strange particles because,
the observable is robust against detection efficiency.
it measures the relative strength of charge-charge, neutral-neutral and charge-neutral correlations
it serves as an indicator of any anomaly in the production of kaon fluctuation which might signal the existence of kaon DCCs
3. Analysis Details
The measurement is based on ALICE data from Pb-Pb collisions at = 2.76 TeV acquired during Run 1 in 2010. 13 M minimum bias events are selected for data analysis. Two Monte-Carlo (MC) event generators, HIJING and AMPT are considered to study the sensitivity of to different particle production dynamics. In this work, 3 M HIJING events are chosen to study. We have taken 3 different tunes of AMPT event generators, (i) string melting ON, rescattering OFF (39 M), (ii) string melting OFF, rescattering ON (53 M), (iii) string melting ON, rescattering ON (38.94 M).
This analysis is based on minimum bias (MB) events. The MB trigger was based on a combination of information of the hits from SPD and two sides of V0 detectors. A vertex cut is applied to select events within 10 cm to maintain uniform acceptance in the detectors and to minimize the variations of the efficiency with “z”. The collision centrality was determined using the V0 multiplicity. We have considered various centralities for this analysis: 0–10%, 10–20%, 20–40%, 40–60% and 60–80%. Charged kaons () are selected based on the signals measured from the combined information of TPC and TOF detectors using Particle Identification (PID) method. The are selected in the kinematic ranges: 0.5 and 0.2 1.5 GeV/c. The measurement of neutral kaons is carried out based on the weak decay . These decays are identified from the decay topology of V0 particle and the invariant mass of . The decay vertex of is reconstructed and calculated from pairs of detected tracks. Standard ALICE topological cuts are used to obtain the neutral kaons. Neutral kaons with a transverse momentum within 0.4 1.5 GeV/c measured in the pseudo-rapidity range 0.5 are selected with a invariant mass cut 0.48 GeV < < 0.515 GeV. Similar cuts are used in MC models to select charged and neutral kaons.
4. Results
Once we obtain the number of
and
in each centrality with specific acceptance, average numbers of singles and pairs can be calculated. Values of
are then acquired for each centrality bins. The values of
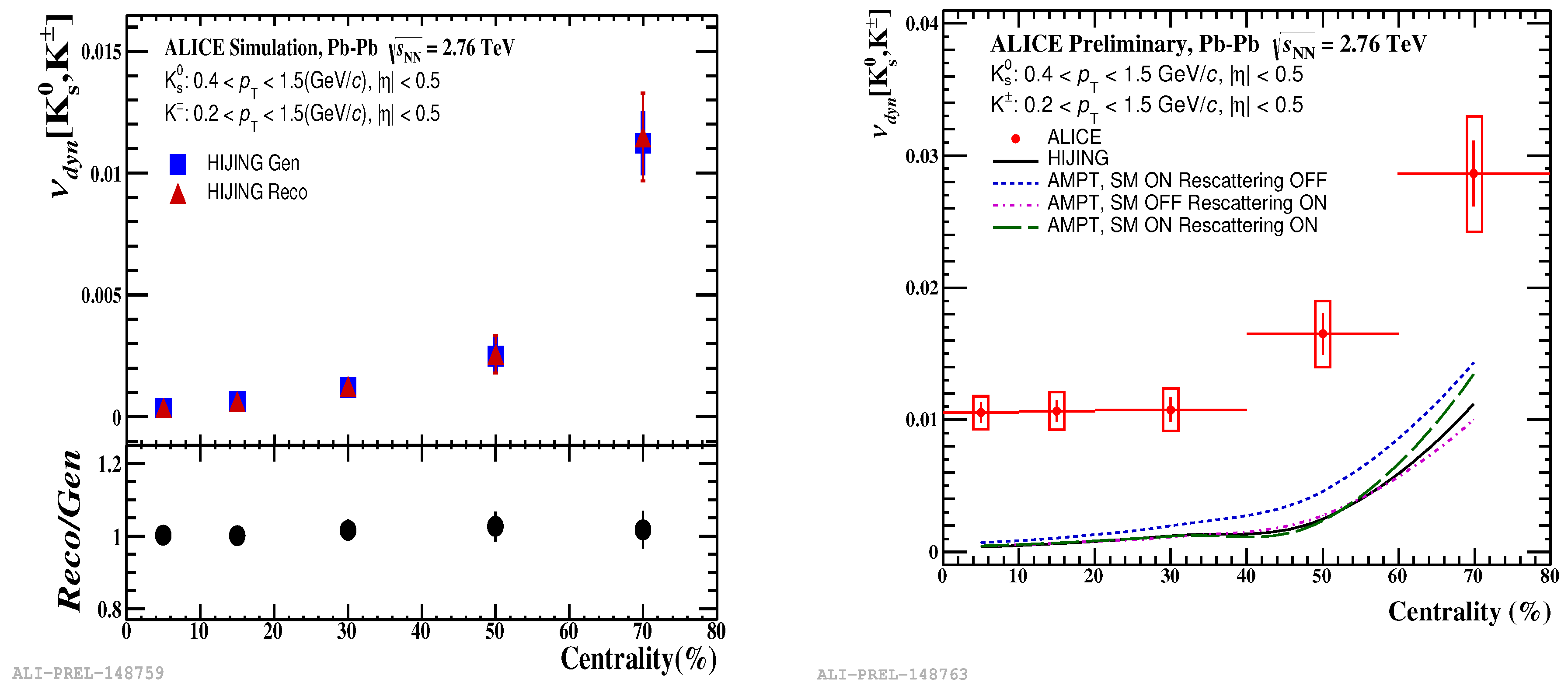
for both HIJING generated and reconstructed level are obtained and shown in the top part of
Figure 2a, for various centralities. Reconstructed HIJING is obtained by passing generated HIJING through GEANT (Geometry and tracking). The values are bin width corrected. The values of
for both HIJING generated and reconstructed are steeply rising and are positive, when measured as a function of collision centrality (towards peripheral collision). The values in each centrality bin are in agreement with each other. The statistical uncertainty in the values of
for HIJING MCs are calculated by sub-sampling method. The Bottom panel of
Figure 2a depicts the ratio of reconstructed to generated values of
as a function of centrality. The values of the ratio are within few percents of unity in all centrality bins. The errors in the ratios are calculated by binomial error propagation method. The measurement of
in HIJING MC is unaffected by the detector efficiencies.
The ALICE data for
are compared to MC model predictions in
Figure 2b. The ALICE data are shown with the red solid circles and coloured dashed lines show HIJING and AMPT model calculations. All values are corrected for centrality bin width. Statistical errors were evaluated with sub-sampling method.
Measured values are positive and significantly larger than those obtained with the model calculations. The trend is different in data compared to model predictions. The values are flat in central to mid-central events (0–40%) and rise towards peripheral collisions (40–80%). The covariance term of becomes positive in charge neutral correlations and cross correlations are weak in data. We observe a violation of 1/n scaling in data, where “n” is the number of sources. Both the models predict 1/n scaling. The two models fail to describe the behaviour of data. The anomalous behaviour in data indicates possible isospin fluctuation in kaon sector.
We observe that the values for AMPT except for string melting (SM) ON, rescattering OFF (blue lines) are in agreement with HIJING in each centrality bin. The values are a little bit higher for SM ON, rescattering OFF, compared to other cases. The hadronic rescattering includes decay of resonance particles, when it is OFF resonance decay ceases. This might influence the decrease in the number of produced particles and increase the value of .
5. Conclusions
The first measurement of isospin fluctuations in kaon sector in Pb-Pb collisions at = 2.76 TeV has been performed. Neutral-charge kaon correlation in the data shows anomalous behaviour (1/n scaling is violated), when studied as a function of collision centrality. This violation might indicate possible isospin fluctuation in kaon sector. HIJING and AMPT, fail to describe the behaviour of data. The values for data are larger compared to models in each centrality. The AMPT results suggest that is sensitive to the production dynamics.