Linear Integrated Interface for Automatic Differential Capacitive Sensing †
Abstract
:1. Introduction
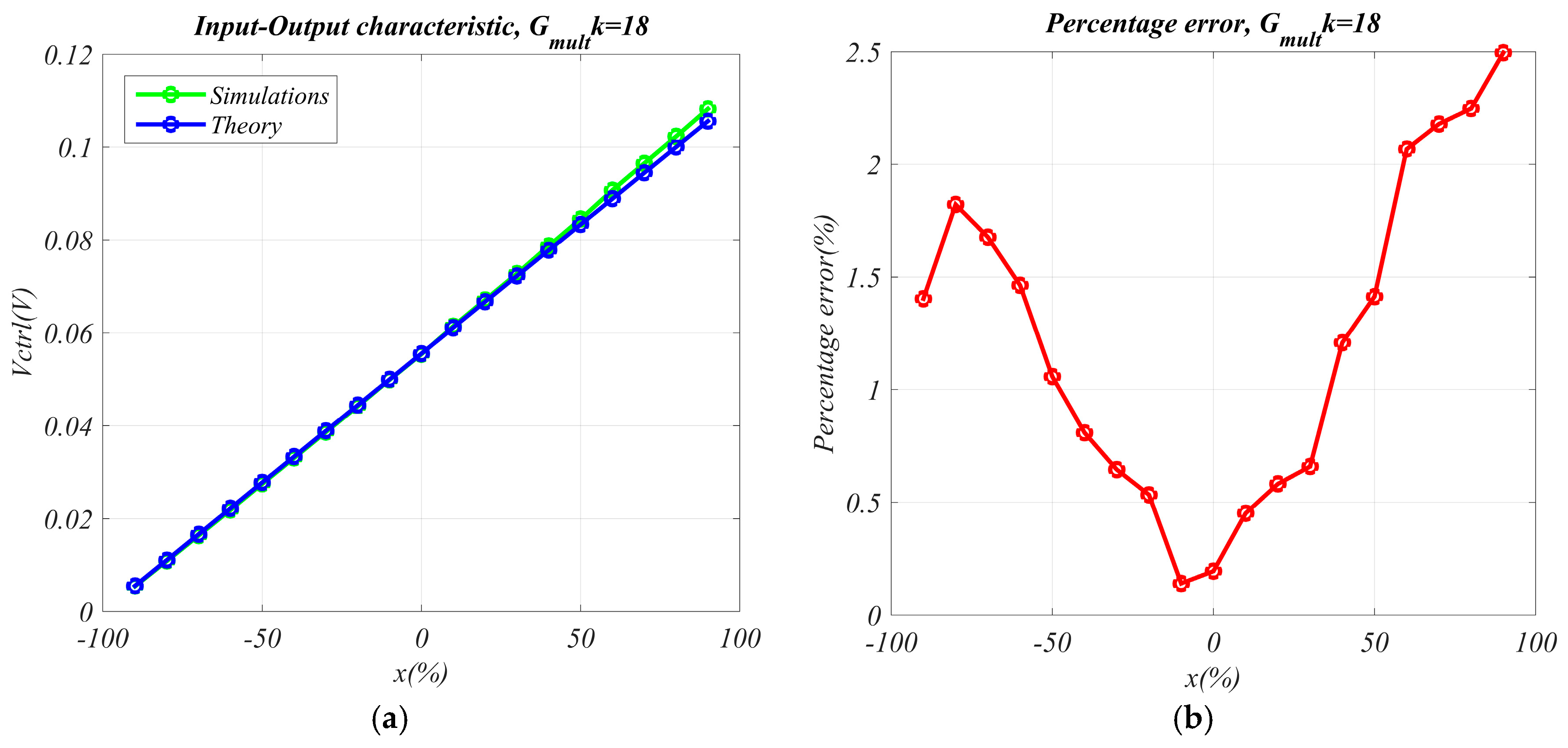
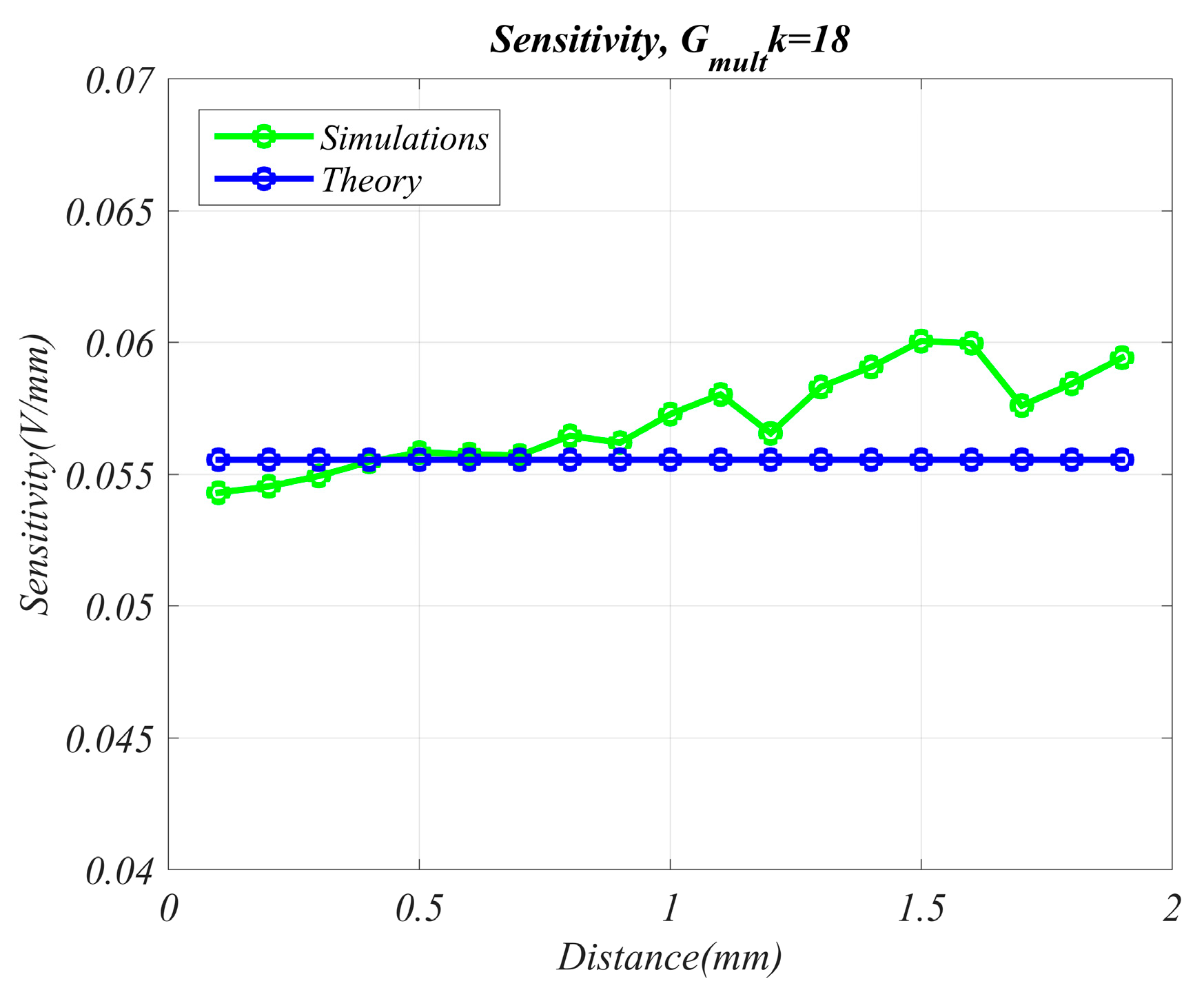
2. The Proposed Interface
3. Conclusions
Conflicts of Interest
References
- De Marcellis, A.; Ferri, G. Analog Circuits and Systems for Voltage-Mode and Current-Mode Sensor Interfacing Applications; Springer: Houten, The Netherlands, 2011. [Google Scholar]
- Baxter, K. Capacitive sensor basics. In Capacitive Sensors: Design and Applications; The Institute of Electrical and Electronics Engineers: New York, NY, USA, 1997; pp. 1–46. [Google Scholar]
- Ko, W.H. Trends and frontiers of MEMS. Sens. Actuators A Phys. 2007, 136, 62–67. [Google Scholar] [CrossRef]
- Kumar, B.; Rajita, G.; Mandal, N. A review on capacitive-type sensor for measurement of height of liquid level. Meas. Control 2014, 47, 219–224. [Google Scholar] [CrossRef]
- Puers, R. Capacitive sensors: when and how to use them. Sens. Actuators A Phys. 1993, A37–A38, 93–105. [Google Scholar] [CrossRef]
- Mochizuki, K.; Watanabe, K.; Masuda, T. A High-Accuracy High-Speed Signal Processing Circuit of Differential-Capacitance Transducers. IEEE Trans. Instrum. Meas. 1998, 47, 1244–1247. [Google Scholar] [CrossRef]
- Ferri, G.; Parente, F.R.; Stornelli, V. Analog current-mode interfaces for differential capacitance sensing. In Proceedings of the IEEE Sensors Applications Symposium (SAS), Catania, Italy, 20–22 April 2016; pp. 1–6. [Google Scholar]
- Lötters, J.C.; Olthuis, W.; Veltink, P.H.; Bergveld, P. A sensitive differential capacitance to voltage converter for sensor applications. IEEE Trans. Instrum. Meas. 1999, 48, 89–96. [Google Scholar] [CrossRef]
- George, B.; Kumar, V.J. Switched capacitor signal conditioning for differential capacitive sensors. IEEE Trans. Instrum. Meas. 2007, 56, 913–917. [Google Scholar] [CrossRef]
- Ferri, G.; Parente, F.R.; Stornelli, V.; D’Amico, A.; Pennazza, G.; Santonico, M. A standard CMOS technology fully-analog differential capacitance sensor front-end. In Proceedings of the IEEE International Workshop on Advances in Sensors and Interfaces (IWASI), Gallipoli, Italy, 18–19 June 2015; pp. 152–157. [Google Scholar]
- Ferri, G.; Stornelli, V.; Parente, F.R.; Barile, G. Full range analog Wheatstone bridge-based automatic circuit for differential capacitance sensor evaluation. Int. J. Circuit Theory Appl. 2016. [Google Scholar] [CrossRef]
- Ferri, G.; Parente, F.R.; Stornelli, V.; Barile, G.; Pantoli, L. Automatic bridge-based interface for differential capacitive full sensing. Procedia Eng. 2016, 168, 1585–1588. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barile, G.; Ferri, G.; Parente, F.R.; Stornelli, V.; Depari, A.; Flammini, A.; Sisinni, E. Linear Integrated Interface for Automatic Differential Capacitive Sensing. Proceedings 2017, 1, 592. https://doi.org/10.3390/proceedings1040592
Barile G, Ferri G, Parente FR, Stornelli V, Depari A, Flammini A, Sisinni E. Linear Integrated Interface for Automatic Differential Capacitive Sensing. Proceedings. 2017; 1(4):592. https://doi.org/10.3390/proceedings1040592
Chicago/Turabian StyleBarile, Gianluca, Giuseppe Ferri, Francesca Romana Parente, Vincenzo Stornelli, Alessandro Depari, Alessandra Flammini, and Emiliano Sisinni. 2017. "Linear Integrated Interface for Automatic Differential Capacitive Sensing" Proceedings 1, no. 4: 592. https://doi.org/10.3390/proceedings1040592
APA StyleBarile, G., Ferri, G., Parente, F. R., Stornelli, V., Depari, A., Flammini, A., & Sisinni, E. (2017). Linear Integrated Interface for Automatic Differential Capacitive Sensing. Proceedings, 1(4), 592. https://doi.org/10.3390/proceedings1040592









