Energy Estimation for Electret Harvester with Nonlinear Spring ^†

Abstract

A design of an electret-type vibration energy harvester using non-linear springs is described. The use of bi-stable springs enabling a snap-through behavior is a well-known technique known for improving the low-frequency performances of energy harvesters. The electrical power from our bi-stable energy harvester concept is estimated using a numerical computing tool and an electrical equivalent circuit model. We conclude that our bi-stable spring harvester concept obtains larger power at lower frequencies compared to a similar linear design.

1. Introduction

Many kinds of vibration sources can be found in our daily life or in industrial activities, etc. Vibration Energy Harvesting (VEH) technologies can produce sufficient electrical power to supply wireless sensors energy. Recently, energy harvesting is expected as an alternative to batteries for Internet of Things (IoT) applications [1,2]. Typical IoT wireless sensor nodes consist of sensors, a microcontroller, a low power wireless communication unit and a battery. The battery replacing or recharging costs prevent the wide spreading of the IoT. Provided that vibration energy harvesters generate enough power from vibration sources, the cost of battery replacement will be erased. The miniaturization of harvesting devices using Micro Electro Mechanical Systems (MEMS) fabrication processes has been considered by many researchers. MEMS energy harvesters are classified by their specific electromechanical conversion mechanisms into electrostatic, electromagnetic and piezoelectric types. Standard MEMS type electrostatic harvesters are designed as linear resonators fabricated by silicon Deep Reactive Ion Etching (DRIE). In a previous study, we have reported a bi-stable spring design for electrostatic harvesters [3]. Compared to other typical types of bi-stable springs design [4], ours does not require an initial compression force to get its bi-stable behavior. The linear resonators have a strong advantage for collecting maximum mechanical power thanks to their higher Q factors [5]. On the other hand, they exhibit a narrower bandwidth which can be an obstacle for efficiently harvesting real vibration sources, since most sources do not present a single frequency power spectrum but rather a widespread one. Due to their non-linear behavior, bi-stable springs present wider bandwidths and thus are more suitable to harvest power in real life applications. The design of this work’s bi-stable springs was carried out in a previous work [3]. In this study, we focus on computing the electrical power output of our bi-stable electret-based electrostatic harvester concept with respect to frequency and load resistance. The benefits of our bi-stable solution are highlighted by comparing its electrical behavior to the one of a similar linear harvester.

2. Materials and Methods

2.1. A Design and Simulation for Non-linear Resonator with Bi-stbale

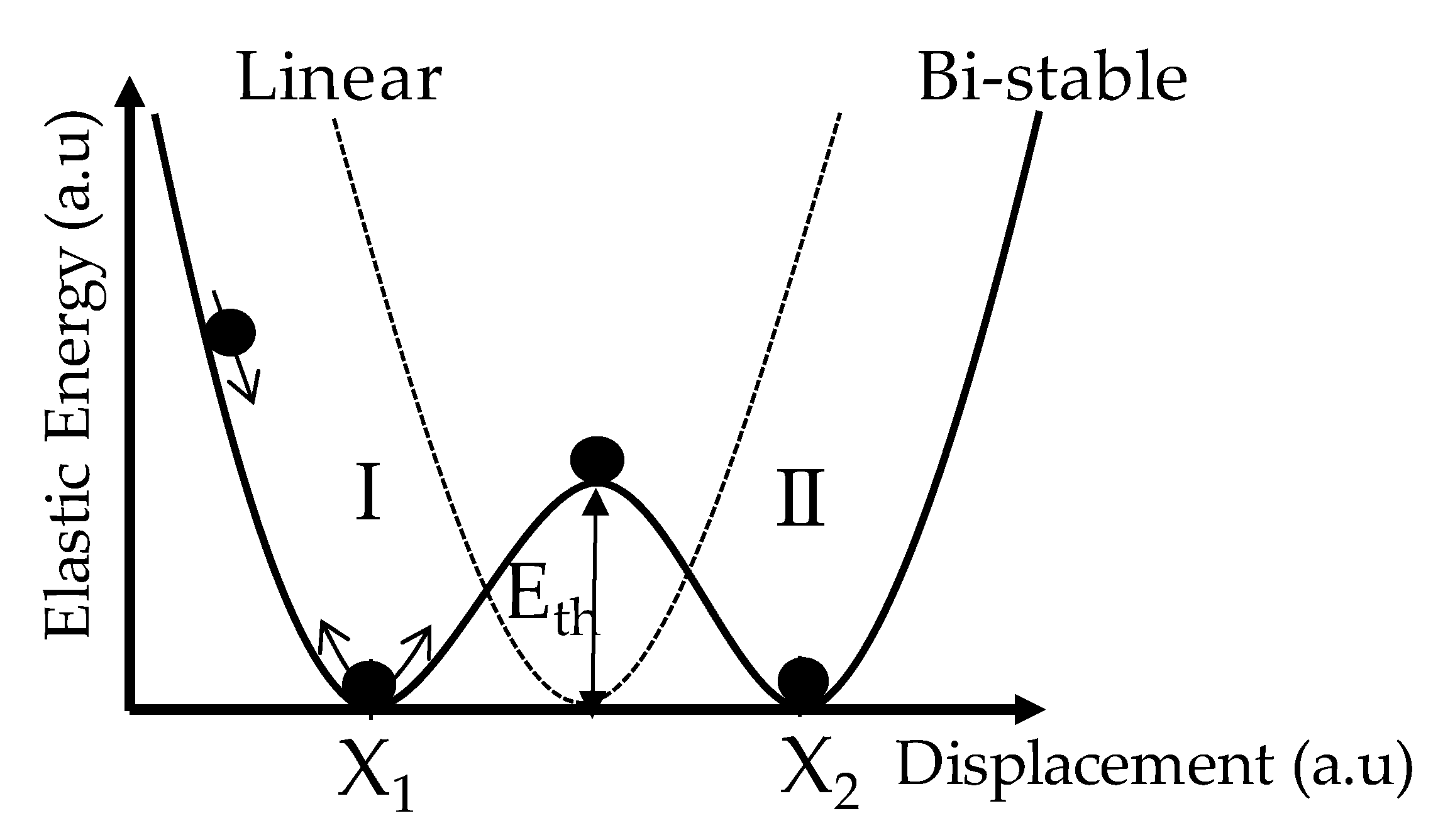
2.1.1. Bi-Stable Behavior

The bi-stable behavior is a non-linear phenomenon. As shown in Figure 1, this non-linearity will induce a double potential energy well profile (defined by Equation (1)) instead of the more classic single well profile exhibited by linear springs (defined by Equation (2)). The two stable positions x₁ and x₂, as well as the energy threshold E_th that has to be overcome to switch from stable state I to stable state II, are defined during the design phase.

Moreover, the bi-stable behavior is characterized by a snap-through motion. This non-linear switching behavior enables the harvesting of a wide range of vibration frequencies as long as the vibration source is powerful enough to trigger the transition. Another feature of our bi-stable harvester is the frequency response dependence over the input acceleration amplitude. As shown later in this article, the spring behavior is linear for small acceleration levels, softening for moderate levels and hardening for large levels.

$${\mathrm{E}}_{\mathrm{Bi}-\mathrm{stable}}=\frac{1}{4}{A}_2{x}^4-\frac{1}{2}{B}_2{x}^2$$

(1)

$$\mathrm{E}{ }_{\mathrm{Linear}}=\frac{1}{2}{A}_1{x}^2$$

(2)

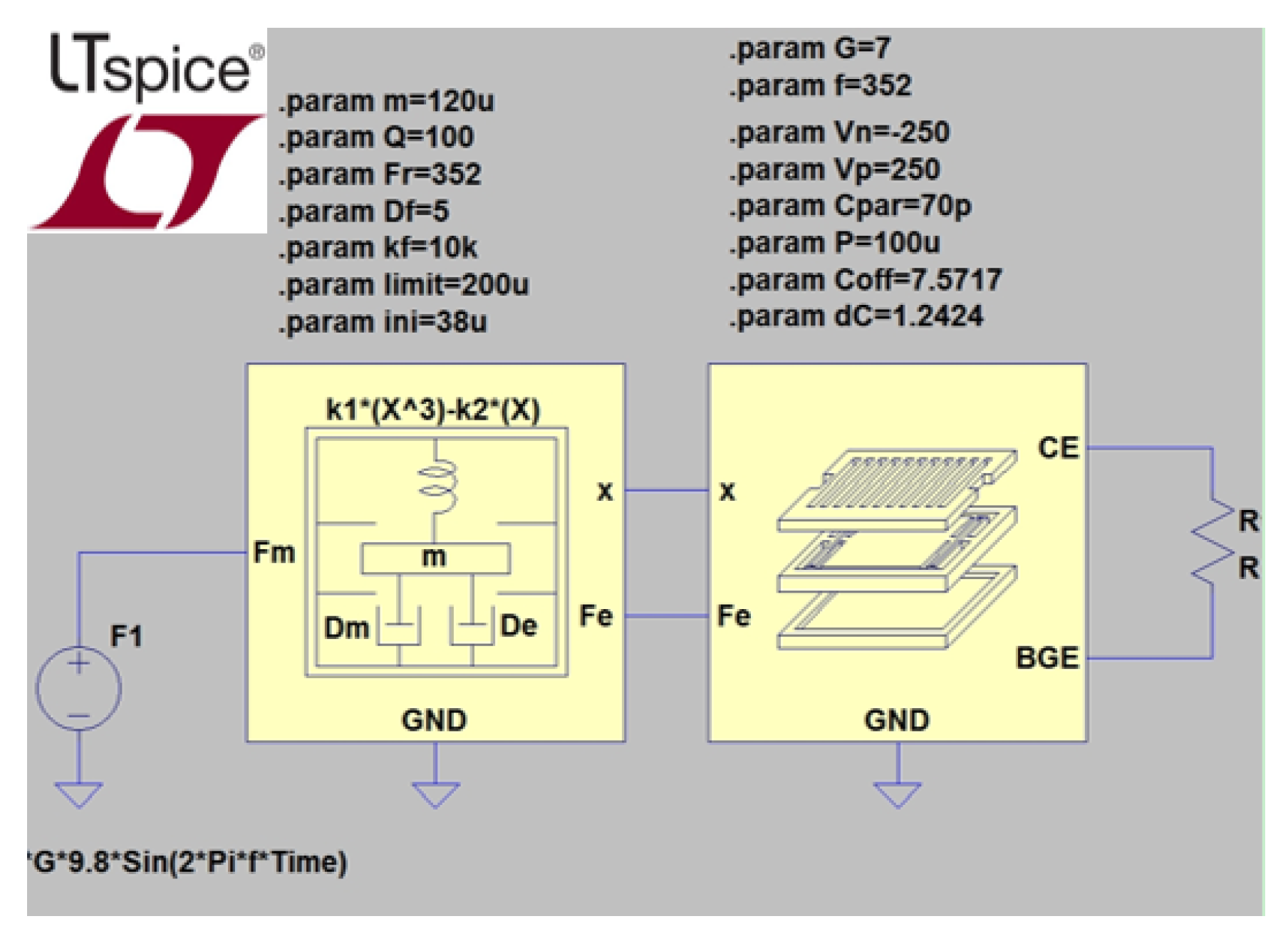
2.1.2. Analysis of Bi-Stable Motion by Finite Element Method (FEM), MATLAB, and SIMULINK

The frequency response of bi-stable motion was analyzed by the combination of structural and numerical analysis software. The structural analysis of our harvester was carried out by ANSYS 16.0, as shown in Figure 2 Each beam is 15 mm-long, 30 μm-wide and 525 μm-deep. The central mass weights 0.12 g. The structure material is silicon with Young’s modulus of 180 GPa and density of 2.33 g/cm³. A zoom on Figure 2 shows that the whole non-linear spring is composed of a parallel pair of two beams separated by a 30 μm space.

The resulting frequency response is shown in Figure 3. The bandwidth becomes wider depending on the applied acceleration. The natural frequency is 93 Hz. In the figure, the up-sweep frequency responses are shown in solid lines. Down-sweep frequency responses are shown in dotted lines. While the response seems to be linear for small amplitudes of applied acceleration (~0.01 G), the response changes from linear to softening and eventually to hardening as the acceleration increases. The two peaks observed around 160 Hz (dotted light blue and red) are harmonic responses due to the non-linearity inherent to the bi-stable spring.

3. Results

3.1. Electrical Power Estimation of Our Bi-Stable Electret-Based Electrostatic Energy Harvester

3.1.1. Equivalent Circuit for Electrostatic Harvester

To estimate the output power from our bi-stable energy harvester design, an equivalent circuit which consists of mechanical and electrical components have been established [5]. The model is shown in Fig.4. The mechanical sub-model was determined based on the equation of motion where parameter D_m is mechanical damping, D_e electrical damping, K₁ and K₂ respectively non-linear and linear spring coefficients, m total weight, and F_m external force. The displacement is transferred to the electrical sub-model for the calculation of electrical power. Electrical-field analysis were carried out to compute the varying capacitance of our electret-type harvester. The electrical power is eventually calculated from the voltage generated on the load resistance.

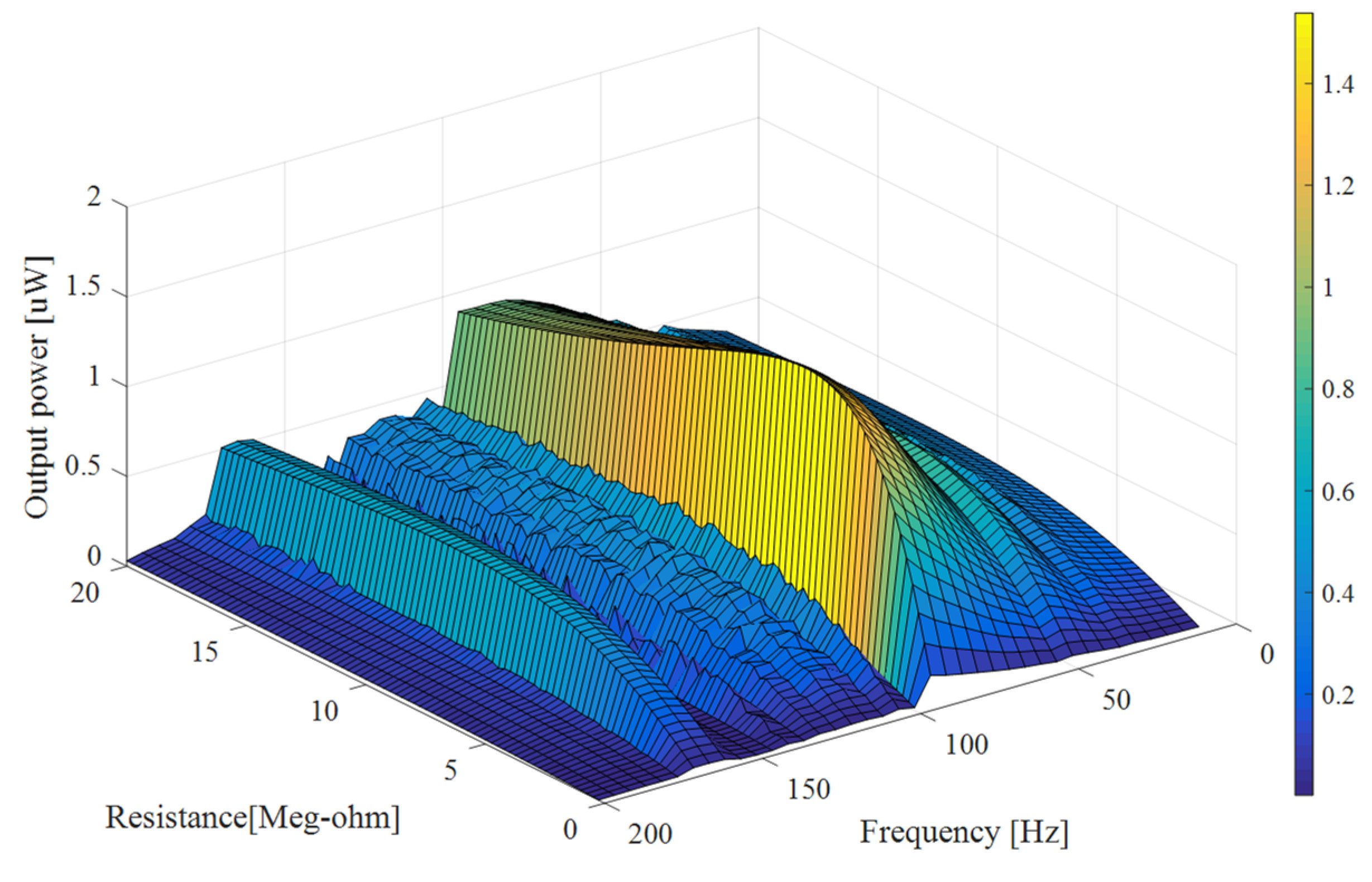
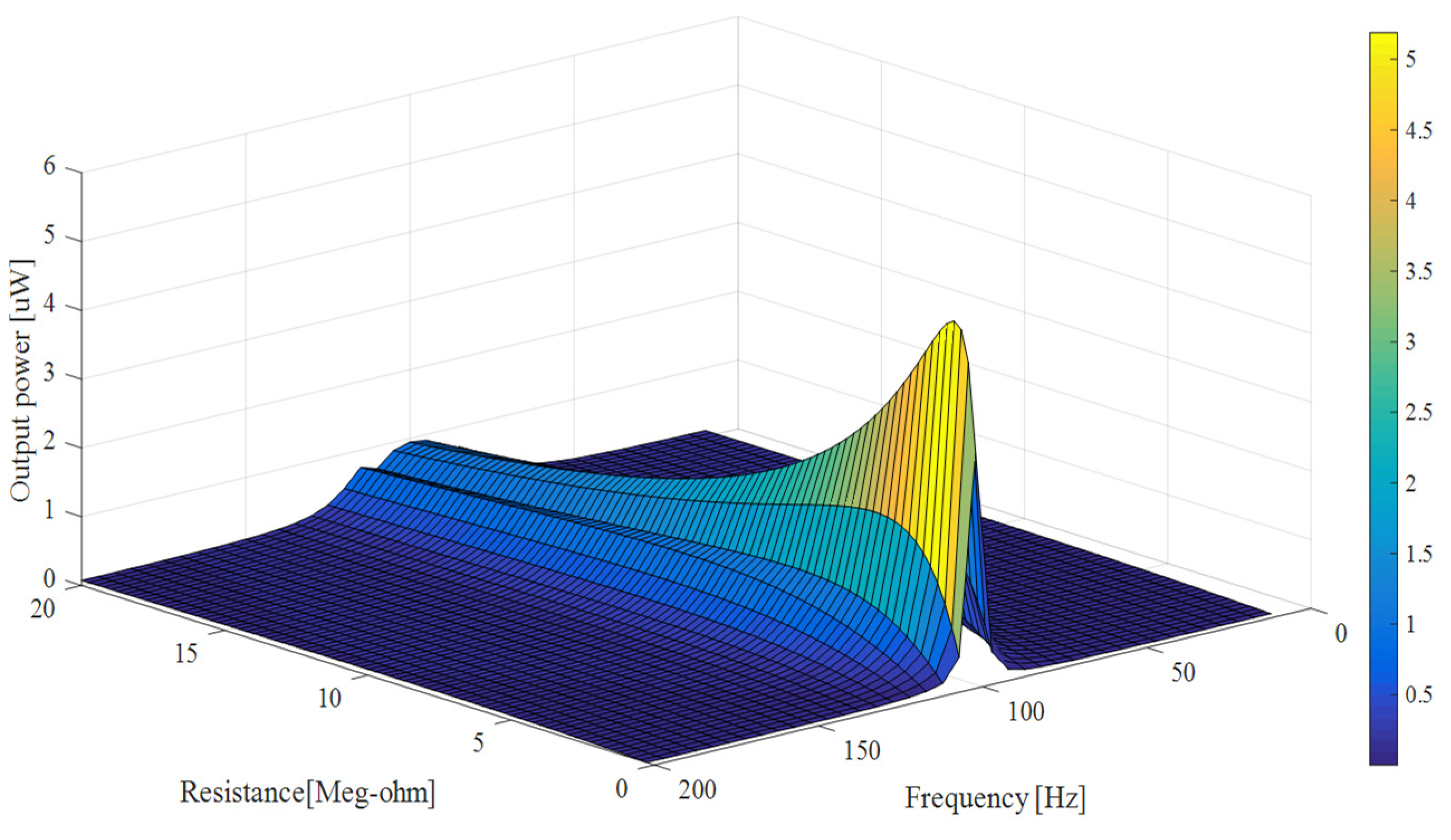
3.1.2. Comparison between Linear and Bi-Stable Harvesters Electrical Power Outputs

To highlight the benefits from our bi-stable design, we compare its power output response with respect to a linear harvester. The latter has the same mass, mechanical quality factor and a designed central frequency of 100 Hz. Simulation results of bi-stable and linear cases are shown in Figure 5 and Figure 6 respectively. The electrical power is plotted against both the load resistance and frequency.

The linear harvester produces a maximum power of 5 μW dissipated through a 1 MΩ load for an excitation frequency of 100 Hz. In the bi-stable case, the maximum electrical power is 1.5 μW for a 95 Hz excitation and a load resistance of 5 MΩ. While the frequency bandwidth of the linear harvester is limited by its mechanical quality factor, the bi-stable type harvester shows a wider bandwidth caused by the non-linear spring hardening effect.

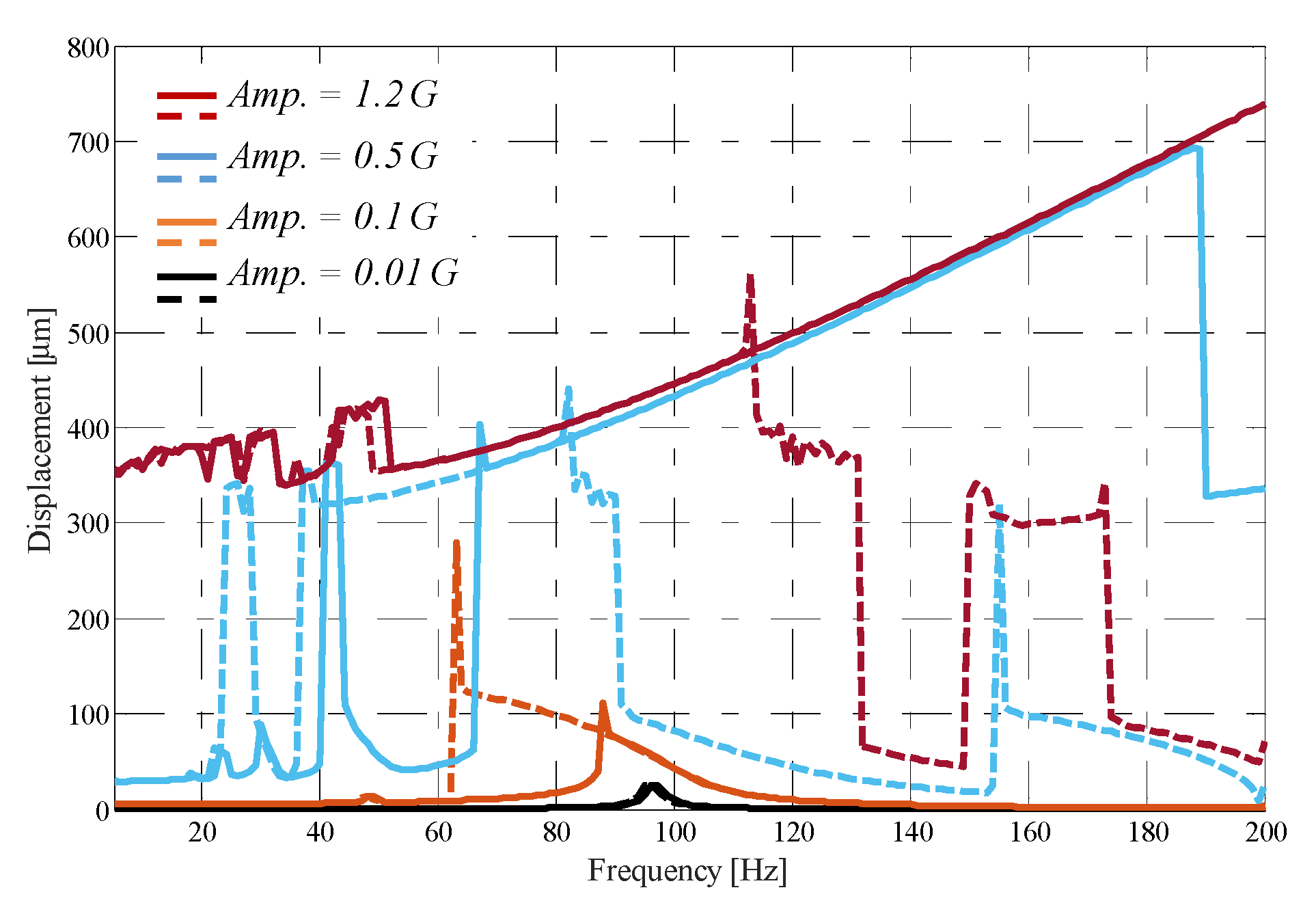
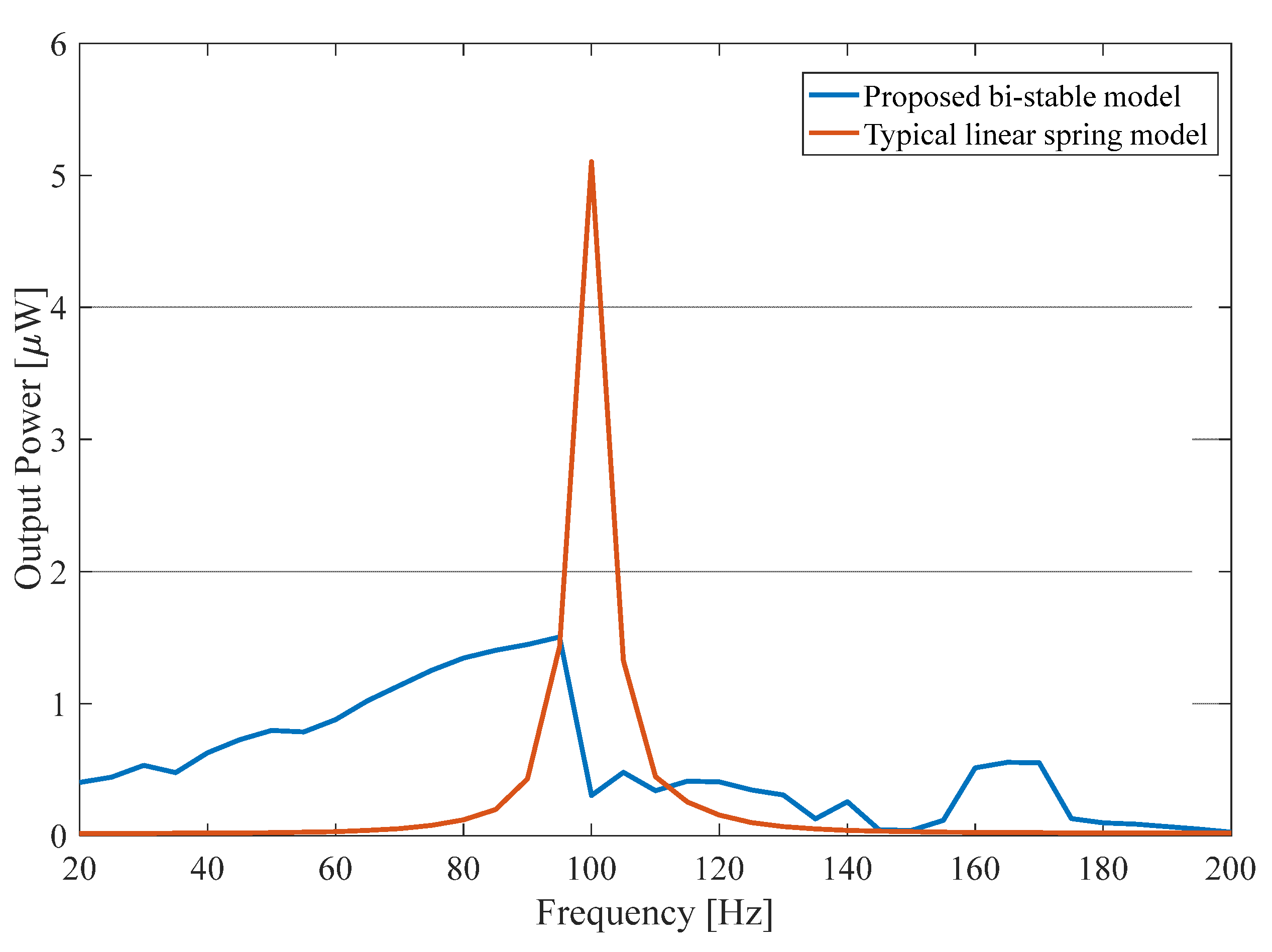
3.1.3. Comparison of Electrical Power Frequency Response between Linear and Bi-Stable Harvesters

To compare the electrical power frequency response between our bi-stable harvester and the similar linear case, the output powers in frequency domain for optimal loads are shown in Figure 7. The non-linear characteristics of the bi-stable generator gets larger output power in the low frequency range. While the linear harvester can generate larger power over a narrow bandwidth, these results demonstrate that our bi-stable energy harvester design is more suitable for scavenging broadband frequency vibration sources.

4. Conclusions

We constructed a structural simulation and an equivalent circuit enabling us to estimate the electrical power of our bi-stable electret-based electrostatic generator. In comparison with a similar linear harvester, we conclude that the use of non-linear bi-stable springs leads to a broader frequency response. Our harvester solution is thus more suitable for scavenging kinetic energy from real vibration sources where most of the power lays in the low frequency spectrum.