Abstract
A piezoelectric tuning fork sensor is evaluated as a physical excitation and sensing device aiming at the detection of crystals and their nucleation behavior in joint fluids, as observed in gout. This device allows to study the crystallization tendency at varying temperatures or at increased uric acid concentrations as predominant in real human joints. In this work, a tuning fork resonator is characterized to enable spatially resolved viscosity and density measurements by calculating the mode shape of the vibration from resonance frequency measurements when immersed in test liquids.
1. Introduction
According to recent studies [1] a stronger prevalence of gout and joint diseases in general is expected. Our long-term aim is to extend the range of available instruments for detecting gout by employing a complementary novel physical microsensor for detection of monosodium urate (MSU) crystals (see Figure 1a) in the synovial fluid of human joints. First experiments using a thickness shear mode (TSM) quartz crystal microbalance for sensing sedimentation of crystals showed insufficient sensitivity. This is mainly attributed to the low penetration depth of the shear waves of approximately 200 nm and the missing mass effect [2] (i.e., the crystals are not rigidly attached to the sensor but form a soft layer). We therefore employed a low frequency piezoelectric quartz tuning fork (TF) sensor setup with a penetration depth of 3.3 µm in water, using the MFA200K44 impedance analyzer from Microresonant with the robust resonance base fitting algorithm [3,4]. Contrary to TSM, using the tuning fork also yields the possibility to separate density and viscosity of the liquid under test [5]. Onset of crystallization is characterized by increasing viscosity. According to the Einstein equation [6], the viscosity of the suspension ηs follows ηs = ηf (1 + 2.5 V) with ηf and V denoting viscosity of the base fluid and volume fraction of the particles. The impact of nucleation on viscosity can therefore be separated from e.g., temperature effects that mainly affect the resonance frequency. Furthermore, the TF setup is used to analyze the depth dependent viscosity and density at the beginning of crystallization. Due of the finite length of the TF, fluid parameters determined from the resonance parameters are spatial averages. In this work, we demonstrate a method where this averaging function is determined from resonance frequency measurements.

Figure 1.
(a) Polarized light image of MSU crystals (growing procedure strictly following [7]); (b) Measurement setup and tuning fork sensor (fr = 32.786 kHz in air); (c) The sensor is used to measure the temperature controlled liquid in the vial at multiple vertical positions using a linear stage.
2. Measurement Setup
The measurement setup shown in Figure 1b, consists of a temperature controlled vial containing the liquid under test. A linear stage is moving the parylene coated TF in vertical direction through the vial. The resonance parameters of the TF sensor are evaluated using a dedicated resonance analyzer.
3. Methods
Two cases are of particular interest. First, the onset of crystallization where small nuclei appear forming a stable density and viscosity distribution and second, the settlement of larger particles, where the viscosity varies over depth and time. This second state is monitored by starting from an initially uniform distribution obtained by stirring the sample. After turning the stirrer off, the particles begin to settle with different speeds according to their morphology and buoyant mass passing the tuning fork sensor. Due to the finite length of the TF, the measured resonance frequency is spatially averaged with the squared displacement distribution (i.e., the square of the mode shape ϕ(z) of the immersed resonator.
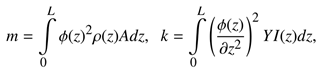
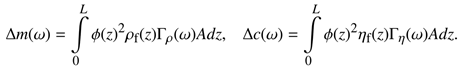
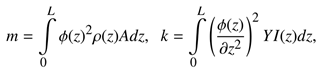
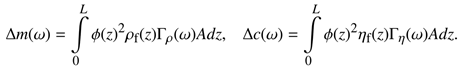
The equivalent mass (m) and stiffness (k) parameters of the unloaded sensors can be determined by Equation (1a) where ρ, A and YI denote mass density, area and bending stiffness, respectively. Due to liquid loading, the equivalent mass is changed by ∆m with a respective frequency dependent hydrodynamic function Γρ [8] and the liquid density ρf. The fluid viscosity ηf introduces a damping factor ∆c associated with a hydrodynamic function Γη (see Equation (1b)). According to [9], these changes follow the functional dependency
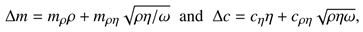 where the constants mρ, mρη, cη and cρη can be determined by model adjust measurements using a set of test liquids [4,9]. The angular resonance frequency ωr and the Q-factor are given by
where the constants mρ, mρη, cη and cρη can be determined by model adjust measurements using a set of test liquids [4,9]. The angular resonance frequency ωr and the Q-factor are given by
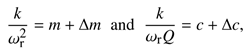 where m and c are the mass and the damping factor of the unloaded sensor, respectively. For spatially resolved viscosity and density measurements, the mode shape of the sensor must be determined. This is achieved by moving the TF through a well-defined liquid/liquid interface with differing density and viscosity. By combining Equations (1)–(3), the mode shape can be determined from the variation of the resonance frequency ωr(z) recorded for the sensor passing the interface
where m and c are the mass and the damping factor of the unloaded sensor, respectively. For spatially resolved viscosity and density measurements, the mode shape of the sensor must be determined. This is achieved by moving the TF through a well-defined liquid/liquid interface with differing density and viscosity. By combining Equations (1)–(3), the mode shape can be determined from the variation of the resonance frequency ωr(z) recorded for the sensor passing the interface
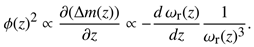
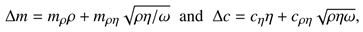
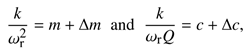
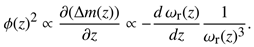
It is expected that the the mode shapes of tuning fork and cantilever are similar and therefore a numerical experiment (see Figure 2) where the resonance frequency of an Euler-Bernoulli cantilever, which is gradually shifted upwards from liquid 2 to liquid 1, is determined. Figure 2c shows the first three mode shapes calculated using Equation (4) and a comparison to the eigenmode of the free vibration [10]. The results are very similar for the first mode even at higher loading, but do only moderately agree for the higher modes. i.e., the loading has a certain influence on the mode shape.
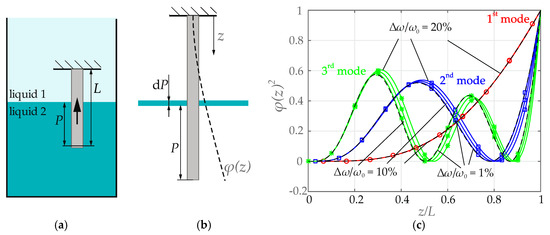
Figure 2.
Figure 2. (a) A resonator is moved from liquid 2 to liquid 1; (b) From the recorded frequency shift, the influence function (i.e., the squared mode shape) of an infinitely thin liquid layer at a certain height P can be determined; (c) Comparison between Equation (4) and the eigenmodes of a free vibrating cantilever.
4. Results
In principle, air could be chosen as liquid 1. However no suitable liquid 2 could be found with negligible capillary action when it is brought in contact with the parylene covered TF and air. We therefore use a liquid/liquid interface formed by ethylene glycol (ρf = 1.1132 g/cm³, ηf = 16.1 mPas at 20 °C) and methyl isobutyl ketone (MIBK) (ρf = 0.802 g/cm³, ηf = 0.58 mPas at 20 °C). The surface energies of these liquids and the parylene coating of the TF are almost equal, but feature very different partial solubility parameters. They therefore form a boundary with nearly zero interfacial surface tension, so the TF does not distort the interface while passing. A comparably abrupt step of viscosity and density is therefore realized. The TF was shifted in steps of 10 µm each 10 s. The resonance analyzer recorded at a rate of four measurements per second. The frequency response is shown in Figure 3a. The function was interpolated and Equation (4) was used to determine the squared mode shape. With knowledge of the mode shape, a viscosity and density distribution can be determined by deconvolution of ∆m from Equations (1)–(3) with ϕ(z)².
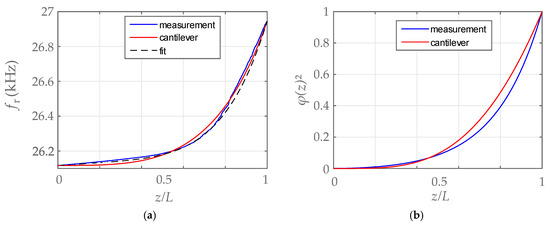
Figure 3.
(a) Measured resonance frequency (approx. 35.000 points) and comparison to cantilever; (b) mode shape calculated using Equation (4) resembling the fundamental cantilever mode.
Author Contributions
All authors contributed to theory, setup, measurement and writing.
Acknowledgments
This work was supported by the Linz Institute of Technology (project LIT-2016-1-SEE-019). Thanks to the Institute for Microsensors, –Actuators and –Systems at the University of Bremen for providing the parylene-C coating of the tuning fork sensors, the Linz Center of Mechatronics for polarized light microscopy and Microresonant (Linz, Austria) for providing the measurement instrument.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Martillo, M.A.; Nazzal, L.; Crittenden, D.B. The crystallization of monosodium urate. Curr. Rrheumatol. Rep. 2014, 16, 400. [Google Scholar] [CrossRef] [PubMed]
- Voinova, M.V.; Jonson, M.; Kasemo, B. Missing mass effect in biosensor’s QCM applications. Biosens. Bioelectron. 2002, 17, 835–841. [Google Scholar] [CrossRef]
- Niedermayer, A.O.; Voglhuber-Brunnmaier, T.; Sell, J.K.; Jakoby, B. Methods for the robust measurement of the resonant frequency and quality factor of significantly damped resonating devices. Meas. Sci. Technol. 2014, 23, 085107. [Google Scholar] [CrossRef]
- Voglhuber-Brunnmaier, T.; Niedermayer, O.A.; Beigelbeck, R.; Jakoby, B. Resonance parameter estimation from spectral data: Cramér–Rao lower bound and stable algorithms with application to liquid sensors. Meas. Sci. Technol. 2014, 25, 105303. [Google Scholar] [CrossRef]
- Voglhuber-Brunnmaier, T.; Heinisch, M.; Niedermayer, A.O.; Abdallah, A.; Reigelbeck, R.; Jakoby, B. Optimal parameter estimation method for different types of resonant liquid sensors. Procedia Eng. 2014, 87, 1581–1584. [Google Scholar] [CrossRef]
- Mardes, E.W.J. Viscosity and Suspensions and the Einstein Equation. Nature 1940, 145, 970. [Google Scholar] [CrossRef]
- Perrin, C.M.; Dobish, M.A.; Van Keuren, E.; Swift, J.A. Monosodium urate monohydrate crystallization. CrystEngComm 2011, 13, 1111. [Google Scholar] [CrossRef]
- Sader, J.E. Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope. J. Appl. Phys. 1998, 84, 64–76. [Google Scholar] [CrossRef]
- Heinisch, M.; Voglhuber-Brunnmaier, T.; Reichel, E.K.; Dufour, I.; Jakoby, B. Reduced order models for resonant viscosity and mass density sensors. Sens. Actuators A Phys. 2014, 220, 76–84. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-hill: New York, NY, USA, 1959. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).