A Novell Hall Magnetometer Using Dynamic Offset Cancellation ^†

Abstract

A novel Hall magnetometer using dynamic offset cancellation principle is presented. It consists from a single triangular silicon plate with three contacts and interface electronics. The proposed dynamic offset-cancelling measurement cycle includes three states. During each state, an external circuit is switched to the plate contacts in a certain way. This way, the direction of current flow through the Hall plate is changed from phase to phase. At the same time, the output voltage is measured. After averaging the obtained three voltages per a measurement cycle, the offset voltage cancelled and this way the offset-free Hall voltage is obtained. The obtained offset reduction factor is very promising, reaching 120–130. The Hall device sensitivity is about 25 V/AT.

1. Introduction

The very important key characteristic of the Hall sensors is the offset voltage V_off, which is its output signal in the absence of magnetic field [1,2,3]. It depends on power supply, temperature, mechanical stress and sometimes it is larger than the Hall voltage V_H (B). Some efforts to reduce the initial offset V_off by hardware consists of orthogonally coupling of two or more matched symmetrical Hall plates [2]. But, after applying this method, the residual offset is large since the matched Hall plates are not identical. An alternative effort to reduce the initial offset V_off, is the spinning current method [3,4,5], or “dynamic offset cancellation” [1]. In the spinning-current method, the direction of current flow in a single symmetrical Hall plate is made to spin around an axis through the center of the Hall plate. At the same time, the output voltage is sampled at the Hall contact pair which is perpendicularly oriented to the current flow [2]. The very common Hall sensors are four terminal devices [1,6,7,8,9,10], where one pair of opposite terminals serves as drive contacts and the other pair as sense contacts; consequently Hall sensors can be operated in two [1] or four [3] different modes. During an offset cancelling measurement cycle, the drive current is spatially rotated through these modes and the corresponding output signals are averaged [1,6,7,8,9,10].

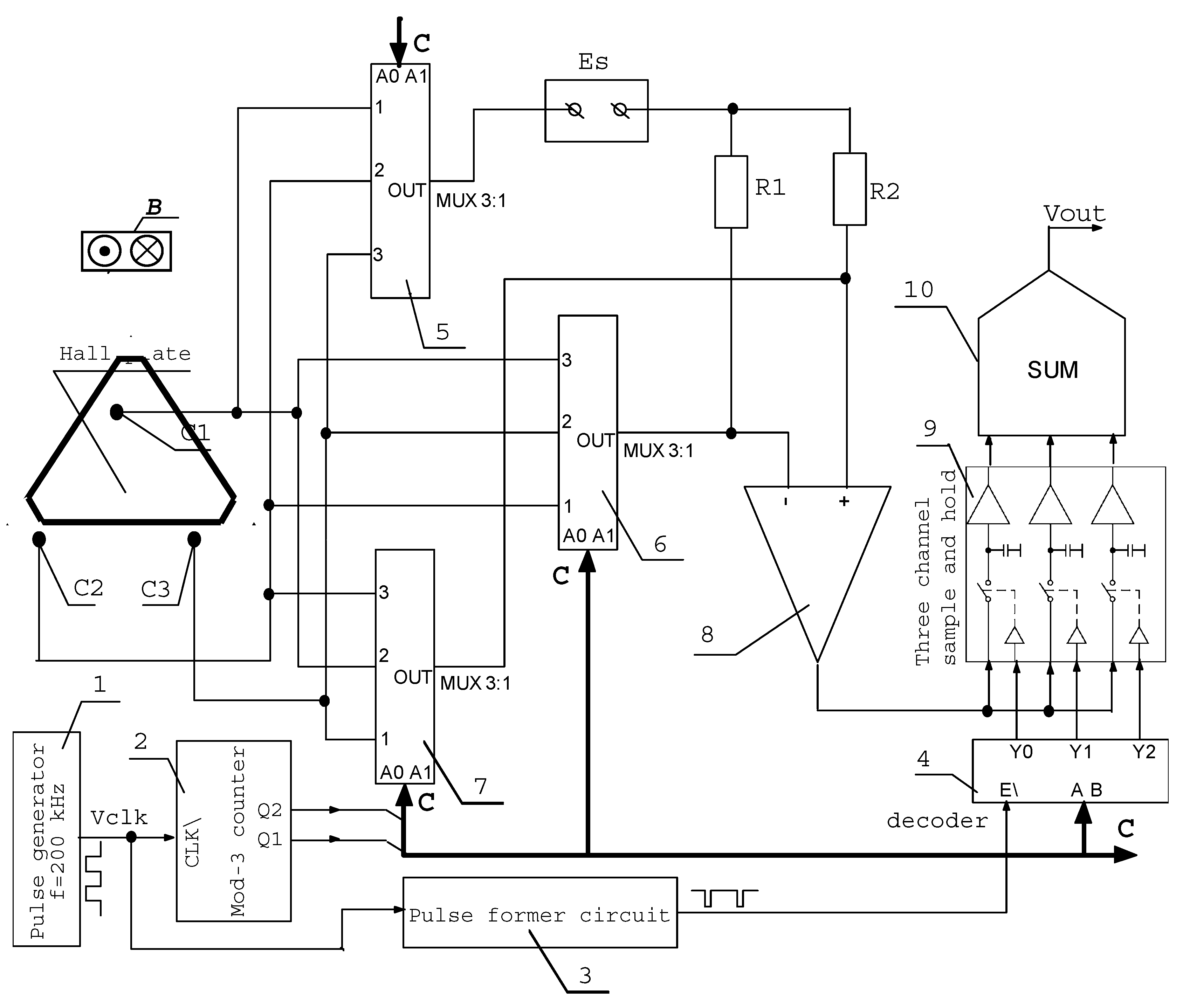
This paper presents a novel Hall magnetometer using dynamic offset cancellation principle, based on a single equilateral triangular n-Si plate with three contacts only. The functions, necessary for obtaining the useful Hall signal and cancelling the offset, are performed by proper interface electronics. Moreover, this device is characterized by high spatial resolution due to the small number of Hall plate contacts (three only).

2. The Hall Plate Design and Magnetometer Operation Principle

The Hall plate consists of a semiconductor n-Si structure in the form of an equilateral triangle, Figure 1. The magnetosensitivity is about 25 V/AT. On the surface of the substrate, near the vertices of the triangle, three n⁺-contacts, C₁, C₂, and C₃ are positioned.

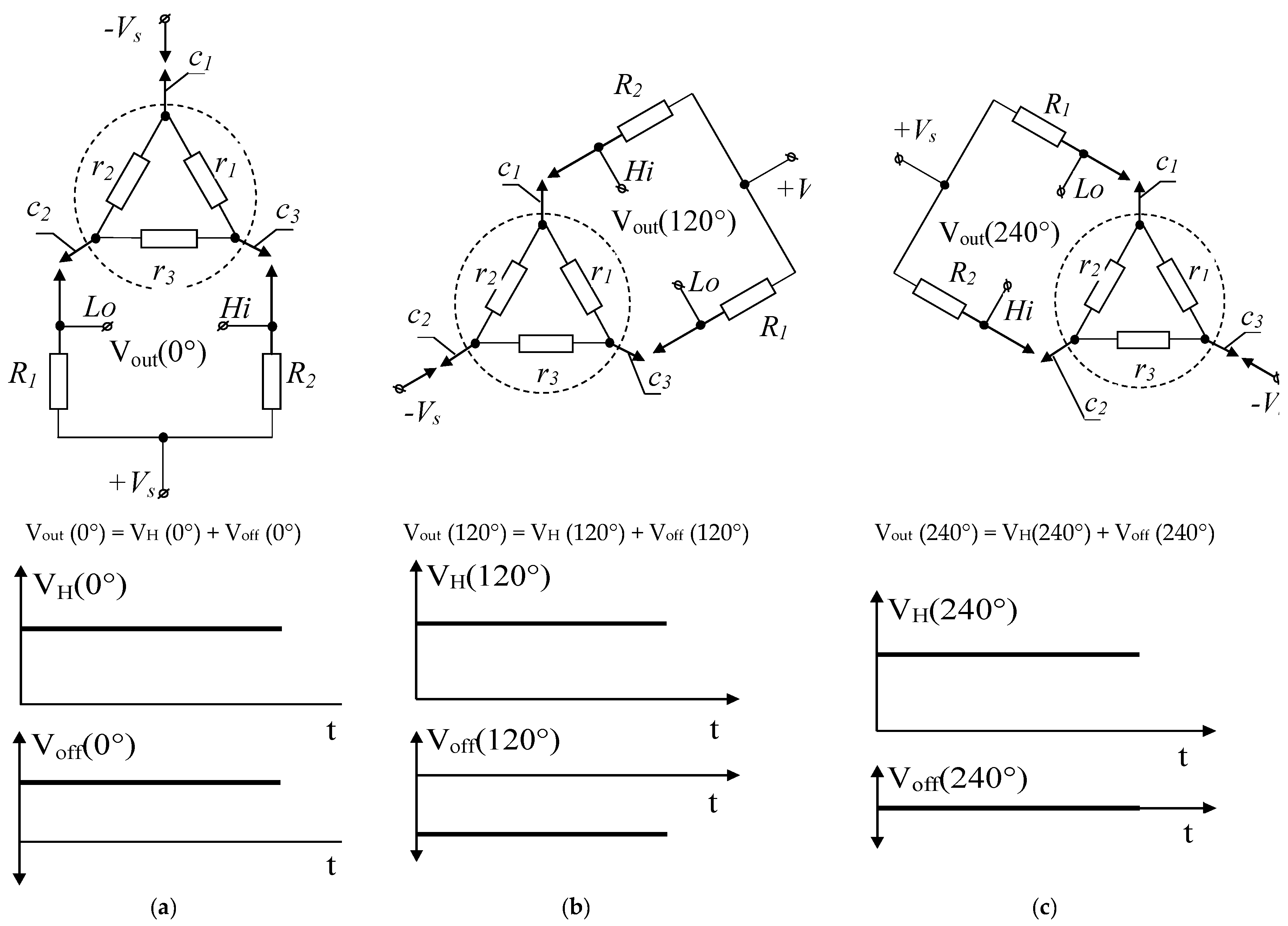
The dynamic offset-cancelling measurement cycle includes three consecutive states, shown in Figure 2a–c. We shall call them 0° state, 120° state and 240° state respectively. In Figure 2a–c, for the convenience of analysis, the Hall element is represented by a model of three connected in triangle resistors—r₁, r₂ and r₃. As is shown, during each state, an external circuit is connected to the plate contacts in a certain way. Such external circuit comprise the power supply with terminals −V_S and +V_S and the resistor network R₁–R₂ (R₁ = R₂ = R). One terminal of R₁ as well as one terminal of R₂ is connected to the power supply terminal +V_S. The other terminal of R₁ as well as the other terminal of R₂ is switched to a certain pair of adjacent plate contacts. To the third plate contact, the power supply terminal −V_S is switched. Between the terminals Lo and Hi, the sensor output voltage V_out is measured. In general, V_out consists of two parts, namely the magnetic field dependent Hall voltage V_H (B) and the offset voltage V_off:

V_out = V_H (B) + V_off

(1)

The Hall plate is fed with constant current as the value of external resistors R₁ and R₂ many times exceed the value of r₁, r₂ and r₃.

The first state of the measurement cycle (0° state) is shown in Figure 2a. The resistor R₁ is switched to contact

C₂, the resistor R₂ is switched to contact c₃, and the power supply terminal −V_S is switched to contact c₁. For an ideal Hall plate, the resistances of r₁, r₂, and r₃ are equal, i.e., r₁ = r₂ = r₃ = r. The resistors r₁, r₂, R₁ and R₂ form Wheatstone bridge. In the absence of magnetic field, the output voltage measured between the terminals Lo and Hi will be zero, because the bridge is balanced. In the presence of magnetic field, the Lorentz force F_L = qV_dr × B deflects the moving carriers laterally; q is the electron charge and V_dr is the velocity of the carriers. As a result, in the vicinity of the contacts C₂ and C₃ additional charges are generated, resulting in appearing of Hall voltage between the contacts Hi and Lo. The Hall voltage is proportional to the magnitude of the magnetic field B, and its sign depend on the direction of the magnetic field B.

Assume that an imbalance, for example due to a mechanical stress, occurs such that the region between the contacts c₁ and c₂ shows a resistance smaller than the rest of the plate, i.e., r₁ = r₃ = r; r₂ = r—Δr. In such case, in absence of magnetic field B, (B = 0), the output voltage V_out between the contacts Lo и Hi will be different from zero as the bridge (r₁–r₂–R₁–R₂) is not balanced due to r₁ ≠ r₂. To the terminal Lo, the resistor r₂ is connected, corresponding to the substrate region with resistance r–Δr, and to the terminal Hi, the resistor r₁ is connected, corresponding to the substrate region with resistance r. Then, the offset voltage V_off (0°) will be measured, Figure 2a. In the presence of magnetic field В (B ≠ 0), the Hall voltage V_H between the contacts Lo и Hi appeared, which is added to the offset voltage V_off (0°). In particular direction of the magnetic field, the Hall voltage V_H (0°) will have the same sign as the offset voltage V_off (0°), as is shown in Figure 2a.

The second state of the measurement cycle (120° state) is shown in Figure 2b. Actually, switching contacts during the transition from the first to second state is carried out in such a way that the external circuit rotated virtually in the Hall element plane around its center to an angle 120° from its initial position, Figure 2b. In such case, the bridge r₂—r₃—R₁—R₂ is not balanced due to r₂ ≠ r₃. To the terminal Lo, the resistor r₃ is connected, corresponding to the substrate region with resistance r, and to the terminal Hi, the resistor r₂ is connected, corresponding to the substrate region with resistance r–Δr. This means that the measured between contacts Lo and Hi offset voltage V₀ (120°) will have the same value but opposite sign compared to the measured offset voltage V₀ (0°) during the first state of the measurement cycle (0° state) shown in Figure 2a. As can be seen from the scheme, the measured Hall voltage V_H (120°) between the output contacts Hi and Lo will have the same sign compared to the measured Hall voltage V_H (0°) during the first state (0° state).

The third state of the measurement cycle (240° state) is shown in Figure 2c. Actually, switching contacts during the transition from the first to third state is carried out in such a way that the external circuit rotated virtually in the Hall element plane around its center to an angle 240° from its initial position, Figure 2c. In such case, the bridge (r₁–r₃–R₁–R₂) is balanced due to r₁ = r₃. This means that the measured between the contacts Lo and Hi offset voltage V₀ (120°) will be zero, i.e., V₀ (120°) = 0. As can be seen from the scheme, the measured Hall voltage V_H (120°) between the output contacts Hi and Lo will have the same sign compared to the measured Hall voltages V_H (0°) and V_H (120°) during the first state (0° state) and second state (120° state).

In the end, the obtained voltages from each of the three consecutive states from the current measurement cycle are summed. This way, the useful Hall signal triples but the offset voltages are cancelled in most cases:

V_out = (V₀ (0°) + V_H) + (V₀ (120°) + V_H) + (V₀ (240°) + V_H) = 3V_H + V_res

(2)

where V_res is so-called residual plate offset, which is very low.

3. Interface Circuitry and Results

The block diagram of the sensor interface circuit is shown in Figure 1. Block 1, “Pulse Generator”, clocks the mod-3 counter (Block 2) by pulse sequence with proper frequency. Block 2 carries out the following functions: (1) generates a sequence to control the switching over the contacts of the Hall plate to the power supply E_S and the resistor network—R₂; and (2) takes part in the formation of proper pulses to control Block 9, “Three channel sample-and-hold”. Based on the control sequence generated by Block 2, the multiplexers 5, 6 and 7 directly switch over the contacts of the microdevice to the power supply E_S and the resistor network R₁–R₂. Block 8 comprises a precise instrumentation amplifier. To obtain offset compensated value of the sensor signal, the output of Block 8 is passed to Block 9, “Three channel sample-and-hold”. Block 4 feeds proper sampling pulses to the sampling inputs of Block 9, so that the outputs of the sample-and-hold circuits hold the output voltages obtained from the current measurement cycle. The summer 10 sums these three voltages. Thus, the obtained Hall voltages from each of the three consecutive states from the current measurement cycle, are summed but the corresponding offset voltages are cancelled in most cases. The offset reduction factor is about 120–130. Despite the fact that the new device uses discrete realization, the obtained performance is promising for various applications in the robotics, automation, low-field magnetometry, navigation etc.