Simulating Rain Droplets Influence on Distance Measurement with a Time-of-Flight Camera Sensor ^†

Abstract

Time-of-Flight (ToF) camera sensors measure simultaneously the light intensity and the scene distance on a pixel basis. Environmental effects, like rain droplets between the scene and the ToF camera, have an impact on the distance accuracy of the sensor. Optical raytracing simulations were performed to study rain influence in detail. The 3D simulation setup comprises all relevant elements including the sensor design, the object/scene geometry and a model for the environmental conditions. Specifically, a setup with small-angle ToF camera optics is investigated and a comparison of the influence of several typical rain intensities is presented. The simulation results serve as an input for developing error-compensation algorithms.

1. Introduction

The development of assisted and autonomous driving vehicles is currently making large progress. The key component for this technology is a reliable sensor network delivering precise information about the vehicle’s environment in real-time. The combination of several sensor types and measurement principles aims at making the network robust against glitches. One very promising sensor type is a ToF-based camera, which is capable of delivering information on the distance between the sensor and objects in its field of view [1]. Here we investigate the influence of different rain intensities on the accuracy of distance measurements using a ToF camera. The rain influence was studied by optical raytracing simulations, as this strategy offers well-defined control of the parameters and test conditions.

2. Simulation Model

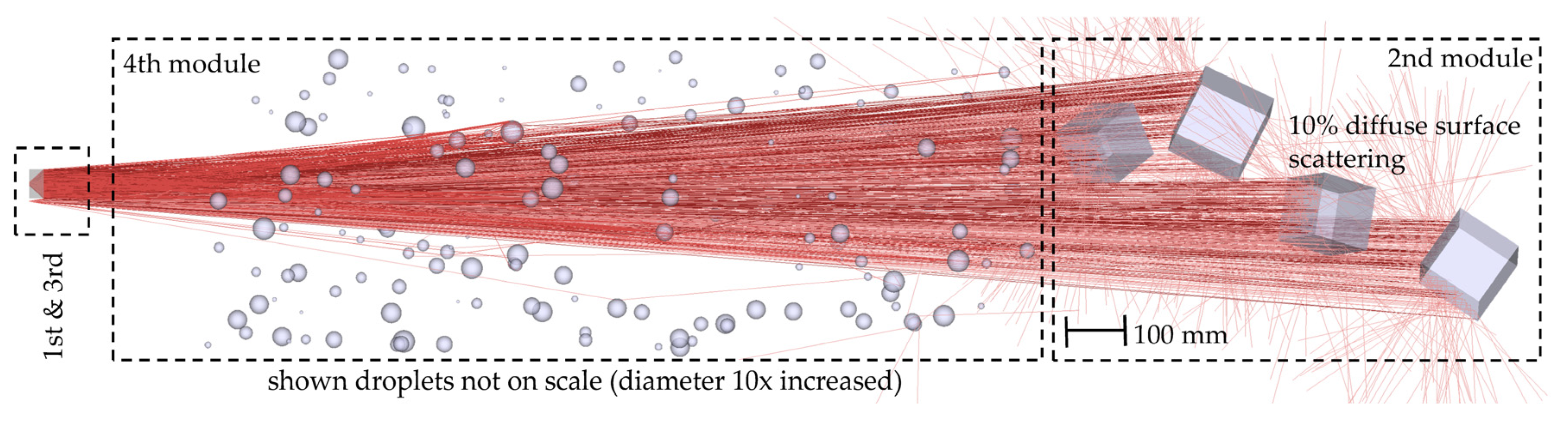
The 3D simulation model is based on geometrical optics raytracing using Zemax^® Optic Studio and accounts effects of material reflection, scattering and absorption. The simulation model can be sectioned into 4 modules regarding their functionality (Figure 1). The emitter optics (1st module) comprises a VCSEL array sending light pulses towards the scene (2nd module). Back-scattering at the scene’s objects traces the light pulses partially back towards the receiver optics and ToF camera sensor unit (3rd module). Rain influence (4th module) is modelled by randomly positioned water spheres placed between the ToF sensor and the scene. As intensity and travel time are analyzed individually for each ray hitting the sensor, the model allows a “per pixel” distance calculation mimicking the phase delay method between emitted and reflected signals [2]. This also allows examination of the same scene under different environmental conditions.

3. Examining Rain Influence

Rain droplet diameters typically range from 0.4 mm to 4 mm with densities from 50 to 1200 drops per m³ [3,4]. Based on literature values, distributions for light and medium rain were modelled and their influence on the sensor signal examined (Figure 2). As intensity and travel time are analyzed individually for each ray hitting the sensor, the model allows a “per pixel” distance comparison for the same scene under different environmental conditions.

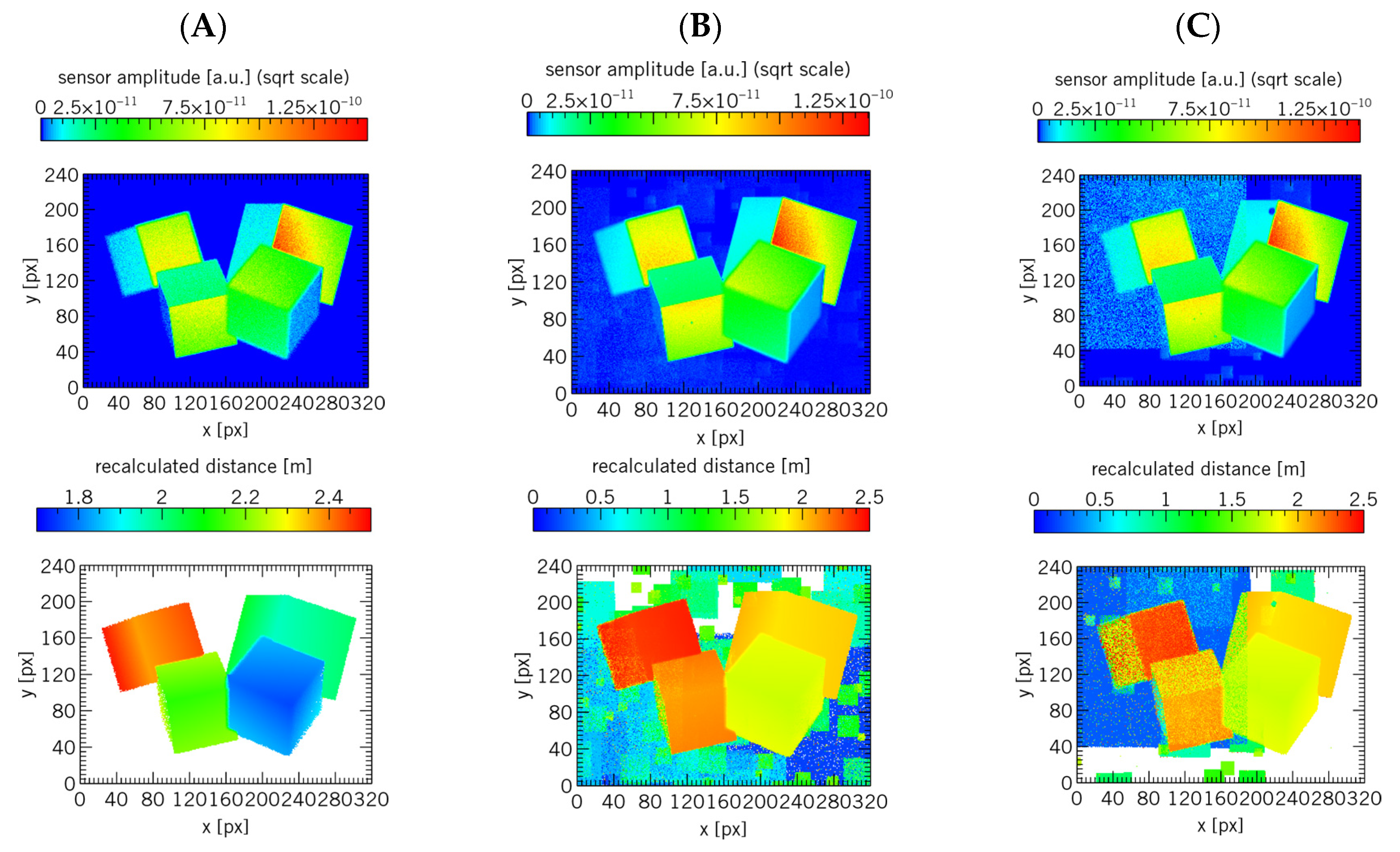
The sensor’s objective is to measure the scene’s objects distances and intensities. The following simple approach was applied to suppress rain influence. The ToF amplitude signals for all examined rain intensities (no rain, light rain and medium rain) were filtered with a minimum threshold, as low amplitude signals are more likely caused by rain droplets (Figure 3). A 2% minimum threshold could successfully suppress most of the rain influence in the depth re-calculation for the light rain setup. In contrast, for medium rain more advanced error suppression methods are needed as even with a 10% minimum threshold a significant distance error caused from the rain droplets is still noticeable.

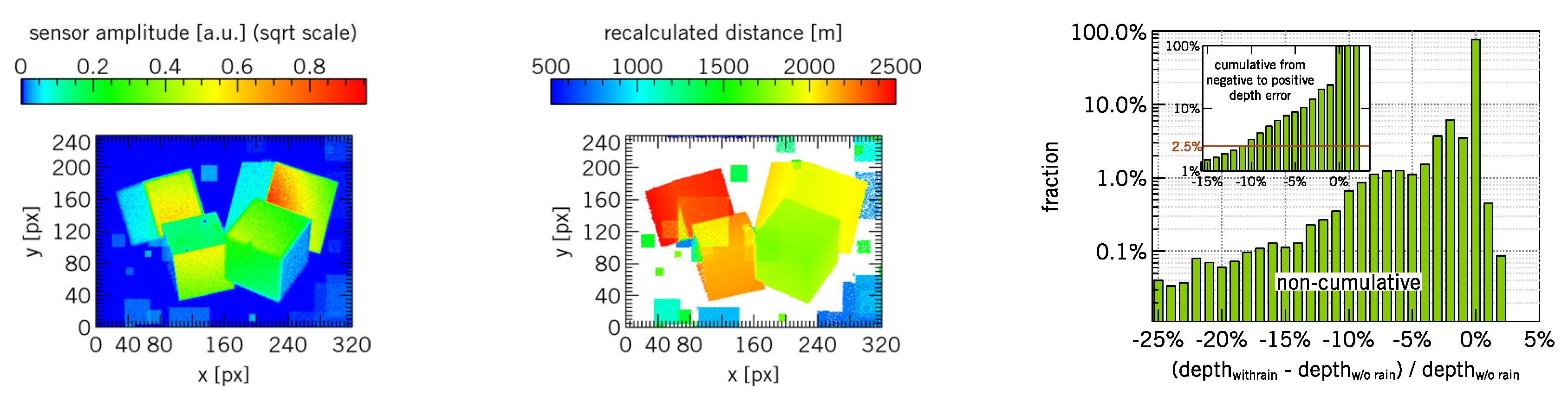
In case the more advanced error suppression methods will not perform as expected, it is important to quantify the erroneous influence of the rain on the signal. We set up and analyzed a “worst-case” model which features a density of 1000 particles/m³ with randomly distributed rain diameters between 0.4 mm and 4 mm. Figure 4 shows the simulation results. The re-calculated distance of the scene objects between “no rain” and “worst-case” model differ less than −10% for 97.5% of the values. The difference is due to overlying refraction and reflection effects from rain drops.

4. Conclusions and Outlook

The distance errors caused by the rain drops in our “light rain” model are mostly below 2% and can be suppressed by cutting all sensor intensity signals below this level. For larger rain drop sizes, as e.g., used in our medium rain model, more sophisticated algorithms filtering the rain influence from the sensor’s signal need to be developed. This will be a topic of future work.

From the additional presented “worst-case” rain model, the presence of rain has a significant impact on the re-calculated distance. For objects at longer distances as considered in our model, even higher distance errors are expected. The presence of raindrops leads to re-calculation of mainly too short distances in average. Regarding safety aspects, at least, this does not make the situation worse.

Distance error could be compensated with averaging of multiple sensor frames. Unfortunately the speed of falling rain drops (10–25 m/s) lies within the car’s speed on motorways and thus averaging only would work for slow driving speeds.

Further investigation of other scenes, as well as experimental verification is ongoing work.