Mechanical Properties and Energy Absorption Characteristics of the Fractal Structure of the Royal Water Lily Leaf Under Quasi-Static Axial Loading

Abstract

Inspired by the self-organizing optimization mechanisms in nature, the leaf venation of the royal water lily exhibits a hierarchically branched fractal network that combines excellent mechanical performance with lightweight characteristics. In this study, a structural bionic approach was adopted to systematically investigate the venation architecture through macroscopic morphological observation, experimental testing, 3D scanning-based reverse reconstruction, and finite element simulation. The influence of key fractal geometric parameters under vertical loading on the mechanical behavior and energy absorption capacity was analyzed. The results demonstrate that the leaf venation of the royal water lily exhibits a core-to-margin gradient fractal pattern, with vein thickness linearly decreasing along the radial direction. At each hierarchical bifurcation, the vein width is reduced to 65–75% of the preceding level, while the bifurcation angle progressively increases with branching order. During leaf development, the fractal dimension initially decreases and then increases, indicating a coordinated functional adaptation between the stiff central trunk and the compliant peripheral branches. The veins primarily follow curved trajectories and form a multidirectional interwoven network, effectively extending the energy dissipation path. Finite element simulations reveal that the fractal venation structure of the royal water lily exhibits pronounced nonlinear stiffness behavior. A smaller bifurcation angle and higher fractal branching level contribute to enhanced specific energy absorption and average load-bearing capacity. Moreover, a moderate branching length ratio enables a favorable balance between yield stiffness, ultimate strength, and energy dissipation. These findings highlight the synergistic optimization between energy absorption characteristics and fractal geometry, offering both theoretical insights and bioinspired strategies for the design of impact-resistant structures.

1. Introduction

Sandwich structures, known for their high strength-to-weight ratio, are widely used in modern industrial applications such as automotive, marine, and aerospace engineering [1,2,3,4]. A typical sandwich panel consists of two face sheets and a core layer: the face sheets primarily provide global stiffness and load-bearing capacity, while the core serves critical roles in support, shear resistance, weight reduction, and energy absorption [5]. With the continuous advancement of intelligent and green transportation equipment, the requirements for safety and lightweight design of key components in automotive and rail vehicles have been increasingly emphasized. However, mere weight reduction without systematic improvements in structural design and material selection can significantly compromise the safety performance of these components.

Although traditional sandwich core structures such as honeycombs and foams have been well established in engineering applications, their energy absorption mechanisms are relatively simple, resulting in limited energy dissipation and difficulty in meeting increasingly stringent performance requirements [6,7]. In recent years, the rise in biomimetics and fractal geometry theory has provided new perspectives and theoretical support for the optimization of sandwich core structures.

Bioinspired sandwich structures, by mimicking the adaptive and self-optimizing characteristics of biological organisms, achieve lightweight design while exhibiting excellent load-bearing and energy absorption capabilities. Numerous studies have systematically explored the mechanical performance of various plant structures. For example, luffa sponge [8] features stable core units and load-bearing shell units, with fiber arrangements demonstrating a stiffness–flexibility coupling effect. During the yielding phase, it can absorb energy ranging from 90.3 to 188.4 kJ/m³ (volumetric basis) or 2.13 to 4.06 J per sample, with the shell units playing a dominant role in axial energy absorption. Bamboo [9,10] exhibits significant anisotropy in compression behavior; its longitudinal compression follows a buckling-induced kink band formation mechanism, and the node regions possess notably higher stiffness than internodes, enhancing axial load capacity. The durian husk [11] achieves specific energy absorption twice that of the mesocarp, and its hemishell structure outperforms individual parts in energy absorption. Reed stalk nodes [12] effectively improve overall strength under axial loading. The pomelo mesocarp [13] dissipates approximately 80 J of energy in free-fall tests without external damage. Coconut shells [14] and nut shells [15] also demonstrate excellent impact resistance and puncture toughness.

Fractal geometry, as a branch of mathematics, not only demonstrates concrete applications in fields such as quantum physics (e.g., properties of two-dimensional quantum rings with various fractal structures and studies of electrostatic shielding potential) and materials science (e.g., characterization of planar fractal curves) [16,17,18], but also provides a precise mathematical framework to describe fractal structures in nature [19,20]. Notably, the mechanical optimization mechanisms embedded in typical fractal structures found in nature offer innovative bioinspired design concepts for engineering structures. The fractal characteristics of biological structures have inspired novel approaches in engineering structural design. For instance, Ajdari et al. [21] constructed fractal structures by replacing vertices of regular hexagonal lattices with smaller hexagons; experimental results showed that, at equal mass, first- and second-order fractal structures exhibited stiffness values approximately 2 and 3.5 times higher than conventional structures, respectively. Zhang et al. [22] designed a fractal honeycomb structure and numerically investigated its out-of-plane crush resistance, revealing that hierarchical architectures significantly enhance compressive strength. Furthermore, Wang et al. [23] proposed thin-walled structures based on Koch fractals; both experimental and numerical studies demonstrated that Koch fractals substantially improve energy absorption, with second-order Koch fractal structures achieving the highest specific energy absorption. Zhang et al. [24] introduced spider web-inspired fractal structures and found that fractal design significantly enhances compressive performance, with the FS2 configuration showing optimal energy absorption. Current research indicates that although scholars worldwide have made progress in characterizing both macroscopic and microscopic biological structures and applying fractal geometry methods, a critical scientific challenge remains: how to effectively integrate biomimetic principles with fractal geometry theory to systematically quantify multiscale fractal features of biological structures, particularly to meet the demands of lightweight design.

Through long-term evolution, the royal water lily’s leaf venation has formed a fractal structure that provides efficient support to the leaf with low mass and outstanding mechanical properties. Its lightweight and high-strength characteristics make it an ideal bioinspired prototype for sandwich core design [25]. As early as 2011, Zou et al. [26] utilized the macroscopic structure and mechanical characteristics of the royal water lily to optimize the design of a vertical lathe rotary table. Finite element analysis indicated that the optimized table exhibited a mass reduction of 280 kg and a deformation decrease of 4.7%. Zhang et al. [27] further drew inspiration from the fractal-like arrangement of the royal water lily leaf veins, extracting equivalent principal stress trajectories and optimizing near-surface stiffeners. The results demonstrated that the optimized model achieved a 28% increase in specific stiffness compared with the conventional design, effectively enhancing the overall structural rigidity. However, the quantitative relationship between the macroscopic fractal architecture of the royal water lily venation and its mechanical properties remains inadequately understood. In this study, based on fractal geometry and biomimetic principles, the royal water lily venation was selected as a bioinspired prototype to analyze its macroscopic structural features. Using 3D scanning technology, a digital reconstruction of the multi-level fractal venation was realized. A parametric finite element model was then developed to systematically conduct quasi-static compression simulations, quantitatively elucidating the effects of key structural parameters such as fractal dimension and branching angle on overall compressive strength and energy absorption. The study integrates fractal geometry with biomimetic design, systematically investigating the relationship between the fractal structure and functional performance of the royal water lily leaf veins. By elucidating the formation mechanisms and evolutionary principles underlying complex natural structures, this work provides novel insights for biomimetic theory and offers technical guidance for the innovative design of lightweight, high-strength sandwich structures.

2. Materials and Methods

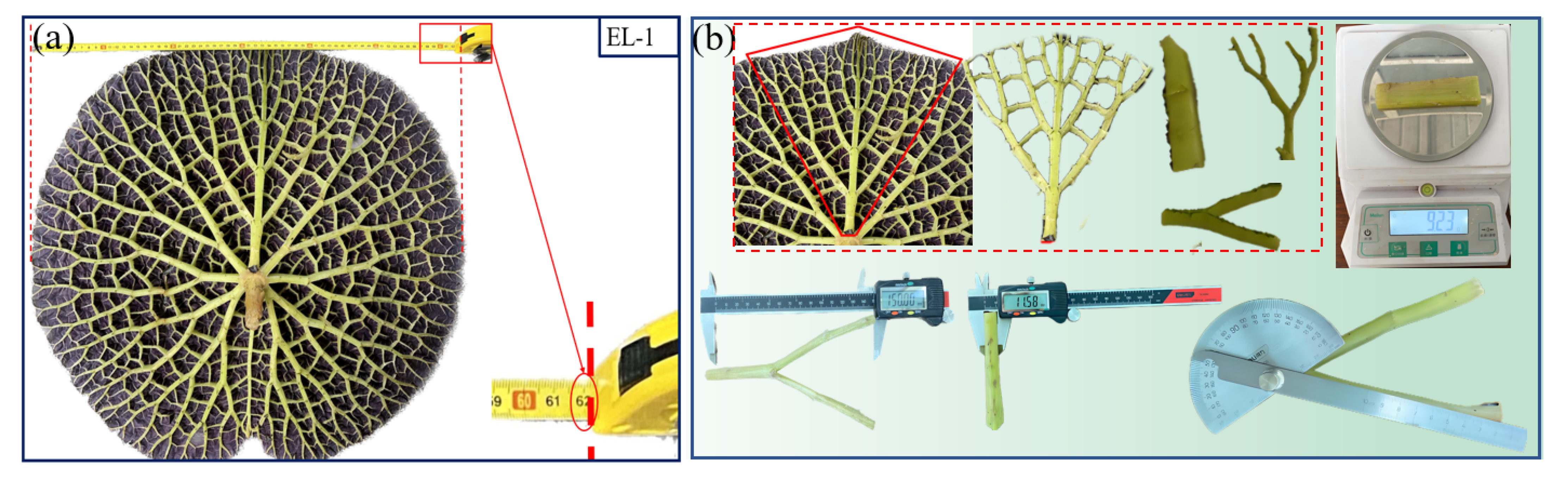
2.1. Sample Collection and Measurement

The royal water lily leaf used in this study was collected in mid-August from the Lotus Pond at Dongshan Scenic Area in Suzhou, China. The sample was labeled as EL-1 (Euryale leaf). The leaf had a diameter of approximately 620 mm, as shown in Figure 1. The venation of the royal water lily exhibits a radial pattern, with thick primary veins and interwoven secondary veins forming a grid-like structure of regularly arranged quadrilaterals. This hierarchical bifurcated pattern not only enhances the flatness of the leaf surface but also helps to disperse external loads, thereby improving overall stability and structural strength.

Considering the bilaterally symmetrical structure of the royal water lily leaf venation, measurements were conducted on the central primary vein and the right-side lateral veins of sample EL-1. For the purpose of parameter comparison and statistical analysis, the primary and secondary veins were sequentially numbered from No.1 to No.5 in a clockwise direction starting from the central axis, as shown in Figure 2a. As illustrated in Figure 2b, the key geometric parameters of the leaf venation include the cross-sectional thickness of the primary vein (T), the in-plane vein width (W), the bifurcation angle (θ), and the branch length ratio (λ), which is defined as the ratio of the length of a secondary branch to that of its immediate upstream branch.

2.2. Three-Dimensional Scanning of the Royal Water Lily Leaf Veins

In this study, a high-precision 3D digital reconstruction of the royal water lily leaf veins was conducted using the EinScan-Pro handheld 3D scanner (Shining 3D Tech Co., Ltd., Hangzhou, China). This device employs structured white light LED technology, offering a single-frame scanning area of 210 × 150 mm and accommodating object sizes ranging from 0.15 to 4 m. By integrating high-speed image acquisition with an intelligent feature-matching algorithm, the scanner enables rapid and accurate capture of the complex three-dimensional morphology of biological structures.

2.3. Three-Dimensional Reconstruction of the Royal Water Lily Leaf Vein Model

2.3.1. Compressive Performance of the Royal Water Lily Leaf Vein

Given the large size of the royal water lily leaf veins, full-scale mechanical testing is impractical. Therefore, this study employed reverse modeling techniques to obtain geometric models of the leaf veins via 3D scanning for subsequent simulation analyses. To ensure accurate construction of the 3D model, the EinScan-Pro handheld 3D scanner was used to perform reverse reconstruction of the leaf veins, as shown in Figure 3a,b. The point cloud data collected through a systematic scanning process were processed using Geomagic Studio 2015 software for noise reduction, hole filling, and surface reconstruction, ultimately yielding a complete 3D model of the leaf veins. Prior to scanning, a thin layer of white developer was uniformly sprayed onto the leaf vein surface to enhance reflectivity and improve the scanner’s ability to capture detailed morphological features, as illustrated in Figure 3c. During the scanning process, the “non-textured high-precision scanning” mode was selected in the EinScan-Pro V1 software. The operator slowly and steadily moved the scanner across the leaf surface to acquire the point cloud data. Real-time monitoring of data integrity was conducted on the computer interface; if any areas were found to be missing, the scanner’s angle and position were adjusted to rescan the deficient regions until the point cloud was complete.

2.3.2. Reverse Engineering and 3D Modeling of Leaf Veins

After completing the 3D scanning, the collected data were saved and processed using Geomagic Studio software. Given the bilateral symmetry of the leaf vein structure, only half of the scanned data required repair; the complete structure was then generated using a mirroring tool. The point cloud was first aligned with the global coordinate system to establish a stable reference frame for subsequent operations. The point cloud was then preprocessed by removing extraneous data around the leaf edge using the “Boundary” toolbar (Figure 4a). The cleaned point cloud was converted into a polygonal mesh via the “Wrap” function (Figure 4b). Mesh repair was performed, including hole filling, surface smoothing, and mirroring operations. The repaired model was saved as shown in Figure 4c. To isolate the leaf veins from the lamina, the precise surface modeling function was employed to create closely connected surface patches. Finally, surface fitting was performed to generate the three-dimensional model of the leaf veins (Figure 4d).

2.4. Validation and Parameters of the Simulation Model

2.4.1. Quasi-Static Compression Test

To validate the accuracy of the finite element simulation model, a quasi-static compression test was conducted on the central primary vein and compared with the simulation results. The experiment was carried out using an ETM 300 kN electronic universal testing machine (Wance Testing Equipment Co., Ltd., Shenzhen, China)at the Key Laboratory of Bionic Engineering (Ministry of Education), Jilin University, as shown in Figure 5a. The central primary vein was selected as the test specimen, and its morphology is illustrated in Figure 5b. To ensure consistent loading conditions, the vein sample was placed flat on a horizontal platform, with the loading direction set vertically downward. The loading speed was maintained at 2 mm/min, and the maximum displacement was set to 15 mm, as depicted in Figure 5c. During the experiment, the system continuously recorded the load–displacement curve, and the data were exported for subsequent analysis.

2.4.2. Simulation Parameters and Conditions

The leaf vein model was first meshed using HyperMesh 2022, and the mesh quality was carefully verified. Upon completion, the mesh was exported and imported into Abaqus CAE 2022 for finite element simulation. In Abaqus CAE, a rigid plate was applied to the upper surface to compress the model vertically downward at a constant speed of 2 mm/min, with a total displacement of 15 mm. Fixed constraints were applied to the bottom of the model and the lower rigid plate, as illustrated in Figure 6a. Based on the structural characteristics, the leaf vein model was divided into three regions, as shown in Figure 6b: the knob region (Knob), the epidermal layer (Epidermis), and the spongy internal tissue (Sponge). The material properties assigned to each region are listed in

Table 1. Specimen parameters for transverse and axial compression testing of the royal water lily leaf vein.

	Specimen Length/mm	Specimen Width/mm	Mass (g)	Young’s Modulus (MPa)	Poisson’s Ratio	Density (t/mm3)
Experiment	100	Upper: 9.67 Lower: 10.89	6.48	—	—	—
Simulation	100	Upper: 9.35 Lower: 11.44	5.73	Knob: 12.5 Epidermis: 9.66	0.3	5.092 × 10−10
Error	—	Upper: 3.42% Lower: 5.05%	13.08%	—	—	—

[28]. Additionally, a friction coefficient of 0.2 was defined for all contact surfaces [29]. After the simulation, the load–displacement curve was extracted for subsequent comparison and analysis.

Figure 7 presents a comparison between the compression test results of the leaf vein and the predictions obtained from finite element simulations. As shown in Figure 7a, the load–displacement curves from both experiment and simulation exhibit similar trends: the load smoothly increases with displacement and, after reaching a peak, enters a relatively stable plateau region. This behavior indicates that the leaf vein undergoes a degree of elastic deformation under external loading. Quantitatively, there are some discrepancies between the two curves. The simulated peak compressive force (PCF) is 24.17 N (at a displacement of 10.5 mm), whereas the experimental value is 28.09 N (at 12 mm displacement), corresponding to a relative error of 13.95%. On the other hand, as shown in Figure 7b, the total energy absorption (EA) predicted by the simulation agrees well with the experimental measurement, with values of 264.85 mJ and 262.05 mJ, respectively, yielding an error of only 1.07%. The slight numerical deviations in the load–displacement response may be attributed to the simplification of the spongy internal microstructure in the finite element model. Given that this microstructure contributes minimally to the macroscopic mechanical behavior, such simplification is deemed reasonable for the current analysis.

In summary, the simulation results show good consistency with experimental data in terms of overall deformation trends and energy absorption capacity. This confirms that the established finite element model can accurately capture the mechanical behavior of the leaf vein and can be reliably used for subsequent mechanical performance studies.

2.5. Evaluation Metrics

To comprehensively assess the mechanical performance of the leaf vein under quasi-static compression simulation, the following evaluation metrics are adopted in this study: total energy absorption (EA), specific energy absorption (SEA), mean crushing force (MCF), and instantaneous stiffness (K) [30,31,32].

Total energy absorption (EA) primarily refers to the energy dissipated by energy-absorbing structures through their own deformation under impact, which can be calculated by integrating the load–displacement curve. The equation is as follows:

$$\mathrm{EA}={\displaystyle {\int }_0^{{\delta }_{\max }}\mathrm{F}(\mathrm{x})dx}$$

(1)

In Equation (4), δ_max is the maximum effective compressive displacement; F(x) is the instantaneous crushing load at the compressive displacement x.

The specific energy absorption (SEA) represents the energy absorbed per unit mass of the energy-absorbing structure, defined as the ratio of the total energy absorption (EA) to the mass (M) of the energy-absorbing structure. A higher SEA value indicates better energy absorption performance. The expression is as follows:

$$\mathrm{SEA}={\displaystyle \frac{\mathrm{EA}}{\mathrm{M}}}$$

(2)

The mean crush force (MCF) represents the impact load per unit compression distance, defined as the ratio of the total energy absorption (EA) to the maximum effective displacement. A higher MCF value indicates better energy absorption performance. The equation is as follows:

$$\mathrm{MCF}={\displaystyle \frac{\mathrm{EA}}{{\delta }_{\max }}}$$

(3)

The instantaneous stiffness K reflects the structure’s resistance to deformation at any given moment during the loading process. It is typically defined as the ratio of load to displacement at a specific point. The equation is as follows:

$$K_i={\displaystyle \frac{F_n-F_{n-1}}{d_n-d_{n-1}}}$$

(4)

where F_n − F_n−1 is the difference in compressive force between two adjacent points, and d_n − d_n−1 is the corresponding difference in displacement.

3. Results and Discussion

3.1. Macrostructural Analysis of Leaf Venation

3.1.1. Thickness and Width Analysis of Midrib Cross-Sections

Figure 8 illustrates the variation in thickness (T) with respect to the distance from the leaf center (L) for five representative leaf veins. The measurement results show a consistent trend across all samples: the thickness decreases linearly from the center toward the leaf edge. At the outermost margin, the thickness values converge to approximately 4.5 mm, with a total reduction of about 11% from the initial thickness at the center. An interesting observation is that the rate of thickness reduction (i.e., the absolute value of the slope of each curve) increases progressively from vein No.1 to No.5. This can be attributed to the fact that although all veins share a similar thickness at the margin, the total length from the center to the edge becomes shorter from No.1 to No.5. As a result, the thickness gradient must be completed over a shorter distance, leading to a steeper decline. Based on the measured data, a linear fitting yields the following empirical relationship between thickness T and distance from the center L: T = −0.11L + 44 mm.

The distribution of leaf vein width exhibits a clear correlation with the bifurcation hierarchy. As shown in Figure 9, the vein width progressively decreases with increasing bifurcation order. The average width of primary (non-bifurcated) veins is 12.61 mm. Following one, two, and three bifurcations, the average widths of the resulting secondary, tertiary, and quaternary veins decrease to 9.15 mm, 6.59 mm, and 4.25 mm, respectively. Calculations indicate that the width of a daughter vein after each bifurcation is approximately 65% to 75% of its parent vein’s width, demonstrating a distinct hierarchical reduction pattern.

3.1.2. Analysis of Vein Bifurcation Angles

The venation system of the royal water lily exhibits a regular bifurcation pattern and symmetrical features. The primary veins (major veins) extend radially and symmetrically from the leaf center outward. Secondary and tertiary veins branching from the primary veins follow a bilateral symmetrical pattern, bifurcating from both sides of the parent vein at similar angles. This hierarchical branching forms a three- to four-level tree-like venation network. To quantitatively analyze the variation in bifurcation angles across hierarchical levels, this study measured the angles of eight primary veins and their subsequent branches, with results shown in Figure 10. Data analysis in Figure 11 reveals that the average bifurcation angle increases with hierarchical level. Specifically, for the first-level bifurcations (8 in total), angles range from 30° to 60°, with an average of 46.61°; for second-level bifurcations (16 in total), angles range from 40° to 70°, averaging 55.98°; and for third-level bifurcations (32 in total), angles range from 30° to 75°, with an average of 58.64°. This phenomenon can be explained by the fact that, as the branching order increases and the veins extend toward the leaf margin, the enlarged bifurcation angles facilitate better distribution and bearing of external loads, thereby reducing local stress concentration and enhancing the overall mechanical stability and damage resistance of the leaf.

3.1.3. Fractal Dimension Analysis of Leaf Veins

Fractal geometry is dedicated to describing irregular, complex, and multi-scale phenomena observed in nature [33]. The core characteristics of fractal geometry are self-similarity and fractal dimension [34,35]. Self-similarity refers to the property whereby the structure exhibits a high degree of morphological resemblance regardless of the scale of observation. The fractal dimension is a quantitative measure of the structural complexity and can be calculated using the recursive method, expressed as:

$$D={\displaystyle \frac{\log (N)}{\log (1/r)}}$$

(5)

where N is the number of self-similar substructures, and r is the scaling ratio of each substructure.

The leaf venation of the royal water lily resembles a structured binary tree, with its fractal dimension reflecting the geometric configuration, branching pattern, and structural complexity. To investigate the variation in fractal dimension, the leaf veins of three representative samples were analyzed using fractal geometry methods. The measurement results are shown in Figure 12. As illustrated, the fractal dimension of the royal water lily veins is not constant but exhibits a dynamic evolution characterized by an initial decrease followed by an increase. In the early stages of development, the veins form a regular backbone with a low fractal dimension, enabling the rapid establishment of a high-stiffness load-bearing framework. This efficiently minimizes material consumption while meeting the demands of concentrated load transfer caused by buoyancy and root tensile forces. In the later stages, the fractal dimension increases in the peripheral regions, resulting in a more complex branching network. This facilitates the dispersion of dynamic loads such as water flow impact and wind disturbances, extends the energy dissipation path, and activates multiscale structural deformation mechanisms. Consequently, the venation system enhances its energy absorption capacity and evolves into a core-to-edge gradient structure. This observation offers a natural prototype for gradient fractal strategies in bioinspired structural design.

3.1.4. Morphological Analysis of Intercostal Veins in the Royal Water Lily

As shown in Figure 13, curved secondary veins account for a higher proportion than parallel ones in the royal water lily vein system, indicating a morphology-function correlation with its energy absorption performance. Structurally, curved veins follow wavy or arched trajectories, whereas parallel veins exhibit nearly uniform alignment. This morphological difference leads to distinct energy dissipation mechanisms: curved veins increase deformation path complexity and prolong energy dissipation duration, as external loads must overcome multi-directional bending resistance. In contrast, parallel veins, constrained by their unidirectional orientation, mainly undergo axial tension or compression, offering limited energy dissipation paths and being prone to forming straight crack propagation channels that cause localized energy release. From an evolutionary perspective, the royal water lily must withstand multi-directional dynamic loads such as water currents, self-weight, and biological loads. The predominance of curved veins helps reduce peak stress under impact, accommodate the uneven self-weight distribution of large floating leaves, and balance material efficiency with structural strength through complex deformation pathways. In addition, the central region of the leaf exhibits densely distributed curved veins to dissipate high-energy impacts, while the marginal areas retain fewer curved veins to avoid stress concentration and fracture typically induced by parallel vein patterns. Compared with the predominantly parallel venation found in grasses, the high proportion of curved veins in the royal water lily represents an evolutionary adaptation to multi-directional loading environments.

3.1.5. Vein Length Analysis

At all hierarchical levels, the royal water lily leaf veins follow a binary branching pattern from parent to daughter veins, in which secondary veins symmetrically branch from both sides of the primary vein, and tertiary veins similarly emerge from the secondary veins. As shown in Figure 14, observational measurements reveal that the vein branch length ratio (λ) is not constant but exhibits a trend of first increasing and then decreasing from the central axis toward the outer branches. This morphological gradient enables hierarchical regulation of mechanical load transfer paths and deformation modes, thereby optimizing the structural functionality of the leaf. In the central region, short branches with low length ratios enhance the connection stiffness between the main vein and primary branches, ensuring stable transmission of high loads and improving local bending rigidity to resist deformation. In contrast, long branches in the peripheral region extend the deformation path, facilitating multiscale structural coordination and significantly enhancing energy absorption efficiency while expanding the energy dissipation domain. The variation in length ratio also disrupts the linear propagation of cracks, forcing crack deflection or bifurcation in the transition zones, thereby mitigating the risk of localized energy release. This gradient distribution aligns with the principle of material efficiency and reflects the plant’s evolutionary adaptation to complex environmental stresses. It provides a natural prototype for the design of bioinspired gradient materials.

3.2. Simulation Results Analysis

3.2.1. Mechanical Performance of the Overall Vein Structure

To simulate the mechanical loading conditions experienced by leaf veins in natural environments, a downward vertical load was applied to the vein model in the simulation. In Abaqus CAE, a rigid plate was set to move downward at a rate of 2 mm/min for a total displacement of 10 mm. To ensure the stability of the loading process, fixed constraints were applied to the bottom elements of the model and the lower rigid plate, as illustrated in Figure 15. The Coulomb friction coefficient between contact surfaces was set to 0.2 [36]. Upon completion of the simulation, the load–displacement curve was obtained as the output.

The simulation results, as shown in Figure 16a, reveal a nonlinear mechanical response of the royal water lily veins under vertical loading. The load–displacement curve can be divided into three distinct stages: In the initial small-displacement region, the central primary vein first bears the load and undergoes elastic deformation, characterized by a weakly nonlinear relationship between load and displacement, with a relatively low slope. As the displacement increases, the central vein transitions into elastic–plastic deformation, and secondary branches begin to contribute to load-bearing. During this stage, the load increases more rapidly with displacement, indicating a strong nonlinear (progressive damage) response, accompanied by an increase in slope. With further displacement, the peripheral fine veins reach their load-bearing limit, leading to a sharp rise in load with displacement. This marks the rapid strengthening stage, where the slope increases steeply until the end of the data range. These results indicate that the royal water lily vein structure absorbs energy through a hierarchical load-bearing mechanism and progressive damage during deformation.

Based on the simulation data, the instantaneous stiffness of the vein structure was further calculated, as shown in Figure 16b. The entire loading process was analyzed in two stages: Firstly, during the initial stage (0–5 mm), the slope of the curve remains relatively small, with the load increasing slowly as displacement progresses. Specifically, within the range of 0–1 mm, the load rises gradually, and the vein structure primarily undergoes elastic deformation, resulting in a low average instantaneous stiffness of 4.62 N/mm. Between 1 and 5 mm, the slope of the curve increases progressively, and the average instantaneous stiffness rises to 15.92 N/mm. Secondly, in the 5–10 mm stage, the load increases rapidly, accompanied by a notable rise in curve slope. From 5 to 7 mm, the average instantaneous stiffness reaches 44.60 N/mm; beyond 7 mm, it sharply increases to 160.09 N/mm. This significant enhancement in stiffness under larger loads indicates a pronounced stiffening effect of the vein structure as deformation progresses.

In summary, under vertical loading, the leaf veins exhibit a nonlinear stiffness response characterized by an initially low stiffness that gradually increases with displacement. This mechanical behavior allows the veins to stably absorb energy under low loads and effectively prevent structural failure under high loads, thereby maintaining the overall structural stability.

3.2.2. Analysis of Fractal Parameters Influencing the Energy Absorption Characteristics of Leaf Veins

The mechanical performance of the leaf veins has been validated in the previous section. Building upon this, the current section focuses on analyzing the effects of key fractal parameters—namely bifurcation angle, fractal branching level, and fractal branch length ratio—on the mechanical behavior of the leaf veins.

(1) Simulation Comparison of Bifurcation Angles

Observations of the leaf vein structure reveal variations in bifurcation angles at different locations. This section selects leaf veins with three distinct bifurcation angles (77°, 66°, and 54°) for finite element simulations to analyze the influence of bifurcation angle on mechanical performance. Figure 17 illustrates the sampling locations and corresponding finite element models for the different bifurcation angles. In Abaqus CAE, a vertical downward load was applied to the leaf vein models, with the upper rigid plate moving downward at a velocity of 2 mm/min to compress the model by 10 mm. The material properties and friction coefficients between contact surfaces remained consistent with previous settings. Load–displacement curves were outputted upon completion of the simulations.

The simulation results in Figure 18 reveal clear variations in the mechanical response of leaf veins with different bifurcation angles. As shown in the load–displacement curves in Figure 18a, increasing the bifurcation angle from 54° to 77° results in a gradual decrease in curve slope, reflecting reduced initial stiffness and load-bearing capacity. However, the curves become smoother overall. Figure 18b presents the specific energy absorption (SEA) and mean crushing force (MCF) for different bifurcation angles. At 54°, the structure exhibits the highest SEA (100.25 mJ/g) and MCF (67.31 N) among the three tested angles. As the angle increases, both SEA and MCF decline, indicating that smaller bifurcation angles enhance the energy absorption performance of the vein structure. Therefore, bifurcation angle can be considered a key structural parameter in the subsequent design of sandwich core structures.

(2) Finite Element Simulation of Fractal Branching Level

The excellent load-bearing capacity of the royal water lily veins is attributed to their hierarchically branched geometric structure. To investigate the influence of fractal branching level on the mechanical performance of the vein structure, this study selected two primary veins on the left side for finite element analysis. Figure 19a illustrates the sampling diagram, where the veins are labeled using the format “vein number-branching level.” The meshing of the vein models was carried out in Hypermesh, and vertical compression loading of 10 mm at a rate of 2 mm/min was applied to the upper rigid plate in Abaqus CAE. Fixed constraints were applied to the bottom elements of the vein and the lower rigid plate. The material properties and the friction coefficient between contact surfaces were consistent with previous settings. The finite element models are shown in Figure 19b. After the simulation, the load–displacement curves were obtained.

The simulation results shown in Figure 20 indicate that the fractal branching level affects the mechanical performance of the leaf vein structures. Figure 20a presents the load–displacement curves, revealing that with increasing fractal branching levels, the load-bearing capacity of the leaf veins increases. In the initial stage, the slopes of the curves for samples 1-1 and 1-2 are similar, whereas the slope for 2-2 is greater than that of 2-1, indicating that the stiffness of vein 2 increases with higher fractal branching levels. Figure 20b illustrates the effects of fractal branching levels on specific energy absorption (SEA) and mean crushing force (MCF). As the fractal branching level increases, the SEA of vein 1 rises from 40.72 mJ/g to 43.33 mJ/g, and its MCF increases from 61.17 N to 158.14 N; for vein 2, the SEA increases from 60.60 mJ/g to 66.33 mJ/g, and the MCF rises from 85.27 N to 189.85 N. These results indicate that increasing the fractal branching level corresponds with improvements in both the energy absorption capacity and load-bearing performance of the leaf vein structures. Therefore, fractal branching level can be considered a key structural parameter in the design of sandwich core materials.

(3) Simulation Comparison of Length Ratio

The royal water lily leaf veins exhibit a characteristic fractal branching structure, where branches at each hierarchical level follow specific geometric scaling rules in length and size. This branching system serves dual mechanical functions: support and cushioning. To further investigate the influence of fractal branching scale ratio (length ratio λ) on energy absorption performance, this study defines λ as the ratio of the current branch length to that of its parent branch. As shown in Figure 21, three finite element models were constructed with λ = 0.5 (short branch), λ = 0.8 (medium branch), and λ = 1.0 (equal-length branch). Under the conditions of maintaining consistent total height and branching angles, quasi-static compression simulations were performed to obtain the corresponding displacement–load response data.

Figure 22a shows the load–displacement curves of the three structures. The structure with λ = 0.5 exhibits a relatively gentle load increase during the initial loading phase (displacement 0–2.5 mm), with the lowest stiffness and poorer energy absorption. Its maximum load is about 10.83 N, mainly because the branches are too short, limiting the load transfer path. This results in an overall soft structure that undergoes early local buckling and insufficient energy dissipation capacity. The structure with λ = 1.0 has the highest initial stiffness, with load rapidly increasing and showing a significant rise between 4 and 6 mm displacement, reaching a maximum load of 11.93 N. However, as displacement increases further, the load growth slows down and even plateaus, indicating insufficient yielding capacity in the later stage. This structure’s high symmetry concentrates stiffness in the central main vein and primary branches, restricting deformation in the branching areas and limiting further energy dissipation. In contrast, the structure with an intermediate length ratio λ = 0.8 demonstrates more balanced mechanical performance. It exhibits good stiffness response in the initial stage (0–4 mm), with steadily increasing load, and maintains a continuous growth trend during the mid-to-late stages (6–11 mm), reaching a maximum load of 13.16 N, significantly higher than the other two groups. This structure, with its moderate scale reduction ratio, provides each branch level with sufficient load-bearing rigidity while maintaining reasonable flexibility. This enables synergistic deformation mechanisms in branching and junction areas, effectively delaying local yielding and enhancing energy dissipation.

Based on the load–displacement curves, the specific energy absorption (SEA) and mean crushing force (MCF) of the three structural models were compared. As shown in Figure 22b, when the length ratio λ = 0.5, the structure exhibits the lowest energy absorption capacity and compression stability, with an SEA of 33.19 J/kg and an MCF of 5.22 N. When λ = 0.8, the SEA increases to 34.51 J/kg, and the MCF rises significantly to 6.40 N, indicating better load stability and energy dissipation efficiency. Although the structure with λ = 1.0 has the highest SEA (37.50 J/kg), its MCF is only 5.75 N, suggesting that while it absorbs more energy per unit mass, its load response fluctuates more noticeably, which may indicate more significant local instability during compression. Overall, despite the higher unit-mass energy absorption of the λ = 1.0 structure, the intermediate length ratio (λ = 0.8) demonstrates a more balanced performance in terms of load–displacement continuity, compression stability, and multi-stage energy absorption capability. This balance between load-bearing and energy dissipation reflects a relatively favorable overall mechanical performance, providing a useful reference for parameter design in biomimetic structures.

In summary, this study demonstrates that the branching angle, fractal branching level, and branch length ratio of royal water lily leaf veins play a critical role in their energy absorption and load-bearing performance. Therefore, these fractal parameters can serve as key control variables in the subsequent structural optimization of sandwich panel cores to enhance their overall mechanical performance and energy absorption characteristics. It should be noted, however, that this study has certain limitations: (1) The finite element models were reconstructed based on point cloud data, with the spongy microstructure of the leaf veins simplified during modeling, making it difficult to fully capture the complex mechanical behavior of the biological material, which may lead to some discrepancies from the real structure; (2) the experimental sample pool was limited, and testing was primarily conducted under quasi-static compression, without exploring dynamic loading or impact conditions; (3) this study focused on key geometric parameters such as branching angle, fractal branching level, and branch length ratio, while other potential factors—such as material anisotropy, variation in vein thickness, leaf age, environmental conditions, and genetic differences—were not systematically investigated; (4) the application of leaf vein fractal structures in engineering faces challenges such as scalability, manufacturing defects, and fatigue under cyclic loading, and although fractal-based biomimetic designs are well-suited to royal water lily veins, their manufacturability, limitations, and broader engineering applicability require further validation. Future research will address these issues to further explore the engineering potential of such fractal structures.

4. Conclusions

This study systematically analyzed the macroscopic structural characteristics of the royal water lily leaf veins, combining 3D modeling, finite element simulation, and experimental testing to investigate the influence of mechanisms of fractal parameters (branching angle, fractal branching level, and branch length ratio) on the mechanical performance and energy absorption capacity under vertical compression loading. The main conclusions are as follows:

(1) The royal water lily leaf veins exhibit a typical gradient-distributed dendritic fractal structure, with thickness gradually decreasing radially and showing a linear relationship with the distance from the center, expressed as T = −0.11L + 44T mm. After each bifurcation, the vein width reduces to approximately 65–75% of the original width, while the branching angle increases progressively with the fractal branching level, forming distinct hierarchical features. The secondary veins predominantly display curved morphologies, constituting a multidirectional interwoven network. Their wavy arrangement combined with large branching angles helps to extend the energy dissipation path.

(2) The royal water lily veins possess a core–edge gradient fractal structure, where the fractal dimension follows a dynamic evolution trend of “decreasing first, then increasing” during growth: the central region features a low fractal dimension forming a rigid main trunk that optimizes load transfer and material usage; the peripheral region develops a high fractal dimension with a complex branching network that effectively disperses environmental impact loads.

(3) Based on 3D scanning and surface reconstruction techniques, the vein surfaces were repaired and reconstructed in Geomagic Studio to establish a 3D vein model. Quasi-static compression tests were conducted on representative central main veins, and finite element models were developed to perform simulations, validating the model’s effectiveness.

(4) The simulation results indicate that the overall leaf vein structure exhibits nonlinear stiffness behavior under vertical loading. Parametric analysis shows that within a certain range, regions with smaller branching angles or higher fractal branching levels exhibit better specific energy absorption (SEA) and mean crushing force (MCF). Additionally, when the fractal length ratio (λ) is at an intermediate level, the post-yield stiffness, ultimate load capacity, and energy dissipation capacity achieve a more balanced performance.

Based on structural bionics and fractal geometry, this study systematically investigated the relationship between the macroscopic structure of the royal water lily leaf veins and their mechanical performance. The findings provide innovative theoretical guidance and technical insights for the development of lightweight, high-strength thin-walled structures inspired by fractal vein architectures. Nevertheless, certain limitations should be acknowledged. The finite element models were reconstructed from point cloud data, which inevitably simplified the spongy internal microstructure and may not fully capture the complex mechanical behavior of natural venation. The experimental tests were restricted to a limited number of samples under quasi-static loading, without considering long-term durability, dynamic impacts, or cyclic fatigue. Moreover, this study primarily focused on fractal parameters such as bifurcation angle, fractal branching level, and length-to-width ratio, while other potential factors (e.g., material anisotropy, vein thickness variation, developmental stage, environmental humidity and temperature, and genetic variability) were not included. Future work could therefore address these limitations by incorporating more comprehensive experimental validation, including long-term fatigue tests and dynamic loading conditions, and by expanding the parametric space to account for biological variability and environmental influences. In addition, integrating sensitivity analysis and cross-species comparative studies would further enhance the robustness of the findings. On the application side, future research may explore the scalability, manufacturability, and practical feasibility of vein-inspired fractal designs, thereby advancing their use in engineering structures that demand both high-strength and superior energy absorption performance.