ABAQUS Subroutine-Based Implementation of a Fractional Consolidation Model for Saturated Soft Soils

Abstract

This paper presents a finite element implementation of a fractional rheological consolidation model in ABQUS, in which the fractional Merchant model governs the mechanical behavior of the soil skeleton, and the water flow is controlled by the fractional Darcy’s law. The implementation generally involves two main parts: subroutine-based fractional constitutive models’ development and their coupling. Considering the formal similarity between the energy equation and the mass equation, the fractional Darcy’s law was implemented using the UMATHT subroutine. The fractional Merchant model was then realized through the UMAT subroutine. Both subroutines were individually verified and then successfully coupled. The coupling was achieved by modifying the stress update scheme based on Biot’s poroelastic theory and the effective stress principle in UMAT, enabling a finite element analysis of the fractional consolidation model. Finally, the model was applied to simulate the consolidation behavior of a multi-layered foundation. The proposed approach may serve as a reference for the finite element implementation of consolidation models incorporating a fractional seepage model in ABAQUS.

1. Introduction

Saturated soft soils are characterized by high water content, low permeability, and pronounced time-dependent behavior, which give rise to distinctive responses such as delayed consolidation, creep deformation, and nonlinear seepage behaviors. To more accurately capture these features, many efforts [1,2,3] have been made to improve classical consolidation theory, among which the application of fractional derivatives provides a novel perspective for describing the consolidation process, generating many fractional models.

Fractional derivatives have attracted increasing attention for their ability to characterize the memory effects observed in various time-dependent processes [4]. Studies have shown that fractional models require relatively few parameters for constitutive modeling while providing accurate descriptions of material behavior [5]. By incorporating fractional constitutive models, consolidation models can more accurately describe the time-dependent deformation and nonlinear diffusion behavior of saturated soft soils [6,7]. Such models have mainly been developed along two directions: mechanical modeling and seepage modeling. In terms of mechanical models, many researchers, inspired by Koeller’s framework [8], have replaced the classical Newtonian viscous body with a fractional viscous body (spring pot) in component models and proposed a variety of fractional mechanical models [9,10]. Further developments have extended these models to account for damage effects in materials [11,12]. In terms of seepage models, approaches using fractional derivatives can generally be categorized into two main types. The first type introduces fractional derivatives into the pressure gradient term. This can be performed by applying a time-fractional derivative to the pressure gradient [13] or by replacing the classical spatial derivative with a spatial fractional derivative [14]. The second type modifies the relationship between seepage velocity and hydraulic gradient by incorporating fractional derivatives into the constitutive expression [15,16].

With the increasing research on the fractional consolidation models of saturated soft soils, significant attention has been paid to their numerical implementation methods. For the fractional consolidation model of saturated soft soil, researchers often simplify the problem to one or two dimensions and employ methods including the finite difference method [17] and Laplace transform method [18,19] to solve the problem. While these approaches are effective for parametric studies, they encounter significant challenges when handling complex boundaries in practical engineering applications [5]. To address this issue, researchers have gradually turned to the secondary development of commercial finite element software. Among these, ABAQUS has become the primary platform for the finite element implementation of fractional models due to its open user-defined subroutine interface and robust solver capabilities.

In ABAQUS 2021, the implementation of fractional consolidation models generally involves three components: the mechanical model, the seepage model, and the coupling method. Currently, several studies have utilized the user-defined subroutine UMAT to implement various fractional viscoelastic models, including the fractional Maxwell model [20], the fractional Kelvin model [21], and the fractional Merchant model [22], providing detailed numerical implementation schemes [22,23]. These efforts have laid a solid foundation for the finite element modeling of fractional consolidation models for saturated soft soils. In contrast, the implementation of fractional seepage models remains in the exploratory stage. This is partly due to the limited research in this area [24], but the main reason is the absence of a dedicated user-defined subroutine interface in ABAQUS for defining seepage constitutive relations. To address this issue, Barrera [25] employed the UMATHT subroutine to indirectly implement a consolidation analysis of saturated soils considering the fractional Darcy’s law.

In summary, current research mainly focuses on the finite element implementation of fractional mechanical models via the UMAT, while the method for implementing fractional seepage models within the finite element framework remains unclear. To this author’s knowledge, the implementation of consolidation models in a finite element context, which incorporates fractional mechanical and seepage constitutive models, has not been addressed in the existing studies.

This study proposes a finite element scheme for a fractional rheological consolidation model in ABAQUS based on user-defined subroutines. Specifically, the fractional Darcy’s law is implemented through the UMATHT subroutine, while the fractional Merchant model is implemented via the UMAT subroutine. These two components are then coupled to simulate the consolidation process of soft soil. The implementation of the models is validated through a comparison with numerical results or analytical solutions. Finally, a comparison of the simulated results and monitoring data indicates that the developed fractional rheological consolidation model is workable and can offer a practical reference for consolidation analysis in engineering applications.

2. Fractional Consolidation Model of Rheological Soils

Various definitions of fractional derivatives have been proposed in the literature, among which the Grünwald–Letnikov, Riemann–Liouville, and Caputo formulations are the most commonly used. Their mathematical definitions of order $\beta$ ($\beta \in \left(0,1\right)$, and $m=1$ are assumed in this paper) are given as follows:

$${}^{GL}D_{a,t}^{\beta }f\left(t\right)=\underset{\begin{array}{l}\mathrm{d}t\to 0\\ n\mathrm{d}t=t\end{array}}{\lim }\mathrm{d}{t}^{-\beta }{\displaystyle \sum _{i=0}^n{\left(-1\right)}^i\left(\begin{array}{c}\beta \\ i\end{array}\right)}f\left(t-i\mathrm{d}t\right)$$

(1)

$${}^{RL}D_{a,t}^{\beta }f\left(t\right)={\displaystyle \frac{1}{\Gamma (m-\beta )}}{\displaystyle \frac{{\mathrm{d}}^m}{\mathrm{d}{t}^m}}{{\displaystyle \int }}_a^t{\left(t-\tau \right)}^{m-\beta -1}f(\tau )\mathrm{d}\tau$$

(2)

$${}^{C}D_{a,t}^{\beta }f(t)={\displaystyle \frac{1}{\Gamma (m-\beta )}}{{\displaystyle \int }}_a^t{\left(t-\tau \right)}^{m-\beta -1}{f}^{\left(m\right)}(\tau )\mathrm{d}\tau$$

(3)

where $f\left(t\right)$ is a function continued on $\left[a,b\right]$. $\Gamma \left(·\right)$ is the Euler Gamma function. The superscripts GL, RL, and C denote the Grunwald–Letnikov, Riemann–Liouville, and Caputo fractional derivatives, respectively.

2.1. Fractional Darcy’s Law

The well-known Darcy’s law is the basic assumption in Biot’s poroelastic theory for porous media. It describes the relation between the water flow $q$ and pressure gradient $\nabla p$ in porous media through the following equation:

$$q=-{\displaystyle \frac{k}{{\gamma }_{\mathrm{f}}}}\nabla p$$

(4)

where $k$ is the permeability coefficient depending on the material; ${\gamma }_{\mathrm{f}}$ denotes the unit weight of water.

To capture the memory effects associated with pore structure evolution during the consolidation process of saturated soils, Feng et al. [7] have introduced the Riemann–Liouville derivative into the seepage model. The pressure–flux relationship of the fractional seepage model is given as follows:

$${\gamma }_{f}q=-(k+k_{\beta }{}^{RL}D_{0,t}^{\beta })\nabla p$$

(5)

where $k_{\beta }$ denotes the anomalous permeability coefficient.

2.2. Fractional Merchant Model

The fractional Merchant model is one of the commonly employed mechanical models in the existing research [18,26] on the fractional consolidation model for saturated soft soil. This model comprises a fractional Kelvin model connected in series with a linear elastic modulus $E_0$, as illustrated in Figure 1.

For the isotropic fractional Merchant model, the constitutive relationship between stress $\sigma$ and strain $\epsilon$ can be expressed as follows:

$$\sigma +{\displaystyle \frac{E_1{V}^{\alpha }}{E_0+E_1}}{}^{C}D_{0,t}^{\alpha }\sigma ={\displaystyle \frac{E_0{E}_1}{E_0+E_1}}\epsilon +{\displaystyle \frac{E_0{E}_1{V}^{\alpha }}{E_0+E_1}}{}^{C}D_{0,t}^{\alpha }\epsilon$$

(6)

where $E_1$ is the elastic modulus; $\eta$ is the viscosity coefficient; and $V$ is viscosity time.

Koeller [8] has derived creep functions of this model:

$$\epsilon (t)={\displaystyle {\int }_0^{t}J(t-\tau )\mathrm{d}\sigma (\tau )}={\displaystyle {\int }_0^{t}J(t-\tau )\frac{\partial \sigma (\tau )}{\partial \tau }\mathrm{d}\tau }$$

(7)

$$J(t)={\displaystyle \frac{1}{E_0}}+{\displaystyle \frac{1}{E_1}}\left\{1-E_{\alpha }\left[-{\left({\displaystyle \frac{t}{V}}\right)}^{\alpha }\right]\right\}$$

(8)

where $J\left(t\right)$ is the creep compliance. $E_{\alpha }(x)={\displaystyle {\sum }_{k=0}^{\infty }{x}^k/\Gamma \left(\alpha k+1\right)}$ is the Mittag-Leffler function.

2.3. Governing Equations Based on Biot’s Poroelastic Theory

Biot’s poroelastic theory provides a fundamental framework for describing the physical processes in saturated porous media. By incorporating the influence of excess pore water pressure, it enables a coupled analysis of fluid flow and deformation of the solid skeleton. This theory serves as the theoretical foundation for the governing equations of the consolidation model for saturated soils.

The derivation of the rheological consolidation model is based on Biot’s work, with the following modifications:

(1)

The deformation of the soil skeleton is governed by the fractional Merchant model;

(2)

The water flow within the soil layer is controlled by the fractional Darcy’s law;

(3)

The influence of mass forces, including gravity, is ignored for simplification.

The framework of Biot’s poroelastic theory in three-dimension can be simplified as follows:

$$\nabla \left({\sigma }^{\prime }+{\alpha }_{b}p{\delta }_{ij}\right)=0$$

(9)

$${\alpha }_p{\displaystyle \frac{\partial p}{\partial t}}+\nabla q+{\alpha }_b{\displaystyle \frac{\partial {\epsilon }_{\mathrm{v}}}{\partial t}}=0$$

(10)

Accordingly, the constitutive equation of the fractional Merchant model should be extended to a three-dimensional form:

$${\sigma }_{ij}^{\prime }+{\displaystyle \frac{E_1{V}^{\alpha }{}^{C}D_{0,t}^{\alpha }{\sigma }_{ij}^{\prime }}{E_0+E_1}}={\displaystyle \frac{E_0{E}_1{\epsilon }_{ij}+E_0{E}_1{V}^{\alpha }{}^{C}D_{0,t}^{\alpha }{\epsilon }_{ij}}{\left(E_0+E_1\right)\left(1+\mu \right)}}+{\displaystyle \frac{\mu \left(3E_0{E}_1{\epsilon }_{\mathrm{v}}+E_0{E}_1{V}^{\alpha }{}^{C}D_{0,t}^{\alpha }{\epsilon }_{\mathrm{v}}\right)}{\left(E_0+E_1\right)\left(1+\mu \right)\left(1-2\mu \right)}}{\delta }_{ij}$$

(11)

where ${\sigma }^{\prime }$ is effective stress; ${\alpha }_b$ is Biot’s coefficient; ${\alpha }_p$ is the water storage coefficient; ${\epsilon }_{\mathrm{v}}$ is volumetric strain; $\mu$ is Poisson’s ratio; and ${\delta }_{ij}$ is the Kronecker delta.

Equations (5) and (9)–(11) represent the governing equations of the fractional consolidation model for saturated soft soils.

3. Numerical Implementation of Fractional Consolidation Model

3.1. Approximation of Fractional Derivative

The Riemann–Liouville fractional derivative of a function $f\left(t\right)$ on the interval $\left[0,t\right]$, for a fractional order $\beta \in \left(0,1\right)$, can be numerically approximated through the discrete scheme of a Grünwald–Letnikov fractional derivative with second-order accuracy [27]:

$$D_{a,t}^{\beta }f\left(t_{n+1}\right)=\underset{\Delta t\to 0}{\lim }\left[\Delta t^{-\beta }{\displaystyle \sum _{m=0}^{n+1}{\lambda }_m^{\left(\beta \right)}f\left(t_{n+1-m}\right)}\right]$$

(12)

The accuracy of the discrete scheme in Equation (12) depends on the binomial coefficient ${\lambda }_m^{\left(\beta \right)}$. Lubich [28] derived expressions corresponding to different orders of accuracy:

Let $\omega \left(t,\beta \right)$ be the generating functions of the ${\lambda }_m^{\left(\beta \right)}$, and expand $\omega \left(t,\beta \right)$ into a Taylor series at the origin:

$$\omega \left(t,\beta \right)={\displaystyle \sum _{m=0}^{\infty }{\lambda }_m^{\left(\beta \right)}{t}^m}$$

(13)

If the generating function takes the following form:

$$\omega \left(t,\beta \right)={\left(1-t\right)}^{\beta }$$

(14)

The binomial coefficients ${\lambda }_m^{\left(\beta \right)}=g_m^{\left(\beta \right)}$ that yield first-order accuracy for the discrete scheme in Equation (12) can be obtained through the fast Fourier transform:

$$g_0^{\left(\beta \right)}=1,\hspace{1em}\hspace{1em}{g}_m^{\left(\beta \right)}=\left(1-{\displaystyle \frac{\beta +1}{m}}\right)g_{m-1}^{\left(\beta \right)}$$

(15)

Similarly, if the generating function is given by the following:

$$\omega \left(t,\beta \right)={\left(1.5-2t+0.5t^2\right)}^{\beta }$$

(16)

The binomial coefficients ${\lambda }_m^{\left(\beta \right)}$ that ensure the second-order accuracy of Equation (12) are as follows:

$${\lambda }_m^{\left(\beta \right)}={1.5}^{\beta }{\displaystyle \sum _{j=0}^m{g}_j^{\left(\beta \right)}}{g}_{m-j}^{\left(\beta \right)}{3}^{-j}$$

(17)

3.2. Implementation and Validation of the Fractional Darcy’s Law

Given the formal similarity between the energy equation and mass equation, and inspired by Barrera’s framework [25], this study utilizes the UMATHT subroutine (originally intended for defining a heat constitutive model) to implement the fractional Darcy’s law.

3.2.1. Numerical Implementation Based on UMATHT

The mass equation and energy equations can be expressed as follows:

$${\alpha }_p{\displaystyle \frac{\partial p}{\partial t}}-\nabla q=0$$

(18)

$$\rho c{\displaystyle \frac{\partial T}{\partial t}}-\nabla q_T=0$$

(19)

where $\rho$ is the density; $c$ is the specific heat; and $q_T$ is the heat flux.

It is noted that the energy equation shares a similar mathematical form with the mass equation. Thus, by setting ${\alpha }_p=1$, the equivalent relationship of the fractional Darcy’s law in the ABAQUS heat transfer module is as follows:

$$q=-\left({\displaystyle \frac{k}{\rho g}}+{\displaystyle \frac{k_{\beta }}{\rho g}}{D}_{0,t}^{\beta }\right)\nabla p\Rightarrow q_T/\rho c=-\left({\displaystyle \frac{K}{\rho c}}+{\displaystyle \frac{K_{\beta }}{\rho c}}{}^{RL}D_{0,t}^{\beta }\right)\nabla T$$

(20)

In the UMATHT subroutine, Dtemdx represents the spatial temperature gradient at the current time increment, and flux denotes the heat flux. Accordingly, the fractional Darcy’s law can be implemented through the definition of flux in the subroutine based on Equations (5) and (12):

$$\mathrm{Flux}\left(t_n\right)=-k\cdot \mathrm{Dtemdx}\left(t_n\right)-k_{\beta }\cdot \underset{\Delta t\to 0}{\lim }\left[\Delta t^{-\beta }{\displaystyle \sum _{m=0}^n{\lambda }_m^{\left(\beta \right)}\mathrm{Dtemdx}\left(t_{n-m}\right)}\right]$$

(21)

According to Equation (21), the calculation of flux at the nth increment requires the spatial temperature gradient data from all previous increments. In Fortran, two common methods are used to store and retrieve historical data. The first employs a Common Block (CB), the structure and size of which depend on the number of elements, nodes, time steps, and model dimensions. While computationally efficient, this approach is limited by a 2 GB memory [22]. The second method involves writing historical data to TXT files, which significantly reduces computational efficiency. To achieve a balance between storage efficiency and computational performance, this study adopts the first approach.

Notably, the binomial coefficients ${\lambda }_m^{\left(\beta \right)}$ in Equation (21) are initially indexed from zero, whereas the arrays in Fortran are by default indexed starting from one. To ensure consistency and correctness in implementation, index adjustment is necessary.

Let $i=m+1$, and rewrite the equation in a forward recursive form:

$$g_1^{\left(\beta \right)}=1,\hspace{1em}\hspace{1em}{g}_i^{\left(\beta \right)}=\left(1-{\displaystyle \frac{\beta +1}{i}}\right)g_{i-1}^{\left(\beta \right)}$$

(22)

$${\lambda }_i^{\left(\beta \right)}={1.5}^{\beta }{\displaystyle \sum _{j=1}^i{g}_j^{\left(\beta \right)}}{g}_{i-j+1}^{\left(\beta \right)}{3}^{1-j}$$

(23)

The implementation scheme of the UMATHT subroutine is summarized in Algorithm 1.

Algorithm 1. Pseudocode of UMATHT subroutine.

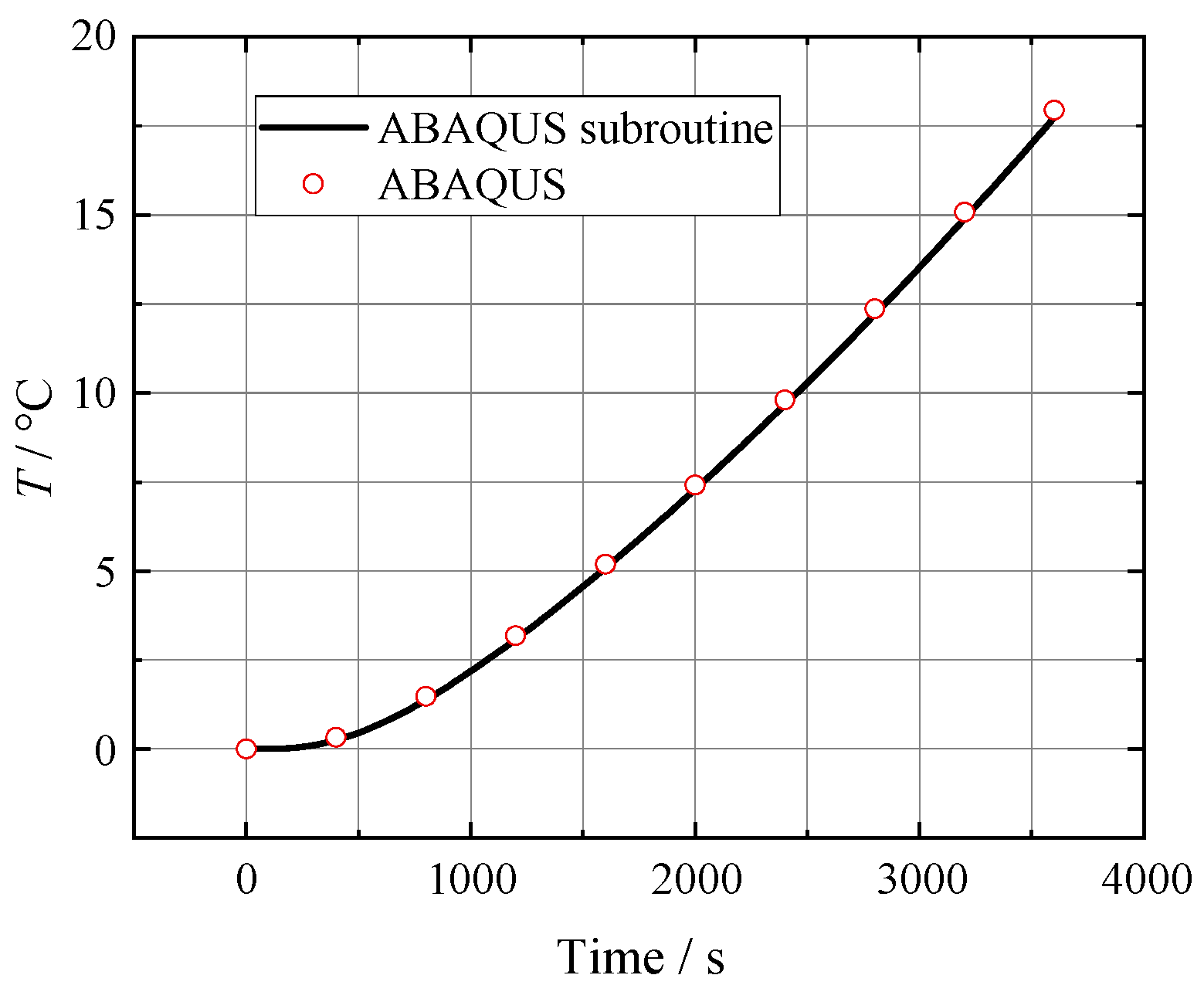
3.2.2. Verification of UMATHT

Based on the numerical scheme described in Section 3.2.1, the UMATHT subroutine for the fractional Darcy’s law was developed. To verify its correctness, two numerical examples are presented.

In ABAQUS, the material parameters associated with the fractional Darcy’s law are defined in the “User Material” and “Density” options under the Property module. The “User Material” should be set to thermal type, requiring input parameters including the conductivity, anomalous conductivity, specific heat capacity, and fractional order.

Example 1: A square domain with a side length of 1.2 m was established in ABAQUS and discretized by the elements named DC2D4. A temperature boundary condition of 0 °C was applied to the top edge, while the remaining edges were defined as insulated, simplifying the model to a one-dimensional heat conduction problem. Additionally, an initial temperature of 60 °C was assigned using the predefined field.

The specific parameters used in the model are as follows: $K=5\mathrm{W}/\left(\mathrm{m}\cdot \mathrm{K}\right)$, $K_{\beta }=5\mathrm{W}/\left(\mathrm{m}\cdot {\mathrm{s}}^{-\beta }\cdot \mathrm{K}\right)$, $\rho =100{\mathrm{kg}/\mathrm{m}}^3$, $c=10\mathrm{J}/(\mathrm{kg}\cdot \mathrm{K})$, $\beta =0.5$.

The geometry of the model is illustrated in Figure 2a, and the boundary conditions and mesh discretization are shown in Figure 2b.

The total simulation time was set to 100 s, with a fixed time increment of 0.5 s. The temperature response at the midpoint of the model (y = 0.6 m) was extracted and compared with the results obtained from the finite difference program developed by Zhang et al. [29]. As shown in Figure 3, the results exhibit excellent agreement, with only minor discrepancies.

Example 2: This example was selected from a heat transfer model provided in the ABAQUS documentation. The geometry of the model is a 10 m × 1 m rectangular, discretized through DC2D4 elements. Heat exchange with the environment occurred along the top edge through a surface film condition, while all other edges were assumed to be insulated. The ambient temperature was defined by an amplitude function: it remains at 100 °C for 3600 s and then instantly rises to 200 °C. The initial temperature of the model was set to 0 °C through the predefined field.

The geometry of the finite element model is illustrated in Figure 4a, and the boundary conditions and mesh discretization are shown in Figure 4b. The physical parameters involved are as follows: $K=1.4\mathrm{W}/\left(\mathrm{m}\cdot \mathrm{K}\right)$, $\rho =7800{\mathrm{kg}/\mathrm{m}}^3$, $c=260\mathrm{J}/(\mathrm{kg}\cdot \mathrm{K})$.

Then, the fractional order in the UMATHT subroutine was set to a value approaching zero, thereby reducing the fractional Darcy’s law to the classical Darcy’s law. This degenerated subroutine was then applied to example 2 for numerical analysis. The parameters inputted in the subroutine are as follows: $K=0.7\mathrm{W}/\left(\mathrm{m}\cdot \mathrm{K}\right)$, $K_{\beta }=0.7\mathrm{W}/\left(\mathrm{m}\cdot {\mathrm{s}}^{-\beta }\cdot \mathrm{K}\right)$, $\rho =7800{\mathrm{kg}/\mathrm{m}}^3$, $c=260\mathrm{J}/(\mathrm{kg}\cdot \mathrm{K})$, $\beta =0.01$.

The temperature response at the midpoint of the model ($y=5\mathrm{m}$) was extracted and compared with the results from the example in the ABAQUS documentation. As shown in Figure 5, the two results exhibit close agreement.

3.3. Implementation and Validation of the Fractional Merchant Model

A previous study [20] demonstrated that when the time step $\Delta t$ is sufficiently small, the numerical results of the Grünwald–Letnikov fractional derivative converge to those of the Caputo fractional derivative. To simplify the development of the subroutine, this study adopts the approximation of the Grünwald–Letnikov derivative, as shown in Equation (12), to implement the fractional Merchant model.

3.3.1. Numerical Implementation Based on UMAT

In the UMAT subroutine, it is necessary to define the Jacobian matrix and the stress update equation. Notably, UMAT employs engineering shear strain, which differs from tensorial shear strain and must be appropriately converted: ${\gamma }_{ij}=2{\epsilon }_{ij}$.

Assuming the material is isotropic, the stress–strain relationship of the fractional Merchant model is given by Equation (11). By incorporating the approximation of the Grünwald–Letnikov fractional derivative, as defined in Equation (12), the general form of the constitutive relation is expressed as follows [22]:

$$\left\{\begin{array}{c}{\sigma }_{ii}\left(n\Delta t\right)=A{\epsilon }_{ii}\left(n\Delta t\right)+B{\epsilon }_{\mathrm{v}}\left(n\Delta t\right)+C{\displaystyle \sum _{m=2}^{n+1}{\lambda }_m^{\left(\alpha \right)}}{\epsilon }_{ii}\left[\left(n+1-m\right)\Delta t\right]\\ \hspace{1em}\hspace{1em}\hspace{1em} +D{\displaystyle \sum _{m=2}^{n+1}{\lambda }_m^{\left(\alpha \right)}}{\epsilon }_{\mathrm{v}}\left[\left(n+1-m\right)\Delta t\right]-E{\displaystyle \sum _{m=2}^{n+1}{\lambda }_m^{\left(\alpha \right)}}{\sigma }_{ii}\left[\left(n+1-m\right)\Delta t\right]\\ {\sigma }_{ij}\left(n\Delta t\right)=0.5A{\gamma }_{ij}\left(n\Delta t\right)+C{\displaystyle \sum _{m=2}^{n+1}0.5{\lambda }_m^{\left(\alpha \right)}}{\gamma }_{ij}\left[\left(n+1-m\right)\Delta t\right]\\ \hspace{1em}\hspace{1em}\hspace{1em} -E{\displaystyle \sum _{m=2}^{n+1}{\lambda }_m^{\left(\alpha \right)}}{\sigma }_{ii}\left[\left(n+1-m\right)\Delta t\right]\end{array}\right.$$

(24)

where

$$\left\{\begin{array}{ccc}A& =& E_0\left(E_1\Delta t^{\alpha }+E_1{V}^{\alpha }\right)/\left(1+\mu \right)/\left[\left(E_0+E_1\right)\Delta t^{\alpha }+E_1{V}^{\alpha }\right]\\ B& =& 3\mu E_0\left(E_1\Delta t^{\alpha }+E_1{V}^{\alpha }\right)/\left(1+\mu \right)/\left(1-2\mu \right)/\left[\left(E_0+E_1\right)\Delta t^{\alpha }+E_1{V}^{\alpha }\right]\\ C& =& E_0{E}_1{V}^{\alpha }/\left(1+\mu \right)/\left[\left(E_0+E_1\right)\Delta t^{\alpha }+E_1{V}^{\alpha }\right]\\ D& =& 3\mu E_0{E}_1{V}^{\alpha }/\left(1+\mu \right)/\left(1-2\mu \right)/\left[\left(E_0+E_1\right)\Delta t^{\alpha }+E_1{V}^{\alpha }\right]\\ E& =& E_1{V}^{\alpha }/\left[\left(E_0+E_1\right)\Delta t^{\alpha }+E_1{V}^{\alpha }\right]\end{array}\right.$$

According to the definition of the Jacobian matrix $\partial \Delta \sigma /\partial \Delta \epsilon$,

$${\displaystyle \frac{\partial \Delta {\sigma }_{ii}}{\partial \Delta {\epsilon }_{ii}}}={\displaystyle \frac{\left(1-\mu \right)E_0\left(E_1\Delta t^{\alpha }+E_1{V}^{\alpha }\right)}{\left(1+\mu \right)\left(1-2\mu \right)\left[\left(E_0+E_1\right)\Delta t^{\alpha }+E_1{V}^{\alpha }\right]}}\hspace{1em}i=x,y,z$$

(25)

$${\displaystyle \frac{\partial \Delta {\sigma }_{ii}}{\partial \Delta {\epsilon }_{jj}}}={\displaystyle \frac{\mu E_0\left(E_1\Delta t^{\alpha }+E_1{V}^{\alpha }\right)}{\left(1+\mu \right)\left(1-2\mu \right)\left[\left(E_0+E_1\right)\Delta t^{\alpha }+E_1{V}^{\alpha }\right]}}\hspace{1em}i=x,y,z,i\ne j$$

(26)

$${\displaystyle \frac{\partial \Delta {\sigma }_{ij}}{\partial \Delta {\gamma }_{ij}}}={\displaystyle \frac{E_0\left(E_1\Delta t^{\alpha }+E_1{V}^{\alpha }\right)}{2\left(1+\mu \right)\left[\left(E_0+E_1\right)\Delta t^{\alpha }+E_1{V}^{\alpha }\right]}}\hspace{1em}i=x,y,z,i\ne j$$

(27)

Thus, the Jacobian matrix of the fractional Merchant model can be obtained:

$$Ja=\left[\begin{array}{llllll}{\displaystyle \frac{\left(1-\mu \right)E_2}{\left(1+\mu \right)\left(1-2\mu \right)}}\hfill & {\displaystyle \frac{\mu E_2}{\left(1+\mu \right)\left(1-2\mu \right)}}\hfill & {\displaystyle \frac{\mu E_2}{\left(1+\mu \right)\left(1-2\mu \right)}}\hfill & 0\hfill & 0\hfill & 0\hfill \\ {\displaystyle \frac{\mu E_2}{\left(1+\mu \right)\left(1-2\mu \right)}}\hfill & {\displaystyle \frac{\left(1-\mu \right)E_2}{\left(1+\mu \right)\left(1-2\mu \right)}}\hfill & {\displaystyle \frac{\mu E_2}{\left(1+\mu \right)\left(1-2\mu \right)}}\hfill & 0\hfill & 0\hfill & 0\hfill \\ {\displaystyle \frac{\mu E_2}{\left(1+\mu \right)\left(1-2\mu \right)}}\hfill & {\displaystyle \frac{\mu E_2}{\left(1+\mu \right)\left(1-2\mu \right)}}\hfill & {\displaystyle \frac{\left(1-\mu \right)E_2}{\left(1+\mu \right)\left(1-2\mu \right)}}\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & {\displaystyle \frac{E_2}{2\left(1+\mu \right)}}\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & {\displaystyle \frac{E_2}{2\left(1+\mu \right)}}\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & {\displaystyle \frac{E_2}{2\left(1+\mu \right)}}\hfill \end{array}\right]$$

(28)

where $E_2={\displaystyle \frac{E_0\left(E_1\Delta t^{\alpha }+E_1{V}^{\alpha }\right)}{\left(E_0+E_1\right)\Delta t^{\alpha }+E_1{V}^{\alpha }}}$.

As presented in Equation (24), the stress at the nth time step in the fractional Merchant model depends on the historical data of stress and strain. Therefore, as discussed in Section 3.2.1, two CBs are defined in the Fortran to store historical data. The implementation scheme of the UMAT subroutine is summarized in Algorithm 2.

Algorithm 2. Pseudocode of UMAT subroutine.

3.3.2. Verification of UMAT

Based on the numerical scheme described in Section 3.3.1, the UMAT subroutine for the fractional Merchant model was developed. To validate its correctness, a verification test was conducted following the method recommended in the ABAQUS documentation, which involves evaluating the strain response of a single element under a load. Specifically, a cubic model with a side length of 1 m was established in ABAQUS, consisting of a single element (C3D8). Under uniaxial loading, the axial displacement of the element corresponds directly to the axial strain.

As illustrated in Figure 6, a uniaxial tensile stress was applied to the top surface, while the bottom and side surfaces were fully constrained in displacement. The material parameters were defined through the “User Material” option in the Property module, with the material type specified as Mechanical. The specific material parameters used are as follows: $E_0=50\mathrm{GPa}$, $E_1=24\mathrm{MPa}$, $\mu =0.3$, $V=10\mathrm{s}$, $\alpha =0.2$.

The loading scheme follows the pulse load used by Zhou [30], in which the load ${\sigma }_0$ is applied instantaneously at $t_1$, maintained for the duration $t_2-t_1$, and then removed instantaneously, as expressed in Equation (29):

$$\sigma \left(t\right)=\left\{\begin{array}{c}0t<t_1\\ {\sigma }_0{t}_1\le t\le t_2\\ 0t_2<t\end{array}\right.$$

(29)

In this verification, the parameters were set as ${\sigma }_0=1\mathrm{Mpa}$, $t_1=2\mathrm{s}$, $t_2=8\mathrm{s}$. Equation (29) was implemented using an amplitude curve in ABAQUS. However, if the amplitude is set to 1 and 0 simultaneously at t₁ and t₂, ABAQUS cannot correctly identify the load at those time points. Therefore, a modified amplitude definition was adopted: the amplitude was set to 0 at 2 s and 8.001 s, and to 1 at 2.001 s and 8 s.

The creep function of the fractional Merchant model is presented in Equation (8), from which the analytical solution of the model under pulse load can be derived:

$$\epsilon \left(t\right)=\left\{\begin{array}{ll}0& t<t_1\\ J\left(t-t_1\right){\sigma }_0\hfill & t_1\le t\le t_2\\ \left[J\left(t-t_1\right)-J\left(t-t_2\right)\right]{\sigma }_0\hfill & t_2<t\end{array}\right.$$

(30)

The time increment for numerical analysis was fixed at 0.05 s, and the Viscosity option was selected in the analysis step. The comparison between the numerical results obtained from the UMAT subroutine and the analytical solution is presented in Figure 7. The results exhibit good agreement, with only minor discrepancies observed. This demonstrates that the UMAT subroutine for the fractional Merchant model is accurate and reliable for simulating the fractional Merchant model.

3.4. Coupling Method of UMAT and UMATHT

3.4.1. Stress Updating

The fractional consolidation model integrates the fractional Darcy’s law and the fractional Merchant model within Biot’s poroelastic framework. Therefore, effectively coupling the two subroutines is essential for the implementation of the fractional consolidation model in ABAQUS.

According to Terzaghi’s effective stress principle and Biot’s poroelastic theory,

$${\sigma }_{ij}^{\prime }={\sigma }_{ij}-{\alpha }_{b}p{\delta }_{ij}$$

(31)

Under the elastic assumption, the constitutive relation of effective stress and strain for saturated porous media is as follows:

$${\sigma }^{\prime }=D\epsilon$$

(32)

where $D$ is the elastic stiffness matrix.

As shown in Equation (32), within Biot’s poroelastic framework, the stress governing the deformation of the solid skeleton is governed by effective stress. Therefore, in the current incremental step of the subroutine, after calculating the stress increment based on the stress–strain relationship, a correction is required to obtain the stress increment under the coupling effect:

$$\Delta {\sigma }_{ij}=\Delta {\sigma }_{ij}-{\alpha }_p\Delta T{\delta }_{ij}$$

(33)

The volumetric strain term in the Equation (10) can be regarded as the heat source term in the heat transfer equation. It can be defined in the RPL in UMAT:

$$\partial {\epsilon }_{\mathrm{v}}/\partial t={\displaystyle \sum \Delta {\epsilon }_{ii}}/\Delta t$$

(34)

3.4.2. Verification of the Coupling Method

In this section, the subroutines for Fourier’s law and the elastic model were developed and coupled according to Section 3.3.1.

The geometric diagram of the model is shown in Figure 8. The simulation represents a one-dimensional consolidation process, in which the initial excess pore water pressure, generated by external loading, dissipates over time. However, since the excess pore water pressure is replaced by the temperature in ABAQUS, directly applying external loads does not result in the expected initial pore pressure (i.e., temperature). To address this, the initial excess pore pressure induced by instantaneous loading is equivalently represented through the assignment of an initial temperature field.

COMSOL 6.2, a finite element software specialized in solving partial differential equations, offers robust numerical computation capabilities and mature algorithms for multi-physics coupling problems. To validate the accuracy of the coupling method for subroutines, the results from COMSOL are used for a comparison.

The finite element model was analyzed through a temperature–displacement coupling analysis step, with a total of 10 elements (CPE4T). The physical parameters used in the model are as follows: $k=5\times {10}^{-8}\mathrm{m}/\mathrm{s}$, $\rho =1000{\mathrm{kg}/\mathrm{m}}^3$, $g=10{\mathrm{m}/\mathrm{s}}^2$, $E=0.1\mathrm{GPa}$, $\mu =0.3$.

The simulation results focus on the temporal evolution of excess pore water pressure and displacement at the midpoint of the model. A comparison between the ABAQUS and COMSOL results is presented in Figure 9. As shown in the figure, the two sets of results exhibit good agreement, with only minor discrepancies.

3.4.3. Coupling Calculation of Subroutines for Fractional Models

Based on Section 3.3.2, the UMATHT for the fractional Darcy’s law and the UMAT for the fractional Merchant model were coupled in ABAQUS. Feng et al. [7] previously proposed the finite difference method (FDM) scheme for a one-dimensional fractional model that adopts the same fractional seepage and mechanical constitutive relations as this study. It can be used as the verification for the fractional consolidation model implemented in ABAQUS. However, the fractional consolidation model in Feng’s paper was derived based on the continuity equation under the framework of Terzaghi’s consolidation theory:

$${\displaystyle \frac{\partial {\epsilon }_{\mathrm{v}}}{\partial t}}=-\nabla q$$

(35)

In ABAQUS, when temperature is used to replace the excess pore water pressure, the temperature–displacement coupling method is equivalent to Biot’s poroelasticity framework as presented in Section 2.3.

Comparing the diffusion Equations (10) and (35) from a mathematical perspective, it can be found that Equation (10) contains an additional term corresponding to the medium’s water storage coefficient ${\alpha }_p$ (assuming ${\alpha }_b=1$). To degenerate Equation (10) into Equation (35) within ABAQUS, the water storage coefficient must be set to zero, which corresponds to setting the specific heat capacity $c=0$. However, in practice, ABAQUS fails to converge when $c$ is set to zero or infinitesimal, resulting in computational failure.

To enable a valid comparison with the ABAQUS simulation, the finite difference scheme from Feng’s paper [7] is modified by incorporating a water storage coefficient term. The revised finite difference scheme is expressed as follows:

For $n=1$,

$$A_1{p}^1=B_1{p}^0+d_1$$

(36)

$$A_1=\left[\begin{array}{ccccc}1& & & & \\ -\left(s+b\right)& J\left({\displaystyle \frac{\mathrm{d}t}{2}}\right)+2s+2b+{\alpha }_p& -\left(s+b\right)& & \\ & \ddots & \ddots & \ddots & \\ & & -\left(s+b\right)& J\left({\displaystyle \frac{\mathrm{d}t}{2}}\right)+2s+2b+{\alpha }_p& -\left(s+b\right)\\ & & & & -2\left(s+b\right)\end{array}\right]$$

(37)

$$B_1=\left[\begin{array}{ccccc}0& & & & \\ sr-s+b& -2\left[sr-s-{\displaystyle \frac{1}{2}}J\left({\displaystyle \frac{\mathrm{d}t}{2}}\right)-{\displaystyle \frac{1}{2}}{\alpha }_p+b\right]& sr-s+b& & \\ & \ddots & \ddots & \ddots & \\ & & sr-s+b& -2\left[sr-s-{\displaystyle \frac{1}{2}}J\left({\displaystyle \frac{\mathrm{d}t}{2}}\right)-{\displaystyle \frac{1}{2}}{\alpha }_p+b\right]& sr-s+b\\ & & & & 2\left(sr-s+b\right)\end{array}\right]$$

(38)

$$d_1={\left[\begin{array}{c}{p}_0^1\\ \mathrm{d}t{f}_1^1+\left(F_1^1-F_1^0\right)J\left({\displaystyle \frac{\mathrm{d}t}{2}}\right)\\ ⋮\\ \mathrm{d}t{f}_{M-1}^1+\left(F_{M-1}^1-F_{M-1}^0\right)J\left({\displaystyle \frac{\mathrm{d}t}{2}}\right)\\ \mathrm{d}t{f}_M^1+\left(F_M^1-F_M^0\right)J\left({\displaystyle \frac{\mathrm{d}t}{2}}\right)\end{array}\right]}_{\left(M+1\right)\times 1}$$

(39)

For $n>1$,

$$\begin{array}{l}{A}_2{p}^n+{\displaystyle \sum _{k=1}^{n-1}\left(J\left[\left(n-k+\frac{1}{2}\right)\mathrm{d}t\right]-J\left[\left(n-k-\frac{1}{2}\right)\mathrm{d}t\right]\right)}\left(p^k-p^{k-1}\right)\\ =B_2{p}^{n-1}-s{\displaystyle \sum _{k=1}^{n-1}\left(a_{n-k-1}-a_{n-k}\right)B{p}^{k-\frac{1}{2}}}+s{\tilde{a}}_{n-1}B{p}^0\\ +{\displaystyle \sum _{k=1}^{n-1}\left(J\left[\left(n-k+\frac{1}{2}\right)\mathrm{d}t\right]-J\left[\left(n-k-\frac{1}{2}\right)\mathrm{d}t\right]\right)}\left(F^k-F^{k-1}\right)+d_2\end{array}$$

(40)

$$A_2=\left[\begin{array}{ccccc}1& & & & \\ -\left({\displaystyle \frac{s}{2}}+b\right)& J\left({\displaystyle \frac{\mathrm{d}t}{2}}\right)+s+2b+{\alpha }_p& -\left({\displaystyle \frac{s}{2}}+b\right)& & \\ & \ddots & \ddots & \ddots & \\ & & -\left({\displaystyle \frac{s}{2}}+b\right)& J\left({\displaystyle \frac{\mathrm{d}t}{2}}\right)+s+2b+{\alpha }_p& -\left({\displaystyle \frac{s}{2}}+b\right)\\ & & & & -2\left({\displaystyle \frac{s}{2}}+b\right)\end{array}\right]$$

(41)

$$B_2=\left[\begin{array}{ccccc}0& & & & \\ {\displaystyle \frac{s}{2}}+b& -\left[s+2b-J\left({\displaystyle \frac{\mathrm{d}t}{2}}\right)-{\alpha }_p\right]& {\displaystyle \frac{s}{2}}+b& & \\ & \ddots & \ddots & \ddots & \\ & & {\displaystyle \frac{s}{2}}+b& -\left[s+2b-J\left({\displaystyle \frac{\mathrm{d}t}{2}}\right)-{\alpha }_p\right]& {\displaystyle \frac{s}{2}}+b\\ & & & & s+2b\end{array}\right]$$

(42)

$$B=\left[\begin{array}{ccccc}0& & & & \\ 1& -2& 1& & \\ & \ddots & \ddots & \ddots & \\ & & 1& -2& 1\\ & & & & 2\end{array}\right]$$

(43)

$$d_2={\left[\begin{array}{c}{p}_0^n\\ \mathrm{d}t{f}_1^{n-{\displaystyle \frac{1}{2}}}+\left(F_1^n-F_1^{n-1}\right)J\left({\displaystyle \frac{\mathrm{d}t}{2}}\right)\\ ⋮\\ \mathrm{d}t{f}_{M-1}^{n-{\displaystyle \frac{1}{2}}}+\left(F_{M-1}^n-F_{M-1}^{n-1}\right)J\left({\displaystyle \frac{\mathrm{d}t}{2}}\right)\\ \mathrm{d}t{f}_M^{n-{\displaystyle \frac{1}{2}}}+\left(F_M^n-F_M^{n-1}\right)J\left({\displaystyle \frac{\mathrm{d}t}{2}}\right)\end{array}\right]}_{\left(M+1\right)\times 1}$$

(44)

where $M$ and $N$ are the number of equally spaced points in the spatial and temporal domain, respectively. The intervals of length in the spatial ($L$) and temporal ($T$) directions are represented by $\mathrm{d}x=L/M$ and $\mathrm{d}t=T/N$. Accordingly, $x_i=i\mathrm{d}x$($0\le i\le M$), and $t_n=n\mathrm{d}t$($0\le n\le N$). Additionally, $r=1-\beta$, $s=\left(k_{\beta }/{\gamma }_{\mathrm{f}}+\mathrm{d}{t}^r\right)/\Gamma (r+1)$, $b=k/{\gamma }_{\mathrm{f}}\cdot \mathrm{d}t/2\mathrm{d}{x}^2$, $a_n={\left(n+1\right)}^r-n^r$, and ${\tilde{a}}_{n-1}=0.5\left(n^{r-1}r+{\left(n-1\right)}^{r-1}r\right)-a_{n-1}$.

The comparison is based on the one-dimensional model described in Section 3.3.2, where an instantaneous constant load is applied to the model boundary. The specific parameters are as follows: $k=6\times {10}^{-5}\mathrm{m}/\mathrm{s}$, $k_{\beta }=6\times {10}^{-5}{\mathrm{m}/\mathrm{s}}^{1-\beta }$, $\rho =1000{\mathrm{kg}/\mathrm{m}}^3$, $g=10{\mathrm{m}/\mathrm{s}}^2$, $E_0=30\mathrm{MPa}$, $E_1=30\mathrm{MPa}$, $\mu =0.3$, ${\alpha }_p=1\times {10}^{-5}{\mathrm{Pa}}^{-1}$.

The variations of excess pore water pressure and displacement at the midpoint of the model are selected for comparison, as shown in Figure 10. The results indicate that the solutions from ABAQUS and FDM are in good agreement, demonstrating the reliability of the fractional rheological consolidation model developed in ABAQUS.

4. Example and Discussion

4.1. Application on the Consolidation of Double-Layered Saturated Soft Soil Foundation

In this section, a foundation model based on the Tianjin port project [31] was established. The foundation had a total depth of 15 m, consisting of a 9 m thick silt layer overlying a 6 m thick soft clay layer. The reinforcement scheme employed vertical drainage boards (spaced 1 m × 1 m) combined with vacuum preloading and surcharge loading, maintaining a pressure of 100 kPa for 120 days. To evaluate the effectiveness of the reinforcement, Zhang et al. [31] installed displacement and pressure monitoring points at various depths, as illustrated in Figure 11.

Based on the layout of the vertical drainage boards, a two-dimensional finite element model was established in ABAQUS to simulate the soil consolidation between two adjacent drainage boards, with a model size of 15 m × 1 m. The saturated soil was assumed to deform only in the vertical direction, and pore water was allowed to dissipate horizontally through the drainage boards. The top and bottom boundaries were set as impermeable, and the bottom boundary was fixed. An initial pore water pressure of 100 kPa was assigned to match the applied loading conditions.

The physical parameters [31] involved in the model are as follows:

Silt: $E_0=1.93\mathrm{MPa}$, $E_1=1.23\mathrm{MPa}$, $\mu =0.3$, $V=0.01\mathrm{d}$, $\alpha =0.6$, $k_h=4.5\times {10}^{-10}\mathrm{m}/\mathrm{s}$, $k_{h\beta }=6\times {10}^{-10}{\mathrm{m}/\mathrm{s}}^{1-\beta }$, $k_{\mathrm{v}}=2.9\times {10}^{-10}\mathrm{m}/\mathrm{s}$, $k_{\mathrm{v}\beta }=2.9\times {10}^{-10}{\mathrm{m}/\mathrm{s}}^{1-\beta }$, ${\alpha }_p=1.371{\mathrm{MPa}}^{-1}$, ${\alpha }_b=1$, $\beta =0.1$.

Soft soil: $E_0=2.35\mathrm{MPa}$, $E_1=1.55\mathrm{MPa}$, $\mu =0.3$, $V=0.2\mathrm{d}$, $\alpha =0.8$, $k_h=2.7\times {10}^{-10}\mathrm{m}/\mathrm{s}$, $k_{h\beta }=2.7\times {10}^{-10}{\mathrm{m}/\mathrm{s}}^{1-\beta }$, $k_{\mathrm{v}}=1.6\times {10}^{-10}\mathrm{m}/\mathrm{s}$, $k_{\mathrm{v}\beta }=1.6\times {10}^{-10}{\mathrm{m}/\mathrm{s}}^{1-\beta }$, ${\alpha }_p=1.0{\mathrm{MPa}}^{-1}$, ${\alpha }_b=1$, $\beta =0.3$.

The monitoring data obtained from the literature indicate that the initial pore pressure distribution varied across different depths. However, by the end of the 120-day monitoring period, the excess pore pressure at all points had decreased by approximately 100 kPa. To facilitate a consistent comparison, the excess pore pressure data were normalized to a range of 100 kPa to 0 kPa:

$$p_{\mathrm{new}}=\mathrm{100,000}\times {\displaystyle \frac{p-p_{\min }}{p_{\max }-p_{\min }}}$$

(45)

In addition, the monitoring data report that the displacement appeared at a depth of 15 m, whereas the bottom boundary of the foundation model in ABAQUS was fixed. To ensure comparability between the simulation and monitoring data, the monitoring displacements were adjusted by subtracting the settlement at the 15 m depth.

Finally, the simulation results of displacement and excess pore water pressure at the midpoint in the horizontal direction were compared with the monitoring data, as shown in Figure 12. This demonstrates that the fractional rheological consolidation model can simulate the consolidation behavior of a double-layered soft soil foundation.

4.2. Comparison Between Different Models

This section compares the consolidation models obtained from different combinations of the fractional Merchant model (FM), the classical Merchant model, the fractional Darcy’s law (FD), and the classical Darcy’s law.

As illustrated in Figure 13, a range of results from different models for the case in Section 4.1 are presented. Given the capacity of these models to be transformed into one another, identical calculation parameters were adopted for the purpose of comparison.

Table 1. Number of parameters, iteration counts, and R-squared.

Consolidation Model	Number of Parameters	Iteration Counts	R2 (Pressure)	R2 (Displacement)
FM + FD	10	4485	0.9770	0.9210
FM + Darcy	8	4385	0.8738	0.7289
Merchant + FD	9	2108	0.8263	0.8974
Merchant + Darcy	7	1103	0.9122	0.7933

summarizes the number of required parameters for each model, as well as the iteration counts in ABAQUS and R-squared for the case study presented in Section 4.1. Due to the memory effect of fractional derivatives, the calculation process needs to access historical results, which tends to impair convergence and consequently increases the number of iterations required for models incorporating fractional constitutive relations. These results indicate that, although the proposed fractional model demands more computational resources and parameters, its predictions are in closer agreement with actual monitoring data.

4.3. Discussion

In the current implementation scheme, temperature is used as a variable to represent excess pore water pressure. However, the temperature field in ABAQUS does not inherently respond to external loading. Consequently, the temperature distribution must be manually prescribed to reflect the pore pressure expected under specific loading conditions. This approach makes the model applicable exclusively to consolidation under constant external loads. Moreover, the consolidation model is constrained by its ability to incorporate temperature effects. To address this limitation, future work could explore the use of the UEL subroutine to enable full thermal–hydraulic–mechanical coupling in the finite element framework, allowing for more accurate and flexible modeling of saturated soft soil behavior under various loading conditions.

In addition, the current approach also requires a fixed time step and exhibits poor numerical convergence in coupled analyses. The computation time further increases as the number of time steps grows, since a larger set of historical results must be stored and retrieved during the analysis. These issues limit the model’s computational efficiency and stability. Future research could focus on improving the robustness of the numerical implementation by introducing adaptive time-stepping schemes and enhancing the convergence performance, to make the model more practical for complex coupled analyses.

5. Conclusions

A finite element implementation scheme for a fractional rheological consolidation model is presented in this study. The implementation is carried out in ABAQUS by developing two user-defined subroutines: UMATHT for the fractional Darcy’s law and UMAT for the fractional Merchant model. The implementation details are discussed, including the formulation, programming scheme, and coupling method. The proposed implementation is verified through numerical results or analytical solutions, and then is applied to simulate the consolidation behavior of the saturated soft soil foundation. Several conclusions can be drawn:

(1)

The user-defined subroutines in ABAQUS provide a practical and adaptable way to incorporate fractional models into finite element analysis.

(2)

The fractional Darcy’s law is implemented through the UMATHT subroutine by utilizing the similarity between the energy equation and mass equation, which makes the development of fractional seepage models feasible.

(3)

Coupled implementation enables the simulation of a foundation model within the ABAQUS platform, and the results show good agreement with monitoring data, demonstrating the applicability of the model.

(4)

The numerical implementation scheme of the fractional models presented in this study can serve as a reference for researchers to further develop fractional consolidation models for saturated soft soils in ABAQUS.