Design and Control of Fractional-Order Systems Based on Fractal Operators

Abstract

In recent years, we have abstracted physical fractal space from biological structures and movements within living organisms, revealing the profound intrinsic connections between fractional order time and fractional-dimensional space, and providing partial explanations for the sources and orders of fractional order. We have confirmed that the topological invariants of fractal cells, the order of physical components, and the mismatch of spatiotemporal order are important factors determining the fractional order of operators. This paper is a continuation of the previous work. Inspired by bone fractal operators, this article attempts to identify other factors that affect the order of operators. Specifically, the following contents are included: (1) originating from the bone fractal operators, we present the construction process of the “apparent half-order” system; (2) using the Schiessel–Blumen model as the comparative object, we analyze the origin and characteristics of the “γ-order” system; (3) using the continued fraction theory and operatorization thought as the link, we establish the design and control method for general fractional-order systems, and discuss the factors affecting the order of fractional-order operators.

1. Introduction

Fractional-order system refers to a mathematical model whose dynamic behavior is dominated by fractional-order differential equations (FDEs). Its core feature is that the order of differential/integral operators can be any real number, not just integers [1,2]. This non-integer order endows the system with unique intrinsic memory and genetic properties: the current output or state of the system depends not only on the input at the moment but also significantly on the weighted accumulation of its entire past history [3]. This inherent temporal non-locality and long-range dependence make the fractional-order model a natural tool for characterizing numerous complex physical phenomena [4,5,6]. For example, it can effectively simulate the non-exponential relaxation or creep behavior observed in biological tissues (such as nerve conduction, drug metabolism) and viscoelastic materials (such as polymers, rubber) [7]. It can also characterize the abnormal diffusion process of fluid or pollutant transport in fractal or porous media such as soil and rock [8,9]. In the field of control engineering, fractional-order controllers provide more flexible gain and phase shaping capabilities than traditional integer-order PID (Proportional–Integral–Derivative) by introducing adjustable real order, significantly improving the robustness of the system to parameter changes and disturbances [10]. Compared to attempting to approximate these complex processes using high-order/integer-order differential equations, fractional-order models can typically achieve more accurate and universal modeling of real-world systems with memory effects, spatial non-uniformity, and scale invariance (fractal features) in a lower-order, more concise form, and a mathematical structure that is more in line with physical essence. They are a powerful framework for dealing with complex dynamic problems across scales [11,12,13].

It is precisely because of the flourishing development of fractional calculus theory that fractional-order systems have been able to demonstrate their unique advantages in numerous engineering and scientific fields and have been widely applied [14,15]. It should be emphasized that there are numerous definitions for fractional-order integrals and differentials, which have led to the lack of a unified research paradigm in their long-term development. The most common approach is to study each fractional-order-characterized ordinary differential or partial differential equation one by one, but the above system is not perfect. A more natural processing method is to use the operational calculus [16]. Heaviside’s proposal to use symbol $p$ instead of differentiation operation ${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}$ in the study of circuits and electromagnetic theory, and the ability to perform various algebraic operations such as addition, subtraction, multiplication, and division on this symbol, marked the birth of the operational calculus theory [17]. At the beginning of the 20th century, the theory of operational calculus underwent significant development, but did not form a fundamental breakthrough [18,19,20,21]. Until 1959, Polish mathematician Mikusiński gave a completely new set of rules for operational calculus: introducing a new way of operator action, wherein the operator action yields outcomes defined as convolution integrals with their associated kernel functions [22]. The above operation to a certain extent laid the foundation of algebraic theory for operational calculus, greatly promoting the development of this discipline [23]. Nowadays, the theory of operational calculus has been widely applied, but there are still some basic problems that need to be solved [24,25,26]. For example, there is still no unified pattern for the representation of operators and their corresponding physical meanings [27,28]. Therefore, how to establish the correlation between operational calculus and other disciplines such as fractal, mechanics, etc., is a research topic worthy of long-term exploration [29,30].

Recent studies have conceptualized multi-level, chain-like topologies derived from muscle/ligament fibers, nerve fibers, and compact bone fibers, while concurrently modeling multi-level micro-elastic cavity topology from arterial blood flows [31]. This framework establishes biologically inspired fractal and fractional-order mechanics based on physical components as basic elements. Strikingly, these distinct systems converge toward shared characteristics: the common physical fractal space, similar fractal operators, and similar fractional-order mechanics. It should be emphasized that this spatial form of describing functional self-similarity is different from geometric fractals, as this system does not possess the concept of measurement in geometry. Due to the absence of measurement, it is impossible to characterize its structural characteristics using classical fractal dimensions. Moreover, the fractal tree features abstracted from the aforementioned biological materials are infinite-level self-identical, while the regular fractal features in textbooks are infinite-level self-similar. Self-identical is a special form of self-similarity. However, infinite-level structures in physics and biology do not exist, they are just idealized limit states, but they do capture the essence of things. For example, in fractional-order circuit design [32,33,34] researchers also extend the hierarchical structure of fractal circuits to infinity and then use finite-level structures to approximate the expected fractional-order systems based on the truncation method. If traditional chain-like circuits are used to construct fractional-order systems, the calculation of each circuit component is generally to four or more decimal places, which is difficult to achieve in practical physical circuits and highlights the necessity of “infinite-level”. Therefore, researchers named this type of spatial form with self-similar characteristic in physical or mechanical behavior as “physical fractal space” or “functional fractal space” [35].

In this new spatial form, researchers have naturally explained the essence of many material mechanics behaviors, such as bone mechanics, intravascular hemodynamics, the viscoelastic properties of coal, and so on [36]. When dealing with the above issues, the classic concept of “element” has certain limitations. Most researchers have overlooked the discreteness of fibers and the self-similarity of structures in biomaterials and have directly extended the continuity hypothesis proposed for inorganic metal materials to biomaterials [37]. Taking the viscoelastic mechanics of biomaterials as an example, researchers have established the classic quasi-linear viscoelastic constitutive model, which functionally corresponds to the time characteristics of different scales in the viscoelastic response of materials, but the fitting ability is limited [38]. Because “element” is continuous, it cannot characterize the discrete arrangement of fibrin in biological fibers. Therefore, the “fractal cell” in the “physical fractal space” can be regarded as the basic mechanical analysis unit of biomaterials, that is, a new “element”. Researchers have found that the method of studying material properties and functions using the algebraic theory of operational calculus is highly effective, providing a new theoretical system and research paradigm for mechanics research. It should be noted that the fractal operators in the physical fractal space are all non-integer-order operators. Such non-integer-order operators are suitable tools for characterizing non-localized effects. In the future, it is worthwhile for researchers to constantly think and explore how to apply this research method to different disciplinary fields.

Non-integer-order operators in the physical fractal space have been widely applied in many disciplines [31,35]. But it still leaves behind some basic issues that make the explanation of the above application seem unnatural. For example, researchers only introduce fractional-order operators phenomenologically without investigating their underlying physical essence. This situation is not difficult to understand, as researchers only use fractional-order operators as “appropriate” tools and do not care where fractional-order operators come from or what factors determine their order. In fact, understanding the influencing factors of order in fractional-order operators is the theoretical basis for designing and controlling general fractional-order systems. In our previous work, we have confirmed that the topological invariants of fractal cells, the order of physical components, and the mismatch of spatiotemporal order are important factors determining the fractional order of operators [36,37]. It can be said that the source of fractional order is not unique, and the factors that determine fractional order are diverse. How to understand this diversity? Are there any other influencing factors? This article attempts to provide answers, including the following contents: (a) a review of the bone fractal operator model and “apparent half-order” system; (b) a comparison between the Schiessel–Blumen model and “$\gamma$-order” system; (c) a design and control method for general fractional-order systems. The classic fractional-order design usually expresses the operators in the complex frequency domain, which inevitably encounters problems such as cumbersome operation when solving the overall response. With the development of the operator kernel function method [38], people gradually realized that the logical foundation of its operator algebra was incomplete and there were some ambiguities. In order to overcome the above limitations, we apply the continued fraction theory and operatorization thought to the design of fractional-order systems. We solve for the overall operator and its kernel function response in the operator domain, greatly simplifying the calculation steps, which is a new attempt in the interdisciplinary fields of mechanics, mathematics, and physics, and also provides a new perspective for understanding the interrelationships between various disciplines.

Section 2 reviews the bone fractal operator model and the “apparent half-order” system. Section 3 presents the Schiessel–Blumen model and the “$\gamma$-order” system. Section 4 analyzes the correlation between continued fraction structures, fractal operators, and fractional-order systems. Section 5 elaborates on the operatorization thought in fractional-order system design. Section 6 provides the operatorization expression of the Schiessel–Blumen model. Section 7 establishes the design and control method for general fractional-order systems. Section 8 discusses the factors affecting the order of fractional-order operators.

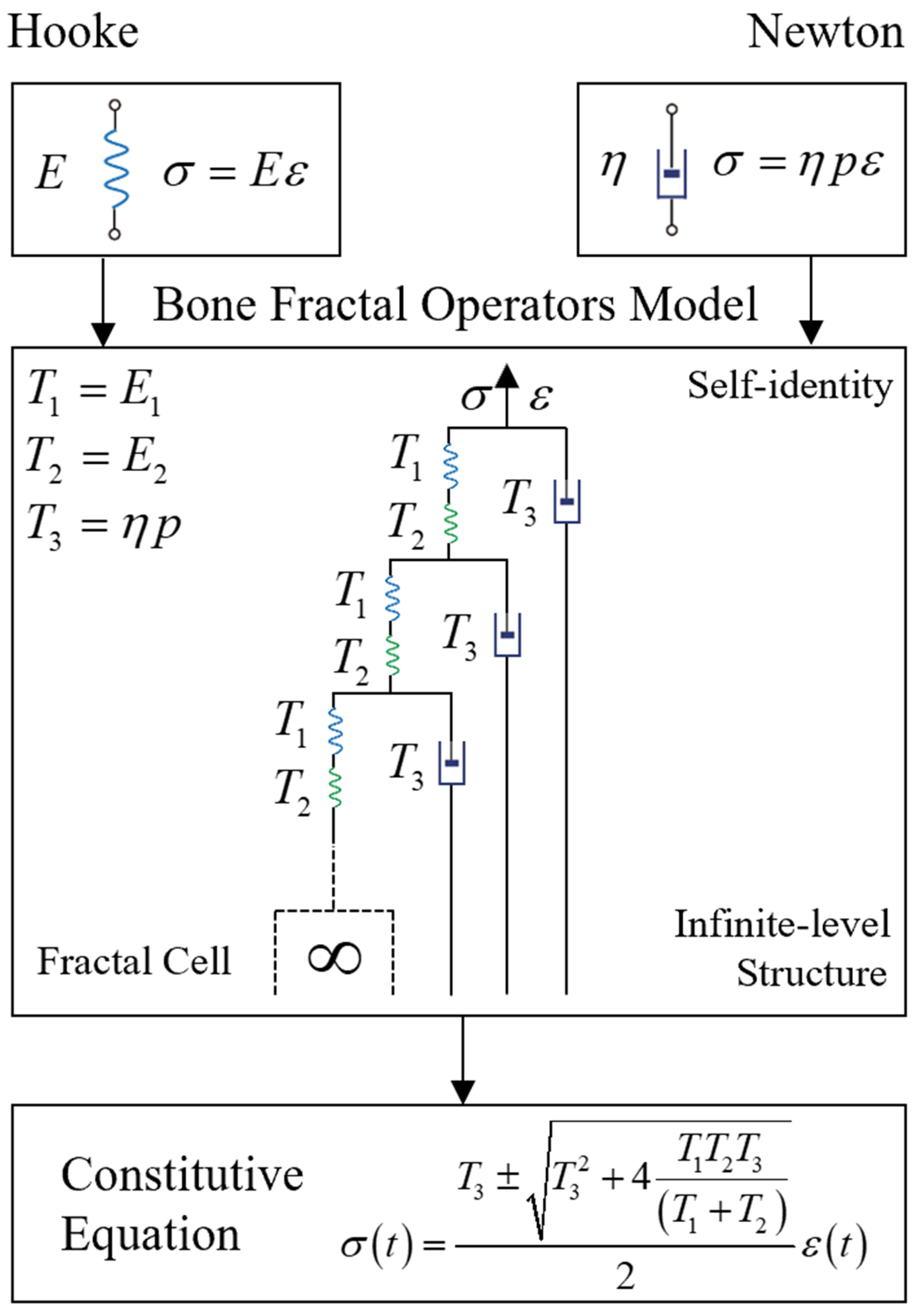
2. Bone Fractal Operator Model and “Apparent Half-Order” System

This section mainly reviews the bone fractal operator model and the “apparent half-order” system. For convenience, we first provide the derivation process of the algebraic expression for bone fractal operator model [31]. According to Mikusiński’s work [22] and the operator structure introduced earlier, the definitions of basic differential operators and integral operators are as follows: If function $f\left(t\right)$ has continuous derivatives at $t\ge 0$, then the basic differential operator $p$ is defined as:

$$pf\left(t\right)={\displaystyle \frac{\mathrm{d}f\left(t\right)}{\mathrm{dt}}}+f\left(0\right)\delta \left(t\right).$$

(1)

The integral operator $l$ is defined as:

$$lf\left(t\right)={\displaystyle \underset{0}{\overset{t}{\int }}f\left(\tau \right)}\mathrm{d}\tau .$$

(2)

The basic differential operator $p$ and integral operator $l$ defined by Equations (1) and (2) are inverse operators to each other, and the combination of these two basic operators has an effect that is independent of the order of action. In the Mikusiński operator field, Equation (3) holds, which is an important foundation of operator algebra theory.

$$l={\displaystyle \frac{1}{p}}.$$

(3)

Based on Equation (3), both the differential operator and integral operator discussed in this article can be regarded as the functions of the basic differential operator $p$ defined in Equation (1), that is, operator-type function $T\left(p\right)$.

When stress $\sigma \left(t\right)$ is applied to bone fibers and strain $\epsilon \left(t\right)$ is generated, then we have the following:

$$\sigma \left(t\right)=T\left(p\right)\epsilon \left(t\right),$$

(4)

where $T\left(p\right)$ is the bone fractal operator in the physical fractal space. Based on the fractal characteristics of compact bone and the transmission patterns of force and deformation along the chain-like fiber, we can abstract a multi-level self-identical element tree and extend it to infinite levels. The invariance of operator fractal space provides the algebraic equation that bone fractal operator $T$ need to satisfy, which is as follows:

$${\displaystyle \frac{1}{\frac{1}{T_1}+\frac{1}{T_2}+\frac{1}{T}}}+T_3=T.$$

(5)

In mechanics, the right-hand side of Equation (5) can be regarded as the stiffness of the fractal component, and the left-hand side can be regarded as the stiffness of the fractal cell, and the two are equivalent. It is further deduced that:

$$\left(T_1+T_2\right)T^2-\left(T_1+T_2\right)T_{3}T-T_1{T}_2{T}_3=0.$$

(6)

Equation (6) is the algebraic equation of the fractal operator $T$. This is a quadratic equation with the following radical solution:

$$T={\displaystyle \frac{T_3\pm \sqrt{T_3^2+4\frac{T_1{T}_2{T}_3}{\left(T_1+T_2\right)}}}{2}}.$$

(7)

So far, the fractal operator $T$ of compact bone is determined, as shown in Equation (7).

Note the presence of symbol √ in the bone fractal operator $T$, whose root √ is derived from a quadratic operator algebraic equation and is independent of the selection of physical components. In other words, regardless of how the physical components in the fractal tree are selected and what the final order of the bone fractal operator $T$ is, its expression will always include √. Therefore, we refer to this √ order caused by the topological index of fractal structure as the “apparent half-order” (operator) system, as shown in Figure 1.

The bone fractal operator model approximates the mechanical behavior of bone by connecting an infinite number of Hooke elastic elements and Newton viscous elements in series and parallel, as shown in Figure 1 [35]. In fact, the physical (functional) fractal spaces that we abstract from biological materials, biological structures, and biological movements all adopt the simplest form of two-branch topology without exception. Its topological index is “2”, which is the smallest prime number and determines the most basic and universal motion laws within the organism [36]. As for why the bone fractal operator model shown in Figure 1 is an “apparent half-order” system? The answer is simple: because the bone fractal operator $T$ satisfies a quadratic algebraic equation (Equation (6)) and its solution contains a quadratic radical (Equation (7)) in apparent form. Therefore, we say that the bone fractal operator $T$ is a 1/2-order operator in apparent form. Here, the reason for adding the restrictive word “apparent” is that the final order of the root √ not only depends on the 1/2-order of the apparent sign √, but also on the order of the operator within the root sign.

Thus, we have reviewed the construction process of the bone fractal operator model and its correlation with the “apparent half-order” system.

3. Schiessel–Blumen Model and “γ-Order” System

This section mainly presents the Schiessel–Blumen model and the “$\gamma$-order” system.

Schiessel–Blumen mentioned in reference [39] that “our models allow a transparent interpretation of the parameters which enter the fractional equations, and reveal that the internal dynamics are hierarchically constrained.” In fact, the S-B model mainly discusses fractional-order relaxation equations, as fractional calculus is an important tool for analyzing slow relaxation phenomena. The construction process of the S-B model is as follows:

Establish a coupled linear differential equation system that the structure satisfies based on the mechanical model shown in Figure 2:

(a)

The additivity of the strains

$${\epsilon }_k^{\mathrm{d}}={\epsilon }_{k+1}^{\mathrm{s}}+{\epsilon }_{k+1}^{\mathrm{d}},$$

(8)

where the subscript $k$ of strain represents the structural hierarchy, that is, the $k$ level structure, the superscript $\mathrm{s}$ represents the spring, and $\mathrm{d}$ represents the dashpot. And $k=0,1,\dots ,n-2$, the strains at the upper and the lower ends of the stepped structure satisfy $\epsilon ={\epsilon }_0^{\mathrm{s}}+{\epsilon }_0^{\mathrm{d}}$ and ${\epsilon }_{n-1}^{\mathrm{d}}={\epsilon }_n^{\mathrm{s}}$, respectively.

(b)

The additivity of the stresses

$${\sigma }_k^{\mathrm{s}}={\sigma }_{k+1}^{\mathrm{s}}+{\sigma }_k^{\mathrm{d}},$$

(9)

where $k=0,1,\dots ,n-1$, and the stress at the lower end of the stepped structure satisfies $\sigma ={\sigma }_0^{\mathrm{s}}$.

(c)

The constitutive equation followed by the physical component of each structural part, which is as follows for spring:

$${\epsilon }_k^{\mathrm{s}}={\displaystyle \frac{1}{E_k}}{\sigma }_k^{\mathrm{s}},$$

(10)

where $E_k$ is the stiffness coefficient of the $k$-th spring. Which is as follows for dashpot:

$${\sigma }_k^{\mathrm{d}}={\eta }_k{\displaystyle \frac{\mathrm{d}{\epsilon }_k^{\mathrm{d}}}{\mathrm{d}t}},$$

(11)

where ${\eta }_k$ is the viscosity coefficient of the $k$-th dashpot.

(d)

Initial conditions

$$\epsilon \left(t\le 0\right)=\sigma \left(t\le 0\right)=0.$$

(12)

Establish the stress–strain relationship in the complex frequency domain after Laplace transform. Substituting Equation (10) into Equation (8), we have:

$$E_{k+1}{\overline{\epsilon }}_k^{\mathrm{d}}\left(s\right)={\overline{\sigma }}_{k+1}^{\mathrm{s}}\left(s\right)+E_{k+1}{\overline{\epsilon }}_{k+1}^{\mathrm{d}}\left(s\right).$$

(13)

By substituting Equation (11) into Equation (9) and combining it with the derivative theorem of Laplace transform, we have:

$${\overline{\sigma }}_k^{\mathrm{s}}\left(s\right)={\overline{\sigma }}_{k+1}^{\mathrm{s}}\left(s\right)+s{\eta }_k{\overline{\epsilon }}_k^{\mathrm{d}}\left(s\right).$$

(14)

Then, by combining the above equations and performing clever mathematical iterations between Equations (13) and (14), and through $n-2$ times iterative operations, the continued fraction representation of the stress–strain relationship in the complex frequency domain can be obtained:

$$E_0{\displaystyle \frac{\overline{\epsilon }\left(s\right)}{\overline{\sigma }\left(s\right)}}=1+{\displaystyle \frac{s^{-1}\frac{E_0}{{\eta }_0}}{1+}}{\displaystyle \frac{s^{-1}\frac{E_1}{{\eta }_0}}{1+}}{\displaystyle \frac{s^{-1}\frac{E_1}{{\eta }_1}}{1+}}{\displaystyle \frac{s^{-1}\frac{E_2}{{\eta }_1}}{1+}}\cdots {\displaystyle \frac{s^{-1}\frac{E_{n-1}}{{\eta }_{n-1}}}{1+}}{\displaystyle \frac{s^{-1}\frac{E_n}{{\eta }_{n-1}}}{1}}.$$

(15)

It should be emphasized that Equation (15) is only the constitutive equation of the n-level structure shown in Figure 2 and does not possess the properties of the “$\gamma$-order” system. Therefore, Schiessel–Blumen attempted to introduce the binomial series from reference [40] as follows:

$$x{\left(x+1\right)}^{\gamma -1}={\displaystyle \frac{x}{1+}}{\displaystyle \frac{\left(1-\gamma \right)x}{1+}}{\displaystyle \frac{\frac{1\cdot \left(0+\gamma \right)}{1\cdot 2}x}{1+}}{\displaystyle \frac{\frac{1\cdot \left(2-\gamma \right)}{2\cdot 3}x}{1+}}{\displaystyle \frac{\frac{2\cdot \left(1+\gamma \right)}{3\cdot 4}x}{1+}}{\displaystyle \frac{\frac{2\cdot \left(3-\gamma \right)}{4\cdot 5}x}{1+}}\cdots .$$

(16)

The advantage of this operation is that the coefficients of Equations (15) and (16) can be matched one-to-one to obtain the material parameters of each structural part of spring and dashpot, and the final main order of the system is $\gamma$. Therefore, we can select the parameters $E_k$ and ${\eta }_k$ according to Equation (17):

$$c_0={\displaystyle \frac{E_0}{{\eta }_0}},{\displaystyle \frac{E_1}{{\eta }_0}}=\left(1-\gamma \right)c_0,{\displaystyle \frac{E_1}{{\eta }_1}}={\displaystyle \frac{1\cdot \left(0+\gamma \right)}{1\cdot 2}}{c}_0,\dots .$$

(17)

It should be noted that the S-B model initially has an n-level structure, while the binomial series of Equation (16) is infinite. This means that choosing Equation (17) as the material parameter design method for the system is based on extending the n-level structure to infinite-level structures. By substituting Equation (17) into Equation (15), we have:

$$E_0{\displaystyle \frac{\overline{\epsilon }\left(s\right)}{\overline{\sigma }\left(s\right)}}=1+{\displaystyle \frac{\frac{c_0}{s}}{1+}}{\displaystyle \frac{\left(1-\gamma \right)\frac{c_0}{s}}{1+}}\cdots {\displaystyle \frac{\frac{\left(n-1\right)\left(n-\gamma \right)}{\left(2n-1\right)\left(2n-2\right)}\frac{c_0}{s}}{1}}.$$

(18)

Therefore, when the hierarchical structure $k$ of the system tends towards infinity, we have:

$$E_0{\displaystyle \frac{\overline{\epsilon }\left(s\right)}{\overline{\sigma }\left(s\right)}}=1+\left({\displaystyle \frac{c_0}{s}}\right){\left({\displaystyle \frac{c_0}{s}}+1\right)}^{\gamma -1}.$$

(19)

Thus, the constitution of Schiessel–Blumen model in the complex frequency domain has been determined, as shown in Equation (19).

The Schiessel–Blumen model approximates the fractional-order relaxation equation by connecting a finite number of Hooke elastic elements and Newton viscous elements in series and parallel, as shown in Figure 2, and extending the finite-order structure (n-level structure) to infinite order according to binomial series and continued fraction theory [39]. Observing Equation (19), it can be seen that the main-order of the S-B system is $\gamma$. This means inputting a coefficient relationship Equation (17) related to the expected fractional-order $\gamma$ to the physical components of the system. In the system of S-B model, only integer-order physical components are used. When the structural hierarchy tends towards infinity, the operator order of the overall structure is also equal to $\gamma$. And the expected fractional-order $\gamma$ is artificially given, so this is a design approach to achieve general $\gamma$ order of the system. If the constraint of the “apparent half-order” system is infinite self-identical, then the constraint of the S-B model is precisely the coefficient expression containing the design parameter $\gamma$ in Equation (17).

Thus, we have demonstrated the construction process of the Schiessel–Blumen model and its correlation with “$\gamma$-order” system.

4. Correlation Between Continued Fraction Structures, Fractal Operators, and Fractional-Order Systems

This section mainly analyzes the correlation between continued fraction structures, fractal operators, and fractional-order systems.

In Section 3, we provided a detailed introduction to the derivation process of the Schiessel–Blumen model. It should be emphasized that when Schiessel–Blumen was searching for a matching binomial series (Equation (16)), the first term did not contain 1, so the continued fraction (Equation (15)) of initial n-level structure and binomial series (Equation (16)) were not congruent, with a difference of 1 between the two. The initial structure of the S-B model is finite level (n-level), and it needs to be extended to infinity before its continued fraction can accurately equal the binomial series (Equation (16)).

In reference [38], inspired by bone fractal operators, we established correlations between various disciplines (fractal geometry, fractional calculus, special function, continued fraction, etc.), while also endowing them with specific mechanical connotations in the physical fractal space. The new understanding of the correlation mentioned above is due to our previous exploration of bone mechanics. Similarly, this section attempts to establish the correlation between continued fraction structures, fractal operators, and fractional-order systems.

In reference [38], we used the theory of a continued fraction to explain the construction process, properties, and characteristics from Golden Meta-Spring to Generalized Meta-Spring, mainly involving the definition and representation of a continued fraction. Generally speaking, the basic form of a continued fraction, namely the continued fraction structure, corresponds precisely to the step topology in the physical fractal space. In other words, this pattern caused by symmetry breaking in tree-like topology is an intrinsic manifestation of the continued fraction structure. It can be said that the existence of continued fractions leads to the existence of stepped topological structures and generalized fractal systems. We can obtain different step topological fractal trees by regulating the continued fraction structure and then calculate the fractal operators based on the stiffness–flexibility calculation method in mechanics. Finally, we can use the spatiotemporal correlation in the physical fractal space to obtain the fractional-order systems.

Essentially, the starting point of the S-B model is to solve a system of linear differential equations, obtain a continued fraction structure through clever mathematical iterations, and finally obtain the fractional order constitution in the complex frequency domain, which is completely different from our operatorization thought. The advantage of the operatorization thought is that it skips the step of initially listing the system of linear differential equations and directly manipulates the research object. Its biggest feature is to separate the intrinsic and extrinsic aspects of the research system and calculate them independently. “Intrinsic” is the operator of the system, which is the intrinsic property of the system and is not affected by external inputs. “Extrinsic” is the external input of the system, that is, external conditions which are not affected by the inherent properties of the system. In other words, the operatorization method is a computational model for decoupling the research system. If we use operatorization method to perform inverse Laplace transform on both sides of Equation (19) simultaneously, we have:

$$\begin{array}{l}{L}^{-1}\overline{\sigma }\left(s\right)=L^{-1}L\left[\sigma \left(t\right)\right]=\sigma \left(t\right)=L^{-1}\left[{\displaystyle \frac{E_0}{1+\left(\frac{c_0}{s}\right){\left(\frac{c_0}{s}+1\right)}^{\gamma -1}}}\overline{\epsilon }\left(s\right)\right]\\ =L^{-1}\left[{\displaystyle \frac{E_0}{1+\left(\frac{c_0}{s}\right){\left(\frac{c_0}{s}+1\right)}^{\gamma -1}}}\right]\ast L^{-1}\left[\overline{\epsilon }\left(s\right)\right]=L^{-1}\left[{\displaystyle \frac{E_0}{1+\left(\frac{c_0}{s}\right){\left(\frac{c_0}{s}+1\right)}^{\gamma -1}}}\right]\ast \epsilon \left(t\right).\end{array}$$

(20)

According to the convolution theorem of operators, we have:

$$\sigma \left(t\right)=T\left(p\right)\epsilon \left(t\right)=K\left(t\right)\ast \epsilon \left(t\right).$$

(21)

The convolution kernel function of the S-B model is:

$$K_{\mathrm{S}\text{-}\mathrm{B}}\left(t\right)=L^{-1}\left[{\displaystyle \frac{E_0}{1+\left(\frac{c_0}{s}\right){\left(\frac{c_0}{s}+1\right)}^{\gamma -1}}}\right].$$

(22)

Therefore, the operator of the S-B model is:

$$T_{\mathrm{S}\text{-}\mathrm{B}}\left(p\right)=L\left[K_{\mathrm{S}\text{-}\mathrm{B}}\left(t\right)\right]\left(p\right)=L{L}^{-1}\left[{\displaystyle \frac{E_0}{1+\left(\frac{c_0}{s}\right){\left(\frac{c_0}{s}+1\right)}^{\gamma -1}}}\right]={\displaystyle \frac{E_0}{1+\left(\frac{c_0}{p}\right){\left(\frac{c_0}{p}+1\right)}^{\gamma -1}}}.$$

(23)

In Equation (23), the main order of the operator is $\gamma$. Note that in the complex frequency domain each term in the continued fraction structure of Equation (15) is included $s^{-1}$, indicating that the continued fraction expression of the S-B model does not match the real physical graph (structure). Because the structure shown in Figure 2 is a system with alternating arrangement of spring and dashpot, if expressed in an operatorization manner it should be a continued fraction structure with an alternating arrangement of constant terms and time differential operator $p$. At this point, we can consider the S-B model to be completely different from our operatorization thought. The former precisely derives the continued fraction expression through clever mathematical iterations when solving a system of linear differential equations with an overall structure, but does not involve the correspondence between the real physical structure and operator. Our bone fractal operator model establishes a one-to-one correspondence between a physical graph, structural topology, and operatorization expression. We believe that whether it is a single physical component or a structural system composed of several physical components, they all correspond to a certain operator. Similarly, any operator theoretically has a combination or combination of physical components that matches it. Essentially, the S-B model attempts to construct a continued fraction form and then search for binomial series corresponding to it in order to derive the proportional relationship satisfied by the parameters of the spring $E_k$ and dashpot ${\eta }_k$ materials. However, each term of the continued fraction in Equation (15) does not correspond to each level of the real physical structure. Therefore, the S-B model is a purely mathematical construction method that does not include physical features, while our operatorization method is a paradigm of the integration of mathematics and mechanics, with fundamental differences between the two. This also highlights the importance of developing an operatorization theoretical system. It should be emphasized that we can use the parameters of the S-B model to validate and calculate its operators, but logically it is inverted. In practical applications, we often focus more on the parameter design of physical components, so it is particularly important to find a general design approach for material parameters in the spring–dashpot system.

Thus, we have established the correlation between continued fraction structures, fractal operators, and fractional-order systems, and introduced the concept of operatorization method, laying a theoretical foundation for the operatorization thought in fractional-order system design.

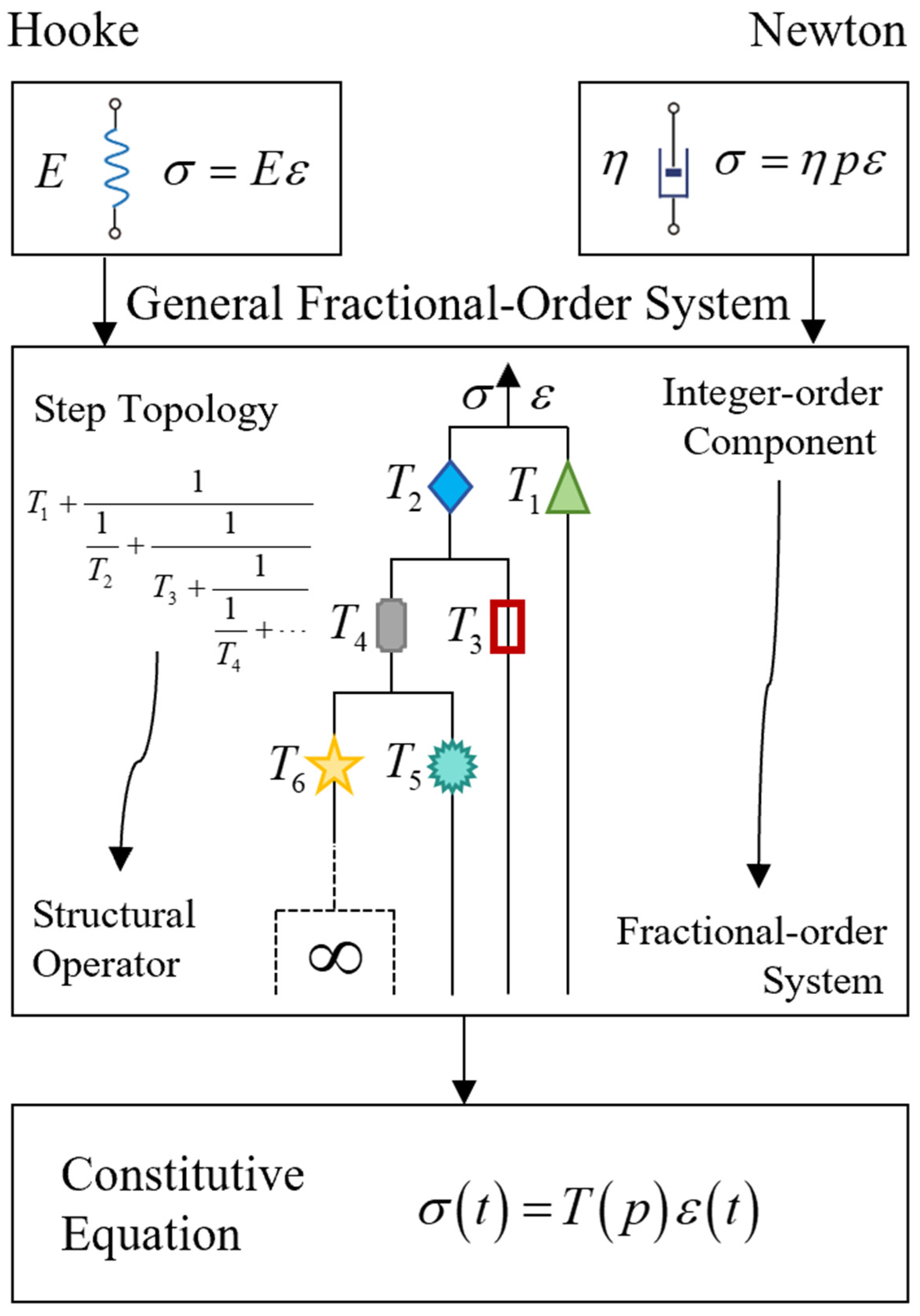
5. Operatorization Thought in Fractional-Order System Design

This section mainly elaborates on the operatorization thought in fractional-order system design.

In Section 4, we established the correlation between continued fraction structures, fractal operators, and fractional-order systems by introducing the concept of operatorization method. In fact, if the concept of “there exists a correspondence between functions and tangible structures in the physical fractal space” in reference [38] is further extended, that is, the research object is extended from the “function domain” to the “operator domain”, the operatorization thought in fractional-order system design can be obtained: “there exists a correspondence between operator-type functions and tangible structures in the physical fractal space”. The difference between the two is that the former attempts to construct a full-spring stiffness system, while the latter does not limit the types of physical components. This means that the former is a constant-type operator system, while the latter is a functional-type operator system. The connection between the two is that they both use the stiffness–flexibility calculation method of a continued fraction to design the system. It should be emphasized that, unlike the definition of a continued fraction in pure mathematics, the physical effects of structural series and parallel connections also need to be considered in the real system design. In reference [38], it is reflected that the equivalent stiffness of the series branch is the reciprocal sum of the stiffness of each physical component, and the equivalent stiffness of the parallel branch is the direct sum of the stiffness of each physical component. In our operatorization thought the equivalent operator of a series branch is the reciprocal sum of the operators of each physical component, while the equivalent operator of a parallel branch is the direct sum of the operators of each physical component. The objective reality differences caused by mechanics or physics mentioned above highlight the necessity of interdisciplinary research and provide a new idea for the design and control of fractional-order systems; with the help of operatorization thought we can express the expected fractional-order system in the form of continued fraction, obtain the operators of each level of physical components according to the stiffness–flexibility calculation method of continued fraction, and then deduce the properties of physical components through the convolution theorem of operators, thus building the entire system. The above is the operatorization thought in fractional-order system design, as shown in Figure 3.

Specifically, we start from the most basic integer-order physical components (such as spring–dashpot model) and build the real system according to the step topology corresponding to the continued fraction. According to the operatorization thought, the final system can be expressed as a structural operator $T_{\mathrm{Structural}}\left(p\right)$:

$$T_{\mathrm{Structural}}\left(p\right)=T_1+{\displaystyle \frac{1}{\frac{1}{T_2}+\frac{1}{T_3+\frac{1}{\frac{1}{T_4}+\cdots }}}}.$$

(24)

By substituting the structural operator $T_{\mathrm{Structural}}\left(p\right)$ into Equation (4), we can obtain the response $\sigma \left(t\right)$ of the system under different input strain $\epsilon \left(t\right)$, that is:

$$\sigma \left(t\right)=\left(T_1+{\displaystyle \frac{1}{\frac{1}{T_2}+\frac{1}{T_3+\frac{1}{\frac{1}{T_4}+\cdots }}}}\right)\epsilon \left(t\right).$$

(25)

Equation (25) and the stiffness expression of the Golden Meta-Spring model in reference [38] satisfy the consistency of the apparent form, because both adopt the stiffness–flexibility calculation method in the step topology structure. As mentioned earlier, the structural operator $T_{\mathrm{Structural}}\left(p\right)$ of the system are intrinsic properties, so the fractional order of $T_{\mathrm{Structural}}\left(p\right)$ is also the fractional order of the overall system. This means that with Equation (25), we can regulate the fractional order of the system. In other words, if we want to design the fractional order of the system, we can choose the material parameters of the physical components in Equation (25).

Structural operator $T_{\mathrm{Structural}}\left(p\right)$ provides convenience for solving the response of the system as once $T_{\mathrm{Structural}}\left(p\right)$ is obtained its convolution can be directly calculated to obtain the output of the system, which is also the core of operatorization thought in fractional-order system design. The advantage of this operation is that it decouples the output problem of solving the overall system into independent calculations of the internal structural operators $T_{\mathrm{Structural}}\left(p\right)$ of the system and their convolutions with external input $\epsilon \left(t\right)$, greatly simplifying the analysis steps and computational complexity. It can be said that the selection of material parameters for physical components is another important factor in determining the fractional order of system operators.

It should be emphasized that the bone fractal operator model and the S-B model, as two typical ways of designing fractional-order systems, have slight differences in operatorization expression. The bone fractal operator model corresponds directly to Figure 3, where all physical components are of integer order. The fractional-order system is obtained through the design concept of infinite-level self-identical. The physical components of the S-B model are also of integer order. By satisfying a certain proportional relationship between the material parameters of the spring–dashpot and extending the structural hierarchy to infinity, the “$\gamma$-order” system is obtained. There are subtle differences in the structural operator $T_{\mathrm{Structural}}\left(p\right)$ between the two. Due to the different forms of system construction, the bone fractal operator model includes the first term $T_1$ in Equation (25), while the S-B model does not. But the solution of system response is completely unaffected by the above differences, which is another advantage of the operatorization thought, namely the convenience brought by decoupling.

Thus, we have elaborated on the operatorization thought in fractional-order system design and provided a computational approach for solving the response of operator system.

6. Operatorization Expression of Schiessel–Blumen Model

This section mainly presents the operatorization expression of the Schiessel–Blumen model.

In Section 4, we obtained the operator $T_{\mathrm{S}\text{-}\mathrm{B}}\left(p\right)$ corresponding to the S-B model. In Section 5, we obtained the structural operator $T_{\mathrm{Structural}}\left(p\right)$ for generalized fractal systems. Next, we will represent the operator $T_{\mathrm{S}\text{-}\mathrm{B}}\left(p\right)$ of the S-B model in the form of a continued fraction. It should be emphasized again that this section further illustrates the advantages of the operatorization thought using the S-B model. In other words, the introduction of the S-B model in Section 3 is essentially a preparation for introducing the operatorization thought. If the conventional S-B model method is used for the system shown in Figure 2, it is required to solve the linear differential equation system shown in Equations (8)–(14). If the operatorization thought is adopted, it is only necessary to correspond with the binomial series shown in Equation (16) with the structural operator $T_{\mathrm{Structural}}\left(p\right)$ shown in Equation (24) one-by-one and the types and parameters of each level of physical components can be obtained sequentially, which once again highlights the power of operatorization thought in fractional-order system design.

Based on the parameter design Equation (17) of the S-B model, we can obtain the material parameters and their operatorization expressions for each level of spring and dashpot. Specifically, assuming $E_0$ and ${\eta }_0$ knowing, according to Equation (24), we have:

$$T_1^{\mathrm{S}\text{-}\mathrm{B}}=E_0,$$

(26)

$$T_2^{\mathrm{S}\text{-}\mathrm{B}}={\eta }_{0}p,$$

(27)

$$T_3^{\mathrm{S}\text{-}\mathrm{B}}=E_1=\left(1-\gamma \right){\eta }_0{\displaystyle \frac{E_0}{{\eta }_0}}=\left(1-\gamma \right)E_0,$$

(28)

$$T_4^{\mathrm{S}\text{-}\mathrm{B}}={\eta }_{1}p={\displaystyle \frac{2E_1}{\gamma c_0}}p={\displaystyle \frac{2}{\gamma }}{\displaystyle \frac{\left(1-\gamma \right)E_0}{\frac{E_0}{{\eta }_0}}}p={\displaystyle \frac{2\left(1-\gamma \right)}{\gamma }}{\eta }_{0}p,\dots .$$

(29)

Therefore, the operator $T_{\mathrm{S}\text{-}\mathrm{B}}\left(p\right)$ of the S-B model can be further expressed as:

$$T_{\mathrm{S}\text{-}\mathrm{B}}\left(p\right)={\displaystyle \frac{1}{\frac{1}{E_0}+\frac{1}{{\eta }_{0}p+\frac{1}{\frac{1}{\left(1-\gamma \right)E_0}+\frac{1}{\frac{2\left(1-\gamma \right)}{\gamma }{\eta }_{0}p+\frac{1}{\frac{1}{\frac{\left(2-\gamma \right)\left(1-\gamma \right)}{3\gamma }{E}_0}+\cdots }}}}}}.$$

(30)

When the hierarchical structure tends towards infinity, Equation (30) becomes Equation (23). Equation (30) indicates that any physical component at any level in the S-B model can be determined and represented using the most basic (initial) material parameters of the spring $E_0$ and dashpot ${\eta }_0$. Observing Equation (23) it is easy to see that the operator $T_{\mathrm{S}\text{-}\mathrm{B}}\left(p\right)$ of the S-B model is mainly determined by the stiffness coefficient $E_0$ of the initial spring, the viscosity coefficient ${\eta }_0$ of the initial dashpot, and the expected order $\gamma$. The above three parameters are all manually selected. For material parameters $E_0$ and ${\eta }_0$, the operator $T_{\mathrm{S}\text{-}\mathrm{B}}\left(p\right)$ of the entire system is directly related to both. The stiffness coefficient $E_0$ of the initial spring and the viscosity coefficient ${\eta }_0$ of the initial dashpot are the basic material parameters of the overall structure, because the material parameters of each level of spring and dashpot can be represented by $E_0$ and ${\eta }_0$. In other words, there are an infinite number of options for selecting values $E_0$ and ${\eta }_0$, which can be combined arbitrarily. Therefore, there are infinitely many types of spring–dashpot systems that can form any $\gamma$-order operator $T_{\mathrm{S}\text{-}\mathrm{B}}\left(p\right)$. For the expected order $\gamma$, according to our operatorization thought, the above process can be understood as follows: if we want to construct a system of any $\gamma$-order, we only need to input a coefficient expression related to $\gamma$ in each level according to Equations (26)–(29).

At this point, based on the S-B model we have provided a construction method for any operator order. The S-B model derives the continued fraction structure through pure mathematical iteration, but their continued fraction form does not correspond one-to-one with the real mechanical structure shown in Figure 2. Therefore, in the S-B model continued fraction and binomial series are only used as pure mathematical methods and do not have physical connotations. But in our operatorization system, the continued fraction itself has rich physical connotations, which are closely related to factors such as the topological structure of fractal trees and the mechanical properties of physical components. Equations (23) and (30) represent a new design approach in our operatorization system; for a system, if we expect it to be designed to any $\gamma$-order, we only need to find a series expansion that satisfies the condition so that it can be expressed in simple continued fraction form, and then use the operatorization thought to solve the parameters of physical components. In other words, the continued fraction form corresponding to the series expansion of Equation (23) is Equation (30). When we represent Equation (23) as a continued fraction (Equation (30)), the material parameters of each level of physical components are also determined and the entire system is determined accordingly.

Thus, we have provided the operatorization expression and continued fraction form of the Schiessel–Blumen model.

7. Design and Control Method for General Fractional-Order Systems

This section mainly establishes the design and control method for general fractional-order systems.

In current research, whether it is a biological model composed of springs and dashpots, or a circuit model composed of resistors, capacitors, and inductors, the basic components that make up the fractal tree structure are of integer order [31,35,36]. By extending the structural hierarchy to infinity and based on the self-identical properties of fractal cells, algebraic equations satisfied by fractal operators can be listed, thus obtaining the explicit expression of fractal operators. In short, we have designed fractional-order systems using only integer-order physical components, which brings new inspiration to fractional-order control.

We naturally think that current fractal operators have an “apparent half-order” property. Can we construct systems of any fractional order through further design? Or can the design and control of any operator order be achieved under the original two-branch step topology? The answer is affirmative.

Firstly, let us dialectically examine this issue. In our system, there are two prerequisites for forming operator algebraic equations: one is infinite level and the other is self-identical. This self-identical prerequisite, or the property that parts are equal to the whole, is a necessary condition for forming an “apparent half-order” system, but it is also essentially a constraint condition. Once this constraint is broken, the properties of the system will change. In Section 4 and Section 5, we have introduced the correlation between continued fraction structures, fractal operators, and fractional-order systems, as well as the operatorization thought in fractional-order system design. It should be emphasized that the consistency between the self-assembly mode of the step topology and the continued fraction form provides theoretical support for the design and control of arbitrary operator order. In other words, step topology is an ideal structural model, and symmetry and symmetry breaking theory play an important role in it [37,38].

Secondly, if we try to break the constraint of being self-identical, can we obtain similar results? The answer is still affirmative, and the S-B model is a typical representative of it. In the S-B model, the physical components at each level are not exactly the same or identical, but when the structural hierarchy tends towards infinity we can still obtain a system with a fractional order of “$\gamma$”, which is a very exciting result. It should be emphasized that the reference [39] does not seem to directly propose the design principle and basis of Equation (17), but this layer-by-layer stacking pattern is very similar to the continued-fraction structure. The S-B model provides a new perspective for clarifying the sources of fractional order: we can obtain systems of any fractional order by selecting material parameters or changing the constraint relationships between material levels which greatly enhances the designability of the system. In the past physical fractal space, our system was identical and of “apparent half-order”. Now, through the above design ideas we have broken the constraints of being self-identical and introduced new constraints, which makes the properties of the new system more diverse and the functions more comprehensive. Thus, we have achieved the design and control of general operator order in the form of the two-branch step topology.

We summarize the design and control method for general fractional-order system as follows: select the expected $\gamma$ order of the system, find a series expansion that satisfies the conditions and includes the $\gamma$ order, and express it in the form of continued fraction. Using the operatorization thought, we obtain the material parameters of each level of physical components to build the overall system. Therefore, the binomial series (Equation (16)) provided in the S-B model is only a design scheme. So, are there other binomial series expansions that can be used to construct any $\gamma$-order system? The answer is affirmative. For example, if the expected order of the system is $\gamma$, a simple series ${\left(p+1\right)}^{\gamma }$ can be used for expansion, as can be seen in the following:

$${\left(p+1\right)}^{\gamma }={\displaystyle \frac{1}{1}}\begin{array}{c}\\ +\end{array}{\displaystyle \frac{\left(-\gamma \right)p}{1}}\begin{array}{c}\\ +\end{array}{\displaystyle \frac{1·\left(1+\gamma \right)p}{2}}\begin{array}{c}\\ +\end{array}{\displaystyle \frac{1·\left(1-\gamma \right)p}{3}}\begin{array}{c}\\ +\end{array}{\displaystyle \frac{2·\left(2+\gamma \right)p}{4}}\begin{array}{c}\\ +\end{array}{\displaystyle \frac{2·\left(2-\gamma \right)p}{5}}\begin{array}{c}\\ +\end{array}\cdots .$$

(31)

It should be emphasized that $p$ in Equation (31) is a time differential operator, and its series expansion is an operator-type function. Here, we further extend the research object from the “function domain” to the “operator domain”. Equation (31) can be further written as:

$$T_{{\left(p+1\right)}^{\gamma }}\left(p\right)={\displaystyle \frac{1}{1+\frac{\left(-\gamma \right)p}{1+\frac{1·\left(1+\gamma \right)p}{2+\frac{1·\left(1-\gamma \right)p}{3+\frac{2·\left(2+\gamma \right)p}{4+\frac{2·\left(2-\gamma \right)p}{5+\cdots }}}}}}}={\displaystyle \frac{1}{1+\frac{1}{\frac{1}{\left(-\gamma \right)p}+\frac{1}{-\frac{2\gamma }{\left(1+\gamma \right)}+\frac{1}{-\frac{3\left(1+\gamma \right)}{\gamma \left(1-\gamma \right)p}+\cdots }}}}}.$$

(32)

Therefore, according to Equation (24) and the operatorization thought, the operators corresponding to each level of physical components can be calculated sequentially as follows:

$${\displaystyle \frac{1}{T_1^{{\left(p+1\right)}^{\gamma }}}}=1,$$

(33)

$$T_2^{{\left(p+1\right)}^{\gamma }}={\displaystyle \frac{1}{\left(-\gamma \right)p}},$$

(34)

$${\displaystyle \frac{1}{T_3^{{\left(p+1\right)}^{\gamma }}}}=-{\displaystyle \frac{2\gamma }{\left(1+\gamma \right)}},$$

(35)

$$T_4^{{\left(p+1\right)}^{\gamma }}=-{\displaystyle \frac{3\left(1+\gamma \right)}{\gamma \left(1-\gamma \right)p}},\dots .$$

(36)

Just follow the pattern shown in Equations (33)–(36), and use the coefficient relationship equation containing the order of “$\gamma$” at each level as the input term for material parameters, we can construct general system with a fractional order of “$\gamma$”. The system here is a broad concept, not limited to the spring–dashpot system in mechanics, but can also be the capacitor–inductor–resistor system in circuits, and so on. Note that time integration operator ${\displaystyle \frac{1}{p}}$ appear in Equations (34) and (36), so the “any order” here is more suitable for building inductance (first-order integral operator) and resistance (constant operator) components in circuit models. It can be said that as long as the series expansion is reasonable, we can always build fractional-order systems that meet the requirements, which means that the design and control methods for general fractional-order systems are not unique. For example, we can find multiple design methods for $\gamma$-order systems. It should be emphasized that Equations (34)–(36) indicate that physical components with “negative” properties will appear in the system. These “negative” materials are widely present in nature, and we can also synthesize structures with “negative” properties through artificial design (such as mechanical metamaterials with negative Poisson’s ratio and negative modulus [41,42,43,44,45]).

Thus, this article provides two parameter selection methods for constructing general “$\gamma$-order” systems, namely Equations (16) and (31). In fact, the parameter selection of general “$\gamma$-order” system depends on the expansion form of the binomial series containing time differential operator $p$. Or in other words, different binomial expansion methods will result in different parameter selection methods, that is, the material parameters of the physical components that make up the overall fractional-order systems are different. For example, the series expansion of Equation (31) can also be expressed as:

$$\begin{array}{l}{\left(p+1\right)}^{\gamma }={\displaystyle \frac{1}{1}}\begin{array}{c}\\ +\end{array}{\displaystyle \frac{\left(-\gamma \right)p}{1}}\begin{array}{c}\\ +\end{array}{\displaystyle \frac{\frac{1·\left(1+\gamma \right)}{1·2}p}{1}}\begin{array}{c}\\ +\end{array}{\displaystyle \frac{\frac{1·\left(1-\gamma \right)}{2·3}p}{1}}\begin{array}{c}\\ +\end{array}{\displaystyle \frac{\frac{2·\left(2+\gamma \right)}{3·4}p}{1}}\begin{array}{c}\\ +\end{array}{\displaystyle \frac{\frac{2·\left(2-\gamma \right)}{4·5}p}{1}}\begin{array}{c}\\ +\end{array}\cdots ,\\ \hspace{1em}\hspace{1em}\hspace{1em}={\displaystyle \frac{1}{1}}\begin{array}{c}\\ +\end{array}{\displaystyle \frac{\left(-\gamma \right)p}{1}}\begin{array}{c}\\ +\end{array}{\displaystyle \frac{\left(1+\gamma \right)p}{2}}\begin{array}{c}\\ +\end{array}{\displaystyle \frac{\left(1-\gamma \right)p}{3}}\begin{array}{c}\\ +\end{array}{\displaystyle \frac{\left(2+\gamma \right)p}{2}}\begin{array}{c}\\ +\end{array}{\displaystyle \frac{\left(2-\gamma \right)p}{5}}\begin{array}{c}\\ +\end{array}{\displaystyle \frac{\left(3+\gamma \right)p}{2}}\begin{array}{c}\\ +\end{array}{\displaystyle \frac{\left(3-\gamma \right)p}{7}}\begin{array}{c}\\ +\end{array}\cdots .\end{array}$$

(37)

Equation (37) provides two additional ways to select parameters. We can calculate the operators corresponding to each level of physical components in sequence according to the patterns shown in Equations (33)–(36), in order to determine the material parameters of each physical component. The specific process will not be repeated here. It can be seen that the parameter selection of physical components at each level is closely related to the expansion of binomial series. Every binomial series containing the time differential operator $p$, when expressed in the continued fraction form, corresponds to a real system whose order is the order of the operator-type function $T\left(p\right)$. Therefore, the design of general “$\gamma$-order” system is not unique and has diversity.

Next, we will provide application examples for constructing general “$\gamma$-order” systems. At present there are two main methods for simulating a general fractional-order system using conventional physical components such as spring and dashpot. One approach is to use methods such as Newton’s method for approximation. Another type is the fractal design mode mentioned in this article. If traditional methods are used to construct fractional-order systems, the calculation of each physical component is generally to four or more decimal places, which is difficult to achieve in practical production and preparation, and this is also the biggest disadvantage of approximation methods. If the fractal design mode is adopted, it usually increases the number of physical components constructed exponentially with the recursive series, which greatly increases the manufacturing cost. Therefore, we can use truncation method to approximate the expected “$\gamma$-order” to the maximum extent with a finite-level structure. In this way, the entire system is composed of finite-level and integer-order physical components, which not only avoids the excessive use of physical components, but also reduces the difficulty of preparing fractional-order components.

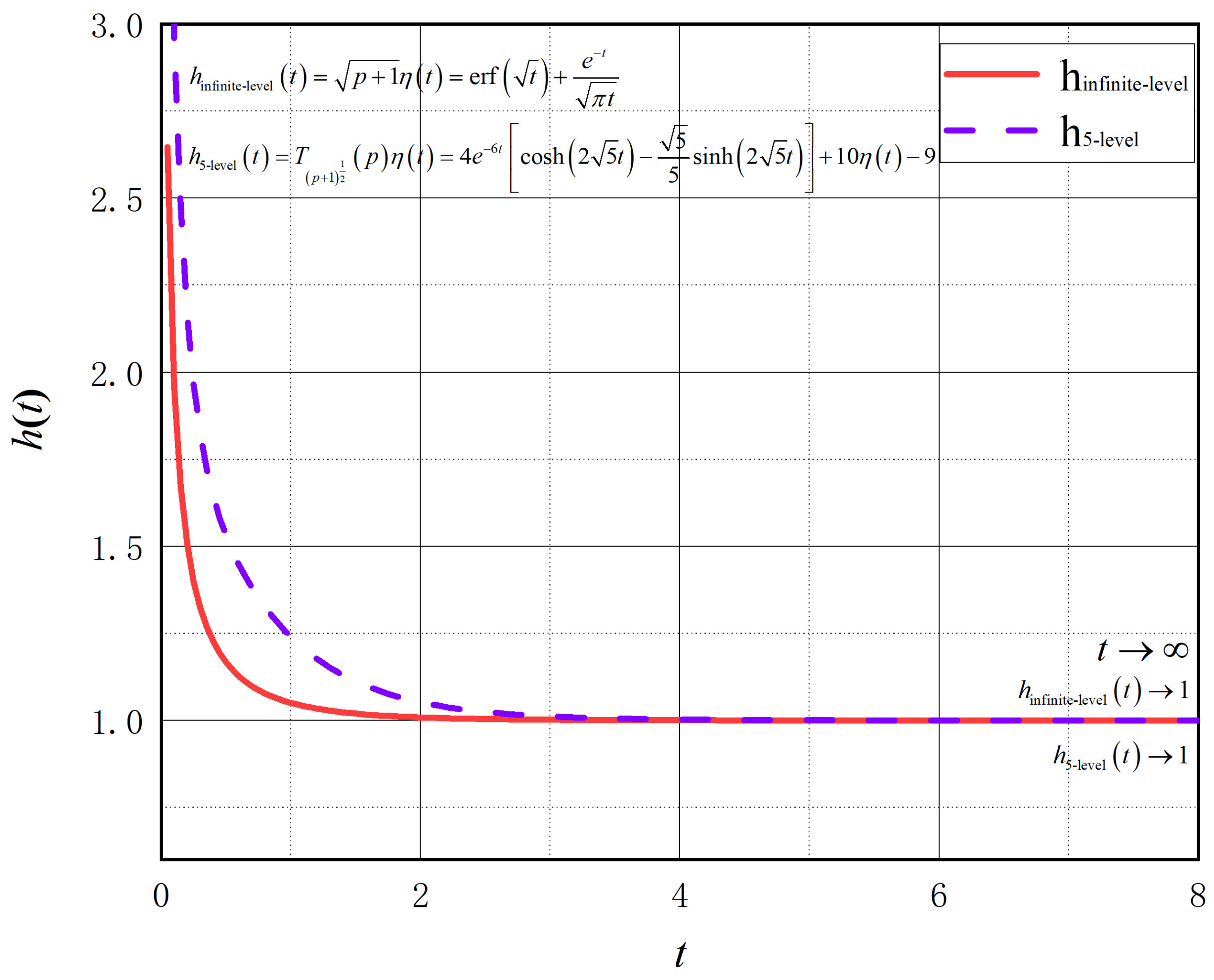
Consider a simple case where a “${\left(p+1\right)}^{\frac{1}{2}}$-order” system is desired to be designed. In reference [36], we have confirmed that when the input strain $\epsilon \left(t\right)$ is the Heaviside unit step function $\eta \left(t\right)$, the stress response of the system is as follows:

$$h_{\infty \text{-}\mathrm{l}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{l}}\left(t\right)=\sqrt{p+1}\eta \left(t\right)=\mathrm{erf}\left(\sqrt{t}\right)+{\displaystyle \frac{e^{-t}}{\sqrt{\pi t}}}.$$

(38)

If only the first five levels of the system are used, that is, only five physical components are used, Equation (32) can be further written as:

$$T_{{\left(p+1\right)}^{\frac{1}{2}}}\left(p\right)={\displaystyle \frac{5p^2+20p+16}{p^2+12p+16}}.$$

(39)

At this point, the stress response of the system is:

$$h_{5\text{-}\mathrm{l}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{l}}\left(t\right)=T_{{\left(p+1\right)}^{\frac{1}{2}}}\left(p\right)\eta \left(t\right)=4e^{-6t}\left[\cosh \left(2\sqrt{5}t\right)-{\displaystyle \frac{\sqrt{5}}{5}}\sinh \left(2\sqrt{5}t\right)\right]+10\eta \left(t\right)-9.$$

(40)

Plot the stress–strain responses corresponding to Equations (38) and (40) together, as shown in Figure 4.

In reference [36], we have confirmed that when $t\to \infty$, $h_{\infty \text{-}\mathrm{l}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{l}}\left(t\right)\to 1$. Figure 4 shows that for Equation (40), it also exists: when $t\to \infty$, $h_{5\text{-}\mathrm{l}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{l}}\left(t\right)\to 1$. Moreover, the five-level structure corresponding to Equation (40) has consistent long-term attenuation characteristics compared to the infinite-level structure corresponding to Equation (38). This means that if we use the truncation method and only use five physical components, we can obtain a relatively ideal fractional-order system, i.e., the expected “${\left(p+1\right)}^{\frac{1}{2}}$-order” system, by following the step-like construction mode shown in Figure 3. The simple example shown in Figure 4 provides theoretical support for the feasibility of designing general fractional-order system. Or in other words, using finite-level structures to approximate the properties of infinite-level structures is an interesting way to add possibilities for practical production, preparation, and construction of expected fractional-order systems. It should be emphasized that this article only considers a simple case where the input strain $\epsilon \left(t\right)$ is the Heaviside unit step function $\eta \left(t\right)$. In the following work, we will discuss in detail the effects of different truncation methods and input signals on the approximation performance and output response of the entire system.

Another approach is to use the Euler’s theorem for continued fraction to represent the series ${\displaystyle \sum _{k=0}^{\infty }{c}_k{z}^k}$ corresponding to the expected order $\gamma$ as continued fraction $b_0+{\displaystyle \sum _{k=1}^{\infty }\left(\frac{a_k}{b_k}\right)}$. Where $c_0=b_0$, $c_{1}z=a_1$, $b_1=1$, $a_k=-{\displaystyle \frac{c_k}{c_{k-1}}}z$, $b_k=1+{\displaystyle \frac{c_k}{c_{k-1}}}z$, and $k=2,3,\dots$. Utilize the correspondence between coefficients to obtain the material parameters of physical components at each level. In addition, attention should be paid to the selection of the expansion point of the series, as the expansion does not converge at any position. Moreover, when using normalization operations to process continued fractions, it is easy to introduce non-linear terms that possess additive properties. This means that once non-linear components appear in the system, the non-linear effects of physical components will become increasingly severe as the structural hierarchy increases. This is not what we expected to see, as the fractional-order system in this article is entirely constructed from integer-order components, and we do not want to add non-linear components to the system, which would pose significant challenges for the preparation of real systems. It should be emphasized that, similar to the operatorization thought proposed in Section 5 and the search for suitable series expansions in Section 7, we further extend the research object from the “functional domain” to the “operator domain”. Therefore, the series and continued fraction here are both on the operator domain, and Euler’s theorem here is essentially on the operator domain. In short, Euler’s theorem for continued fraction provides a new approach for the design and control of any operator order. We will discuss the application of Euler’s theorem for continued fraction in future work.

Thus, we have established the design and control method for general fractional-order systems, and it is exciting that the components make up the fractional-order systems are of integer order, which classical mechanical models do not possess.

8. Discussion on the Factors Influencing the Order of Fractional-Order Operators

In previous research [31,35,36,37,38], we have focused on answering the fundamental question: Where do fractional-order operators come from? What factors determine the order of fractional-order operators?

For the first question, we provide a reasonable explanation: the biological fractal operators in the physical fractal space. Based on the bone fractal operators, it can be confirmed that there is a profound intrinsic correlation between the fractional order time and fractional-dimensional space. The fractional-dimensional space inevitably leads to the fractional order time. Fractional-dimensional space, as well as the motion in fractional-dimensional space, must be characterized by fractional-order-time operators. So far, we have answered the important question of the origin of fractional-order operators.

For the second question, we found that the source of fractional order is not unique, and the factors that determine fractional order are diverse. For example, the topological invariants of fractal cells, the order of physical components, and the mismatch of spatiotemporal order, etc. Of course, we can obtain different types of fractal operators by regulating structural topology and component properties. These fractal operators share a commonality: the “apparent half-order”. This commonality arises from the quadratic algebraic equation satisfied by fractal operators. If the self-identical constraint in the physical fractal space is lifted we can also design fractional-order systems by adjusting the proportional relationship of coefficients between physical components, where the S-B model is a typical representative. Essentially, the derivation process of the S-B model is a mechanical manifestation of continued fraction iteration. The S-B model obtains a set of material parameters for the spring and dashpot through the corresponding equality of binomial coefficients. The use of Equation (17) in reference [39] is only one scenario. In theory, as long as the binomial series is selected appropriately, there are infinite design methods for the material parameters of spring and dashpot. Moreover, the general design method for any fractional-order system proposed in Section 7 also indicates that the series expansion method is not unique, and the system design method is also not unique. Essentially, whether it is the bone fractal operator model or the S-B model, their fractional-order operators are derived from a series of operators of infinite integer-order physical components that are stacked in a continued fraction pattern. In other words, the order of fractional-order operators is directly influenced by the material parameters of each level of physical components. Therefore, the research results of this article provide another strong evidence for explaining the source of fractional order, that is, the selection of material parameters or changing the constraint relationship between material levels are important factors determining the fractional order of operators.

The novelty of this article lies in the application of operatorization thought to the design of general fractional-order systems. It should be emphasized that Mikusiński’s operator algebra theory does not provide a general method for determining kernel functions by operators. In references [35,36], we established the correlation between kernel function and operator using integral transformation, summarized the general solution process of operator kernel function method, and understood it as the operatorization thought in the physical fractal space. The above ideas are fundamentally different from the classical fractional-order system design theory; the operatorization thought is based on operations in the operator domain, while the classical theory is often based on complex frequency domain. Taking the design of impedance approximation circuit as an example [34], traditional circuit design requires the impedance $Z\left(s\right)$ to be established in the complex frequency domain, where $Z$ is the complex number and $s$ is a variable in the complex plane. If the operatorization thought is used to construct the same system, the impedance $Z\left(s\right)$ will be represented as an operator-type function $T\left(p\right)$, where the independent variable $p$ is the derivative with respect to time, which is a sign rather than a parameter. The biggest advantage of operatorization thought is that it transforms all problems into the operator domain for computation. This operation is precise and simple, and compared with traditional methods it avoids the tedious steps of repeatedly using Laplace transform or inverse Laplace transform when solving system response. Or, in other words, with the operatorization thought the definition and operation of fractional calculus have been unified. We do not need to provide different fractional-order definitions for different problems, we just need to use the operatorization thought to calculate the convolution of the operator and its kernel function of the overall system, which is also the core of operatorization thought. However, designing fractional-order systems based on the continued fraction theory and operatorization thought also has limitations; when expanding the operators $T\left(p\right)$ of the overall system into continued fraction, operators and physical components with “negative” properties often appear, which increases the cost and complexity of actual production and preparation. From a mathematical perspective, this limitation arises from the symmetry breaking of the step topology corresponding to the continued fraction structure during its formation [37,38]. In the future, we will further optimize the continued fraction structure and fractal tree pattern and simplify the parameter selection of physical components and the construction method of overall system. Meanwhile, we will also discuss in detail the practical applications of operatorization thought in different fields, such as fractional-order circuit design, in our upcoming work.

Thus, apart from the topological invariants of fractal cells, the order of physical components, and the mismatch of spatiotemporal order, we have provided the fourth main influencing factor of the fractional order.

9. Conclusions

This article takes the bone fractal operator model and the Schiessel–Blumen model as the background and establishes the design and control method for general fractional-order systems based on the continued fraction theory and operatorization thought. It is worth mentioning that the components make up fractional-order systems are of integer-order, which is not present in classical mechanical models. The operatorization thought transforms the calculation of the operator and its kernel function response of the overall system from the traditional complex frequency domain to the operator domain, making the solving steps precise and simple. This is a new attempt in the interdisciplinary fields of mechanics, mathematics, and systems science. In the future, how to apply operatorization thought to different fields is a research topic worth exploring for a long time.

With operator series expansion as the core, this article confirms that general fractional-order operator can be obtained by adjusting the material parameters of physical components or changing the constraint relationships between material levels, which greatly enhances the designability of the system. The selection of material parameters is an important factor in determining the fractional order of operators, and the bone fractal operator in the physical fractal space provides a new perspective for understanding this wonderful correlation.