A Discrete Model to Solve a Bifractional Dissipative Sine-Gordon Equation: Theoretical Analysis and Simulations

Abstract

In this work, we consider a generalized form of the classical $(2+1)$-dimensional sine-Gordon system. The mathematical model considers a generalized reaction term, and the two-dimensional Laplacian includes the presence of space-fractional derivatives of the Riesz type with two different differentiation orders in general. The system is equipped with a conserved quantity that resembles the energy functional in the integer-order scenario. We propose a numerical model to approximate the solutions of the fractional sine-Gordon equation. A discretized form of the energy-like quantity is proposed, and we prove that it is conserved throughout the discrete time. Moreover, the analysis of consistency, stability, and convergence is rigorously carried out. The numerical model is implemented computationally, and some computer simulations are presented in this work. As a consequence of our simulations, we show that the discrete energy is approximately conserved throughout time, which coincides with the theoretical results.

1. Introduction

Fractional calculus, or more precisely, arbitrary-order calculus, has seen enormous development within the mathematical community in recent years due to its ability to model phenomena with complex behavior [1]. Amongst these complex phenomena, we can cite long-term memory dynamic effects and randomness or stochasticity with changing distributions, which in many cases result in simpler fractional models compared to their integer-order counterparts [2,3,4,5,6,7]. There is also evidence that fractional models provide equally good (or even better) descriptions for real-world processes than classical models in the sense of a closer match between modeled data and experimental measurements [8]. Some examples of the applications of fractional calculus can be found in the field of biological sciences, where fractional-order models have been used to describe the spread of infectious diseases such as dengue [9], as well as pharmacokinetic and pharmacodynamic processes [10], and even technological processes like fermentation [11]. In material engineering, there are also interesting applications, such as modeling viscoelasticity through the use of fractional derivatives [12,13]. Similarly, in physics, the use of fractional calculus can be observed in the investigation of Stefan problems with fractional time [14], in fractional Bloch–Torrey equations [15], in fluid mechanics [16], in quantum mechanics [17], and in some non-homogeneous Div-Curl systems [18], to mention just a few examples.

On the other hand, in recent times, numerical methods in fractional calculus have seen substantial advances [19]. This is partly due to the fact that fractional differential equations (FDEs) have gained prominence in modeling various real-world phenomena [20]. Indeed, various models have been extended to the fractional case, like Schrödinger’s equation [21], the Klein–Gordon equation [22], some reaction–diffusion equations [23,24], and Havriliak–Negami models [25], among other systems. One commonly employed method for solving these types of problems is the finite-difference method and its variations. These methods are particularly useful for FDEs with Caputo or Riemann–Liouville derivatives [26,27,28]. However, these methods can be computationally intensive, especially for high-dimensional problems, due to their global nature. Also, we can find spectral and pseudospectral methods for solving FDEs. Spectral methods have proven valuable for solving FDEs with high accuracy. The application of these methods includes the use of Chebyshev or Legendre polynomials, which convert fractional problems into systems of algebraic equations [29,30,31]. In turn, pseudospectral methods further enhance computational efficiency by reducing the number of function evaluations needed during simulations, albeit with a reduction in precision. Periodic conditions at the boundary are also needed [32]. We can also find the fractional version of the finite-element method. This method is of great interest due to its generality, convergence, and ease with which it allows the introduction of complex domains [33]. While this approach is a staple in classical areas like heat transfer, fluid dynamics, and electromagnetic modeling, its versatility does not end there. Surprisingly, it has also emerged as a key tool for unraveling fractional equations in quantum mechanics and statistical mechanics, as recent studies highlight [34,35,36,37].

One of the models that has been extensively studied in the literature (both analytically and numerically) is the sine-Gordon equation (SGE). This model is a well-known nonlinear partial differential equation. As an extended two-dimensional and integer-order model, the SGE takes the following form:

$$\begin{array}{cc}\hfill \frac{{\partial }^{2}u\left(x,y,t\right)}{\partial t^2}+\gamma \frac{\partial u\left(x,y,t\right)}{\partial t}-\lambda \Delta u(x,y,t)& =-\varphi (x,y)sinu(x,y,t)\hfill \\ \hfill & +F\left(x,y,t\right)+G^{\prime }(u(x,y,t)).\hfill \end{array}$$

(1)

Here, $u:{\mathbb{R}}^2\times {\mathbb{R}}^{\ge 0}\to \mathbb{R}$ represents a sufficiently smooth function dependent on $(x,y,t)$, where $(x,y)\in {\mathbb{R}}^2$ are spatial coordinates and $t\in {\mathbb{R}}^{\ge 0}$ denotes time. The function $\varphi (x,y)$ is continuous and varies over space with $(x,y)$, while $F(x,y,t)$ is also a continuous function that depends on both space and time. Additionally, $G:\mathbb{R}\to \mathbb{R}$ is a continuously differentiable function. The parameters $\gamma$ and $\lambda$, both real constants, have direct physical interpretations: $\gamma$ corresponds to a damping coefficient and $\lambda$ quantifies constant spatial diffusion. Here, $\Delta$ represents the two-dimensional Laplacian operator acting over x and y.

Originally emerging from differential geometry and surface theory, the sine-Gordon equation has become a cornerstone of nonlinear science due to its mathematical depth and wide range of applications across physics [38,39]. A defining feature of this equation is its ability to support soliton solutions and localized, stable waveforms that retain their shape and velocity over time, even during interactions with other solitons. This property classifies the sine-Gordon equation as an integrable system, solvable via advanced methods such as Bäcklund transformations and the inverse scattering technique [40,41]. The equation’s relevance spans multiple domains of applied physics. In solid-state physics, for instance, it models magnetic flux dynamics in long Josephson junctions, where solitons manifest as “fluxons” (quantized magnetic flux units) [42]. Similarly, in nonlinear optics, it describes specific light pulse behaviors, offering critical insights into optical soliton propagation in fiber optics [43]. The equation also serves as a foundational model in quantum field theory for studying $(1 + 1)$-dimensional field theories [44,45].

In this work, we introduce a second-order finite difference model for the dissipative 2D sine-Gordon equation with bifractional damping using Riesz operators in space (30). Two main contributions are presented in this manuscript. The first one is a structure-preserving formulation that satisfies a discrete energy-dissipation (conservation for the undamped case) law (1). The second one is a fully discrete numerical scheme with proven consistency, stability, and convergence in two dimensions (3)–(5). These developments extend existing 1D or non-dissipative models and offer a solid, efficient tool for exploring the interplay of nonlinearity and fractional damping.

The rest of this paper is organized as follows. In Section 2, we introduce the notation and basic properties of Riesz space-fractional derivatives and set up the framework for the problem. Section 3 presents the discrete finite-difference scheme: we define the temporal Crank–Nicolson two-step method, the centered-difference approximation of Riesz operators, and the discrete energy. In Section 4, we analyze the scheme’s numerical properties, proving its consistency (second order in space and time), conditional stability via a discrete Gronwall argument, and convergence to the exact solution. Section 5 offers a suite of MATLAB simulations, first validating against a known analytic solution, then exploring the effects of varying fractional orders on the analytic solution and in soliton profiles, and finally demonstrating both conservative and dissipative dynamics of a circular ring soliton. Section 6 summarizes our main findings, highlights the practical advantages of the method, and outlines potential directions for future work. Appendix A presents a collection of the full MATLAB code used to generate all numerical experiments.

2. Preliminaries

In this work, we consider $T>0$ as a fixed temporal period. For convenience, we take a fixed one-dimensional spatial domain of the form $D=(a,b)$, with $a<b$ and $D^2=D\times D$. Let $\Omega =D^2\times \left(0,T\right)\subseteq {\mathbb{R}}^3$ represent the space–time domain, and agree that $\overline{\Omega }$ represents the closure of $\Omega$ in ${\mathbb{R}}^3$ under the standard topology. It is obvious that $\overline{D^2}=[a,b]\times [a,b]$. For the remainder of this work, we will let $u:\overline{\Omega }\to \mathbb{R}$ be sufficiently smooth. Motivated by the form of the SGE described in Equation (1), we will let $\varphi :\overline{D^2}\to \mathbb{R}$ and $F:\overline{\Omega }\to \mathbb{R}$ be continuous functions, and let $G:\Omega \to \mathbb{R}$ be continuously differentiable. Throughout, we will suppose that $\varphi$ and G are non-negative functions. As expected, $\lambda$ and $\gamma$ will be non-negative real numbers with the property that $\gamma >0$. Moreover, $\alpha$ and $\beta$ will denote real numbers in $(1, 2]$. These conventions will be observed throughout this work.

Definition 1

(Podlubny [46]). Suppose that $n\in \mathbb{N}$ and $\alpha \in \mathbb{R}$ satisfy $n-1<\alpha <n$. Let us recall now that the Riesz fractional derivative of order α of the function u at the point $(x,y,t)\in \Omega$ with respect to x is provided by the following:

$$\frac{{\partial }^{\alpha }u(x,y,t)}{{\partial \left|x\right|}^{\alpha }}=\frac{-1}{2cos(\frac{\pi \alpha }{2})\Gamma (n-\alpha )}\frac{{\partial }^n}{\partial x^n}{\int }_{-\infty }^{\infty }\frac{u(\xi ,y,t)}{{|x-\xi |}^{\alpha -n+1}}d\xi .$$

(2)

Here, Γ denotes the usual gamma function. In the case that $\alpha =n$, let us agree that the Riesz fractional derivative of u with respect to x coincides with the usual integer-order nth derivative of u with respect to x. In a similar fashion, if $n-1<\beta <n$, then we define the Riesz fractional derivative of order β of u with respect to y at the point $(x,y,t)\in \Omega$ as follows:

$$\frac{{\partial }^{\beta }u(x,y,t)}{{\partial \left|y\right|}^{\beta }}=\frac{-1}{2cos(\frac{\pi \beta }{2})\Gamma (n-\beta )}\frac{{\partial }^n}{\partial y^n}{\int }_{-\infty }^{\infty }\frac{u(x,\xi ,t)}{{|y-\xi |}^{\beta -n+1}}d\xi .$$

(3)

As expected, we define the Riesz derivative of order $\beta =2$ of u with respect to y as the classical second-order derivative of u with respect to y. For the sake of commodity, we introduce the fractional Laplacian operator of order $(\alpha ,\beta )$ of u at the point $(x,y,t)$ as follows:

$${\Delta }^{\alpha ,\beta }u(x,y,t)=\frac{{\partial }^{\alpha }u(x,y,t)}{{\partial \left|x\right|}^{\alpha }}+\frac{{\partial }^{\beta }u(x,y,t)}{{\partial \left|y\right|}^{\beta }}.$$

(4)

Finally, we define the fractional gradient operator of order $(\alpha ,\beta )$ of u at $(x,y,t)$ as the following vector:

$${\nabla }^{\alpha ,\beta }u(x,y,t)=\left(\frac{{\partial }^{\alpha }u(x,y,t)}{{\partial \left|x\right|}^{\alpha }},\frac{{\partial }^{\beta }u(x,y,t)}{{\partial \left|y\right|}^{\beta }}\right).$$

(5)

With these conventions, the fractional form of the two-dimensional SGE investigated in the present work is the nonlinear partial differential equation provided by the following:

$$\begin{array}{cc}\hfill \frac{{\partial }^{2}u(x,y,t)}{\partial t^2}+\gamma \frac{\partial u(x,y,t)}{\partial t}-\lambda {\Delta }^{\alpha ,\beta }u(x,y,t)& =-\varphi (x,y)sinu(x,y,t)\hfill \\ \hfill & +F\left(x,y,t\right)-G^{\prime }(u(x,y,t))\hfill \end{array}$$

(6)

for each $(x,y,t)\in \Omega$. For the remainder of this work, we will let ${\psi }_1,{\psi }_2$: $\overline{D^2}\to \mathbb{R}$ be sufficiently smooth functions that are equal to zero at the boundary of $\overline{D^2}$. We will also consider the following initial and boundary conditions:

$$\begin{array}{cc}\hfill u(x,y,0)& ={\psi }_1(x,y),\forall (x,y)\in D^2,\hfill \\ \hfill \frac{\partial u}{\partial t}(x,y,0)& ={\psi }_2(x,y),\forall (x,y)\in D^2,\hfill \\ \hfill u(x,y,t)& =0,\forall (x,y,t)\in \partial D^2\times \left(0,T\right).\hfill \end{array}$$

(7)

Here, we observe that the functions ${\psi }_1$ and ${\psi }_2$ describe the initial position and velocity of the problem, respectively. For the remainder of the present manuscript, Equation (6) will be called the fractional 2D sine-Gordon equation (FSG). It is worthwhile noticing that, when $\alpha =\beta =2$, this equation is equal to the mathematical model (1).

In implementing the Riesz fractional derivative discretely on a bounded grid, we adopt homogeneous Dirichlet boundary conditions $u=0$ outside and on $\partial \Omega$. This zero-extension simplifies the non-local integral to vanish outside the domain. Our finite-difference scheme respects summation-by-parts identities, mirroring integration-by-parts in the continuous case, and supports discrete energy-dissipation properties [27]. Additionally, truncation error of far-field contributions is controlled via domain size and mesh resolution, following established bounds for finite-difference and quadrature approximations of the fractional Laplacian [47].

In some real physical systems, a sine-Gordon equation with a space-fractional (Riesz) derivative offers a more realistic model than its classical (integer-order) form. For example, in crystal dislocations and lattice defects, long-range interactions in the atomic lattice can be captured more accurately by a spatial fractional model. These nonlocal interactions justify the use of the Riesz operator in space, while the displacement of atoms at the boundary can be fixed at the edges of a finite crystal sample [48]. In nonlocal Josephson junctions, the phase dynamics along junction arrays with nonlocal coupling correspond to a space-fractional sine-Gordon form [49]. In nonlinear supratransmission problems in continuum media, a spatial fractional sine-Gordon equation better reproduces wave propagation through media with long-range dispersion [50].

Definition 2.

Let $p\in [1,\infty )$. In what follows, we use $L^p(D^2)$ to represent the space of all p-integrable functions on $\overline{D^2}$. We will use $L^p(\Omega )$ to denote the set of all functions $v:\overline{\Omega }\to \mathbb{R}$ that vanish at the boundary of $D^2$ at all times, and for which $v(·,·,t)\in L^p(D^2)$, for each $t\in [0,T]$. In particular, if $v,w\in L^2(\Omega )$, then we define

$${⟨v,w⟩}_{L^2(\Omega )}={\int }_{\overline{D^2}}v(x,y,t)w(x,y,t)dxdy,\forall t\in [0,T].$$

(8)

Here, place emphasis on the fact that ${⟨v,w⟩}_{L^2(\Omega )}$ is a function of t. It is well known that $⟨·,·⟩$ is an inner product in $L^2(\Omega )$. For the remainder of this section, we will use ${\parallel ·\parallel }_{L^2(\Omega )}$ to denote the Euclidean norm induced by $⟨·,·⟩$. Moreover, for each $v\in L^1(\Omega )$, we let

$${\parallel v\parallel }_{L^1(\Omega )}={\int }_{\overline{D^2}}\left|v(x,y,t)\right|dxdy,\forall t\in [0,T].$$

(9)

Finally, we agree that

$${∥{\nabla }^{\alpha /2,\beta /2}u∥}_{L^2(\Omega )}^2={∥\frac{{\partial }^{\alpha /2}u}{{\partial \left|x\right|}^{\alpha /2}}∥}_{L^2(\Omega )}^2+{∥\frac{{\partial }^{\beta /2}u}{{\partial \left|y\right|}^{\beta /2}}∥}_{L^2(\Omega )}^2,\forall t\in [0,T].$$

(10)

Definition 3.

Let u be a solution of Equation (6) subject to the initial boundary conditions (7). Then, the total energy of the system at time $t\in [0,T]$ is provided by the following:

$$E(t)=\frac{1}{2}{∥\frac{\partial u}{\partial t}∥}_{L^2(\Omega )}^2+\frac{\lambda }{2}{∥{\nabla }^{\alpha /2,\beta /2}u∥}_{L^2(\Omega )}^2+{∥\varphi \left(1-cosu\right)∥}_{L^1(\Omega )}+{\parallel G(u)\parallel }_{L^1(\Omega )}.$$

(11)

One of the well-known properties of the classical integer-order SGE is the conservation of energy over time in the undamped case [27,51]. Motivated by this fact, we wish to prove a similar result for our fractional extension of the SGE. To that end, we will use the fact that Riesz spatial derivatives satisfy a generalization of the formula for integration by parts [52]. More precisely, if $\alpha , \beta \in (1, 2)$, then the following formulas hold for all $u,v\in L^2(D^2)$:

$$\begin{array}{cc}\hfill {⟨-\frac{{\partial }^{\alpha }u}{{\partial \left|x\right|}^{\alpha }},v⟩}_{L^2(\Omega )}& ={⟨u,-\frac{{\partial }^{\alpha }v}{{\partial \left|x\right|}^{\alpha }}⟩}_{L^2(\Omega )}={⟨\frac{{\partial }^{\frac{\alpha }{2}}u}{{\partial \left|x\right|}^{\frac{\alpha }{2}}},\frac{{\partial }^{\frac{\alpha }{2}}v}{{\partial \left|x\right|}^{\frac{\alpha }{2}}}⟩}_{L^2(\Omega )},\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill {⟨-\frac{{\partial }^{\beta }u}{{\partial \left|y\right|}^{\beta }},v⟩}_{L^2(\Omega )}& ={⟨u,-\frac{{\partial }^{\beta }v}{{\partial \left|y\right|}^{\beta }}⟩}_{L^2(\Omega )}={⟨\frac{{\partial }^{\frac{\beta }{2}}u}{{\partial \left|y\right|}^{\frac{\beta }{2}}},\frac{{\partial }^{\frac{\beta }{2}}v}{{\partial \left|y\right|}^{\frac{\beta }{2}}}⟩}_{L^2(\Omega )}.\hfill \end{array}$$

(13)

Theorem 1.

If u is a solution to (6) subject to the conditions (7), then

$$E^{\prime }(t)=-\gamma {∥\frac{\partial u}{\partial t}∥}^2+{⟨F,\frac{\partial u}{\partial t}⟩}_{L^2(\Omega )},\forall t\in [0,T].$$

(14)

The system is conservative in case $\gamma =0$ and $F\equiv 0$.

Proof. 

In the first step, we will take the derivative of E with respect to t. Next, we will exchange the derivative operator with the integral sign and apply the chain rule. The property of integration by parts for Riesz fractional operators will be applied next, and Equation (6) will be substituted. In addition, recall that $\varphi$ and G are non-negative functions. As a consequence, we obtain the following chain of identities:

$$\begin{array}{cc}\hfill E^{\prime }(t)& ={⟨\frac{{\partial }^{2}u}{\partial t^2},\frac{\partial u}{\partial t}⟩}_{L^2(\Omega )}+\lambda {⟨\frac{{\partial }^{\alpha /2}}{{\partial \left|x\right|}^{\alpha /2}}\frac{\partial u}{\partial t},\frac{{\partial }^{\alpha /2}u}{{\partial \left|x\right|}^{\alpha /2}}⟩}_{L^2(\Omega )},\hfill \\ \hfill & +\lambda {⟨\frac{{\partial }^{\beta /2}}{{\partial \left|y\right|}^{\beta /2}}\frac{\partial u}{\partial t},\frac{{\partial }^{\beta /2}u}{{\partial \left|y\right|}^{\beta /2}}⟩}_{L^2(\Omega )}+{⟨\varphi sinu,\frac{\partial u}{\partial t}⟩}_{L^2(\Omega )}+{⟨G^{\prime }(u),\frac{\partial u}{\partial t}⟩}_{L^2(\Omega )},\hfill \\ \hfill & ={⟨\frac{{\partial }^{2}u}{\partial t^2},\frac{\partial u}{\partial t}⟩}_{L^2(\Omega )}-\lambda {⟨\frac{{\partial }^{\alpha }u}{{\partial \left|x\right|}^{\alpha }},\frac{\partial u}{\partial t}⟩}_{L^2(\Omega )}-\lambda {⟨\frac{{\partial }^{\beta }u}{{\partial \left|y\right|}^{\beta }},\frac{\partial u}{\partial t}⟩}_{L^2(\Omega )},\hfill \\ \hfill & +{⟨\varphi sinu,\frac{\partial u}{\partial t}⟩}_{L^2(\Omega )}+{⟨G^{\prime }(u),\frac{\partial u}{\partial t}⟩}_{L^2(\Omega )},\hfill \\ \hfill & ={⟨\frac{{\partial }^{2}u}{\partial t^2}-\lambda {\nabla }^{\alpha ,\beta }u+\varphi sinu+G^{\prime }(u),\frac{\partial u}{\partial t}⟩}_{L^2(\Omega )},\hfill \\ \hfill & =-\gamma {∥\frac{\partial u}{\partial t}∥}_{L^2(\Omega )}^2+{⟨F,\frac{\partial u}{\partial t}⟩}_{L^2(\Omega )},\forall t\in [0,T].\hfill \end{array}$$

(15)

This is what we wanted to prove. From here, if $\gamma =0$ and $F\equiv 0$, then the energy is preserved over time. In another case, the energy will dissipate.    □

The following is a straightforward consequence of Theorem 1.

Corollary 1.

Suppose that $F\equiv 0$ and u is a solution of (6) subject to conditions (7). Then, both $\frac{\partial u}{\partial t}$ and ${\nabla }^{\alpha /2,\beta /2}u$ belong to $L^2(\Omega )$.

Before closing this stage of our investigation, we wish to rewrite the partial differential Equation (6) as a system of two first-order differential equations. More precisely, notice that Equation (6) is equivalent to the following system:

$$\left\{\begin{array}{cc}\hfill \frac{\partial u(x,y,t)}{\partial t}& =v(x,y,t),\forall (x,y,t)\in \Omega ,\hfill \\ \hfill \frac{\partial v(x,y,t)}{\partial t}& =-\gamma v(x,y,t)+\lambda {\Delta }^{\alpha ,\beta }u(x,y,t)-\varphi (x,y)sinu(x,y,t)\hfill \\ \hfill & +F\left(x,y,t\right)-G^{\prime }(u(x,y,t)),\forall (x,y,t)\in \Omega .\hfill \end{array}\right.$$

(16)

As a consequence, the energy of the system can be rewritten as follows:

$$E(t)=\frac{1}{2}{∥v∥}_{L^2(\Omega )}^2+\frac{\lambda }{2}{∥{\nabla }^{\alpha /2,\beta /2}u∥}_{L^2(\Omega )}^2+{∥\varphi \left(1-cosu\right)∥}_{L^1(\Omega )}+{\parallel G(u)\parallel }_{L^1(\Omega )}.$$

(17)

Convenient discretization of this system of temporally first-order partial differential equations will be provided and analyzed in the following sections.

3. Numerical Model

In the present section, we propose the finite-difference discretization of the mathematical model (16). To that end, we will consider regular partitions of the interval $\overline{D}$ in both the x- and y-directions, as well as a regular partition of $[0,T]$. Spatially, we will fix partition norms $\Delta x$ and $\Delta y$ in the x and y directions, respectively, which satisfy $\Delta x=\Delta y=h$. Moreover, we will temporally fix a partition norm $\Delta t=\tau$. We define $M=(b-a)/h$ and $N=T/\tau$ as positive integers. The spatial and temporal domains are divided into uniform partitions: $x_i=a+ih$, $y_j=a+jh$, and $t_k=k\tau$, where $0\le i,j\le M$ and $0\le k\le N$. For clarity, we define $u_{i,j}^k=u(x_i,y_j,t_k)$ as the exact solution at grid point $x_i,y_j,t_k$, while $U_{i,j}^k$ will represent its numerical approximation at the same point.

Next, let $R_h$ denote the spatial mesh, which consists of all points $(x_i,y_j)$ generated by $x_i=a+ih$ and $y_j=a+jh$. We also define ${𝒱}_h$ as the linear space over $\mathbb{R}$ of all real-valued functions defined on the grid $R_h$ that vanish at the grid’s boundary. For any two functions $f,g\in {𝒱}_h$, the discrete inner product $⟨·,·⟩:{𝒱}_h\times {𝒱}_h\to \mathbb{R}$ and discrete norms ${\parallel ·\parallel }_1,{\parallel ·\parallel }_2:{𝒱}_h\to \mathbb{R}$ are defined as follows:

$$\begin{array}{cc}\hfill ⟨f,g⟩& =h^2\sum _{i,j=0}^{M-1}{f}_{i,j}{g}_{i,j},\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill {∥f∥}_1& =h^2\sum _{i,j=1}^{M-1}\left|f_{i,j}\right|,\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill {∥f∥}_2& =\sqrt{⟨f,f⟩}.\hfill \end{array}$$

(20)

In what follows, let us assume that ${(U^k)}_{k=0}^K$ is a sequence of ${𝒱}_h$. For the remainder of this work, we will employ the following discrete operators:

$$\begin{array}{cc}\hfill {\delta }_t{U}_{i,j}^{k+\frac{1}{2}}& =\frac{U_{i,j}^{k+1}-U_{i,j}^k}{\tau },\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill {\mu }_t{U}_{i,j}^{k+\frac{1}{2}}& =\frac{U_{i,j}^{k+1}+U_{i,j}^k}{2}.\hfill \end{array}$$

(22)

Similarly, we will employ the following nonlinear difference operator to consistently approximate the derivative of $F(u)$ with respect to u:

$${\delta }_{u,t}F(U_{i,j}^{k+\frac{1}{2}})=\left\{\begin{array}{cc}\frac{F(U_{i,j}^{k+1})-F(U_{i,j}^k)}{U_{i,j}^{k+1}-U_{i,j}^k}\hfill & \mathrm{if} U_{i,j}^{k+1}\ne U_{i,j}^k,\hfill \\ F^{\prime }(U_{i,j}^{k+\frac{1}{2}})\hfill & \mathrm{if} U_{i,j}^{k+1}=U_{i,j}^k.\hfill \end{array}\right.$$

(23)

In order to approximate the space fractional derivatives of our mathematical model, we require the following definition from the literature.

Definition 4

(Ortigueira [53]). For function $f:\mathbb{R}\to \mathbb{R}$, $h>0$, and $\alpha >-1$, whenever it exists, the fractional centered difference of order α of f at x is provided by the following:

$${\Delta }_h^{\alpha }f(x)=\sum _{l=-\infty }^{\infty }{g}_l^{(\alpha )}f(x-lh),\forall x\in \mathbb{R},$$

(24)

where

$$g_l^{(\alpha )}=\frac{{\left(-1\right)}^l\Gamma \left(\alpha +1\right)}{\Gamma \left(\frac{\alpha }{2}+l+1\right)\Gamma \left(\frac{\alpha }{2}-l+1\right)},\forall k\in \mathbb{Z}.$$

(25)

It is worth recalling that if f is sufficiently smooth at on its domain and $\alpha \in (0,1)\cup \left(1,2\right]$, then we obtain the following:

$$\frac{{\partial }^{\alpha }f(x)}{{\partial \left|x\right|}^{\alpha }}=-\frac{{\Delta }_h^{\alpha }f(x)}{h^{\alpha }}+𝒪(h^2),\forall x\in \mathbb{R}.$$

(26)

Motivated by these properties and the definition above, we define the discrete finite-difference operators for the space fractional derivatives as follows:

$$\begin{array}{cc}\hfill {\delta }_x^{(\alpha )}{U}_{i,j}^k& =-\frac{1}{h^{\alpha }}\sum _{l=0}^M{g}_{i-l}^{\left(\alpha \right)}{U}_{l,j}^k,\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill {\delta }_y^{(\beta )}{U}_{i,j}^k& =-\frac{1}{h^{\beta }}\sum _{l=0}^M{g}_{j-l}^{(\beta )}{U}_{i,l}^k.\hfill \end{array}$$

(28)

In turn, the fractional Laplacian and gradient of order $(\alpha ,\beta )$ will be estimated using the operators ${\delta }_{x,y}^{\alpha ,\beta }={\delta }_x^{(\alpha )}+{\delta }_y^{(\beta )}$ and ${\tilde{\nabla }}^{\alpha ,\beta }=({\delta }_x^{(\alpha )},{\delta }_y^{(\beta )})$, respectively. Finally, as in the continuous-case scenario, we will agree that

$$\parallel {\tilde{\nabla }}^{\alpha /2,\beta /2}{U}^k{\parallel }_2^2 = \parallel {\delta }_x^{(\alpha /2)}{U}^k{\parallel }_2^2 + {\parallel {\delta }_y^{(\beta /2)}{U}^k\parallel }_2^2,\forall k\in \{0,1,\dots ,K\}.$$

(29)

As a consequence of the previous discussion, we will approximate the solutions of (16) over the space–time domain $\Omega$ using the nonlinear finite-difference scheme:

$$\left\{\begin{array}{cc}\hfill {\delta }_t{U}_{i,j}^{k+\frac{1}{2}}& ={\mu }_t{V}_{i,j}^{k+\frac{1}{2}},\hfill \\ \hfill {\delta }_t{V}_{i,j}^{k+\frac{1}{2}}& =-\gamma {\mu }_t{V}_{i,j}^{k+\frac{1}{2}}+\lambda {\delta }_{x,y}^{\alpha ,\beta }{\mu }_t{U}_{i,j}^{k+\frac{1}{2}}-{\varphi }_{i,j}{\delta }_{u,t}cos{U}_{i,j}^{k+\frac{1}{2}},\hfill \\ \hfill & +F_{i,j}^{k+\frac{1}{2}}-{\delta }_{u,t}G(U_{i,j}^{k+\frac{1}{2}}),\hfill \end{array}\right.$$

(30)

with the following discrete initial-boundary conditions:

$$\begin{array}{cc}\hfill {\mu }_t{U}_{i,j}^{\frac{1}{2}}& ={\psi }_1(x_i,y_j),\forall i,j\in \left\{1,\dots ,M-1\right\},\hfill \\ \hfill {\mu }_t{V}_{i,j}^{\frac{1}{2}}& ={\psi }_2(x_i,y_j),\forall i,j\in \left\{1,\dots ,M-1\right\},\hfill \\ \hfill U_{i,j}^k=V_{i,j}^k& =0,\forall k\in \{0,1,\dots ,K\},\forall (i,j)\in \partial D^2.\hfill \end{array}$$

(31)

Here, we use $\partial D^2$ to represent the points of the grid on the boundary of $D^2$. Moreover, we agree that $F_{i,j}^{k+\frac{1}{2}}=F(x_i,y_j,t_{k+\frac{1}{2}})$ and $t_{k+\frac{1}{2}}={\mu }_t{t}_k$ for each $k=0,1,\dots ,K-1$.

Definition 5.

Let $(U,V)$ be a solution of the finite-difference model (30). Then, the total energy of the system at time $k\in \{0,1,\dots ,K\}$ is provided by the following:

$$E^k=\frac{1}{2}\parallel V^k{\parallel }_2^2+\frac{\lambda }{2}\parallel {\tilde{\nabla }}^{\alpha /2,\beta /2}{U}^k{\parallel }_2^2+\parallel \varphi (1-cos{U}^k){\parallel }_1+{\parallel G(U^k)\parallel }_1.$$

(32)

The next lemma is necessary to demonstrate the energy conservation property of the discrete system (30). For briefness, we will use U and V to represent sequences ${(U^k)}_{k=0}^K$ and ${(V^k)}_{k=0}^K$, respectively, in ${𝒱}_h$.

Lemma 1

(Macías-Díaz [27]). If $\alpha ,\beta \in (1,2]$ and $U,V\in {𝒱}_h$, then

$$\begin{array}{cc}\hfill ⟨-{\delta }_x^{\left(\alpha \right)}U,V⟩& =⟨{\delta }_x^{\left(\alpha /2\right)}U,{\delta }_x^{\left(\alpha /2\right)}V⟩=⟨U,-{\delta }_x^{\left(\alpha \right)}V⟩,\hfill \\ \hfill ⟨-{\delta }_y^{\left(\beta \right)}U,V⟩& =⟨{\delta }_y^{\left(\beta /2\right)}U,{\delta }_y^{\left(\beta /2\right)}V⟩=⟨U,-{\delta }_y^{\left(\beta \right)}V⟩.\hfill \end{array}$$

(33)

Theorem 2.

Let $(U,V)$ be a solution of the discrete system (30) subject to the initial-boundary conditions (31). Then,

$${\delta }_t{E}^k=-\gamma {\parallel {\delta }_t{u}^k\parallel }_2^2+⟨F^{k+\frac{1}{2}},{\delta }_t{U}^{k+\frac{1}{2}}⟩.$$

(34)

As a consequence, the discrete system is conservative when $\gamma =0$ and $F\equiv 0$.

Proof. 

We start the proof by taking the inner product on both sides of the second equation in (30) with ${\delta }_t{U}^k$ and substitute the first equation in the term multiplied by $\gamma$. In this way, we obtain the following expression:

$$\begin{array}{cc}\hfill ⟨{\delta }_t{V}^{k+\frac{1}{2}},{\delta }_t{U}^{k+\frac{1}{2}}⟩& =-\gamma \parallel {\delta }_t{U}^{k+\frac{1}{2}}{\parallel }_2^2+\lambda ⟨{\delta }_x^{(\alpha )}{\mu }_t{U}^{k+\frac{1}{2}}+{\delta }_y^{(\beta )}{\mu }_t{U}^{k+\frac{1}{2}},{\delta }_t{U}^{k+\frac{1}{2}}⟩,\hfill \\ \hfill & -⟨\varphi {\delta }_{u,t}\left[1-cos{U}^{k+\frac{1}{2}}\right],{\delta }_t{U}^{k+\frac{1}{2}}⟩-⟨{\delta }_{u,t}G(U^{k+\frac{1}{2}}),{\delta }_t{U}^{k+\frac{1}{2}}⟩,\hfill \\ \hfill & +⟨F^{k+\frac{1}{2}},{\delta }_t{U}^{k+\frac{1}{2}}⟩\hfill \end{array}$$

(35)

for each $k=0,1,\dots ,K-1$. Next, we will calculate each of the terms appearing in Equation (35). First, notice that the term on the left-hand side can be simplified using the first identity of the finite-difference scheme. In that way, obtain the following:

$$\begin{array}{cc}\hfill ⟨{\delta }_t{V}^{k+\frac{1}{2}},{\delta }_t{U}^{k+\frac{1}{2}}⟩& =⟨{\delta }_t{V}^{k+\frac{1}{2}},{\mu }_t{V}^{k+\frac{1}{2}}⟩=\frac{1}{2\tau }⟨V^{k+1}-V^k,V^{k+1}+V^k⟩,\hfill \\ \hfill & =\frac{1}{2\tau }\left(\parallel V^{k+1}{\parallel }_2^2-{\parallel V^k\parallel }_2^2\right)=\frac{1}{2}{\delta }_t\parallel V^{k+\frac{1}{2}}{\parallel }_2^2,\forall k=0,1,\dots ,K-1.\hfill \end{array}$$

(36)

We proceed to calculate the second term on the right-hand side of Equation (35). In this case, we employ the properties of fractional-centered differences to obtain the following:

$$\begin{array}{cc}\hfill ⟨{\delta }_x^{(\alpha )}{\mu }_t{U}^{k+\frac{1}{2}},{\delta }_t{U}^{k+\frac{1}{2}}⟩& =\frac{1}{2\tau }⟨{\delta }_x^{(\alpha )}\left(U^{k+1}+U^k\right),U^{k+1}-U^k⟩,\hfill \\ \hfill & =-\frac{1}{2\tau }\left(\parallel {\delta }_x^{\left(\alpha /2\right)}{U}^{k+1}{\parallel }_2^2-{\parallel {\delta }_x^{\left(\alpha /2\right)}{U}^k\parallel }_2^2\right),\hfill \\ \hfill & =-\frac{1}{2}{\delta }_t\parallel {\delta }_x^{\left(\alpha /2\right)}{U}^{k+\frac{1}{2}}{\parallel }_2^2\hfill \end{array}$$

(37)

for each $k=0,1,\dots ,K-1$. In a similar way, we can obtain an equivalent expression for the term $⟨{\delta }_x^{(\alpha )}{\mu }_t{U}^{k+\frac{1}{2}},{\delta }_t{U}^{k+\frac{1}{2}}⟩$. Next, we simplify the third and fourth terms on the right-hand side of (35). As a consequence, we obtain the following formulas:

$$\begin{array}{cc}\hfill ⟨\varphi {\delta }_t\left[1-cos{U}^{k+\frac{1}{2}}\right],{\delta }_t{U}^{k+\frac{1}{2}}⟩& ={\delta }_t{\parallel \varphi (1-cos{U}^k)\parallel }_1,\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill ⟨{\delta }_{u,t}G(U^{k+\frac{1}{2}}),{\delta }_t{U}^{k+\frac{1}{2}}⟩& ={\delta }_t{\parallel G(U^k)\parallel }_1.\hfill \end{array}$$

(39)

Using (36), (37), and these last identities, together with some algebraic manipulations, we reach the conclusion of this theorem.    □

4. Numerical Properties

The purpose of this section is to establish the most important numerical properties of the discrete model presented in this work. More precisely, we will establish the second-order consistency of the scheme, the property of conditional stability, and the convergence os the second order in both space and time.

To prove the consistency, numerical stability, and convergence of the method we define the continuous operators ${\mathcal{L}}_1$ and ${\mathcal{L}}_2$ as follows:

$$\begin{array}{cc}\hfill {\mathcal{L}}_1\left(u,v\right)& =\frac{\partial v}{\partial t}+\gamma \frac{\partial u}{\partial t}-\lambda {\Delta }^{\alpha ,\beta }u+\varphi (\mathbf{x})sinu-F(\mathbf{x},t)-G^{\prime }(u),\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill {\mathcal{L}}_2\left(u,v\right)& =\frac{\partial u}{\partial t}-v,\hfill \end{array}$$

(41)

where $\mathbf{x}=(x,y)$. These operators correspond to the residual forms of the first and second equations in (16). For the numerical approximations $U_{i,j}^k$ and $V_{i,j}^k$, the discrete operators $L_1$ and $L_2$ are defined as follows:

$$\begin{array}{cc}\hfill L_1(U_{i,j}^k,V_{i,j}^k)& ={\delta }_t{V}_{i,j}^k+\gamma {\mu }_t{V}_{i,j}^k-\lambda {\delta }_{x,y}^{\alpha ,\beta }{\mu }_t{U}_{i,j}^k-{\varphi }_{i,j}{\delta }_{u,t}cos{U}_{i,j}^k-{\delta }_{u,t}G(U_{i,j}^k)-F_{i,j}^{k+\frac{1}{2}},\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill L_2(U_{i,j}^k,V_{i,j}^k)& ={\delta }_t{U}_{i,j}^k-{\mu }_t{V}_{i,j}^k.\hfill \end{array}$$

(43)

These operators mirror the structure of (40) and (41), representing the residuals of the equations in the discretized system (30).

The following result summarizes the consistency properties of the finite-difference scheme (30) under suitable regularity assumptions.

Theorem 3

(Consistency). Assume $u\in {\mathcal{C}}_{x,y,t}^{4,4,3}\left(\overline{\Omega }\right)$ and $v\in {\mathcal{C}}_{x,y,t}^{3,3,2}\left(\overline{\Omega }\right)$. Then, there exists a constant $C>0$, independent of h and τ, such that for all $i,j\in \{0,\dots ,M\}$ and $k\in \{0,\dots ,N\}$,

$$\left|\left({\mathcal{L}}_1+{\mathcal{L}}_2\right)(u,v)-\left(L_1+L_2\right)(U_{i,j}^k,V_{i,j}^k)\right|\le C\left(h^2+{\tau }^2\right).$$

(44)

Proof. 

Applying Taylor’s theorem to u and v at $(x_i,y_j,t_{k+\frac{1}{2}})$, we derive the following truncation error bounds for the discrete operators, where $C_1,\dots ,C_7$ depend on the maximum norms of the fourth-order spatial and third-order temporal derivatives of u and v:

$$\begin{array}{cc}\hfill \left|{\delta }_t{U}_{i,j}^k-{\partial }_{t}u(x_i,y_j,t_{k+\frac{1}{2}})\right|& \le C_1{\tau }^2,\hfill \\ \hfill \left|{\delta }_t{V}_{i,j}^k-{\partial }_{t}v(x_i,y_j,t_{k+\frac{1}{2}})\right|& \le C_2{\tau }^2,\hfill \\ \hfill \left|{\mu }_t{V}_{i,j}^k-v(x_i,y_j,t_{k+\frac{1}{2}})\right|& \le C_3{\tau }^2,\hfill \\ \hfill \left|{\delta }_{u,t}cos{U}_{i,j}^k-sinu(x_i,y_j,t_{k+\frac{1}{2}})\right|& \le C_4{\tau }^2,\hfill \\ \hfill \left|{\delta }_{u,t}G(U_{i,j}^k)-G^{\prime }(u(x_i,y_j,t_{k+\frac{1}{2}}))\right|& \le C_5{\tau }^2,\hfill \\ \hfill \left|F_{i,j}^{k+\frac{1}{2}}-F(x_i,y_j,t_{k+\frac{1}{2}})\right|& \le C_6{\tau }^2,\hfill \\ \hfill \left|{\delta }_{x,y}^{\alpha ,\beta }{\mu }_t{U}_{i,j}^k-{\Delta }^{\alpha ,\beta }u(x_i,y_j,t_{k+\frac{1}{2}})\right|& \le C_7(h^2+{\tau }^2).\hfill \end{array}$$

(45)

Summing these inequalities via the triangle inequality and defining

$$C=\sum _{i=1}^7{C}_i+(\gamma -1)C_3+(\lambda -1)C_7,$$

(46)

we obtain (44). Under the regularity assumptions of this theorem, it is obvious that the constant C is independent of both h and $\tau$.    □

The goal of the following discussion is to establish the properties of stability and convergence. To that end, several lemmas will be required.

Lemma 2.

Let $G\in {\mathcal{C}}^2(\mathbb{R})$ with $G^{″}\in {\mathcal{L}}^{\infty }(\mathbb{R})$. Suppose that sequences ${(U_a^k)}_{k=0}^N$, ${(U_b^k)}_{k=0}^N$, and ${(V_a^k)}_{k=0}^N,$ ${(V_b^k)}_{k=0}^N\subseteq {\mathbb{R}}^{(M-1)\times (M-1)}$ satisfy

$$\begin{array}{cc}\hfill {\delta }_t{U}_a^{k+\frac{1}{2}}& ={\mu }_t{V}_a^{k+\frac{1}{2}},\hfill \\ \hfill {\delta }_t{U}_b^{k+\frac{1}{2}}& ={\mu }_t{V}_b^{k+\frac{1}{2}}.\hfill \end{array}$$

(47)

Define the error quantities as ${\epsilon }_u^k=U_a^k-U_b^k$, ${\epsilon }_v^k=V_a^k-V_b^k$, and ${\tilde{G}}^k={\delta }_{u_a,t}G(U_a^k)-{\delta }_{u_b,t}G(U_b^k)$. Then, there exist positive constants $C_1,C_2,C_3$ depending only on G, such that

$$\begin{array}{cc}\hfill \left|⟨{\tilde{G}}^k,{\delta }_t{\epsilon }_u^k⟩\right|& \le C_1\left(\parallel {\epsilon }_u^{k+1}{\parallel }_2^2+ \parallel {\epsilon }_u^k{\parallel }_2^2+ \parallel {\epsilon }_v^{k+1}{\parallel }_2^2+\parallel {\epsilon }_v^k{\parallel }_2^2\right),\hfill \end{array}$$

(48)

$$\begin{array}{cc}\hfill \left|2\tau \sum _{k=0}^{n-1}⟨{\tilde{G}}^k,{\delta }_t{\epsilon }_u^k⟩\right|& \le C_2\parallel {\epsilon }_u^0{\parallel }_2^2+C_3\tau \sum _{k=0}^n\parallel {\epsilon }_v^k{\parallel }_2^2.\hfill \end{array}$$

(49)

Proof. 

Let $C_0={\parallel G^{″}\parallel }_{\infty }$. Using the mean value theorem, we readily establish that

$$|{\tilde{G}}_{i,j}^k| \le C_0\left(|{({\epsilon }_u^{k+1})}_{i,j}| + |{({\epsilon }_u^k)}_{i,j}|\right)\forall (i,j)\in \left\{1,\dots ,M-1\right\}.$$

(50)

Applying the Cauchy–Schwarz inequality, we obtain the following:

$$\begin{array}{cc}\hfill |⟨{\tilde{G}}^k,{\delta }_t{\epsilon }_u^{k+\frac{1}{2}}⟩|& \le \frac{C_0}{4}\left(\parallel {\epsilon }_u^{k+1}{\parallel }_2^2+ \parallel {\epsilon }_u^k{\parallel }_2^2+ \parallel {\epsilon }_v^{k+1}{\parallel }_2^2+ {\parallel {\epsilon }_v^k\parallel }_2^2\right).\hfill \end{array}$$

(51)

Now, inequality (48) readily follows with $C_1=\frac{C_0}{4}$. To derive the cumulative bound (49), observe that the relationship ${\delta }_t{\epsilon }_u^{k+\frac{1}{2}}={\mu }_t{\epsilon }_v^{k+\frac{1}{2}}$ implies the following:

$${\epsilon }_u^n={\epsilon }_u^0+\frac{\tau }{2}\sum _{k=0}^{n-1}\left({\epsilon }_v^{k+1}+{\epsilon }_v^k\right).$$

(52)

Applying the Cauchy–Schwarz inequality again to (52) and using ${(a+b)}^2\le 2a^2+2b^2$, we obtain the following inequality:

$$\begin{array}{cc}\hfill \parallel {\epsilon }_u^n{\parallel }_2^2& \le 2\parallel {\epsilon }_u^0{\parallel }_2^2+2T\tau \sum _{k=0}^n{\parallel {\epsilon }_v^k\parallel }_2^2.\hfill \end{array}$$

(53)

Substitute (53) into (48), multiply it by $2\tau$, and sum over $k=0,\dots ,n-1$. In that way, we can readily derive the inequality as follows:

$$\begin{array}{cc}\hfill 2\tau C_1\sum _{k=0}^{n-1}({\parallel {\epsilon }_u^{k+1}\parallel }_2^2& + \parallel {\epsilon }_u^k{\parallel }_2^2+ \parallel {\epsilon }_v^{k+1}{\parallel }_2^2+ {\parallel {\epsilon }_v^k\parallel }_2^2),\hfill \\ \hfill & \le C_1\sum _{k=0}^{n-1}[8T\parallel {\epsilon }_u^0{\parallel }_2^2+ 8T{\tau }^2\sum _{i=0}^{k+1}{\parallel {\epsilon }_v^i\parallel }_2^2,\hfill \\ \hfill & +2\tau \left(\parallel {\epsilon }_v^{k+1}{\parallel }_2^2+ {\parallel {\epsilon }_v^k\parallel }_2^2\right)].\hfill \end{array}$$

(54)

Realizing that ${\tau }^2{\sum }_{i=0}^{n+1}\parallel {\epsilon }_v^i{\parallel }_2^2 \le T\tau {\sum }_{i=0}^{n+1}{\parallel {\epsilon }_v^i\parallel }_2^2$ and combining like terms yields, we derive (49) by letting $C_2=8NT{C}_1$ and $C_3=(8T^2+4)C_1$.    □

The following technical result was taken from the literature. It is a discrete form of the well-known Gronwall inequality.

Lemma 3

(Pen-Yu [54]). Let ${\left({\omega }^n\right)}_{n=0}^N$, ${\left({\rho }^n\right)}_{n=0}^N$ be non-negative sequences satisfying the following:

$${\omega }^n\le {\rho }^n+C\tau \sum _{k=0}^{n-1}{\omega }^k\forall n\in \{0,\dots ,N\}$$

(55)

for some $C\ge 0$. Then, ${\omega }^n\le {\rho }^n{e}^{Cn\tau }$ for all $n\in \{0,\dots ,N\}$.

In the next result, constants $C_2$ and $C_3$ are the same as in Lemma 2, while $C_1$ is redefined as $C_1=max\left\{{∥\varphi ∥}_{\infty },{∥G^{″}∥}_{\infty }\right\}$. In the following result, we let ${\psi }_a=\left({\left({\psi }_1\right)}_a,{\left({\psi }_2\right)}_a\right)$ and ${\psi }_b=\left({\left({\psi }_1\right)}_b,{\left({\psi }_2\right)}_b\right)$ denote two distinct sets of initial conditions for the system (30).

Theorem 4

(Numerical Stability). Let $G\in {\mathcal{C}}^2(\mathbb{R})$ with $G^{″}\in {\mathcal{L}}^{\infty }(\mathbb{R})$, and assume the temporal step size $\tau >0$ satisfies the following condition:

$$(2T+C_3)\tau <1.$$

(56)

For the two sets of initial conditions ${\psi }_a,{\psi }_b$, we let ${(U_a^k,V_a^k)}_{k=0}^N$ and ${(U_b^k,V_b^k)}_{k=0}^N$ be the corresponding solutions of the system (30). Define ${\widetilde{cos}}^k={\delta }_{u_a,t}cos(U_a^k)-{\delta }_{u_b,t}cos(U_b^k)$. Then, there exist constants $C_4,C_5>0$, such that

$$\parallel {\epsilon }_u^n{\parallel }_2^2+ \parallel {\epsilon }_v^n{\parallel }_2^2+ \lambda \parallel {\tilde{\nabla }}^{\alpha /2,\beta /2}{\epsilon }_u^n{\parallel }_2^2 \le C_4\left(\parallel {\epsilon }_u^0{\parallel }_2^2+ \parallel {\epsilon }_v^0{\parallel }_2^2+ \lambda \parallel {\tilde{\nabla }}^{\alpha /2,\beta /2}{\epsilon }_u^0{\parallel }_2^2\right)e^{C_{5}n\tau }.$$

(57)

Proof. 

Note that ${\epsilon }_u^k$ and ${\epsilon }_v^k$ satisfy the following:

$$\begin{array}{cc}\hfill {\delta }_t{\epsilon }_u^k& ={\mu }_t{\epsilon }_v^k,\hfill \end{array}$$

(58)

$$\begin{array}{cc}\hfill {\delta }_t{\epsilon }_v^k& =-\gamma {\delta }_t{\epsilon }_u^k+\lambda {\delta }_{x,y}^{\alpha ,\beta }{\mu }_t{\epsilon }_u^k+\varphi {\widetilde{cos}}^k+{\tilde{G}}^k.\hfill \end{array}$$

(59)

Taking the inner product of ${\delta }_t{\epsilon }_u^k$ with both sides of (59), summing from 0 to n, and applying the discrete energy identities from Theorem 2 along with Lemma 2 we obtain the following:

$$\begin{array}{cc}\hfill \parallel {\epsilon }_v^n{\parallel }_2^2& + \lambda \parallel {\tilde{\nabla }}^{\alpha /2,\beta /2}{\epsilon }_u^n{\parallel }_2^2\hfill \\ \hfill & \le \parallel {\epsilon }_v^0{\parallel }_2^2+ \lambda \parallel {\tilde{\nabla }}^{\alpha /2,\beta /2}{\epsilon }_u^0{\parallel }_2^2+ C_2\parallel {\epsilon }_u^0{\parallel }_2^2+ C_3\tau \sum _{k=0}^n{\parallel {\epsilon }_v^k\parallel }_2^2.\hfill \end{array}$$

(60)

Defining the composite error ${\epsilon }^k= \parallel {\epsilon }_u^k{\parallel }_2^2+ \parallel {\epsilon }_v^k{\parallel }_2^2+ \lambda \parallel {\tilde{\nabla }}^{\alpha /2,\beta /2}{\epsilon }_u^k{\parallel }_2^2$, we obtain the following:

$$\begin{array}{cc}\hfill {\epsilon }^n& \le (2+C_2){\epsilon }^0+(2T+C_3)\tau \sum _{k=0}^n{\epsilon }^k.\hfill \end{array}$$

(61)

We apply Lemma 3 with

$$\begin{array}{cc}\hfill C_4& =\frac{2+C_2}{1-(2T+C_3)\tau },\hfill \\ \hfill C_5& =\frac{2T+C_3}{1-(2T+C_3)\tau }.\hfill \end{array}$$

(62)

This completes the proof.    □

Finally, we establish the property of convergence.

Theorem 5

(Convergence). Let $u\in {\mathcal{C}}^{4,4,3}(\overline{\Omega })$ and $v\in {\mathcal{C}}^{3,3,2}(\overline{\Omega })$ be exact solutions of system (16), with $G\in {\mathcal{C}}^2(\mathbb{R})$ satisfying $G^{″}\in L^{\infty }(\mathbb{R})$. Let ${(U^k)}_{k=0}^n$ and ${(V^k)}_{k=0}^N$ denote the numerical solutions of system (30) with initial boundary conditions ψ. We define the approximation errors as follows:

$$\begin{array}{cc}\hfill {\epsilon }_u^k& =u(t_k)-U^k,\hfill \\ \hfill {\epsilon }_v^k& =v(t_k)-V^k.\hfill \end{array}$$

(63)

If the inequality

$$(8C_1{T}^2+2T+6)\tau <1$$

(64)

is satisfied, then there exists a constant $C>0$, independent of h and τ, such that

$$\underset{0\le k\le N}{max}\left(\parallel {\epsilon }_u^k{\parallel }_2+ {\parallel {\epsilon }_v^k\parallel }_2\right)\le C({\tau }^2+h^2).$$

(65)

Proof. 

Let $R_{i,j}^k$ and $S_{i,j}^k$ denote the local truncation errors at grid point $(x_i,y_j,t_k)$. From Theorem 3, there exists $C_{RS}>0$, such that

$$\parallel R^k{\parallel }_2+ {\parallel S^k\parallel }_2\le C_{RS}({\tau }^2+h^2),0\le k\le N.$$

(66)

Notice that the approximation errors satisfy

$$\begin{array}{cc}\hfill {\delta }_t{\epsilon }_u^{k+\frac{1}{2}}& ={\mu }_t{\epsilon }_v^{k+\frac{1}{2}}+R^{k+\frac{1}{2}},\hfill \end{array}$$

(67)

$$\begin{array}{cc}\hfill {\delta }_t{\epsilon }_v^{k+\frac{1}{2}}& =-\gamma {\delta }_t{\epsilon }_u^{k+\frac{1}{2}}+\lambda {\delta }_{x,y}^{\alpha ,\beta }{\mu }_t{\epsilon }_u^{k+\frac{1}{2}}+\varphi {\widetilde{cos}}^k+{\tilde{G}}^k+S^{k+\frac{1}{2}}.\hfill \end{array}$$

(68)

Following arguments similar to those used in the proof of Theorem 4, we establish the following:

$$\begin{array}{c}\hfill \parallel {\epsilon }_v^n{\parallel }_2^2+ {\parallel {\epsilon }_u^n\parallel }_2^2\le C_2\tau \sum _{k=0}^n\left(\parallel {\epsilon }_v^k{\parallel }_2^2+ {\parallel {\epsilon }_u^k\parallel }_2^2\right)+C_3({\tau }^4+h^4),\end{array}$$

(69)

where $C_2=8C_1{T}^2+2T+6$ and $C_3=5T{C}_{RS}^2$. Applying Lemma 3 with ${\omega }^n= \parallel {\epsilon }_v^n{\parallel }_2^2+ {\parallel {\epsilon }_u^n\parallel }_2^2$ and ${\rho }^n=C_2({\tau }^4+h^4)$, we can readily obtain that

$$\underset{0\le k\le N}{max}\left(\parallel {\epsilon }_u^k{\parallel }_2^2+ {\parallel {\epsilon }_v^k\parallel }_2^2\right)\le C_4{e}^{C_{5}T}({\tau }^4+h^4),$$

(70)

with suitable positive constants $C_4$ and $C_5$. By taking square roots and letting $C=\sqrt{C_4{e}^{C_{5}T}}$, we readily obtain the inequality (65).    □

5. Simulations

The purpose of the present section is to provide some computer simulations that illustrate the capability of the scheme to preserve the total energy and explore how solutions to (16) behave under different fractional orders, $\alpha$ and $\beta$. Our simulations were obtained using the MATLAB code of our finite-difference scheme based on a fixed-point approach. All simulations were conducted on a Lenovo LOQ 15ARP9 laptop equipped with an AMD Ryzen 7 7435HS 8-core/16-thread processor, paired with an NVIDIA Laptop GPU, featuring 3072 CUDA cores and 8 GB GDDR6 VRAM (128-bit interface). The system had 24 GB DDR5-4800 RAM and a 512 GB NVMe SSD.

To verify our numerical method’s accuracy, we considered the following analytical solution:

$$\begin{array}{cc}\hfill u(x,y,t)& =cos(\pi x)cos(\pi y)cos(t),\hfill \end{array}$$

(71)

$$\begin{array}{cc}\hfill v(x,y,t)& =-cos(\pi x)cos(\pi y)sin(t),\hfill \end{array}$$

(72)

on $\overline{\Omega }=\left[-\frac{1}{2},\frac{1}{2}\right]\times \left[-\frac{1}{2},\frac{1}{2}\right]\times \left[0, 5\right]$ with $\varphi (x,y)=1$, $\alpha =\beta =2$, $\gamma =0$, $\lambda =\frac{1}{2{\pi }^2}$, $F(x,y,t)=sin\left(cos(\pi x)cos(\pi y)cos(t)\right)$, and $G\equiv 0$. Initial conditions correspond to (71) and (72).

Figure 1 and Figure 2 compare analytical and numerical solutions at $t=0.8$ and $t=3$ using the spatial step $h=0.025$ and the time step $\tau =0.1$. Both solutions show strong visual agreement at these times. Figure 3 confirms this by plotting the $L^2$-error over time, which remains below $1.6\times {10}^{-2}$ and peaks near the simulation’s end.

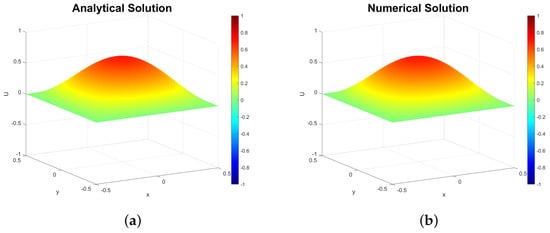
Figure 1. (a) Analytical solution (71) at $t=0.8$. (b) Numerical approximation ($h=0.025$ and $\tau =0.1$).

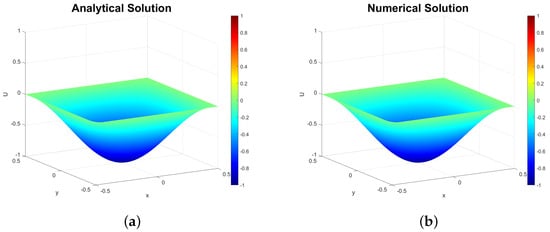
Figure 2. (a) Analytical solution (71) at $t=3$. (b) Numerical approximation ($h=0.025$ and $\tau =0.1$).

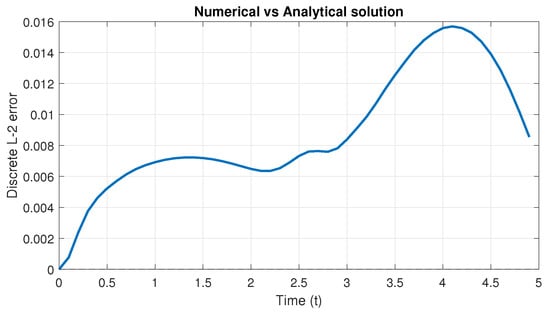
Figure 3. $L^2$-error between the analytical solution (71) and numerical approximation ($h=0.025$, $\tau =0.1$).

5.1. Impact of Fractional Orders $\alpha$ and $\beta$

Figure 4, Figure 5 and Figure 6 demonstrate how changing the fractional orders $\alpha$ and $\beta$ affects solution behavior. The most noticeable difference from the integer-order case is the wave amplitude: for $\alpha =\beta =1.1$ and $1.5$ (Figure 4 and Figure 5), amplitudes exceed 8, but decrease toward the non-fractional amplitude of 1 as $\alpha ,\beta$ tend to 2 (Figure 6). We also observe waveform deformations near the wave center when $\alpha$ and $\beta$ deviate from 2 (e.g., panels (d) in Figure 4 and Figure 5). These resemble deformations in vibrating membrane problems, contrasting with the integer-order solutions in Figure 1 and Figure 2. As expected, deformations diminish as orders approach integer values.

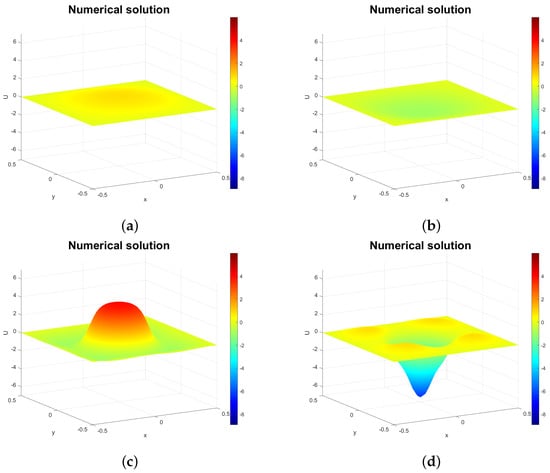
Figure 4. Solution profiles for $\alpha =\beta =1.1$ at (a) $t=1$, (b) $t=3$, (c) $t=10$, and (d) $t=14$ ($h=0.025$ and $\tau =0.1$).

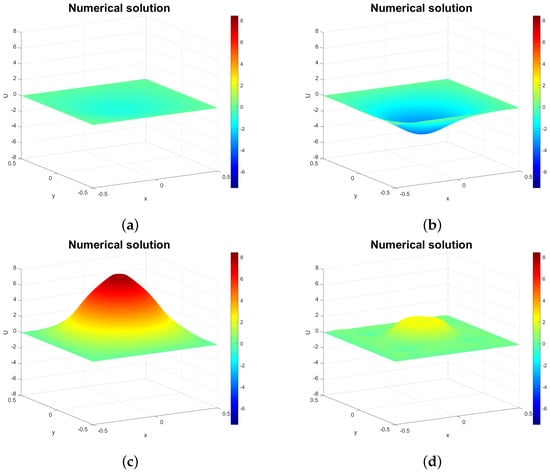
Figure 5. Solution profiles for $\alpha =\beta =1.5$ at (a) $t=3$, (b) $t=10$, (c) $t=15$, and (d) $t=25$ ($h=0.025$ and $\tau =0.1$).

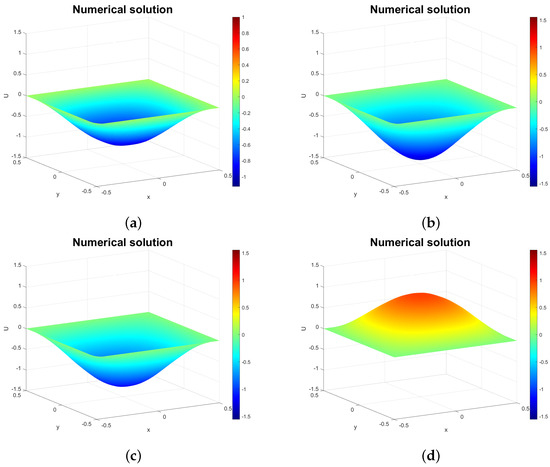
Figure 6. Solution profiles for $\alpha =\beta =1.9$ at (a) $t=3$, (b) $t=10$, (c) $t=15$, and (d) $t=25$ ($h=0.025$ and $\tau =0.1$).

5.2. Evolution of a Circular Ring Soliton

In the second scenario, we examine a localized, radially symmetric wave (“pulson”) on the spatial domain $D=[-4, 4]$ with parameters $\gamma =0$ (conservative case), $\gamma =0.5$ (dissipative case), and $\lambda =1$, and no external forcing ($F\equiv 0,G\equiv 0$). The initial conditions are as follows:

$$\begin{array}{cc}\hfill {\psi }_1(x,y)& =2arctan\left(e^{3-5\sqrt{x^2+y^2}}\right),\hfill \end{array}$$

(73)

$$\begin{array}{cc}\hfill {\psi }_2(x,y)& =0,\hfill \end{array}$$

(74)

as in [55]. We compare three different grid choices:

1.

Long-time wave evolution: $h=\tau =0.1$ over $0\le t\le 30$,

2.

Conservation of energy: $h=0.1$, $\tau =0.005$ over $0\le t\le 1.5$,

3.

Dissipation of energy: $h=0.1$, $\tau =0.01$ over $0\le t\le 5$.

In the first two experiments, we compare solutions with fractional orders $\alpha =\beta =1.5$ against the integer case $\alpha =\beta =2$, while the third experiment examines both fractional orders (1.1, 1.4, and 1.7) and the integer order 2. Figure 7 shows that at $t=0$, the ring soliton shrinks similarly for both fractional and integer solutions. However, different derivative orders produce distinct oscillation patterns by $t=5$ and $t=10$ (panels c–f). These differences diminish by $t=20$, where both solutions develop nearly identical structures (panels g–h). Despite variations in oscillation formation and radiation patterns, the overall evolution aligns with observations in [56,57].

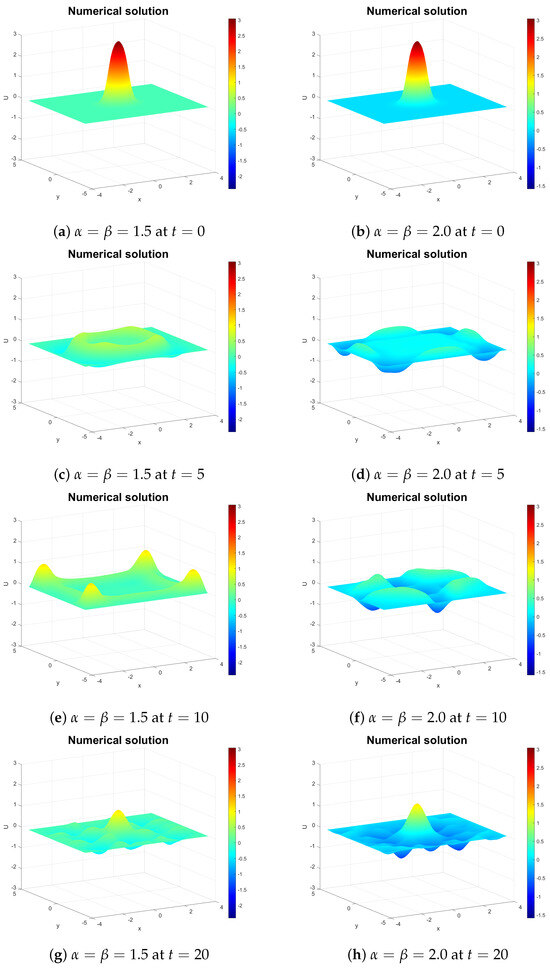
Figure 7. Numerical profiles at $t=0, 5, 10, 20$ for (left) the fractional order $\alpha =\beta =1.5$ and (right) integer order $\alpha =\beta =2.0$. All runs use $h=\tau =0.1$.

Figure 8 confirms energy conservation in both cases. For $\alpha =\beta =1.5$ (panel a), the maximum deviation is approximately $6.1\times {10}^{-3}$, while for $\alpha =\beta =2$ (panel b), it reaches $2.9\times {10}^{-3}$. Figure 9 shows the dissipative case with $\gamma =0.5$. Together, Figure 8 and Figure 9 demonstrate that $\alpha$ and $\beta$ do not affect energy behavior, they only $\gamma$ control energy conservation/dissipation, confirming Theorem 2.

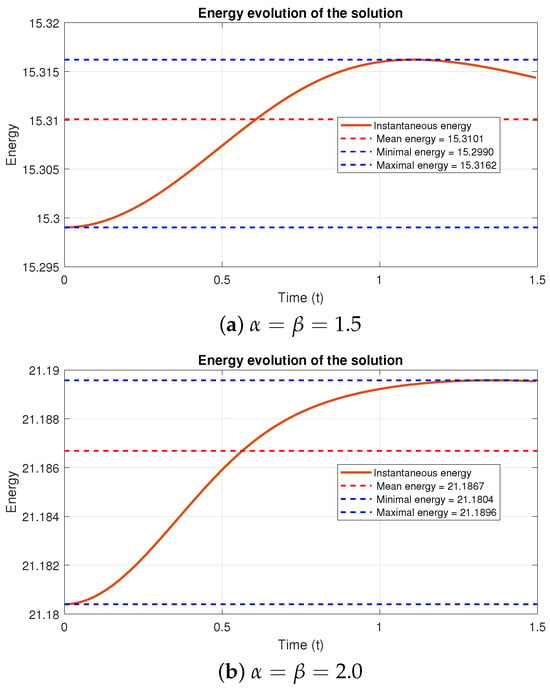
Figure 8. Energy versus time for the same runs shown in Figure 7, with $\tau =0.005$ and $h=0.1$ over $0\le t\le 1.5$.

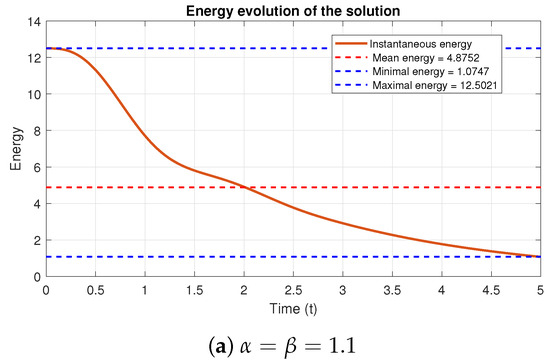
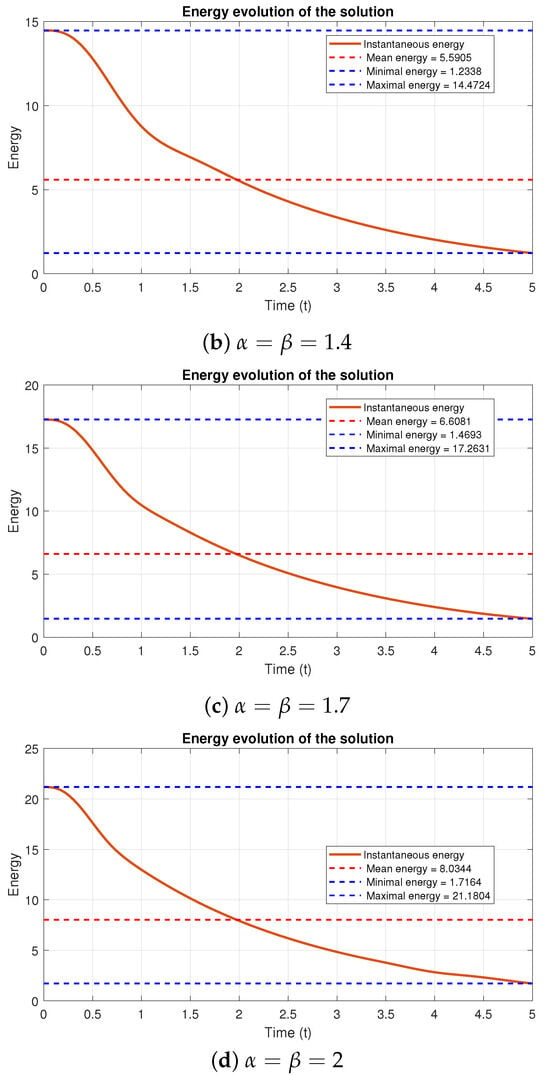
Figure 9. Energy dissipation for different derivative orders $\alpha$ and $\beta$ with fixed $\gamma =0.5$, $\tau =0.01$, $h=0.1$, and $0\le t\le 5$.

5.3. Numerical Study of Convergence

Before closing this section, we provide a brief numerical experiment to confirm the order of convergence of the scheme. To that end, we consider the setting used in Section 5.1 and fix $\alpha =\beta =1.5$. As an approximate to the exact solution, we employ values of $\tau =0.0001$ and $h=0.001$. Under these circumstances, Table 1 and Table 2 provide numerical studies of the convergence of the scheme with respect to space and time, respectively. Notice that the standard convergence rates are, at most, of the second order in space and time in the $L^2$-norm. These results confirm the conclusion of the theorem on the convergence of the scheme, which states that the finite-difference method proposed in this work has second-order convergence in the $L^2$-norm.

Table 1. Numerical study of the temporal convergence of the finite-difference scheme (30). Various values for parameters $\tau$ and h were employed to that end. We provide the errors in the $L^2$-norm and the standard convergence rate in time.

	$\mathit{h}=0.05$		$\mathit{h}=0.025$
$\mathbf{\tau }$	Error	Rate	Error	Rate
$0.1/2^0$	$2.8589\times {10}^{-2}$	−	$1.0034\times {10}^{-2}$	−
$0.1/2^1$	$8.6063\times {10}^{-3}$	$1.7320$	$3.3118\times {10}^{-3}$	$1.5992$
$0.1/2^2$	$2.6621\times {10}^{-3}$	$1.6928$	$9.9304\times {10}^{-4}$	$1.7377$
$0.1/2^3$	$7.5022\times {10}^{-4}$	$1.8272$	$2.7521\times {10}^{-4}$	$1.8513$

Table 2. Numerical study of the spatial convergence of the finite-difference scheme (30). Various values for parameters $\tau$ and h were employed to that end. We provide the errors in the $L^2$-norm and the standard convergence rate in space.

	$\mathit{\tau }=0.05$		$\mathit{\tau }=0.025$
$\mathbf{h}$	Error	Rate	Error	Rate
$0.05/2^0$	$8.6063\times {10}^{-3}$	−	$2.6621\times {10}^{-3}$	−
$0.05/2^1$	$3.3118\times {10}^{-3}$	$1.3777$	$9.9304\times {10}^{-4}$	$1.4213$
$0.05/2^2$	$1.0198\times {10}^{-3}$	$1.6992$	$3.7077\times {10}^{-4}$	$1.7828$
$0.05/2^3$	$3.3695\times {10}^{-4}$	$1.5978$	$1.1811\times {10}^{-4}$	$1.6503$

6. Conclusions

In this manuscript, a double space-fractional generalization of the sine-Gordon equation in two spatial dimensions was investigated. The generalization considered in this work uses space-fractional derivatives of the Riesz type in both spatial dimensions, with not necessarily equal orders of differentiation in the interval $(1, 2]$. In our model, a generalized potential was employed, and the sine-Gordon potential function is one of the summands. Suitable initial conditions were considered, and homogeneous Neumann data were imposed as boundary conditions on the spatial domain. Using the properties of Riesz fractional derivatives, we rigorously established that the system is dissipative in the most general case. Moreover, under suitable conditions, the energy of the system is conserved over time. Some corollaries on the regularity of the solutions of the system were obtained as a consequence of the property of the dissipativity of the energy.

Motivated by these analytical results, we proposed a numerical scheme to approximate the solution. The discrete model was obtained using finite differences. To approximate the Riesz fractional operators, we used fractional-order centered differences in space. The methodology is a nonlinear two-step Crank–Nicolson-type scheme that yields second-order approximations in both space and time. Together with the numerical integrator for the mathematical model, we also proposed a discrete form of the energy functional. As in the continuous counterpart, we showed that the discrete energy is dissipative in general, and it is conserved over the discrete time interval under the same assumptions imposed on the mathematical model. Moreover, by using a fixed-point theorem, we proved that the discrete model is always solvable.

From a theoretical point of view, we established the second-order consistency of the scheme in both space and time. The properties of convergence and stability were also proved theoretically using a suitable discrete form of Gronwall’s inequality. The uniqueness of the numerical solutions was a consequence of the conditional stability of the scheme. Computationally, the numerical model was implemented using a form of the fixed-point method. Various numerical simulations were carried out in order to assess the validity of some of our theoretical results. For example, we confirmed that the numerical model was dissipative in general and conservative under the theoretical assumptions made in this work. Other simulations considered the integer-order case, and the solutions obtained in this work qualitatively agree with the known solutions for the sine-Gordon equation. For the sake of convenience, the MATLAB code used to produce the simulations of this work is provided in Appendix A at the end of the manuscript.

Before closing this work, we would like to address some interesting comments and limitations of the present work that were noted by some of our reviewers:

• To start with, the case with different fractional orders $\alpha$ and $\beta$ is mainly mentioned but not deeply explored numerically in the present work. We do not consider this case in light of the fact that the outcomes are qualitatively similar to the case when $\alpha =\beta$. However, it is important to discuss the physical significance and additional challenges of this anisotropy. The classical sine-Gordon equation is usually referred to as certain mechanical systems in quantum mechanics. In that context, the different orders of the fractional derivatives could represent different degrees of elasticity or damping in different directions, affecting the response of the material to external forces. Evidently, this can result in complex dynamics that merit attention in future works.
• Theorem 1 is satisfied for sufficiently regular solutions of (6). In this case, the meaning of ‘sufficiently regular’ is evidently ambiguous, since various hypotheses on the smoothness of the solutions of (6) may lead to the same conclusion of the theorem. For example, since the spatial domain has a finite area, we may require solutions of the continuous system to possess continuous derivatives up to order 2, in addition to requiring that homogeneous Dirichlet conditions be satisfied at the boundary. Also, functions $\varphi$ and F must be continuous, while G needs to be continuously differentiable and non-negative. Evidently, more general conditions could be imposed in order to reach the same conclusion of the theorem.
• As one of the reviewers pointed out, the fractional centered difference scheme approximates Riesz fractional derivatives with second-order accuracy, but no stability analysis specific to this discretization is provided. Unfortunately, this is one of the various limitations that are inherent to the current approach. However, on the other hand, the use of fractional centered differences has the advantage that its computational implementation is relatively straightforward, especially when it is compared to other approaches available in the literature [58].
• The theorem on the convergence property of the finite-difference scheme imposes very restrictive assumptions on the regularity of the solutions. Those assumptions were established in the article [53], and the proof of the consistency property of those discrete operators relies on Taylor’s theorem and the mean-value theorem. In light of those facts, the regularity assumptions are indispensable, indeed. Obviously, these conditions are an important limitation in our approach. Evidently, they can be fixed by using a different approach, such as the use of weighted-shifted Grünwald differences [58]. Unfortunately, this last methodology requires a more complicated computational implementation, which leads to longer computational time.