Efficient Numerical Methods for Time-Fractional Diffusion Equations with Caputo-Type Erdélyi–Kober Operators

Abstract

This study proposes an L1 discretization scheme (an accurate second-order finite difference method) for time-fractional diffusion equations involving the Caputo-type Erdélyi–Kober operator, which models anomalous diffusion. Our key contributions include the following: (i) reformulation of the original problem into an equivalent fractional integral equation to facilitate analysis; (ii) development of a novel L1 scheme for temporal discretization, which is rigorously proven to realize second-order accuracy in time; (iii) derivation of positive definiteness properties for discrete kernel coefficients; (iv) discretization of the spatial derivative using the classical second-order centered difference scheme, for which its second-order spatial convergence is rigorously verified through numerical experiments (this results in a fully discrete scheme, enabling second-order accuracy in both temporal and spatial dimensions); (v) a fast algorithm leveraging sum-of-exponential approximation, reducing the computational complexity from $O\left(N^2\right)$ to $O(NlogN)$ and memory requirements from $O\left(N\right)$ to $O(logN)$, where N is the number of grid points on a time scale. Our numerical experiments demonstrate the stability of the scheme across diverse parameter regimes and quantify significant gains in computational efficiency. Compared to the direct method, the fast algorithm substantially reduces both memory requirements and CPU time for large-scale simulations. Although a rigorous stability analysis is deferred to subsequent research, the proven properties of the coefficients and numerical validation confirm the scheme’s reliability.

1. Introduction

In recent decades, fractional integro-differential equations have emerged as critical mathematical tools in interdisciplinary scientific and engineering research [1,2,3,4]. Within this framework, fractional diffusion equations occupy a central position due to their ability to model anomalous transport phenomena. These equations exhibit remarkable versatility in capturing the multi-regime diffusion dynamics and characteristic crossover behaviors observed in complex heterogeneous systems [5,6,7]. To address such diverse physical scenarios, multiple fractional operator definitions have been developed, including the Riemann–Liouville calculus, Grünwald–Letnikov integral, Caputo derivative, Hadamard calculus, and Erdélyi–Kober calculus. While numerical methods for equations involving the first four operator types have reached considerable maturity, the analysis of Erdélyi–Kober fractional operators remains an open research frontier. This gap in the existing literature serves as the primary motivation for our research on developing systematic numerical approaches for this understudied operator class.

The Erdélyi–Kober fractional integral operator, originally introduced by Erdélyi and Hermann K. in 1940 [8] through integral boundary condition formulations, has gained significant traction in modeling multiscale physical systems [9,10,11]. The fundamental properties of these operators—particularly the relationship between Caputo-type Erdélyi–Kober derivatives and their classical counterparts—have been systematically detailed in [2,12,13]. Recent advances in Erdélyi–Kober fractional integro-differential equations have yielded several key developments. The authors of [14,15] used the fixed-point theorem to analyze the existence and uniqueness of solutions for Erdélyi–Kober fractional nonlinear integral equations. Płociniczak [16] established a dimension-reduction framework for fractional porous media equations via non-dimensionalization, transforming the original equation into tractable integro-differential forms and thus greatly reducing the complexity of the solution. Moreover, the Erdélyi–Kober operator’s equivalence to hyper-Bessel differential operators has enabled novel solution strategies for hyper-Bessel fractional equations [17,18,19].

The inherent non-locality of fractional operators renders analytical solutions computationally prohibitive, necessitating advanced numerical approximations for practical applications. Despite extensive work on Riemann–Liouville/Caputo operators [20,21,22], numerical methods for Erdélyi–Kober operators remain underdeveloped. The current limitations in this domain include the following: Płociniczak et al. [23] proposed rectangular, midpoint, and trapezoidal formulations for Erdélyi–Kober fractional integral operators; however, they did not provide error bounds or theoretical justification. Odibat et al. [24] implemented a predictor-correction method for Caputo-type Erdélyi–Kober fractional differential equations without convergence analysis. Existing semi-discrete schemes [25] yield suboptimal first-order accuracy under weak initial regularity assumptions, and the stability and convergence of these schemes were analyzed using the Galerkin–Hermite method. Crucially, there is no high-order scheme with a fast algorithm for diffusion equations involving Caputo-type Erdélyi–Kober operators. Beyond fractional calculus, high-order numerical methods are critical in solving nonlinear dynamical systems. For instance, center-focus and integrability analyses [26,27,28,29] employ high-order techniques to study stability and bifurcations in ordinary differential equations. These methods inspired our development of a high-order scheme for fractional operators, as similar precision is required for complex Caputo dynamics in anomalous diffusion models. This study bridges these gaps by proposing novel high-order finite difference schemes using a fast algorithm for Caputo-type Erdélyi–Kober fractional diffusion equations.

In the following sections, we focus on the following initial boundary value problem of Caputo-type Erdélyi–Kober time fractional diffusion models:

$$\{\begin{array}{}\mathrm{(1)}& {\phantom{.}}_{CEK}{\mathrm{D}}_{0,t;\sigma ,\eta }^{\alpha }u(x,t)=u_{xx}(x,t)+f(x,t),(x,t)\in (0,L)\times (0,T],\mathrm{(2)}& u(x,0)=\phi \left(x\right),x\in (0,L),\mathrm{(3)}& u(0,t)=0,u(L,t)=0,t\in (0,T],\end{array}$$

where f and $\phi$ are provided with suitably smooth functions, and Caputo-type the Erdélyi–Kober fractional derivative ${\phantom{.}}_{CEK}{\mathrm{D}}_{0,t;\sigma ,\eta }^{\alpha }p\left(t\right)$ is defined via the following [24]:

$${\phantom{.}}_{CEK}{\mathrm{D}}_{0,t;\sigma ,\eta }^{\alpha }p\left(t\right)={\displaystyle \frac{t^{-\sigma \eta }}{\Gamma (1-\alpha )}}{\int }_0^t{(t^{\sigma }-s^{\sigma })}^{-\alpha }{\delta }_{\sigma }\left[s^{\sigma (\alpha +\eta )}p\left(s\right)\right]\mathrm{d}{s}^{\sigma },\alpha \in (0,1),\sigma >0,\eta \in \mathbb{R},$$

(4)

where ${\delta }_{\sigma }={\displaystyle \frac{1}{\sigma s^{\sigma -1}}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}s}}$ is the scaled derivative operator, $\alpha \in (0,1)$ is the fractional order, $\sigma >0$ is the scaling parameter, and $\eta \in \mathbb{R}$ is the shift parameter.

As observed, when $\sigma =1$ and $\eta =0,$ the operator defined in (4) reduces to

$${\phantom{.}}_{CEK}{\mathrm{D}}_{0,t;1,0}^{\alpha }p\left(t\right)={\displaystyle \frac{1}{\Gamma (1-\alpha )}}{\int }_0^t{(t-s)}^{-\alpha }{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathrm{s}}}q\left(s\right)\mathrm{d}s={\phantom{.}}_C{D}_{0,t}^{\alpha }q\left(t\right),$$

where $q\left(s\right)=s^{\alpha }p\left(s\right),$${\phantom{.}}_C{D}_{0,t}^{\alpha }q$ represents the standard Caputo derivative. Therefore, the Erdélyi–Kober operator studied here can be regarded as an extension of the classical problem rather than a special case. See details in Table 1.

Table 1. A comparison between the classical Caputo model and proposed model (1).

Model	Operator	Parameters	Physical Interpretation
Classical Caputo [20,21,22]	${\displaystyle \frac{1}{\Gamma (1-\alpha )}}{\int }_0^t{(t-s)}^{-\alpha }{u}^{\prime }\left(s\right)\mathrm{d}\mathrm{s}$	$\alpha \in (0,1)$	Standard anomalous diffusion
Proposed model (Equation (1))	${\phantom{.}}_{CEK}{\mathrm{D}}_{0,t;\sigma ,\eta }^{\alpha }p\left(t\right)$ (Equation (4))	$\alpha \in (0,1),\sigma >0,\eta \in \mathbb{R}$	Generalized scaling in time;
			$\sigma \ne 1$ models multi-scale transport [9,10]

To facilitate subsequent analyses, we apply the Erdélyi–Kober fractional integral ${\phantom{.}}_{EK}{\mathrm{D}}_{0,t;\sigma ,\eta }^{-\alpha }$ to both sides of Equation (1), yielding an equivalent form [12]:

$$u(x,t){=}_{EK}{\mathrm{D}}_{0,t;\sigma ,\eta }^{-\alpha }{u}_{xx}(x,t)+F(x,t),(x,t)\in (0,L)\times (0,T],$$

(5)

where

$${\phantom{.}}_{EK}{\mathrm{D}}_{0,t;\sigma ,\eta }^{-\alpha }{u}_{xx}(x,t)={\displaystyle \frac{t^{-\sigma (\alpha +\eta )}}{\Gamma \left(\alpha \right)}}{\int }_0^t{(t^{\sigma }-s^{\sigma })}^{\alpha -1}{s}^{\sigma \eta }{u}_{xx}(x,s)\mathrm{d}{s}^{\sigma },$$

$$F(x,t)={\displaystyle \frac{t^{-\sigma (\alpha +\eta )}}{\Gamma \left(\alpha \right)}}{\int }_0^t{(t^{\sigma }-s^{\sigma })}^{\alpha -1}{s}^{\sigma \eta }f(x,s)\mathrm{d}{s}^{\sigma }.$$

The remainder of this study is organized as follows. In Section 2, an L1-type discretization formula is developed for the Erdélyi–Kober fractional integral operator, accompanied by a detailed analysis of the truncation errors. Furthermore, we rigorously establish the positive definiteness of the discrete kernel coefficients, which lays the groundwork for future stability analyses. Building upon these theoretical foundations, we derive a finite difference scheme to solve Equation (5). To enhance computational efficiency, Section 3 introduces a rapid implementation algorithm for the difference scheme. The numerical example presented in Section 4 validates the theoretical predictions and demonstrates the effectiveness of our method. Finally, concluding remarks, along with our perspectives, are provided in Section 5.

We compare our L1 scheme to limitations in existing studies: (i) Plociniczak et al. [23] lack error bounds for their quadrature rules, while our L1 scheme provides rigorous $O\left({\tau }^2\right)$ truncation error estimates (Theorems 1 and 2). (ii) Odibat et al. [24] offered no convergence analysis, whereas we establish coefficient properties (Lemmas 1 and 3) that are foundational for stability. (iii) Semi-discrete schemes [25] only enable first-order accuracy; however, our fully discrete method enables second-order accuracy in time and space (Table 2 and Table 4). Crucially, we introduce the first rapid algorithm ($O(NlogN)$ complexity) for this operator.

2. A Direct L1 Difference Scheme

This section focuses on constructing an L1-type difference scheme based on linear interpolation for approximating fractional derivatives. The scheme derives its name from the ‘L1-norm’ error minimization inherent in piecewise linear approximations. We developed this scheme for Equation (5), coupled with its governing initial boundary value conditions (2) and (3). We firstly introduce some spatial notations. Given a positive constant $M,$ we denote $h=L/M.$ Let $x_i=ih(0\le i\le M),$ and ${\Omega }_h=\left\{x_i\right|0\le i\le M\}.$ Then, the grid function space is defined by

$${\mathcal{V}}_h=\left\{u\right|u=(u_0,u_1,\dots ,u_M)\},{\stackrel{\circ }{\mathcal{V}}}_h=\left\{u\right|u\in {\mathcal{V}}_h;u_0=u_M=0\}.$$

For any $u\in {\mathcal{V}}_h,$ introduce the following notation:

$${\delta }_x^{\mathrm{bw}}{u}_i={\displaystyle \frac{1}{h}}(u_i-u_{i-1}),{\delta }_x^2{u}_i={\displaystyle \frac{1}{h^2}}(u_{i+1}-2u_i+u_{i-1}).$$

For any $u,v\in {\stackrel{\circ }{\mathcal{V}}}_h$, the inner products and norms are defined by

$$(u,v)=h\sum _{i=1}^{M-1}{u}_i{v}_i,\parallel u\parallel =\sqrt{(u,u)},$$

$$({\delta }_{x}u,{\delta }_{x}v)=h\sum _{i=1}^M{\delta }_x{u}_{i-{\displaystyle \frac{1}{2}}}{\delta }_x{v}_{i-{\displaystyle \frac{1}{2}}},\parallel {\delta }_{x}u\parallel =\sqrt{({\delta }_{x}u,{\delta }_{x}u)}.$$

The operator ${\delta }_x^{\mathrm{bw}}$ denotes the first-order backward difference at $x_i$, while ${\delta }_x^2$ represents the second-order central difference at $x_i.$ This notation aligns with the inner product definition $({\delta }_{x}u,{\delta }_{x}v),$ where backward differences are explicitly summed over spatial indices.

The Derivation of the Difference Scheme

For any fixed $T,$ take a positive integer $N.$ Moreover, denote $\tau =T^{\sigma }/N,$$t_0=0,$$t_k={(t_{k-1}^{\sigma }+\tau )}^{{\displaystyle \frac{1}{\sigma }}},k=1,2,\dots ,N.$

We denote $g(x,t)\triangleq t^{\sigma \eta }{u}_{xx}(x,t).$ Considering Equation (5) at point $t=t_n,$ we have

$$\begin{array}{cc}\hfill u(x,t_n)=& {\displaystyle \frac{t_n^{-\sigma (\alpha +\eta )}}{\Gamma \left(\alpha \right)}}{\int }_0^{t_n}{(t_n^{\sigma }-s^{\sigma })}^{\alpha -1}g(x,s)\mathrm{d}{s}^{\sigma }+F(x,t_n)\hfill \\ \hfill =& {\displaystyle \frac{t_n^{-\sigma (\alpha +\eta )}}{\Gamma \left(\alpha \right)}}\sum _{k=0}^{n-1}{\int }_{t_k}^{t_{k+1}}{(t_n^{\sigma }-s^{\sigma })}^{\alpha -1}g(x,s)\mathrm{d}{s}^{\sigma }+F(x,t_n),x\in (0,L),1\le n\le N.\hfill \end{array}$$

(6)

Let ${\Pi }_{1,k}p\left(s\right)$ be the linear interpolation polynomial of any function p defined on an interval $[t_k,t_{k+1}],k=0,1,\dots ,N-1.$ We obtain

$${\Pi }_{1,k}p\left(s\right)={\displaystyle \frac{t_{k+1}^{\sigma }-s^{\sigma }}{\tau }}p\left(t_k\right)+{\displaystyle \frac{s^{\sigma }-t_k^{\sigma }}{\tau }}p\left(t_{k+1}\right),$$

(7)

with the truncation error

$${\theta }_p\left(s\right)={\Pi }_{1,k}p\left(s\right)-p\left(s\right)={\displaystyle \frac{1}{2}}(s^{\sigma }-t_{k+1}^{\sigma })(s^{\sigma }-t_k^{\sigma }){\delta }_{\sigma }^{2}p\left({\xi }_k\left(s\right)\right),{\xi }_k\left(s\right)\in (t_k,t_{k+1}),0\le k\le N.$$

(8)

Here, ${\delta }_{\sigma }^2={\delta }_{\sigma }\left({\delta }_{\sigma }\right),$ where ${\delta }_{\sigma }={\displaystyle \frac{1}{{\sigma }^{\sigma -1}}}{\displaystyle \frac{d}{ds}}.$ Thus, ${\delta }_{\sigma }^{2}p\left(s\right)={\displaystyle \frac{1}{{\sigma }^2{s}^{2\sigma -2}}}{\displaystyle \frac{d^{2}p}{d{s}^2}}-{\displaystyle \frac{(\sigma -1)dp}{{\sigma }^2{s}^{2\sigma -1}ds}}.$

We now develop an L1-type discretization formula for the temporal convolution integral in (6). Let us ignore the spatial variable x for now. We extend the classical Caputo L1 approach [21,22] to address the generalized kernel ${(t^{\sigma }-s^{\sigma })}^{\alpha -1}$, ensuring second-order temporal accuracy. Using (7), we have

$$\begin{array}{cc}\hfill & {\phantom{.}}_{EK}{D}_{0,t;\sigma ,\eta }^{-\alpha }{g\left(t\right)|}_{t=t_n}={\displaystyle \frac{t_n^{-\sigma (\alpha +\eta )}}{\Gamma \left(\alpha \right)}}\sum _{k=0}^{n-1}{\int }_{t_k}^{t_{k+1}}{(t_n^{\sigma }-s^{\sigma })}^{\alpha -1}g\left(s\right)\mathrm{d}{s}^{\sigma }\hfill \\ \hfill \approx & {\displaystyle \frac{t_n^{-\sigma (\alpha +\eta )}}{\Gamma \left(\alpha \right)}}\sum _{k=0}^{n-1}{\int }_{t_k}^{t_{k+1}}{(t_n^{\sigma }-s^{\sigma })}^{\alpha -1}\left[{\displaystyle \frac{t_{k+1}^{\sigma }-s^{\sigma }}{\tau }}g\left(t_k\right)+{\displaystyle \frac{s^{\sigma }-t_k^{\sigma }}{\tau }}g\left(t_{k+1}\right)\right]\mathrm{d}{s}^{\sigma }\hfill \\ \hfill =& {\displaystyle \frac{t_n^{-\sigma (\alpha +\eta )}}{\Gamma \left(\alpha \right)}}\sum _{k=0}^{n-1}\left[{\int }_{t_k}^{t_{k+1}}{(t_n^{\sigma }-s^{\sigma })}^{\alpha -1}(t_{k+1}^{\sigma }-s^{\sigma })\mathrm{d}{s}^{\sigma }{\displaystyle \frac{g\left(t_k\right)}{\tau }}+{\int }_{t_k}^{t_{k+1}}{(t_n^{\sigma }-s^{\sigma })}^{\alpha -1}(s^{\sigma }-t_k^{\sigma })\mathrm{d}{s}^{\sigma }{\displaystyle \frac{g\left(t_{k+1}\right)}{\tau }}\right]\hfill \\ \hfill =& {\displaystyle \frac{t_n^{-\sigma (\alpha +\eta )}}{\Gamma \left(\alpha \right)}}[{\displaystyle \frac{1}{\alpha (\alpha +1)}}{A}_{n,n-1}^{(\sigma ,\alpha )}{\displaystyle \frac{g\left(t_n\right)}{\tau }}+\sum _{k=1}^{n-1}{\displaystyle \frac{1}{\alpha (\alpha +1)}}(A_{n,k-1}^{(\sigma ,\alpha )}-A_{n,k}^{(\sigma ,\alpha )}){\displaystyle \frac{g\left(t_k\right)}{\tau }}\hfill \\ \hfill & +(-{\displaystyle \frac{A_{n,0}^{(\sigma ,\alpha )}}{\alpha (\alpha +1)}}+{\displaystyle \frac{\tau }{\alpha }}{t}_n^{\sigma \alpha }){\displaystyle \frac{g\left(t_0\right)}{\tau }}]\hfill \\ \hfill =& {\displaystyle \frac{t_n^{-\sigma (\alpha +\eta )}}{\Gamma \left(\alpha \right)}}\sum _{k=0}^n{C}_{n,k}^{(\sigma ,\alpha )}{\displaystyle \frac{g\left(t_k\right)}{\tau }}\triangleq {\phantom{.}}_{EK}{\mathbb{D}}_{0,t;\sigma ,\eta }^{-\alpha }g\left(t_n\right),\hfill \end{array}$$

(9)

Here,

$$A_{n,k}^{(\sigma ,\alpha )}={(t_n^{\sigma }-t_k^{\sigma })}^{\alpha +1}-{(t_n^{\sigma }-t_{k+1}^{\sigma })}^{\alpha +1},0\le k\le n-1,$$

$$C_{n,k}^{(\sigma ,\alpha )}=\left\{\begin{array}{c}{\displaystyle \frac{\tau }{\alpha }}{t}_n^{\sigma \alpha }-{\displaystyle \frac{1}{\alpha (\alpha +1)}}\left[t_n^{\sigma (\alpha +1)}-{(t_n^{\sigma }-t_1^{\sigma })}^{\alpha +1}\right],k=0,\hfill \\ {\displaystyle \frac{1}{\alpha (\alpha +1)}}\left[{(t_n^{\sigma }-t_{k-1}^{\sigma })}^{\alpha +1}-2{(t_n^{\sigma }-t_k^{\sigma })}^{\alpha +1}+{(t_n^{\sigma }-t_{k+1}^{\sigma })}^{\alpha +1}\right],1\le k\le n-1,\hfill \\ {\displaystyle \frac{1}{\alpha (\alpha +1)}}{\tau }^{\alpha +1},k=n.\hfill \end{array}\right.$$

In this case, $A_{n,k}^{(\sigma ,\alpha )}$ captures the integral of ${(t_n^{\sigma }-s^{\sigma })}^{\alpha -1}$ over $[t_k,t_{k+1}],$ and $C_{n,k}^{(\sigma ,\alpha )}$ denotes the discrete convolution weights for the L1 scheme.

For the truncation error of the L1 formula ${\phantom{.}}_{EK}{\mathbb{D}}_{0,t;\sigma ,\eta }^{-\alpha }g\left(t_n\right),$ we outline the estimate below.

Theorem 1.

Suppose $g\in C^2[t_0,t_n],$$\alpha \in (0,1).$ We denote

$$r_n={\phantom{.}}_{EK}{D}_{0,t;\sigma ,\eta }^{-\alpha }{g\left(t\right)|}_{t=t_n}-{\phantom{.}}_{EK}{\mathbb{D}}_{0,t;\sigma ,\eta }^{-\alpha }g\left(t_n\right),n=1,2,\dots ,N.$$

Then, we have

$$|r_n|\le {\displaystyle \frac{t_n^{-\sigma \eta }}{8\Gamma (1+\alpha )}}\underset{t_0<{\xi }_k\left(s\right)<t_n}{max}\left|{\delta }_{\sigma }^{2}g\left({\delta }_k\left(s\right)\right)\right|{\tau }^2.$$

Proof. 

With the help of Equation (8), we obtain

$$\begin{array}{cc}\hfill |r_n|=& {\displaystyle \frac{t_n^{-\sigma (\alpha +\eta )}}{\Gamma \left(\alpha \right)}}\sum _{k=0}^{n-1}{\int }_{t_k}^{t_{k+1}}{(t_n^{\sigma }-s^{\sigma })}^{\alpha -1}|g\left(s\right)-{\Pi }_{1,k}g\left(s\right)|\mathrm{d}{s}^{\sigma }\hfill \\ \hfill \le & {\displaystyle \frac{t_n^{-\sigma (\alpha +\eta )}}{2\Gamma \left(\alpha \right)}}\sum _{k=0}^{n-1}{\int }_{t_k}^{t_{k+1}}{(t_n^{\sigma }-s^{\sigma })}^{\alpha -1}(t_{k+1}^{\sigma }-s^{\sigma })(s^{\sigma }-t_k^{\sigma })|{\delta }_{\sigma }^{2}g\left({\xi }_k\left(s\right)\right)|\mathrm{d}{s}^{\sigma }\hfill \\ \hfill \le & {\displaystyle \frac{t_n^{-\sigma (\alpha +\eta )}}{8\Gamma \left(\alpha \right)}}{\tau }^2\underset{t_0<{\xi }_k\left(s\right)<t_n}{max}|{\delta }_{\sigma }^{2}g\left({\xi }_k\left(s\right)\right)|\sum _{k=0}^{n-1}{\int }_{t_k}^{t_{k+1}}{(t_n^{\sigma }-s^{\sigma })}^{\alpha -1}\mathrm{d}{s}^{\sigma }\hfill \\ \hfill =& {\displaystyle \frac{t_n^{-\sigma \eta }}{8\Gamma (1+\alpha )}}\underset{t_0<{\xi }_k\left(s\right)<t_n}{max}|{\delta }_{\sigma }^{2}g\left({\xi }_k\left(s\right)\right)|{\tau }^2.\hfill \end{array}$$

Thus, we complete the proof. □

In the above theorem $g=t^{\sigma \eta }{u}_{xx}\in C^2[t_0,t_n],$ which implies that $u\in C^2[0,T].$ Therefore, this requirement ensures that Theorem 1’s truncation error holds. If the regularity of the solution decreases, the convergence order will not reach second-order accuracy. This aligns with the fractional calculus literature.

Unlike classical Caputo operators, we assume $g\in C^2[0,T]$ to address the composition of ${\delta }_{\sigma }$ and $s^{\alpha +\eta }$ in Equation (9). This ensures that ${\delta }_{\sigma }^{2}g\left({\xi }_k\left(s\right)\right)$ in Theorem 1 remains bounded.

The coefficient $\left\{C_{n,k}^{(\sigma ,\alpha )}\right\}$ defined in (9) has the following properties.

Lemma 1.

For $\left\{C_{n,k}^{(\sigma ,\alpha )}{|}_{k=0}^n\right\}$ defined in (9), it holds that

$$\begin{array}{}\mathrm{(10)}& \begin{array}{cc}\hfill & 2C_{n,n}^{(\sigma ,\alpha )}>C_{n,n-1}^{(\sigma ,\alpha )}>\dots >C_{n,2}^{(\sigma ,\alpha )}>C_{n,1}^{(\sigma ,\alpha )}>2C_{n,0}^{(\sigma ,\alpha )}>0;\hfill \end{array}\hfill \mathrm{(11)}& \begin{array}{cc}\hfill & C_{n,k}^{(\sigma ,\alpha )}-2C_{n,k-1}^{(\sigma ,\alpha )}+C_{n,k-2}^{(\sigma ,\alpha )}>0,3\le k\le n-1;\hfill \end{array}\hfill \mathrm{(12)}& \begin{array}{cc}\hfill & 2C_{n,0}^{(\sigma ,\alpha )}-2C_{n,1}^{(\sigma ,\alpha )}+C_{n,2}^{(\sigma ,\alpha )}>0,C_{n,n-2}^{(\sigma ,\alpha )}-2C_{n,n-1}^{(\sigma ,\alpha )}+2C_{n,n}^{(\sigma ,\alpha )}>0.\hfill \end{array}\hfill \end{array}$$

Proof. 

(1) Proof of Equation (10): It is straightforward to show that

$$C_{n,0}^{(\sigma ,\alpha )}={\displaystyle \frac{\tau }{\alpha }}\left[t_n^{\sigma \alpha }-{(t_n^{\sigma }-{\xi }_1)}^{\alpha }\right]>{\displaystyle \frac{\tau }{\alpha }}\left[t_n^{\sigma \alpha }-t_n^{\sigma \alpha }\right]=0,{\xi }_1\in (0,t_1^{\sigma }).$$

For $2\le k\le n-1,$ we have

$$\begin{array}{cc}\hfill & C_{n,k}^{(\sigma ,\alpha )}-C_{n,k-1}^{(\sigma ,\alpha )}\hfill \\ \hfill =& {\displaystyle \frac{1}{\alpha (\alpha +1)}}\left[-{(t_n^{\sigma }-t_{k-2}^{\sigma })}^{\alpha +1}+3{(t_n^{\sigma }-t_{k-1}^{\sigma })}^{\alpha +1}-3{(t_n^{\sigma }-t_k^{\sigma })}^{\alpha +1}+{(t_n^{\sigma }-t_{k+1}^{\sigma })}^{\alpha +1}\right]\hfill \\ \hfill =& (1-\alpha ){\int }_0^{\tau }\mathrm{d}{z}_1{\int }_0^{\tau }\mathrm{d}{z}_2{\int }_0^{\tau }{(t_n^{\sigma }-t_{k+1}^{\sigma }+z_1+z_2+z_3)}^{\alpha -2}\mathrm{d}{z}_3>0.\hfill \\ \hfill & 2C_{n,n}^{(\sigma ,\alpha )}-C_{n,n-1}^{(\sigma ,\alpha )}\hfill \\ \hfill =& {\displaystyle \frac{2}{\alpha (\alpha +1)}}{\tau }^{\alpha +1}-{\displaystyle \frac{1}{\alpha (\alpha +1)}}\left[{(t_n^{\sigma }-t_{n-2}^{\alpha })}^{\alpha +1}-2{\tau }^{\alpha +1}\right]\hfill \\ \hfill =& {\displaystyle \frac{{\tau }^{\alpha +1}}{\alpha (\alpha +1)}}[4-2^{\alpha +1}]>0.\hfill \\ \hfill & C_{n,1}^{(\sigma ,\alpha )}-2C_{n,0}^{(\sigma ,\alpha )}\hfill \\ \hfill =& {\displaystyle \frac{1}{\alpha (\alpha +1)}}\left[3t_n^{\sigma (\alpha +1)}-4{(t_n^{\sigma }-t_1^{\sigma })}^{\alpha +1}+{(t_n^{\sigma }-t_2^{\sigma })}^{\alpha +1}\right]-{\displaystyle \frac{2\tau }{\alpha }}{t}_n^{\sigma \alpha }\hfill \\ \hfill =& {\displaystyle \frac{{\tau }^{\alpha +1}}{\alpha }}P(n,\alpha ),\hfill \end{array}$$

where $P(n,\alpha )={\displaystyle \frac{1}{\alpha +1}}\left[3n^{\alpha +1}-4{(n-1)}^{\alpha +1}+{(n-2)}^{\alpha +1}\right]-2n^{\alpha }.$ To prove $C_{n,1}^{(\sigma ,\alpha )}-2C_{n,0}^{(\sigma ,\alpha )}>0$, we only need to prove $P(n,\alpha )>0.$ By Taylor’s formula, we have

$$\begin{array}{cc}\hfill P(n,\alpha )=& {\displaystyle \frac{1}{\alpha +1}}[3n^{\alpha +1}-4n^{\alpha +1}+4(\alpha +1)n^{\alpha }-2\alpha (\alpha +1)n^{\alpha -1}-{\displaystyle \frac{2}{3}}\alpha (\alpha +1)(1-\alpha ){(n-1+{\xi }_1)}^{\alpha -2}\hfill \\ \hfill & +n^{\alpha +1}-2(\alpha +1)n^{\alpha }+2\alpha (\alpha +1)n^{\alpha -1}+{\displaystyle \frac{4}{3}}\alpha (\alpha +1)(1-\alpha ){(n-2+{\xi }_2)}^{\alpha -2}]-2n^{\alpha }\hfill \\ \hfill =& {\displaystyle \frac{2}{3}}\alpha (1-\alpha )\left[2{(n-2+{\xi }_2)}^{\alpha -2}-{(n-1+{\xi }_1)}^{\alpha -2}\right],\hfill \end{array}$$

in which ${\xi }_1\in (0,1),{\xi }_2\in (0,2).$

It can readily be verified that

$$P(n,\alpha )>{\displaystyle \frac{2}{3}}\alpha (1-\alpha )[2n^{\alpha -2}-{(n-1)}^{\alpha -2}]>0\mathrm{for}n\ge 4.$$

In addition, when $n=2,3,$$P(n,\alpha )>0$ can be proved using a simple calculation.

(2) Proof of Equation (11):

$$\begin{array}{cc}\hfill & C_{n,k}^{(\sigma ,\alpha )}-2C_{n,k-1}^{(\sigma ,\alpha )}+C_{n,k-2}^{(\sigma ,\alpha )}\hfill \\ \hfill =& {\displaystyle \frac{1}{\alpha (\alpha +1)}}\left[{(t_n^{\sigma }-t_{k-3}^{\sigma })}^{\alpha +1}-4{(t_n^{\sigma }-t_{k-2}^{\sigma })}^{\alpha +1}+6{(t_n^{\sigma }-t_{k-1}^{\sigma })}^{\alpha +1}-4{(t_n^{\sigma }-t_k^{\sigma })}^{\alpha +1}+{(t_n^{\sigma }-t_{k+1}^{\sigma })}^{\alpha +1}\right]\hfill \\ \hfill =& (1-\alpha )(2-\alpha ){\int }_0^{\tau }\mathrm{d}{z}_1{\int }_0^{\tau }\mathrm{d}{z}_2{\int }_0^{\tau }\mathrm{d}{z}_3{\int }_0^{\tau }{(t_n^{\sigma }-t_{k+1}^{\sigma }+z_1+z_2+z_3+z_4)}^{\alpha -3}\mathrm{d}{z}_4>0.\hfill \end{array}$$

We note that Equation (11) holds for $k\ge 3$, as $C_{n,k-2}^{(\sigma ,\alpha )}$ requires $k-2\ge 1.$ The case $k=2$ is covered separately in Equation (12).

(3) Proof of Equation (12):

$$\begin{array}{cc}\hfill & 2C_{n,0}^{(\sigma ,\alpha )}-2C_{n,1}^{(\sigma ,\alpha )}+C_{n,2}^{(\sigma ,\alpha )}\hfill \\ \hfill =& {\displaystyle \frac{2\tau }{\alpha }}{t}_n^{\sigma \alpha }+{\displaystyle \frac{1}{\alpha (\alpha +1)}}\left[-4t_n^{\sigma (\alpha +1)}+7{(t_n^{\sigma }-t_1^{\sigma })}^{\alpha +1}-4{(t_n^{\sigma }-t_2^{\sigma })}^{\alpha +1}+{(t_n^{\sigma }-t_3^{\sigma })}^{\alpha +1}\right]\hfill \\ \hfill =& {\displaystyle \frac{{\tau }^{\alpha +1}}{\alpha }}\left\{2n^{\alpha }+{\displaystyle \frac{1}{\alpha +1}}\left[-4n^{\alpha +1}+7{(n-1)}^{\alpha +1}-4{(n-2)}^{\alpha +1}+{(n-3)}^{\alpha +1}\right]\right\}.\hfill \end{array}$$

Similarly to the treatment of $P(n,\alpha ),$ one can also prove that $2C_{n,0}^{(\sigma ,\alpha )}-2C_{n,1}^{(\sigma ,\alpha )}+C_{n,2}^{(\sigma ,\alpha )}>0.$

$$\begin{array}{cc}\hfill & C_{n,n-2}^{(\sigma ,\alpha )}-2C_{n,n-1}^{(\sigma ,\alpha )}+2C_{n,n}^{(\sigma ,\alpha )}\hfill \\ \hfill =& {\displaystyle \frac{1}{\alpha (\alpha +1)}}\left[{(t_n^{\sigma }-t_{n-3}^{\sigma })}^{\alpha +1}-4{(t_n^{\sigma }-t_{n-2}^{\sigma })}^{\alpha +1}+7{\tau }^{\alpha +1}\right]\hfill \\ \hfill =& {\displaystyle \frac{{\tau }^{\alpha +1}}{\alpha (\alpha +1)}}\left(3^{\alpha +1}-4·2^{\alpha +3}+7\right)>0.\hfill \end{array}$$

Therefore, the proof is complete. □

The coefficients’ properties (Equations (10)–(12)) critically depend on $\sigma >0$ and $\alpha \in (0,1).$ As $\sigma \to 0^{+},$ the operator degenerates into the Riemann–Liouville form, resulting in a loss of monotonicity for the coefficient $\left\{C_{n,k}^{(\sigma ,\alpha )}\right\}.$ When $\alpha \to 1^{-},$ the scheme reduces to the classical L1 formula but imposes stricter regularity requirements. Critically, the positive definiteness and monotonicity of the coefficients $\left\{C_{n,k}^{(\sigma ,\alpha )}\right\}$ imply that the discrete convolution kernel satisfies the following inequality [30]:

$$\sum _{s=1}^n\left(\sum _{k=0}^s{\widehat{C}}_{n,k}^{(\sigma ,\alpha )}{u}^{n-s}\right)u^n\ge 0,$$

where

$${\widehat{C}}_{s,0}^{(\sigma ,\alpha )}=2C_{s,0}^{(\sigma ,\alpha )},{\widehat{C}}_{s,k}^{(\sigma ,\alpha )}=C_{s,k}^{(\sigma ,\alpha )}(k=1,2,\dots ,s-1),{\widehat{C}}_{s,s}^{(\sigma ,\alpha )}=2C_{s,s}^{(\sigma ,\alpha )}.$$

Combined with the discrete Grönwall inequality, this ensures unconditional stability. A complete energy estimate requires novel tools for Erdélyi–Kober operators, which are currently under active development.

Now, we devote the following sections to presenting a second-order difference scheme in order to solve problems (1)–(3). Suppose that $u(x,t)\in C^{(4,2)}([0,L]\times [0,T]).$ Denote

$$U_i^n=u(x_i,t_n),F_i^n=F(x_i,t_n),0\le n\le N;{\phi }_i=\phi \left(x_i\right),0\le i\le M.$$

Considering Equation (5) at the point $(x_i,t_n),$ we obtain

$$u(x_i,t_n)={\displaystyle \frac{t_n^{-\sigma (\alpha +\eta )}}{\Gamma \left(\alpha \right)}}{\int }_0^{t_n}{(t_n^{\sigma }-s^{\sigma })}^{\alpha -1}{s}^{\sigma \eta }{u}_{xx}(x_i,s)\mathrm{d}{s}^{\sigma }+F(x_i,t_n),1\le i\le M-1,1\le n\le N.$$

Applying Equation (9) to approximate the Erdélyi–Kober fractional integral and the central difference quotient to the spatial derivative $u_{xx}$, we obtain

$$U_i^n={\displaystyle \frac{t_n^{-\sigma (\alpha +\eta )}}{\Gamma \left(\alpha \right)}}\sum _{k=0}^n{C}_{n,k}^{(\sigma ,\alpha )}{\displaystyle \frac{t_k^{\sigma \eta }}{\tau }}{\delta }_x^2{U}_i^k+F_i^n+R_i^n,1\le i\le M-1,1\le n\le N,$$

(13)

where

$$R_i^n=r_i^n+{\displaystyle \frac{t_n^{-\sigma (\alpha +\eta )}}{\Gamma \left(\alpha \right)}}\sum _{k=0}^n{C}_{n,k}^{(\sigma ,\alpha )}{\displaystyle \frac{t_k^{\sigma \eta }}{\tau }}\left[u_{xx}(x_i,t_k)-{\delta }_x^2{U}_i^k\right].$$

We notice that, in Theorem 1, there exists a positive constant $c_1$ such that

$$\begin{array}{cc}\hfill |R_i^k|\le & |r_i^n|+{\displaystyle \frac{c_1{t}_n^{-\sigma \alpha }}{\Gamma \left(\alpha \right)\tau }}{h}^2\sum _{k=0}^n{C}_{n,k}^{(\sigma ,\alpha )}\hfill \\ \hfill \le & {\displaystyle \frac{t_n^{-\sigma \eta }}{8\Gamma (1+\alpha )}}\underset{t_0<{\xi }_k\left(s\right)<t_n}{max}\left|{\delta }_{\sigma }^{2}g\left({\delta }_k\left(s\right)\right)\right|{\tau }^2+{\displaystyle \frac{c_1{t}_n^{-\sigma \alpha }}{\Gamma \left(\alpha \right)\tau }}{h}^2·{\displaystyle \frac{\tau }{\alpha }}{t}_n^{\sigma \alpha }\hfill \\ \hfill =& {\displaystyle \frac{t_n^{-\sigma \eta }}{8\Gamma (1+\alpha )}}\underset{t_0<{\xi }_k\left(s\right)<t_n}{max}\left|{\delta }_{\sigma }^{2}g\left({\delta }_k\left(s\right)\right)\right|{\tau }^2+{\displaystyle \frac{c_1{h}^2}{\Gamma (\alpha +1)}}.\hfill \end{array}$$

(14)

Noticing the initial boundary value conditions (2) and (3), we have

$$\{\begin{array}{}\mathrm{(15)}& U_i^0={\phi }_i,1\le i\le M-1,\hfill \mathrm{(16)}& U_0^n=0,U_M^n=0,0\le n\le N.\hfill \end{array}$$

Omitting the small terms in Equation (13) and replacing the grid function $U_i^n$ with its numerical approximation $u_i^n,$ we construct a direct second-order difference scheme to solve problems (1)–(3) as follows:

$$\{\begin{array}{}\mathrm{(17)}& u_i^n={\displaystyle \frac{t_n^{-\sigma (\alpha +\eta )}}{\Gamma \left(\alpha \right)}}\sum _{k=0}^n{C}_{n,k}^{(\sigma ,\alpha )}{\displaystyle \frac{t_k^{\sigma \eta }}{\tau }}{\delta }_x^2{u}_i^k+F_i^n,1\le i\le M-1,1\le n\le N,\hfill \mathrm{(18)}& u_i^0={\phi }_i,1\le i\le M-1,\hfill \mathrm{(19)}& u_0^n=0,u_M^n=0,0\le n\le N.\hfill \end{array}$$

3. A Fast Difference Scheme

The inherent non-locality of fractional operators poses significant implementation challenges in practical computation. To address this fundamental limitation, we implement the fast algorithm developed by Jiang et al. [31] within our methodological framework.

3.1. Fast Approximation of the Erdélyi–Kober Integral

The following lemma is fundamental and needed.

Lemma 2.

For the given $\gamma \in (0,1)$ and tolerance error $ϵ$ [31], cut-off time restriction $\delta$, and final time $T,$ there is one positive integer $N_{exp}^{\left(\gamma \right)},$ positive point $\left\{s_l^{\left(\gamma \right)}\right|l=1,2,\dots ,N_{exp}^{\left(\gamma \right)}\},$ and corresponding positive weight $\left\{w_l^{\left(\gamma \right)}\right|l=1,2,\dots ,N_{exp}^{\left(\gamma \right)}\}$, such that

$$|t^{-\gamma }-\sum _{l=1}^{N_{exp}^{\left(\gamma \right)}}{w}_l^{\left(\gamma \right)}{e}^{-s_l^{\left(\gamma \right)}t}|\le ϵ,\forall t\in [\delta ,T],$$

where

$$N_{exp}^{\left(\gamma \right)}=O\left((log{\displaystyle \frac{1}{ϵ}})(loglog{\displaystyle \frac{1}{ϵ}}+log{\displaystyle \frac{T}{\delta }})+(log{\displaystyle \frac{1}{\delta }})(loglog{\displaystyle \frac{1}{ϵ}}+log{\displaystyle \frac{1}{\delta }})\right).$$

As observed, $N_{exp}^{\left(\gamma \right)}$ is of the order $O(logN)$ for $T\ge 1$, or is of the order ${log}^{2}N$ for $T\approx 1$ in fixed accuracy $ϵ$ cases. In particular, as $\alpha \to 1^{-},$$\gamma =1-\alpha \to 0^{+},$ requiring $N_{exp}=O(log{\displaystyle \frac{1}{ϵ}}+log{\displaystyle \frac{1}{\gamma }})$ terms for accuracy $ϵ$.

Now, we derive a fast algorithm for computing the Erdélyi–Kober integral ${\phantom{.}}_{EK}{D}_{0,t;\sigma ,\eta }^{-\alpha }{g\left(t\right)|}_{t=t_n}.$ Let $\delta =\tau /2$:

$$\begin{array}{cc}\hfill & {\phantom{.}}_{EK}{D}_{0,t;\sigma ,\eta }^{-\alpha }{g\left(t\right)|}_{t=t_n}\hfill \\ \hfill =& {\displaystyle \frac{t_n^{-\sigma (\alpha +\eta )}}{\Gamma \left(\alpha \right)}}\sum _{k=0}^{n-1}{\int }_{t_k}^{t_{k+1}}{(t_n^{\sigma }-s^{\sigma })}^{\alpha -1}g\left(s\right)\mathrm{d}{s}^{\sigma }\hfill \\ \hfill =& {\displaystyle \frac{t_n^{-\sigma (\alpha +\eta )}}{\Gamma \left(\alpha \right)}}\left[\sum _{k=0}^{n-2}{\int }_{t_k}^{t_{k+1}}{(t_n^{\sigma }-s^{\sigma })}^{\alpha -1}g\left(s\right)\mathrm{d}{s}^{\sigma }+{\int }_{t_{n-1}}^{t_n}{(t_n^{\sigma }-s^{\sigma })}^{\alpha -1}g\left(s\right)\mathrm{d}{s}^{\sigma }\right]\hfill \\ \hfill \approx & {\displaystyle \frac{t_n^{-\sigma (\alpha +\eta )}}{\Gamma \left(\alpha \right)}}\left[\sum _{l=1}^{N_{exp}^{(1-\alpha )}}{w}_l^{(1-\alpha )}\sum _{k=0}^{n-2}{\int }_{t_k}^{t_{k+1}}{e}^{-s_l^{(1-\alpha )}(t_n^{\sigma }-s^{\sigma })}{\Pi }_{1,k}g\left(s\right)\mathrm{d}{s}^{\sigma }+{\int }_{t_{n-1}}^{t_n}{(t_n^{\sigma }-s^{\sigma })}^{\alpha -1}{\Pi }_{1,n-1}g\left(s\right)\mathrm{d}{s}^{\sigma }\right]\hfill \\ \hfill =& {\displaystyle \frac{t_n^{-\sigma (\alpha +\eta )}}{\Gamma \left(\alpha \right)}}\left[\sum _{l=1}^{N_{exp}^{(1-\alpha )}}{w}_l^{(1-\alpha )}{F}_l^n+{\displaystyle \frac{{\tau }^{\alpha }}{\alpha +1}}g\left(t_{n-1}\right)+{\displaystyle \frac{{\tau }^{\alpha }}{\alpha (\alpha +1)}}g\left(t_n\right)\right],\hfill \end{array}$$

(20)

where

$$\begin{array}{cc}\hfill & F_l^1=0;\hfill \\ \hfill & F_l^n=\sum _{k=0}^{n-2}{\int }_{t_k}^{t_{k+1}}{e}^{-s_l^{(1-\alpha )}(t_n^{\sigma }-s^{\sigma })}{\Pi }_{1,k}g\left(s\right)\mathrm{d}{s}^{\sigma }.\hfill \end{array}$$

The integral $F_l^n$ can be evaluated using a recursive algorithm:

$$\begin{array}{cc}\hfill F_l^n=& e^{-s_l^{(1-\alpha )}\tau }\sum _{k=0}^{n-3}{\int }_{t_k}^{t_{k+1}}{e}^{-s_l^{(1-\alpha )}(t_{n-1}^{\sigma }-s^{\sigma })}{\Pi }_{1,k}g\left(s\right)\mathrm{d}{s}^{\sigma }+{\int }_{t_{n-2}}^{t_{n-1}}{e}^{-s_l^{(1-\alpha )}(t_n^{\sigma }-s^{\sigma })}{\Pi }_{1,n-2}g\left(s\right)\mathrm{d}{s}^{\sigma }\hfill \\ \hfill =& e^{-s_l^{(1-\alpha )}\tau }{F}_l^{n-1}+A_l{\displaystyle \frac{g\left(t_{n-2}\right)}{\tau }}+B_l{\displaystyle \frac{g\left(t_{n-1}\right)}{\tau }},n=2,3,\dots ,\hfill \end{array}$$

where, for $1\le l\le N_{exp}^{(1-\alpha )},$ we have the following:

$$\begin{array}{cc}\hfill & A_l={\displaystyle \frac{1}{s_l^{(1-\alpha )}}}\left\{-\tau e^{-2s_l^{(1-\alpha )}\tau }+{\displaystyle \frac{1}{s_l^{(1-\alpha )}}}\left[e^{-s_l^{(1-\alpha )}\tau }-e^{-2s_l^{(1-\alpha )}\tau }\right]\right\},\hfill \\ \hfill & B_l={\displaystyle \frac{1}{s_l^{(1-\alpha )}}}\left\{\tau e^{-s_l^{(1-\alpha )}\tau }-{\displaystyle \frac{1}{s_l^{(1-\alpha )}}}\left[e^{-s_l^{(1-\alpha )}\tau }-e^{-2s_l^{(1-\alpha )}\tau }\right]\right\}.\hfill \end{array}$$

In addition, one can show that

$$\begin{array}{cc}\hfill & {\phantom{.}}_{EK}{D}_{0,t;\sigma ,\eta }^{-\alpha }{g\left(t\right)|}_{t=t_n}\hfill \\ \hfill \approx & {\displaystyle \frac{t_n^{-\sigma (\alpha +\eta )}}{\Gamma \left(\alpha \right)}}[\sum _{l=1}^{N_{exp}^{(1-\alpha )}}{w}_l^{(1-\alpha )}\sum _{k=0}^{n-2}{\int }_{t_k}^{t_{k+1}}{e}^{-s_l^{(1-\alpha )}(t_n^{\sigma }-s^{\sigma })}\left({\displaystyle \frac{t_{k+1}^{\sigma }-s^{\sigma }}{\tau }}g\left(t_k\right)+{\displaystyle \frac{s^{\sigma }-t_k^{\sigma }}{\tau }}g\left(t_{k+1}\right)\right)\mathrm{d}{s}^{\sigma }\hfill \\ \hfill & +{\int }_{t_{n-1}}^{t_n}{(t_n^{\sigma }-s^{\sigma })}^{\alpha -1}\left({\displaystyle \frac{t_n^{\sigma }-s^{\sigma }}{\tau }}g\left(t_{n-1}\right)+{\displaystyle \frac{s^{\sigma }-t_{n-1}^{\sigma }}{\tau }}g\left(t_n\right)\right)\mathrm{d}{s}^{\sigma }]\hfill \\ \hfill =& {\displaystyle \frac{t_n^{-\sigma (\alpha +\eta )}}{\Gamma \left(\alpha \right)}}[{\int }_{t_{n-1}}^{t_n}{(t_n^{\sigma }-s^{\sigma })}^{\alpha -1}(s^{\sigma }-t_{n-1}^{\sigma })\mathrm{d}{s}^{\sigma }·{\displaystyle \frac{g\left(t_n\right)}{\tau }}\hfill \\ \hfill & +\left(\sum _{l=1}^{N_{exp}^{(1-\alpha )}}{w}_l^{(1-\alpha )}{\int }_{t_{n-2}}^{t_{n-1}}{e}^{-s_l^{(1-\alpha )}(t_n^{\sigma }-s^{\sigma })}(s^{\sigma }-t_{n-2}^{\sigma })\mathrm{d}{s}^{\sigma }+{\int }_{t_{n-1}}^{t_n}{(t_n^{\sigma }-s^{\sigma })}^{\alpha }\mathrm{d}{s}^{\sigma }\right)·{\displaystyle \frac{g\left(t_{n-1}\right)}{\tau }}\hfill \\ \hfill & +\sum _{l=1}^{N_{exp}^{(1-\alpha )}}{w}_l^{(1-\alpha )}\sum _{k=1}^{n-2}\left({\int }_{t_k}^{t_{k+1}}{e}^{-s_l^{(1-\alpha )}(t_n^{\sigma }-s^{\sigma })}(t_{k+1}^{\sigma }-s^{\sigma })\mathrm{d}{s}^{\sigma }+{\int }_{t_{k-1}}^{t_k}{e}^{-s_l^{(1-\alpha )}(t_n^{\sigma }-s^{\sigma })}(s^{\sigma }-t_{k-1}^{\sigma })\mathrm{d}{s}^{\sigma }\right)·{\displaystyle \frac{g\left(t_k\right)}{\tau }}\hfill \\ \hfill & +\sum _{l=1}^{N_{exp}^{(1-\alpha )}}{w}_l^{(1-\alpha )}{\int }_0^{t_1}{e}^{-s_l^{(1-\alpha )}(t_n^{\sigma }-s^{\sigma })}(t_1^{\sigma }-s^{\sigma })\mathrm{d}{s}^{\sigma }·{\displaystyle \frac{g\left(t_0\right)}{\tau }}]\hfill \\ \hfill =& {\displaystyle \frac{t_n^{-\sigma (\alpha +\eta )}}{\Gamma \left(\alpha \right)}}\sum _{k=0}^n{\widehat{C}}_{n,k}^{(\sigma ,\alpha )}{\displaystyle \frac{g\left(t_k\right)}{\tau }}\triangleq {\phantom{.}}_{FEK}{\mathbb{D}}_{0,t;\sigma ,\eta }^{-\alpha }g\left(t_n\right),\hfill \end{array}$$

in which

$${\widehat{C}}_{n,k}^{(\sigma ,\alpha )}=\left\{\begin{array}{c}\sum _{l=1}^{N_{exp}^{(1-\alpha )}}{w}_l^{(1-\alpha )}{\int }_0^{t_1}{e}^{-s_l^{(1-\alpha )}(t_n^{\sigma }-s^{\sigma })}(t_1^{\sigma }-s^{\sigma })\mathrm{d}{s}^{\sigma },k=0,\hfill \\ \sum _{l=1}^{N_{exp}^{(1-\alpha )}}{w}_l^{(1-\alpha )}({\int }_{t_k}^{t_{k+1}}{e}^{-s_l^{(1-\alpha )}(t_n^{\sigma }-s^{\sigma })}(t_{k+1}^{\sigma }-s^{\sigma })\mathrm{d}{s}^{\sigma }\hfill \\ +{\int }_{t_{k-1}}^{t_k}{e}^{-s_l^{(1-\alpha )}(t_n^{\sigma }-s^{\sigma })}(s^{\sigma }-t_{k-1}^{\sigma })\mathrm{d}{s}^{\sigma }),1\le k\le n-2,\hfill \\ \sum _{l=1}^{N_{exp}^{(1-\alpha )}}{w}_l^{(1-\alpha )}{\int }_{t_{n-2}}^{t_{n-1}}{e}^{-s_l^{(1-\alpha )}(t_n^{\sigma }-s^{\sigma })}(s^{\sigma }-t_{n-2}^{\sigma })\mathrm{d}{s}^{\sigma }+{\displaystyle \frac{1}{\alpha +1}}{\tau }^{\alpha +1},k=n-1,\hfill \\ {\displaystyle \frac{1}{\alpha (\alpha +1)}}{\tau }^{\alpha +1},k=n.\hfill \end{array}\right.$$

Using the definition of $C_{n,k}^{(\sigma ,\alpha )}$ and ${\widehat{C}}_{n,k}^{(\sigma ,\alpha )},$ it is straightforward to show that

$$C_{n,n}^{(\sigma ,\alpha )}-{\widehat{C}}_{n,n}^{(\sigma ,\alpha )}=0;|C_{n,k}^{(\sigma ,\alpha )}-{\widehat{C}}_{n,k}^{(\sigma ,\alpha )}|\le ϵ,0\le k\le n-1.$$

Lemma 3.

The coefficient $\left\{{\widehat{C}}_{n,k}^{(\sigma ,\alpha )}{|}_{k=0}^n\right\}$ satisfies

$$\begin{array}{cc}\hfill & 2{\widehat{C}}_{n,n}^{(\sigma ,\alpha )}>{\widehat{C}}_{n,n-1}^{(\sigma ,\alpha )}>\dots >{\widehat{C}}_{n,2}^{(\sigma ,\alpha )}>{\widehat{C}}_{n,1}^{(\sigma ,\alpha )}>2{\widehat{C}}_{n,0}^{(\sigma ,\alpha )}>0;\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & {\widehat{C}}_{n,k}^{(\sigma ,\alpha )}-2{\widehat{C}}_{n,k-1}^{(\sigma ,\alpha )}+{\widehat{C}}_{n,k-2}^{(\sigma ,\alpha )}>0,3\le k\le n-1;\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill & 2{\widehat{C}}_{n,0}^{(\sigma ,\alpha )}-2{\widehat{C}}_{n,1}^{(\sigma ,\alpha )}+{\widehat{C}}_{n,2}^{(\sigma ,\alpha )}>0,{\widehat{C}}_{n,n-2}^{(\sigma ,\alpha )}-2{\widehat{C}}_{n,n-1}^{(\sigma ,\alpha )}+2{\widehat{C}}_{n,n}^{(\sigma ,\alpha )}>0.\hfill \end{array}$$

(23)

Proof. 

It is clear that all ${\widehat{C}}_{n,k}^{(\sigma ,\alpha )}$ instances are positive. For $1\le k\le n-2,$ the mean value theorem yields

$$\begin{array}{cc}\hfill & {\widehat{C}}_{n,k}^{(\sigma ,\alpha )}\hfill \\ \hfill =& \sum _{l=1}^{N_{exp}^{(1-\alpha )}}{w}_l^{(1-\alpha )}\left({\displaystyle \frac{1}{s_l^{(1-\alpha )}}}{\int }_{t_k^{\sigma }}^{t_{k+1}^{\sigma }}(t_{k+1}^{\sigma }-s)\mathrm{d}{e}^{-s_l^{(1-\alpha )}(t_n^{\sigma }-s)}+{\displaystyle \frac{1}{s_l^{(1-\alpha )}}}{\int }_{t_{k-1}^{\sigma }}^{t_k^{\sigma }}(s-t_{k-1}^{\sigma })\mathrm{d}{e}^{-s_l^{(1-\alpha )}(t_n^{\sigma }-s)}\right)\hfill \\ \hfill =& \sum _{l=1}^{N_{exp}^{(1-\alpha )}}{\displaystyle \frac{w_l^{(1-\alpha )}}{s_l^{(1-\alpha )}}}\left({\int }_{t_k^{\sigma }}^{t_{k+1}^{\sigma }}{e}^{-s_l^{(1-\alpha )}(t_n^{\sigma }-s)}\mathrm{d}s-{\int }_{t_{k-1}^{\sigma }}^{t_k^{\sigma }}{e}^{-s_l^{(1-\alpha )}(t_n^{\sigma }-s)}\mathrm{d}s\right)\hfill \\ \hfill =& \sum _{l=1}^{N_{exp}^{(1-\alpha )}}{\displaystyle \frac{w_l^{(1-\alpha )}}{s_l^{(1-\alpha )}}}{\int }_{t_k^{\sigma }}^{t_{k+1}^{\sigma }}{e}^{-s_l^{(1-\alpha )}(t_n^{\sigma }-s)}(1-e^{-s_l^{(1-\alpha )}\tau })\mathrm{d}s\hfill \\ \hfill =& \sum _{l=1}^{N_{exp}^{(1-\alpha )}}{\displaystyle \frac{w_l^{(1-\alpha )}}{s_l^{(1-\alpha )}}}(1-e^{-s_l^{(1-\alpha )}\tau })\tau e^{-s_l^{(1-\alpha )}(t_n^{\sigma }-{\xi }_k)},{\xi }_k\in (t_k^{\sigma },t_{k+1}^{\sigma }),\hfill \end{array}$$

which means that ${\widehat{C}}_{n,k}^{(\sigma ,\alpha )}$ increases monotonically with respect to k and is convex:

$$\begin{array}{cc}\hfill & {\widehat{C}}_{n,n-1}^{(\sigma ,\alpha )}-{\widehat{C}}_{n,n-2}^{(\sigma ,\alpha )}\hfill \\ \hfill =& \sum _{l=1}^{N_{exp}^{(1-\alpha )}}{w}_l^{(1-\alpha )}\left({\int }_{t_{n-2}^{\sigma }}^{t_{n-1}^{\sigma }}{e}^{-s_l^{(1-\alpha )}(t_n^{\sigma }-s)}(s-t_{n-2}^{\sigma })\mathrm{d}s-{\int }_{t_{n-3}^{\sigma }}^{t_{n-2}^{\sigma }}{e}^{-s_l^{(1-\alpha )}(t_n^{\sigma }-s)}(s-t_{n-3}^{\sigma })\mathrm{d}s\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{\alpha +1}}{\tau }^{\alpha +1}-\sum _{l=1}^{N_{exp}^{(1-\alpha )}}{w}_l^{(1-\alpha )}{\int }_{t_{n-2}^{\sigma }}^{t_{n-1}^{\sigma }}{e}^{-s_l^{(1-\alpha )}(t_n^{\sigma }-s)}(t_{n-1}^{\sigma }-s)\mathrm{d}s\hfill \\ \hfill \ge & \sum _{l=1}^{N_{exp}^{(1-\alpha )}}{w}_l^{(1-\alpha )}{\int }_{t_{n-2}^{\sigma }}^{t_{n-1}^{\sigma }}{e}^{-s_l^{(1-\alpha )}(t_n^{\sigma }-s)}(s-t_{n-2}^{\sigma })(1-e^{-s_l^{(1-\alpha )}\tau })\mathrm{d}s\hfill \\ \hfill & +{\displaystyle \frac{1}{\alpha +1}}{\tau }^{\alpha +1}-{\int }_{t_{n-2}^{\sigma }}^{t_{n-1}^{\sigma }}\left[ϵ+{(t_n^{\sigma }-s)}^{\alpha -1}\right](t_{n-1}^{\sigma }-s)\mathrm{d}s\hfill \\ \hfill \ge & {\displaystyle \frac{{\tau }^{\alpha +1}}{\alpha (\alpha +1)}}(1-\alpha )(2^{\alpha }-1)-{\displaystyle \frac{ϵ}{2}}{\tau }^2>0\mathrm{for}ϵ<{\displaystyle \frac{2{\tau }^{\alpha -1}}{\alpha (\alpha +1)}}(1-\alpha )(2^{\alpha }-1).\hfill \end{array}$$

Similarly, we have

$$\begin{array}{cc}\hfill & 2{\widehat{C}}_{n,n}^{(\sigma ,\alpha )}-{\widehat{C}}_{n,n-1}^{(\sigma ,\alpha )}\hfill \\ \hfill \ge & {\displaystyle \frac{2{\tau }^{\alpha +1}}{\alpha (\alpha +1)}}(2-2^{\alpha })-{\displaystyle \frac{ϵ}{2}}{\tau }^2>0\mathrm{for}ϵ<{\displaystyle \frac{4{\tau }^{\alpha -1}}{\alpha (\alpha +1)}}(2-2^{\alpha }).\hfill \end{array}$$

Furthermore, we have

$$\begin{array}{cc}\hfill & {\widehat{C}}_{n,1}^{(\sigma ,\alpha )}-2{\widehat{C}}_{n,0}^{(\sigma ,\alpha )}\hfill \\ \hfill \ge & {\int }_{t_1}^{t_2}{(t_n^{\sigma }-s^{\sigma })}^{\alpha -1}(t_2^{\sigma }-s^{\sigma })\mathrm{d}{s}^{\sigma }+{\int }_0^{t_1}{(t_n^{\sigma }-s^{\sigma })}^{\alpha -1}{s}^{\sigma }\mathrm{d}{s}^{\sigma }-2{\int }_0^{t_1}{(t_n^{\sigma }-s^{\sigma })}^{\alpha -1}(t_1^{\sigma }-s^{\sigma })\mathrm{d}{s}^{\sigma }\hfill \\ \hfill & -ϵ{\int }_{t_1}^{t_2}(t_2^{\sigma }-s^{\sigma })\mathrm{d}{s}^{\sigma }-ϵ{\int }_0^{t_1}{s}^{\sigma }\mathrm{d}{s}^{\sigma }-2ϵ{\int }_0^{t_1}(t_1^{\sigma }-s^{\sigma })\mathrm{d}{s}^{\sigma }\hfill \\ \hfill \ge & C_{n,1}^{(\sigma ,\alpha )}-2C_{n,0}^{(\sigma ,\alpha )}-2ϵ{\tau }^2>0\mathrm{for}ϵ<\left(C_{n,1}^{(\sigma ,\alpha )}-2C_{n,0}^{(\sigma ,\alpha )}\right)/\left(2{\tau }^2\right),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & 2{\widehat{C}}_{n,0}^{(\sigma ,\alpha )}-2{\widehat{C}}_{n,1}^{(\sigma ,\alpha )}+{\widehat{C}}_{n,2}^{(\sigma ,\alpha )}\hfill \\ \hfill \ge & 2C_{n,0}^{(\sigma ,\alpha )}-2C_{n,1}^{(\sigma ,\alpha )}+C_{n,2}^{(\sigma ,\alpha )}-4ϵ{\tau }^2>0\mathrm{for}ϵ<\left(2C_{n,0}^{(\sigma ,\alpha )}-2C_{n,1}^{(\sigma ,\alpha )}+C_{n,2}^{(\sigma ,\alpha )}\right)/\left(4{\tau }^2\right).\hfill \end{array}$$

In addition, one has

$$\begin{array}{cc}\hfill & {\widehat{C}}_{n,n-2}^{(\sigma ,\alpha )}-2{\widehat{C}}_{n,n-1}^{(\sigma ,\alpha )}+2{\widehat{C}}_{n,n}^{(\sigma ,\alpha )}\hfill \\ \hfill \ge & C_{n,n-2}^{(\sigma ,\alpha )}-2C_{n,n-1}^{(\sigma ,\alpha )}+2C_{n,n}^{(\sigma ,\alpha )}-2ϵ{\tau }^2\hfill \\ \hfill =& {\displaystyle \frac{{\tau }^{\alpha +1}}{\alpha (\alpha +1)}}(3^{\alpha +1}-2^{\alpha +3}+7)-2ϵ{\tau }^2>0\mathrm{for}ϵ<{\displaystyle \frac{3^{\alpha +1}-2^{\alpha +3}+7}{2\alpha (\alpha +2)}}{\tau }^{\alpha -1}.\hfill \end{array}$$

□

Theorem 2.

Suppose the function $g\in C^2[t_0,t_n],$$\alpha \in (0,1).$ We have

$$\begin{array}{cc}\hfill & {|}_{EK}{D}_{0,t;\sigma ,\eta }^{-\alpha }g\left(t\right){|}_{t=t_n}-{\phantom{.}}_{FEK}{\mathbb{D}}_{0,t;\sigma ,\eta }^{-\alpha }g\left(t_n\right)|\hfill \\ \hfill \le & {\displaystyle \frac{t_n^{-\sigma \eta }}{8\Gamma (1+\alpha )}}\underset{t_0<{\xi }_k\left(s\right)<t_n}{max}|{\delta }_{\sigma }^{2}g\left({\delta }_k\left(s\right)\right)|{\tau }^2+{\displaystyle \frac{ϵt_n^{-\sigma (\alpha +\eta -1)}}{\Gamma \left(\alpha \right)}}\underset{t_0\le t\le t_{n-1}}{max}\left|g\left(t\right)\right|,n=1,2,\dots ,N.\hfill \end{array}$$

Proof. 

The proof is provided as follows:

$$\begin{array}{cc}\hfill & {\phantom{.}}_{EK}{D}_{0,t;\sigma ,\eta }^{-\alpha }{g\left(t\right)|}_{t=t_n}-{\phantom{.}}_{FEK}{\mathbb{D}}_{0,t;\sigma ,\eta }^{-\alpha }g\left(t_n\right)\hfill \\ \hfill =& \left[{\phantom{.}}_{EK}{D}_{0,t;\sigma ,\eta }^{-\alpha }{g\left(t\right)|}_{t=t_n}-{\phantom{.}}_{EK}{\mathbb{D}}_{0,t;\sigma ,\eta }^{-\alpha }g\left(t_n\right)\right]+\left[{\phantom{.}}_{EK}{\mathbb{D}}_{0,t;\sigma ,\eta }^{-\alpha }g\left(t_n\right)-{\phantom{.}}_{FEK}{\mathbb{D}}_{0,t;\sigma ,\eta }^{-\alpha }g\left(t_n\right)\right]\hfill \\ \hfill =& r_n+{\widehat{r}}_n.\hfill \end{array}$$

(24)

With the help of Theorem 1, we obtain

$$|r_n|\le {\displaystyle \frac{t_n^{-\sigma \eta }}{8\Gamma (1+\alpha )}}\underset{t_0<{\xi }_k\left(s\right)<t_n}{max}\left|{\delta }_{\sigma }^{2}g\left({\delta }_k\left(s\right)\right)\right|{\tau }^2.$$

On the other hand, Lemma 2 yields

$$\begin{array}{ccc}|{\widehat{r}}_n|\hfill & =\hfill & {\displaystyle \frac{t_n^{-\sigma (\alpha +\eta )}}{\Gamma \left(\alpha \right)}}\sum _{k=0}^{n-2}{\int }_{t_k}^{t_{k+1}}{\Pi }_{1,k}g\left(s\right)|{(t_n^{\sigma }-s^{\sigma })}^{\alpha -1}-\sum _{l=1}^{N_{exp}^{(1-\alpha )}}{w}_l^{(1-\alpha )}{e}^{-s_l^{(1-\alpha )}(t_n^{\sigma }-s^{\sigma })}|\mathrm{d}{s}^{\sigma }\hfill \\ \hfill & \le \hfill & {\displaystyle \frac{ϵt_n^{-\sigma (\alpha +\eta )}}{\Gamma \left(\alpha \right)}}{\int }_{t_0^{\sigma }}^{t_{n-1}^{\sigma }}\left|g\left(s\right)\right|\mathrm{d}s\le {\displaystyle \frac{ϵt_n^{-\sigma (\alpha +\eta -1)}}{\Gamma \left(\alpha \right)}}\underset{t_0\le t\le t_{n-1}}{max}\left|g\left(t\right)\right|.\hfill \end{array}$$

Thus, we complete the proof. □

3.2. The Fast Difference Scheme

In this section, we present a fast difference scheme for problems (1)–(3). Similarly to the treatment of the direct difference scheme, applying (20) in the temporal direction, we obtain

$$\{\begin{array}{}\mathrm{(25)}& \begin{array}{c}{U}_i^n={\displaystyle \frac{t_n^{-\sigma (\alpha +\eta )}}{\Gamma \left(\alpha \right)}}\left[\sum _{l=1}^{N_{exp}^{(1-\alpha )}}{w}_l^{(1-\alpha )}{F}_{l,i}^n+{\displaystyle \frac{{\tau }^{\alpha }}{\alpha +1}}{t}_{n-1}^{\sigma \eta }{\delta }_x^2{U}_i^{n-1}+{\displaystyle \frac{{\tau }^{\alpha }}{\alpha (\alpha +1)}}{t}_n^{\sigma \eta }{\delta }_x^2{U}_i^n\right]\\ +F_i^n+{\widehat{R}}_i^n,1\le i\le M-1,1\le n\le N,\end{array}\hfill \mathrm{(26)}& F_{l,i}^1=0,1\le l\le N_{exp}^{(1-\alpha )},1\le i\le M-1,\hfill \mathrm{(27)}& \begin{array}{c}{F}_{l,i}^n=e^{-s_l^{(1-\alpha )\tau }}{F}_{l,i}^{n-1}+A_l{\displaystyle \frac{t_{n-2}^{\sigma \eta }}{\tau }}{\delta }_x^2{U}_i^{n-2}+B_l{\displaystyle \frac{t_{n-1}^{\sigma \eta }}{\tau }}{\delta }_x^2{U}_i^{n-1},\\ 1\le l\le N_{exp}^{(1-\alpha )},1\le i\le M-1,2\le n\le N,\end{array}\hfill \end{array}$$

where there exists a constant $c_2$ such that

$$|{\widehat{R}}_i^n|\le c_2({\tau }^2+h^2+ϵ),1\le i\le M-1,1\le n\le N.$$

(28)

Omitting the small term ${\widehat{R}}_i^n$ in (25), replacing the grid functions $\{U_i^n,F_{l,i}^n\}$ with their numerical approximations $\{u_i^n,f_{l,i}^n\}$, and observing the initial boundary value conditions (15) and (16), we arrive at the following fast difference scheme:

$$\{\begin{array}{}\mathrm{(29)}& \begin{array}{c}{u}_i^n={\displaystyle \frac{t_n^{-\sigma (\alpha +\eta )}}{\Gamma \left(\alpha \right)}}\left[{\displaystyle \sum _{l=1}^{N_{exp}^{(1-\alpha )}}}{w}_l^{(1-\alpha )}{f}_{l,i}^n+{\displaystyle \frac{{\tau }^{\alpha }}{\alpha +1}}{t}_{n-1}^{\sigma \eta }{\delta }_x^2{u}_i^{n-1}+{\displaystyle \frac{{\tau }^{\alpha }}{\alpha (\alpha +1)}}{t}_n^{\sigma \eta }{\delta }_x^2{u}_i^n\right]\\ +F_i^n,1\le i\le M-1,1\le n\le N,\end{array}\hfill \mathrm{(30)}& f_{l,i}^1=0,1\le l\le N_{exp}^{(1-\alpha )},1\le i\le M-1,\hfill \mathrm{(31)}& \begin{array}{c}{f}_{l,i}^n=e^{-s_l^{(1-\alpha )\tau }}{f}_{l,i}^{n-1}+A_l{\displaystyle \frac{t_{n-2}^{\sigma \eta }}{\tau }}{\delta }_x^2{u}_i^{n-2}+B_l{\displaystyle \frac{t_{n-1}^{\sigma \eta }}{\tau }}{\delta }_x^2{u}_i^{n-1},\\ 1\le l\le N_{exp}^{(1-\alpha )},1\le i\le M-1,2\le n\le N,\end{array}\hfill \mathrm{(32)}& u_i^0={\phi }_i,1\le i\le M-1,\hfill \mathrm{(33)}& u_0^n=0,u_M^n=0,0\le n\le N.\hfill \end{array}$$

For 3D problems ($M_x\times M_y\times M_z$ grid), a direct scheme costs $O\left(M_x{M}_y{M}_z{N}^2\right)$ in terms of storage. The fast algorithm reduces this to $O(M_x{M}_y{M}_{z}NlogN).$ While the fast algorithm reduces scaling, memory ($O(M_x{M}_y{M}_{z}logN)$) remains demanding. GPU parallelization and reduced-order models will be explored.

4. Numerical Analysis

This section provides numerical validation demonstrating the effectiveness of our novel discretization framework for Erdélyi–Kober integration operators. Through a detailed comparative analysis of the CPU times between the direct difference scheme ((17)–(19)) and the fast difference scheme ((29)–(33)), our computational experiments reveal that the accelerated algorithm significantly enhances computational efficiency, with complexity reduced from $O\left(N^2\right)$ to $O(NlogN)$. The absolute tolerance error $ϵ={10}^{-12}$ is adopted in our numerical simulations.

Example 1.

We chose the exact solution of problem (5) to be $u(x,t)=t^{\alpha +2-\sigma \eta }sinx.$ The right-hand-side function is determined via the exact solution as follows:

$$F(x,t)=\left[1+{\displaystyle \frac{\Gamma (1+\frac{\alpha +2}{\sigma })}{\Gamma (\alpha +1+\frac{\alpha +2}{\sigma })}}\right]t^{\alpha +2-\sigma \eta }sinx.$$

Let the final time be $T=1,$ and the spatial domain is $\Omega =(0,2\pi ).$ To examine the accuracy and efficiency of the difference schemes, the $L^2$-norm error

$$E(h,\tau )=\underset{0\le n\le N}{max}\parallel U^n-u^n\parallel$$

is recorded in each run, and the experimental orders are evaluated using

$$R_{\tau }={log}_2\left({\displaystyle \frac{E(h,2\tau )}{E(h,\tau )}}\right),R_h={log}_2\left({\displaystyle \frac{E(2h,\tau )}{E(h,\tau )}}\right).$$

The accuracy tests are performed by taking the parameters $\eta =0.2$ and $\sigma =0.9$ for three fractional orders $\alpha =0.1,0.5$, and $0.9.$ The error analyses of both the direct and accelerated difference schemes establish an asymptotic convergence order of $O({\tau }^2+h^2)$, with the theoretical upper bounds demonstrating remarkable agreement with the empirical convergence rates observed in our numerical simulations.

Table 2 shows the numerical accuracy and CPU time of the two difference schemes. To isolate temporal errors, we employ a refined spatial discretization with $h=\pi /2500.$ The numerical verification results confirm that our scheme enables second-order temporal accuracy, outperforming the first-order method reported by the authors of [25].

Table 2. Temporal errors and convergence orders for varying $\alpha$ values ($\sigma =0.9,\eta =0.2$, and $h=\pi /2500$).

$\mathit{\alpha }$	N	Direct Difference Scheme (17)–(19)			Fast Difference Scheme (29)–(33)
		$\mathit{E}(\mathit{h},\mathit{\tau })$	${\mathit{R}}_{\mathit{\tau }}$	CPU (s)	$\mathit{E}(\mathit{h},\mathit{\tau })$	${\mathit{R}}_{\mathit{\tau }}$	CPU (s)
0.1	80	1.02 × 10−5		34.98	1.02 × 10−5		33.46
	160	2.67 × 10−6	1.9323	78.63	2.67 × 10−6	1.9323	75.52
	320	6.60 × 10−7	2.0159	214.52	6.60 × 10−7	2.0159	161.22
	640	1.50 × 10−7	2.1320	325.09	1.50 × 10−7	2.1320	320.56
0.5	80	2.78 × 10−5		34.74	2.78 × 10−5		38.59
	160	6.97 × 10−6	1.9943	89.78	6.97 × 10−6	1.9943	78.55
	320	1.72 × 10−6	2.0195	155.16	1.72 × 10−6	2.0195	157.49
	640	3.97 × 10−7	2.1129	326.34	3.97 × 10−7	2.1129	316.44
0.9	80	3.09 × 10−5		53.27	3.09 × 10−5		33.52
	160	7.70 × 10−6	2.0035	141.53	7.70 × 10−6	2.0039	73.62
	320	1.91 × 10−6	2.0158	278.45	1.91 × 10−6	2.0147	154.67
	640	4.55 × 10−7	2.0661	468.05	4.46 × 10−7	2.0954	314.03

Table 2. Temporal errors and convergence orders for varying $\alpha$ values ($\sigma =0.9,\eta =0.2$, and $h=\pi /2500$).

$\mathit{\alpha }$	N	Direct Difference Scheme (17)–(19)			Fast Difference Scheme (29)–(33)
		$\mathit{E}(\mathit{h},\mathit{\tau })$	${\mathit{R}}_{\mathit{\tau }}$	CPU (s)	$\mathit{E}(\mathit{h},\mathit{\tau })$	${\mathit{R}}_{\mathit{\tau }}$	CPU (s)
0.1	80	1.02 × 10−5		34.98	1.02 × 10−5		33.46
	160	2.67 × 10−6	1.9323	78.63	2.67 × 10−6	1.9323	75.52
	320	6.60 × 10−7	2.0159	214.52	6.60 × 10−7	2.0159	161.22
	640	1.50 × 10−7	2.1320	325.09	1.50 × 10−7	2.1320	320.56
0.5	80	2.78 × 10−5		34.74	2.78 × 10−5		38.59
	160	6.97 × 10−6	1.9943	89.78	6.97 × 10−6	1.9943	78.55
	320	1.72 × 10−6	2.0195	155.16	1.72 × 10−6	2.0195	157.49
	640	3.97 × 10−7	2.1129	326.34	3.97 × 10−7	2.1129	316.44
0.9	80	3.09 × 10−5		53.27	3.09 × 10−5		33.52
	160	7.70 × 10−6	2.0035	141.53	7.70 × 10−6	2.0039	73.62
	320	1.91 × 10−6	2.0158	278.45	1.91 × 10−6	2.0147	154.67
	640	4.55 × 10−7	2.0661	468.05	4.46 × 10−7	2.0954	314.03

In addition, to assess parameter effects, we tested $(\sigma ,\eta )=\left\{\right(0.3,0.4),(0.6,0.3),(1,0.6\left)\right\}$ with $\alpha =0.5.$ Table 3 shows that time accuracy is still in the second-order form for different parameters $(\sigma$ and $\eta ).$

Table 3. Temporal errors and convergence orders for varying $(\sigma ,\eta )$ ($\alpha =0.5$ and $h=\pi /2500$).

$(\mathit{\sigma },\mathit{\eta })$	N	Direct Difference Scheme (17)–(19)			Fast Difference Scheme (29)–(33)
		$\mathit{E}(\mathit{h},\mathit{\tau })$	${\mathit{R}}_{\mathit{\tau }}$	CPU (s)	$\mathit{E}(\mathit{h},\mathit{\tau })$	${\mathit{R}}_{\mathit{\tau }}$	CPU (s)
(0.3, 0.4)	80	2.02 × 10−4		8.46	2.02 × 10−4		8.05
	160	5.16 × 10−5	1.9706	19.86	5.16 × 10−5	1.9706	17.18
	320	1.30 × 10−5	1.9891	39.27	1.30 × 10−5	1.9891	40.60
	640	3.18 × 10−6	2.0288	83.10	3.18 × 10−6	2.0288	80.38
(0.6, 0.3)	80	6.05 × 10−5		7.64	6.05 × 10−5		7.31
	160	1.52 × 10−5	1.9926	16.00	1.52 × 10−5	1.9926	15.13
	320	3.71 × 10−6	2.0336	36.30	3.71 × 10−6	2.0336	34.93
	640	8.12 × 10−7	2.1934	76.77	8.12 × 10−7	2.1934	70.73
(1, 0.6)	80	2.78 × 10−5		7.23	2.78 × 10−5		7.84
	160	7.45 × 10−6	2.0000	15.25	7.45 × 10−6	1.9000	16.12
	320	2.00 × 10−6	1.9000	34.22	2.00 × 10−6	1.9000	36.38
	640	5.35 × 10−7	1.9999	71.86	5.35 × 10−7	1.9000	75.73

To enhance readability, we also provide the error curve of the direct differential scheme (17)–(19) and fast difference scheme (29)–(33) for $\sigma =0.9,\alpha =0.5,$ and $\eta =0.2,$ see Figure 1. This also verifies the validity of the two difference schemes.

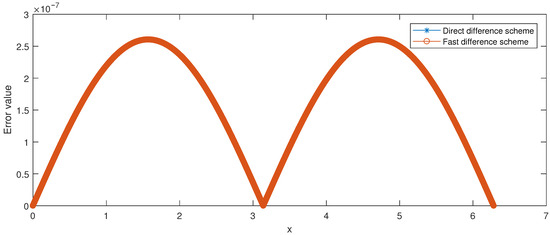
Figure 1. The error curve of the direct differential scheme (17)–(19) and fast difference scheme (29)–(33) for $\sigma =0.9,\alpha =0.5,\eta =0.2,$$\tau =1/640$, and $h=\pi /2500$.

Next, we tested the numerical accuracy and corresponding CPU times of two difference schemes in space. We fixed a fine temporal step size $\tau =1/\mathrm{20,000}$, such that the spatial errors dominate the temporal errors. Table 4 records the numerical results of two difference schemes when solving the example for different $\alpha$ values. Compared to the results reported by the authors of [23], which lack error bounds, our approach reduces spatial errors. Furthermore, the computational cost of the direct difference scheme is largely higher than that of the fast difference scheme, which also reflects the high efficiency of the fast algorithm.

Table 4. Spatial errors and convergence orders for varying $\alpha$ values ($\sigma =0.9,\eta =0.2,\tau =1/20,000$).

$\mathit{\alpha }$	M	Direct Difference Scheme (17)–(19)			Fast Difference Scheme (29)–(33)
		$\mathit{E}(\mathit{h},\mathit{\tau })$	${\mathit{R}}_{\mathit{h}}$	CPU (s)	$\mathit{E}(\mathit{h},\mathit{\tau })$	${\mathit{R}}_{\mathit{h}}$	CPU (s)
0.1	8	2.44 × 10−2		2315.75	2.44 × 10−2		0.85
	6	6.09 × 10−3	2.0038	5880.66	6.09 × 10−3	2.0038	0.95
	32	1.52 × 10−3	2.0010	3411.01	1.52 × 10−3	2.0010	1.08
	64	3.80 × 10−4	2.0003	2217.43	3.80 × 10−4	2.0003	2.06
0.5	8	1.78 × 10−2		2214.54	1.78 × 10−2		0.88
	16	4.46 × 10−3	1.9968	5235.00	4.46 × 10−3	1.9968	0.99
	32	1.12 × 10−3	1.9992	2617.88	1.12 × 10−3	1.9992	1.14
	64	2.79 × 10−4	1.9998	5548.97	2.79 × 10−4	1.9998	2.02
0.9	8	1.10 × 10−2		2791.54	1.10 × 10−2		1.25
	16	2.78 × 10−3	1.9896	2885.54	2.78 × 10−3	1.9899	1.12
	32	6.95 × 10−4	1.9974	2475.10	6.94 × 10−4	1.9987	1.41
	64	1.74 × 10−4	1.9994	2438.99	1.73 × 10−4	2.0044	2.32

Table 4. Spatial errors and convergence orders for varying $\alpha$ values ($\sigma =0.9,\eta =0.2,\tau =1/20,000$).

$\mathit{\alpha }$	M	Direct Difference Scheme (17)–(19)			Fast Difference Scheme (29)–(33)
		$\mathit{E}(\mathit{h},\mathit{\tau })$	${\mathit{R}}_{\mathit{h}}$	CPU (s)	$\mathit{E}(\mathit{h},\mathit{\tau })$	${\mathit{R}}_{\mathit{h}}$	CPU (s)
0.1	8	2.44 × 10−2		2315.75	2.44 × 10−2		0.85
	6	6.09 × 10−3	2.0038	5880.66	6.09 × 10−3	2.0038	0.95
	32	1.52 × 10−3	2.0010	3411.01	1.52 × 10−3	2.0010	1.08
	64	3.80 × 10−4	2.0003	2217.43	3.80 × 10−4	2.0003	2.06
0.5	8	1.78 × 10−2		2214.54	1.78 × 10−2		0.88
	16	4.46 × 10−3	1.9968	5235.00	4.46 × 10−3	1.9968	0.99
	32	1.12 × 10−3	1.9992	2617.88	1.12 × 10−3	1.9992	1.14
	64	2.79 × 10−4	1.9998	5548.97	2.79 × 10−4	1.9998	2.02
0.9	8	1.10 × 10−2		2791.54	1.10 × 10−2		1.25
	16	2.78 × 10−3	1.9896	2885.54	2.78 × 10−3	1.9899	1.12
	32	6.95 × 10−4	1.9974	2475.10	6.94 × 10−4	1.9987	1.41
	64	1.74 × 10−4	1.9994	2438.99	1.73 × 10−4	2.0044	2.32

Example 2.

We also test problem (5) with the exact solution $u(x,t)=t^{\alpha +3/2}sin\pi x.$ Thus, the right-hand-side function is as follows:

$$F(x,t)=\left[1+{\displaystyle \frac{{\pi }^2\Gamma (1+\eta +\frac{\alpha +3/2}{\sigma })}{\Gamma (\alpha +\eta +1+\frac{\alpha +3/2}{\sigma })}}\right]t^{\alpha +3/2}sin\pi x.$$

We chose $T=1$ and $L=1.$ Table 5 and Table 6 verify the temporal and spatial accuracy of the direct difference scheme ((17)–(19)) and the fast difference scheme ((29)–(33)), respectively. It can be observed that the convergence accuracy of all schemes is second-order in nature, which is consistent with the theoretical results. Furthermore, the obvious advantages of the fast algorithm can also be observed in Table 6.

Table 5. Temporal errors and convergence orders for varying $\alpha$ values ($\sigma =0.5,\eta =0.7$, and $h=1/2500$).

$\mathit{\alpha }$	N	Direct Difference Scheme (17)–(19)			Fast Difference Scheme (29)–(33)
		$\mathit{E}(\mathit{h},\mathit{\tau })$	${\mathit{R}}_{\mathit{\tau }}$	CPU (s)	$\mathit{E}(\mathit{h},\mathit{\tau })$	${\mathit{R}}_{\mathit{\tau }}$	CPU (s)
0.1	80	5.97 × 10−5		7.58	5.97 × 10−5		8.22
	160	1.61 × 10−5	1.8940	16.10	1.61 × 10−5	1.8940	17.78
	320	4.21 × 10−6	1.9310	38.82	4.21 × 10−6	1.9310	39.76
	640	1.03 × 10−6	2.0305	83.76	1.03 × 10−6	2.0305	80.96
0.5	80	1.82 × 10−4		7.85	1.82 × 10−4		8.15
	160	4.60 × 10−5	1.9824	16.41	4.60 × 10−5	1.9824	17.67
	320	1.15 × 10−5	1.9960	38.31	1.15 × 10−5	1.9960	39.44
	640	2.82 × 10−6	2.0304	78.76	2.82 × 10−6	2.0304	79.82
0.9	80	2.32 × 10−4		10.04	2.32 × 10−4		8.24
	160	5.79 × 10−5	2.0005	20.53	5.79 × 10−5	2.0007	17.01
	320	1.44 × 10−5	2.0058	37.52	1.44 × 10−5	2.0052	38.03
	640	3.54 × 10−6	2.0256	79.13	3.50 × 10−6	2.0415	77.87

Table 6. Spatial errors and convergence orders for varying $\alpha$ values ($\sigma =0.5,\eta =0.7,$ and $\tau =1/20,000$).

$\mathit{\alpha }$	M	Direct Difference Scheme (17)–(19)			Fast Difference Scheme (29)–(33)
		$\mathit{E}(\mathit{h},\mathit{\tau })$	${\mathit{R}}_{\mathit{h}}$	CPU (s)	$\mathit{E}(\mathit{h},\mathit{\tau })$	${\mathit{R}}_{\mathit{h}}$	CPU (s)
0.1	8	1.16 × 10−2		1987.44	1.16 × 10−2		0.92
	6	2.88 × 10−3	2.0069	2001.05	2.88 × 10−3	2.0069	0.97
	32	7.19 × 10−4	2.0017	2009.06	7.19 × 10−4	2.0017	1.20
	64	1.80 × 10−4	2.0004	2049.78	1.80 × 10−4	2.0004	2.24
0.5	8	1.04 × 10−2		2015.86	1.04 × 10−2		0.92
	16	2.60 × 10−3	2.0056	2014.54	2.60 × 10−3	2.0057	0.99
	32	6.50 × 10−4	2.0014	1994.91	6.50 × 10−4	2.0014	1.24
	64	1.62 × 10−4	2.0004	2015.61	1.62 × 10−4	2.0003	2.19
0.9	8	8.36 × 10−3		2114.65	8.35 × 10−3		1.19
	16	2.08 × 10−3	2.0034	2109.88	2.08 × 10−3	2.0052	1.35
	32	5.21 × 10−4	2.0009	2123.43	5.17 × 10−4	2.0080	1.55
	64	1.30 × 10−4	2.0002	2763.77	1.27 × 10−4	2.0293	2.45

The computational results in Table 2, Table 3, Table 4, Table 5 and Table 6 reveal the asymmetric efficiency gains of the fast difference scheme: while the acceleration effect is minimal when refining the temporal resolution (increasing N), it becomes pronounced when refining the spatial resolution (increasing M values). This asymmetry arises from the distinct computational complexities of the direct and fast schemes. In fact, the speed-up becomes significant for $N\ge {10}^4.$ For small N values, the direct scheme is preferred due to the overhead associated with SOE initialization.

The direct scheme requires $O\left(N^2\right)$ operations per spatial grid point due to non-local temporal convolution, whereas the fast scheme reduces this to $O(NlogN)$. However, for moderate N values (e.g., $N\le 640$ in Table 2 and Table 5), the overhead associated with evaluating exponential sums in the fast scheme (including recursive updates and memory access) offsets the theoretical complexity advantage. Consequently, the CPU time reduction remains marginal. In contrast, spatial refinement (increasing M values) linearly scales the computational load for both schemes. The fast scheme’s reduced cost per time step (from N to $O(logN)$ then translates to significant gains when N is large (e.g., $N=20,000$ in Table 4 and Table 6), as evidenced by the speed-up factors exceeding $1000\times$ for $\alpha =0.1$ and $M=8$ (2315.75 s vs. 0.85 s).

Furthermore, the $\alpha$ dependence of CPU times arises from two factors. (i) Direct Scheme: The computing coefficient $C_{n,k}^{(\sigma ,\alpha )}$ involves fractional power $t^{\sigma \alpha }.$ The computational cost of these operations varies slightly with $\alpha ,$ especially near $\alpha =0$ or 1. (ii) Fast Scheme: The number of exponential terms, $N_{exp}$, increases as $\alpha \to 1$ (as $\gamma =1-\alpha \to 0$), slowing kernel decay and requiring more terms for accurate approximation (Lemma 2). This explains the reduced speed-up at $\alpha =0.9$ (Table 2, $N=640$: 314.03 s vs. direct’s 468.05 s) compared to $\alpha =0.1$ (320.56 s vs. 325.09 s).

These insights highlight the fast scheme’s superiority for large-scale simulations, particularly in high-resolution spatial domains or long-time integration.

The following are some advantages of the proposed methods:

• High accuracy: A temporal second-order scheme for a Caputo-type Erdélyi–Kober operator is obtained.
• Rigor: Coefficient analysis (Lemmas 1 and 3) and error bounds (Theorems 1 and 2) surpass heuristic approaches [24,25].
• Efficiency: Near-optimal memory $O(logN)$ is obtained, and $O(NlogN)$ is computed.

5. Concluding Remarks

This study developed two spatiotemporal second-order difference schemes for solving time-fractional diffusion equations with the Caputo-type Erdélyi–Kober operator. For temporal discretization, an L1-type formula with rigorous error analyses was employed, while the spatial component utilizes a standard second-order centered difference scheme with numerically validated convergence. The combined approach enables optimal accuracy in both dimensions. Crucially, we established a complete theoretical foundation by proving the essential properties of the discrete kernel coefficients (Lemmas 1 and 3) and deriving truncation error estimates (Theorems 1 and 2). These results form the core framework supporting the scheme’s stability and convergence for the Erdélyi–Kober operator.

The proposed method offers significant advantages:

(i)

Unified framework: It seamlessly addresses both generalized operators $(\sigma \ne 1)$ and classical Caputo cases $(\sigma =1),$ enhancing applicability across scenarios requiring adaptive scaling in time or space.

(ii)

Computational efficiency: A fast sum-of-exponential algorithm reduces the complexity to $O(NlogN)$ and memory to $O(logN).$ For example, simulations with $N={10}^6$ time steps have computation times reduced from 1 month (direct scheme) to $<1$ day on a four-core CPU, enabling large-scale fractional PDE modeling.

While specialized, the Caputo-type Erdélyi–Kober operator is critical for modeling multi-scale systems such as anomalous transport in heterogeneous media, e.g., contaminant diffusion in fractured rocks [9,10].

While the present study establishes efficient numerical methods for time-fractional diffusion equations with Caputo-type Erdélyi–Kober operators, several extensions warrant future investigation. First, rigorous stability and convergence proofs building upon the proven coefficients’ properties will be developed. Second, while addressing computational bottlenecks for 3D extensions remains critical despite the fast algorithm’s efficiency, high-dimensional extensions require hybrid CPU–GPU architectures to manage memory bottlenecks. Third, our analysis assumes solution regularity $u\in C^{(4,2)}.$ Theorem 1 indicates that weakened regularity (e.g., $u\notin C^2[0,T]$) reduces the temporal order below second-order. Future research will address low-regularity scenarios via graded meshes [32]$t_k={(k/N)}^{r}T$, with $r>1$ recovering $O\left(N^{-2}\right)$ convergence. In addition, adaptive schemes that balance $\tau$ and h near singularities are also planned. Fourth, extension to nonlinear models (e.g., $f\left(u\right)=u^p$) requires further analysis. Beyond these methodological enhancements, interdisciplinary applications leveraging recent advances in applied mathematics offer promising directions, including the following:

(a)

Modeling HIV dynamics with fractional operators: The anomalous diffusion framework proposed here could be extended to analyze HIV infection models with logistic target-cell growth and cell-to-cell transmission [33]. By replacing classical derivatives with Caputo-type Erdélyi–Kober operators, one may capture memory effects in viral spread dynamics, such as delayed immune responses or heterogeneous infection rates. This aligns with the non-local nature of fractional calculus in biological systems.

(b)

Fractional center analysis: Classical center conditions [34,35] characterize equilibrium points with periodic orbits in ODEs. Extending this to fractional-order switching systems (using our operator) may reveal memory-dependent stability transitions, leveraging Lemma 1’s positivity.

(c)

Bifurcations under fractional dynamics: Symmetric vector fields [27,36] exhibit Hopf bifurcations near nilpotent singularities. Our fast summation algorithm could efficiently compute such bifurcations for fractional perturbations, linking geometric methods with non-local calculus.

These future research directions could bridge fractional PDEs with dynamical systems theory, opening interdisciplinary avenues for both numerical analysis and applied modeling.