Exact Solitary Wave Solutions and Sensitivity Analysis of the Fractional (3+1)D KdV–ZK Equation
Abstract
1. Introduction
2. Methodology
- Step 1: Consider NLPDE as follows:
- Step 2: Utilize the following traveling wave transformation:
- Step 4: The solution of (3) is as follows:
- Step 5: The solutions of (5) are given as follows:
- Case I: If and , we have:
- Case II: If and , we have:
- Case III: If and , afterward:
- Case IV: If and , afterward:
3. Execution of Methodology
- Case I: If , and , we have
- Case II: If and , we have
- Case III: If and , we have:
- Case IV: If and , we have
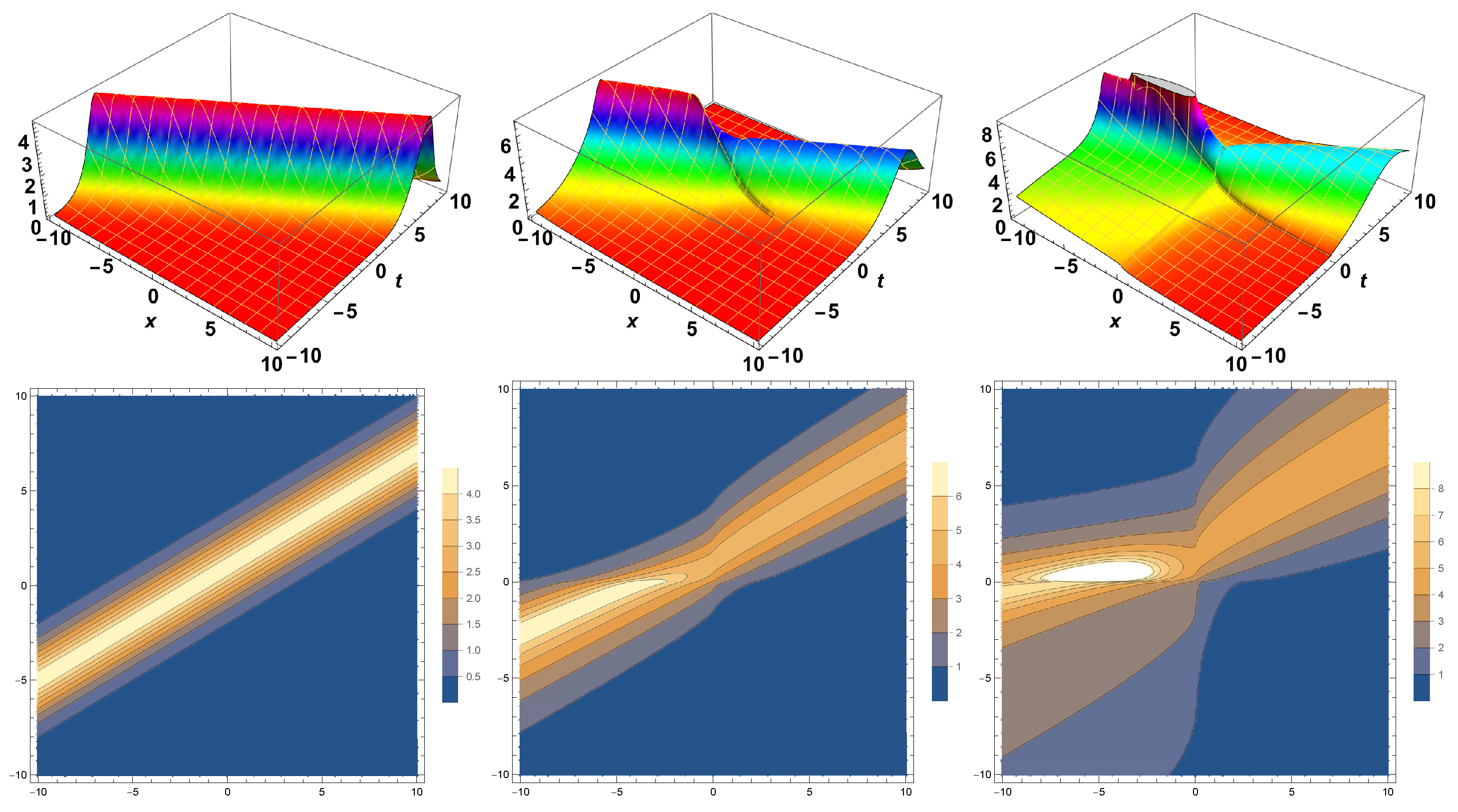
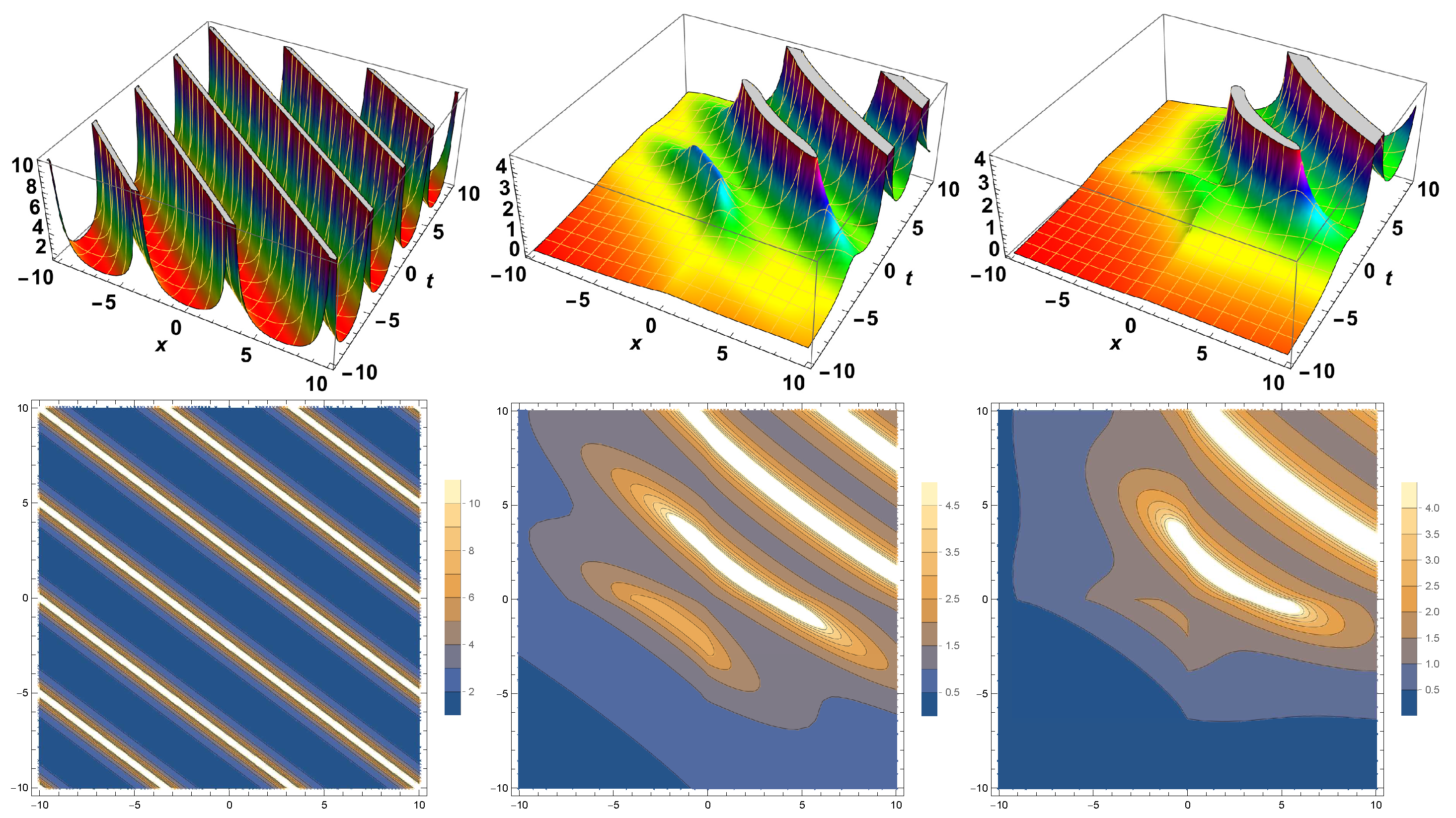
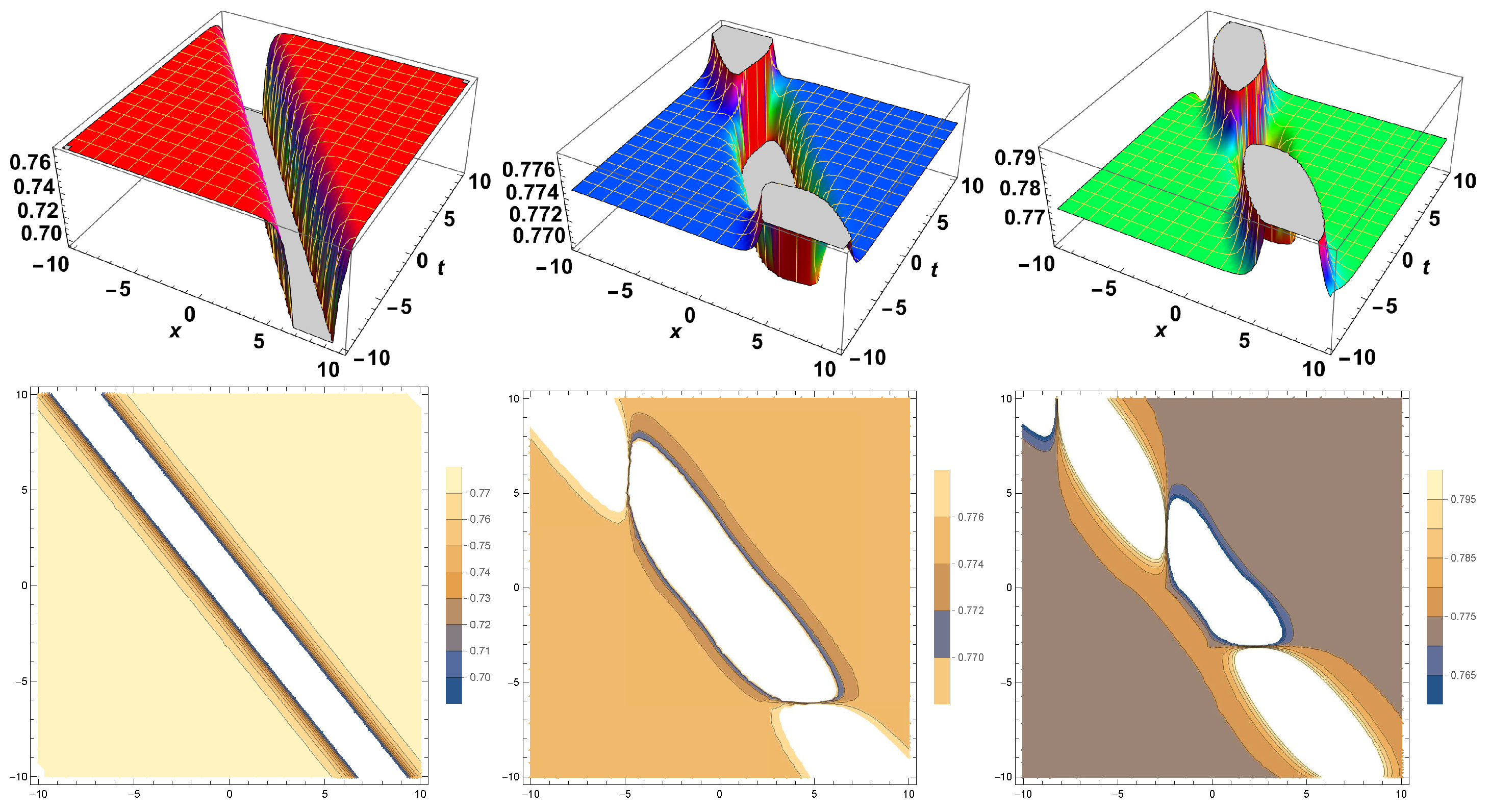
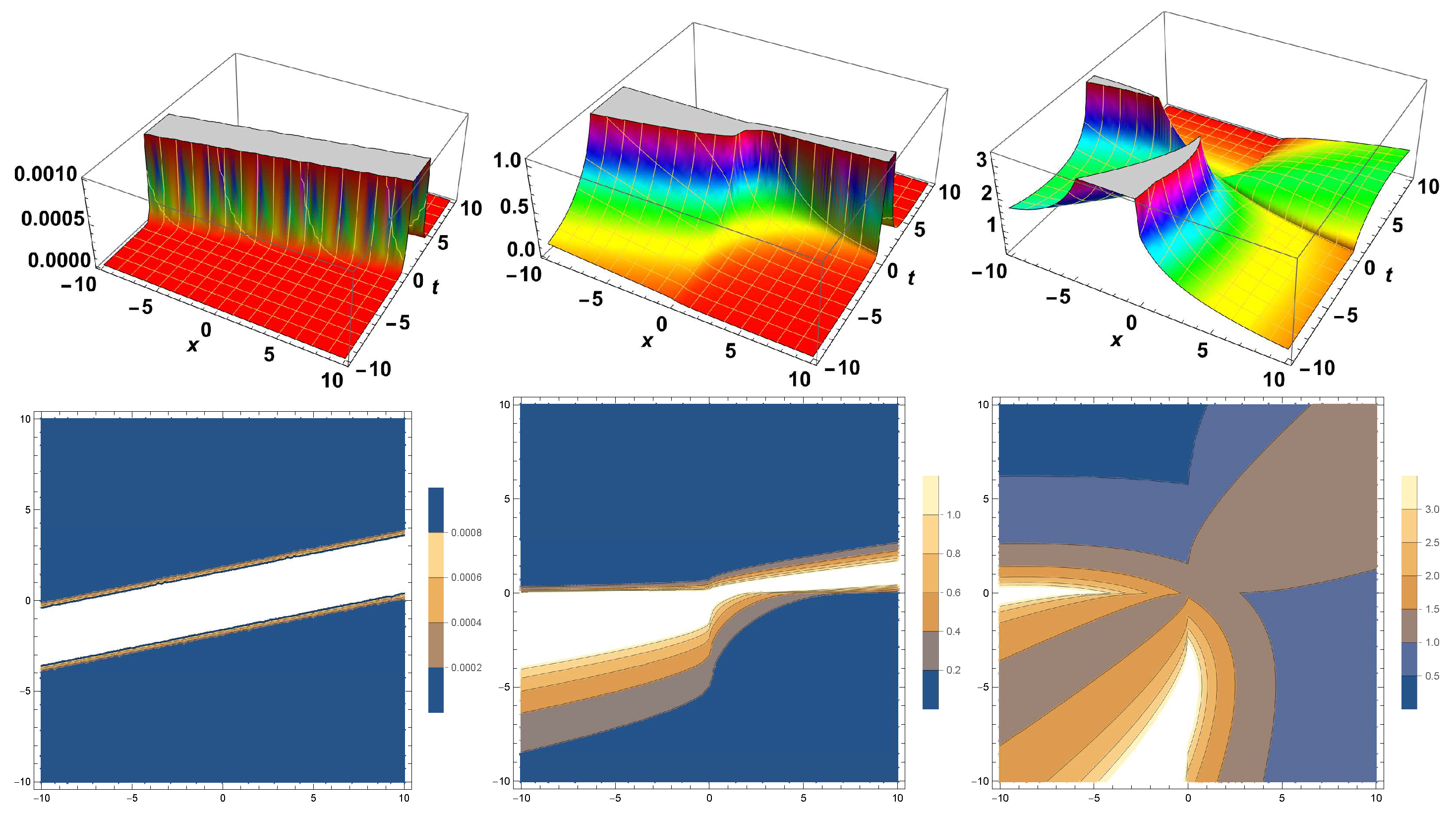
4. Simulation and Discussion
Results Comparison
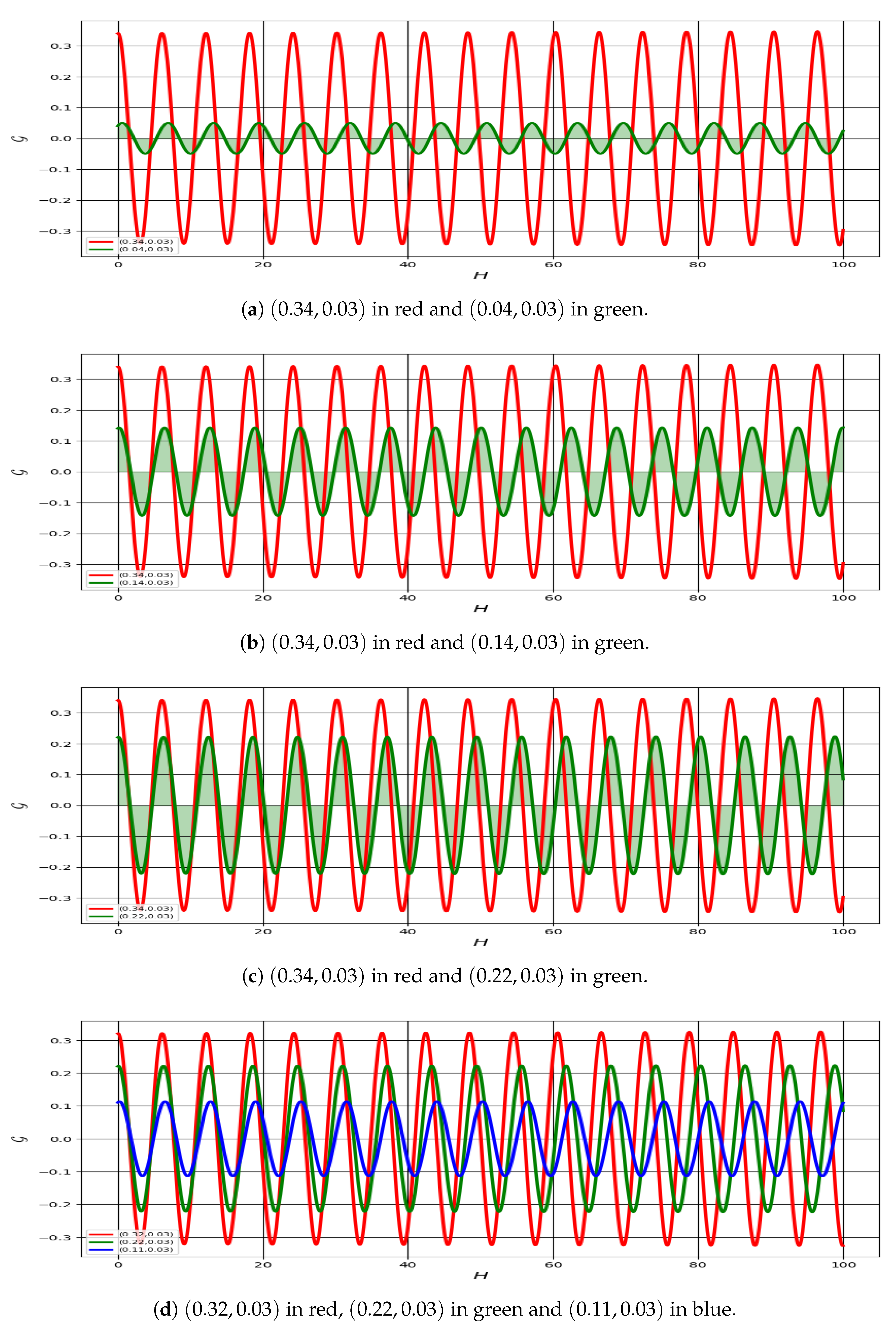
5. Sensitivity Analysis
6. Conclusions
7. Future Scope of Study
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bao, W.; Liu, H.; Wang, F.; Du, J.; Wang, Y.; Li, H.; Ye, X. Keyhole critical failure criteria and variation rule under different thicknesses and multiple materials in K-TIG welding. J. Manuf. Processes 2024, 126, 48–59. [Google Scholar] [CrossRef]
- Yi, X.; Zhao, R.; Lin, Y. The impact of nighttime car body lighting on pedestrians’ distraction: A virtual reality simulation based on bottom-up attention mechanism. Saf. Sci. 2024, 180, 106633. [Google Scholar] [CrossRef]
- Zhang, Z.; Lin, M.; Li, D.; Wu, R.; Lin, R.; Yang, C. An AUV-enabled dockable platform for long-term dynamic and static monitoring of marine pastures. IEEE J. Ocean. Eng. 2025, 50, 276–293. [Google Scholar] [CrossRef]
- Zhao, L.; Weng, W.; Ni, M.; Shen, H.; Zhang, S.; Chen, Y.; Wang, Y. Rubidium salt can effectively relieve the symptoms of DSS-induced ulcerative colitis. Biomed. Pharmacother. 2024, 181, 117574. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.; Liang, J.; Chen, X.; Lin, J.; Wei, J.; Huang, D.; Zhao, L. Isolation and identification of chemical constituents from Zhideke Granules by ultra-performance liquid chromatography coupled with mass spectrometry. J. Anal. Methods Chem. 2020, 2020, 8889607. [Google Scholar] [CrossRef] [PubMed]
- Sobolev, S.L. Partial Differential Equations of Mathematical Physics: Adiwes International Series in Mathematics; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Harisa, S.A.; Ravichandran, C.; Nisar, K.S.; Faried, N.; Morsy, A. New exploration of operators of fractional neutral integro-differential equations in Banach spaces through the application of the topological degree concept. AIMS Math 2022, 7, 15741–15758. [Google Scholar] [CrossRef]
- Murugesan, M.; Muthaiah, S.; Vadivel, R.; Unyong, B. Existence of Solutions for Coupled System of Sequential Liouville–Caputo-Type Fractional Integrodifferential Equations. Fractal Fract. 2023, 7, 800. [Google Scholar] [CrossRef]
- Naz, S.; Rani, A.; Ul Hassan, Q.M.; Ahmad, J.; Rehman, S.U.; Shakeel, M. Dynamic study of new soliton solutions of time-fractional longitudinal wave equation using an analytical approach. Int. J. Mod. Phys. B 2024, 38, 2450420. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Khatun, M.M.; Algolam, M.S.; Sidaoui, R.; Akbar, M.A. Analytical Solitary Wave Solutions of Fractional Tzitzéica Equation Using Expansion Approach: Theoretical Insights and Applications. Fractal Fract. 2025, 9, 438. [Google Scholar] [CrossRef]
- Guner, O.; Aksoy, E.; Bekir, A.; Cevikel, A.C. Different methods for (3+1)-dimensional space–time fractional modified KdV–Zakharov–Kuznetsov equation. Comput. Math. Appl. 2016, 71, 1259–1269. [Google Scholar] [CrossRef]
- Demontis, F. Exact solutions of the modified Korteweg-de Vries equation. Theor. Math. Phys. 2011, 168, 886–897. [Google Scholar] [CrossRef]
- Ansari, A.R.; Jhangeer, A.; Imran, M.; Beenish; Inc, M. A study of self-adjointness, Lie analysis, wave structures, and conservation laws of the completely generalized shallow water equation. Eur. Phys. J. Plus 2024, 139, 489. [Google Scholar] [CrossRef]
- Jhangeer, A.; Ansari, A.R.; Imran, M.; Riaz, M.B. Conserved quantities and sensitivity analysis influence of damping effect in ferrites materials. Alex. Eng. J. 2024, 86, 298–310. [Google Scholar] [CrossRef]
- Samreen, M. Analytical solutions and dynamical insights of the modified Benjamin–Bona–Mahony equation with applications in nonlinear optics. J. Appl. Math. Comput. 2025. [Google Scholar] [CrossRef]
- Beenish; Samreen, M.; Alshammari, F.S. Exploring Solitary Wave Solutions of the Generalized Integrable Kadomtsev–Petviashvili Equation via Lie Symmetry and Hirota’s Bilinear Method. Symmetry 2025, 17, 710. [Google Scholar] [CrossRef]
- Jumarie, G. Modified Riemann-Liouville derivative and fractional Taylor series of nondifferentiable functions further results. Comput. Math. Appl. 2006, 51, 1367–1376. [Google Scholar] [CrossRef]
- Jumarie, G. Table of some basic fractional calculus formulae derived from a modified Riemann–Liouville derivative for non-differentiable functions. Appl. Math. Lett. 2009, 22, 378–385. [Google Scholar] [CrossRef]
- Liu, W.; Chen, K. The functional variable method for finding exact solutions of some nonlinear time-fractional differential equations. Pramana 2013, 81, 377–384. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Shirzadi, A. The first integral method for modified Benjamin–Bona–Mahony equation. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1759–1764. [Google Scholar] [CrossRef]
- Bekir, A.; Guner, O.; Cevikel, A. The exp-function method for some time-fractional differential equations. IEEE/CAA J. Autom. Sin. 2016, 4, 315–321. [Google Scholar] [CrossRef]
- Ibragimov, N.H.; Ibragimov, R.N. Applications of Lie group analysis to mathematical modelling in natural sciences. Math. Model. Nat. Phenom. 2012, 7, 52–65. [Google Scholar] [CrossRef][Green Version]
- Yomba, E. The extended Fan’s sub-equation method and its application to KdV–MKdV, BKK and variant Boussinesq equations. Phys. Lett. A 2005, 336, 463–476. [Google Scholar] [CrossRef]
- Odabasi, M.; Misirli, E. On the solutions of the nonlinear fractional differential equations via the modified trial equation method. Math. Methods Appl. Sci. 2018, 41, 904–911. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Simplest equation method to look for exact solutions of nonlinear differential equations. Chaos Solitons Fractals 2005, 24, 1217–1231. [Google Scholar] [CrossRef]
- Akram, S.; ur Rahman, M.; AL-Essa, L.A. A comprehensive dynamical analysis of (2+1)-dimensional nonlinear electrical transmission line model with Atangana–Baleanu derivative. Phys. Lett. A 2025, 555, 130762. [Google Scholar] [CrossRef]
- San, S.; Beenish; Alshammari, F.S. Analytical and Dynamical Study of Solitary Waves in a Fractional Magneto-Electro-Elastic System. Fractal Fract. 2025, 9, 309. [Google Scholar] [CrossRef]
- Yang, Z.Q.; Hou, K.P.; Guo, T.T. Research on time-varying behavior of cement grouts of different water-cement ratios. Appl. Mech. Mater. 2011, 71, 4398–4401. [Google Scholar] [CrossRef]
- Yang, Z.Q.; Hou, K.P.; Cheng, Y.; Yang, B. Study of column-hemispherical penetration grouting mechanism based on power-law fluid. Chin. J. Rock Mech. Eng. 2014, 33, 3840–3846. [Google Scholar]
- Yang, Z.Q.; Zhu, Y.Y.; Zou, D.S. Formation conditions and risk evaluation of glacial debris flow disasters along International Karakorum Highway (KKH). Ital. J. Eng. Geol. Environ. 2011, 1031–1037. [Google Scholar] [CrossRef]
- Yang, Z.; Xiong, J.; Zhao, X.; Meng, X.; Wang, S.; Li, R.; Xu, H. Column-hemispherical penetration grouting mechanism for Newtonian fluid considering the tortuosity of porous media. Processes 2023, 11, 1737. [Google Scholar] [CrossRef]
- Gao, J. Friction coefficient estimation of the clutch in automatic transmission based on improved persistent excitation condition. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; IEEE: Piscataway, NJ, USA, 2018; p. 5647. [Google Scholar]
- Wu, Z.; Wang, J.; Zhang, X.; Cao, M.; Wu, A. Preliminary studies on diagnostic cast of peptic ulcer based on saliva proteome and bioinformatics. In Proceedings of the 2011 4th International Conference on Biomedical Engineering and Informatics (BMEI), Shanghai, China, 15–17 October 2011; IEEE: Piscataway, NJ, USA, 2011; Volume 3, pp. 1597–1600. [Google Scholar]
- Wu, Z.Z.; Wang, J.G.; Zhang, X.L.; Cao, M.Q. Preliminary study on saliva proteomics of different furs in digestive system diseases. In Proceedings of the 2009 IEEE International Symposium on IT in Medicine & Education, Jinan, China, 14–16 August 2009; IEEE: Piscataway, NJ, USA, 2009; Volume 1, pp. 56–61. [Google Scholar]
- Xiang, D.; He, D.; Sun, H.; Gao, P.; Zhang, J.; Ling, J. HCMPE-Net: An unsupervised network for underwater image restoration with multi-parameter estimation based on homology constraint. Opt. Laser Technol. 2025, 186, 112616. [Google Scholar] [CrossRef]
- Guan, Y.; Cui, Z.; Zhou, W. Reconstruction in off-axis digital holography based on hybrid clustering and the fractional Fourier transform. Opt. Laser Technol. 2025, 186, 112622. [Google Scholar] [CrossRef]
- Ni, Z.L.; Ma, J.S.; Liu, Y.; Li, B.H.; Nazarov, A.A.; Li, H.; Wang, X.X. Numerical analysis of ultrasonic spot welding of Cu/Cu joints. J. Mater. Eng. Perform. 2025. [Google Scholar] [CrossRef]
- Fang, Q.; Sun, Q.; Ge, J.; Wang, H.; Qi, J. Multidimensional Engineering of Nanoconfined Catalysis: Frontiers in Carbon-Based Energy Conversion and Utilization. Catalysts 2025, 15, 477. [Google Scholar] [CrossRef]
- Mace, R.L.; Hellberg, M.A. The Korteweg–de Vries–Zakharov–Kuznetsov equation for electron-acoustic waves. Phys. Plasmas 2001, 8, 2649–2656. [Google Scholar] [CrossRef]
- Kopçasız, B. Qualitative analysis and optical soliton solutions galore: Scrutinizing the (2+1)-dimensional complex modified Korteweg–de Vries system. Nonlinear Dyn. 2024, 112, 21321–21341. [Google Scholar] [CrossRef]
| Aspect | Current Study | Guner et al. [11] |
|---|---|---|
| Analytical Approach | Sardar sub-equation (SSEM); exact wave solutions | The exp-function method, the generalized Kudryashov method and -expansion method are applied. |
| Sensitivity Analysis | Includes Galilean-based sensitivity analysis | Sensitivity analysis are not discuss in Literature |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, A.; Alshammari, F.S.; Yasin, S.; Beenish. Exact Solitary Wave Solutions and Sensitivity Analysis of the Fractional (3+1)D KdV–ZK Equation. Fractal Fract. 2025, 9, 476. https://doi.org/10.3390/fractalfract9070476
Khan A, Alshammari FS, Yasin S, Beenish. Exact Solitary Wave Solutions and Sensitivity Analysis of the Fractional (3+1)D KdV–ZK Equation. Fractal and Fractional. 2025; 9(7):476. https://doi.org/10.3390/fractalfract9070476
Chicago/Turabian StyleKhan, Asif, Fehaid Salem Alshammari, Sadia Yasin, and Beenish. 2025. "Exact Solitary Wave Solutions and Sensitivity Analysis of the Fractional (3+1)D KdV–ZK Equation" Fractal and Fractional 9, no. 7: 476. https://doi.org/10.3390/fractalfract9070476
APA StyleKhan, A., Alshammari, F. S., Yasin, S., & Beenish. (2025). Exact Solitary Wave Solutions and Sensitivity Analysis of the Fractional (3+1)D KdV–ZK Equation. Fractal and Fractional, 9(7), 476. https://doi.org/10.3390/fractalfract9070476









