A Structure-Preserving Finite Difference Scheme for the Nonlinear Space Fractional Sine-Gordon Equation with Damping Based on the T-SAV Approach
Abstract
1. Introduction
2. Equivalent System Based on T-SAV Approach
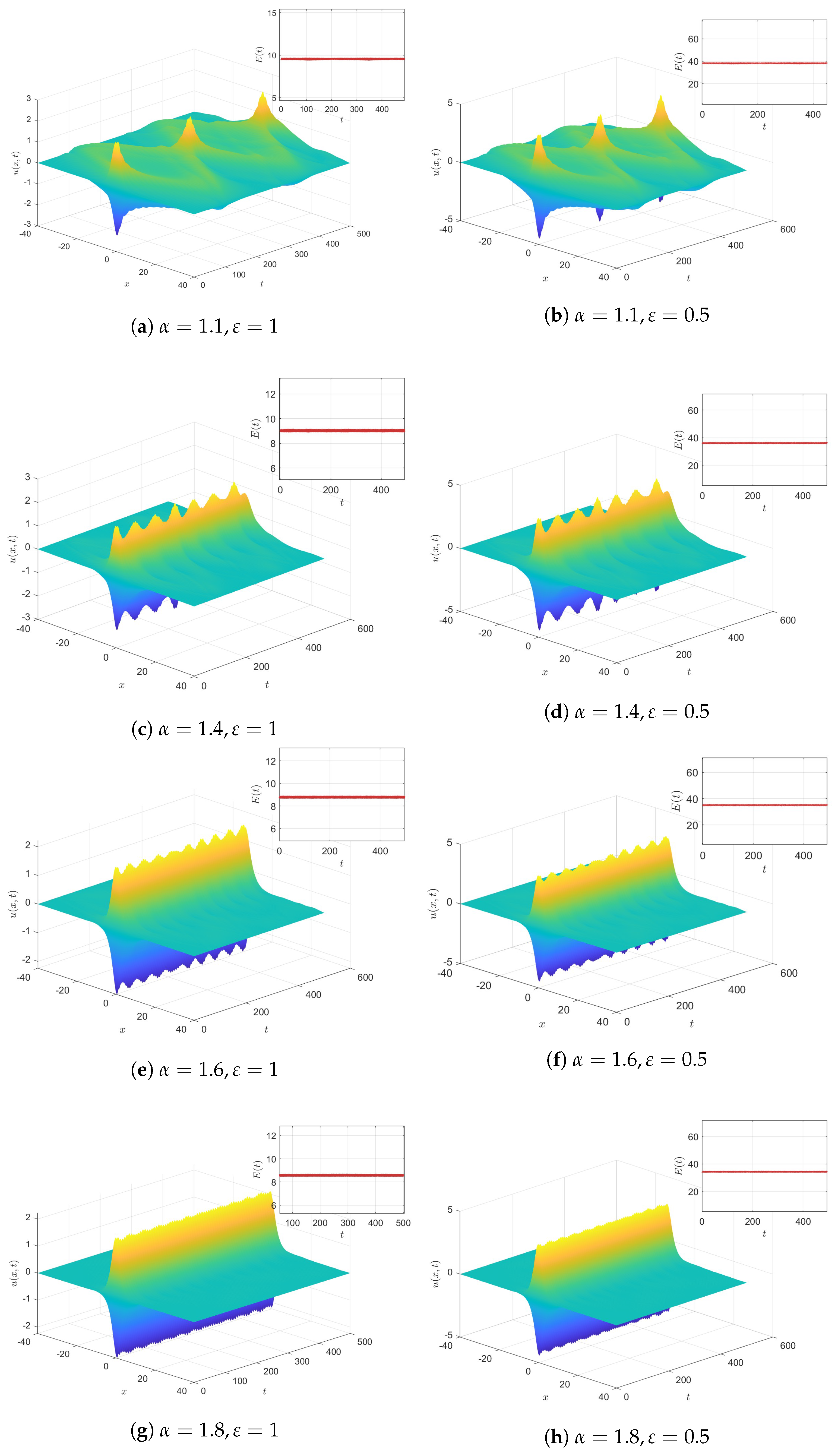
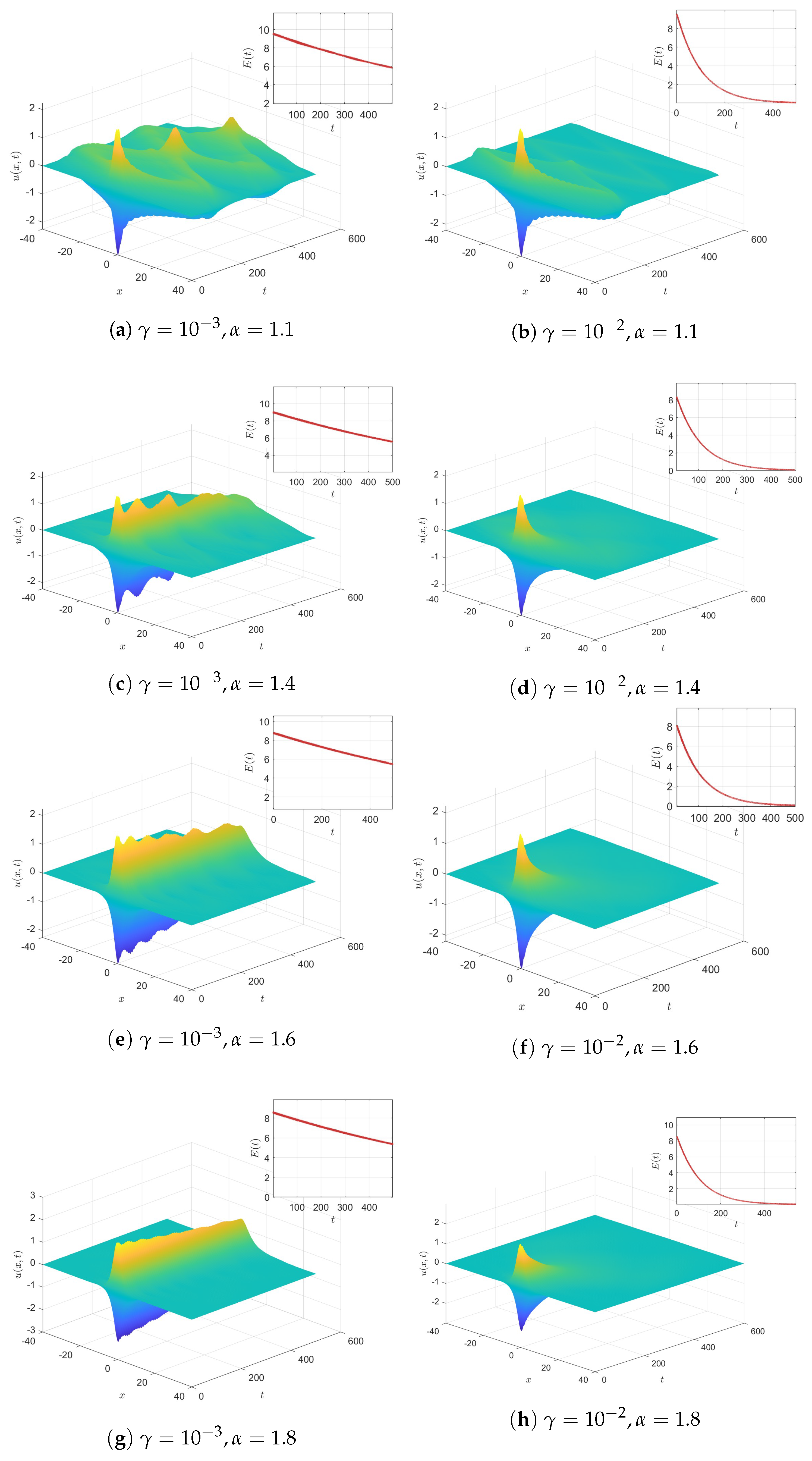
- When , it holds that , indicating energy conservation in the system.
- When , the energy dissipates over time, demonstrating the physical effect of the damping term.
3. Structure-Preserving Finite Difference Scheme
3.1. Approximations for Spatial Fractional Laplacian
3.2. Derivation of Structure-Preserving Difference Scheme
4. Numerical Analysis
4.1. Discrete Energy Dissipation Law
4.2. Boundedness
4.3. Convergence
5. Numerical Examples
5.1. Convergence Rate
5.2. Energy Dissipation or Conservation
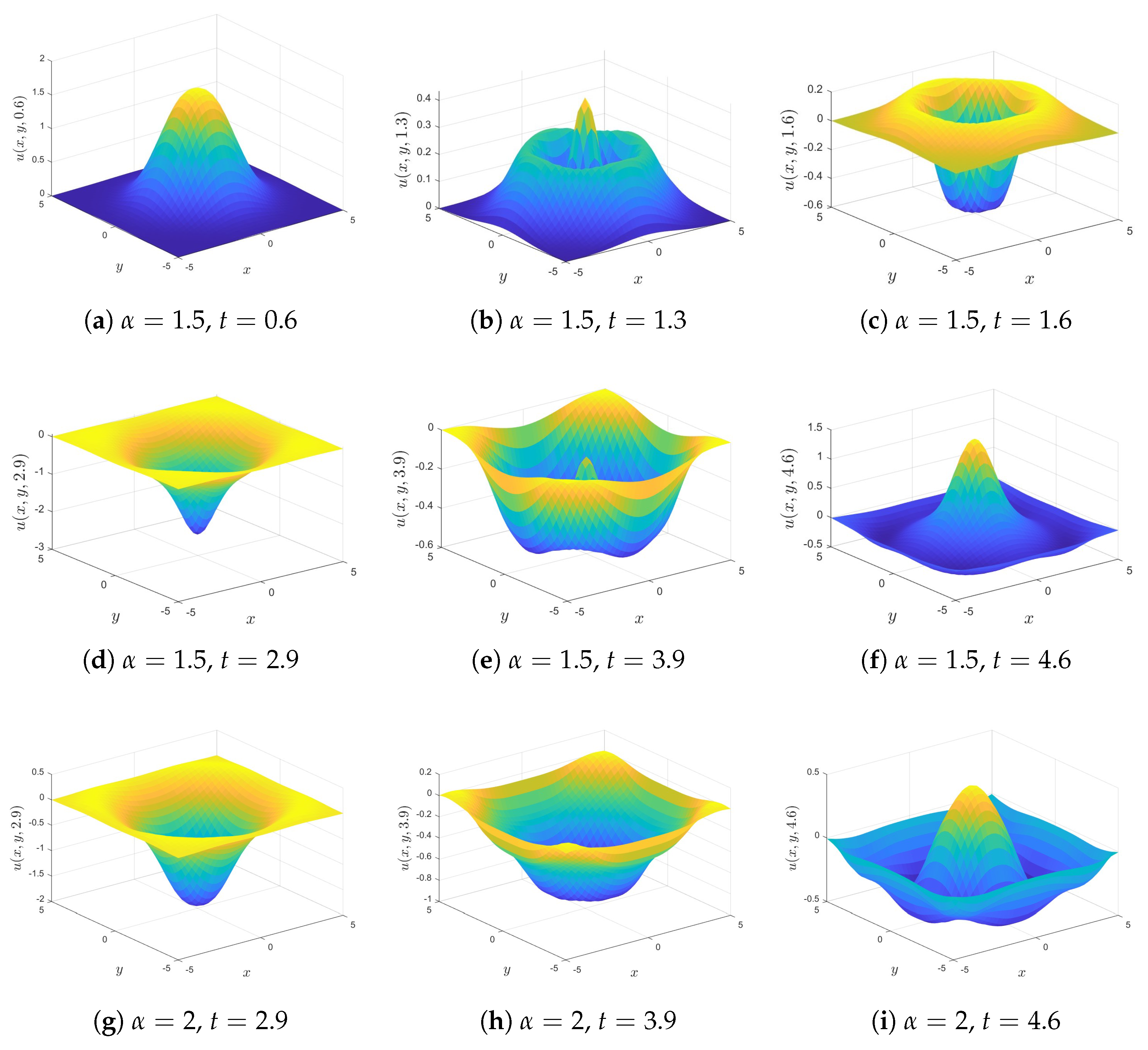
5.3. Two-Dimensional Problem
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NSFSGE | Nonlinear space fractional sine-Gordon equation |
| T-SAV | Triangular Scalar Auxiliary Variable |
| EOC | Experimental order of convergence |
References
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Gu, X.M.; Zhao, Y.L.; Zhao, X.L.; Carpentieri, B.; Huang, Y.Y. A note on parallel preconditioning for the all-at-once solution of Riesz fractional diffusion equations. Numer. Math. Theory Methods Appl. 2021, 14, 1003–1026. [Google Scholar] [CrossRef]
- Zhao, J.J.; Jiang, X.Z.; Xu, Y. A kind of generalized backward differentiation formulae for solving fractional differential equations. Appl. Math. Comput. 2022, 419, 126872. [Google Scholar] [CrossRef]
- Fu, Y.Y.; Cai, W.J.; Wang, Y.S. A linearly implicit structure-preserving scheme for the fractional Sine-Gordon equation based on the IEQ approach. Appl. Math. Comput. 2021, 404, 126281. [Google Scholar] [CrossRef]
- Korabel, N.; Zaslavsky, G.M.; Tarasov, V.E. Coupled oscillators with power-law interaction and their fractional dynamics analogues. Commun. Nonlinear Sci. Numer. Simul. 2007, 12, 1003–1017. [Google Scholar] [CrossRef]
- Macías-Díaz, J.E. Numerical study of the process of nonlinear supratransmission in Riesz space-fractional Sine-Gordon equations. Commun. Nonlinear Sci. Numer. Simul. 2017, 46, 89–102. [Google Scholar] [CrossRef]
- Amabili, M.; Balasubramanian, P.; Ferrari, G. Nonlinear vibrations and damping of fractional viscoelastic rectangular plates. Nonlinear Dyn. 2021, 103, 1–29. [Google Scholar] [CrossRef]
- Jia, J.H.; Zheng, X.C.; Wang, H. Numerical discretization and fast approximation of a variably distributed-order fractional wave equation. ESAIM. Math. Model. Numer. Anal. 2021, 55, 2211–2232. [Google Scholar] [CrossRef]
- Tarasov, V.E.; Aifantis, E.C. Non-standard extensions of gradient elasticity: Fractional non-locality, memory and fractality. Int. J. Eng. Sci. 2014, 83, 1–22. [Google Scholar] [CrossRef]
- Huang, Y.; Oberman, A. Numerical methods for the fractional Laplacian: A finite difference-quadrature approach. SIAM J. Numer. Anal. 2014, 52, 3056–3084. [Google Scholar] [CrossRef]
- Lischke, A.; Pang, G.F.; Gulian, M.; Song, F.Y.; Glusa, C.; Zheng, X.N.; Mao, Z.P.; Cai, W.; Meerschaert, M.M.; Ainsworth, M. What is the fractional Laplacian? A comparative review with new results. J. Comput. Phys. 2019, 404, 109023. [Google Scholar] [CrossRef]
- Jia, J.; Jiang, X.; Chi, X. Improved uniform error bounds of Lawson-type exponential integrator method for long-time dynamics of the high-dimensional space fractional Sine-Gordon equation. Numer. Algorithms 2024, 97, 1179–1214. [Google Scholar] [CrossRef]
- Hu, D.D.; Cai, W.J.; Xu, Z.Z.; Bo, Y.H.; Wang, Y.S. Dissipation-preserving Fourier pseudo-spectral method for the space fractional nonlinear Sine-Gordon equation with damping. Math. Comput. Simul. 2021, 188, 1–18. [Google Scholar] [CrossRef]
- Nikan, O.; Avazzadeh, Z.; Machado, J.A.T. Numerical investigation of fractional nonlinear sine-Gordon and Klein-Gordon models arising in relativistic quantum mechanics. Eng. Anal. Bound. Elem. 2020, 120, 223–237. [Google Scholar] [CrossRef]
- Ran, M.; Zhang, C. Compact difference scheme for a class of fractional-in-space nonlinear damped wave equations in two space dimensions. Comput. Math. Appl. 2016, 71, 1151–1162. [Google Scholar] [CrossRef]
- Alfimov, G.; Pierantozzi, T.; Vázquez, L. Numerical study of a fractional Sine-Gordon equation. J. Phys. A Math. Gen. 2004, 37, 10767–10781. [Google Scholar] [CrossRef]
- Mirzaei, D.; Dehghan, M. Boundary element solution of the two-dimensional Sine-Gordon equation using continuous linear elements. Eng. Anal. Bound. Elem. 2009, 33, 12–24. [Google Scholar] [CrossRef]
- Achouri, T.; Simos, T.E. Conservative finite difference scheme for the nonlinear fourth-order wave equation. Appl. Math. Comput. 2019, 359, 121–131. [Google Scholar] [CrossRef]
- Tlili, K. On the L∞-convergence of two conservative finite difference schemes for fourth-order nonlinear strain wave equations. Comput. Appl. Math. 2021, 40, 1–31. [Google Scholar] [CrossRef]
- Yang, J.X.; Kim, J. The stabilized-trigonometric scalar auxiliary variable approach for gradient flows and its efficient schemes. J. Eng. Math. 2021, 129, 1–26. [Google Scholar] [CrossRef]
- Shen, J.; Xu, J. Convergence and error analysis for the scalar auxiliary variable schemes to gradient flows. SIAM J. Numer. Anal. 2018, 56, 2895–2912. [Google Scholar] [CrossRef]
- Hou, D.M.; Azaiez, M.; Xu, C.J. A variant of scalar auxiliary variable approaches for gradient flows. J. Comput. Phys. 2019, 395, 26. [Google Scholar] [CrossRef]
- Shen, J.; Xu, J.; Yang, J. A new class of efficient and robust energy stable schemes for gradient flows. J. Sci. Comput. 2017, 73, 218–245. [Google Scholar] [CrossRef]
- Fu, Y.Y.; Hu, D.D.; Wang, Y.S. High-order structure-preserving algorithms for the multi-dimensional fractional nonlinear Schrödinger equation based on the SAV approach. Math. Comput. Simul. 2021, 185, 1–20. [Google Scholar] [CrossRef]
- Fu, Y.Y.; Cai, W.J.; Wang, Y.S. A structure-preserving algorithm for the fractional nonlinear Schrödinger equation based on the SAV approach. Commun. Nonlinear Sci. Numer. Simul. 2019, 72, 105–121. [Google Scholar] [CrossRef]
- Hao, Z.; Zhang, Z.; Du, R. Fractional centered difference scheme for high-dimensional integral fractional Laplacian. J. Comput. Phys. 2021, 424, 109851. [Google Scholar] [CrossRef]
- Hu, D.; Cai, W.; Fu, Y.; Wang, Y. Fast dissipation-preserving difference scheme for nonlinear generalized wave equations with the integral fractional Laplacian. Commun. Nonlinear Sci. Numer. Simul. 2021, 99, 105786. [Google Scholar] [CrossRef]
- Tian, Z.H.; Ran, M.H.; Liu, Y. Higher-order energy-preserving difference scheme for the fourth-order nonlinear strain wave equation. Comput. Math. Appl. 2023, 128, 221–235. [Google Scholar] [CrossRef]
- Scherer, R.; Kalla, S.L.; Tang, Y.; Huang, J. The Grunwald-Letnikov method for fractional differential equations. Comput. Math. Appl. 2011, 62, 902–917. [Google Scholar] [CrossRef]
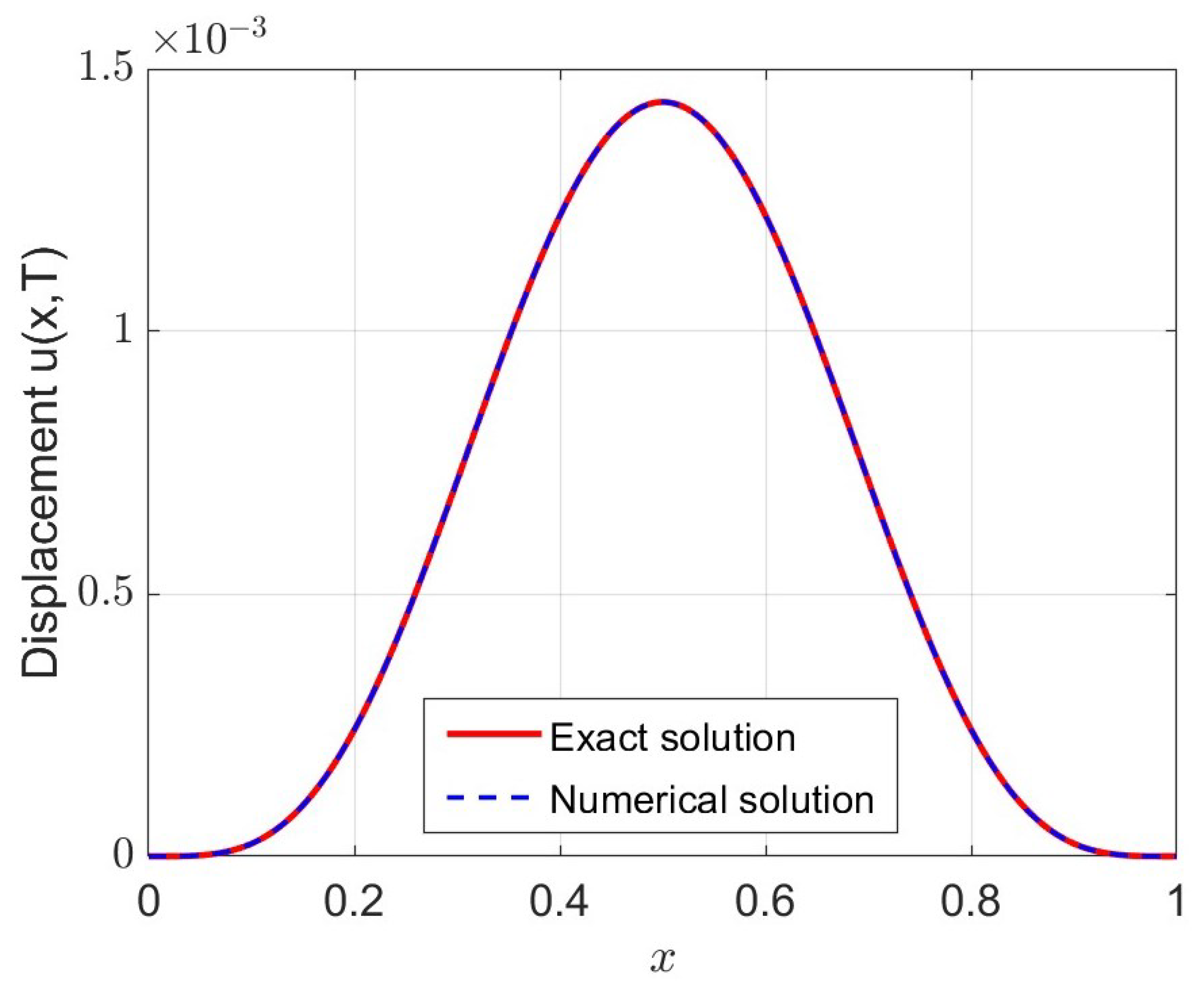
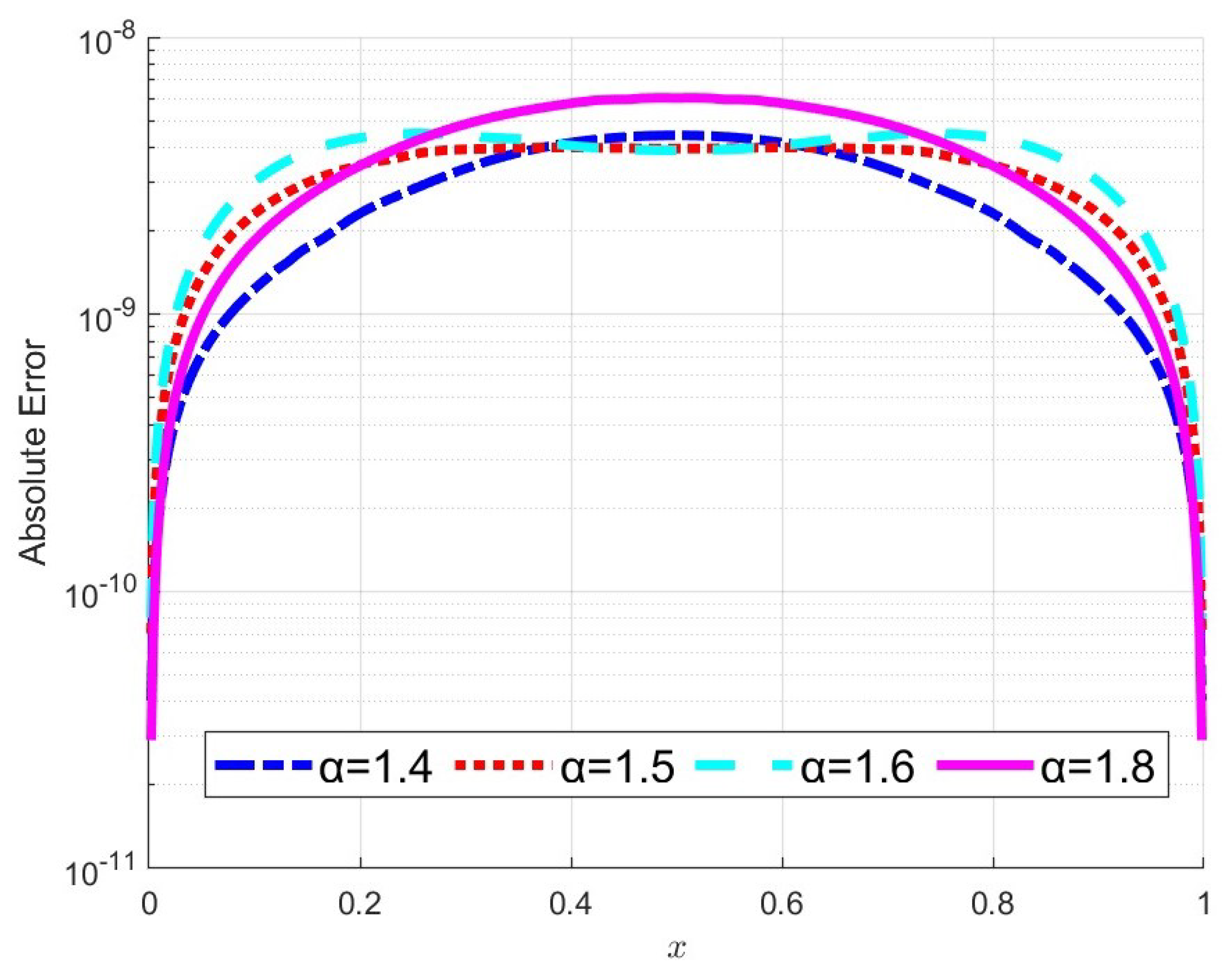
| Present | EGL | Present | EGL | Present | EGL | ||||||||
| EOC | EOC | EOC | EOC | EOC | EOC | ||||||||
| 0 | 1/32 | – | – | – | – | – | – | ||||||
| 1/64 | 1.17 | 0.90 | 2.24 | 0.95 | 2.55 | 0.98 | |||||||
| 1/128 | 1.90 | 0.85 | 2.22 | 0.86 | 2.40 | 0.84 | |||||||
| 1/256 | 1.97 | 0.61 | 2.08 | 0.54 | 2.16 | 0.66 | |||||||
| 1/512 | 1.99 | 0.72 | 2.02 | 0.68 | 2.05 | 0.75 | |||||||
| 0.5 | 1/32 | – | – | – | – | – | – | ||||||
| 1/64 | 1.87 | 0.52 | 2.21 | 0.35 | 2.57 | 0.42 | |||||||
| 1/128 | 1.87 | 0.61 | 2.23 | 0.68 | 2.41 | 0.63 | |||||||
| 1/256 | 1.96 | 0.51 | 2.09 | 0.47 | 2.16 | 0.52 | |||||||
| 1/512 | 1.99 | 0.81 | 2.02 | 0.78 | 2.05 | 0.80 | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, P.; Li, Y. A Structure-Preserving Finite Difference Scheme for the Nonlinear Space Fractional Sine-Gordon Equation with Damping Based on the T-SAV Approach. Fractal Fract. 2025, 9, 455. https://doi.org/10.3390/fractalfract9070455
Jiang P, Li Y. A Structure-Preserving Finite Difference Scheme for the Nonlinear Space Fractional Sine-Gordon Equation with Damping Based on the T-SAV Approach. Fractal and Fractional. 2025; 9(7):455. https://doi.org/10.3390/fractalfract9070455
Chicago/Turabian StyleJiang, Penglin, and Yu Li. 2025. "A Structure-Preserving Finite Difference Scheme for the Nonlinear Space Fractional Sine-Gordon Equation with Damping Based on the T-SAV Approach" Fractal and Fractional 9, no. 7: 455. https://doi.org/10.3390/fractalfract9070455
APA StyleJiang, P., & Li, Y. (2025). A Structure-Preserving Finite Difference Scheme for the Nonlinear Space Fractional Sine-Gordon Equation with Damping Based on the T-SAV Approach. Fractal and Fractional, 9(7), 455. https://doi.org/10.3390/fractalfract9070455






