Quantitative Fractal Analysis of Fracture Mechanics and Damage Evolution in Recycled Aggregate Concrete Beams: Investigation of Dosage-Dependent Mechanical Response Under Incremental Load

Abstract

This study investigated the fracture behavior of concrete beams with recycled coarse aggregate (RCA) and recycled fine aggregate (RFA) using the box-counting method to measure crack fractal dimensions under load. Beams with RCA showed higher fractal dimensions due to RCA’s lower elastic moduli and compressive strengths, resulting in reduced deformation resistance, ductility, and more late-stage crack propagation. A direct proportional relationship existed between RCA/RFA replacement ratios and crack fractal dimensions. Second-order and third-order polynomial trend surface-fitting techniques were applied to examine the complex relationships among RFA/RCA dosage, applied load, and crack fractal dimension. The results indicated that the RFA dosage had a negative quadratic influence, while load had a positive linear effect, with dosage impact increasing with load. A second-order functional relationship was found between mid-span deflection and crack fractal dimension, reflecting nonlinear behavior consistent with concrete mechanics. This study enhances the understanding of recycled aggregate concrete beam fracture behavior, with the crack fractal dimension serving as a valuable quantitative indicator for damage state and crack complexity assessment. These findings are crucial for engineering design and application, enabling better evaluation of structural performance under various conditions.

1. Introduction

The global construction industry faces an unprecedented challenge: meeting the escalating demand for infrastructure while mitigating the environmental footprint of conventional materials [1]. As the second most commonly consumed substance worldwide after water, concrete plays a pivotal role in this dilemma. Its production accounts for 8% of global CO₂ emissions, primarily due to the extraction and processing of virgin aggregates—a non-renewable resource depleting at a rate of 50 billion tons annually [2]. The quest for sustainability has driven innovations in recycled aggregate concrete (RAC), which incorporates construction and demolition waste (CDW) as a substitute for natural aggregates. Despite progress in characterizing RAC’s compressive strength and durability, critical gaps persist in understanding its fracture behavior under dynamic loading conditions—a knowledge deficit with profound implications for structural safety and service life prediction. The integration of recycled coarse aggregate (RCA) and recycled fine aggregate (RFA) into concrete mixtures is beneficial in sustainable construction. RCA, derived from crushed concrete debris, retains residual mortar that introduces inherent heterogeneity, while RFA—typically finer than 5 mm—exhibits higher water absorption due to porous microstructures [3,4,5,6,7]. Early studies highlighted RCA’s 10–30% reduction in elastic modulus and 15–40% decrease in compressive strength compared to natural aggregates, attributes linked to weak interfacial transition zones (ITZs) and microcrack propagation [8,9,10]. Conversely, RFA’s filler effect has been shown to enhance the particle packing density, potentially offsetting strength losses when substituted at ≤30% by volume.

However, these macroscopic properties only partially explain RAC’s mechanical performance. Fracture processes in concrete—characterized by crack initiation, propagation, and coalescence—are governed by mesoscale interactions between aggregates, mortar, and ITZs [11,12]. Traditional linear elastic fracture mechanics (LEFMs), which relies on stress intensity factors and energy release rates, often fails to capture the stochastic nature of crack paths in heterogeneous materials like RAC. This limitation necessitates a shift toward nonlinear, multiscale approaches capable of quantifying crack morphological complexity. The advent of fractal geometry has provided a practical investigation tool used for probing into construction materials [13]. The fractal dimensions (D_f) quantify the geometric complexity of fracture surfaces, offering a dimensionless metric that correlates with material toughness and damage evolution and provides a lens into material heterogeneity. He et al. [14] developed a fractal theory-based methodology integrated with image processing techniques to quantify fracture morphology and crack geometry in critical bridge components. Their research demonstrates that fractal dimension analysis provides a practical metric for tracking crack propagation dynamics and characterizing structural degradation processes. By establishing quantitative correlations between fractal parameters and mechanical degradation indicators, this approach offers an enhanced resolution for monitoring damage evolution compared to conventional evaluation methods. This enhancement arises because the fractal dimension of crack networks reflects the interplay between aggregate distribution, ITZ quality, and loading-induced stress redistributions [15,16].

Early applications of fractal analysis in cementitious materials focused on post-failure fracture surfaces, where D_f values between 1.1 and 1.3 indicated quasi-brittle failure, while D_f > 1.5 suggested ductile behavior. More recent studies have extended this concept to in situ crack monitoring using digital image correlation and box-counting algorithms to track fractal evolution under sustained loads. For instance, a previous study demonstrated that concrete specimens with RCA had higher fractal dimensions during peak loading compared to natural aggregate counterparts, attributing this to RCA’s lower fracture energy and increased microcracking [17]. Despite these advances, existing research suffers from three critical limitations: (1) fragmented analysis of RCA and RFA effects, (2) neglect of dosage-dependent nonlinearities, and (3) reliance on linear fracture models that fail to capture load-path dependencies. This study addresses these gaps through a systematic investigation of RAC beams under incremental loading, employing second-order and third-order polynomial trend surfaces to model the interplay between aggregate replacement ratios, applied loads, and crack fractal dimensions.

The fracture behavior of RAC is governed by competing mechanisms at micro-, meso-, and macroscales. At the microscale, RCA’s porous ITZs act as stress concentrators, promoting microcrack nucleation at lower strain levels than in natural aggregates [18,19,20]. RFA, with its finer particle size and higher specific surface area, enhances hydration product formation but also increases the likelihood of agglomeration, creating weak planes for crack propagation. At the mesoscale, the spatial distribution of recycled aggregates dictates crack path tortuosity. RCA’s irregular shapes and residual mortar coatings force cracks to detour around aggregates, increasing fracture surface roughness (and thus fractal dimension). Conversely, RFA’s uniform grading may stabilize crack propagation by filling voids, though excessive substitution can lead to matrix softening. Macroscopically, these interactions manifest as nonlinear load–deflection responses. RAC beams typically exhibit reduced ultimate flexural strength (15–25% lower than control mixtures) but an enhanced energy absorption capacity due to prolonged crack propagation phases. The fractal dimension serves as a bridge between these scales, providing a unified metric to quantify damage accumulation from microcrack initiation to macroscopic failure.

The box-counting method—a cornerstone of fractal analysis—partitions digital images into grids of decreasing size (ε) and counts the number of boxes (N(ε)) containing crack pixels [21,22]. The fractal dimension D is derived from the slope of log(N(ε)) vs. log(1/ε), with higher D values indicating greater spatial complexity [23]. While computationally intensive, this technique offers a practical and easy way to capture crack features. To model the three-dimensional interplay between RCA/RFA dosage, applied load, and fractal dimension, this study employs polynomial trend surface fitting. Second-order (quadratic) and third-order (cubic) polynomials capture nonlinearities absent in linear regression, enabling the isolation of main effects (RCA/RFA dosage and load) and interaction terms.

This study seeks to advance the mechanistic understanding of RAC’s fracture behavior through three interrelated objectives: to quantify the dosage-dependent effects of RCA and RFA on crack fractal dimensions under incremental loading; to elucidate the load-path dependency of fractal evolution in RAC beams; to develop predictive models linking aggregate replacement ratios, applied loads, and mid-span deflections to fractal dimensions. This research offers three contributions to the field of sustainable concrete technology: (1) Quantitative Damage Metric—by establishing fractal dimension as a surrogate for damage severity, engineers can replace qualitative failure criteria with data-driven thresholds. (2) Design Optimization—the polynomial models enable prescriptive guidelines for RCA/RFA substitution limits under specific loading scenarios, balancing sustainability and performance. (3) Theoretical Advancement—the multiscale framework links aggregate-scale heterogeneity to macroscopic fracture, resolving inconsistencies in prior RAC studies. The remainder of this paper is structured as follows. First, it details the experimental program, including material properties, beam specifications, and fractal analysis protocols. Then, it presents the fractal dimension results, comparing RCA and RFA effects across linear, surface, and network crack regimes. At length, it develops the polynomial trend surface models, while also discussing the theoretical and practical implications for sustainable concrete design. By merging fractal theory with advanced statistical modeling, this study integrates recycled aggregates into construction practices while acknowledging the complexities of their fracture behavior. It also bridges the gap between sustainable material innovation and mechanistic performance prediction, offering a roadmap for the next generation of resilient, low-carbon infrastructure.

2. Experimental Details

2.1. Materials

The cement utilized is grade 42.5 Ordinary Portland Cement (OPC), and its detailed chemical composition is presented in

Table 1. Chemical compositions of the cement.

Notation, %	CaO	SiO2	Al2O3	Fe2O3	SO2	MgO	LOI
Cement	64.09	22.01	5.27	4.21	1.98	1.17	1.27
RA	38.07	45.87	5.43	4.63	1.24	2.34	2.42

Note: LOI—loss of ignition, RA—recycled coarse aggregate (RCA) and recycled fine aggregate (RFA).

. Aggregates, encompassing both fine and coarse fractions, are categorized into natural river sand and recycled fine aggregates for the fine category, as well as natural crushed stone and recycled coarse aggregates for the coarse category. The particle size distribution curves of these aggregates are presented in Figure 1, whilst the primary physical properties of coarse aggregates are shown in

Table 2. Primary physical properties of coarse aggregates.

Notation	Apparent Density kg/m3	Bulk Density kg/m3	Crushing Value %	Water Absorption %
RCA	2587	1270	20.8	3.26
NCA	2682	1694	13.7	0.42
RS	2580	1569	-	0.65
RFA	2192	1209	-	9.52

Note: RCA—recycled coarse aggregate; NCA—natural coarse aggregates; RS—river sand; RFA—recycled fine aggregate.

. The water used is common tap water, with a pH value c.a.7.5.

2.2. Sample Preparation

The concrete was prepared in accordance with the mix proportions specified in

Table 3. Mix proportion of concrete (kg/m³).

Notation	w/c	Water	Cement	NCA	RS	RCA	RFA	Extra Water
Control	0.5	189	378	1249	588	-	-	-
RCA25	0.5	189	378	937	588	312	-	10
RCA50	0.5	189	378	625	588	625	-	21
RCA75	0.5	189	378	312	588	937	-	31
RCA100	0.5	189	378	-	588	1249	-	41
RFA25	0.5	189	378	1249	441	-	147	12
RFA50	0.5	189	378	1249	294	-	294	24
RFA75	0.5	189	378	1249	147	-	441	35
RFA100	0.5	189	378	1249	-	-	588	47

Note: w/c—water to cement ratio; NCA—natural coarse aggregate; RS—river sand; RCA—recycled coarse aggregate; RFA—recycled fine aggregate.

. To achieve the saturated surface-dry (SSD) condition for recycled aggregates, supplementary water (extra water) was incorporated into the mixture. Compensatory water adjustment was implemented to offset the pre-determined water absorption capacity of recycled aggregates, thereby attaining the designated SSD state. This procedural intervention ensures uniformity in the effective water–cement ratio across all mixture formulations, which is critical for maintaining consistent workability and mechanical performance parameters in concrete applications.

A total of 18 beam specimens were designed across 9 groups, with each group comprising 2 identical beams. The experimental variables included different replacement ratios and substitution forms of recycled aggregates. The specific group configuration was as follows: the control was constructed with conventional concrete. Groups RFA25, RFA50, RFA75, and RFA100 incorporated recycled fine aggregates as a partial replacement for natural river sand, with replacement ratios of 25%, 50%, 75%, and 100%, respectively. Groups RCA25, RCA50, RCA75, and RCA100 utilized recycled coarse aggregate as a substitute for crushed stone, maintaining the same replacement ratios.

The beam dimensions were standardized at 2000 mm (length) × 300 mm (width) × 150 mm (depth), with a concrete cover thickness of 25 mm. For longitudinal reinforcement, 16 mm diameter HRB400 hot-rolled ribbed bars were employed. HPB300 plain round bars with an 8 mm diameter were selected for stirrups and structural reinforcement, resulting in an overall reinforcement ratio of 1.03%. To eliminate the influence of shear forces transmitted from supports on crack development in the flexural zone of recycled aggregate concrete beams, a 600 mm pure bending segment was implemented at the beam mid-span. This configuration ensured that the critical flexural section experienced a pure bending moment without shear interference. Stirrups and structural reinforcement were strategically placed in the adjacent flexural shear zones to prevent premature shear failure. The reinforcement details are illustrated in Figure 2 for visual reference.

Based on the pre-calculated mix proportions, the requisite masses of constituent materials for each beam specimen group were pre-weighed. Prior to concrete placement, the interior surfaces of wooden formwork were treated with a release agent to facilitate subsequent demolding operations, followed by strategic placement of the prefabricated steel reinforcement cages within the formwork assemblies. As a preliminary mixing protocol, the mixer apparatus underwent thorough purging with potable water. To ensure optimal homogenization, a two-stage mixing regimen was implemented: (1) a dry mixing phase involving the sequential introduction of fine aggregates and cement into the mixing drum, with a 3 min duration to achieve uniform cementitious matrix dispersion; (2) a wet mixing phase comprising incremental addition of measured mixing water and coarse aggregates, followed by additional 3 min agitation to produce workable concrete consistency.

The fresh concrete matrix was initially deposited at beam extremities within the specimen molds to ensure reinforcement cage stabilization, followed by systematic filling of remaining formwork volumes. During material placement, intentional headspace was maintained above mold rims to accommodate compaction requirements. Subsequent multi-point vibration compaction was executed using immersion vibrators to achieve full compaction criteria. Post-vibration surface finishing operations employed steel trowels for smooth levelling, culminating in protective polyethylene sheeting application to mitigate moisture loss through evaporation.

Following a 48 h initial setting period meeting specified compressive strength thresholds, specimens underwent careful demolding procedures with the avoidance of mechanical disturbances. The curing regimen was conducted under standardized environmental conditions (20 ± 5) °C and 95% relative humidity for a 28-day duration within controlled laboratory facilities.

Upon curing completion, five strategically positioned adhesive foil strain gauges were bonded to each beam’s lateral surface. These gauges featured 100 mm × 3 mm sensitive grid dimensions with a configuration. Adhesive bonding procedures ensured complete wetting of substrate interfaces to eliminate interfacial voids, with subsequent quality verification through ohmmetric resistance measurements. For experimental investigation of flexural crack propagation mechanisms, both beam flanks received uniform application of crack-detecting putty coating with a controlled thickness to prevent geometric interference with fracture patterns. Post-curing surface preparation involved grid delineation using 50 mm × 50 mm spacing with engineering markers, establishing a reference framework for subsequent fractal analysis and crack morphology documentation.

2.3. Testing

Figure 3 illustrates the schematic diagram of the loading device. It features a simply supported beam with a trisection loading arrangement, comprising pinned support at the left extremity and roller support at the right extremity, each offset 100 mm from the beam ends. Load application was facilitated through a distribution beam with a 600 mm spacing between loading points, connected to a hydraulic jack and a 60-ton load cell positioned concentric to the distribution beam’s geometric center. A comprehensive instrumentation suite was employed, including linear variable differential transformers (LVDTs) for displacement measurement—two units above each support assembly for settlement tracking and three units at mid-span for deflection profiling—alongside a DH3816 static strain analysis system for real-time strain acquisition from steel reinforcement and concrete matrix.

Digital crack width gauges with a sub-millimeter resolution enabled precise fracture quantification during testing. The loading protocol comprised two sequential phases: an initial preconditioning regimen to establish contact continuity, stabilize measurement systems, verify instrument functionality, and confirm data integrity, with a preload magnitude set at 50% of the theoretically derived cracking load; followed by a sustained loading sequence with initial increments corresponding to 5% of the calculated ultimate load capacity, transitioning to 10 kN stages post-cracking. Each load step was maintained for 3–5 min intervals, facilitating thorough documentation of crack evolution patterns through optical microscopy-based width measurements and coordinate-based spatial tracking using engineer’s blue dye marking. Upon reaching the ultimate load capacity, defined by catastrophic loss of load-bearing capacity or excessive deflection, testing ceased to allow high-resolution digital imaging for final fracture pattern documentation, coordinate-based fractal analysis of crack networks, and post-mortem failure mode examination. This systematic approach enabled the comprehensive capture of structural performance parameters across the entire loading continuum, providing critical insights into the flexural response characteristics of recycled aggregate concrete beam systems.

2.4. Fractal Dimension-Based Processing of Crack Patterns

2.4.1. Crack Propagation Under Incremental Loading

As a preparatory measure prior to mechanical testing, the lateral surfaces of all beam specimens underwent systematic grid pattern delineation to establish a reference framework for subsequent fractographic analysis. During the experimental bending protocol, crack propagation patterns were documented through sequential marker tracing synchronized with continuous high-resolution video recording. This dual-modality approach enabled the comprehensive capture of temporal and spatial crack evolution dynamics. Post-testing, digital fractographic reconstruction was performed. Within these digital representations, red colorimetric encoding was specifically implemented to enhance crack visibility and facilitate quantitative analysis. Herein, it focuses on the progressive crack development observed in the beam specimen RFA50 across the applied load spectrum. A representative fractographic progression is graphically depicted in Figure 4, illustrating the characteristic crack morphology evolution under incremental loading conditions.

2.4.2. Box-Counting Method for Calculating Fractal Dimension

The box-counting method represents the most widely adopted algorithm for quantifying fractal dimensions in engineering applications [22]. This technique operates on the fundamental principle of multi-resolution analysis, where a hierarchical grid system with progressively finer spatial resolutions (r) is superimposed over the crack distribution pattern. For each grid iteration, the algorithm systematically records the minimum number of boxes (N) required to fully encapsulate the observed crack network. This methodology enables the establishment of a direct mathematical relationship between grid coarseness (r) and the corresponding crack-occupied cell count [N(r)], forming the basis for fractal dimension calculation.

The fractal dimension (D) is derived through logarithmic transformation of these variables, expressed as Equations (1) and (2) by mathematical derivation.

$$\begin{array}{c}N\left(r\right)=r^{-D}\end{array}$$

(1)

$$\begin{array}{c}D=-{\displaystyle \frac{lnN\left(r\right)}{\mathit{ln}\left(r\right)}}\end{array}$$

(2)

where

• D = Box-counting dimension (fractal dimension).
• r = Grid cell dimension.

To investigate the correlation between crack morphology complexity and structural flexural resistance, the experimental protocol focused on the pure bending regions of beam specimens—the primary zone for flexural crack development. High-fidelity digital representations of crack propagation patterns were generated and subsequently subjected to systematic grid partitioning. The pure bending zone crack networks were discretized using seven distinct grid resolutions (100 mm, 50 mm, 30 mm, 25 mm, 20 mm, 10 mm, and 5 mm), with the crack-occupied cell counts (N(r)) recorded for each spatial scale. As an illustrative example, Figure 5 demonstrates the grid partitioning scheme applied to the crack propagation map of beam specimen RFA50 at the ultimate failure state. This standardized protocol was uniformly implemented across all experimental specimens to ensure data consistency.

Employing the box-counting algorithm, the fractal dimension of the beam specimen RFA50 at the ultimate failure state was quantitatively determined through computational analysis. The raw box count data were subjected to bivariate regression analysis. This analysis generated the lnN(r)-ln[1/r] relationship plot, with the slope of the linear regression line yielding the fractal dimension estimate. This multi-scale analytical approach enables comprehensive characterization of crack morphology complexity across multiple spatial domains, providing valuable insights into the fractal nature of concrete crack propagation under flexural loading.

3. Results and Discussion

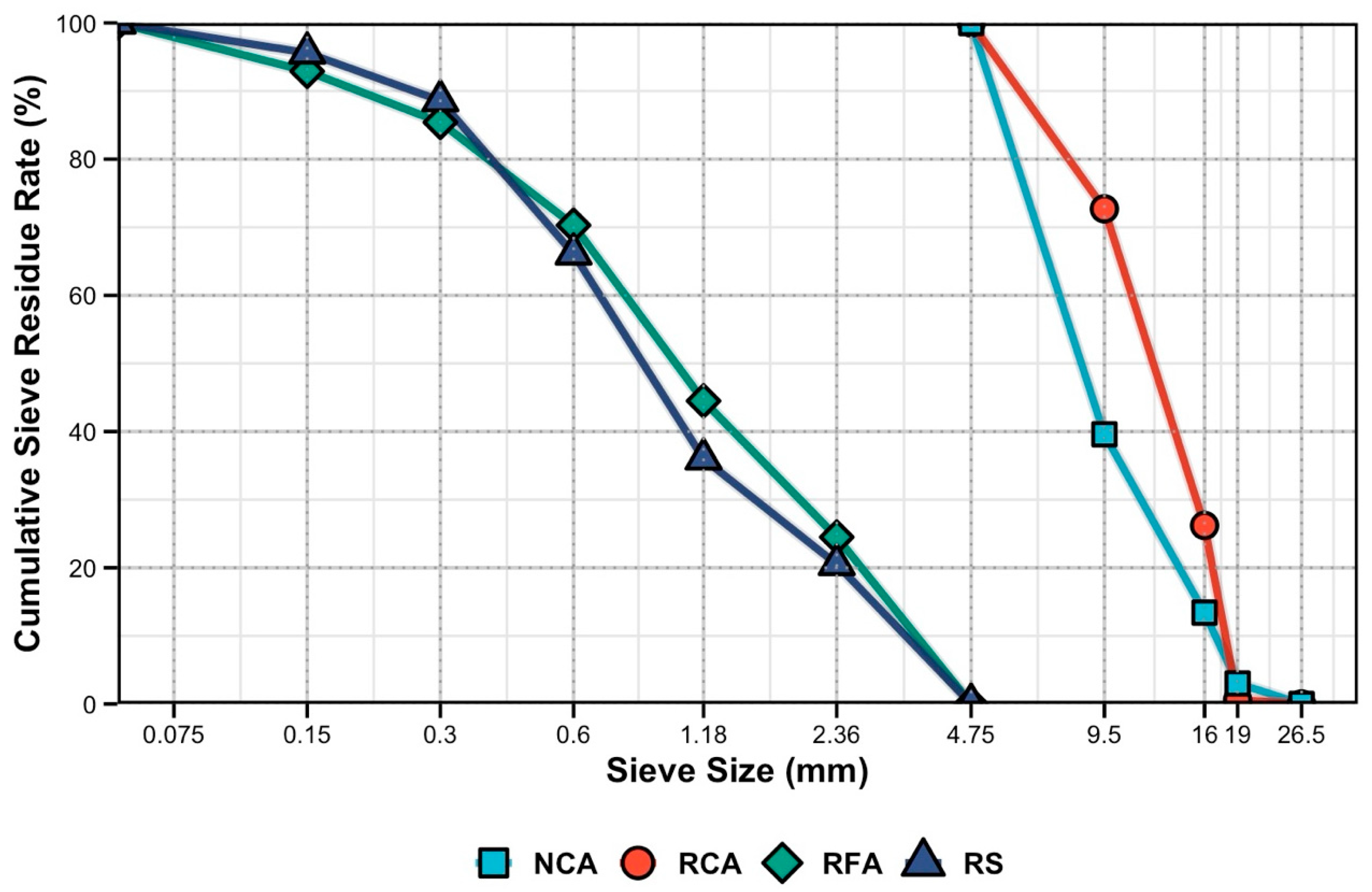
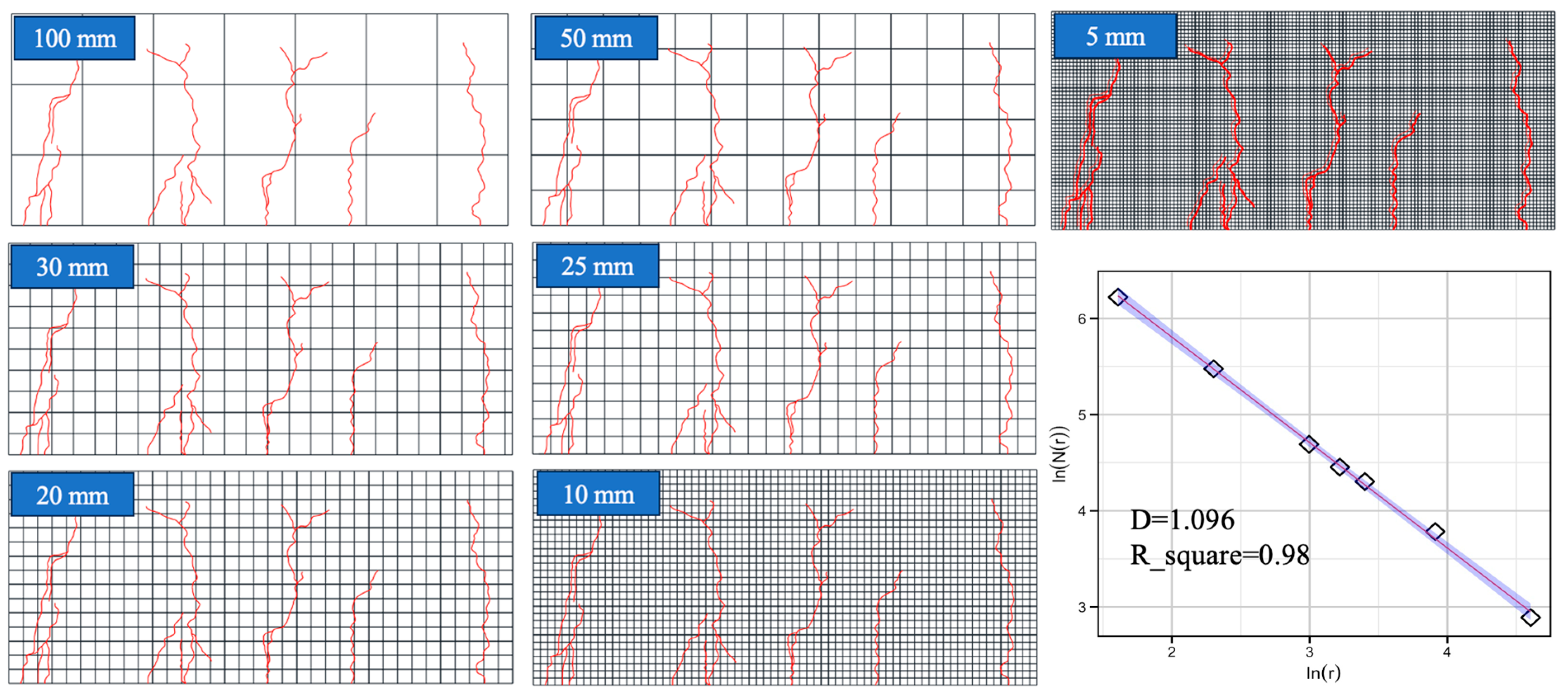
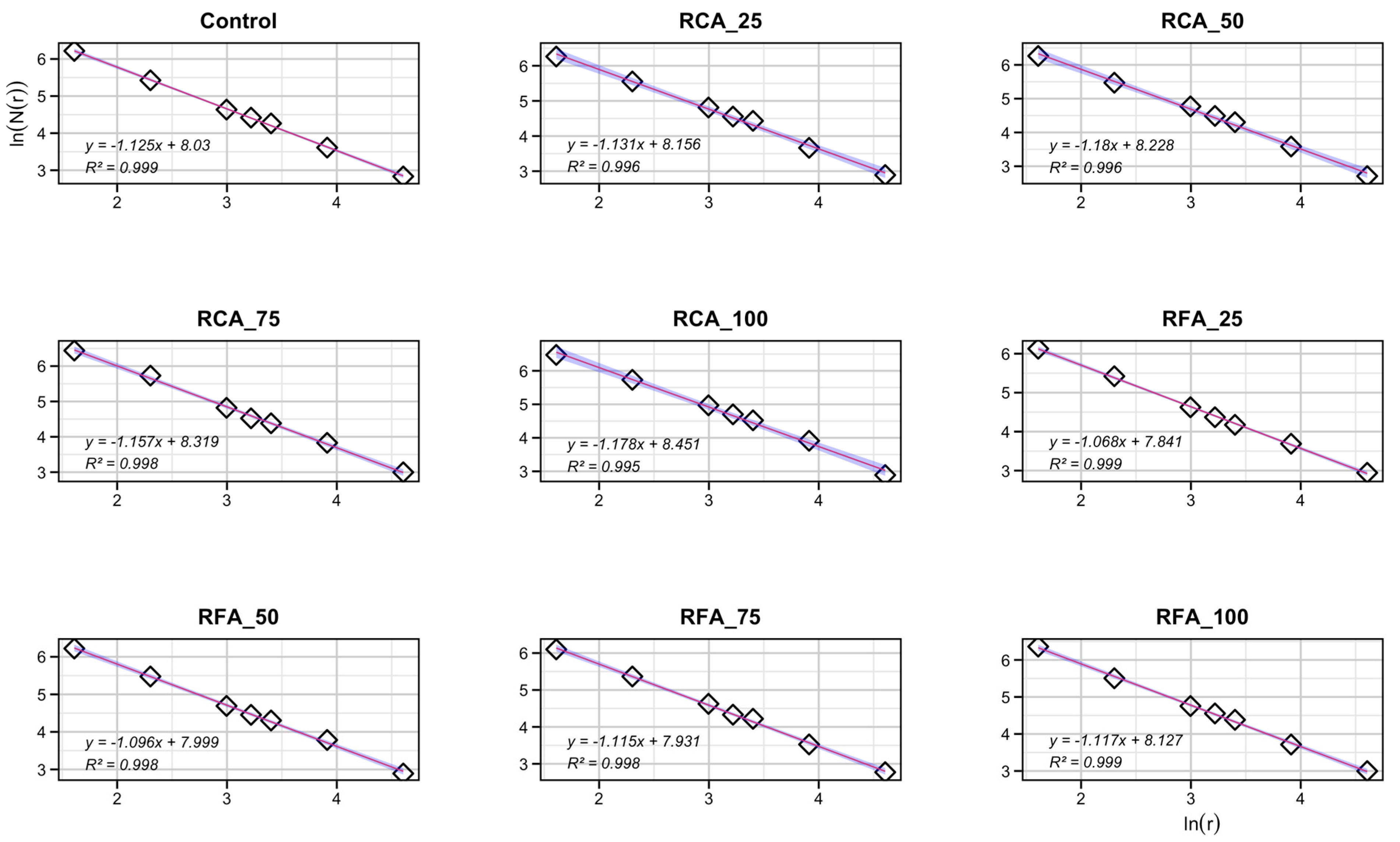
3.1. Fractal Characterization of Cracks in the Pure Bending Zone at Ultimate Failure State

Following the ultimate failure in all nine beam specimens, the crack patterns within their respective pure bending zones underwent systematic grid partitioning using the previously described methodology. The crack-occupied cell counts derived from this multi-scale analysis are used for illustration. Scatter plots depicting the relationship between lnN(r) and ln(r) were subsequently generated for each specimen, followed by linear regression analysis. This analytical sequence culminated in the determination of fractal dimensions (D) for each beam specimen at their ultimate failure state, with results graphically presented in Figure 6. From the scatter plots of linear regression for lnN(r) vs. ln(r) at ultimate failure states, it is evident that all test specimens exhibit linear correlations. This observation indicates that the crack propagation patterns in recycled aggregate concrete beams during flexural loading demonstrate self-similar characteristics, thereby validating the applicability of fractal theory for crack analysis. The fractal dimensions, as illustrated in Figure 7, were determined through the slopes of these linear regressions.

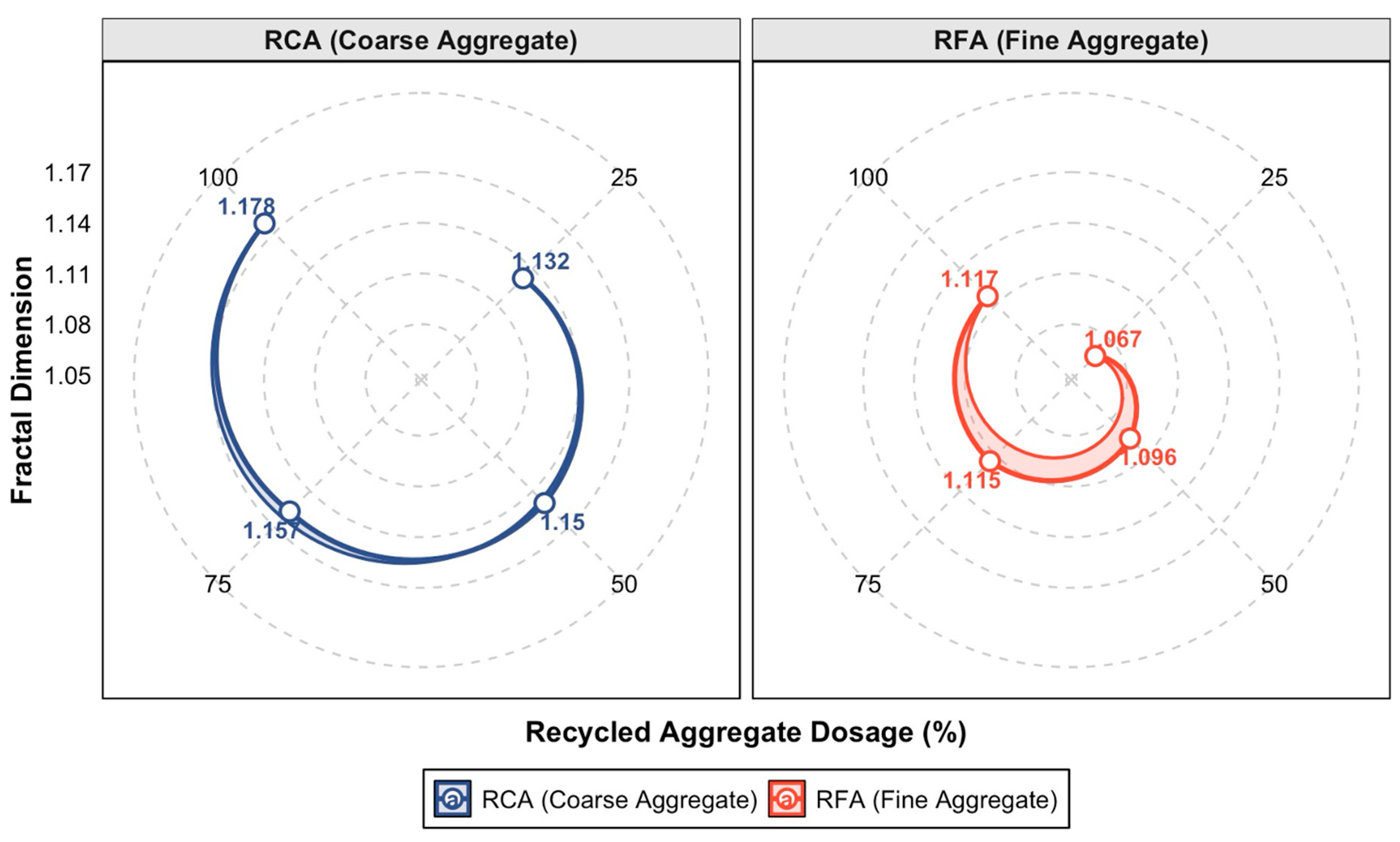
As illustrated in Figure 7, the fractal dimensions of the analyzed beam specimens exhibit values ranging from 1.0 to 1.2. Notably, the RCA100 beam demonstrates the highest fractal dimension, while the RFA25 beam presents the lowest. Under equivalent replacement ratios, concrete beams containing recycled coarse aggregates consistently exhibit higher fractal dimensions compared to those with recycled fine aggregates. This observation stems from the inherent material properties of recycled coarse aggregates, characterized by relatively lower elastic moduli and compressive strengths when contrasted with fine aggregate counterparts [6,7]. During the failure regime, following the yielding and subsequent withdrawal from service of tensile reinforcement, the compressed concrete zone assumes primary load-bearing responsibility. Experimental evidence indicates that recycled coarse aggregate concrete beams manifest diminished deformation resistance and reduced ductility relative to fine aggregate variants, resulting in more pronounced late-stage crack propagation. Given the established correlation between fractal dimension and crack morphological complexity, it follows logically that recycled coarse aggregate concrete beams exhibit elevated fractal dimensions. For specimens with identical replacement configurations, a direct proportionality exists between crack fractal dimensions and recycled coarse aggregate replacement ratios, implying that increased coarse aggregate substitution promotes more extensive crack development and exacerbates damage severity. Conversely, recycled fine aggregate replacement ratios demonstrate a nonlinear relationship with crack fractal dimensions, exhibiting an initial decrease followed by a subsequent increase.

Consistently, recycled fine aggregate concrete beams exhibit lower fractal dimensions compared to conventional ordinary concrete beams. This phenomenon primarily arises from the angular surface morphology and irregular particle shape of recycled fine aggregates, which induce an interlocking effect with neighboring aggregate components. Furthermore, the enhanced bond performance between recycled fine aggregates and steel reinforcement, when compared to conventional concrete matrices, results in superior interface anchorage characteristics. Collectively, these factors contribute to the crack-inhibiting properties of recycled fine aggregate incorporation, demonstrating a marked crack-arresting effect in reinforced concrete elements.

3.2. Fractal Characteristics of Cracks in Pure Bending Sections Under Varying Loads

The fractal analysis of crack evolution in recycled aggregate concrete beams under pure bending conditions reveals significant load-dependent morphological complexity (see Figure 8, Figure 9, Figure 10 and Figure 11). Utilizing a box-counting algorithm, the fractal dimensions (D) of surface fractures were quantified across varying load regimes, establishing a direct correlation between mechanical stress and crack self-organization patterns. In the initial elastic phase, crack propagation exhibited limited spatial development, with lnN(r)-ln(r) slopes below unity, indicating negligible self-similarity. However, as applied loads approached ultimate capacity, the fracture network underwent a marked topological transformation. The observed monotonic increase in fractal dimensions demonstrates a power-law relationship between stress intensity and geometric complexity. Notably, all specimens demonstrated fractal scaling exceeding their topological dimensions (D > D₀), with R² > 0.95 confirming statistical self-affinity across measurement scales. A parametric investigation established a linear growth model (F = aD + b) relating the applied load magnitude (F) to the resultant fractal dimension (D). This empirical relationship, validated through multivariable regression analysis, enables predictive modeling of fracture evolution in recycled aggregate concrete systems. Microstructural examination suggests that increasing load induces hierarchical branching mechanisms, transitioning from primary crack propagation to secondary fracture network formation.

The crack morphology exhibits three distinct fractal regimes: (1) a linear distribution (1.10 ≤ D ≤ 1.40) characterized by isolated fracture paths, (2) a surface distribution (1.30 ≤ D ≤ 1.60) featuring interacting crack families, and (3) a network distribution (1.50 ≤ D ≤ 1.90) showing percolating fracture patterns. Experimental observations confirm that recycled aggregate concrete beams predominantly operate within the linear fractal regime under service loads, with critical failure marked by a sudden transition to surface distribution patterns. These findings contribute to damage mechanics frameworks by establishing the fractal dimension as a quantitative damage index. The observed load-dependent fractal escalation provides critical insight into energy-dissipation mechanisms and failure precursors in cementitious composites.

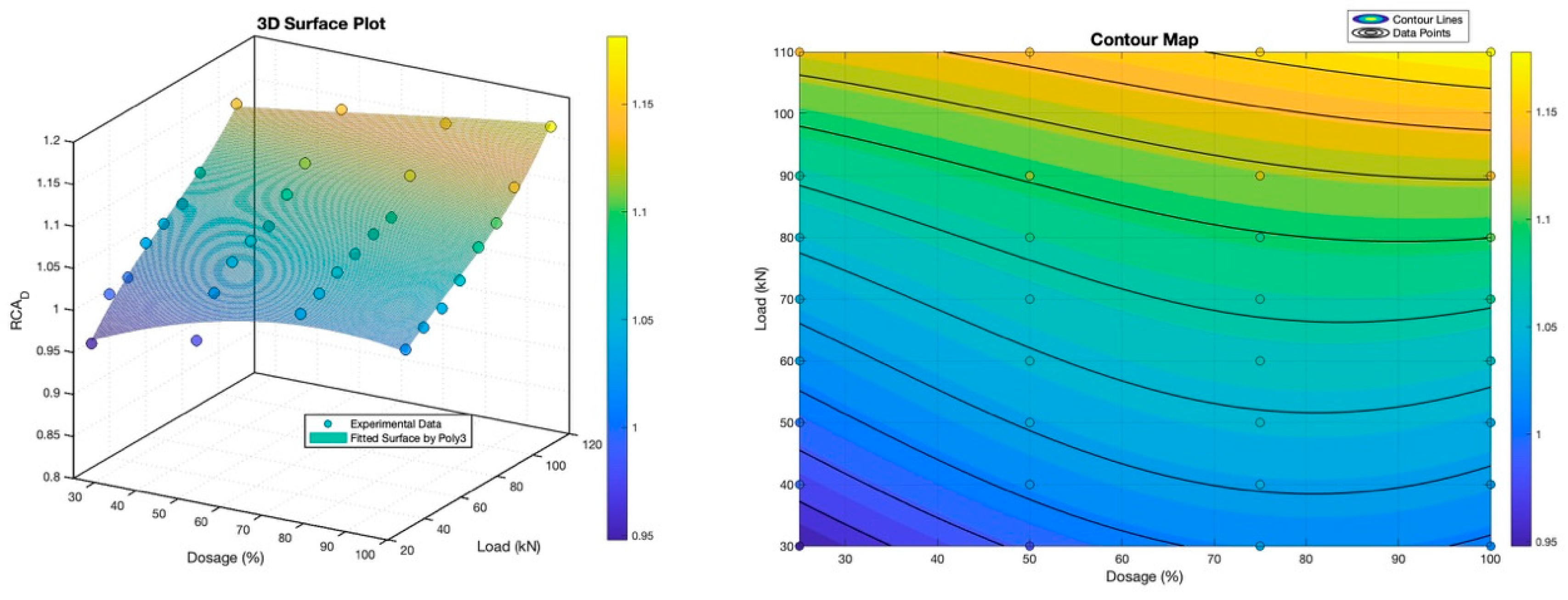
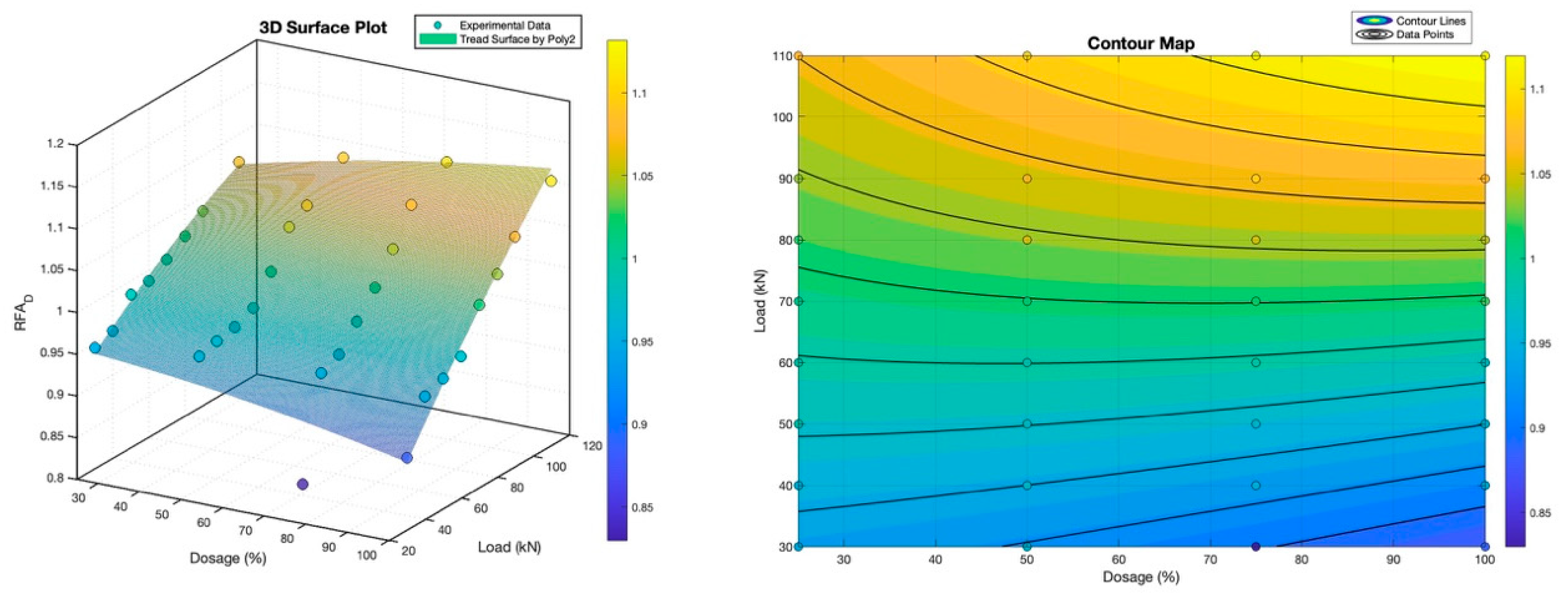
The four charts collectively illustrate the intricate relationships between the dosage of RFA and RCA, applied load, and the fractal dimension (D) of crack propagation in concrete beams, employing both second-order and third-order polynomial trend surface fitting. These figures are used to assess the implications of recycled aggregate-induced crack complexity variations. Figure 8, depicting a 3D surface plot and contour map for RFA_D, reveals a fitted formula indicating a negative quadratic influence of dosage and a positive linear effect of load on RFA_D, suggesting that while an increased RFA dosage initially reduces crack complexity, higher loads amplify it. The R-squared value of 0.9201 underscores the model’s strong explanatory power. 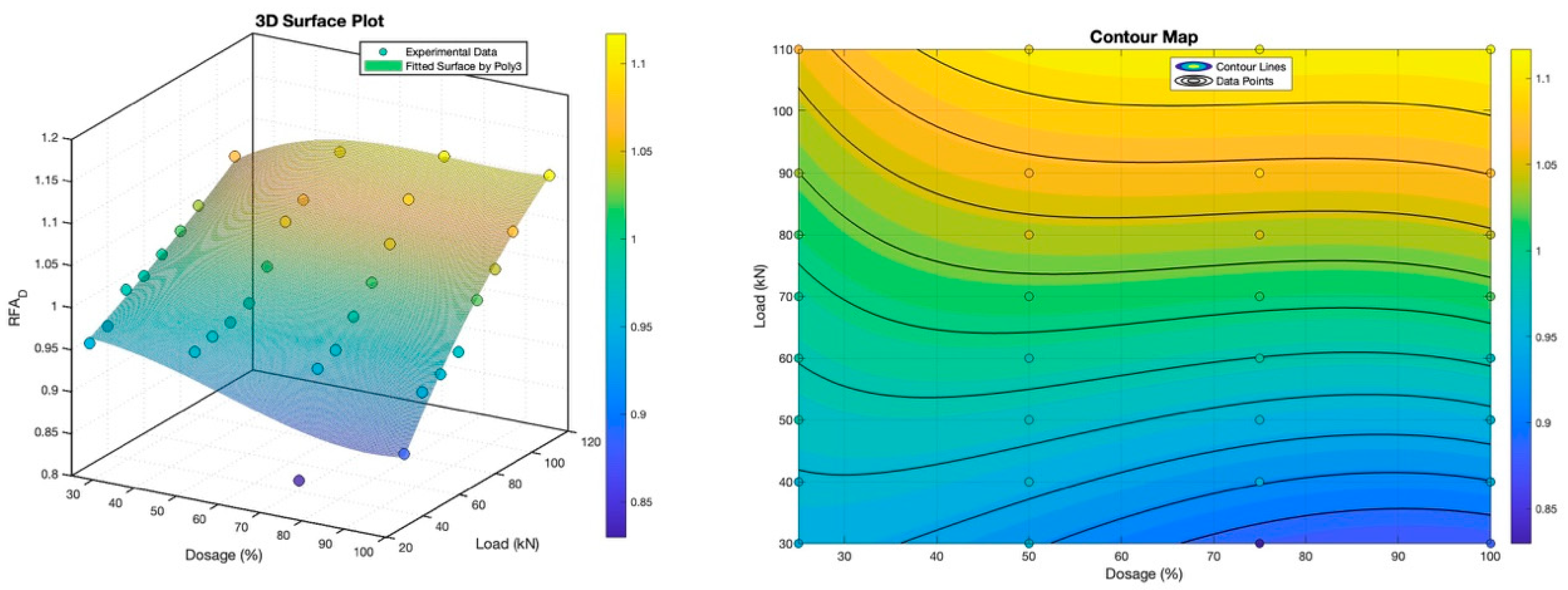Figure 9, focusing on RFA dosage variation under incremental loading, corroborates the negative dosage effect and positive load impact, with an interaction term highlighting that the dosage’s influence on RFA_D becomes more pronounced with rising load, as evidenced by an R-squared of 0.9353. Shifting focus to RCA, Figure 10, utilizing a second-order polynomial, demonstrates positive linear relationships between RCA dosage, load, and RCA_D, implying that a higher RCA content and increased load both elevate crack complexity. The negligible interaction term suggests a minimal combined effect, yet the model explains 96.53% of RCA_D variance. 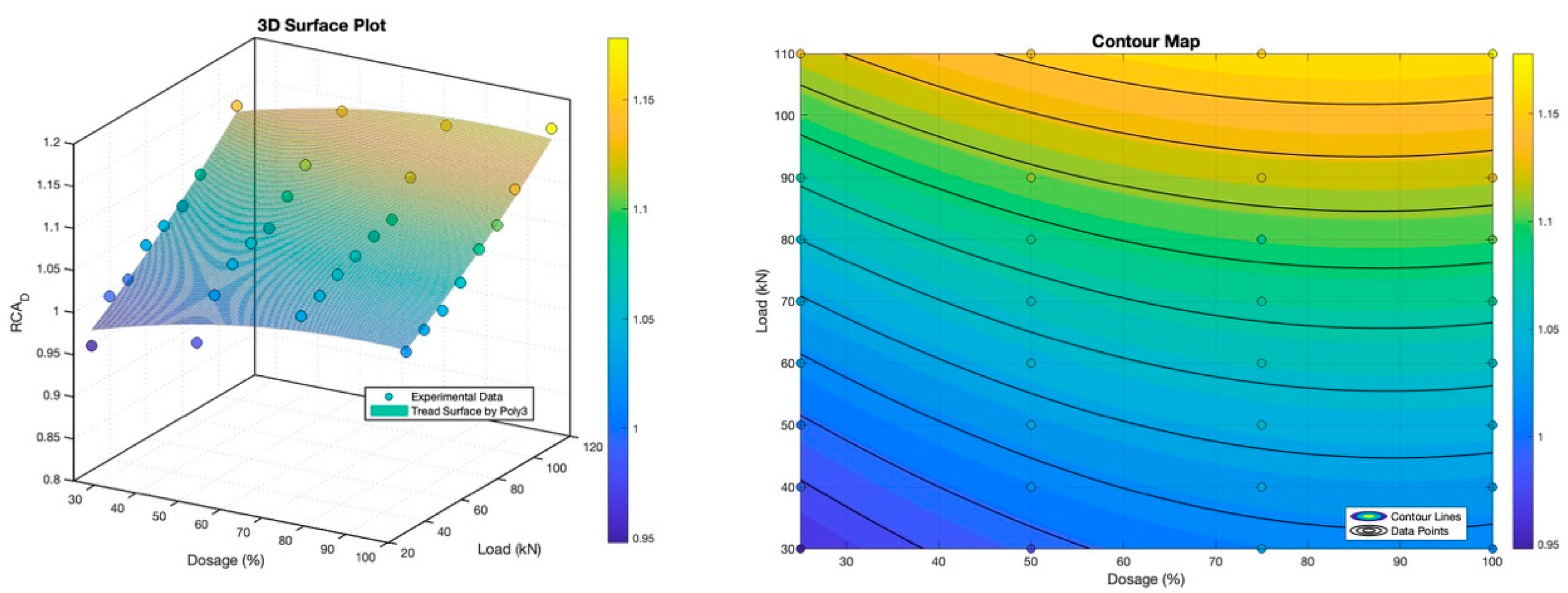Figure 11, employing a third-order polynomial for RCA dosage analysis, reveals a more nuanced relationship: while RCA dosage and load positively influence RCA_D linearly, negative quadratic and cubic terms indicate a potential plateau or reversal in crack complexity at extremely high dosages or loads. The exceptional R-squared value of 0.9779 attests to the model’s remarkable fit.

The observed disparities in crack propagation behavior between RFA and RCA-incorporated concretes can be attributed to the inherent physicochemical characteristics of these recycled aggregate types. RFA, typically characterized by a higher water absorption capacity and porous structure compared to natural fine aggregates, may introduce more micro-voids and weak interfaces within the concrete matrix [24]. These defects can act as stress concentrators, potentially promoting localized crack initiation and coalescence under load. However, the negative quadratic relationship between RFA dosage and RFA_D suggests that beyond a certain threshold, the increased porosity and weakened interfacial transition zone might lead to a more homogeneous crack propagation path, thereby reducing the fractal complexity. Conversely, RCA, often containing a significant portion of adhered mortar and exhibiting a rougher surface texture than natural coarse aggregates, can enhance the mechanical interlocking and friction at the aggregate–cement paste interface. This improved interfacial bonding could contribute to a more tortuous crack path, as cracks are forced to deviate around the angular RCA particles, thereby increasing the fractal dimension (RCA_D). The positive linear relationship between RCA dosage and RCA_D supports this notion, indicating that higher RCA content amplifies this crack deviation mechanism. Furthermore, the applied load plays a pivotal role in modulating crack propagation. Higher loads accelerate crack initiation and propagation, amplifying the inherent tendencies dictated by the aggregate type and dosage. The interaction terms observed in the fitting formulas suggest that the effect of aggregate dosage on fractal dimension is load-dependent, highlighting the synergistic interplay between material composition and mechanical loading in governing the fracture behavior of concrete. Collectively, these charts elucidate that RFA and RCA exert opposing effects on crack fractal dimension, with dosage and load interacting to modulate crack propagation patterns. These findings offer valuable insights for optimizing concrete mixtures, balancing recycled aggregate utilization with desired structural performance, while also highlighting the need for cautious extrapolation beyond the tested dosage and load ranges.

3.3. Relationship Between Fractal Dimension and Mid-Span Deflection

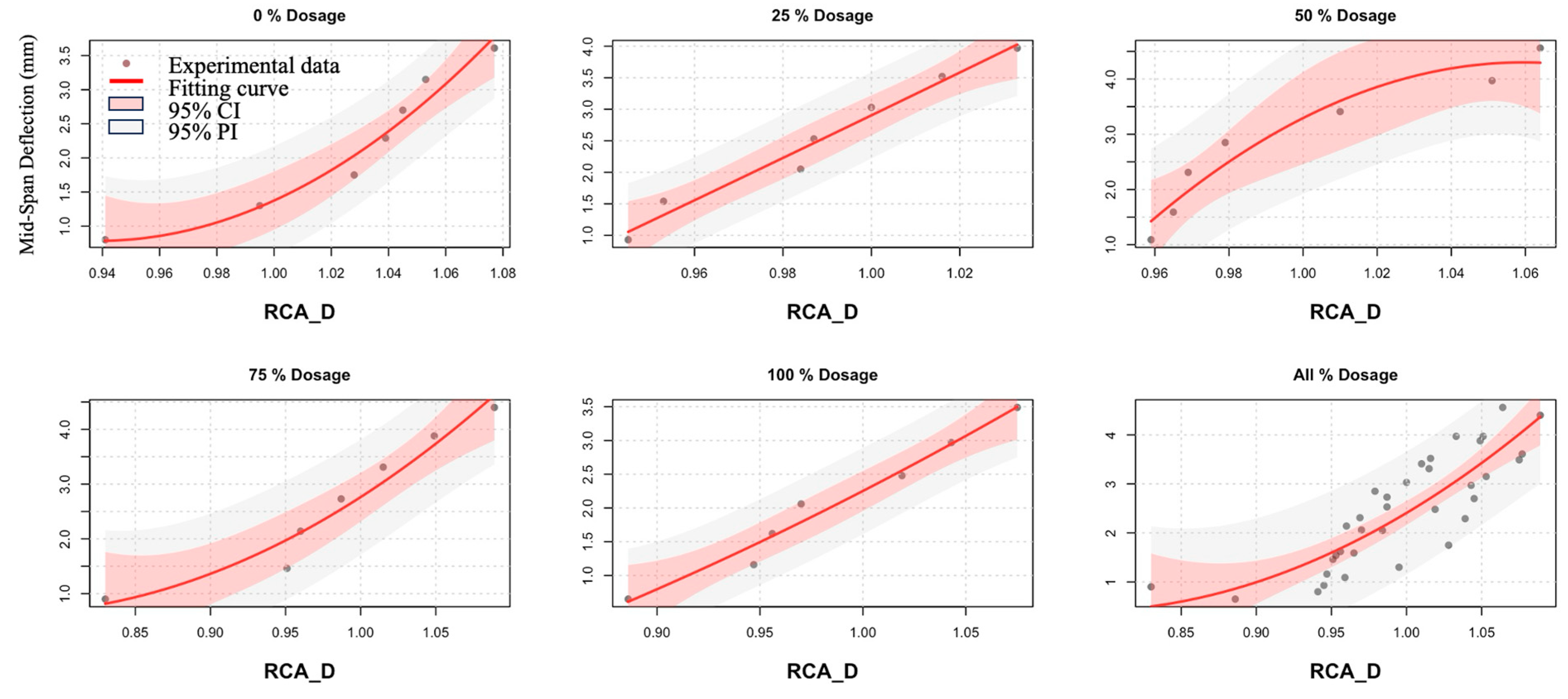
Figure 12 presents a series of graphs that show the correlation between the fractal dimension of cracks (RCA_D) and the mid-span deflection of concrete beams incorporating varying proportions of recycled coarse aggregate (RCA). The different proportions examined are 0%, 25%, 50%, 75%, and 100%, along with a comprehensive “All Dosages” category. Each graph is composed of data points (depicted as gray dots), a quadratic regression curve (shown in red), and 95% confidence intervals (represented by the red-shaded area).

At a 0% recycled coarse aggregate dosage, the quadratic regression equation Deflection = 137.5 − 291.5RCA_D + 155.3RCA_D², with an R² of 0.94, demonstrates a strong fit of the quadratic model to the experimental data. As the fractal dimension of cracks increases, the mid-span deflection of the beam exhibits a nonlinear upward trend. In the absence of recycled coarse aggregate, the beam possesses a specific level of inherent stiffness. With the growth in crack complexity (quantified by the fractal dimension), the deflection gradually escalates as the beam’s ability to carry loads diminishes. When the recycled coarse aggregate dosage reaches 25%, the equation Deflection = 95.33 − 212.1RCA_D + 118.4RCA_D², with an R² of 0.96, shows a clear nonlinear relationship between deflection and the crack fractal dimension. Compared to the 0% dosage scenario, the initial deflection is lower. This can be attributed to the impact of the recycled coarse aggregate on the beam’s material properties, which makes the beam slightly more deformable or reduces its initial stiffness.

At a 50% recycled coarse aggregate dosage, the equation Deflection = −27.84 + 20.48RCA_D + 7.498RCA_D² (R² = 0.92) indicates a nonlinear increase in deflection as the crack fractal dimension rises. The presence of 50% recycled coarse aggregate heightens the beam’s sensitivity to crack development, resulting in more significant deflection changes for a given change in the fractal dimension. For a 75% recycled coarse aggregate dosage, the quadratic regression Deflection = −332.3 + 584.4RCA_D − 253.5RCA_D² shows a nonlinear increase in deflection with the crack fractal dimension. The relatively high coefficients compared to lower dosages suggest that at this high level of recycled coarse aggregate content, the beam’s behavior is greatly influenced by the recycled material, leading to a more pronounced deflection response as cracks develop. At a 100% recycled coarse aggregate replacement, the equation Deflection = −158.5 + 273.2RCA_D − 114.1RCA_D², with an R² of 0.95, shows that the nonlinear relationship between deflection and the crack fractal dimension persists. The initial deflection is relatively low, and the increase in deflection with the fractal dimension is determined by the unique characteristics of the fully recycled coarse aggregate beam. The “All Dosages” combined graph presents an overall nonlinear trend of deflection increasing with the crack fractal dimension across all recycled coarse aggregate dosages. The data points from different dosages are dispersed around the quadratic regression curve, and the 95% confidence interval provides an estimate of the uncertainty associated with the regression model.

The underlying mechanisms behind these observed relationships are closely related to the properties of recycled coarse aggregate. Recycled coarse aggregate typically has different physical and mechanical characteristics compared to natural aggregate, such as higher porosity, lower density, and weaker interfacial transition zones between the aggregate and the cement paste [10,25,26]. These factors reduce the overall stiffness and strength of the concrete beam. As the dosage of recycled coarse aggregate increases, the beam becomes more susceptible to deformation under load, which is reflected in the increasing deflection with the development of cracks (higher fractal dimension). Additionally, the nonlinear relationship between the fractal dimension and deflection can be explained by the nonlinear decrease in the beam’s load-carrying capacity as cracks develop and coalesce. The dosage-dependent behavior is due to the cumulative effect of the recycled coarse aggregate’s properties on the beam’s performance, with different dosages leading to varying degrees of influence on the deflection–crack fractal dimension relationship.

Figure 13 presents a set of graphs and comprehensively depicts the relationship between the fractal dimension of cracks (RFA_D) and the mid-span deflection of beams under varying dosages of recycled fine aggregate (RFA), encompassing 0%, 25%, 50%, 75%, 100%, and an “All Dosages” scenario. Each graph is equipped with data points (gray dots), a quadratic fit curve (red line), and 95% confidence intervals (shaded red area), providing a detailed and nuanced view of this relationship.

At a 0% dosage of recycled fine aggregate, the quadratic fit equation Deflection = 137.5 − 291.5RFA_D + 155.3RFA_D², with an R² value of 0.94, indicates a relatively good fit of the quadratic model to the data. This implies a nonlinear increasing trend in the mid-span deflection of the beam as the fractal dimension of cracks increases. In the absence of recycled fine aggregate, the beam possesses a certain inherent stiffness. As the complexity of cracks, represented by the fractal dimension, rises, the deflection gradually increases due to the weakening of the beam’s load-carrying capacity as cracks propagate. When the dosage of recycled fine aggregate is 25%, the equation Deflection = −25.92 + 23.76RFA_D + 5.054RFA_D², with an R² of 0.9732, shows a nonlinear increase in deflection with the increase in the crack fractal dimension as well. Compared to the 0% dosage case, the initial deflection value is lower. This can be attributed to the influence of the recycled fine aggregate on the material properties of the beam. The recycled fine aggregate may alter the beam’s stiffness, making it slightly more flexible or reducing its initial resistance to deformation.

At a 50% dosage, the equation Deflection = −314.9 + 602.6RFA_D − 284.4RFA_D² (R² = 0.96) further illustrates the nonlinear relationship. The higher coefficients compared to lower dosages suggest that at this level of recycled fine aggregate content, the beam’s response to crack development is more sensitive. A given change in the fractal dimension results in larger deflection changes, indicating that the presence of a significant amount of recycled fine aggregate amplifies the beam’s susceptibility to deformation as cracks become more complex. For a 75% dosage, the quadratic fit Deflection = 21.6 + −55.33RFA_D + 36.5RFA_D², R² = 0.9517, still shows a nonlinear increase in deflection with the crack fractal dimension. The relatively lower coefficients compared to the 50% dosage case may imply that as the recycled fine aggregate dosage approaches 75%, the beam’s behavior starts to stabilize to some extent. However, it still clearly demonstrates a relationship with crack complexity, as the propagation of more complex cracks continues to cause deflection. At a 100% recycled fine aggregate replacement, the equation Deflection = −1.75 + −7.728RFA_D + 11.73RFA_D², R² = 0.9726, shows that the nonlinear relationship between deflection and the crack fractal dimension persists. The initial deflection is relatively low, and the increase in deflection with the fractal dimension is more moderate compared to some intermediate dosages. This could be due to the unique properties of the fully recycled fine aggregate beam, where the beam’s behavior may be dominated by the characteristics of the recycled fine aggregate, leading to a more stable or moderate increase in deflection as cracks develop. The combined “All Dosages” graph presents an overall nonlinear trend of deflection increasing with the crack fractal dimension across all recycled fine aggregate dosages. The data points from different dosages are scattered around the quadratic fit curve, and the 95% confidence interval provides an estimate of the uncertainty in the fit, offering a comprehensive view of the general pattern.

The underlying mechanisms behind these observed relationships are multifaceted. Firstly, recycled fine aggregate typically exhibits different physical and mechanical properties compared to natural aggregate. It often has higher porosity, lower density, and weaker interfacial transition zones between the aggregate and the cement paste. These factors collectively reduce the overall stiffness and strength of the concrete beam. As the dosage of recycled fine aggregate increases, the beam becomes more prone to deformation under load, which is reflected in the increasing deflection with the development of cracks (higher fractal dimension). Secondly, the fractal dimension of cracks serves as a measure of their complexity. As the load on the beam increases, micro-cracks initiate and propagate. In beams with recycled fine aggregate, the weaker interfacial zones and lower overall strength may lead to more complex crack patterns (higher fractal dimensions) at a given load level [27,28,29]. The propagation of these complex cracks causes the beam to deflect more. The nonlinear relationship between the fractal dimension and deflection can be attributed to the fact that as cracks develop and coalesce, the beam’s load-carrying capacity decreases nonlinearly, resulting in a more rapid increase in deflection. Lastly, the dosage-dependent behavior can be explained as follows. At low dosages of recycled fine aggregate, the influence on the beam’s properties is relatively small, and the deflection–crack fractal dimension relationship is similar to that of the control (0% dosage), but with some differences in initial stiffness. As the dosage increases, the cumulative effect of the recycled fine aggregate’s inferior properties becomes more pronounced, leading to larger deflections for a given crack fractal dimension. However, at very high dosages (e.g., 100%), the beam may reach a state where its behavior is dominated by the recycled fine aggregate properties, and the increase in deflection with the crack fractal dimension may become more stable or moderate. In conclusion, the relationship between the fractal dimension of cracks and the mid-span deflection of beams is significantly influenced by the dosage of recycled fine aggregate. The nonlinear relationship is a result of the complex interaction between the recycled fine aggregate’s properties and the crack development process in the concrete beam.

Theoretically, the fractal dimension demonstrates superior sensitivity to microstructural changes, capturing early-stage crack coalescence that remains undetected by displacement measurements. This spatial complexity metric also enables precise damage localization, a resolution unattainable through global deflection analysis. Practically, the fractal approach facilitates cost-effective non-contact monitoring using standard imaging systems, achieving high-level correlation with laser displacement data while reducing sensor costs when integrated into a hierarchical structural health monitoring framework. Fractal dimension spikes precede critical deflection thresholds, serving as an earlier failure precursor. In addition, by fusing fractal dimension with deflection metrics in a hybrid damage index, prediction accuracy can be improved compared to single-parameter models. This dual-parameter approach enables real-time image-based screening complemented by targeted deflection verification, maintaining high-level failure prediction reliability. The findings position fractal analysis as a practical tool for early damage detection, data-driven prognostic modeling, and economically viable bridge assessment systems, with future work focused on automating damage classification through machine learning and full-scale field validation.

4. Conclusions

This research conducted an in-depth investigation into the fracture behavior of concrete beams incorporating RCA and RFA through the application of the box-counting method to quantify the fractal dimension of cracks under loading conditions. The results demonstrated that concrete beams with RCA exhibited significantly higher fractal dimensions of cracks compared to those with RFA. This phenomenon can be attributed to the inherent material properties of RCA, characterized by relatively lower elastic moduli and compressive strengths. Consequently, recycled coarse aggregate concrete beams displayed diminished deformation resistance and reduced ductility, resulting in more pronounced late-stage crack propagation. A direct proportional relationship was identified between the RCA and RFA replacement ratios and the crack fractal dimensions, indicating that an increase in both RCA and RFA substitution promotes more extensive crack development and exacerbates the severity of damage.

The application of polynomial trend surface fitting techniques facilitated a comprehensive examination of the intricate relationships among RFA/RCA dosage, applied load, and the fractal dimension of crack propagation. For RFA, the dosage exerted a negative quadratic influence, while the load had a positive linear effect on the fractal dimension. The presence of an interaction term further highlighted that the influence of RFA dosage on the fractal dimension became more pronounced with increasing load. Moreover, a second-order functional relationship was established between the mid-span deflection and the fractal dimension of cracks. This nonlinear correlation implies that as the complexity of cracks, as quantified by the fractal dimension, increases, the mid-span deflection of the concrete beam also changes in a nonlinear manner, consistent with the nonlinear mechanical behavior of concrete structures under load. In summary, the findings of this study advance the understanding of the fracture behavior of recycled aggregate concrete beams. The fractal dimension of cracks serves as a powerful quantitative metric for evaluating the damage state and crack complexity of concrete beams.