Abstract
Triangular shapes have been studied from different perspectives over a wide temporal frame since ancient times. Initially, fundamental theorems were formulated to demonstrate their geometrical properties. Philosophy and art leveraged the peculiar aspects of triangles as building blocks for more complex geometrical shapes. This paper will review triangles by adopting a multidisciplinary approach, recalling ancient science and Plato’s arguments in relation to their connection with philosophy. It will then consider the artistic utilization of triangles, particularly in compositions created during the medieval era, as exemplified by the Cosmati Italian family’s masterpieces. Various scientific environments have explored triangular 2D and 3D shapes for different purposes, which will be briefly reviewed here. After that, Sierpiński geometry and its properties will be introduced, focusing on the equilateral shape and its internal complexity generated by subdividing the entire triangle into smaller sub-triangles. Finally, examples of triangular planar shapes that fulfill the Sierpiński geometry will be presented as an application in signal processing for high-frequency signals in the microwave and millimeter-wave range.
1. Introduction
This paper reviews the meaning of triangles from different perspectives, including mathematics, philosophy, and art. It discusses the applications of triangular shapes as resonating elements for microwave planar components and antennas.
Numbers initially motivated the Greek philosophers and mathematicians, who tried to reduce the interpretation of the world to specific numeric combinations and geometrical shapes. From this perspective, triangles were a focal point of the mathematical and philosophical efforts of Pythagoras and Plato, giving rise to the famous theorems and the dialogue known as Timaeus [1,2,3,4]. Sierpiński also published about Pythagorean triangles in [5]. Of course, the number “3” is also related to triangles because of the three edges of the geometrical figure. It has been invoked for reasons pertaining to its magic and religious nature, encompassing Catholic culture and several examples since the early historical ages.
In many ancient traditions, “3” is the counterpart to “4”, comparing the male and female principle or the complementarity of the sky and the earth. The number “4” has also been related to the four essential elements studied in the early stage of philosophy and science, i.e., water, air, earth, and fire. “3” + “4” gave rise to the number “7”, also considered “magic” for other reasons (one-fourth of the lunar cycle; the so-called “planets” of antiquity, including the moon and sun, the Pleiades, etc.) [6].
Concerning art, reutilizing small marble pieces coming from the destruction of old Roman temples, mainly columns and wall or floor slides, a medieval Roman family of marble workers invented the so-called Cosmatesque style, whose products are visible in many Catholic churches in Italy, but sometimes also abroad [7,8,9]. Geometrical representations with squares, circles, or spirals were manufactured from the XI to the XIII Century by the Cosmati family, and triangles were available in many compositions as building blocks of picturesque wide floors that looked like mosaics. More ancient artifacts are available in other places. It is interesting to see a handmade decoration from the Museum of Malta, La Valletta, which can be considered a preliminary fractal geometry (see Figure 1).

Figure 1.
Piece of a decoration exhibited in the Archeological Museum of La Valletta (Malta) with inner triangles embedded in a triangular frame (900 B.C., approximately; personal photo).
The Sierpiński triangles are figures belonging to the more general group of fractals [10,11]. They are obtained by a progressive subdivision of whole triangles into many internal triangles of decreasing size. From a mathematical point of view, many publications, software tools, and potential applications have been considered in past decades [12,13,14,15,16]. Triangles are possible elementary cells in the finite element method (FEM) of calculation for electromagnetic 2D and 3D simulations, where each side can represent a lumped element [17]. They are building blocks in manufacturing processes like 3D printing, contributing to mechanically stable structures, especially when combined in hexagons [18].
Finally, equilateral triangles can be seen as regular shapes resonating at specific frequencies when adequately sized and excited by a feeding system. A key point about resonators and antennas for high frequencies is the need for a feeding network to achieve an effective resonant response and good radiative performance for the antennas. This is especially important when the triangles are characterized by an additional internal complexity, as in Sierpiński geometry [19,20]. Like any other resonator, the coupling degree (electrical matching) determines the quality factor and bandwidth. In the case of planar components or antennas, the specific difference between them is necessary for substrates compatible with manufacturing processes for electronic components (high dielectric constant) or radiative elements (low dielectric constant). In both cases, the intrinsic frequency is determined by the size and the choice of substrate. Moreover, triangles are building blocks that are suitable for applications in resonating or radiative arrays, properly combining several of them [20].
In this paper, the triangle is presented from a complementary viewpoint rather than its applications, and some configurations inspired by the Sierpiński geometry will also be proposed for specific configurations in high-frequency signal processing.
The visual representation proposed in this paper serves as a tool for introducing the general reader to the topic. This contribution compiles examples from various scientific, philosophical, and artistic fields that showcase the triangular shape, aiming to provide a comprehensive review and highlight the inspiration derived from this shape in diverse applications. Consequently, the sections of this paper that introduce the Sierpinski and simple triangles have been extended and detailed, focusing not only on the microwave engineering aspects, which are reserved for the final section, where high-frequency applications are discussed.
The introductory part of the present contribution can be considered a review that demonstrates the intriguing characteristics of and fascination with triangular shapes, as well as their utilization as basic forms in various contexts. Starting from this approach, the same shapes have been studied for microwave engineering purposes, proposing full and Sierpinski geometries in guided wave structures and free propagation, discussing applications for signal filtering and antennas of equilateral shapes. The main advantage of fractal Sierpiński configurations, as discussed in this paper, is the possibility of using them as building blocks in arrays to design both microwave filters and antennas. This approach allows for the combination of resonance frequencies or tuning them due to the increasing internal complexity while maintaining the same edge length. This characteristic is particularly fascinating when designing edge-coupled configurations, as it influences the structure’s central frequency and bandwidth. Limitations of Sierpiński triangles in microwave applications include the more complex design due to the high number of discontinuities generated by their internal subdivisions, as well as the necessity to account for grating widths or non-equilateral shapes. On the other hand, the triangular shape and other fractal geometries are also invoked for miniaturization purposes. In our case, coplanar resonators are presented as counterparts to the devices already studied with microstrip feeding, and specific bowtie Sierpiński antennas with an original feeding system are also presented.
2. Philosophy, Mathematics, and Art
Early philosophical currents have always considered mathematics and geometry interrelated and able to bring an inner meaning to understanding the natural order through symbols and specific shapes. This initial thinking was usual when no specialization was present among the scientific disciplines, and ancient thinkers had an intermediate profile between science and philosophy, trying to propose a unitary vision of the world based on general concepts linked to many knowledge fields, like astronomy and basic mathematics. Such a holistic vision of the world is also typical of Eastern philosophy, but in that case, another, more spiritual approach is pursued. In ancient Greece, a logical and scientific methodology puzzled scientists and philosophers, who were able to open schools with the ambition to select people able to understand matters considered “esoteric”, i.e., reserved for a selected group of students. This definition has nothing to do with other currents inspired by the magic meaning of numbers and shapes, which was trendy, especially in the XIX century.
2.1. Plato
The Timaeus essay of Plato, dating back to 360 B.C., treats the triangle as a building block figure giving rise to solid figures. His understanding of reality was based on the World of Ideas and Forms, such that the original theory of the four elements evolved considering the presence of basic shapes, which are regular geometrical solids: Tetrahedron (fire), Octahedron (air), Icosahedron (water), and Cube (earth). Following this approach, the shapes correspond one by one to the four fundamental elements introduced in previous times to model reality. All the natural manifestations resemble their counterparts in the World of Ideas, with the possibility of exchanging their nature and being transformed into another shape. This way of proceeding preludes to the development of alchemy during the Renaissance period, to study the possibility of transforming basic materials into noble ones. The typical goal was to start from lead to obtain gold using one of the properties of the so-called philosopher’s stone [21]. Paracelsus was one of the most famous alchemists, introducing new concepts and materials even in toxicology [22]. Without forcing the comparison, we can say that the intuition of Plato, and successively that of the Alchemists, also preludes to modern findings, with chemical and nuclear reactions able to obtain different elements from proper initial conditions, energy, and involved elements or materials. It can be noted that the term “alchemical” is still used to indicate a process during which a chemical species is transformed into another via a pathway of nonphysical (alchemical) states, as discussed in [23,24] concerning free energy calculations. The Arab alchemist Jabir ibn Hayyan is considered one of the first to link the four elements to alchemy, a term derived from the Arab language meaning “chemistry”. In ancient times, Aristotle introduced the principles of heat or cold and dryness or moisture, relating them to the four basic elements. In the historic alchemical approach, dating mainly to the so-called Renaissance period (15th–16th centuries), the reason for using triangles was to indicate the preferred direction of the four basic elements. So air and fire are described by triangles pointing upward, while water and earth are symbolized by triangles pointing downward. In particular, the triangles representing earth and air are plotted with a line bisecting the triangle, as shown in Figure 2 [25].
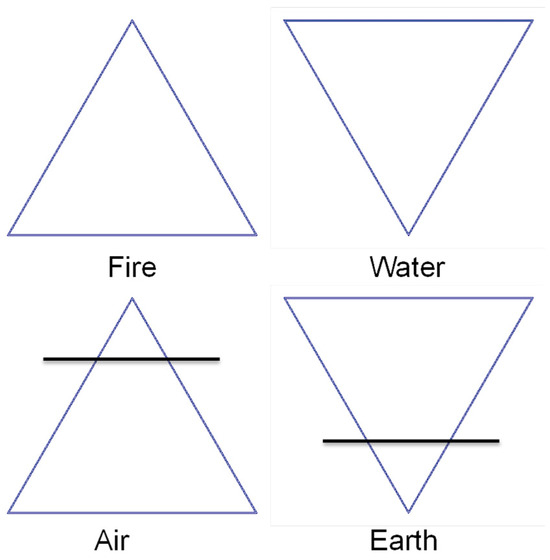
Figure 2.
Alchemical representation of the four basic elements. The shape, the orientation, and the segment distinguishing the up or down position are the signature of each element.
Returning to Plato, his perfect polyhedral shapes comprise triangular faces with internal angles of 30–60–90 and 45–45–90 degrees, respectively. In detail, half of a square and half of an equilateral triangle are considered by Plato to be the fairest geometrical figures, able to give rise to all the others. See, for instance, [26]. An interesting recent book about ancient mathematics, including Plato’s approach to philosophy using geometry, is [27]. That book emphasizes that studying ancient mathematics means forgetting about analytical developments, as this kind of formalism is a recent advancement. Formulas cannot be immediately applied to geometrical and physical scenarios that only now have a synthetic representation using equations. Sometimes, it is questionable even to translate the Greek term “ἀριϴμoν” with “number”. In [27], it is also remembered that Plato defined God as a geometer, citing other authors who claimed the role of God as a mathematician. The above consideration exemplifies a well-known phenomenon in previous times, when philosophy and science were part of a unique discipline, sometimes mediated by religious aspects. In Plato’s case, his personal growth was mainly in philosophy, first as a student of Socrates and after that following a personal path proposing his approach to an ideal state. Returning to Athens after long periods spent in Sicily with tyrants Dionysius I and II, he founded the Academia, inviting high-level students with different backgrounds, including mathematics. He was so enthusiastic about mathematics that he mixed that matter with his philosophical interests, giving rise to an original theory to use special triangles to obtain 2D and 3D polygons and linking ideal shapes to the above-mentioned four basic elements. It is sometimes difficult to translate correctly an ancient text that has been written colloquially, and nowadays, there are still doubts about an authentic interpretation of Plato’s texts. The complete picture of Plato’s philosophical approach to nature includes the presence of a Demiurge, i.e., an alternative definition of a God that is not a Creator but a superior entity creating order using pre-existent elements. From this point of view, the Platonic Solids are building blocks linked to the four basic elements, plus the presence of a fifth one, considered later in the Medieval Age and defined as a quintessence, identified with the dodecahedron. A description of the Platonic Solids and their relationships with fire, air, water, and earth can be found in the original essay of Johannes Kepler [28], and it is reproduced in Figure 3.
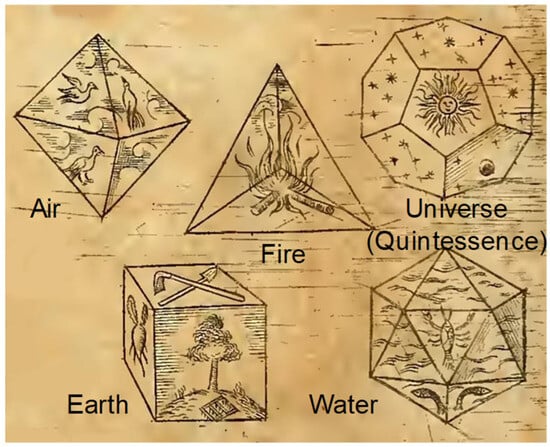
Figure 3.
Platonic Solids and their relationships with basic natural elements: cube is earth, tetrahedron is fire, icosahedron is water, octahedron is air, and dodecahedron is universe. Later, the fifth solid figure was interpreted as quintessence. Re-elaboration from [28].
Using a simple geometrical approach, all the 2D polygons can be subdivided using triangles (equilateral, rectangular, and isosceles). A triangle can be used as a building block for creating 2D polygons and, in the limit for a small angle α in the upper corner (or vanishing length s of the circular sector), a circle. An example of this construction is shown in Figure 4.
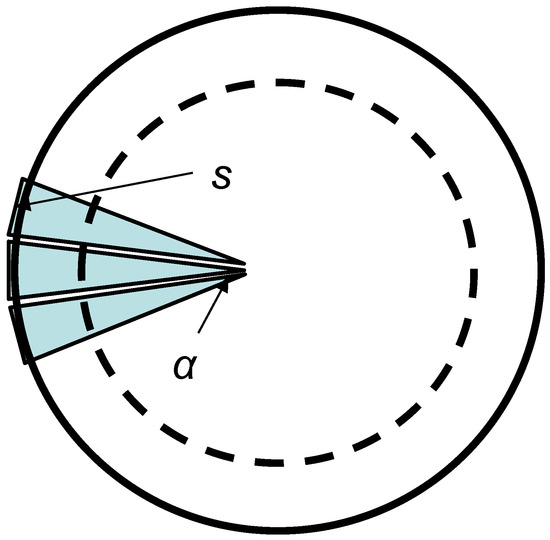
Figure 4.
Construction of a planar polygonal shape using triangles, leading to a circle in the limit conditions. The blue sections are elementary slices, with small arcs s and corresponding angles α, and the dashed line indicates the path to fill the entire circle.
The same procedure can be applied to 3D figures using a tetrahedral pyramid, i.e., a polyhedron that connects a polygonal square base and the apex. In this case, we can even produce a sphere for the same limit conditions, considering a volumetric extension of the infinitesimal pyramid.
An interesting paper about art and mathematics discussing the Platonic Solids in this framework is given in [29]. It is also stressed that the number of regular polygons is infinite but the number of regular solids is finite.
It is worth noting that Plato’s approach was affected by an error, as Johannes Müller von Königsberg (1436–1476), better known as Regiomontanus, demonstrated and discussed in [30]. Using a more precise demonstration, not affected by the understandable approximations of the initial approach, probably due to the utilization of imperfect wood models, we can conclude that an approximately 7° angle is still needed to complete a solid figure using only tetrahedra.
2.2. Ancient Art and Cosmatesque Decorations
In the Introduction, it was underlined that despite their symbolic meaning, triangles are part of many artistic decorations. Crossing lines was probably one of the initial ways humans created shapes, together with other preliminary techniques, continuing with artistic hunting scenes and everyday life pictures in the caves. After that, many authors have used numbers and shapes with specific intents over the centuries [31,32], with alchemical meanings or indications that someone belongs to a group. The triangle is the Catholic symbol that means the triple God identity (Father, Son, and Saint Spirit). That symbol, with the same meaning, is even used in the American one-dollar banknote.
After the fall of the Roman Empire, several ancient buildings were destroyed by external populations, conquering the previous domain of Rome. Marble from the Mediterranean area, initially used for columns, floors, and walls in buildings belonging to the emperor and rich families, was abandoned and no longer maintained. Then, pieces of precious marble could be reutilized in decorative items, arranged in fragments, and proposed in original designs. In this framework, the Cosmati family developed a style based on geometrical configurations, primarily used for church floors, in response to the Pope’s requirements [7]. A mathematical approach, accompanied by a detailed description of Cosmatesque triangles and carpets, is interpreted using Sierpiński theory, as presented in [33,34]. A few examples of Cosmatesque representations, including Sierpiński triangles, are shown in Figure 5 from the Roman church “San Lorenzo fuori le mura” (San Lorenzo outside the walls), but several other examples can be easily found, where triangles are used as the main shape or are part of a more complicated figure, like in Figure 6 and Figure 7. Another classic example of Cosmatesque art is in the Saint Nilo Abbey (an orthodox church with a Christian rite, in Grottaferrata, a small town very close to Roma), as shown in Figure 8. From all of these examples, it is evident that triangular shapes sometimes have an inner meaning, like indicating a direction to be followed, or they are just an easy geometrical shape to be produced from the original pieces.

Figure 5.
Roman church of “San Lorenzo fuori le mura” (outside the walls). Two examples of a Sierpiński-like floor decoration made by fragments of old imperial material. Medieval age, around 1200 (personal photo).


Figure 6.
Triangles used in a Cosmatesque floor: above, from the dome in Civita Castellana, near Roma (internet photo from https://cosmati.wordpress.com/category/pavimenti-cosmateschi/ (accessed on 29 June 2025), by Nicola Severino) and below from the church “Santa Maria in Trastevere” (personal photo).

Figure 7.
Labyrinth symbolizing the path toward the truth in the dome of Ravenna, Italy (personal photo).


Figure 8.
Cosmatesque style with triangles from the Saint Nilo abbey in Grottaferrata, near Roma (personal photo).
2.3. Other Cultural Environments Using Triangles
Several other fields, both scientific and non-scientific, utilize triangles for various purposes. In psychology, Robert Sternberg from Cornell University developed the triangular theory of love to explain passion, intimacy, and commitment as building blocks in human relationships [35].
Several examples of triangular arrangements of stars and planets are found in astronomy. Even if we know that constellations do not exist, in the sense that sometimes we see a specific shape using stars that only apparently belong to the same group or are close to each other, in some cases a “conjunction” can be claimed using the positions of planets and satellites as we see them from the Earth. In many instances, it is rare to see a triangular geometry involving planets, stars, and satellites, as is the case with the moon and planets within the solar system. An example is from the National Geographic Magazine in [36], where the Moon–Jupiter–Venus conjunction is photographed in a triangular configuration, whose next appearance will be in 2040.
Triangles can be illusions, like the Kanisza triangle, which is the result of an elaboration of our mind but does not exist as a real triangle. The above case is part of the general topic about illusory contours, i.e., the figures resulting from boundary conditions that lead the observer to the conviction that a specific shape is present even when it is not plotted [37].
Additionally, the triangular shape is used in other scientific contexts, which are also quite distinct. A typical example is the prism utilized in optics to decompose the spectrum of visible light into the wavelengths that give rise to the colors of a rainbow. Another example is using a triangular diagram to study the equilibrium state of a compound formed by three different chemical species in the right thermodynamic conditions for temperature and pressure, which is helpful in material science and medical applications [38].
A relatively new result for using triangular shapes is in manufacturing processes based on 3D printing to enhance a structure’s mechanical properties [39].
3. Mathematics and Geometry of Sierpiński Fractals
Triangles are categorized into distinct groups based on their shape. Equilateral, isosceles, and rectangular triangles are all suitable for arrangement in a more complicated planar structure. Still, equilateral ones are easier to subdivide and combine in an array, especially for applicative purposes.
Sierpiński triangles can be considered a fractal geometry derived from creating a series of internal triangles with decreasing size. Starting from the initial one, you can subdivide it by considering empty or full triangles and a frame with a specific thickness surrounding all the created sub-triangles. Independent of the above choice, Equation (1) describes the total number of triangles created by the internal subdivision:
where n is the complexity level and Nt is the number of sub-triangles generated. So far, n = 0 means an entire single triangle, and n = 1 means three sub-triangles plus an empty triangular shape, and so on. This situation is represented in Figure 9, where, for completeness, Sierpiński triangles are shown by creating holes in the usual way or the complementary one. As an example related to high-frequency engineering, the generation of Sierpiński triangles for the design of antennas using neural networks was considered in [40]. The “negative” subdivision is complementary and gives back empty triangles surrounded by a frame. Choosing “positive” or “negative” (empty) sub-triangles is crucial in specific applications, such as high-frequency signal processing. It corresponds to a metalized or empty area photolithographically obtained onto the substrate.
Nt = 3n,
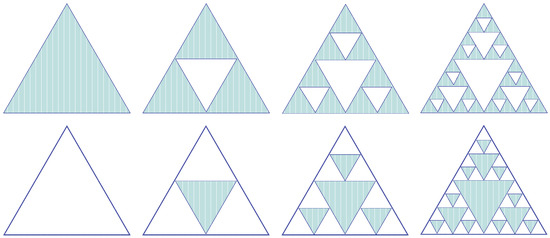
Figure 9.
Iterations to obtain the third level of complexity in the Sierpiński triangle for both positive (top line) and negative (bottom line) shapes. Dark areas and white areas represent the presence and absence of material in the plotted shape. For high-frequency structures it means to have a metallized or non-metallized area.
Sierpiński’s contribution was essential in obtaining a mathematical approach to formalize a theory supporting this specific shape, even if this geometry was already known, as discussed before, for different reasons. Since then, a mathematical formulation of the number of positive and negative sub-triangles and the area as a function of the internal complexity is available. In particular, the complexity level generates several internal sub-triangles, whose number is defined through Equation (1), with the side length decreasing as 1/2n, the total perimeter going to infinity, and the area vanishing when n grows. P = 3n+1/2n gives the perimeter for a triangle with a unitary edge length, while the area is A = (3/4)nA0, where A0 = √3/4. These simple rules can be used to verify their consistency with a possible general law that predicts the frequency of resonance in high-frequency resonators. Sierpiński triangles are typically considered to originate from an equilateral initial shape, but generalized approaches based on non-equilateral shapes are also available [41].
4. High-Frequency Applications
The utilization of equilateral triangles and their fractal evolution, namely Sierpiński ones, in antennas and resonators has been documented since the 1980s up to evolutions for carpet Sierpiński geometries [42].
Several configurations have been studied, including different feeding solutions, to capitalize on the unique characteristics that enable the modulation of geometry and the generation of multiple frequencies. Most of the literature is focused on equilateral triangles, but modifications are suggested to calibrate the frequency and control the spectrum. This task is not trivial because the analytical approach to predicting the resonance frequency is already complex, and electromagnetic simulations must often be used to support it for a direct comparison. The primary challenge is accounting for a structure that presents three significant electromagnetic discontinuities in the simple triangle and an increasing complexity when internal figures are introduced. For this reason, some papers are missing the spectra, probably because they match the expected resonances but are poorly excited [43]. In other papers, it was possible to make a comparison using simulations and experiments, but not formulae [44]. To the best of my knowledge, only in [45,46] was a numerical approach supported by measures successful in the spectrum prediction. Most other papers discuss comparisons between different methods, but they are often only occasionally supported by an experiment, even when suggesting valuable modifications to the original theory. An interesting approach is given in [47]. Additional considerations can be found in [48,49,50,51].
The engineering applications proposed in this paper encompass both planar devices (resonators) and free-space propagation (antennas). Some results have already been presented in other contributions, where the optimization of resonators’ performance is also discussed as a function of the distance between the triangle and several developed prototypes. Additionally, this section presents results confirming the predicted performance, including prototypes for GPS applications and radiation patterns. Other results presented here are numerical and were obtained for heuristic purposes. Nevertheless, various findings are confirmed by feeding the single resonators or more complex structures in [50].
It is important to note that several parameters should be considered for a general approach in studying this specific fractal figure. Additionally, other fractal structures, not necessarily triangular, are often examined by focusing on a particular geometry, without aiming to generalize the theoretical framework. Among these parameters, two are critical for analyzing the Sierpiński geometry for microwave engineering purposes: the feeding method and the width of the planar grating. Notably, the second parameter limits the potential for increasing internal complexity, based on the fundamental understanding of the photolithographic processes needed to manufacture the Sierpiński triangle. Typically, for the mass production of planar microwave devices, the minimum strip metal width on a dielectric substrate is around 10 µm. The reasonable maximum number of internal triangles depends on the grating width used to separate them. Even in the lowest microwave bands, below the X-frequencies (i.e., below 12 GHz), higher complexity does not reasonably exceed C5. When plotting a Sierpiński triangle, it is evident that the grating could be absent, which is an intriguing mathematical characteristic to consider regarding internal complexity, such as a perturbation of the whole patch (when the grating is present) or a collection of tightly connected individual triangles (when the grating is absent). Another challenge in generalizing the concept is studying non-equilateral triangles, which is explored in some detail in the paper [41]. For these reasons, several papers on Sierpiński triangles for use in microwave subsystems are now available. However, all of them focus on specific geometries, boundary conditions, or feeding solutions (microstrips or coplanar waveguides) [20,50].
Examining the studied devices, we can distinguish between the typical performance required by resonators and antennas, as both are resonating structures, but with distinct applications and specific definitions. The common feature of both structures is the frequency spectrum, and it is derived from the theory developed in [52] for equilateral triangles. On the other hand, a direct comparison between theory (an analytical approach or electromagnetic simulation) and experiment is possible when the triangular structure is excited by a feeding that is ideally electrically matched with the triangle; otherwise, the equivalent electrical circuit involving the feeding network and the triangle should include parasitic elements that are able to substantially modify the resonance frequency, the bandwidth, and, consequently, the quality factor. Classical antennas, like the patch ones with circular or square shape, were compared in [20] to demonstrate that the triangular choice helps mainly for three reasons: (i) the edge length determines the frequency of resonance, and a triangle has a smaller planar size than a square with the same edge by a factor of almost 2; (ii) the comparison with a square demonstrates that higher frequencies are possible for the main mode of this structure; and (iii) they are suitable for edge coupling instead of the well-known circles, which easy to design but impossible to be used side-by-side. Further, in the case of a Sierpinski arrangement including C0 and C1, or other combinations of Sierpinski geometry, the pattern can benefit from beam steering in a well-defined direction by design, as demonstrated later by comparing the C0, C1, and C0-C1 antennas.
The simulation software used in this contribution is Microwave Office Release 17.1 by AWR-CADENCE. I utilized the AXIEM environment implemented in this software, which is based on the method of moments, specifically examining the in-plane currents of the microwave structure. The frequency range for evaluating the high-frequency performance of the simulated structures spans from GPS to K-Band frequencies for antenna applications and includes X-Band frequencies for the resonators. This does not limit the use of such a geometry, as the primary resonance mode occurs at a frequency that strictly depends on the planar size and the substrate’s dielectric constant. The proposed geometries can serve as guidelines for design, tailored to specific applications, with no restrictions on frequency selection, except for the internal complexity associated with higher frequencies, such as millimeter waves, which demand extremely high resolution in manufacturing processes.
4.1. Resonance Frequencies
Polygonal shapes and their resonance frequencies for microwave applications were studied decades ago using precise electromagnetic field calculations. Microstrip-excited polygonal planar structures have been reviewed in [51,53], based, for triangles, on the analytical developments in [52]. Triangles were initially proposed with attention given to both theoretical and experimental findings, because they slightly enhance the quality factor of resonators and may be used as magnetic materials with this specific shape for circulator applications [54]. The simulated contour of the electromagnetic field indicates a higher value at the vertices of the triangles; this finding suggests that the vertex could be the ideal location to place the feeding of a triangular shape for resonators and antennas. However, we will see that general agreement with the first analytically derived mode is achieved through lateral coupling, thus favoring the edge, at least for planar resonators. In contrast, antennas require further investigation to reach the optimal solution for the radiation properties of the configuration. Despite the efficiency of excitation at resonance, the modes excited in a triangular shape are obtained using well-established formulas that consider the indices of the transverse magnetic and electric excitation modes. Three indices must be defined, fulfilling the basic equation m + n + l = 0, to solve the wave equation for the EM field components, where the abovementioned indices are all related to field components and are not independent variables. The fundamental mode is described by the (1, 0, −1) set of index values, from which the resonance wavevector value is k = 4π/3a, where a is the edge length of the triangle. The resonance frequency of the fundamental mode is given by [43]:
where c is the light speed in a vacuum and ε is the dielectric constant. From preliminary phenomenological evaluations about the necessity of introducing an effective size or an effective dielectric constant, it appeared that ε must not be corrected, while changing a to an effective value give us a more precise prediction of the resonating frequency [43]. Other modes can be excited, belonging to a series of resonances determined by the change of the indices [52]. It should also be noted that the resonance frequency prediction is a theoretical result of the bare structure when the excitation is optimized, ensuring electrical matching. It is well known that feeding is critical for efficient coupling with the desired resonance mode; otherwise, a significant frequency shift and modifications to the band shape are experienced. In the following paragraphs, this item will be considered again for resonators and antennas. Like any other geometrical figure manufactured for planar high-frequency applications, a triangle is a structure with resonance frequencies determined by its size. Additional properties can be considered if magnetic materials, such as Permalloy [55] or the classical garnets and ferrites [56], or ferroelectric materials [57] are used for tunability. As discussed above, the feeding network is crucial for enhancing the antenna’s radiation capabilities. A reasonably accurate design procedure for triangular antennas and arrays is described in [51,58]. The reason for having a microstrip excitation on the opposite side of the antenna is the necessity of avoiding metal radiative contributions on the same side, especially for substrates with a lower dielectric constant, where the microstrip can be broad and comparable to the antenna size. Another contribution to predicting the resonance frequencies for Sierpiński antennas is given in [40]. The fractal dimension enables the creation of a multi-band response, which is enhanced compared to the simple triangle. A good review of fractal configurations useful for radiation and filtering applications is given in [59]. The internal complexity of the Sierpiński geometry or a combination in an array can also modulate the expected resonance frequency. Still, we shall see that it can affect other radiator properties [60]. Many parameters are involved to determine the resonance frequency of a Sierpiński triangle, and equations governing this prediction should include (i) complexity level; (ii) grating width; (iii) a possible representation of the triangle with “positive” or “negative” complexity, i.e., with empty or full sub-triangles; (iv) a feeding solution and its coupling efficiency; (v) the modification of the resonance frequency when coupled triangles are considered; (vi) substrate material; and additional details still to be considered. This task is deferred to other possible papers, or even to a book. The current scientific literature gives a solution to the triangle’s spectrum based on the entire patch and not for Sierpinski figures. For the latter, a software-supported prediction is often considered in comparison to experimental results. Of course, more equations should be helpful, and not only one, to predict the resonance frequencies. Iterations in the increase in the Sierpinski complexity have been performed for microwave applications, primarily to ensure nearly the same coupling efficiency between the resonators or antennas and the feeding system while achieving frequency tuning due to the increased number of sub-triangles. The electromagnetic response of the Sierpinski structures changes because the electromagnetic field is locally altered, and the spectrum is consequently altered. In reference [44], only resonators on silicon wafers have been studied by feeding them in a CPW environment. In contrast, this paper uses microstrips for feeding, changes the substrate materials, alters the edge size and operational frequencies, and treats antennas, not only resonators.
4.2. Antennas
An example of the frequency response of the sequence from C0 to C3 (from the 0th to the 3rd iteration in the internal complexity) of a Sierpiński antenna is given in the simulations shown in Figure 10, where the substrate is the commercially available material Rogers 5880 (RO5880), with a dielectric constant ε = 2.2 and dielectric losses tanδ = 0.0009 for frequencies higher than 10 GHz [61]. A low dielectric constant impedes the excitation of substrate modes, otherwise lowering the overall antenna performance. The substrate thickness has been fixed at d = 1.575 mm, which is typical for commercially available ones. The metal thickness is t = 35 µm, which is also better for power applications, and the antenna is grounded. A frame of 200 µm surrounds the entire structure and each sub-triangle. A bowtie configuration with internal feeding has been chosen to show how the spectrum can be complicated by the internal sub-triangles of the antenna, whose feeding might be optimized depending on the frequency and the application. In Figure 10, the simulated configurations and the spectrum of the antennas are plotted, with evidence of a complicated response, with an increase in the number of the excitation modes as a function of the sub-divisions, even if identifying the modes to be compared is still subject to interpretation, as also the frequency shift appears to be not monotone with internal complexity. The excited mode strictly depends on the coupling solution. The S-parameters used to represent the electromagnetic response of resonators and antennas are typical quantities in microwave engineering, obtained as ratios between reflected and input voltage signals (S11 and S22) or between output and input signals (S21 and S12). They are a matrix of normalized non-dimensional quantities, often expressed in dB. In the simple case of passive structures, S21 = S12, with a reciprocal and symmetric response.
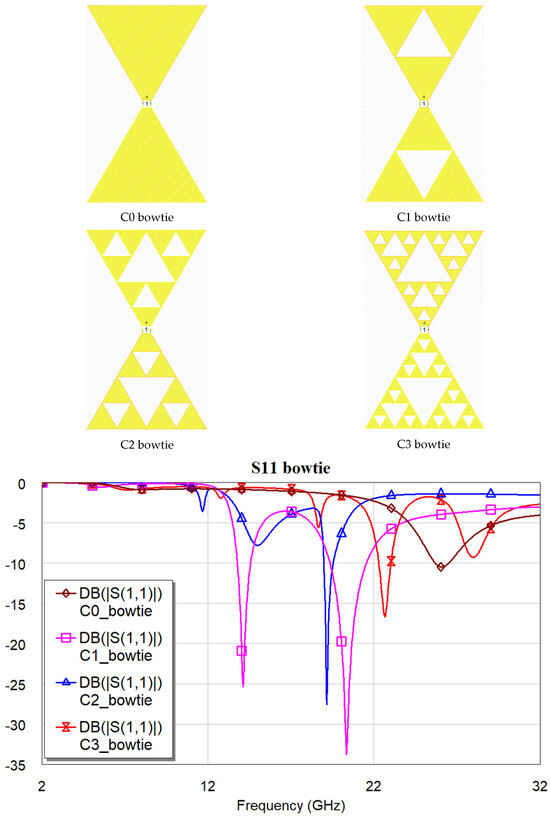
Figure 10.
Configurations and spectrum (in dB) of the Sierpiński bowties. Simulation by Microwave Office 17.1.
The radiation pattern at resonance exhibits a narrow lobe when measured in the middle of the two wings. It is broader in the 90° position, as shown in the plot in Figure 11 at resonance for C0, i.e., at approximately 26 GHz. The expected antenna gain is on the order of 7 dB. Qualitatively, the same radiation pattern is predicted for all the configurations at resonance. Nevertheless, better matching is obtained for C1, which exhibits a gain of around 7.8 dB at 20 GHz and enhanced sidelobe suppression, as shown in Figure 12. The presence of a substrate and the ground condition alter the response of the naked structure. Still, it is necessary to simulate a situation closer to the experimental one, where a feeding line should be present, and the ground helps improve the antenna gain.
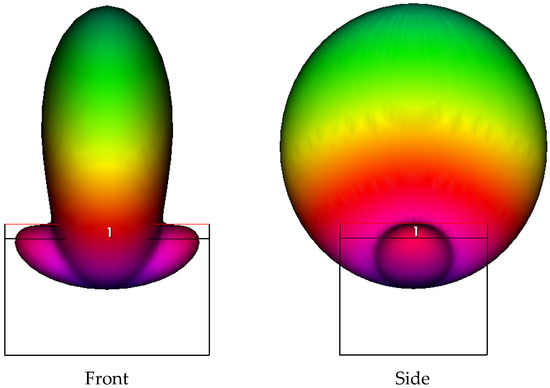
Figure 11.
Front and side view of the radiation pattern for the C0 configuration at 26 GHz. The black profile is a schematic of the transversal size of the antenna, while the colors represent the normalized intensity of the power emitted by the radiator, from the maximum value (green) to the lowest (red and pink).
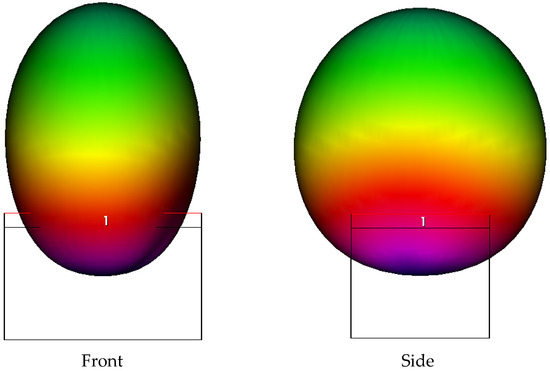
Figure 12.
Front and side view of the radiation pattern for the C1 configuration at 20.3 GHz. black lines are the front and side schematic representation of the antenna size, while the colors indicate the normalized power radiated from the antenna; green on the top is the maximum value, while the other colors measure a decreasing intensity (red and pink).
Concerning the feeding network, having a line on the opposite side of the antenna helps vanish its contribution for radiation purposes, and the radiation and gain are related mainly to the antenna itself and not to the feeding lines. Moreover, the microstrip will be narrow if designed on a substrate with a higher dielectric constant than the antenna. Two options can be used to excite the radiating element: a direct connection with a via hole or a slot. We shall see the simulation results using a via hole combined with a particular shape for the slot. The antennas previously studied with “internal ports” were fed using a microstrip line designed onto a 254 μm thick RO3006 substrate with ε = 6.5. A via hole was introduced to connect the microstrip to the center of the bowtie, and the coupling between the microstrip and the antenna was optimized using a slot geometry with the shape of a St. Andrew cross, designed on the ground plane of the feeding microstrip. Passing close to the antenna edges, the electric field appears better coupled instead of using conventional circular or rectangular slots. A few antennas have been studied for possible GPS frequency applications.
An array makes a natural implementation of single radiating elements, primarily to obtain improvements in the power handling and antenna gain. In this case, triangles or shapes like triangles can be arranged to obtain more complicated structures [62]. While the bowtie is suitable for preliminary information because of its straightforward structure, an array needs a proper feeding network to be studied, accounting for the initial information on the single elements [63,64]. The above consideration implies that the heuristic approach used with internal ports to evaluate the behavior of single triangles fails for a structure that includes more elements. For this reason, bowties are studied in this section, accounting for feeding using a 50 ohm microstrip placed on a substrate on the opposite side of the radiator and with a via hole connecting the feeding line to the central position of the antenna. Of course, this approach requires a different formulation and definition of the boundary conditions. In a 2.5D simulation typical of the AXIEM simulation environment for the software Microwave Office release 17.1 distributed by AWR-CADENCE, an additional metal plane with a finite size has been included to provide the ground for the microstrip. Specifically, a 330 µm wide microstrip, designed onto a RO3006 substrate with ε = 6.5, tanδ = 0.002 and thickness t = 254 µm, is used to excite the antennas, with a via hole passing through the ground plane with a diameter equal to the microstrip width and an external hole in the ground with a diameter doubled compared to the microstrip width.
Four antennas were simulated, also accounting for details of the packaging, designed as a metal box surrounding the antennas and electrically matched with the internal ground planes using via holes. The antennas have the same internal complexity studied for the ones excited using an internal port, but a different stack-up with a thick RO5880 (2 × 3.175 mm, i.e., a superposition of two standard values for this material) and a 0.254 mm thick RO3006 hosting on the backside the feeding microstrip and metallized at the interface with the antenna substrate. A 10 mm separation was imposed between the microstrip plane and the metal ground of the antenna packaging.
The four simulated antennas are shown in Figure 13, while Figure 14 gives the resonance curves, and the resonance frequencies are labeled. All the simulations were performed using Microwave Office release 17, and the same boundary conditions and size for the antennas, changing the internal complexity of the Sierpiński triangles forming the bowtie.
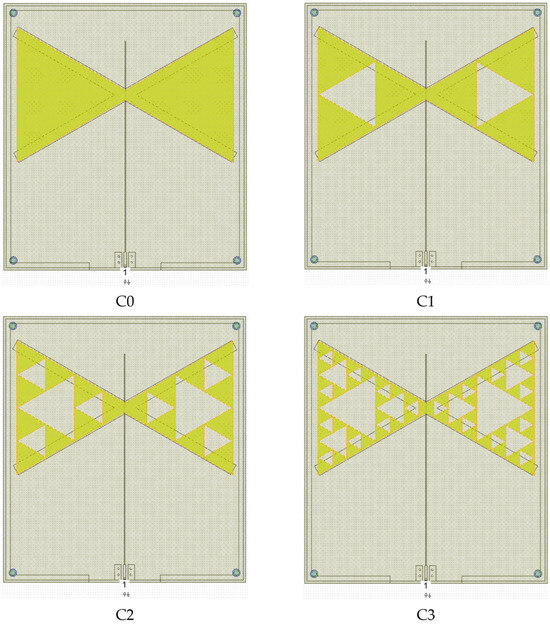
Figure 13.
Four antennas were simulated by Microwave Office to study the resonance properties of a structure suitable for immediate GPS applications, including a feeding microstrip line and a metal packaging, with a 10 mm separation from the bottom side of a metal box. The edge length is 5.66 cm. The St. Andrew Cross used to feed the antennas is visible below the radiating elements. The yellow color represents the top of the structure, where the antenna has been manufactured, while external black color is the frame of the metal box hosting the antenna. The central black line is the microstrip feeding antenna manufactured on the back side of the substrate. The four circles on the corners are the screws fixing the antenna in the metal box.
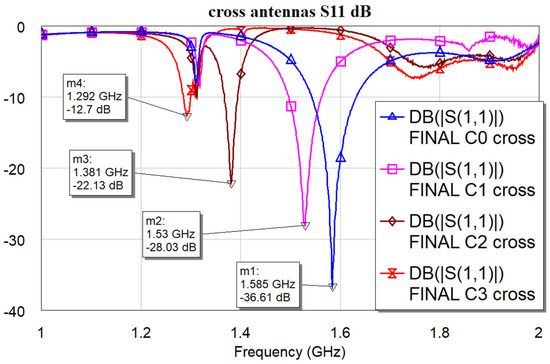
Figure 14.
Resonance response of the simulated antennas, namely four bowties with Sierpiński geometry having internal complexity of C0, C1, C2, and C3, respectively.
From the analysis of Figure 14, it is evident that a modulation of the frequency is possible by changing the Cn-complexity, even if an optimization is still needed, accounting for the variation of the metal border interfacing the feeding line. The best coupling condition is obtained when the triangle has a homogeneously filled edge. In contrast, a decrease in the coupling efficiency is recorded when the fragmentation of the edge is imposed, and inhomogeneities in the electric field between the triangle and the feeding structure are caused. Nevertheless, a good response is expected up to C2 complexity, while C3 needs further improvements. It is worth noting the decrease in the resonance frequency with an increase in internal complexity, thus providing shape-dependent frequency tuning.
Three breadboards were manufactured to demonstrate the expected response for the most promising configurations, i.e., C0 and C1, coupled by a cross and a via hole to the microstrip feeding. Additionally, a mixed structure was created to verify the steering effect introduced by this specific combination because of the non-symmetric configuration of the triangular radiators in the bow-tie arrangement. The three experimentally tested antennas are shown in Figure 15.

Figure 15.
Antennas C0 (on the upper-left corner), C1 (on the upper-right corner), and C0C1 (lower-left corner) were experimentally tested. They were manufactured according to the materials and parameters used for the simulations, i.e., Rogers substrates RO5880 (ε = 2.2) and RO3006 (ε = 6.5).
In Figure 16, the radiation pattern at resonance for the manufactured antennas is plotted, providing evidence of an almost overlapping radiation pattern at the experimental resonance frequencies for each antenna. However, for C0C1, there is a 20-degree shift of the maximum due to the asymmetry of the chosen configuration.
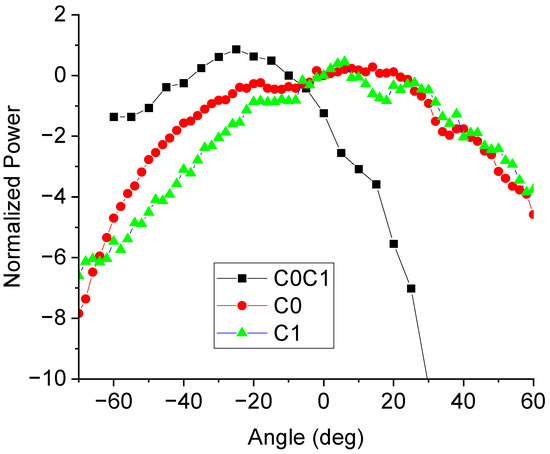
Figure 16.
Radiation pattern for the three experimentally measured antennas at resonance: C0, C1, and C0C1.
In Figure 17, the resonance for C0 and C1 is plotted as a function of frequency, demonstrating the trend in obtaining a decrease in the resonance frequency for the first level of complexity but also the necessity to improve the feeding system when a different Cn is considered. An additional resonance mode is also measured for C1 at lower frequencies.
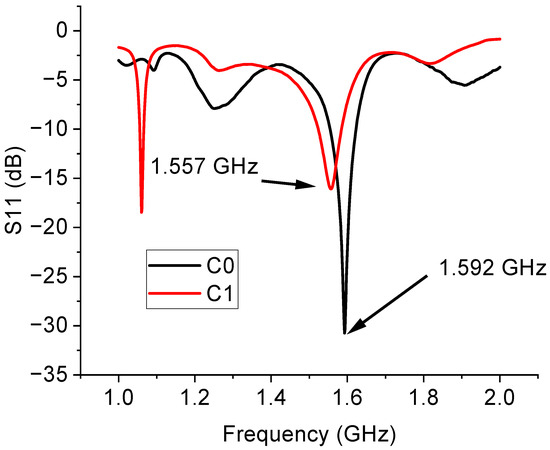
Figure 17.
Comparison between the experimentally measured antennas C0 and C1.
4.3. Resonators
The same fractal configurations used to present antenna applications are suitable for resonating planar structures. Planar filters fed by a coplanar waveguide configuration (CPW) based on triangles have been studied in [20]. In alternative, this section will present some examples of resonators for notch filters fed by microstrips.
Moreover, a possible interpretation in terms of metamaterial structures has been discussed in [65].
Following the same idea, simulations of microstrip-excited Sierpiński triangles will be analyzed in this section. The planar structure is now minded for planar signal processing. Unlike antennas, the high-frequency signal must not be radiated; instead, the substrate has a high dielectric constant to confine the electromagnetic field along the propagation path. A standard configuration is proposed here using a 525 µm thick high-resistivity silicon wafer, for which a 420 µm wide microstrip is utilized to get a 50-ohm impedance for the feeding line. For the sake of simplicity, we shall use the same triangles previously introduced to propose K-band antennas with an edge 6 mm long.
Figure 18 shows the simulated structures, with a 5 μm thick metallization shape suitable to be manufactured by photolithography on the Si substrate, followed by ordinary electroplating. For completeness, asymmetric and symmetric configurations have been studied to show the best response regarding the excited modes and their electrical matching. Figure 19 shows the simulated spectrum for the asymmetric and symmetric structures.
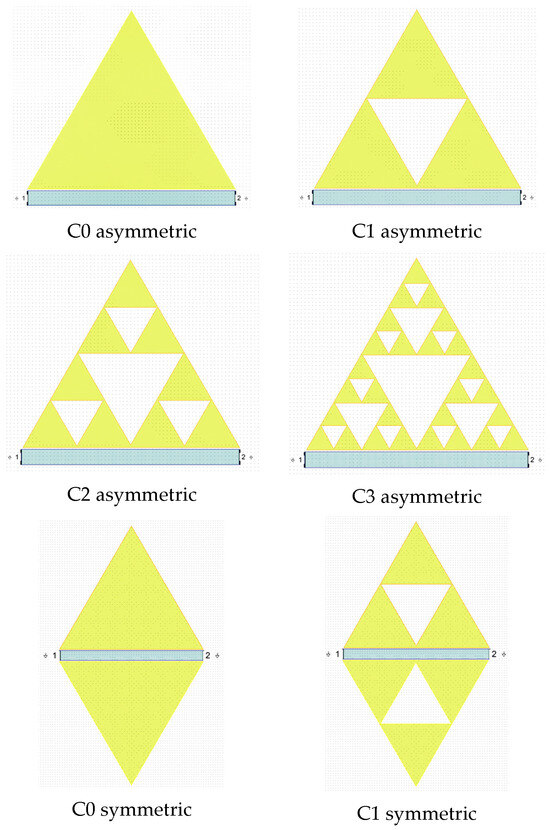
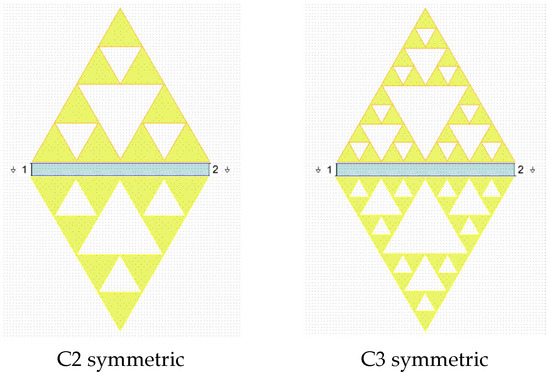
Figure 18.
Simulated resonating structures. (above) The four asymmetric configurations are shown. (below) The four symmetric ones are seen. The blue line is the feeding microstrip, 50 μm from the triangle edge. The metallization is always 5 μm.
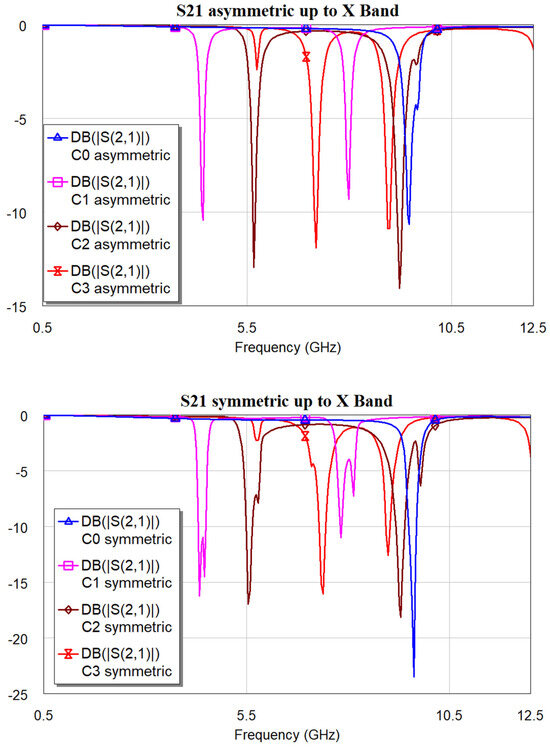
Figure 19.
Simulated response of the S21 trasmission parameter (in dB) for the asymmetric and symmetric resonators. Modes excited up to the X-Band (12 GHz) are shown in both cases. Simulation by Microwave Office 17.1.
Compared to the CPW excited resonators, where the separation from the central conductor, i.e., the separation between the microwave path and the side coupled resonating structure, was also 50 μm, some results are confirmed, with deeper notches when the symmetric device is considered. Nevertheless, asymmetric configurations also achieve acceptable performance, which must be considered when spatial occupancy is limited.
It is worth noting that it is easier to electrically match the microstrip-fed band-stop structure in comparison with the coplanar excitation 20, with a very low loss for the microstrip transducer outside the resonance peaks. The selectivity of the entire triangle C0 compared to the multi-resonance of the C1-C2-C3 structures gives another exciting characteristic of the modes in the investigated band. Table 1 shows the frequency position and separation for all the simulated devices in the asymmetric and symmetric configurations within the X-band.

Table 1.
Frequency of resonance for the simulated structures (asymmetric and symmetric). C0 symmetric and asymmetric do not show additional resonances in the same frequency range.
When two peaks close to each other are present, the more intense one is chosen. Further investigations are needed to interpret the simulated spectrum correctly.
Since all the proposed configurations are also suitable for higher-frequency resonances, this can also help in different microwave bands.
Still, the spectrum is more difficult to interpret or manipulate for a specific application. This is evident in Figure 20, which shows the predicted full spectrum of the C3 configuration, with promising results, especially in the K-band.
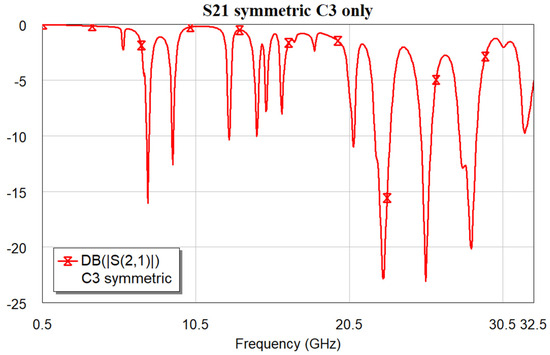
Figure 20.
Simulated spectral response for the S21 parameter (in dB) of the C3 resonator in the symmetric configuration up to 32 GHz.
So far, Sierpiński triangles can easily be considered for a multi-resonance response, and a proper, non-canonical reorganization of the internal triangles, even renouncing the classical equilateral shape for the building block, can help calibrate the desired resonance frequencies.
4.4. Further Considerations, Limitations, and Future Work for Microwave Applications
The long-term debate about triangular shapes, dating back to the Greek philosophers, is not marked by a consistent effort to use triangles for any particular purpose. Nevertheless, despite the various fields inspired by this shape, triangles have been successfully utilized in a wide range of applications. Initially, the quest for an elementary shape to understand reality was the primary guideline followed by Plato, which inspired many pre-scientists, alchemists, and philosophers for centuries. Their work involved the reinterpretation and evolution of the original knowledge system, based on the elements of air, water, earth, and fire. Subsequently, triangles were employed for simple decorations (e.g., mosaics), plotting purposes (e.g., chemical phase state representations), and structural strength (e.g., 3D printing) and as basic shapes in the mesh for electromagnetic simulations. Notably, the last two examples illustrate how triangles serve as building blocks not only for knowledge but also for technological applications, creating a long connection between ancient philosophers and modern scientists. Resonators and antennas have long been a focus in high-frequency engineering, and we discussed how to leverage this distinctive shape to achieve more compact notch filters and radiators that can be easily arranged in arrays. The potential to enhance triangle properties through unconventional geometry, such as that proposed by Sierpiński, has opened a new perspective on modulating the response of a microwave subsystem for engineering purposes. The current work, which utilizes planar resonators and antennas, demonstrates the feasibility of devices based on the Sierpiński geometry in single configurations, implementing feeding mechanisms for both types of devices. A second level of complexity is represented in the case of the antennas by the utilization of the bowtie configuration, which combines two Sierpiński triangles that are, in principle, different from one another. Further work is in progress, both theoretical and experimental, to predict the spectrum involving the increase in complexity of the internal subdivisions, and to determine the conditions for the optimal coupling of the resonators and antennas with the feeding system, as well as the edge-by-edge coupling to achieve arrays of filters and antennas. A specific point to be discussed soon will be the opportunity to use microstrips or CPW to obtain the best electrical results and integration capabilities.
5. Conclusions
The triangle figure, with a focus on the equilateral one and its Sierpiński variants, has been discussed in this contribution from different points of view. It was always an intriguing figure, animating discussions in philosophy and mathematics about its relationships with the elemental constituents of reality. A few examples of Cosmati art were also presented to demonstrate its use in creating original and unique decorations. Then, microwave engineering applications for planar signal processing and antennas have been proposed with a very basic design, exhibiting promising responses in different frequency bands. The possibility of obtaining a multi-frequency response has been stressed thanks to the internal complexity generated by the Sierpiński geometry. Additional non-canonical variants of the internal geometry can adequately tailor the excited resonance modes for specific multi-resonance applications of antennas and resonators.
Funding
This research received no external funding.
Data Availability Statement
Upon requirement.
Acknowledgments
The author thanks all the colleagues who have contributed to this subject in past and current cooperations, specifically, Emanuela Proietti, Giovanni Capoccia, and Giovanni Maria Sardi for design, processing, and measurement activities at CNR-IMM; Flavio Giacomozzi, Jacopo Iannacci, and Girolamo Tagliapietra from FBK Foundation in Trento, for design and technologies activities; and Alina Cismaru from IMT Bucharest for design optimization of resonating and antenna structures. This paper is an extension of an invited article published on the Proceedings of the 2024 CAS Conference, by Romolo Marcelli: “Philosophy, Art, Mathematics, and High-Frequency Applications of Triangular Shapes: From Plato to Sierpiński and beyond”, 2024 International Semiconductor Conference, Sinaia, Romania, 9–11 October 2024 [66].
Conflicts of Interest
The author declares no conflict of interest.
References
- The Editors of Encyclopaedia Britannica. Pythagorean theorem. In Encyclopedia Britannica; Britannica: Chicago, IL, USA, 2024; Available online: https://www.britannica.com/science/Pythagorean-theorem (accessed on 14 June 2024).
- Burgin, M. Platonic Triangles and Fundamental Triads as the Basic Elements of the World. Athens J. Humanit. Arts 2018, 5, 29–44. [Google Scholar] [CrossRef]
- Artmann, B.; Schaefer, L. On Plato’s Fairest Triangles (Timaeus 54a). Hist. Math. 1993, 20, 255–264. [Google Scholar] [CrossRef]
- Lloyd, D.R. Symmetry and Beauty in Plato. Symmetry 2010, 2, 455–465. [Google Scholar] [CrossRef]
- Sierpiński, W. Pythagorean Triangles; Dover Publications Inc.: New York, NY, USA, 2003; Available online: https://www.softouch.on.ca/kb/data/Pythagorean%20Triangles.pdf (accessed on 25 June 2025).
- Stewart, I. Number Symbolism; Encyclopedia Britannica: Chicago, IL, USA, 2024; Available online: https://www.britannica.com/topic/number-symbolism (accessed on 19 June 2024).
- Williams, K. Paloma Pajares-Ayuela—Cosmatesque Ornament: Flat Polychrome Geometric Patterns in Architecture; W.W. Norton: London, UK; New York, NY, USA, 2001. [Google Scholar]
- Rodwell, W.; Neal, D.S. The Cosmatesque Mosaics of Westminster Abbey: The Pavements and Royal Tombs: History, Archaeology, Architecture and Conservation; Oxbow Books: Oxford, UK, 2019. [Google Scholar]
- Severino, N. “COSMATI: La Firma Dell’Artista. I Tratti Inequivocabili Dell’arte Cosmatesca Della Bottega di Lorenzo tra il XII e il XIII Secolo. Alla Scoperta del Repertorio Cosmatesco vero e Definitivo di Lorenzo, Iacopo, Cosma e Figli. Studi sui Pavimenti Cosmateschi,” ilmiolibro.it, Cromografica, Roma, Marzo 2014. Edizione Digitale Libera su Academia.edu. Questa Versione è Stata Corretta e Modificata il 15 Ottobre 2014. (In Italian). Available online: https://www.academia.edu/39870500/COSMATI_La_firma_dellArtista_I_tratti_inequivocabili_dell_arte_cosmatesca_della_bottega_di_Lorenzo_tra_il_XII_e_il_XIII_secolo_Alla_scoperta_del_repertorio_cosmatesco_vero_e_definitivo_di_Lorenzo_Iacopo_Cosma_e_Figli (accessed on 25 June 2025).
- Mandelbrot, B.B. The Fractal Geometry of Nature; Henry Holt and Company: New York, NY, USA, 1983; ISBN 0716711869/9780716711865. [Google Scholar]
- Falconer, K. Fractal Geometry: Mathematical Foundations and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2003; ISBN 978-0-470-84862-3. [Google Scholar]
- Sierpiński, W. Sur une courbe dont tout point est un point de ramification. Comptes Rendus Acad. Sci. Paris 1915, 160, 302–305. [Google Scholar]
- Bickle, A. Properties of Sierpiński Triangle Graphs. In Combinatorics, Graph Theory and Computing; SEICCGTC 2021; Hoffman, F., Holliday, S., Rosen, Z., Shahrokhi, F., Wierman, J., Eds.; Springer Proceedings in Mathematics & Statistics; Springer: Cham, Switzerland, 2024; Volume 448. [Google Scholar] [CrossRef]
- Sun, Q.; Cai, L.; Ma, H.; Yuan, C.; Xu, W. On-surface construction of a metal–organic Sierpiński triangle. Chem. Commun. 2015, 51, 14164. [Google Scholar] [CrossRef]
- Available online: https://it.mathworks.com/matlabcentral/fileexchange/158786-Sierpiński-triangle-generator (accessed on 7 July 2024).
- Available online: https://download.cnet.com/Sierpiński-triangle/3000-18498_4-75864275.html?ex=RAMP-2070.4 (accessed on 7 July 2024).
- Available online: https://www.comsol.it/multiphysics/finite-element-method (accessed on 7 July 2024).
- Guo, S.; Chen, W.; Wang, H.; Qiu, Z.; Wei, B.; Cheng, J.; Yuan, H.; Zhou, Y.; Luo, H. Simulation and experimental research on the cavitation phenomenon of wedge-shaped triangular texture on the surface of 3D-printed titanium alloy materials. Tribol. Int. 2024, 198, 109869. [Google Scholar] [CrossRef]
- Mishra, G.P.; Maharana, M.S.; Modak, S.; Mangaraj, B.B. Study of Sierpiński Fractal Antenna and Its Array with Different Patch Geometries for Short Wave Ka Band Wireless Applications. Procedia Comput. Sci. 2017, 115, 123–134. [Google Scholar] [CrossRef]
- Marcelli, R.; Capoccia, G.; Sardi, G.M.; Bartolucci, G.; Margesin, B.; Iannacci, J.; Tagliapietra, G.; Giacomozzi, F.; Proietti, E. Metamaterials based RF microsystems for telecommunication applications. Ceram. Int. 2023, 49 Pt B, 24379–24389. [Google Scholar] [CrossRef]
- Available online: https://en.wikipedia.org/wiki/Philosopher%27s_stone (accessed on 14 March 2025).
- Goodrick-Clarke, N., Translator; Paracelsus: Essential Readings, North Atlantic Books: Berkeley, CA, USA, 1999.
- Shirts, M.R.; Mobley, D.L.; Chodera, J.D. Chapter 4 Alchemical Free Energy Calculations: Ready for Prime Time? Spellmeyer, D.C., Wheeler, R., Eds.; Annual Reports in Computational Chemistry; Elsevier: Amsterdam, The Netherlands, 2007; Volume 3, pp. 41–59. ISSN 1574-1400. ISBN 9780444530882. Available online: https://www.sciencedirect.com/science/article/pii/S1574140007030046 (accessed on 25 June 2025). [CrossRef]
- Khuttan, S.; Azimi, S.; Wu, J.Z.; Gallicchio, E. Alchemical Transformations for Concerted Hydration Free Energy Estimation with Explicit Solvation. arXiv 2005, arXiv:2005.06504. [Google Scholar] [CrossRef]
- Holmyard, E.J. Alchemy; Dover Publication: New York, NY, USA, 1990; ISBN 10 0486262987. Originally published: Penguin, Harmondsworth, Middlesex, UK, 1957. [Google Scholar]
- Plato. Timaeus; Kalkavage, P., Translator; Focus Publishing/R Pullins & Co.: Newburyport, MA, USA, 2016. [Google Scholar]
- Herrmann, D. Ancient Mathematics—History of Mathematics in Ancient Greece and Hellenism; Springer: Berlin/Heidelberg, Germany, 2023; ISBN 978-3-662-66493-3/978-3-662-66494-0. [Google Scholar] [CrossRef]
- Kepler, J. 1571–1630; “Harmonices Mundi”, Ptolemy, 2nd cent; Fludd, Robert, 1574-1637; Tambach, Gottfried, fl. 1607–1632, Publisher; Planck, Johann, fl. 1615–1627, Printer; Burndy Library, Donor. DSI. Available online: https://archive.org/details/ioanniskepplerih00kepl/mode/2up (accessed on 25 June 2025).
- Emmer, M. Art and Mathematics: The Platonic Solids. Leonardo 1982, 15, 277–282. Available online: https://muse.jhu.edu/article/600238 (accessed on 25 June 2025). [CrossRef]
- Huylebrouck, D. Dark and Bright Mathematics: Hidden Harmony in Art, History and Culture; Copernicus Books; Birkhäuser: Basel, Switzerland, 2023; ISBN 978-3-031-36254-5/978-3-031-36255-2. [Google Scholar] [CrossRef]
- Kalvesmaki, J. The Theology of Arithmetic: Number Symbolism in Platonism and Early Christianity; Hellenic Studies Series 59; Center for Hellenic Studies: Washington, DC, USA, 2013; Available online: http://nrs.harvard.edu/urn-3:hul.ebook:CHS_KalvesmakiJ.The_Theology_of_Arithmetic.2013 (accessed on 25 June 2025).
- Cirlot, J.E. A Dictionary of Symbols: Revised and Expanded Edition, 1st ed.; Sage, J.; Miles, V., Translators; Victoria Cirlot (Afterword), Herbert Read (Foreword); NYRB Classics (1963 First Ed., 2020); New York Review of Books: New York, NY, USA, 2020; ISBN 10 1681371979/13 978-1681371979. [Google Scholar]
- Conversano, E.; Lalli, L.T. Sierpiński Triangles in Stone, on Medieval Floors in Rome. Aplimat J. Appl. Math. 2011, 4, 113–122. [Google Scholar]
- Brunori, P.; Magrone, P.; Tedeschini, L.L. Imperial Porphyry and Golden Leaf: Sierpiński Triangle in a Medieval Roman Cloister. In Advances in Intelligent Systems and Computing; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; Volume 809, pp. 595–609. ISBN 9783319955872. [Google Scholar] [CrossRef]
- Available online: https://en.wikipedia.org/wiki/Triangular_theory_of_love (accessed on 25 June 2025).
- Available online: https://www.nationalgeographic.com/science/article/see-a-rare-alignment-of-all-the-planets-in-the-night-sky (accessed on 25 June 2025).
- Available online: https://en.wikipedia.org/wiki/Illusory_contours (accessed on 25 June 2025).
- Alany, R.G.; Tucker, I.G.; Davies, N.M.; Rades, T. Characterizing colloidal structures of pseudoternary phase diagrams formed by oil/water/amphiphile systems. Drug Dev. Ind. Pharm. 2001, 27, 32–38. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Q.; Yin, J.; Wen, J.; Yu, D. Mechanical properties of 3D-printed hierarchical structures based on Sierpiński triangles. Int. J. Mech. Sci. 2023, 247, 108172. Available online: https://www.sciencedirect.com/science/article/pii/S0020740323000747 (accessed on 25 June 2025). [CrossRef]
- Dhaliwal, B.S.; Pattnaik, S.S. Artificial Neural Network Analysis of Sierpiński Gasket Fractal Antenna: A Low Cost Alternative to Experimentation. Adv. Artif. Neural Syst. 2013, 2013, 560969. [Google Scholar] [CrossRef]
- Steemson, K.; Williams, C. Generalised Sierpiński Triangles. arXiv 2018, arXiv:1803.00411. [Google Scholar]
- Gurjar, R.; Upadhyay, D.K.; Kanaujia, B.K.; Kumar, A. A compact modified Sierpiński carpet fractal UWB MIMO antenna with square-shaped funnel-like ground stub. AEU-Int. J. Electron. Commun. 2020, 117, 153126. [Google Scholar] [CrossRef]
- Dahele, J.; Lee, K. On the resonant frequencies of the triangular patch antenna. IEEE Trans. Antennas Propag. 1987, 35, 100–101. [Google Scholar] [CrossRef]
- Marcelli, R.; Sardi, G.M.; Proietti, E.; Capoccia, G.; Iannacci, J.; Tagliapietra, G.; Giacomozzi, F. Triangular Sierpiński Microwave Band-Stop Resonators for K-Band Filtering. Sensors 2023, 23, 8125. [Google Scholar] [CrossRef]
- Mishra, R.K.; Ghatak, R.; Poddar, D.R. Design Formula for Sierpiński Gasket Pre-Fractal Planar-Monopole Antennas [Antenna Designer’s Notebook]. IEEE Antennas Propag. Mag. 2008, 50, 104–107. [Google Scholar] [CrossRef]
- Anuradha, A.P.; Sinha, S.N. Design of Custom-Made Fractal Multi-Band Antennas Using ANN-PSO [Antenna Designer’s Notebook]. IEEE Antennas Propag. Mag. 2011, 53, 94–101. [Google Scholar] [CrossRef]
- Mukherjee, P.; Mukherjee, A.; Chatterjee, K. Artificial Neural Network based Dimension Prediction of Rectangular Microstrip Antenna. J. Inst. Eng. 2022, 103, 1033–1039. [Google Scholar] [CrossRef]
- Kumprasert, N.; Kiranon, W. Simple and accurate formula for the resonant frequency of the equilateral triangular microstrip patch antenna. IEEE Trans. Antennas Propag. 1994, 42, 1178–1179. [Google Scholar] [CrossRef]
- Priya, S.K.; Bhandari, J.K.; Chaitanya, M.K. Design and Research of Rectangular, Circular and Triangular Microstrip Patch Antenna. Int. J. Innov. Technol. Explor. Eng. 2019, 8, 10. [Google Scholar] [CrossRef]
- Cismaru, A.; Giacomozzi, F.; Pasteanu, M.; Marcelli, R. Design Optimization of RF MEMS-Driven Triangular Resonators with Sierpinski Geometry for Dual-Band Applications. Micromachines 2025, 16, 446. [Google Scholar] [CrossRef]
- Guney, K.; Kurt, E. Effective side length formula for resonant frequency of equilateral triangular microstrip antenna. Int. J. Electron. 2016, 103, 261–268. [Google Scholar] [CrossRef]
- Helszajn, J.; James, D.S. Planar Triangular Resonators with Magnetic Walls. IEEE Trans. Microw. Theory Tech. 1978, 26, 95–100. [Google Scholar] [CrossRef]
- Bahl, I.; Barthia, P. Microwave Solid State Circuit Design; John Wiley and Sons: New York, NY, USA, 1988. [Google Scholar]
- Akaiwa, Y. Operation Modes of a Waveguide Y Circulator (Short Papers). IEEE Trans. Microw. Theory Tech. 1974, 22, 954–960, Erratum in IEEE Trans. Microw. Theory Tech. 1979, 27, 709. [Google Scholar] [CrossRef]
- Aldrigo, M.; Cismanu, A.; Dragoman, M.; Iordanescu, S.; Proietti, E.; Sardi, G.M.; Bartolucci, G.; Marcelli, R. Amplitude and Phase Tuning of Microwave Signals in Magnetically Biased Permalloy Structures. IEEE Access 2020, 8, 190843–190854. [Google Scholar] [CrossRef]
- Geiler, M.; Gillette, S.; Shukla, M.; Kulik, P.; Geiler, A.L. Microwave Magnetics and Considerations for Systems Design. IEEE J. Microw. 2021, 1, 438–446. [Google Scholar] [CrossRef]
- Tagantsev, A.K.; Sherman, V.O.; Astafiev, K.F.; Venkatesh, J.; Setter, N. Ferroelectric Materials for Microwave Tunable Applications. J. Electroceramics 2003, 11, 5–66. [Google Scholar] [CrossRef]
- Sotyohadi; Afandi, R.; Hadi, D.R. Design and Bandwidth Optimization on Triangle Patch Microstrip Antenna for WLAN 2.4 GHz. In MATEC Web of Conferences; EDP Science: Les Ulis, France, 2018; Volume 164, p. 01042. [Google Scholar] [CrossRef]
- Patel, K.; Pandav, S.; Behera, S.K. Reconfigurable Fractal Devices. IEEE Microw. Mag. 2024, 25, 41–62. [Google Scholar] [CrossRef]
- Dwivedy, B.; Behera, S.K.; Singh, V.K. A Versatile Triangular Patch Array for Wideband Frequency Alteration with Concurrent Circular Polarization and Pattern Reconfigurability. IEEE Trans. Antennas Propag. 2019, 67, 1640–1649. [Google Scholar] [CrossRef]
- Rogers Corporation. RO5880 Data Sheet. Available online: https://www.rogerscorp.com/-/media/project/rogerscorp/documents/advanced-electronics-solutions/english/data-sheets/rt-duroid-5870---5880-data-sheet.pdf (accessed on 7 July 2024).
- Feng, G.; Qi, T.; Li, M.; Li, J.; Wang, X.-W.; Yang, H.-L. A low-profile broadband crossed-dipole antenna with fractal structure and inverted-L plates. Sci. Rep. 2022, 12, 14960. [Google Scholar] [CrossRef]
- Priya, S.S.; Nalini, S.; Sandhiya, R.; Sneha, S. Performance and Analyze of Cross Dipole Antenna with Parasitic Elements. Int. Res. J. Eng. Technol. 2020, 7, 915–919. [Google Scholar]
- Karunakar, G.; Dinesh, V. Analysis of microstrip triangular fractal antennas for wireless application. Int. J. Innov. Res. Electr. Electron. Instrum. Control. Eng. 2014, 2, 2216–2219. [Google Scholar]
- Marcelli, R. Equivalent Circuits for Microwave Metamaterial Planar Components. Sensors 2024, 24, 2212. [Google Scholar] [CrossRef]
- Marcelli, R. Philosophy, Art, Mathematics, and High-Frequency Applications of Triangular Shapes: From Plato to Sierpiński and beyond. In Proceedings of the 2024 International Semiconductor Conference, Sinaia, Romania, 9–11 October 2024. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).