Synchronization of Short-Memory Fractional Directed Higher-Order Networks

Abstract

This paper addresses the synchronization problem in complex networks characterized by short-memory fractional dynamics and directed higher-order interactions. Sufficient conditions for global synchronization are rigorously derived using Lyapunov-based analysis and an effective pinning control strategy. To further enhance the adaptability and robustness of the network, an adaptive control law is constructed, accommodating uncertainties and time-varying coupling strengths. An improved predictor–corrector numerical algorithm is also proposed to efficiently solve the underlying short-memory systems. A numerical simulation is conducted to demonstrate the validity of the proposed theoretical results. This work deepens the theoretical understanding of synchronization in higher-order fractional networks and provides practical guidance for the design and control of complex systems with short-memory and higher-order effects.

1. Introduction

Networks have become essential tools for studying complex systems and are typically represented by structures of nodes and edges [1]. Traditional networks, however, focus solely on pairwise relationships, limiting their ability to capture the group interactions common in social [2], biological, and technological contexts [3]. To overcome this limitation, higher-order networks such as hypergraphs and simplicial complexes have been developed, which capture multi-node relationships and thus offer a richer, more accurate framework for analyzing complex dynamics [4,5,6]. Various studies have made significant progress in modeling and analyzing collective dynamics and spreading processes on such higher-order structures [7].

Fractional calculus is known for its long-term memory effect, as the present state always depends on the entire history of the function [8]. For example, the Riemann–Liouville derivative integrates all past values $[t_0,t]$, making numerical computation costly and complex [9]. However, for large times, the influence of the distant past can often be neglected—a concept referred to as the “principle of dissipation of hereditary action” [10]. To address the computational challenges, Podlubny introduced the short-memory principle, which approximates fractional derivatives by considering only the recent history $[t-L,t]$, significantly improving efficiency [11]. Studies indicate that short-memory fractional derivatives are better suited for modeling systems exhibiting short-term memory effects, including impulse systems [12], neural networks [13], memristors [14,15], and fast image encryption [16]. This paper aims to advance the theory and application of such operators, further enriching the field of fractional calculus.

Synchronization refers to the process by which individual units within a network adjust their dynamics to achieve coordinated behavior [17]. This fundamental phenomenon is crucial for understanding the collective functioning of complex systems across disciplines, including physics, biology, neuroscience, and engineering [18,19]. Traditional synchronization studies often focus on integer-order dynamic systems; however, fractional-order systems, characterized by memory effects and hereditary properties, have recently become prominent due to their more accurate representation of various physical and biological phenomena [11,18]. Synchronization phenomena have been further expanded with the rise in fractional higher-order networks [20], such as higher-order neural systems [21], hypergraph-based complex systems [22], neutral higher-order neural networks [23], and multiplex higher-order networks [24]. Despite these advances, critical gaps persist in integrating short-memory fractional dynamics with directed higher-order topologies—particularly regarding synchronization control mechanisms. Therefore, the coupling of short-memory fractional dynamics with higher-order network structures introduces novel challenges and opportunities in studying synchronization.

The present study addresses this gap by proposing a novel framework for analyzing synchronization in directed higher-order networks influenced by short-memory fractional dynamics. The main contributions of this paper are summarized as follows:

• A new complex network framework featuring directed, high-order interactions governed by short-memory fractional dynamics is introduced. Unlike traditional models [13,14,15], more diverse and realistic connection patterns are captured by this formulation, enabling deeper insights into the collective behavior of complex systems.
• The synchronization of a generally short-memory fractional directed higher-order network using a pinning control scheme is investigated.
• An improved predictor–corrector algorithm for solving short-memory fractional systems is proposed. Based on this algorithm, a numerical simulation is conducted to verify the effectiveness of the derived theoretical results.

This paper is organized as follows: Section 2 introduces essential concepts, definitions, and lemmas. Section 3 presents the main results, including the model’s construction and its pinning synchronization. Section 4 details the predictor–corrector algorithms and numerical simulations. Finally, Section 5 concludes the paper.

2. Preliminaries

In this section, fundamental concepts, definitions, and relevant lemmas are presented.

Definition 1

([9]). Let $f\left(t\right)\in AC[t_0,+\infty )$. The short-memory fractional integral of $f\left(t\right)$ can be defined as

$${}_{s_L\left(t\right)}\widehat{I}_t^{\alpha }f\left(t\right)={\displaystyle \frac{1}{\mathrm{\Gamma }\left(\alpha \right)}}{\int }_{s_L\left(t\right)}^t{(t-\xi )}^{\alpha -1}f\left(\xi \right)d\xi ,$$

where $0<\alpha <1$, $L>0$ is the fixed memory length and

$${}_{s_L\left(t\right)}=\left\{\begin{array}{cc}{t}_0,\hfill & t\in [t_0,t_0+L),\hfill \\ t-L,\hfill & t\in [t_0+L,+\infty ).\hfill \end{array}\right.$$

(1)

Definition 2

([9]). Let $f\left(t\right)\in AC[t_0,+\infty )$. The short-memory Caputo fractional derivative is defined as

$${}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }f\left(t\right)={\displaystyle \frac{1}{\mathrm{\Gamma }(1-\alpha )}}{\int }_{s_L\left(t\right)}^t{(t-\xi )}^{-\alpha }{f}^{\prime }\left(\xi \right)d\xi ,$$

(2)

where $0<\alpha <1$.

Remark 1.

According to Equations (1) and (2), for $t\in [t_0,t_0+L)$, the short-memory fractional derivative ${}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }f\left(t\right)$ coincides with the Caputo derivative from $t_0$, that is, ${}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }f\left(t\right)={}_{t_0}{}^{C}D_t^{\alpha }f\left(t\right).$ As $L\to \infty$, this equality extends for all $t\ge t_0$, rendering the operator in Equation (2) a natural generalization of the classical Caputo derivative.

Lemma 1

([25]). Let $\upsilon :\mathbb{R}\to {\mathbb{R}}^n$ be a differentiable vector function. For any time instant $t\ge t_0$, the following inequality holds:

$$\begin{array}{c}\hfill {}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }\left({\upsilon }^T\left(t\right)P\upsilon \left(t\right)\right)\le 2{\upsilon }^T\left(t\right)P {}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }\upsilon \left(t\right),\end{array}$$

where $P\in {\mathbb{R}}^{n\times n}$ is a positive definite matrix and $0<\alpha <1$.

Assumption 1

(QUAD condition). Assume that $f\left(t\right)\in AC[t_0,+\infty )$, and there exists a positive definite matrix $\Theta =\mathrm{diag}({\theta }_1,{\theta }_2,\dots ,{\theta }_n)$ such that the following inequality holds:

$$\begin{array}{c}\hfill {(u-\nu )}^T(f\left(u\right)-f\left(\nu \right))\le {(u-\nu )}^T\Theta (u-\nu ),\end{array}$$

for all $u,\nu \in {\mathbb{R}}^n$.

Remark 2.

The QUAD condition is fundamental to achieving synchronization in complex networks, as highlighted in [26,27,28]. Notably, many classical systems—including the Lorenz system, Chua’s circuit, and Chen’s system—satisfy this condition.

Lemma 2

([25]). Let $V:\mathrm{\Omega }\subseteq {\mathbb{R}}^n\to \mathbb{R}$ be a continuously differentiable function defined on a domain Ω that contains the origin, satisfying $V\left(0\right)=0$ and $V\left(x\right)>0$ for all $x\in \mathrm{\Omega }\setminus \left\{0\right\}$. Let $W:\mathrm{\Omega }\to \mathbb{R}$ be a continuous, nonnegative function. Suppose that

$$\begin{array}{c}\hfill {}_{s_{L\left(t\right)}}{}^C\widehat{D}_t^{\alpha }V\left(x\right)\le -W\left(x\right),\forall x\in \mathrm{\Omega },\end{array}$$

(3)

and there exists a constant $\eta >0$ such that

$$\begin{array}{c}\hfill \underset{\parallel x\parallel \to 0}{lim}{\displaystyle \frac{W\left(x\right)}{V\left(x\right)}}\ge \eta >{\displaystyle \frac{1}{L^{\alpha }\mathrm{\Gamma }(1-\alpha )sin\left(\frac{\alpha \pi }{2}\right)}}.\end{array}$$

Then, the equilibrium point at the origin of system (3) is asymptotically stable.

Lemma 3

([29]). Let A and B be $n\times n$ symmetric matrices. Then, for each $k=1,2,\dots ,n$, the following inequalities hold:

$$\begin{array}{c}\hfill {\lambda }_k\left(A\right)+{\lambda }_n\left(B\right)\le {\lambda }_k(A+B)\le {\lambda }_k\left(A\right)+{\lambda }_1\left(B\right),\end{array}$$

where ${\lambda }_1(·)\ge {\lambda }_2(·)\ge \cdots \ge {\lambda }_n(·)$ denote the eigenvalues of a symmetric matrix, arranged in non-increasing order.

Lemma 4

([30]). Let $P_1=P_1^T$ and $P_3=P_3^T$. The linear matrix inequality (LMI)

$$\left[\begin{array}{cc}{P}_1& P_2\\ \ast & P_3\end{array}\right]<0$$

is equivalent to the following conditions:

$$\begin{array}{c}\hfill \left(1\right)P_3<0\mathit{and}{P}_1-P_2{P}_3^{-1}{P}_2^T<0,\\ \hfill \left(2\right)P_1<0\mathit{and}{P}_3-P_2^T{P}_1^{-1}{P}_2<0.\end{array}$$

3. Main Result

3.1. Model Description

Consider a higher-order network composed of N coupled dynamical nodes, whose structure is described by a hypergraph $\mathcal{G}=(\mathcal{V},\mathcal{E})$. Here, $\mathcal{V}=\{v_1,v_2,\dots ,v_N\}$ denotes the set of vertices (nodes), and $\mathcal{E}=\{{\sigma }_1,{\sigma }_2,\dots ,{\sigma }_M\}$ is the set of hyperedges, where each hyperedge is a subset of nodes. For any distinct $d+1$ vertices $v_{j_0},v_{j_1},\dots ,v_{j_d}$, we define an undirected d-hyperedge as $\tau =[v_{j_0},v_{j_1},\dots ,v_{j_d}]$, where d represents the hyperedge’s order, and a directed d-hyperedge as $\sigma =⟨v_{j_0},v_{j_1},\dots ,v_{j_d}⟩$, with $v_{j_0}$ acting as the source and $v_{j_d}$ as the sink. The order of the hypergraph, denoted by D, is the maximum order among all hyperedges in $\mathcal{G}$. In this framework, directed d-hyperedges are employed to represent directed $(d+1)$-body interactions. Each d-hyperedge can be encoded by a d-order adjacency tensor $A^{\left(d\right)}=\left\{a_{i{j}_1\dots j_d}^{\left(d\right)}\right\}\in {\mathbb{R}}^{N\times \dots \times N}$, where, for a directed d-hyperedge $⟨i,j_1,\dots ,j_d⟩$, we set $a_{i{j}_1\dots j_d}^{\left(d\right)}=1$. In contrast, for an undirected d-hyperedge, the tensor entries satisfy permutation symmetry, i.e., $a_{\pi (i,j_1,\dots ,j_d)}^{\left(d\right)}=1$ for any permutation $\pi$ of the indices.

Consider the following fractional directed higher-order network model with a short-memory property:

$$\begin{array}{cc}\hfill {}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }{x}_i\left(t\right)=& g\left(x_i\left(t\right)\right)+c_1\sum _{j_1=1}^N{a}_{i{j}_1}^{\left(1\right)}\mathrm{\Phi }\left(x_{j_1}\left(t\right)-x_i\left(t\right)\right)+c_2\sum _{j_1=1}^N\sum _{j_2=1}^N{a}_{i{j}_1{j}_2}^{\left(2\right)}\mathrm{\Phi }{f}^{\left(2\right)}(x_i,x_{j_1},x_{j_2})\hfill \\ \hfill & +\cdots +c_D\sum _{j_1=1}^N\dots \sum _{j_D=1}^N{a}_{i{j}_1\dots j_D}^{\left(D\right)}\mathrm{\Phi }{f}^{\left(D\right)}(x_i,x_{j_1},\dots ,x_{j_D}),\hfill \end{array}$$

(4)

where $x_i\left(t\right)=\left(x_{i1}\left(t\right),x_{i2}\left(t\right),\dots ,x_{iN}\left(t\right)\right)\in {\mathbb{R}}^N$ denotes the state vector of the i-th node. The function $g:{\mathbb{R}}^N\to {\mathbb{R}}^N$ describes the nonlinear local dynamics of each node. The positive constants $c_d>0$ for $d=1,2,\dots ,D$ represent coupling strengths, and $\mathrm{\Phi }$ is the inner coupling matrix characterizing the interaction structure. The adjacency tensors $A^{\left(d\right)}=\left\{a_{i{j}_1\dots j_d}^{\left(d\right)}\right\}\in {\mathbb{R}}^{N\times \cdots \times N}$ correspond to interactions of order d. The entries satisfy the rule that for $d=1$, if $i=j_1$, then $a_{i{j}_1}^{\left(1\right)}=0$ (preventing self-connections), while for $i\ne j_1$, $a_{i{j}_1}^{\left(1\right)}\ne 0$ indicates the presence of a connection. For higher-order directed hyperedges $⟨i,j_1,\dots ,j_d⟩$, the entry $a_{i{j}_1\dots j_d}^{\left(d\right)}=1$ if such a hyperedge exists; otherwise, $a_{i{j}_1\dots j_d}^{\left(d\right)}=0$.

For simplicity, let $f^{\left(d\right)}(x_i,x_{j_1},\dots ,x_{j_d})={\displaystyle \frac{1}{d}}\left(x_{j_1}\left(t\right)+\cdots +x_{j_d}\left(t\right)-d{x}_i\left(t\right)\right)$ for $d=1,2,\dots ,D$. By substituting this form into Equation (4), we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }{x}_i\left(t\right)=& g\left(x_i\left(t\right)\right)+c_1\sum _{j_1=1}^N{a}_{i{j}_1}^{\left(1\right)}\mathrm{\Phi }(x_{j_1}\left(t\right)-x_i\left(t\right))\hfill \\ \hfill & +c_2\sum _{j_1=1}^N\sum _{j_2=1}^N{a}_{i{j}_1{j}_2}^{\left(2\right)}\mathrm{\Phi }{\displaystyle \frac{1}{2}}\left[x_{j_1}\left(t\right)+x_{j_2}\left(t\right)-2x_i\left(t\right)\right]+\cdots \hfill \\ \hfill & +c_D\sum _{j_1=1}^N\cdots \sum _{j_D=1}^N{a}_{i{j}_1\cdots j_D}^{\left(D\right)}\mathrm{\Phi }{\displaystyle \frac{1}{d}}\left[x_{j_1}\left(t\right)+\cdots +x_{j_d}\left(t\right)-d{x}_i\left(t\right)\right]\hfill \\ \hfill =& g\left(x_i\left(t\right)\right)+c_1\sum _{j_1=1}^N{a}_{i{j}_1}^{\left(1\right)}\mathrm{\Phi }{x}_{j_1}\left(t\right)\hfill \\ \hfill & +{\displaystyle \frac{c_2}{2}}\sum _{j_1=1}^N\left(\sum _{j_2=1}^N{a}_{i{j}_1{j}_2}^{\left(2\right)}\right)\mathrm{\Phi }{x}_{j_1}\left(t\right)+{\displaystyle \frac{c_2}{2}}\sum _{j_2=1}^N\left(\sum _{j_1=1}^N{a}_{i{j}_1{j}_2}^{\left(2\right)}\right)\mathrm{\Phi }{x}_{j_2}\left(t\right)\hfill \\ \hfill & +\cdots +{\displaystyle \frac{c_D}{d}}\sum _{j_1=1}^N\left(\sum _{j_2=1}^N\cdots \sum _{j_D=1}^N{a}_{i{j}_1\cdots j_D}^{\left(D\right)}\right)\mathrm{\Phi }{x}_{j_1}\left(t\right)+\cdots \hfill \\ \hfill & +{\displaystyle \frac{c_D}{d}}\sum _{j_D=1}^N\left(\sum _{j_1=1}^N\cdots \sum _{j_{D-1}=1}^N{a}_{i{j}_1\cdots j_D}^{\left(D\right)}\right)\mathrm{\Phi }{x}_{j_D}\left(t\right)\hfill \\ \hfill & -\left[c_1\sum _{j_1=1}^N{a}_{i{j}_1}^{\left(1\right)}+c_2\sum _{j_1,j_2=1}^N{a}_{i{j}_1{j}_2}^{\left(2\right)}+\cdots +c_D\sum _{j_1,...,j_D=1}^N{a}_{i{j}_1...j_D}^{\left(D\right)}\right]\mathrm{\Phi }{x}_i\left(t\right).\hfill \end{array}\end{array}$$

(5)

Introducing the notation

$$\begin{array}{c}\hfill k_i^{\left(d\right)}=\sum _{j_1=1}^N\dots \sum _{j_d=1}^N{a}_{i{j}_1\dots j_d}^{\left(d\right)},k_{ij}^{\left(d\right)}=\sum _{j_1=1}^N\dots \sum _{j_{d-1}=1}^N{a}_{i,j,j_1,...,j_{d-1}}^{\left(d\right)},\end{array}$$

and setting

$$\begin{array}{c}\hfill q_{ij}^{\left(d\right)}=\left\{\begin{array}{cc}{k}_{ij}^{\left(d\right)},\hfill & i\ne j,\hfill \\ -k_i^{\left(d\right)},\hfill & i=j,\hfill \end{array}\right.\end{array}$$

Equation (5) can be compactly written as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }{x}_i\left(t\right)=& g\left(x_i\left(t\right)\right)+c_1\sum _{j=1}^N{q}_{ij}^{\left(1\right)}\mathrm{\Phi }{x}_j\left(t\right)+c_2\sum _{j=1}^N{q}_{ij}^{\left(2\right)}\mathrm{\Phi }{x}_j\left(t\right)\hfill \\ \hfill & +\dots +c_D\sum _{j=1}^N{q}_{ij}^{\left(D\right)}\mathrm{\Phi }{x}_j\left(t\right).\hfill \end{array}\end{array}$$

(6)

We define the multi-Laplacian matrix as

$$\begin{array}{c}\hfill {\mathcal{Q}}^{\left(D\right)}=c_1{Q}^{\left(1\right)}+c_2{Q}^{\left(2\right)}+\cdots +c_D{Q}^{\left(D\right)},\end{array}$$

where each $Q^{\left(d\right)}={\left(q_{ij}^{\left(d\right)}\right)}_{N\times N}$ for $d=1,2,\dots ,D$ is an asymmetric real-valued matrix with zero row sums. System (6) can be obtained directly such that

$$\begin{array}{c}\hfill {}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }{x}_i\left(t\right)=g\left(x_i\left(t\right)\right)+\sum _{j=1}^N{\mathcal{Q}}_{ij}^{\left(D\right)}\mathrm{\Phi }{x}_j\left(t\right),i=1,2,\dots ,N,\end{array}$$

(7)

which indicates that the short-memory higher-order network can be equivalently represented as a classical pairwise network governed by the multi-Laplacian matrix ${\mathcal{Q}}^{\left(D\right)}$.

Synchronization in higher-order network (7) is achieved by introducing feedback control inputs $u_i\left(t\right)$ applied to a subset of the nodes. Specifically, the control acts on only the first m nodes, aiming to synchronize these nodes so as to influence the entire network. Without the loss of generality, nodes $i=1,2,\dots ,m$ are considered to be controlled. Consequently, the short-memory controlled network is represented by

$$\begin{array}{cccc}\hfill {}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }{x}_i\left(t\right)& =g\left(x_i\left(t\right)\right)+\sum _{j=1}^N{\mathcal{Q}}_{ij}^{\left(D\right)}\mathrm{\Phi }{x}_j\left(t\right)+u_i\left(t\right),\hfill & \hfill i& =1,2,\dots ,m,\hfill \\ \hfill {}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }{x}_i\left(t\right)& =g\left(x_i\left(t\right)\right)+\sum _{j=1}^N{\mathcal{Q}}_{ij}^{\left(D\right)}\mathrm{\Phi }{x}_j\left(t\right),\hfill & \hfill i& =m+1,m+2,\dots ,N.\hfill \end{array}$$

(8)

The control input is defined as

$$u_i\left(t\right)=-h_i\mathrm{\Phi }\left(x_i\left(t\right)-s\left(t\right)\right),i=1,2,\dots ,m,$$

where the control gains satisfy $h_i>0$.

To guarantee the synchronization of the higher-order network, this paper focuses on strongly connected directed higher-order networks. Let $s\left(t\right)$ be a reference trajectory satisfying

$${}_{s_L\left(t\right)}{}^{C}D_t^{\alpha }s\left(t\right)=g\left(s\left(t\right)\right).$$

If

$$\underset{t\to \infty }{lim}\parallel x_i\left(t\right)-s\left(t\right)\parallel =0,$$

where $\parallel ·\parallel$ denotes the Euclidean norm; then the network (8) is said to achieve synchronization.

Denote the synchronization error by $e_i\left(t\right)=x_i\left(t\right)-s\left(t\right)$. The corresponding error dynamics are described by

$$\begin{array}{cc}\hfill {}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }{e}_i\left(t\right)& =g\left(x_i\left(t\right)\right)-g\left(s\left(t\right)\right)+\sum _{j=1}^N{\mathcal{Q}}_{ij}^{\left(D\right)}\mathrm{\Phi }{e}_j\left(t\right)-h_i\mathrm{\Phi }{e}_i\left(t\right),i=1,2,\dots ,m,\hfill \\ \hfill {}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }{e}_i\left(t\right)& =g\left(x_i\left(t\right)\right)-g\left(s\left(t\right)\right)+\sum _{j=1}^N{\mathcal{Q}}_{ij}^{\left(D\right)}\mathrm{\Phi }{e}_j\left(t\right),i=m+1,m+2,\dots ,N.\hfill \end{array}$$

(9)

3.2. Synchronization of Short-Memory Directed Higher-Order Networks

Theorem 1.

The controlled network described by Equation (8) achieves global synchronization if the following condition is satisfied:

$$\begin{array}{c}\hfill {\lambda }_{max}\left(\Theta \otimes I_N+({\widehat{\mathcal{Q}}}^{\left(D\right)}-H)\otimes \mathrm{\Phi }\right)<-{\displaystyle \frac{1}{2L^{\alpha }\mathrm{\Gamma }(1-\alpha )sin\left(\frac{\alpha \pi }{2}\right)}},\end{array}$$

(10)

where Φ is a positive definite matrix, $H=diag(h_1,h_2,\dots ,h_m,0,\dots ,0)$ is the pinning control matrix, ${\widehat{\mathcal{Q}}}^{\left(D\right)}={\displaystyle \frac{1}{2}}\left({\mathcal{Q}}^{\left(D\right)}+{\mathcal{Q}}^{{\left(D\right)}^T}\right)$, and $I_N$ denotes the $N\times N$ identity matrix.

Proof. 

Consider the Lyapunov function

$$V\left(t\right)={\displaystyle \frac{1}{2}}\sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right).$$

Applying Lemma 1, the Caputo derivative of $V\left(t\right)$ along the system trajectories satisfies

$$\begin{array}{cc}\hfill {}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }V\left(t\right)& ={}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }\left({\displaystyle \frac{1}{2}}\sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right)\right)\hfill \\ \hfill & \le \sum _{i=1}^N{e}_i^T\left(t\right){}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }{e}_i\left(t\right)\hfill \\ \hfill & =\sum _{i=1}^N{e}_i^T\left(t\right)\left(g\left(x_i\left(t\right)\right)-g\left(s\left(t\right)\right)+\sum _{j=1}^N{\mathcal{Q}}_{ij}^{\left(D\right)}\mathrm{\Phi }{e}_j\left(t\right)\right)-\sum _{i=1}^m{e}_i^T\left(t\right)h_i\mathrm{\Phi }{e}_i\left(t\right).\hfill \end{array}$$

By invoking Assumption 1, we have

$$\begin{array}{cc}\hfill {}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }V\left(t\right)\le & \sum _{i=1}^N{e}_i^T\left(t\right)\Theta e_i\left(t\right)+\sum _{i=1}^N\sum _{j=1}^N{e}_i^T\left(t\right){\mathcal{Q}}_{ij}^{\left(D\right)}\mathrm{\Phi }{e}_j\left(t\right)-\sum _{i=1}^m{e}_i^T\left(t\right)h_i\mathrm{\Phi }{e}_i\left(t\right)\hfill \\ \hfill =& E^T\left(t\right)(\Theta \otimes I_N)E\left(t\right)+E^T\left(t\right)\left({\displaystyle \frac{{\mathcal{Q}}^{\left(D\right)}+{\mathcal{Q}}^{{\left(D\right)}^T}}{2}}\otimes \mathrm{\Phi }\right)E\left(t\right)\hfill \\ \hfill & -E^T\left(t\right)(H\otimes \mathrm{\Phi })E\left(t\right)\hfill \\ \hfill =& E^T\left(t\right)\left(\Theta \otimes I_N+({\widehat{\mathcal{Q}}}^{\left(D\right)}-H)\otimes \mathrm{\Phi }\right)E\left(t\right),\hfill \end{array}$$

where

$$E^T\left(t\right)=\left(e_1^T\left(t\right),e_2^T\left(t\right),\dots ,e_N^T\left(t\right)\right).$$

Since $\Theta \otimes I_N+({\widehat{\mathcal{Q}}}^{\left(D\right)}-H)\otimes \mathrm{\Phi }$ is symmetric, it becomes negative definite when the control gains $h_i$ are sufficiently large. This implies that

$${\lambda }_{max}\left(\Theta \otimes I_N+({\widehat{\mathcal{Q}}}^{\left(D\right)}-H)\otimes \mathrm{\Phi }\right)<0.$$

Let

$$\zeta =-2{\lambda }_{max}\left(\Theta \otimes I_N+({\widehat{\mathcal{Q}}}^{\left(D\right)}-H)\otimes \mathrm{\Phi }\right)>0;$$

then it follows that

$$\begin{array}{cc}\hfill {}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }V\left(t\right)& \le 2{\lambda }_{max}\left(\Theta \otimes I_N+({\widehat{\mathcal{Q}}}^{\left(D\right)}-H)\otimes \mathrm{\Phi }\right)V\left(t\right)\hfill \\ \hfill & =-\zeta V\left(t\right).\hfill \end{array}$$

Therefore, by Lemma 2 and condition (10), controlled system (8) achieves global synchronization, provided that the control gains are sufficiently large. □

Remark 3.

In this paper, a short-memory higher-order network model is considered, represented by a D-order hypergraph, and its synchronization conditions are established. When $D=1$, higher-order network (8) reduces to the classical complex network model, where the synchronization condition stated in Theorem 1 remains applicable [31].

Remark 4.

For an undirected d-hyperedge, the d-order adjacency tensor $A^{\left(d\right)}$ and the Laplacian matrix ${\mathcal{Q}}^{\left(D\right)}$ are symmetric, so the symmetrization of ${\mathcal{Q}}^{\left(D\right)}$ is no longer necessary. Consequently, synchronization condition (10) in Theorem 1 is replaced by

$${\lambda }_{max}\left(\Theta \otimes I_N+({\mathcal{Q}}^{\left(D\right)}-H)\otimes \mathrm{\Phi }\right)<-{\displaystyle \frac{1}{2L^{\alpha }\mathrm{\Gamma }(1-\alpha )sin\left(\frac{\alpha \pi }{2}\right)}}.$$

Let ${\theta }^{*}=max\{{\theta }_i,i=1,2,\dots ,n\},{\mathrm{\Phi }}^{*}={\lambda }_{min}\left(\mathrm{\Phi }\right)$; then another sufficient condition for the synchronization of short-memory higher-order network (8) can be obtained using the linear matrix inequality.

Corollary 1.

If the inequality

$$\begin{array}{c}\hfill {\theta }^{*}+{\mathrm{\Phi }}^{*}·{\lambda }_{min}({\widehat{\mathcal{Q}}}^{\left(D\right)}-H)<-{\displaystyle \frac{1}{2L^{\alpha }\mathrm{\Gamma }(1-\alpha )sin\left(\frac{\alpha \pi }{2}\right)}}\end{array}$$

(11)

holds, then network (8) is globally synchronized.

Proof. 

Utilizing Lemma 3, one derives

$$\begin{array}{cc}\hfill {\lambda }_k(\Theta \otimes I_N+(\widehat{{\mathcal{Q}}^{\left(D\right)}}-H)\otimes \mathrm{\Phi })\le & {\lambda }_k(\Theta \otimes I_N)+{\lambda }_{max}((\widehat{{\mathcal{Q}}^{\left(D\right)}}-H)\otimes \mathrm{\Phi })\hfill \\ \hfill =& {\lambda }_k(\Theta ){\lambda }_k\left(I_N\right)+{\lambda }_{max}(\widehat{{\mathcal{Q}}^{\left(D\right)}}-H)){\lambda }_{min}\left(\mathrm{\Phi }\right)\hfill \\ \hfill \le & {\theta }^{*}+{\mathrm{\Phi }}^{*}·{\lambda }_{max}(\widehat{{\mathcal{Q}}^{\left(D\right)}}-H),\hfill \end{array}$$

where $k=1,2,\dots ,nN$. By (11), one has

$$\begin{array}{c}\hfill {\lambda }_{max}(\Theta \otimes I_N+({\widehat{\mathcal{Q}}}^{\left(\mathcal{D}\right)}-H)\otimes \mathrm{\Phi })<-{\displaystyle \frac{1}{2L^{\alpha }\mathrm{\Gamma }(1-\alpha )sin\left(\frac{\alpha \pi }{2}\right)}}.\end{array}$$

Therefore, network (8) can be globally synchronized. □

Let $\xi ={\displaystyle \frac{1}{2L^{\alpha }\mathrm{\Gamma }(1-\alpha )sin\left(\frac{\alpha \pi }{2}\right)}}$, ${\widehat{\mathcal{Q}}}^{\left(D\right)}=\left[\begin{array}{ccc}{\widehat{\mathcal{Q}}}_m^{\left(D\right)}& {\widehat{\mathcal{Q}}}_{12}^{\left(D\right)}& \\ {\widehat{\mathcal{Q}}}_{21}^{\left(D\right)}& {\widehat{\mathcal{Q}}}_{N-m}^{\left(D\right)}& \end{array}\right]$ and $G^{*}=({\theta }^{*}+\xi )I_N+{\mathrm{\Phi }}^{*}({\widehat{\mathcal{Q}}}^{\left(D\right)}-H)$. The matrix $G^{*}$ can be expressed in the following block form:

$$\begin{array}{cc}\hfill G^{*}=& \left[\begin{array}{ccc}{G}_m^{*}& G_{12}^{*}& \\ G_{21}^{*}& G_{N-m}^{*}& \end{array}\right]\hfill \\ \hfill =& \left[\begin{array}{ccc}({\theta }^{*}+\xi )I_m+{\mathrm{\Phi }}^{*}({\widehat{\mathcal{Q}}}_m^{\left(D\right)}-H_m)& {\mathrm{\Phi }}^{*}{\widehat{\mathcal{Q}}}_{12}^{\left(D\right)}& \\ {\mathrm{\Phi }}^{*}{\widehat{\mathcal{Q}}}_{21}^{\left(D\right)}& ({\theta }^{*}+\xi )I_{N-m}+{\mathrm{\Phi }}^{*}{\widehat{\mathcal{Q}}}_{N-m}^{\left(D\right)}& \end{array}\right],\hfill \end{array}$$

where $H_m=diag\{h_1,h_2,\dots ,h_m\}$.

Corollary 2.

Global synchronization of controlled network (8) can be achieved if the control gains $h_i$, $i=1,2,\dots ,m$ are sufficiently large and the condition

$$\begin{array}{c}\hfill G_{N-m}^{*}=({\theta }^{*}+\xi )I_{N-m}+{\mathrm{\Phi }}^{*}{\widehat{\mathcal{Q}}}_{N-m}^{\left(D\right)}<0\end{array}$$

(12)

is satisfied.

Proof. 

Sufficiently large control gains $h_i$ are selected to ensure that $G_m^{*}<0$ and $G_m^{*}-G_{12}^{*}{\left(G_{N-m}^{*}\right)}^{-1}{\left(G_{12}^{*}\right)}^T<0$ hold. Together with condition (12) and Lemma 4, this implies that inequality (11) is satisfied, thereby completing the proof. □

Based on the definition of ${\widehat{\mathcal{Q}}}^{\left(D\right)}$, the diagonal elements are characterized by

$${\widehat{\mathcal{Q}}}_{ii}^{\left(D\right)}=-\left(c_1{k}_i^{\left(1\right)}+c_2{k}_i^{\left(2\right)}+\cdots +c_D{k}_i^{\left(D\right)}\right).$$

The following conclusion can then be drawn:

Corollary 3.

To satisfy condition (11), it is required that

$$\left\{\begin{array}{cc}{G}_{ii}^{*}={\theta }^{*}-{\mathrm{\Phi }}^{*}\left(c_1{k}_i^{\left(1\right)}+c_2{k}_i^{\left(2\right)}+\cdots +c_D{k}_i^{\left(D\right)}\right)-{\mathrm{\Phi }}^{*}{h}_i<-\xi ,\hfill & 1\le i\le m,\hfill \\ G_{ii}^{*}={\theta }^{*}-{\mathrm{\Phi }}^{*}\left(c_1{k}_i^{\left(1\right)}+c_2{k}_i^{\left(2\right)}+\cdots +c_D{k}_i^{\left(D\right)}\right)<-\xi ,\hfill & m+1\le i\le N,\hfill \end{array}\right.$$

where $k_i^{\left(d\right)}$ denotes the number of d-hyperedges in which the i-th node acts as a sink.

Proof. 

The condition $G_{ii}^{*}<-\xi$ is necessary for condition (11) to hold. □

3.3. Adaptive Synchronization of Short-Memory Fractional Higher-Order Directed Networks

Consider the following short-memory fractional directed higher-order network with adaptive coupling strengths:

$$\begin{array}{cc}\hfill {}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }{x}_i\left(t\right)=& g\left(x_i\left(t\right)\right)+c_1\left(t\right)\sum _{j_1=1}^N{a}_{i{j}_1}^{\left(1\right)}\mathrm{\Phi }\left(x_{j_1}\left(t\right)-x_i\left(t\right)\right)\hfill \\ \hfill & +c_2\left(t\right)\sum _{j_1=1}^N\sum _{j_2=1}^N{a}_{i{j}_1{j}_2}^{\left(2\right)}\mathrm{\Phi }{f}^{\left(2\right)}\left(x_i,x_{j_1},x_{j_2}\right)+\cdots \hfill \\ \hfill & +c_D\left(t\right)\sum _{j_1=1}^N\cdots \sum _{j_D=1}^N{a}_{i{j}_1\dots j_D}^{\left(D\right)}\mathrm{\Phi }{f}^{\left(D\right)}\left(x_i,x_{j_1},\dots ,x_{j_D}\right).\hfill \end{array}$$

(13)

Similarly, the error system corresponding to Equation (13) can be expressed as

$${}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }{e}_i\left(t\right)=g\left(x_i\left(t\right)\right)-g\left(s\left(t\right)\right)+\sum _{j=1}^N{\mathcal{Q}}_{ij}^{\left(D\right)}\mathrm{\Phi }{e}_j\left(t\right)-h_i\mathrm{\Phi }{e}_i\left(t\right),i=1,2,\dots ,m,$$

where ${\mathcal{Q}}_{ij}^{\left(D\right)}=c_1\left(t\right)Q_{ij}^{\left(1\right)}+c_2\left(t\right)Q_{ij}^{\left(2\right)}+\cdots +c_D\left(t\right)Q_{ij}^{\left(D\right)}$. For convenience, select the first m nodes to add controllers. The controlled network can be represented as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }{e}_i\left(t\right)& =g\left(x_i\left(t\right)\right)-g\left(s\left(t\right)\right)+\sum _{j=1}^N{\mathcal{Q}}_{ij}^{\left(D\right)}\mathrm{\Phi }{e}_j\left(t\right)-h_i\mathrm{\Phi }{e}_i\left(t\right),i=1,2,\dots ,m,\hfill \\ \hfill {}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }{e}_i\left(t\right)& =g\left(x_i\left(t\right)\right)-g\left(s\left(t\right)\right)+\sum _{j=1}^N{\mathcal{Q}}_{ij}^{\left(D\right)}\mathrm{\Phi }{e}_j\left(t\right),i=m+1,m+2,\dots ,N.\hfill \end{array}\end{array}$$

(14)

The adaptive coupling strengths are designed in the following form:

$$\begin{array}{c}\hfill {}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }{c}_d\left(t\right)={\displaystyle \frac{{\rho }_d}{N}}\sum _{i=1}^N{e}_i^T\left(t\right)\mathrm{\Phi }{e}_i\left(t\right),\end{array}$$

(15)

where the adjustment rate of $c_d\left(t\right)$ is determined by the adaptive gain coefficients ${\rho }_d$ and $d=1,2,\dots ,D$.

Theorem 2.

If the following inequality holds:

$$\begin{array}{c}\hfill {\mu }_{max}\left(\Theta \otimes I_N+\sum _{d=1}^D{c}_d\left(t\right)\left({\widehat{Q}}^{\left(d\right)}\otimes \mathrm{\Phi }\right)-H\otimes \mathrm{\Phi }\right)<-{\displaystyle \frac{1}{2L^{\alpha }\mathrm{\Gamma }(1-\alpha )sin\left(\frac{\alpha \pi }{2}\right)}},\end{array}$$

(16)

then network (14) achieves global synchronization.

Proof. 

Let us consider the Lyapunov function defined by

$$\begin{array}{c}\hfill V\left(t\right)={\displaystyle \frac{1}{2}}\sum _{i=1}^N{e}_i^T\left(t\right)e_i\left(t\right).\end{array}$$

(17)

By taking the Caputo fractional derivative of Equation (17) from Lemma 1, we get

$$\begin{array}{cc}\hfill {}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }V\left(t\right)\le & \sum _{i=1}^N{e}_i^T{\left(t\right)}_{s_L\left(t\right)}^C{\widehat{D}}_t^{\alpha }{e}_i\left(t\right)\hfill \\ \hfill \le & \sum _{i=1}^N{e}_i^T\left(t\right)\left(g\left(x_i\left(t\right)\right)-g\left(s\left(t\right)\right)+\sum _{j=1}^N{\mathcal{Q}}_{ij}^{\left(D\right)}\mathrm{\Phi }{e}_j\left(t\right)\right)-\sum _{i=1}^m{e}_i^T\left(t\right)h_i\mathrm{\Phi }{e}_i\left(t\right).\hfill \end{array}$$

By applying Assumption 1, we obtain

$$\begin{array}{cc}\hfill {}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }V\left(t\right)\le & \sum _{i=1}^N{e}_i^T\left(t\right)\Theta e_i\left(t\right)+\sum _{i=1}^N\sum _{j=1}^N{e}_i^T\left(t\right){\mathcal{Q}}_{ij}^{\left(D\right)}\mathrm{\Phi }{e}_j\left(t\right)-\sum _{i=1}^m{e}_i^T\left(t\right)h_i\mathrm{\Phi }{e}_i\left(t\right)\hfill \\ \hfill =& \sum _{i=1}^N{e}_i^T\left(t\right)\Theta e_i\left(t\right)+\sum _{i=1}^N\sum _{j=1}^N{e}_i^T\left(t\right)\sum _{d=1}^D{c}_d\left(t\right)Q_{ij}^{\left(d\right)}\mathrm{\Phi }{e}_j\left(t\right)-\sum _{i=1}^m{e}_i^T\left(t\right)h_i\mathrm{\Phi }{e}_i\left(t\right)\hfill \\ \hfill =& E^T\left(t\right)(\Theta \otimes I_N)E\left(t\right)+E^T\left(t\right)\left[\sum _{d=1}^D{c}_d\left(t\right)\left({\displaystyle \frac{Q^{\left(d\right)}+Q^{\left(d\right)T}}{2}}\right)\otimes \mathrm{\Phi }\right]E\left(t\right)\hfill \\ \hfill & -E^T\left(t\right)(H\otimes \mathrm{\Phi })E\left(t\right)\hfill \\ \hfill =& E^T\left(t\right)\left[\Theta \otimes I_N+\sum _{d=1}^D{c}_d\left(t\right)({\widehat{Q}}^{\left(d\right)}\otimes \mathrm{\Phi })-H\otimes \mathrm{\Phi }\right]E\left(t\right),\hfill \end{array}$$

(18)

where $E^T\left(t\right)=(e_1^T\left(t\right),e_2^T\left(t\right),\dots ,e_N^T\left(t\right))$.

Let $\kappa =-2{\mu }_{max}(\Theta \otimes I_N+{\sum }_{d=1}^D{c}_d\left(t\right)({\widehat{Q}}^{\left(d\right)}\otimes \mathrm{\Phi })-H\otimes \mathrm{\Phi })$. When $h_i$ is large enough, one can see that $\kappa >0$; then

$$\begin{array}{cc}\hfill & {}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }V\left(t\right)\hfill \\ \hfill \le & {\mu }_{max}\left(\Theta \otimes I_N+\sum _{d=1}^D{c}_d\left(t\right)({\widehat{Q}}^{\left(d\right)}\otimes \mathrm{\Phi })-(H\otimes \mathrm{\Phi })\right)E^T\left(t\right)E\left(t\right)\hfill \\ \hfill =& -\kappa V\left(t\right).\hfill \end{array}$$

Thus, it follows from Lemma 2 and Equation (16) that network (14) can achieve global synchronization. □

Remark 5.

The adaptive control strategy proposed in Theorem 2 is shown to achieve significant performance improvements over the fixed-gain control scheme described in Theorem 1 by dynamically adjusting the coupling strength $c_d\left(t\right)$. The controller employs the global synchronization error metric, ${\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{e}_i^T\left(t\right)\mathrm{\Phi }{e}_i\left(t\right)$, as the feedback signal, and the adaptive rate parameter ${\rho }_d>0$ is optimized to effectively reduce control energy consumption while maintaining rapid convergence. Consequently, the synchronization robustness and flexibility of short-memory fractional directed higher-order networks are substantially enhanced through this adaptive mechanism.

4. Numerical Implementation

4.1. Predictor–Corrector Algorithm

In this section, the numerical solution for a short-memory fractional system is given using the Adams–Bashforth–Moulton algorithm [15]. The following short-memory fractional system is considered:

$$\left\{\begin{array}{c}{}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }x\left(t\right)=f(t,x\left(t\right)),\hfill \\ x\left(t_0\right)=x_0,t\in [t_0,+\infty ),\hfill \end{array}\right.$$

(19)

where $0<\alpha <1$. According to reference [25], Equation (19) can be rewritten as

$${}_{t_0}{}^C\widehat{D}_t^{\alpha }x\left(t\right)=\left\{\begin{array}{cc}f(t,x(t\left)\right),\hfill & t\in [t_0,t_0+L),\hfill \\ f(t,x\left(t\right))+{\displaystyle \frac{1}{\mathrm{\Gamma }(1-\alpha )}}[{\displaystyle \frac{x(t-L)}{L^{\alpha }}}-{\displaystyle \frac{x\left(t_0\right)}{{(t-t_0)}^{\alpha }}}\hfill \\ -\alpha {\int }_{t_0}^{t-L}{(t-\tau )}^{-\alpha -1}x\left(\tau \right)d\tau ],\hfill & t\in [t_0+L,+\infty ).\hfill \end{array}\right.$$

(20)

Assume a uniform grid $\{t_n=nh\mid n=0,1,\dots ,N\}$ with step size $h={\displaystyle \frac{T}{N}}$, where N is a non-negative integer. For $t\in [t_0,t_0+L)$, let $m=\lfloor {\displaystyle \frac{L}{h}}\rfloor$; then the fractional predictor–corrector algorithm [15] can be applied to obtain the numerical solution $x_h\left(t_0\right),\dots ,x_h\left(t_m\right)$ for Equation (19).

Next, our primary focus is on the interval $t\in [t_0+L,+\infty )$. Let

$$\begin{array}{c}\hfill g(t,x\left(t\right))=f(t,x\left(t\right))+{\displaystyle \frac{1}{\mathrm{\Gamma }(1-\alpha )}}\left[{\displaystyle \frac{x(t-L)}{L^{\alpha }}}-{\displaystyle \frac{x\left(t_0\right)}{{(t-t_0)}^{\alpha }}}-\alpha {\int }_{t_0}^{t-L}{(t-\tau )}^{-\alpha -1}x\left(\tau \right)d\tau \right].\end{array}$$

(21)

Integrating both sides of Equation (20) yields

$$\begin{array}{c}\hfill x\left(t\right)=x\left(t_0\right)+{\displaystyle \frac{1}{\mathrm{\Gamma }\left(\alpha \right)}}{\int }_{t_0}^t{(t-\tau )}^{\alpha -1}g(\tau ,x\left(\tau \right))d\tau .\end{array}$$

(22)

Using the Adams–Bashforth–Moulton method [15], the corrector formula is given by

$$x_h\left(t_{n+1}\right)=x_0+{\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }(\alpha +2)}}g\left(t_{n+1},x_h^P\left(t_{n+1}\right)\right)+{\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }(\alpha +2)}}\sum _{j=0}^n{a}_{j}g\left(t_j,x_h\left(t_j\right)\right),$$

where the coefficients $a_j$ are defined as

$$a_j=\left\{\begin{array}{cc}{n}^{\alpha +1}-(n-\alpha ){(n+1)}^{\alpha },\hfill & j=0,\hfill \\ {(n-j+2)}^{\alpha +1}+{(n-j)}^{\alpha +1}-2{(n-j+1)}^{\alpha +1},\hfill & 1\le j\le n,\hfill \\ 1,\hfill & j=n+1,\hfill \end{array}\right.$$

and $n=m,\dots ,N-1$. The predicted value $x_h^P\left(t_{n+1}\right)$ is given by

$$x_h^P\left(t_{n+1}\right)=x_0+{\displaystyle \frac{1}{\mathrm{\Gamma }\left(\alpha \right)}}\sum _{j=0}^n{b}_{j}g\left(t_j,x_h\left(t_j\right)\right),$$

where the weights $b_j$ are calculated as

$$b_j={\displaystyle \frac{h^{\alpha }}{\alpha }}\left({(n+1-j)}^{\alpha }-{(n-j)}^{\alpha }\right).$$

As for $g(t_j,x_h\left(t_j\right))$, using the trapezoidal formula and Equation (21), we obtain

$$\begin{array}{c}\hfill g(t_j,x_h\left(t_j\right))=f(t_j,x_h\left(t_j\right))+{\displaystyle \frac{1}{\mathrm{\Gamma }(1-\alpha )}}\left[{\displaystyle \frac{x_h\left(t_{j-m}\right)}{L^{\alpha }}}-{\displaystyle \frac{x_0}{{(t_j-t_0)}^{\alpha }}}-{\displaystyle \frac{h^{-\alpha }}{2}}\sum _{i=0}^{j-m}{\omega }_{i,j}{x}_h\left(t_i\right)\right],\end{array}$$

where

$${\omega }_{i,j}=\left\{\begin{array}{cc}{(j-1)}^{-\alpha }-j^{-\alpha },\hfill & i=0,\hfill \\ {(j-i-1)}^{-\alpha }-{(j-i+1)}^{-\alpha },\hfill & 1\le i\le j-m-1,\hfill \\ m^{-\alpha }-{(m+1)}^{-\alpha },\hfill & i=j-m.\hfill \end{array}\right.$$

Similarly,

$$\begin{array}{cc}\hfill g(t_{n+1},x_h^P\left(t_{n+1}\right))=& f(t_{n+1},x_h^P\left(t_{n+1}\right))+{\displaystyle \frac{1}{\mathrm{\Gamma }(1-\alpha )}}[{\displaystyle \frac{x_h\left(t_{n+1-m}\right)}{L^{\alpha }}}-{\displaystyle \frac{x_0}{{(t_{n+1}-t_0)}^{\alpha }}}\hfill \\ \hfill & -{\displaystyle \frac{h^{-\alpha }}{2}}\sum _{i=0}^{n+1-m}{\omega }_{i,n+1}{x}_h\left(t_i\right)].\hfill \end{array}$$

The description of the numerical algorithm is now completed. It is shown in [32] through mathematical analysis that the error can be expected to behave as

$$\underset{j=0,1,\dots ,N}{max}\left|x\left(t_j\right)-x_h\left(t_j\right)\right|=O\left(h^p\right),$$

where $p=min(2,1+\alpha )$.

4.2. Numerical Examples

In this part, a classic example is given to verify the synchronization and adaptive synchronization of a short-memory higher-order network.

Consider a directed 2-hypergraph network with six nodes, denoted by the vertex set $V=\{1,2,3,4,5,6\}$, as illustrated in Figure 1. The network contains directed 1-hyperedges $\left(\right\{1,2\},\{2,3\},\{2,5\},\{3,5\},\{4,3\}$, and $\{6,1\})$ and directed 2-hyperedge $\left(\right\{1,5,6\}$ and $\{3,5,4\})$. For convenience, controllers are added to the first three nodes. The node dynamics are governed by a short-memory Caputo fractional Lorenz system

$$\left\{\begin{array}{c}{}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }{s}_1\left(t\right)=a(s_2\left(t\right)-s_1\left(t\right)),\hfill \\ {}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }{s}_2\left(t\right)=b{s}_1\left(t\right)-s_1\left(t\right)s_3\left(t\right)-s_2\left(t\right),\hfill \\ {}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }{s}_3\left(t\right)=s_1\left(t\right)s_2\left(t\right)-c{s}_3\left(t\right),\hfill \end{array}\right.$$

(23)

where $L=0.2$, $a=10,b=22,$ and $c={\displaystyle \frac{3}{8}}$. The chaotic orbits are shown in Figure 2 for $\alpha =0.98$.

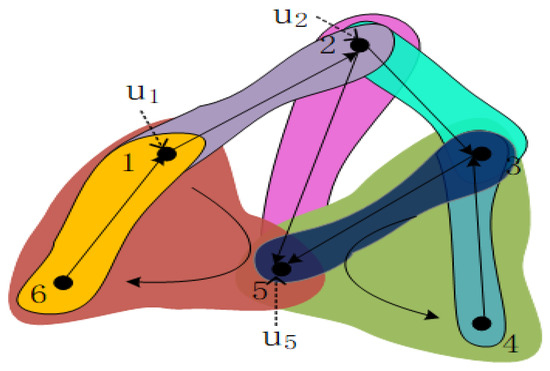
Figure 1. A directed 2-hypergraph network.

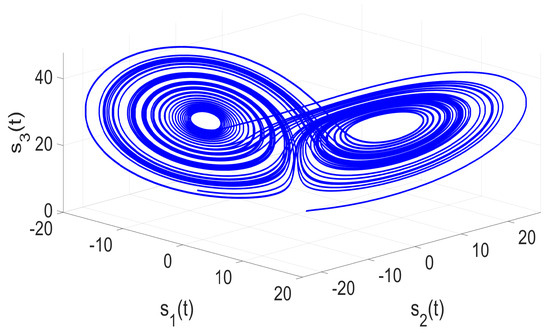
Figure 2. The chaotic orbits of short-memory fractional Lorenz system (23).

Consider the following network:

$$\begin{array}{cc}\hfill {}_{s_L\left(t\right)}{}^C\widehat{D}_t^{\alpha }{x}_i\left(t\right)& =g\left(x_i\left(t\right)\right)+\sum _{j=1}^6{\mathcal{Q}}_{ij}\mathrm{\Phi }{x}_j\left(t\right)-h_i\mathrm{\Phi }(x_i\left(t\right)-s\left(t\right)),\hfill \end{array}$$

where

$$g\left(x_i\left(t\right)\right)=\left(\begin{array}{c}a(x_{i2}\left(t\right)-x_{i1}\left(t\right))\\ b{x}_{i1}\left(t\right)-x_{i1}\left(t\right)x_{i3}\left(t\right)-x_{i2}\left(t\right)\\ x_{i1}\left(t\right)x_{i2}\left(t\right)-c{x}_{i3}\left(t\right)\end{array}\right).$$

Here are the corresponding Laplace matrices:

$$Q_1=\left[\begin{array}{cccccc}-1& 1& 0& 0& 0& 0\\ 0& -2& 1& 0& 1& 0\\ 0& 0& -1& 0& 1& 0\\ 0& 0& 1& -1& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 1& 0& 0& 0& 0& -1\end{array}\right],Q_2=\left[\begin{array}{cccccc}-1& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& -1& 0& 1& 0\\ 0& 0& 1& -1& 0& 0\\ 0& 0& 0& 1& -2& 1\\ 1& 0& 0& 0& 0& -1\end{array}\right].$$

To quantify the short-memory fractional network synchronization, the synchronization mean error is defined as

$$E\left(t\right)={\displaystyle \frac{1}{6}}\sum _{i=1}^6{\parallel x_i\left(t\right)-s\left(t\right)\parallel }_2.$$

Choose the coupling strengths $c_1=c_2=25$ and control gains $h_i=15,i=1,2,3$, while the remaining nodes remain uncontrolled. Let $\mathrm{\Phi }$ be the identity matrix and $\Theta =\mathrm{diag}(2,2,\dots ,2)$. According to the conditions of Theorem 1, the largest eigenvalue

$${\lambda }_{max}\left(\Theta \otimes I_N+({\widehat{\mathcal{Q}}}^{\left(D\right)}-H)\otimes \mathrm{\Phi }\right)=-3.4887,$$

and

$$-{\displaystyle \frac{1}{2L^{\alpha }\mathrm{\Gamma }(1-\alpha )sin\left(\frac{\alpha \pi }{2}\right)}}=-0.0490,$$

which satisfies condition (10). Therefore, the synchronization of controlled network (9) is achieved. The node errors are illustrated in Figure 3, and as shown in Figure 4, the mean synchronization errors asymptotically converge to zero across different fractional orders $\alpha$, demonstrating successful synchronization of system (9).

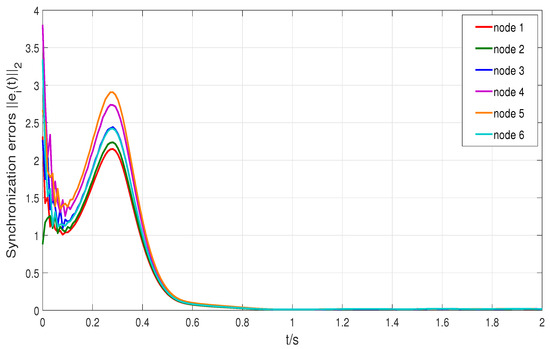
Figure 3. Synchronization errors of network (9).

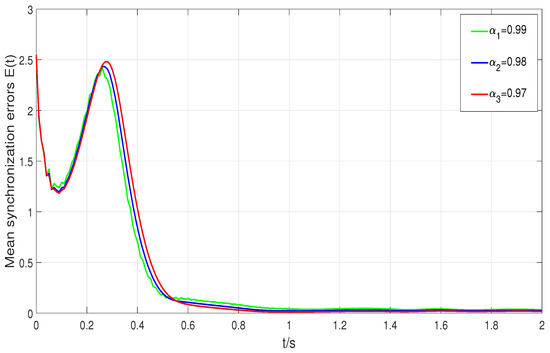
Figure 4. Mean synchronization errors under different fractional orders $\alpha$.

Furthermore, the synchronization control problem for directed higher-order networks (14) is further addressed by employing an adaptive coupling strategy to enhance control efficiency. The proposed adaptive coupling mechanisms are defined as in Equation (15), with initial conditions set as $c_d\left(0\right)=1.0$ for $d=1,2$, adaptation rates of ${\alpha }_1=0.12$ and ${\alpha }_2=0.15$, and all other parameters unchanged. The evolution of the adaptive coupling strengths is illustrated in Figure 5, where the coupling strengths initially start small and gradually increase until synchronization is attained. The maximum eigenvalue

$${\mu }_{max}\left(\Theta \otimes I_N+\sum _{d=1}^D{c}_d\left(t\right)({\widehat{Q}}^{\left(d\right)}\otimes \mathrm{\Phi })-H\otimes \mathrm{\Phi }\right)=-0.1788<-0.0490,$$

confirms that condition (16) is satisfied. Consequently, the synchronization of directed higher-order network (14) is successfully achieved through the adaptive coupling strength defined in Equation (15). The synchronization errors of the nodes are shown in Figure 6, and as depicted in Figure 7, the mean synchronization error converges to zero for different fractional orders $\alpha$.

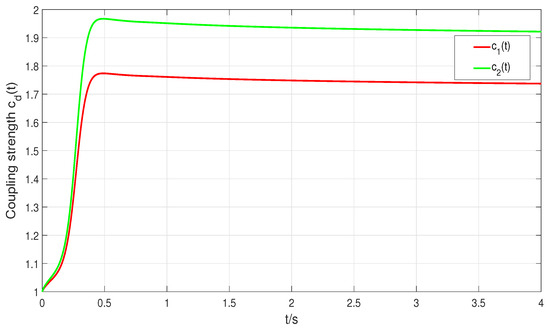
Figure 5. The evolutionary dynamics of adaptive coupling strength (15).

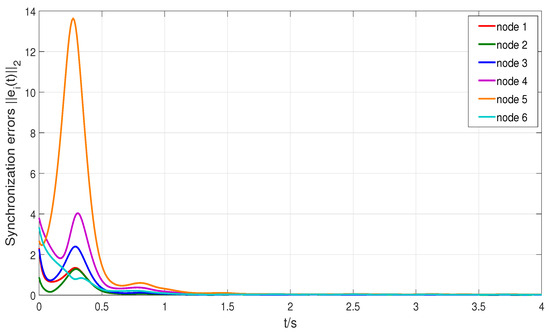
Figure 6. Synchronization errors of network (14).

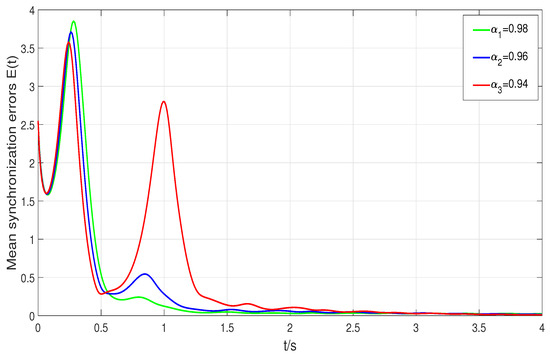
Figure 7. Mean synchronization errors under fractional orders $\alpha$.

5. Conclusions

In this study, the synchronization control problem of short-memory fractional directed higher-order networks has been systematically addressed. A novel network model was constructed by integrating hypergraph theory with higher-order adjacency tensors, enabling an accurate characterization of multi-body interactions beyond traditional pairwise frameworks. Based on the short-memory property of the Caputo fractional derivative, a pinning control strategy was developed, and sufficient synchronization conditions were rigorously derived through Lyapunov function analysis and matrix techniques. These results clarify the intrinsic relationships among control gains, coupling strength, network topology, and fractional order. To enhance robustness under realistic, time-varying coupling scenarios, an adaptive control law was introduced. Furthermore, an improved predictor–corrector algorithm was proposed for general fractional systems with short memory, providing efficient numerical solutions.

The generality of the approaches developed here not only advances the study of synchronization in higher-order networks but also contributes to the broader development of short-memory fractional calculus theory. The synchronization of stochastic short-memory fractional systems will be investigated in future research to advance both theory and application.