Fuzzy-Immune Adaptive Fractional-Order LQI Control for Robust and Intelligent Heart Rate Regulation in Cardiac Pacemakers

Abstract

Cardiac pacemakers are standard implantable medical devices that regulate and treat heart rhythm disorders, primarily aiming to improve patient health outcomes. This study presents the systematic design, implementation, and simulation-based validation of a novel fuzzy-immune adaptive Fractional-Order Linear Quadratic Integral (FO-LQI) control strategy for heart rate (HR) regulation using cardiac pacemakers. Unlike the conventional LQI controller, the proposed approach replaces the integer-order integrator with a fractional-order integral operator to enhance the controller’s design flexibility and dynamic response. To address the implementation challenges of fixed fractional exponents, a fuzzy-immune adaptation mechanism is introduced to modulate the fractional order in real time. This adaptive scheme improves the controller’s robustness across varying physiological states, enabling more responsive HR adaptation to the patient’s metabolic demands. The proposed controller is modeled and simulated in MATLAB/Simulink using physiologically relevant test cases. Comparative simulation results show that the fuzzy-immune adaptive FO-LQI controller outperforms the baseline LQI and fixed FO-LQI controllers in achieving time-optimal HR regulation. These findings validate the reliability and enhanced robustness of the proposed control scheme for simulating cardiac behavior under diverse physiological conditions.

1. Introduction

A cardiac pacemaker is an invasive biomedical device typically implanted in the chest near the collarbone and connected to the atrium or the ventricle [1]. It delivers periodic electrical impulses to the heart, effectively functioning as an artificial pulse generator [2]. Widely used in the healthcare sector, cardiac pacemakers are designed to treat various cardiovascular conditions, including arrhythmia, bradycardia, and tachycardia—disorders often caused by sinus node dysfunction, heart block, chronotropic incompetence, atrial fibrillation, or other cardiac anomalies [3,4].

Pacemakers may be classified as either temporary or permanent [5]. Temporary pacemakers are primarily used during medical procedures when the patient’s heart cannot maintain a safe intrinsic rhythm [5]. In contrast, permanent pacemakers are implanted in patients with persistent cardiac rhythm disturbances that necessitate long-term intervention [6]. Recent studies have also explored memristor-based chaotic dynamical models for generating electrocardiogram signals, offering promising applications in low-power, wearable, and implantable cardiac systems [7]. Such approaches highlight the growing role of memristive circuits in next-generation bioelectronics and motivate the development of adaptive, energy-efficient control strategies for pacemakers.

Effective cardiac pacing requires precise control of several parameters, such as heart rate, atrioventricular (AV) delay, pacing voltage, respiratory rate, and blood pH levels [8]. Since deviations from the normal heart rate range of 60–100 beats per minute (bpm) are clinically undesirable, heart rate regulation and control remain a critical objective in pacemaker design [9]. Parameters like pacing voltage and AV delay significantly influence heart rate, and their robust control determines the overall effectiveness of a pacemaker system [10]. A reliable HR control system enables the pacemaker to improve the patient’s cardiac output and enhance their safety and comfort across different activity levels and conditions [11].

1.1. Literature Review

Extensive research has been conducted on heart rate (HR) regulation via cardiac pacemakers [12], resulting in various control strategies, each with distinct advantages and limitations. These can be systematically categorized based on their dependence on system modeling and adaptability: model-based vs. model-free, and fixed-gain vs. adaptive-gain control schemes.

1.1.1. Model-Free Fixed Control Strategies

The Proportional–Integral–Derivative (PID) controller remains popular due to its simplicity, low computational cost, and well-established tuning methods [13]. However, it performs poorly in systems with large delays and nonlinear dynamics, and its fixed gains render it inadequate under physiological disturbances [14]. Gain optimization approaches employing heuristic tuning rules and nature-inspired algorithms such as the artificial bee colony have been proposed to enhance PID performance, albeit at the cost of increased complexity, undermining its primary strength [15]. The Fractional-Order PID (FOPID) controller improves robustness and transient performance by introducing fractional integral and derivative orders [16,17]. Despite its flexible design and agile control yield, the fractional orders’ tuning poses a challenge [18]. The Sliding Mode Control (SMC) offers strong robustness against disturbances and system uncertainties by enforcing motion along a defined sliding surface [19]. While effective for nonlinear systems, SMC suffers from chattering due to high-frequency switching, which may damage cardiac tissue and reduce device lifespan [20].

1.1.2. Model-Based Fixed Control Strategies

The Model Predictive Control (MPC) optimizes control actions by predicting future system behavior while handling constraints explicitly [21]. Despite its effectiveness, real-time implementation is limited by high computational demands and sensitivity to model inaccuracies, making it less suitable for implantable devices with power and resource constraints [22]. The ubiquitous Linear Quadratic Regulator (LQR) control minimizes a quadratic cost function by optimizing state-feedback gains through the algebraic Riccati equation [23]. While straightforward to design, LQR lacks robustness to nonlinearity and disturbances, requires full state feedback, and often exhibits steady-state offsets [24]. Integrating an additional integral action, as in Linear Quadratic Integrator (LQI), can eliminate steady-state errors and improve disturbance rejection [25].

1.1.3. Adaptive Control Strategies

The adaptive controllers adjust controller parameters in real-time based on tracking errors relative to a reference [26]. The adaptive control schemes offer adaptability to system uncertainties, but slow convergence and the requirement for continuous stimulation pose practical limitations, particularly in biomedical applications [27]. The adaptive PID control strategy proposed in [28] serves to enhance the chronotropic efficiency in pacemakers, demonstrating improved heart rate regulation under varying physiological demands. The ubiquitous rate-adaptive intracardiac pacemaker tends to adjust the pacing based on sensed physiological parameters, offering improved responsiveness in fully implantable devices [29]. The incorporation of intelligent backstepping controllers in implantable pacemakers has also garnered a lot of traction by achieving improved robustness and adaptability in heart rate tracking [30]. The model reference adaptive control (MRAC) approach has also demonstrated promising results in cardiac hemodynamic regulation [31].

1.1.4. Intelligent Control Strategies

The Fuzzy Logic Control (FLC) offers model-free control suitable for nonlinear and uncertain environments [32]. It translates inputs into linguistic rules using membership functions, enabling smooth and intuitive control [33]. However, FLC design is often heuristic and patient-specific, which increases complexity in biomedical contexts. Hybrid FLC schemes combining PID or FOPID have demonstrated enhanced performance [34]. The neural networks (NNs) offer powerful nonlinear modeling capabilities and adaptive control through learning-based weight updates [35]. Although highly flexible, they are probabilistic and may exhibit unpredictable behavior, limiting reliability in critical systems [10]. Recently, data-driven approaches such as reinforcement learning have emerged, showing promise for precision control in repeated biomedical processes [36].

1.2. Main Contributions

This article presents the systematic design, implementation, and simulation-based validation of a novel fuzzy-immune adaptive fractional-order LQI (FIFO-LQI) control strategy for cardiac pacemakers. The proposed controller introduces a real-time fuzzy-immune mechanism to adaptively regulate the fractional-order integral term, thereby enhancing tracking accuracy, transient response, and disturbance rejection under physiologically realistic scenarios. The proposed approach builds upon the conventional LQI controller as a baseline, enhancing its control flexibility by substituting its integer-order integrator with a fractional-order operator. The fractional order in the FO-LQI controller is optimized offline through a multi-objective tuning process. To obviate the necessity of fixed offline tuning and improve controller adaptability, the fractional exponent is modulated online using a bio-inspired fuzzy-immune adaptation mechanism. This modification transforms the FO-LQI controller into an intelligent self-adaptive control scheme. The adaptive system, modeled after biological immune responses, dynamically adjusts the control trajectory based on real-time physiological variations. As a result, the heart rate control mechanism becomes more responsive and resilient to changes in metabolic demand across different physical states. The main contributions of this work are listed as follows:

• Development of a novel FO-LQI controller for cardiac pacemakers, based on a nominal state-space model.
• Integration of a fuzzy-immune adaptive system to dynamically regulate the fractional-order operator in real time.
• Simulation-based validation of the proposed controller in MATLAB/Simulink under physiologically relevant scenarios.

The proposed control framework offers several key advantages. Firstly, it enhances HR regulation by exploiting the design flexibility rendered by the fractional operators. Secondly, it introduces a fuzzy-immune adaptation mechanism to provide a practical framework for the intelligent control of implantable biomedical devices. The artificial immune adaptive system is particularly advantageous for gain adaptation in controllers due to its strong self-regulating and self-learning capabilities, inspired by the human immune system’s ability to respond dynamically to changing environments. It enables real-time adjustment of controller parameters in response to external disturbances or internal state variations, enhancing robustness and adaptability. Hence, fuzzy immune augmentation significantly improves the closed-loop system’s disturbance rejection and tracking capability across diverse metabolic states.

1.3. Distinctive Features of the Proposed Work

The conventional integer-order controllers such as PID and LQI controllers, while simple and widely used, often exhibit limited adaptability and suboptimal performance under nonlinear, time-varying physiological conditions common in cardiac systems. Specifically, fixed-gain PID or LQI controllers may lead to integral windup, slow convergence, or steady-state offsets when the heart’s dynamics change due to disease progression (such as reduced myocardial compliance) or external disturbances (such as stress-induced heart rate fluctuations). In contrast, the proposed fuzzy-immune adaptive FO-LQI controller introduces a fractional-order integrator whose order is dynamically modulated in real time. This allows the integral action to scale smoothly during transient and steady-state phases, effectively managing overshoot, windup, and convergence behavior. The conventional integer-order controllers struggle to overcome the aforementioned limitations.

The proposed controller introduces a novel convergence of model-based and intelligent adaptive control. Unlike fixed FO-LQI controllers, the proposed method:

• Self-adapts the fractional order online via a fuzzy-immune system, eliminating the need for fixed fractional exponent tuning.
• Incorporates biological immune principles for dynamic gain regulation, offering fast disturbance recovery and enhanced robustness.
• Balances optimality and adaptability by retaining the LQI’s structured optimal control framework while injecting real-time responsiveness.

This hybridization differentiates our approach from both traditional fixed-gain integer-order controllers and heuristic rule-based systems. It addresses both the rigidity of integer-order control and the lack of adaptability in conventional schemes, offering a more robust and flexible solution for HR regulation in pacemakers.

The adaptive tuning of a single fractional-order term in an LQI controller using a fuzzy-immune mechanism, for robust-optimal heart rate regulation in cardiac pacemakers, has not been reported in the existing scientific literature. This article, therefore, centers on the systematic formulation and validation of this novel control strategy.

The structure of the paper is as follows: Section 2 presents the derivation of the nominal state-space model and the design of the baseline LQI controller. Section 3 details the proposed self-adaptive FO-LQI control framework. Section 4 outlines the offline tuning methodology. Section 5 provides a comparative analysis of the baseline and proposed controllers and a discussion of simulation results. The study concludes in Section 6 with a summary and future directions.

2. System Description

A cardiac pacemaker is a biomedical device implanted to regulate heart rhythm by delivering electrical pulses to the myocardium, ensuring consistent cardiac contractions [37]. The device consists of a pulse generator containing battery and electronic circuits that generate electric impulses, sensing electrodes that continuously monitor the heart’s electrical activity and provide feedback to the control system, and insulated electrodes that deliver pulses from the generator to the heart tissue. The closed-loop control of a cardiac pacemaker involves continuously monitoring physiological signals such as heart rate (HR) and adjusting the pacing pulses accordingly to maintain optimal HR in response to varying physical or metabolic demands. The system’s closed-loop block diagram is shown in Figure 1. The controller interprets the sensed feedback and computes the appropriate pacing rate to synchronize cardiac activity with the body’s needs. This control mechanism helps compensate for intrinsic deficiencies in the heart’s electrical system by dynamically re-adjusting the bio-electric control signals.

2.1. Model Derivation

The model of the pacemaker and the heart is derived in this section [38]. The heart’s intrinsic dynamics can be modeled as a second-order system with a natural frequency ${\omega }_n$ and damping ratio $\delta$. The corresponding open-loop transfer function is expressed in (1) [15].

$$G_C\left(s\right)={\displaystyle \frac{{\omega }_n^2}{s\left(s+2\delta {\omega }_n\right)}}$$

(1)

where $s$ is the Laplace operator. The pacemaker’s output can be approximated by a first-order filter, typically represented as shown in (2) [15].

$$G_P\left(s\right)={\displaystyle \frac{m}{1+s \tau }}$$

(2)

where $m$ is the filter gain and $\tau$ is the time constant. In the rest condition, the cardiac system should behave like an under-damped system. Hence, in this study, the values of natural frequency and damping ratio for a patient are heuristically set at ${\omega }_n=12.57$ and $\delta =0.8$ [15]. The empirical settings of the pacemaker, used in this study, are $K=1$ and $\tau ={\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$8$}\right.}$ [15]. The transfer functions of $G_C\left(s\right)$ and $G_P\left(s\right)$ are identified in (3).

$$G_C\left(s\right)={\displaystyle \frac{169}{s\left(s+20.8\right)}}, G_P\left(s\right)={\displaystyle \frac{8}{s+8}}$$

(3)

The combined transfer function representing the heart-pacemaker dynamics is derived by taking the product of the transfer function of the heart $G_C\left(s\right)$ with the transfer function of the pacemaker $G_P\left(s\right)$, as shown in (4).

$$G_{CP}\left(s\right)=G_C\left(s\right)\times G_P\left(s\right)$$

(4)

The transfer function representing the action of the cardiac pacemaker on the heart is identified as shown by (5).

$$G_{CP}\left(s\right)={\displaystyle \frac{R\left(s\right)}{U\left(s\right)}}={\displaystyle \frac{1352}{s^3+28.8s^2+166.4s}}$$

(5)

where $R\left(s\right)$ is the actual heart rate, and $U\left(s\right)$ is the bio-electrical signal generated by the pacemaker to normalize the HR. The transfer function in (5) is written as shown below to create the state space model for the cardiac pacemaker system.

$$\left(s^3+28.8s^2+166.4s\right) R\left(s\right)=1352 U\left(s\right)$$

(6)

The above expression is simplified and transformed into a differential equation time domain, as expressed in (7).

$$\stackrel{⃛}{r}\left(t\right)+28.8 \ddot{r}\left(t\right)+166.4 r\left(t\right)=1352 u\left(t\right)$$

(7)

where $r\left(t\right)$ is the actual heart rate and $u\left(t\right)$ is the bio-electric control input signal. The pacemaker-heart dynamics are represented in state space form as expressed in (8).

$$\dot{x}\left(t\right)=\mathit{A}x\left(t\right)+\mathit{B}u\left(t\right), y\left(t\right)=\mathit{C}x\left(t\right)+\mathit{D}u\left(t\right)$$

(8)

where $x\left(t\right)$ is the state vector, $y\left(t\right)$ is the output vector, and $u\left(t\right)$ is the bio-electrical control signal. Here, $\mathit{A}$ is the system matrix, $\mathit{B}$ is the control input matrix, $\mathit{C}$ is the output matrix, and $\mathit{D}$ is the feedforward matrix. The state variables of the cardiac pacemaker system are expressed as follows.

$$x\left(t\right)={\left[\begin{array}{ccc}r\left(t\right)& \dot{r}\left(t\right)& \ddot{r}\left(t\right)\end{array}\right]}^T$$

(9)

where $\dot{r}\left(t\right)$ represents the rate of change in HR, and $\ddot{r}\left(t\right)$ represents the HR acceleration. The state space matrices are expressed in companion form in (10).

$$\begin{gathered} \mathit{A}=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 0& -166.4& -28.8\end{array}\right], \mathit{B}=\left[\begin{array}{c}0\\ 0\\ 1352\end{array}\right], \\ \mathit{C}=\left[\begin{array}{ccc}1& 0& 0\end{array}\right], \mathit{D}=\left[0\right] \end{gathered}$$

(10)

To improve the pacemaker system’s disturbance rejection and setpoint tracking ability, an integral of the error term is also introduced as an auxiliary state variable in the system. The integral of error $\epsilon \left(t\right)$ is computed as shown in (11).

$$\epsilon \left(t\right)=\int e\left(t\right)dt$$

(11)

such that, $e\left(t\right)=r\left(t\right)-r_d$, where $e\left(t\right)$ is the error between the desired HR, $r_d$, and the actual HR of the patient. With the inclusion of $\epsilon \left(t\right)$ as a new state variable, the system’s state-space model is modified as shown below.

$$\dot{x}\left(t\right)=\mathit{A}x\left(t\right)+\mathit{B}u\left(t\right)+\mathit{G}{r}_d, y\left(t\right)=\mathit{C}x\left(t\right)+\mathit{D}u\left(t\right)$$

(12)

where

$$\mathit{A}=\left[\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& -166.4& -28.8& 0\\ 1& 0& 0& 0\end{array}\right], \mathit{B}=\left[\begin{array}{c}0\\ 0\\ \begin{array}{c}1352\\ 0\end{array}\end{array}\right], \mathit{G}=\left[\begin{array}{c}0\\ 0\\ 0\\ -1\end{array}\right], \mathit{C}=\left[\begin{array}{cccc}1& 0& 0& 0\end{array}\right], \mathit{D}=\left[0\right]$$

The modified state vector is expressed in (13).

$$x\left(t\right)={\left[\begin{array}{ccc}r\left(t\right)& \dot{r}\left(t\right)& \begin{array}{cc}\ddot{r}\left(t\right)& \epsilon \left(t\right)\end{array}\end{array}\right]}^T$$

(13)

These state space matrices can be used to obtain the transfer function of the cardiac pacemaker system with the integral of error, as shown in (14).

$$G_{CPI}\left(s\right)={\displaystyle \frac{1352s}{s^4+28.8s^3+166.4s^2}}$$

(14)

2.2. Baseline LQI Control Law

The LQI controller extends the conventional LQR by incorporating an integral action into the state-feedback loop [39]. This modification enhances the system’s ability to track reference signals more accurately and reduces transient deviations such as overshoots and undershoots [25].

2.2.1. Controller Formulation

The controller is synthesized by minimizing a quadratic performance index that penalizes state error and control effort, ensuring optimal performance over an infinite time horizon. This performance index is defined as follows [40].

$$J_{lqi}={\displaystyle \frac{1}{2}}{\int }_0^{\mathrm{\infty }}\left({x\left(t\right)}^T\mathit{Q}x\left(t\right)+{u\left(t\right)}^T\mathit{R}u\left(t\right)\right)dt$$

(15)

Here, $\mathit{Q}$ $\in$ ℝ^4×4 is a positive semi-definite matrix that weights the state variables, while $\mathit{R}$ $\in$ ℝ is a positive definite scalar that penalizes the control input. These matrices are designed to strike an appropriate balance between accurate tracking and minimal control effort. The weighting matrices for the proposed cardiac pacemaker are defined in (16).

$$\mathit{Q}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(\begin{array}{cc}\begin{array}{cc}{q}_r& q_{\dot{r}}\end{array}& \begin{array}{cc}{q}_{\ddot{r}}& q_{\epsilon }\end{array}\end{array}\right), \mathit{R}=p$$

(16)

To ensure asymptotic stability, the weighting coefficients must satisfy: $q_r\ge 0$, $q_{\dot{r}}\ge 0$, $q_{\ddot{r}}\ge 0$, $q_{\mathsf{\epsilon }}\ge 0$, and $p>0$. The offline tuning procedure employed for selecting these coefficients is detailed in Section 4. Once these matrices are configured, the optimal feedback gain is computed by solving the Hamilton–Jacobi–Bellman (HJB) equation, which results in the Algebraic Riccati Equation (ARE) expressed below [40].

$${\mathit{A}}^T\mathit{P}+\mathit{P}\mathit{A}-\mathit{P}\mathit{B}{\mathit{R}}^{-1}{\mathit{B}}^T\mathit{P}+\mathit{Q}=0$$

(17)

The solution of ARE may exhibit numerical stiffness in embedded applications. Hence, in embedded applications, the ARE is typically solved by using specialized numerical techniques such as the Kleinman iteration, Chandrasekhar-type factorization, or semi-implicit ODE solvers, which are better suited to real-time and memory-constrained environments [41,42]. The symmetric positive definite solution $\mathit{P}$ $\in$ ℝ^4×4 of this ARE determines the optimal gain vector formulated in (18).

$$\mathit{K}={\mathit{R}}^{-1}{\mathit{B}}^T\mathit{P}$$

(18)

Accordingly, the optimal control input is expressed in (19).

$$u\left(t\right)=-\mathit{K}x\left(t\right)$$

(19)

where $\mathit{K}=\left[\begin{array}{cc}\begin{array}{cc}{k}_r& k_{\dot{r}}\end{array}& \begin{array}{cc}{k}_{\ddot{r}}& k_{\epsilon }\end{array}\end{array}\right]$. The integral action embedded within the state vector eliminates steady-state error and strengthens the system’s rejection of persistent disturbances. The control law can be rewritten as shown below.

$$u\left(t\right)=-k_r r\left(t\right)-k_{\dot{r}} \dot{r}\left(t\right)-k_{\ddot{r}} \ddot{r}\left(t\right)-k_{\epsilon }\int e\left(t\right)dt$$

(20)

2.2.2. Stability Proof

The stability of the LQI controller is validated using a Lyapunov-based approach. Consider the following candidate Lyapunov function [25].

$$V\left(t\right)={x\left(t\right)}^T\mathit{P}x\left(t\right)>0, \mathrm{f}\mathrm{o}\mathrm{r} x\left(t\right)\ne 0$$

(21)

Taking the time derivative of $V\left(t\right)$ yields the following expression.

$$\dot{V}\left(t\right)=2{x\left(t\right)}^T\mathit{P}\dot{x}\left(t\right)=2{x\left(t\right)}^T\mathit{P}\left(\mathit{A}-\mathit{B}\mathit{K}\right)x\left(t\right)=2{x\left(t\right)}^T\mathit{P}\left(\mathit{A}-\mathit{B}{\mathit{R}}^{-1}{\mathit{B}}^T\mathit{P}\right)x\left(t\right)$$

(22)

Rewriting this expression as shown in (23).

$$\dot{V}\left(t\right)={x\left(t\right)}^T\left(\mathit{P}\mathit{A}+{\mathit{A}}^T\mathit{P}\right)x\left(t\right)-2{x\left(t\right)}^T\left(\mathit{P}\mathit{B}{\mathit{R}}^{-1}{\mathit{B}}^T\mathit{P}\right)x\left(t\right)$$

(23)

By substituting the ARE in (17) into (23), $\dot{V}\left(t\right)$ simplifies as shown below [26].

$$\dot{V}\left(t\right)=-{x\left(t\right)}^T\mathit{Q}x\left(t\right)-{x\left(t\right)}^T\left(\mathit{P}\mathit{B}{\mathit{R}}^{-1}{\mathit{B}}^T\mathit{P}\right)x\left(t\right)<0$$

(24)

As long as $\mathit{R}={\mathit{R}}^T>0$ and $\mathit{Q}={\mathit{Q}}^T\ge 0$, the expression for $\dot{V}\left(t\right)$ will remain negative definite. This confirms that the closed-loop system governed by the LQI controller is asymptotically stable. The LQI control architecture applied for regulating the HR is illustrated in Figure 2.

3. Proposed Control Methodology

This section presents the methodical formulation of the proposed fuzzy immune adaptive FO-LQI control law for the cardiac pacemaker system.

3.1. Fixed Fractional-Order LQI (FO-LQI) Control Law

Fractional calculus extends the classical concepts of differentiation and integration to non-integer (fractional) orders, providing a powerful framework for modeling and controlling systems with intricate dynamics [43]. One can enhance system performance by incorporating fractional-order (FO) elements into control strategies, especially in complex dynamical environments [44]. The operator $D^{\mathsf{\lambda }}$ denotes a fractional derivative or integral, where $\mathsf{\lambda }$ is the fractional order. The three commonly used definitions of fractional derivatives—Grünwald–Letnikov, Riemann–Liouville, and Caputo—are presented below [45]. The Grünwald–Letnikov formulation is expressed in (25).

$$D^{\mathsf{\lambda }}f\left(t\right)=\underset{h\to 0}{\lim }{\displaystyle \frac{1}{h^i}}\sum _{i=0}^{(t-a)/h}{\left(-1\right)}^i\left(\begin{array}{c}\mathsf{\lambda }\\ i\end{array}\right)f\left(t-ih\right)$$

(25)

where $\left(\begin{array}{c}\mathsf{\lambda }\\ i\end{array}\right)=\Gamma \left(\mathsf{\lambda }+1\right)/\Gamma \left(i+1\right)\Gamma \left(\mathsf{\lambda }-i+1\right)$, and $h$ is the step size. The Riemann–Liouville definition is expressed in (26).

$$D^{\mathsf{\lambda }}f\left(t\right)={\displaystyle \frac{1}{\Gamma \left(n-\mathsf{\lambda }\right)}}{\displaystyle \frac{d^n}{{dt}^n}}{\int }_a^t{\displaystyle \frac{f\left(\tau \right)}{{\left(t-\tau \right)}^{\mathsf{\lambda }-n+1}}}d\tau$$

(26)

where $\Gamma \left(x\right)$ is the Euler gamma function, $n$ is an integer such that $n-1<\mathsf{\lambda }<\mathrm{n}$. The Caputo definition is expressed in (27).

$$D^{\mathsf{\lambda }}f\left(t\right)={\displaystyle \frac{1}{\Gamma \left(\mathsf{\lambda }-n\right)}}{\int }_a^t{\displaystyle \frac{f^n\left(\tau \right)}{{\left(t-\tau \right)}^{\mathsf{\lambda }-n+1}}}d\tau$$

(27)

Standard integer-order derivatives and integrals are replaced with fractional counterparts in fractional-order control, offering enhanced flexibility in control law design [44]. This added flexibility allows the controller to exhibit dynamic behaviors unattainable through traditional integer-order techniques. In this context, the conventional LQI controller is extended to an FO-LQI formulation as described in (28).

$$u\left(t\right)=-k_r r\left(t\right)-k_{\dot{r}} \dot{r}\left(t\right)-k_{\ddot{r}} \ddot{r}\left(t\right)-k_{\epsilon }\left(D^{\mathsf{\lambda }}e\left(t\right)\right)$$

(28)

Here, the FO term introduces a new parameter, $\mathsf{\lambda }$, representing the order of the fractional integral applied to $e\left(t\right)$. This addition enhances the responsiveness and adaptability of the controller. It is important to note that when the fractional order $\mathsf{\lambda }$ lies within the range $0<\mathsf{\lambda }<1$, the operator exhibits derivative-like behavior, with $\mathsf{\lambda }=1$ corresponding to a conventional first-order derivative. Conversely, for $-1<\mathsf{\lambda }<0$, the operator exhibits integral-like behavior, with $\mathsf{\lambda }=-1$ representing a standard first-order integral operator [43].

In regulation control problems, the desired reference signal $r_d$ is constant. Consequently, the tracking error simplifies to $e\left(t\right)=r\left(t\right)$. Under this condition, the control law can be expressed in a simplified form as follows.

$$u\left(t\right)=-k_r r\left(t\right)-k_{\dot{r}} \dot{r}\left(t\right)-k_{\ddot{r}} \ddot{r}\left(t\right)-k_{\epsilon }\left(D^{\mathsf{\lambda }}r\left(t\right)\right)$$

(29)

The corresponding transfer functions are expressed as shown in (30).

$${\displaystyle \frac{u\left(s\right)}{r\left(s\right)}}=-k_r-k_{\dot{r}} s-k_{\ddot{r}} s^2-k_{\epsilon } s^{\mathsf{\lambda }}$$

(30)

Since implementing fractional powers of $s$ (i.e., $s^{\mathsf{\lambda }}$) directly is not feasible in practice, the Oustaloup recursive approximation is used [46]. This approximation of the fractional-order term $s^{\mathsf{\lambda }}$ is defined as follows [47].

$$s^{\mathsf{\lambda }}=M\prod _{i=1}^N{\displaystyle \frac{1+\left(\raisebox{1ex}{$s$}\!\left/ \!\raisebox{-1ex}{$w_{z,i}$}\right.\right)}{1+\left(\raisebox{1ex}{$s$}\!\left/ \!\raisebox{-1ex}{$w_{p,i}$}\right.\right)}}$$

(31)

such that, ${ w}_{z,i}=w_l{\left({\displaystyle \raisebox{1ex}{$w_h$}\!\left/ \!\raisebox{-1ex}{$w_l$}\right.}\right)}^{{\displaystyle \raisebox{1ex}{$2i-1-\mathsf{\lambda }$}\!\left/ \!\raisebox{-1ex}{$2N$}\right.}},w_{p,i}=w_l{\left({\displaystyle \raisebox{1ex}{$w_h$}\!\left/ \!\raisebox{-1ex}{$w_l$}\right.}\right)}^{{\displaystyle \raisebox{1ex}{$2i-1+\mathsf{\lambda }$}\!\left/ \!\raisebox{-1ex}{$2N$}\right.}}$, where $N$ is the filter order, $w_l$ and $w_h$ represent the lower and upper frequency bounds, and $M$ is a scaling constant chosen to ensure ${\left|jw\right|}^{\mathsf{\lambda }}=1$ at $w=1.0$ rad/s. The filter used in this study is characterized by $N=5$, $w_l={10}^{-3}$ rad/s, and $w_h={10}^3$ rad/s [46].

The LQI controller’s stability conditions, $\mathit{R}={\mathit{R}}^T>0$ and $\mathit{Q}={\mathit{Q}}^T\ge 0$ remain valid for the FO-LQI approach [44]. This is because the FO-LQI controller modifies only the estimate of one state integral provided to the control law, without altering the core structure of the state-feedback gains. To implement the FO-LQI control law with fixed fractional order, the parameter $\mathsf{\lambda }$ is tuned offline by using the procedure outlined in Section 4. The block diagram illustrating the FO-LQI structure is shown in Figure 3.

3.2. Fuzzy-Immune Adaptive FO-LQI Control Law

The Fuzzy Immune System (FIS) is an intelligent processing mechanism that autonomously modulates the system’s immune-like behavior, thereby enhancing its adaptability and responsiveness in mitigating external disturbances [48].

3.2.1. Artificial Immune System

Inspired by the biological immune response, this model draws from the roles played by antibodies and lymphocytes within the natural immune system [49]. Specifically, helper T cells ($T_H$), suppressor T cells ($T_S$), and B cells collectively participate in lymphocyte generation. The B cells assess the magnitude of invading antigens and, upon evaluation, initiate the activation of $T_H$ cells to promote plasma cell formation. These plasma cells then secrete antibodies to counteract the intrusion. Once the antigen threat diminishes, $T_S$ cells become active to suppress further antibody production. This dynamic interplay between $T_H$ and $T_S$ cells adaptively regulates the antibody generation process, striking a balance between activation and inhibition.

As a result, the system exhibits flexible damping characteristics and ensures a rapid transient response. The cumulative stimulation of B cells at the $n^{th}$ generation is mathematically defined in (32) [50].

$$c\left(n\right)=T_H\left(n\right)-T_S\left(n\right)$$

(32)

where $T_H\left(n\right)=\alpha d\left(n\right),T_S\left(n\right)=\alpha \beta v\left(c\left(n\right),\dot{c}\left(n\right)\right)d\left(n\right)$

In this formulation, $c\left(n\right)$ denotes the B-cell stimulation at the $n^{th}$ cycle. The terms $T_H\left(n\right)$ and $T_S\left(n\right)$ represent the concentrations of helper and suppressor T cells, respectively. The variable $d\left(n\right)$ corresponds to the antigen concentration, while $v\left(.\right)$ is a nonlinear suppression function that adaptively modulates the antibody regulation rate. The parameters $\alpha$ and $\beta$ are predefined constants representing the stimulation and suppression factors, respectively. The compact form of B-cell stimulation is formulated in (33).

$$v\left(n\right)=\alpha \left(1-\beta v\left(c\left(n\right),\dot{c}\left(n\right)\right)\right)d\left(n\right)$$

(33)

Analogous to biological systems, physical control systems are also prone to degradation due to random disturbances. Therefore, the FIS framework is adapted in this study to effectively modulate stimulation in a control context. The mapping between the biological and cyber-physical control systems is outlined in the

Table 1. Comparison of analogous parameters between biological and physical systems.

Biological System		Physical System
Immune system	→	Cardiac pacemaker
Antibody generation, $n$	→	Sampling instant, $t$
Antigen concentration, $d\left(n\right)$	→	Error variable, $e\left(t\right)$
B-cell stimulation, $c\left(n\right)$	→	Control input, $u\left(t\right)$

as follows.

Based on this analogy, the resulting immune-inspired feedback control law is expressed as follows [50].

$$u\left(t\right)=f\left(t\right) e\left(t\right)$$

(34)

where $u\left(t\right)$ is the control input generated by multiplying the instantaneous error $e\left(t\right)$ with a time-varying immune-inspired gain $f\left(t\right)$, expressed in (35).

$$f\left(t\right)=\alpha \left(1-\beta v\left(u,\dot{u}\right)\right)$$

(35)

This formulation enables adaptive gain modulation based on the system’s control dynamics, emulating the natural immune system’s self-regulatory behavior to improve control performance under uncertain and disturbed environments.

3.2.2. Rationale

In conventional control systems, the integral component plays a pivotal role in eliminating steady-state errors by accumulating the error over time. However, its influence must be judiciously managed across different operational phases to ensure optimal performance and prevent adverse effects such as integral windup [39].

During transient or disturbed conditions, characterized by significant deviations from the setpoint, a strong integral action can lead to excessive accumulation of the error term, a phenomenon known as integral windup. This causes the control input signal to saturate, resulting in overshoot, prolonged settling times, or instability. The integral gain is minimized (or gradually increased) to mitigate these risks during transient phases. This approach allows the proportional and derivative components to address immediate discrepancies effectively, ensuring a faster and more stable transient response. The error diminishes once the system transitions into a steady state or equilibrium condition. At this juncture, the integral action modulates the control effort to eliminate any residual steady-state errors [51].

This study achieves the aforementioned control behavior by adjusting the parameter $\mathsf{\lambda }$, which dynamically reconfigures the integral control effort. The following rationale is thus used to adapt the value of $\mathsf{\lambda }$ online.

• During transient or disturbed conditions, $\mathsf{\lambda }$ is reduced and set closer to zero, effectively reducing the integral action. This suppression prevents the accumulation of excessive error, thereby avoiding integral windup and allowing for a faster response.

• As the system approaches steady-state, $\mathsf{\lambda }$ is gradually decreased towards −1, enhancing the integral action. This adjustment eliminates any residual steady-state errors, leading to a smooth and accurate convergence to the desired setpoint.

The control input $u\left(t\right)$ and its time derivative $\dot{u}\left(t\right)$ are precise indicators of the presence and magnitude of external disturbances affecting the system. By monitoring these variations, the integral control action can be adapted in real time to mitigate the impact of disturbances. Hence, by dynamically adjusting $\mathsf{\lambda }$ in response to the system’s control input variations, the proposed controller balances rapid disturbance rejection and precise steady-state performance, enhancing overall system robustness and efficiency. In this article, an immune-inspired adaptive gain function is used for the online adaptive adjustment of the FO. The self-adjusting FO is expressed in (36).

$$\mathsf{\lambda }\left(t\right)=\alpha \left(1-\beta v\left(u,\dot{u}\right)\right)$$

(36)

To comply with the aforementioned rationale for the online modulation of integral control action, the suppression function $v\left(u,\dot{u}\right)$ is realized via a customized fuzzy immune adaptation function, and the parameters $\beta$ and $\alpha$ are selected such that $\beta >0$ and $\alpha =-1$.

3.2.3. Fuzzy Immune Adaptation Scheme

In this study, the stimulus-suppression function $v\left(u,\dot{u}\right)$ is realized through a Fuzzy Inference System (FIS) [50]. The control signal $u\left(t\right)$ and its time derivative $\dot{u}\left(t\right)$ are the inputs to the FIS, whereas the output is the modulation signal $v\left(u,\dot{u}\right)$. Both inputs are defined over a normalized range of [−1, 1] before processing by using the hyperbolic tangent functions, as shown below.

$$u_n\left(t\right)=\tanh \left(u\left(t\right)\right), {\dot{u}}_n\left(t\right)=\tanh \left(\dot{u}\left(t\right)\right)$$

(37)

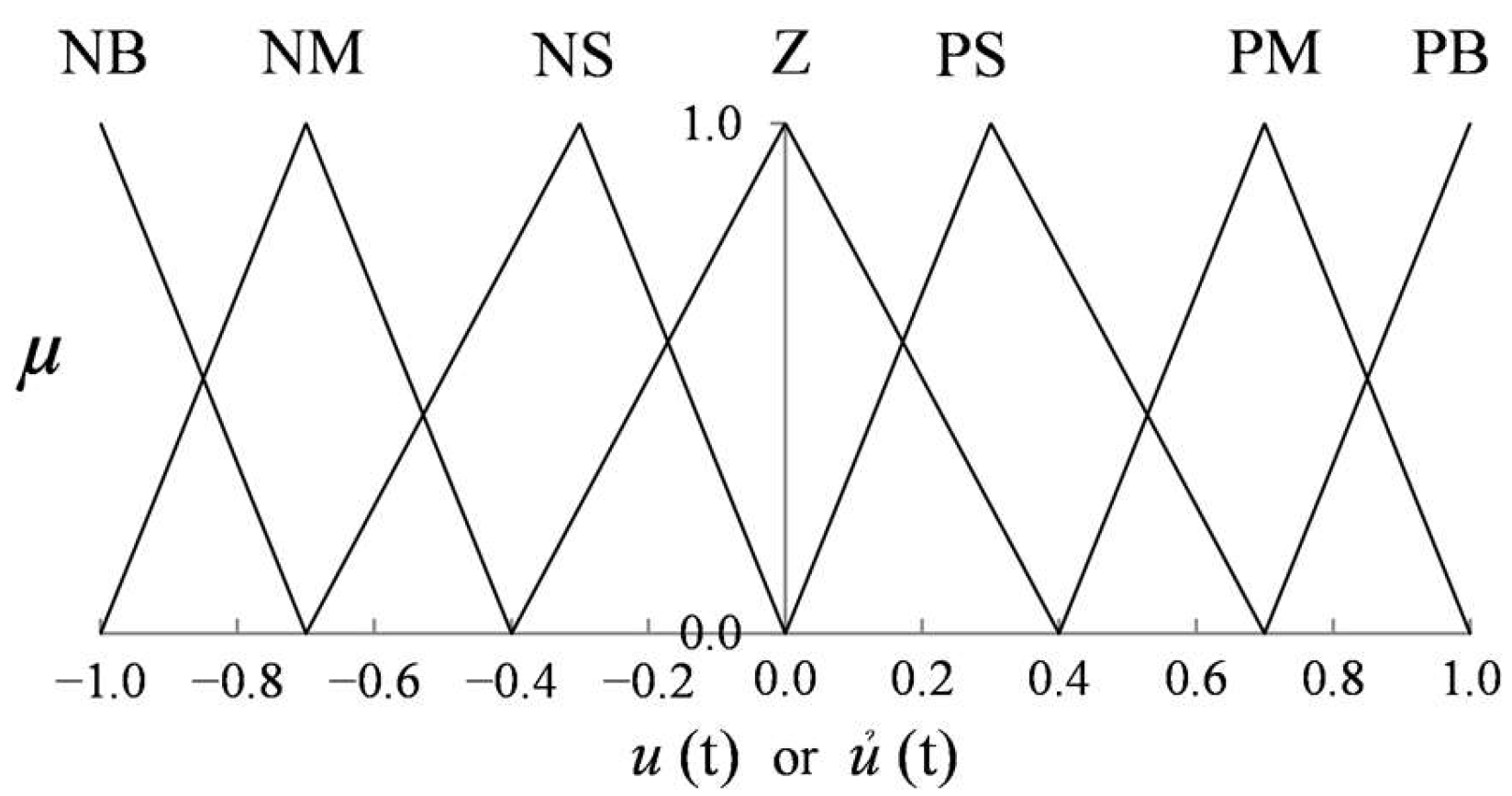
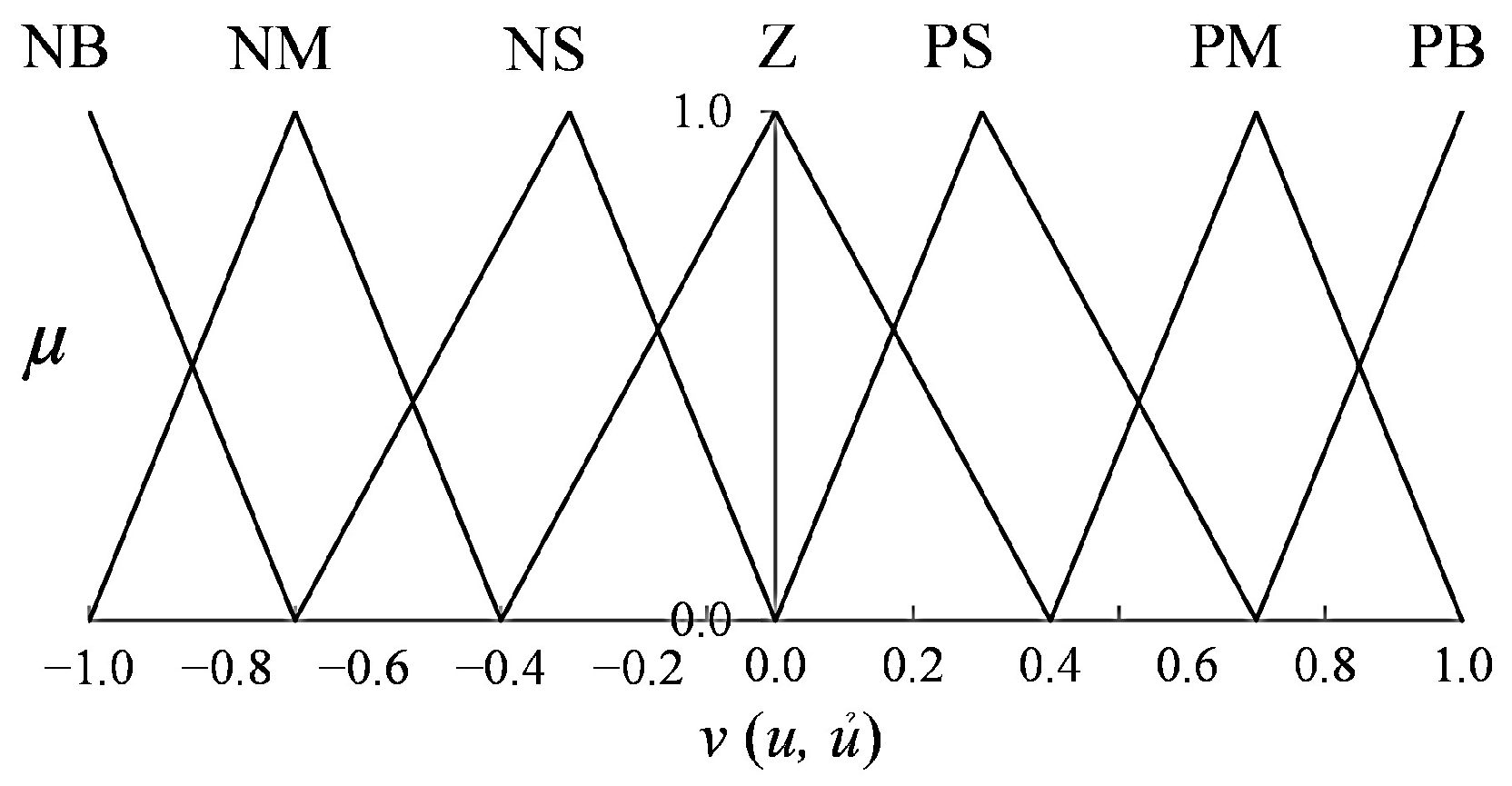
where $\tanh \left(.\right)$ represents the hyperbolic tangent function. The output $v\left(u,\dot{u}\right)$ is normalized within the range [0, 1]. Seven linguistic terms are employed to describe the fuzzy variables: Negative Big (NB), Negative Medium (NM), Negative Small (NS), Zero (Z), Positive Small (PS), Positive Medium (PM), and Positive Big (PB). These are used uniformly across the input and output domains.

Table 2. Fuzzy rule base for the stimulus-suppression function. The arrows point to the first column and first row.

${\mathit{u}}_{\mathit{n}}\downarrow /{\dot{\mathit{u}}}_{\mathit{n}}\to$	NB	NM	NS	Z	PS	PM	PB
NB	PB	PB	PM	PM	PS	PS	Z
NM	PB	PM	PM	PS	PS	Z	PS
NS	PM	PM	PS	PS	Z	PS	PS
Z	PM	PS	PS	Z	PS	PS	PM
PS	PS	PS	Z	PS	PS	PM	PM
PM	PS	Z	PS	PS	PM	PM	PB
PB	Z	PS	PS	PM	PM	PB	PB

outlines the fuzzy rule base used to construct the function $v\left(.\right)$. The fuzzy reasoning is performed using the Mamdani inference method [41], specifically the max–min operation, as expressed in (38).

$${\mu }_{ij}=\mathit{min}\left(h_{i1}\left(u_n\right),h_{j2}\left({\dot{u}}_n\right)\right)$$

(38)

Here, $\mu$ denotes the degree of activation of the fuzzy rule, and $h_{ij}\left(u\right)$ represents the membership function (MF), modeled as an asymmetric triangular shape defined below.

$$h_{ij}\left(g\right)=\left\{\begin{array}{c}1+{\displaystyle \frac{g-c_{ij}}{{b_{i,j}}^{-}}}, {-b_{ij}}^{-}\le g-c_{ij}\le 0\\ 1-{\displaystyle \frac{g-c_{ij}}{{b_{ij}}^{+}}}, 0\le g-c_{ij}\le {b_{ij}}^{+}\\ 0, otherwise\end{array}\right.$$

(39)

In this formulation, $g$ represents the normalized value of either $u_n$ or ${\dot{u}}_n$, while ${b_{ij}}^{+}$, ${b_{ij}}^{-}$, and $c_{ij}$ correspond to the right half-width, left half-width, and center of the $j^{th}$ MF of the $i^{th}$ input, respectively. Symmetrical triangular membership functions (MFs) are used to maintain reasonable design flexibility, computational efficiency, and interpretability. The MF plots for inputs and outputs are illustrated in Figure 4 and Figure 5, respectively. The final crisp output $v\left(u,\dot{u}\right)$ is obtained through defuzzification using the center-of-gravity method, given by (40).

$$v\left(u,\dot{u}\right)={\displaystyle \frac{{\displaystyle {\sum }_{i=1}^7}{\displaystyle {\sum }_{j=1}^7}\left({\mu }_{ij}{\times w}_{ij}\right)}{{\displaystyle {\sum }_{i=1}^7}{\displaystyle {\sum }_{j=1}^7}{\mu }_{ij}}}$$

(40)

where $w_{ij}$ represents the centroid of the activated output MF. The output is normalized within the range [0, 1] by using the squared hyperbolic tangent function, as shown below.

$$\overline{v}\left(u,\dot{u}\right)={\left(\tanh \left(v\left(u,\dot{u}\right)\right)\right)}^2$$

(41)

The updated value of $\overline{v}\left(u,\dot{u}\right)$ is then used to compute the re-adjusted FO, $\mathsf{\lambda }\left(t\right)$, according to the following expression.

$$\mathsf{\lambda }\left(t\right)=-\left(1-\beta \overline{v}\left(u,\dot{u}\right)\right)$$

(42)

The parameter $\beta >0$ is tuned within the range [0, 1]. The parameter values selected for this implementation are quantified in Section 4. Incorporating the self-adaptive FO in the typical FO-LQI law modifies the control law as shown below.

$$u\left(t\right)=-k_r r\left(t\right)-k_{\dot{r}} \dot{r}\left(t\right)-k_{\ddot{r}} \ddot{r}\left(t\right)-k_{\epsilon }\left(D^{\mathsf{\lambda }\left(t\right)} e\left(t\right)\right)$$

(43)

The block diagram illustrating the fuzzy immune adapted FO-LQI (FIFO-LQI) structure is shown in Figure 6.

In Figure 6, the ${\displaystyle \raisebox{1ex}{$d$}\!\left/ \!\raisebox{-1ex}{$dt$}\right.}$ block, used as an input to the fuzzy-immune system, is implemented numerically via a discrete-time backward difference approximation, owing to its suitability for real-time embedded execution. The fractional-order control block is realized via a rational approximation of the fractional operator via the Oustaloup recursive filter. This implementation serves a functional role in shaping the controller’s memory and frequency response, enabling smoother transient behavior and improved disturbance rejection. While only one fractional-order term is introduced for practical reasons, extending the full system to fractional order is possible, but it was deliberately avoided to maintain real-time feasibility for embedded biomedical applications.

4. Controller Parameterization

This section outlines the offline tuning methodology employed to optimize the state and control weighting matrices coefficients, defined in Equation (17), for the baseline LQI controller, along with the critical parameters associated with the proposed adaptive control framework. The tuning process is driven by minimizing the cost function in (44).

$$J_e={\int }_0^{\mathrm{T}}\left[{\left(e\left(t\right)\right)}^2+{\left(u\left(t\right)\right)}^2\right]dt$$

(44)

where $\mathrm{T}$ represents the total time span of a single simulation trial. This cost function is designed to penalize the tracking error $e\left(t\right)$ and the control effort $u\left(t\right)$ equally, thereby promoting precise state regulation while minimizing energy consumption. The elements of the LQI weighting matrices are selected from within the range [0, 100], and the fractional exponent of the fixed FO-LQI controller is restricted within the interval [−1, 0]. The hyper-parameter $\beta$ of the fuzzy immune block is confined to the interval [0, 1]. 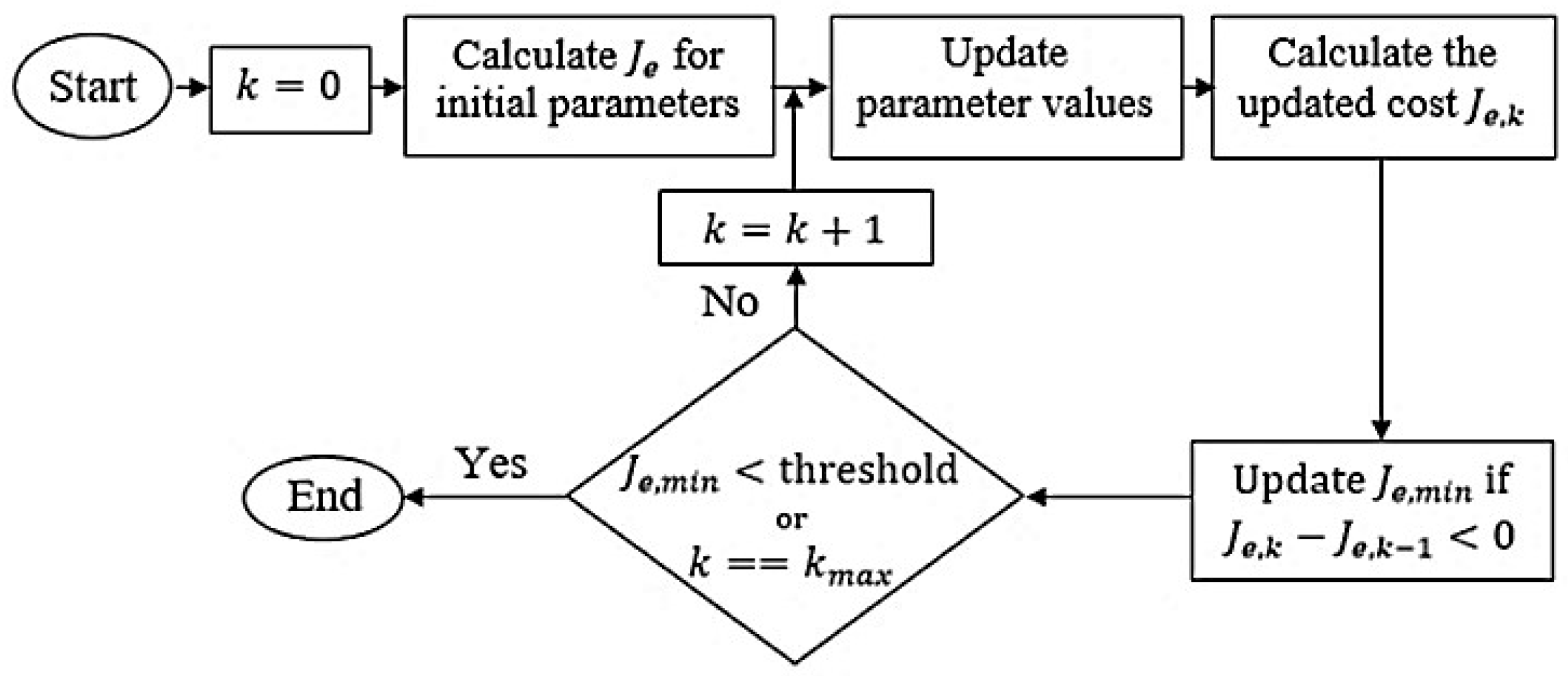Section 5 elaborates on the simulation setup used to perform this tuning. Initially, all parameters are set to unity to standardize the starting point. The complete tuning process is depicted in Figure 7 [44].

The iterative optimization routine starts with the initial parameter configuration [44]. In each iteration, the pacemaker is commanded to follow a step reference HR signal over a 5 s interval, during which the cost $J_{e,k}$ is computed for the $k^{th}$ trial. The algorithm searches for an improved parameter set by moving along the negative gradient of the cost function. If a trial yields a lower cost $J_{e,k}$ than the previous one $J_{e,k-1}$, the current minimum cost $J_{e,min}$ is updated accordingly.

The optimization continues until either the maximum number of trials $k_{max}$ is exhausted or the cost drops below a pre-established threshold. This threshold is empirically determined based on the initial cost value, denoted as $J_{e,min}^0\approx 3.0\times {10}^5$, and is scaled by a heuristic factor of 0.02. This scaling balances computational effort with solution fidelity—smaller factors may halt the process prematurely, while larger ones can lead to excessive computation time. Thus, the stopping condition is defined as $J_{e,min}\le 0.02\times J_{e,min}^0$, corresponding to a threshold value of $6.0\times {10}^3$. The maximum trial count is set to $k_{max}=50$.

Following optimization, the resulting state and control weighting matrices are $\mathit{Q}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(\begin{array}{cc}\begin{array}{cc}12.841& 2.612\end{array}& \begin{array}{cc}0.144& 1.063\end{array}\end{array}\right)$ and $\mathit{R}=1.029$. These yield the LQI state-feedback gain vector, $\mathit{K}=\left[\begin{array}{cc}\begin{array}{cc}4.158& 2.255\end{array}& \begin{array}{cc}0.353& -1.014\end{array}\end{array}\right]$. The optimized FO of the fixed FO-LQI is 0.781. The optimized hyperparameter for the fuzzy immune adaptation block is determined to be $\beta =0.892$.

5. Simulation Results and Analysis

This study employs a phased validation approach, initiating with detailed simulations to assess the proposed controller’s performance. It focuses on comprehensive simulation-based validation under physiologically realistic scenarios, serving as a low-risk, cost-effective environment for design iteration, performance benchmarking, and controller refinement. These simulations would serve to facilitate iterative refinement and optimization, thus establishing a robust foundation before engaging in resource-intensive hardware-in-the-loop experiments. Furthermore, due to current limitations in access to pacemaker-compatible experimental platforms, real-time hardware validation could not be performed at this stage. Accordingly, this section presents simulation results and a comprehensive comparative analysis of the time-domain behavior of the heart rate control techniques for cardiac pacemakers.

5.1. Simulation Setup

The claims regarding disturbance rejection and steady-state performance of the proposed controller are supported through extensive simulation-based validation under physiologically relevant conditions. The reference tracking capabilities of the LQI, FO-LQI, and the proposed FIFO-LQI controller were assessed through time-domain simulations under various conditions, including a nominal HR condition, sudden stress, sustained physical activity, rhythmic activities, and pacemaker parameter variations. These simulations were conducted using MATLAB/Simulink R2020b on a 64-bit embedded computer equipped with a 2.1 GHz CPU and 12 GB RAM, operating at a sampling frequency of 250 Hz [52]. While this platform indeed exceeds typical embedded hardware in computational capacity, the prescribed controllers are implemented using computationally economical structures compatible with embedded deployment, including a single fractional-order term. The sampling frequency of 250 Hz was chosen to reflect common clinical pacing rates, ensuring physiological relevance. Pacemakers typically operate at pulse rates up to 180 bpm (~3 Hz) with high timing precision. A 250 Hz sampling rate provides a 4.0 ms resolution, which is sufficient to accurately capture heart rate dynamics and pacing intervals [53].

The fractional-order control block is realized using the FOMCON toolbox in MATLAB, which employs a rational approximation of the fractional operator via the Oustaloup recursive filter. The standard cardiac pacemaker model, derived in Section 2.1, was used to evaluate the controller’s effectiveness in reference HR tracking and disturbance rejection. To emulate typical sensor noise encountered during cardiac pace-making operations, band-limited white noise was added to the control input, configured with a noise power of 10⁻³ and a sampling time of 4.0 ms. Finally, to prevent control input saturation, the control input signal $u\left(t\right)$ was constrained within a range of 0 to 1.5 volts. A 1.5 V input setting balances effective cardiac stimulation with the minimization of battery drain, thereby ensuring patient safety and device efficiency [53].

To ensure that the test cases are physiologically relevant and representative of real-world cardiac and pacemaker operating conditions, key system parameters such as the natural frequency (${\omega }_n=1.0$), damping ratio (ζ $=0.7$), and pacemaker dynamics ($K_f=1.0$ and $\tau =0.4$) were selected based on established cardiac control models reported in prior literature [14]. To enhance simulation realism, additive noise was introduced to emulate sensor imperfections, while control input saturation was applied to reflect clinically accepted stimulation thresholds typically enforced in implantable pacemaker devices [46].

5.2. Simulation Results

The performance of the proposed FIFO-LQI controller was benchmarked against the LQI and the FO-LQI controller across five distinct simulation scenarios, each reflecting a different physiological condition. Additive White Gaussian Noise (AWGN) was introduced into the system’s input in each simulation to emulate real-world sensor noise encountered during cardiac operations.

 A. 

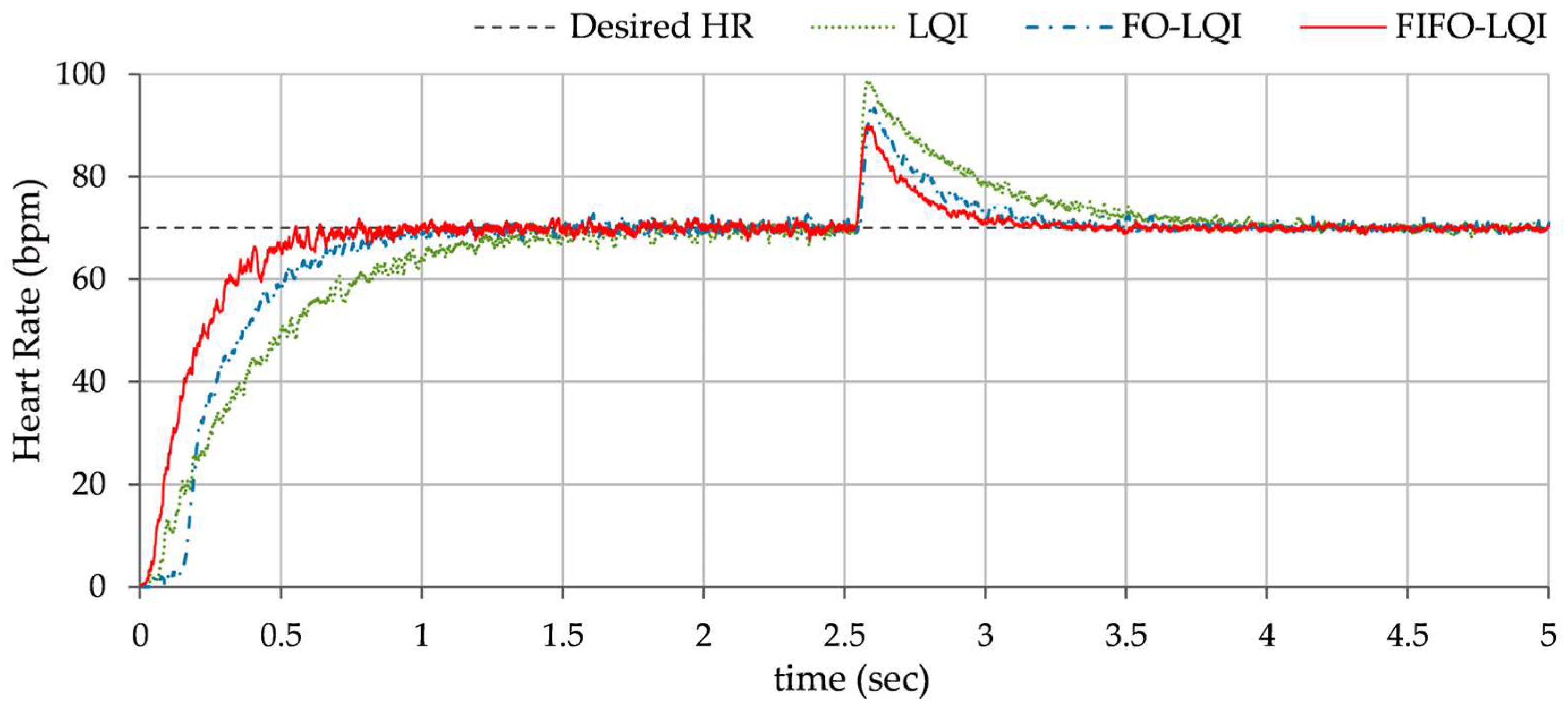
Step reference tracking: This simulation case is the foundational test to assess the controller’s ability to track the HR reference of 70 bpm under normal, undisturbed conditions. The variations in HR, exhibited by each controller, are shown in Figure 8. The steady-state error profile of the HR is depicted in Figure 9.

 B. 

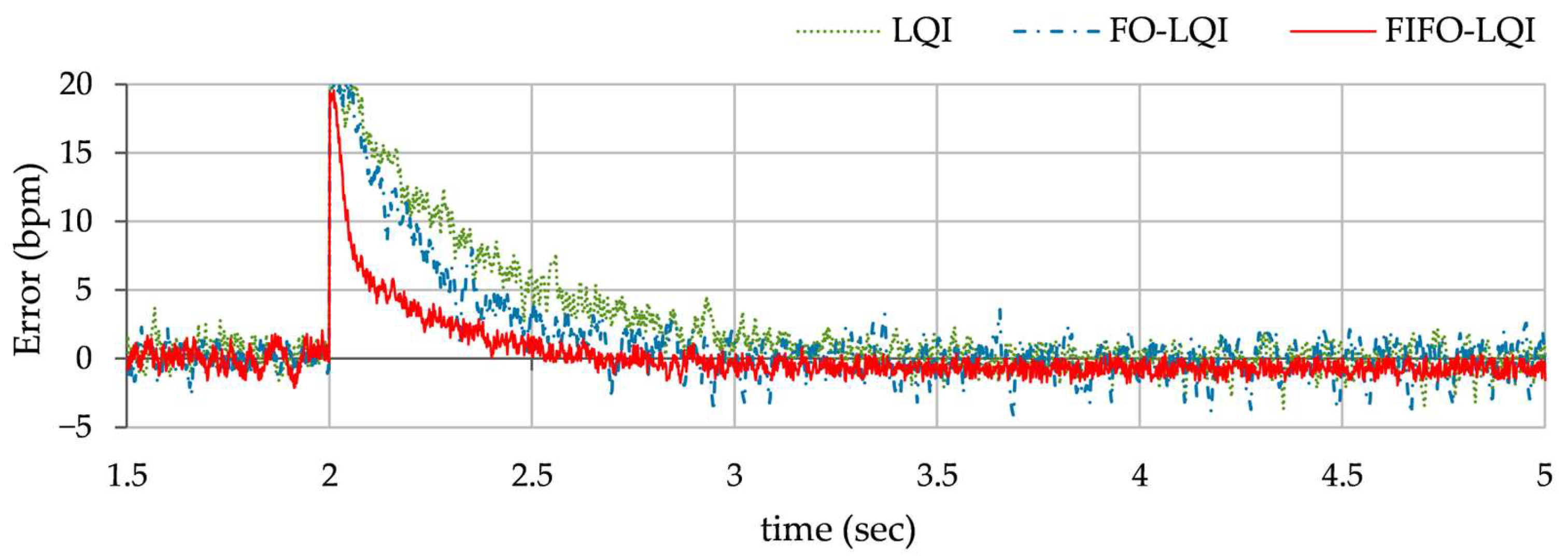
Multi-step reference tracking: This scenario examines the controller’s ability to track a sudden increase in heart rate under normal conditions. This is typically caused by dehydration, emotional stress, or anxiety. A step change in the HR reference, from 72 bpm to 110 bpm, is applied at t = 2.0 s. to conduct the test. The corresponding variations in the HR, exhibited by each controller, are shown in Figure 10. The error profile of the HR is depicted in Figure 11.

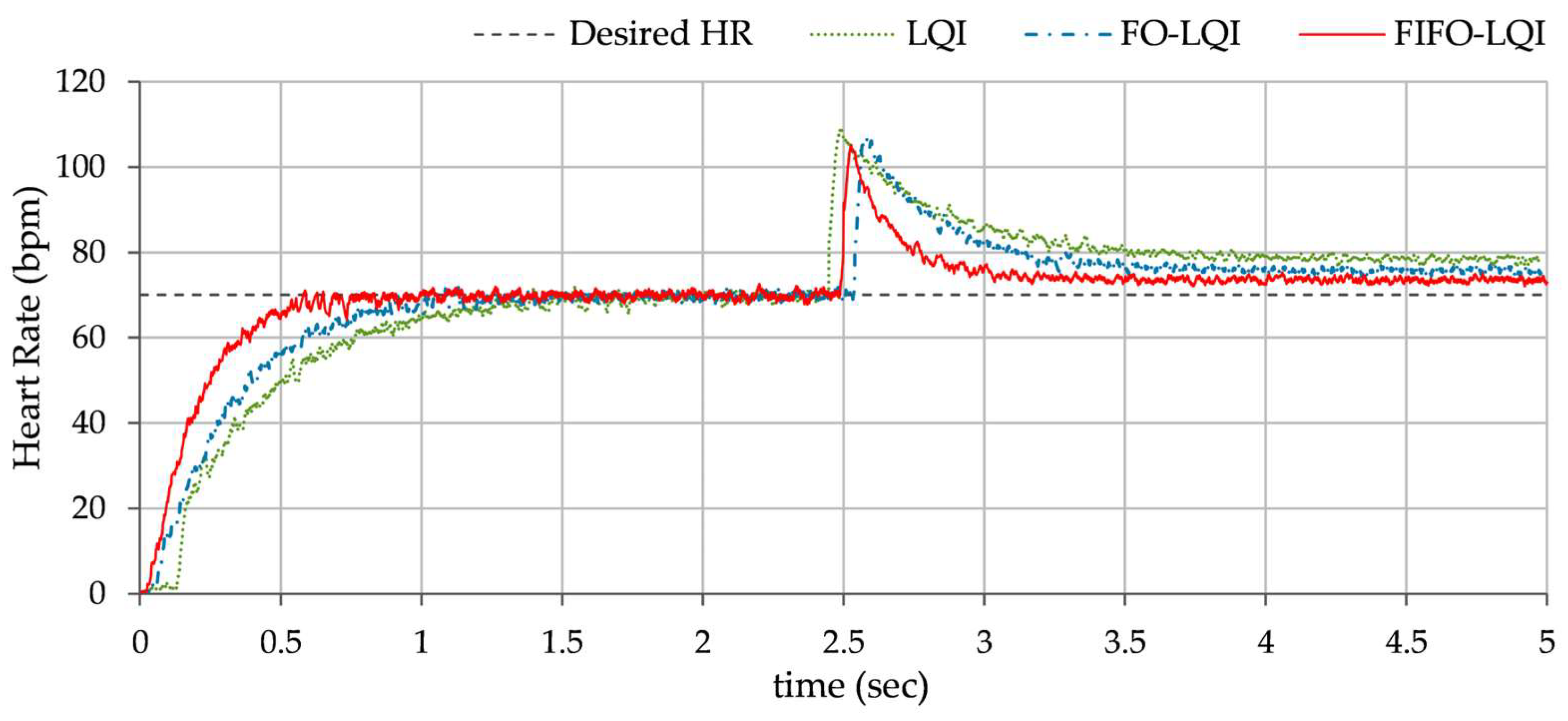
 C. 

Impulsive disturbance rejection: This simulation evaluates the controller’s robustness to abrupt external disturbances, typically caused by a sudden increase in metabolic demand, an unexpected stressor, or an abrupt posture change. To carry out the test, an external pulse of +0.5 V magnitude and 100 msec. duration is introduced in the control input at t ≈ 2.5 s. The consequent HR profiles, exhibited by each controller, are shown in Figure 12.

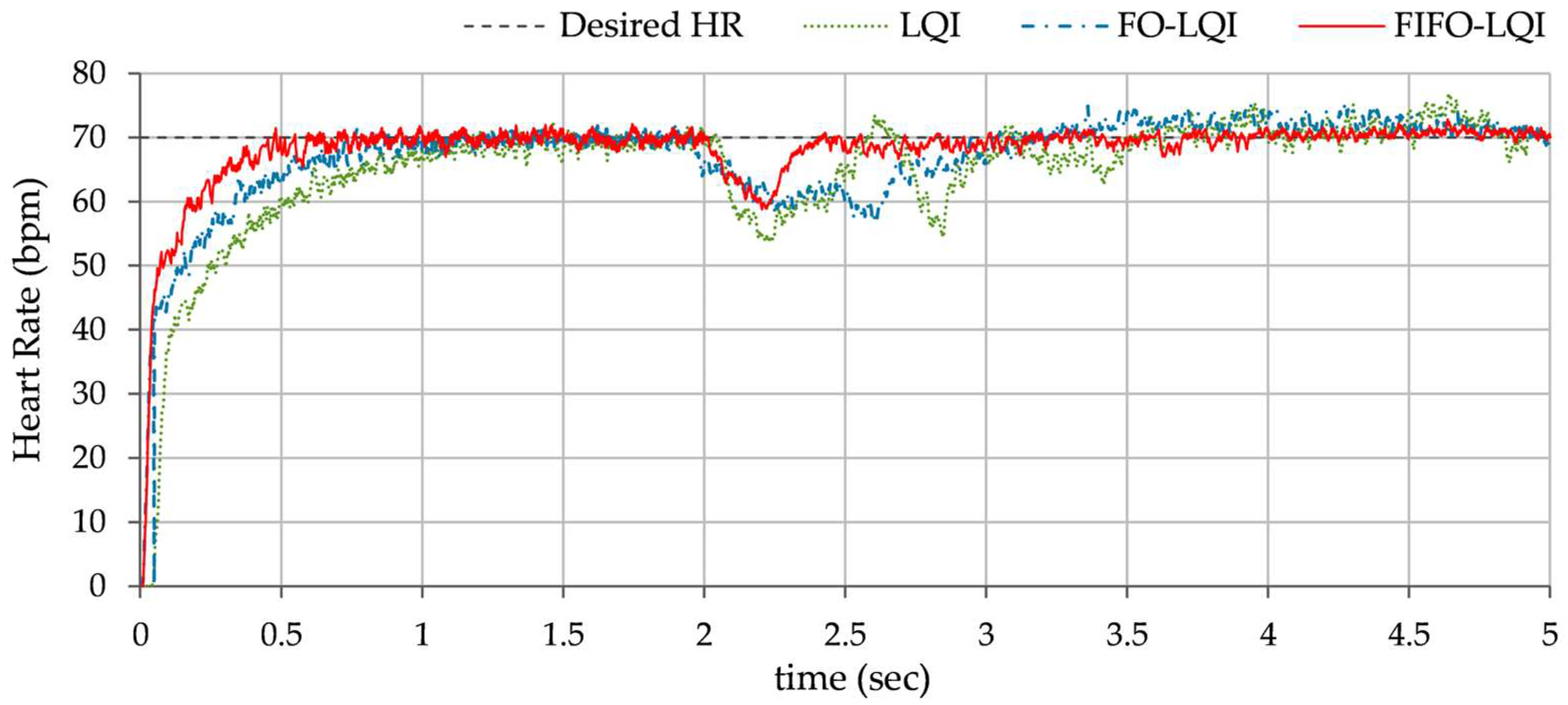
 D. 

Step disturbance compensation: This test examines the controller’s performance under sustained disturbances, such as prolonged physical activity, exercise, emotional stress, or an increased oxygen demand. A step disturbance signal of +0.5 V magnitude is injected in the control input at t ≈ 2.0 s. The consequent HR profiles, exhibited by each controller, are shown in Figure 13.

 E. 

Model uncertainties compensation: This test analyzes the controller’s robustness against model inaccuracies by introducing variations in the pacemaker’s hardware settings to simulate uncertainties in patient-specific cardiac dynamics. To carry out the test, the pacemaker’s filter gain $m$ is decreased by 20% at t ≈ 2.0 s, emulating potential miscalibrations or hardware inconsistencies in a pacemaker. This variation alters the coefficients of the system’s state-space model, changing the pacemaker’s control characteristics and potentially impacting its HR reference tracking behavior. In practice, decreasing the filter gain reduces the magnitude of the system’s output in response to the same metabolic demands, resulting in a slight drop in HR due to reduced control action intensity. The HR profiles, contributed by each controller, are shown in Figure 14.

5.3. Performance Evaluation and Discussion

In the simulation tests (A–E), the performance of the proposed FIFO-LQI controller was compared against LQI and FO-LQI controllers under various conditions to assess tracking accuracy and disturbance rejection capabilities. The simulation outcomes are evaluated using key performance metrics to assess the controller’s effectiveness:

• RMSE: This metric calculates the root mean square of the error, $e\left(t\right)$, in HR. It is calculated as shown in (45).

$$RMSE=\sum \sqrt{{\displaystyle \frac{{\left(e\left(n\right)\right)}^2}{n}}}$$

(45)

where $n$ represents the total number of samples.

• Overshoot (OS): The peak deviation of the HR during the initial transient phase of the response.
• Settling Time (T_set): The time required for the HR response to remain within ±2% of the reference value after a disturbance.
• Maximum Peak (M_peak): The highest deviation (either overshoot or undershoot) following a disturbance.
• Recovery Time (T_rec): The time taken by the response to fall within ±2% of the reference HR after experiencing a disturbance.
• Offset Error (E_offset): The offset in the tracking response under step disturbance.

Table 3. Summary of experimental results.

Simulation	Performance Index		Control Law
	Symbol	Unit	LQI	FO-LQI	FIFO-LQI
A	RMSE	bpm	17.00	13.98	9.34
	OS	bpm	2.71	2.84	2.11
	Tset	sec.	1.22	0.84	0.57
B	RMSE	bpm	14.20	11.85	8.35
	OS	bpm	2.70	2.87	2.14
	Tset	sec.	1.23	0.85	0.58
C	RMSE	bpm	16.98	15.05	10.80
	OS	bpm	2.70	2.85	2.12
	Tset	sec.	1.27	0.85	0.58
	Mpeak	bpm	28.5	23.98	19.11
	Trec	sec.	1.02	0.64	0.42
D	RMSE	bpm	19.40	16.47	12.15
	OS	bpm	2.70	2.87	2.13
	Tset	sec.	1.23	0.86	0.57
	Mpeak	bpm	39.31	37.24	35.20
	Eoffset	bpm	10.07	7.19	5.29
	Trec	sec.	1.08	0.78	0.47
E	RMSE	bpm	13.79	8.01	6.45
	OS	bpm	2.72	2.86	2.15
	Tset	sec.	1.22	0.84	0.58
	Mpeak	bpm	−16.41	−13.20	−11.23
	Trec	sec.	2.61	2.02	1.15

summarizes these metrics, demonstrating that the proposed FIFO-LQI controller enhances control performance by balancing damping control effort and time optimality. In this study, all simulations were performed using double-precision arithmetic in MATLAB/Simulink, with filter realizations designed to minimize truncation and roundoff errors.

In Test A, the LQI controller exhibited moderate performance, with noticeable overshoot, oscillations, and prolonged settling time. The FO-LQI controller achieved better tracking accuracy, characterized by reduced overshoot, faster convergence, and reduced steady-state fluctuations. The FIFO-LQI controller manifests a smooth and accurate tracking of the desired HR with minimal overshoot and settling time, demonstrating the controller’s efficacy in nominal conditions.

In Test B, the LQI controller maintained an oscillatory response and showed sensitivity to the disturbances, resulting in lag and degraded tracking accuracy. The FO-LQI controller manifested relatively enhanced reference tracking accuracy. In contrast, the FIFO-LQI controller demonstrated enhanced robustness and adaptability, effectively tracking the multi-step trajectory while optimizing control resource allocation. In Test C, the LQI-controlled system showed significant deviations from the reference trajectory, followed by slow recovery. The FO-LQI controller exhibited relatively enhanced damping against the disturbances, restoring the system to its reference position and attenuating peak overshoots. The FIFO-LQI controller’s ability to quickly recover and maintain the desired HR setpoint after the disturbance reflects its resilience and adaptability to sudden changes. In Test D, the LQI controller struggled to maintain steady-state accuracy post-disturbance and exhibited slower transient recovery and the highest post-disturbance offset in HR tracking behavior. The FO-LQI controller improved reference tracking accuracy by adapting to the step disturbance. Despite the ongoing disturbance, the FIFO-LQI controller quickly dampened the oscillations and minimized the post-disturbance offset from the desired HR, showcasing its capability to handle prolonged stressors. In Test E, the LQI controller demonstrated poor compensation, with large fluctuations in response. In contrast, the FO-LQI controller reasonably improved disturbance attenuation, resulting in a smoother response. The FIFO-LQI controller ability to maintain accurate HR tracking despite the aforementioned discrepancies indicates its robustness and adaptability to model variations.

As compared to the FO-LQI controller, the FIFO-LQI controller exhibits a 33.3% improvement in RMSE, a 25.7% improvement in OS, and a 32.1% improvement in T_set under normal conditions. Under impulsive disturbance conditions, in comparison to the FO-LQI controller, the FIFO-LQI controller demonstrates a 20.3% reduction in M_peak and a 34.4% reduction in T_rec. Under step disturbance conditions, in comparison to the FO-LQI controller, the FIFO-LQI controller demonstrates a 5.5% reduction in M_peak, a 39.7% reduction in T_rec, and a 26.7% improvement in E_offset. Finally, under model variations, the FIFO-LQI controller demonstrates a 14.9% reduction in M_peak and a 43.1% reduction in T_rec in comparison to the FO-LQI controller. Overall, the FIFO-LQI controller consistently outperformed the LQI and FO-LQI controllers across all tests, showcasing its adaptability in various scenarios.

5.4. Statistical Analysis of Simulation Results

The simulation results are statistically evaluated to validate the performance improvements achieved by the proposed controller. A 95% confidence interval (CI) analysis is employed to assess the reliability and statistical significance of the outcomes across simulations A–E for each control scheme. The CI provides a quantitative measure of uncertainty, indicating that there is a 95% probability that the true mean HR levels lie within the specified interval.

Table 4. Statistical analysis of simulation results.

Simulation	Tool (bpm)	LQI	FO-LQI	FIFO-LQI
A	Mean	64.11	66.30	68.13
	Median	69.47	69.57	69.80
	Standard Dev.	14.33	11.88	7.89
	CI (95%)	0.56	0.47	0.31
	Upper CI (95%)	64.68	66.77	68.44
	Lower CI (95%)	63.55	65.84	67.82
B	Mean	77.47	78.76	80.39
	Median	84.27	87.18	89.06
	Standard Dev.	14.46	14.63	12.88
	CI (95%)	0.56	0.57	0.51
	Upper CI (95%)	78.04	79.34	80.90
	Lower CI (95%)	76.90	78.19	79.89
C	Mean	66.23	66.64	68.04
	Median	69.94	69.84	69.99
	Standard Dev.	15.63	14.68	10.62
	CI (95%)	0.61	0.57	0.42
	Upper CI (95%)	66.84	67.22	68.46
	Lower CI (95%)	65.61	66.07	67.63
D	Mean	70.62	70.10	70.08
	Median	77.48	71.10	72.37
	Standard Dev.	18.77	15.73	12.15
	CI (95%)	0.74	0.62	0.48
	Upper CI (95%)	71.36	70.72	70.56
	Lower CI (95%)	69.89	69.48	69.60
E	Mean	65.16	67.17	68.18
	Median	68.17	69.56	69.70
	Standard Dev.	10.28	7.48	6.18
	CI (95%)	0.41	0.29	0.24
	Upper CI (95%)	65.57	64.47	68.42
	Lower CI (95%)	64.76	66.88	67.93

summarizes the CI results for state variations under each experimental condition. The analysis demonstrates that the FIFO-LQI controller consistently outperforms the LQI and FO-LQI controllers, reflecting improved robustness and reduced variability across all test scenarios.

5.5. Practical Considerations

The proposed control procedure ensures that the additional computational burden is minimal, particularly because the fractional operator is implemented via a fixed-order Oustaloup approximation. Moreover, the proposed approach uses a single FO exponent that is self-adjusted online to balance transient and steady-state performance. The resulting computational overhead remains well within the capabilities of modern embedded processors, especially when compared with high-complexity methods like MPC or neural network controllers. The adoption of a fractional integral operator is functionally motivated. It allows real-time modulation of integral action to address phenomena like windup and is embedded within an optimal control framework rather than used for novelty alone.

In this work, the fractional operator is approximated using the Oustaloup recursive filter, which replaces the non-integer-order integrator with a rational transfer function realizable via a finite number of first-order filters. The selected filter parameters (order = 5) are intentionally kept low to balance approximation accuracy and computational complexity. Since only a single fractional-order integral term is used, the computational and memory demands are modest. This allows the controller to be implemented efficiently on modern low-power microcontrollers or DSPs that support fixed-point arithmetic and basic filter operations. Finally, the FIFO-LQI formulation avoids real-time differentiation or inversion of matrices and uses a static state-feedback structure, which further supports its feasibility for embedded deployment.

6. Conclusions

This study has presented an adaptive FO-LQI controller for cardiac pacing, in which the integral control action is modulated online via a fuzzy-immune adaptation law. Through a series of MATLAB/Simulink simulations, which include step reference tracking under impulsive, sustained disturbances, and model uncertainties, the proposed controller demonstrated faster convergence, lower overshoot, and superior disturbance rejection compared to the conventional LQI and fixed FO-LQI scheme. By suppressing integral action during large error conditions (avoiding windup) and enhancing it as the response approaches steady state, the controller achieves both rapid disturbance recovery and precise elimination of steady-state fluctuations. These results confirm the effectiveness and robustness of the FIFO-LQI control law for regulating HR under physiological changes. The FIFO-LQI controller achieves improved transient responses and maintains steady-state accuracy, validating its robustness in tracking and disturbance rejection compared to the typical LQI and FO-LQI controllers.

While the proposed FIFO-LQI controller demonstrates superior robustness and performance across a range of simulated physiological scenarios, it is not without limitations. First, the controller’s effectiveness relies on the accuracy of the underlying nominal heart-pacemaker model. Although the fuzzy-immune adaptation provides resilience to moderate uncertainties, large deviations from the modeled dynamics or unmodeled nonlinearities (e.g., time-varying patient-specific cardiovascular responses) may degrade performance. Second, the fuzzy-immune rule base and membership functions are manually designed, which introduces potential suboptimality, especially for patient-specific adaptation. Third, while computationally more efficient than methods like MPC or neural networks, real-time implementation of the FIFO-LQI controller in resource-constrained pacemaker hardware still requires further validation, particularly with respect to memory, energy consumption, and timing constraints. Lastly, the current validation is simulation-based; hence, real-world performance, sensor delays, and actuator nonlinearities remain to be addressed in future hardware-in-the-loop or clinical validation studies.

There is a lot of room for improvement in the future. Firstly, the proposed control scheme can be validated via hardware-in-the-loop experiments using a pacemaker test bench and in vitro cardiac tissue models to assess real-time performance and robustness. Additionally, the proposed adaptive controller can be benchmarked against mainstream intelligent control strategies, such as MPC and neural network-based controllers, to further evaluate its general applicability and comparative performance. Furthermore, the use of machine learning and soft-computing techniques can be investigated for online adaptive modulation of the fractional exponent and automatic tuning or refinement of the fuzzy rule base. For ultra-low-power applications, such as implantable pacemakers, future efforts can focus on the implementation of fixed-point arithmetic and simplified filter structures to minimize computational and energy overhead. Finally, the control framework can be extended to nonlinear and patient-specific cardiac models to more accurately capture the complex, time-varying dynamics of the cardiovascular system. This would facilitate personalized controller design and improve the clinical relevance and effectiveness of the proposed approach.