Fractal Characterization and NMR Analysis of Curing-Dependent Pore Structures in Cemented Tailings Waste RockBackfill
Abstract
1. Introduction
2. Materials and Methods
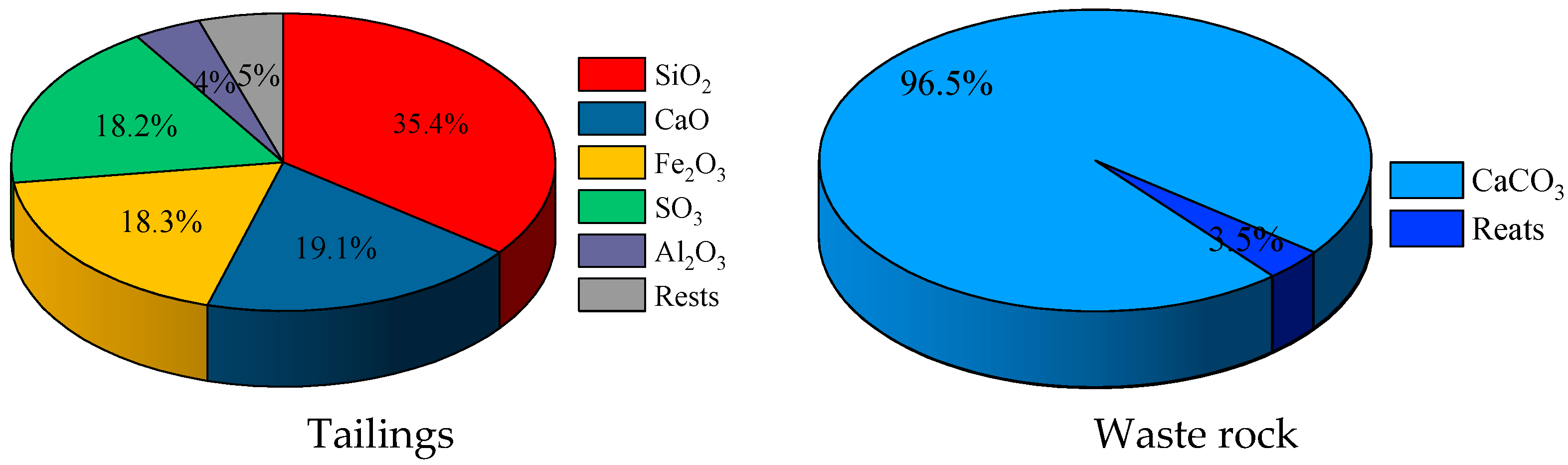
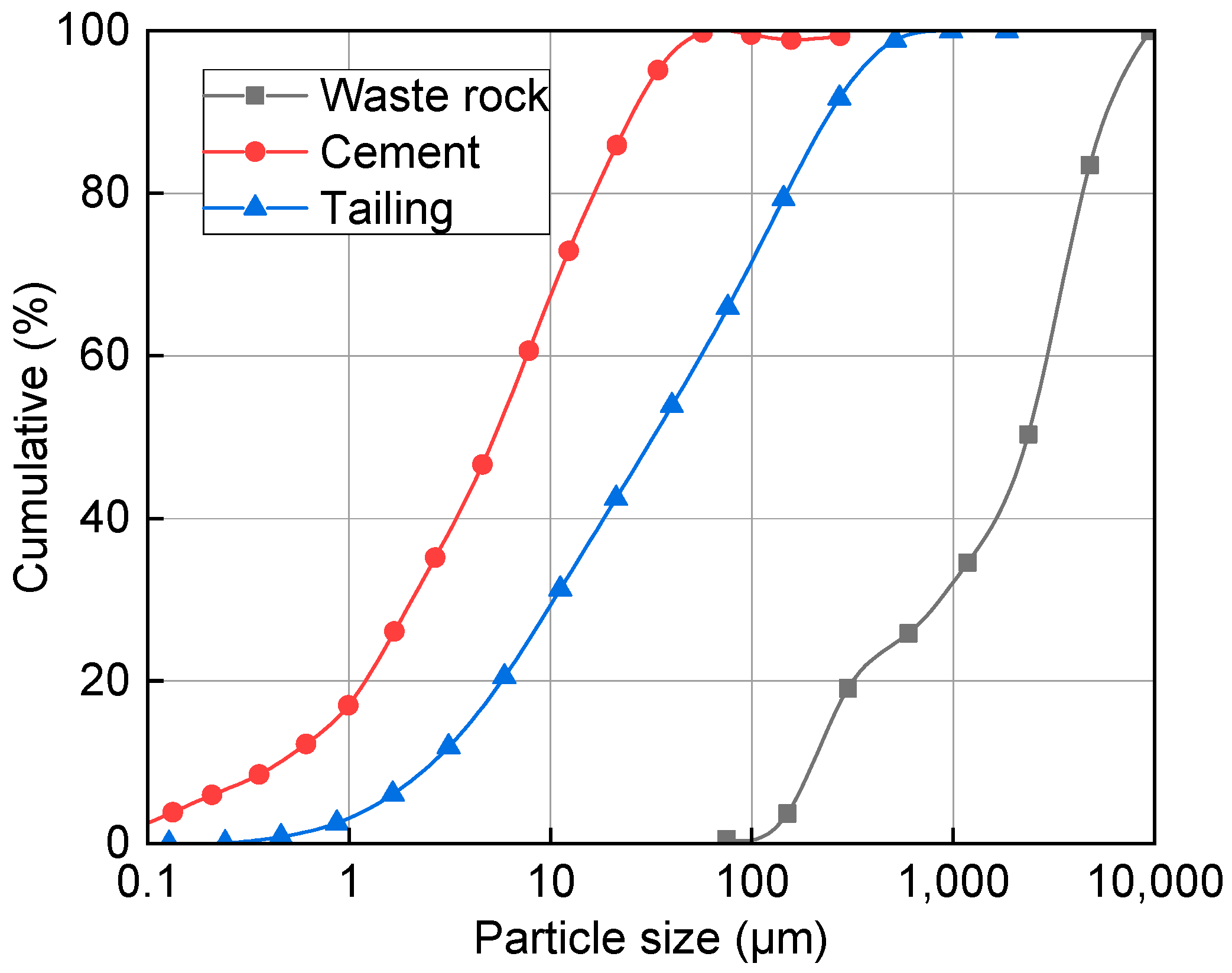
2.1. Raw Materials
2.2. Mix Design and Specimen Preparation
2.3. Experimental Method and Equipment
2.3.1. Low-Field Nuclear Magnetic Resonance (NMR)
2.3.2. Uniaxial Compression Strength Test
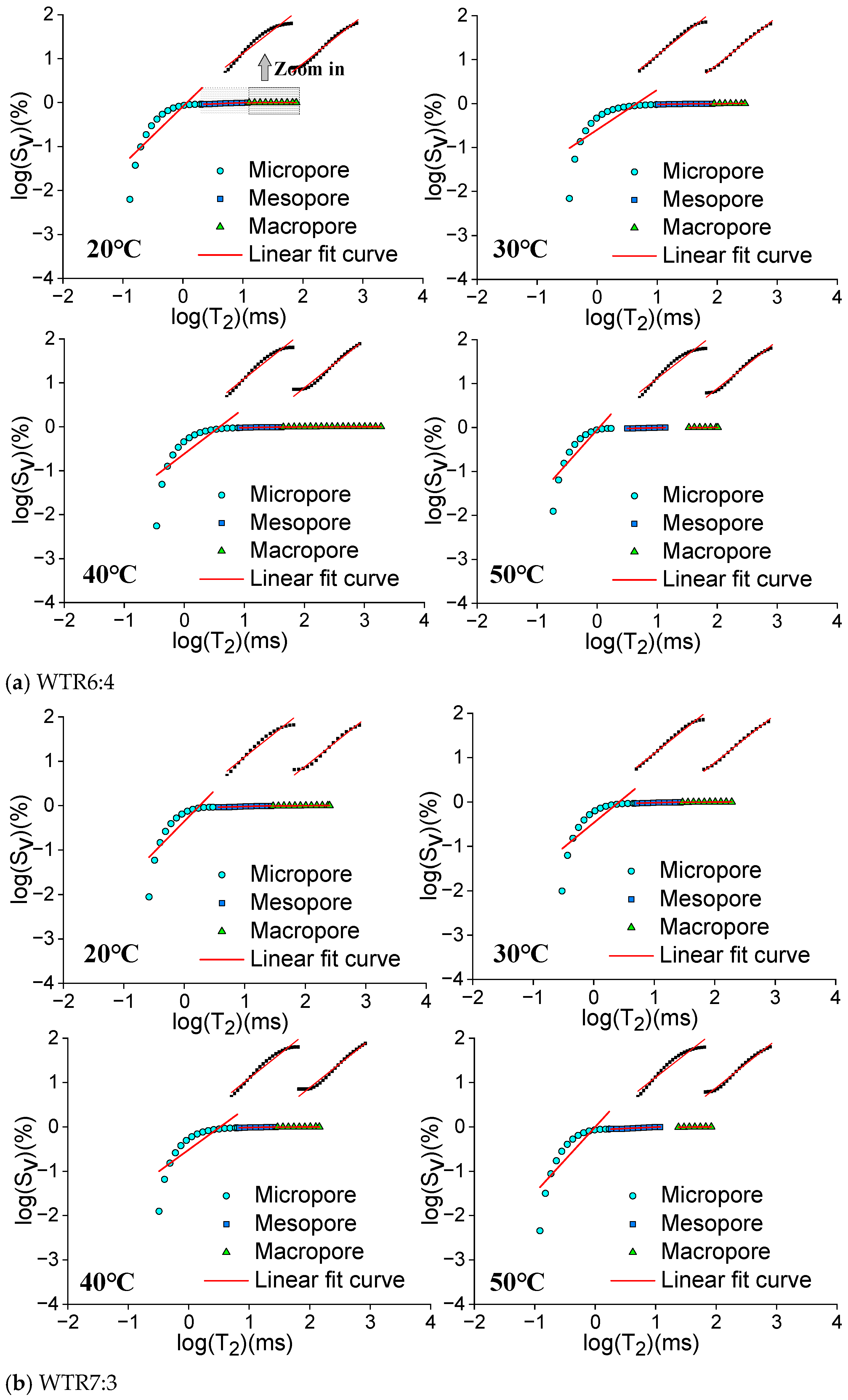
2.3.3. Fractal Theory and Dimension
3. Results
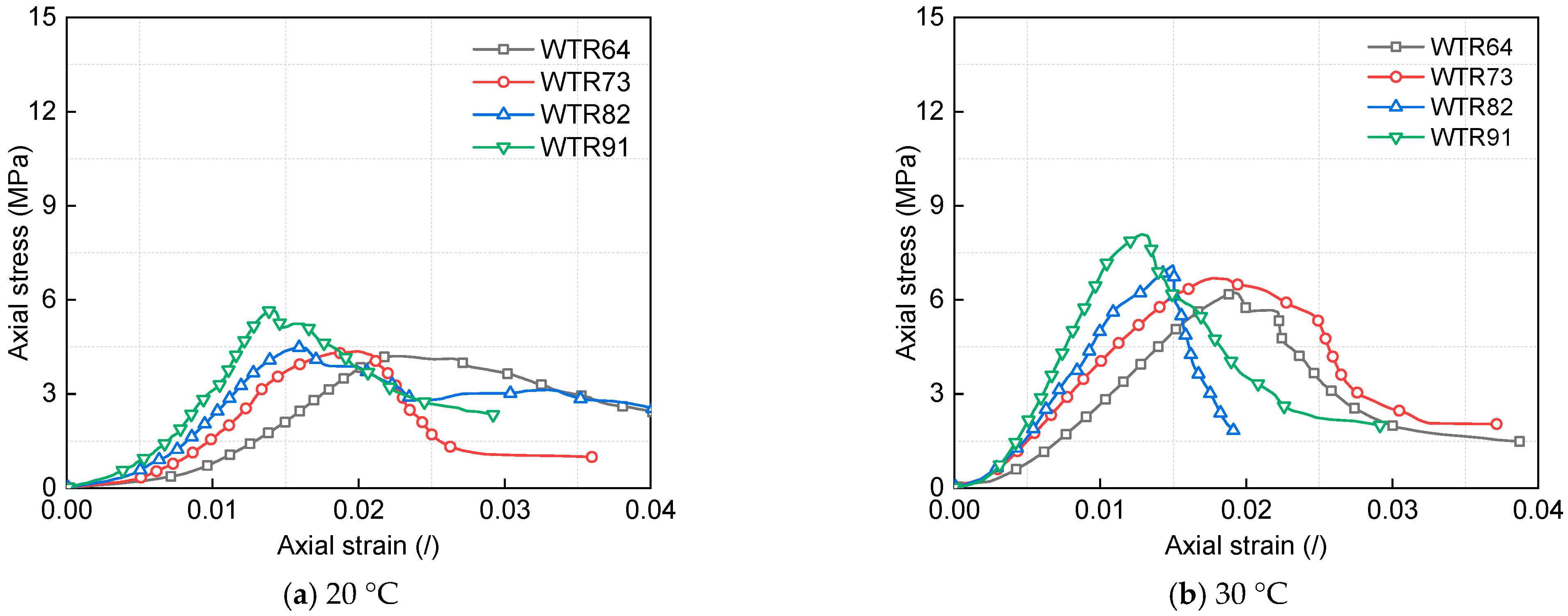
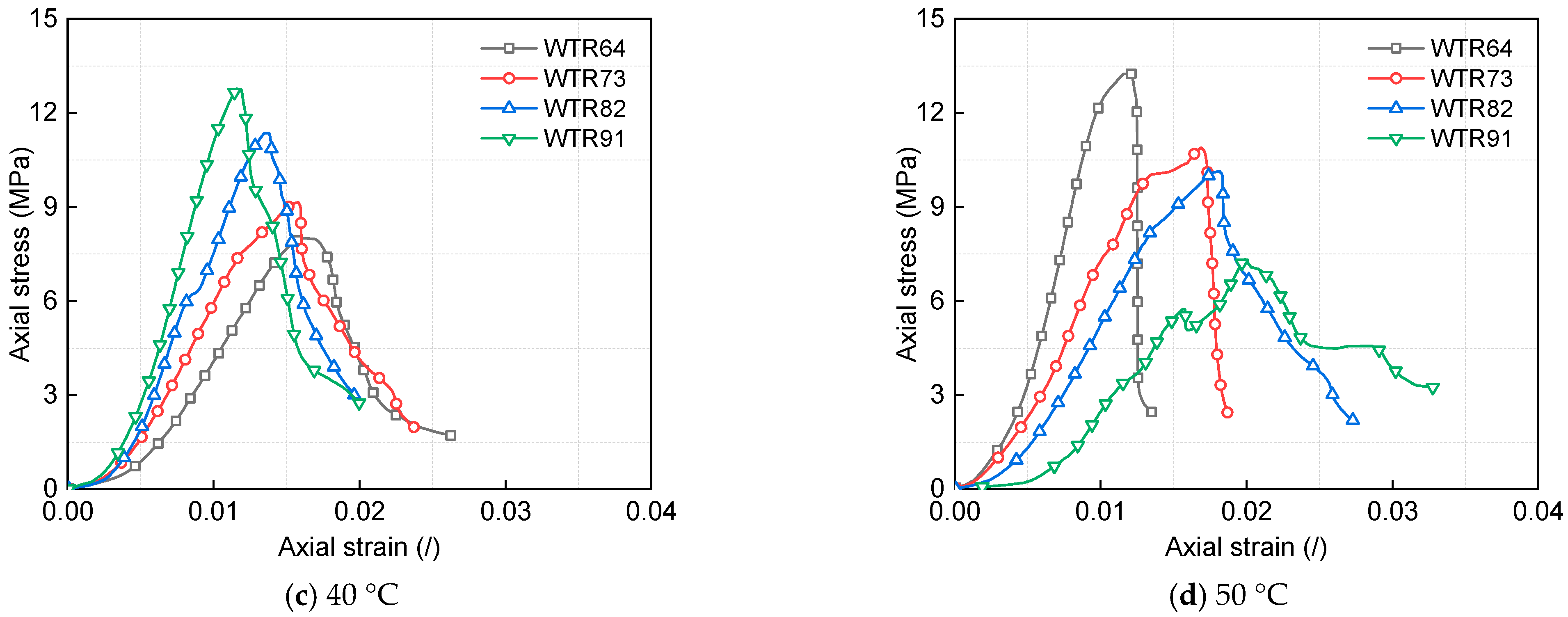
3.1. Mechanical Behavior
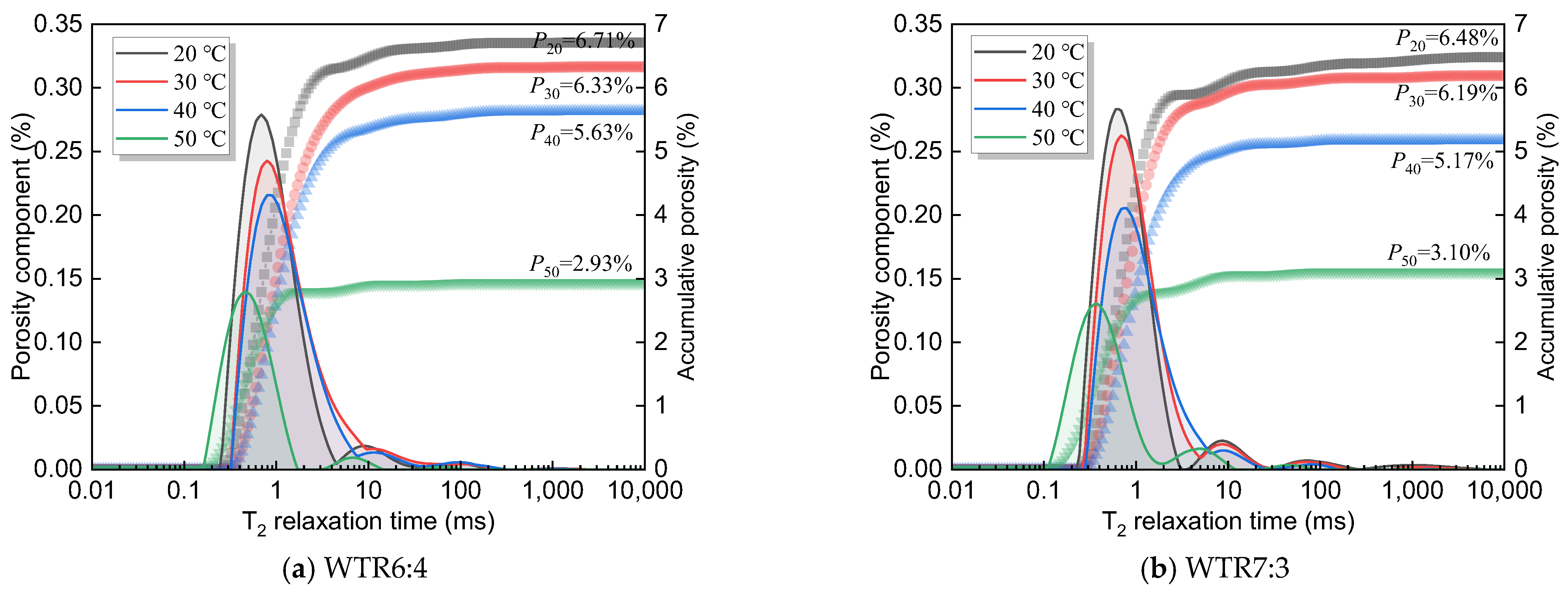
3.2. T2 Spectrum Distribution Curves
4. Discussion
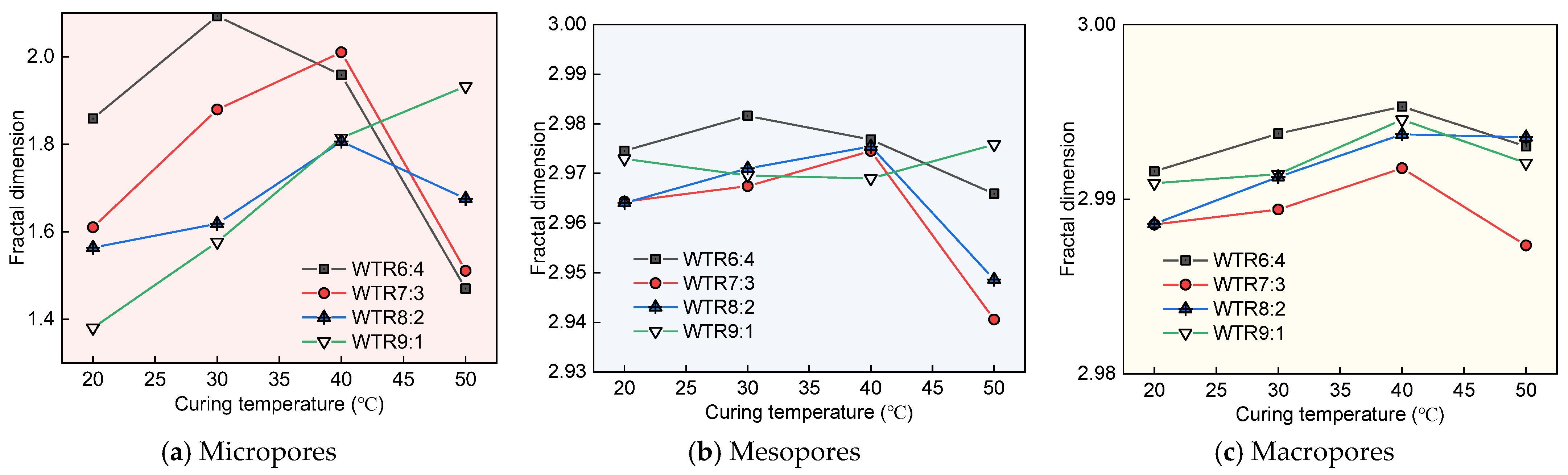
4.1. Fractal Dimension of Pore Structure
4.2. Cross-Scale Analysis
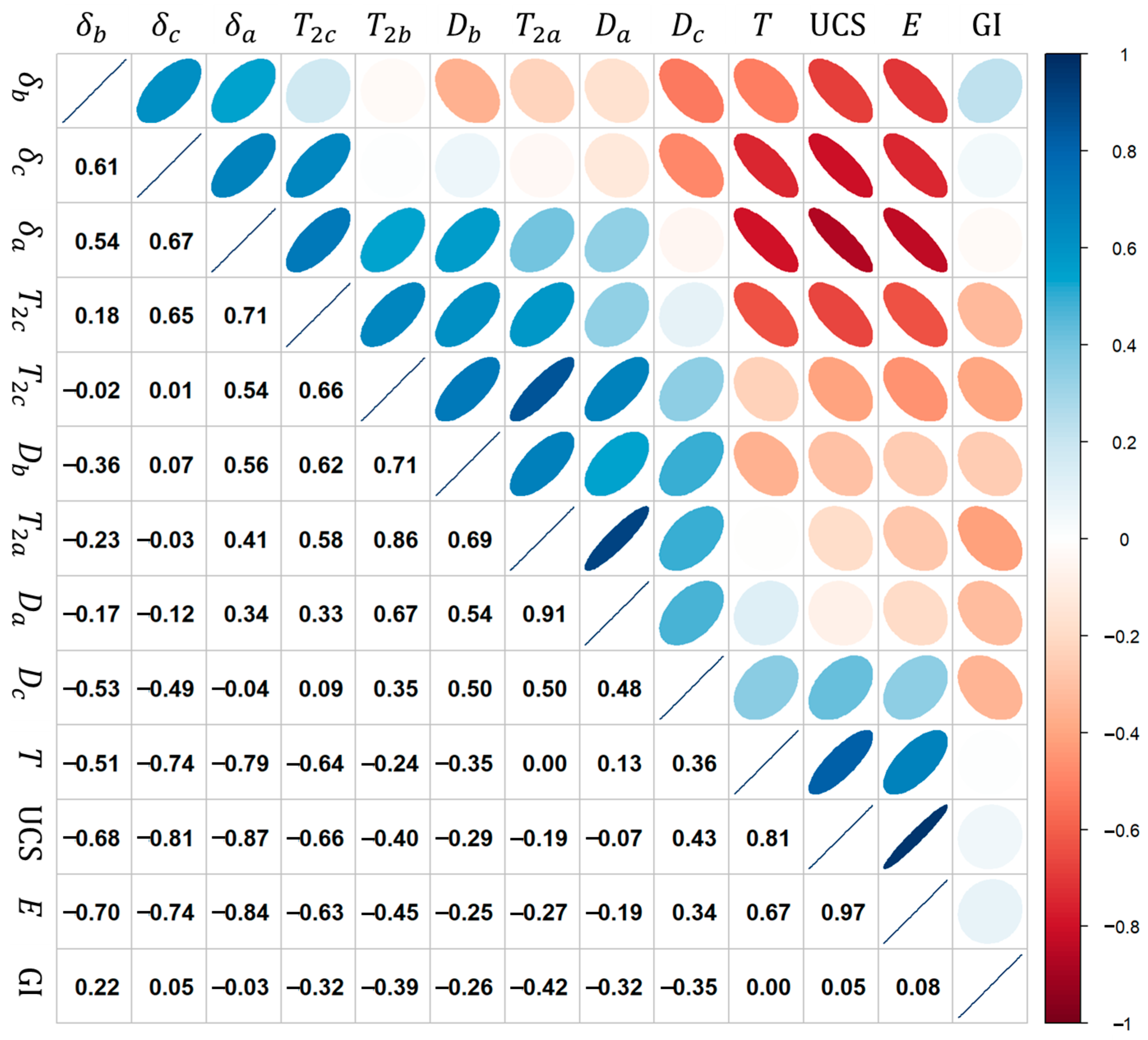
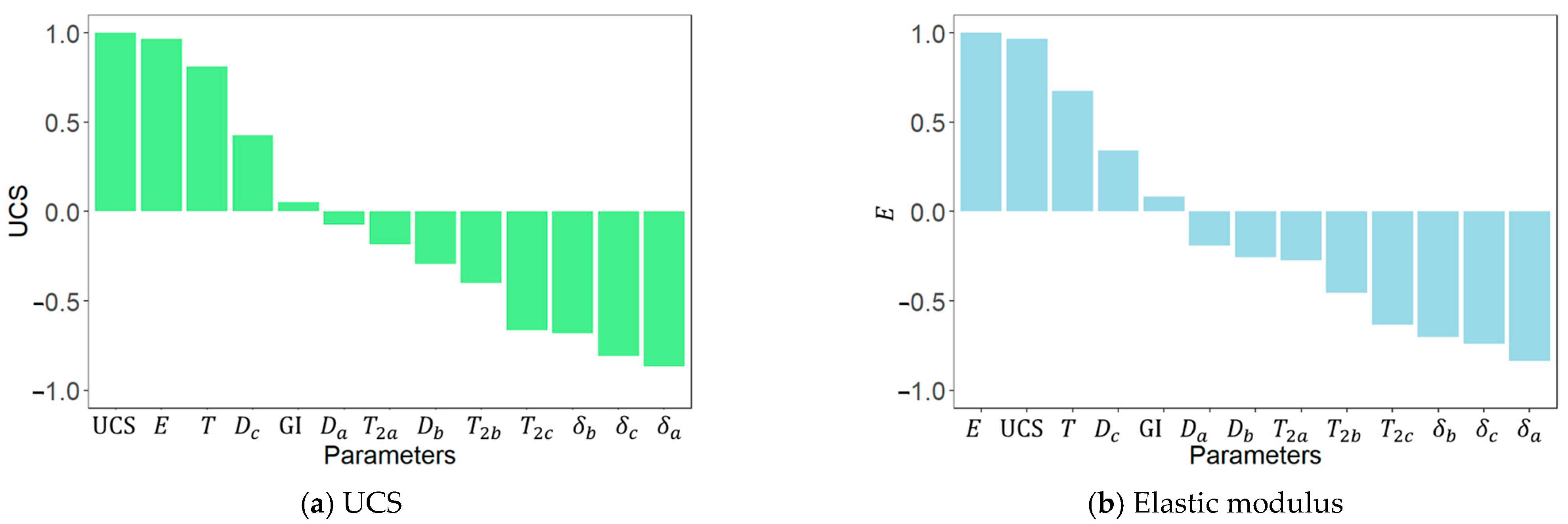
4.3. Interdependency Between Fractal Dimensions and Pore Structure Indicators
4.4. Microstructural Control Pathways on Strength
5. Conclusions
- The mechanical performance and pore structure of CTRB are strongly influenced by the combined effect of aggregate gradation and curing temperature. Optimal performance is achieved at WTRs of 60–80% and curing temperatures between 20 °C and 40 °C, while excessive curing temperature (50 °C) leads to structural degradation and reduced strength;
- The hierarchical sensitivity of fractal dimensions follows the order: Da (micropores) > Db (mesopores) > Dc (macropores), indicating that finer pores are more responsive to compositional and environmental changes, and serve as key indicators of microstructural complexity;
- The fine matrix phase plays a critical role in forming a well-connected micropore network. An increase in coarse aggregate content reduces this matrix, leading to simpler, less space-filling structures with lower fractal dimensions and weaker mechanical performance;
- A nonlinear thermal response was observed: moderate heat promotes secondary hydration products and enhances particle packing, whereas excessive temperature causes hydration instability, microcracking, and coarsened pore structure;
- Pore volume fractions at all scales (δa, δb, δc) exhibit strong negative correlations with both UCS and E, with micropores showing the highest impact (R = −0.87). Reduced porosity and more compact pore structure significantly improve quality of backfill material through better particle packing, denser microstructure, and improved stress transfer;
- Strong internal correlations were identified between NMR-derived pore size, relaxation time, fractal dimension, and porosity, validating the utility of fractal theory as a reliable descriptor for pore structure evolution in cemented materials;
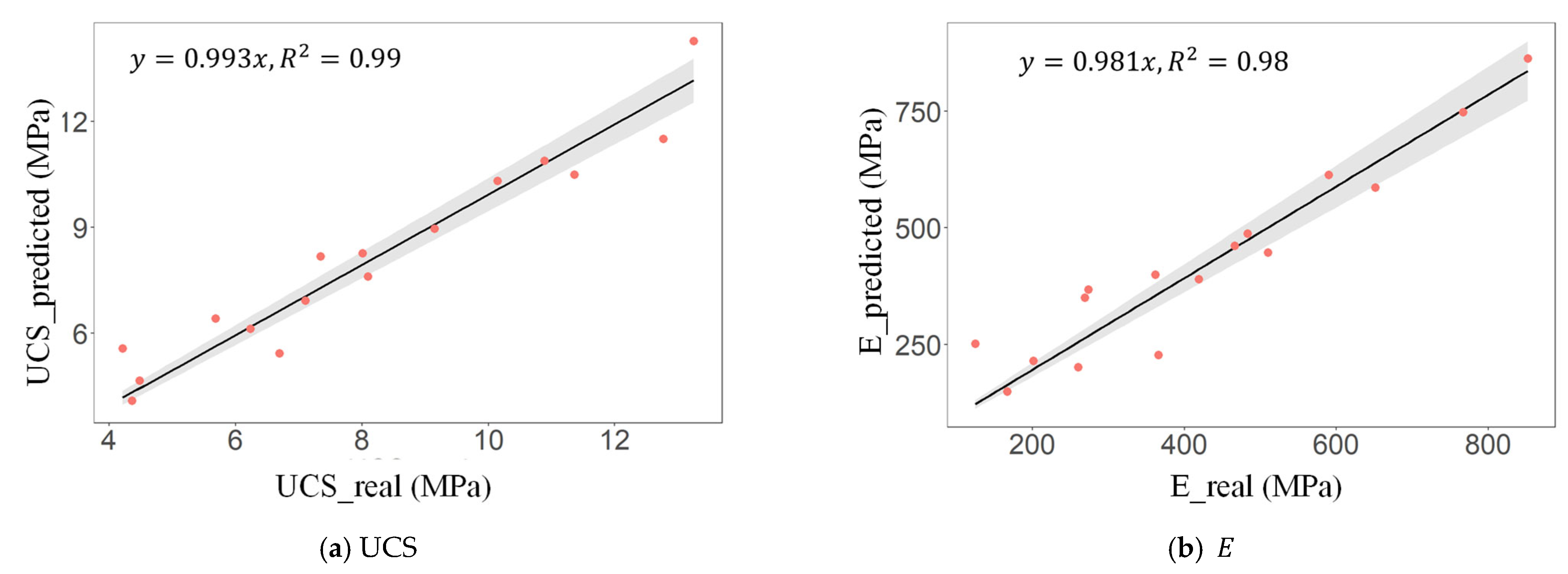
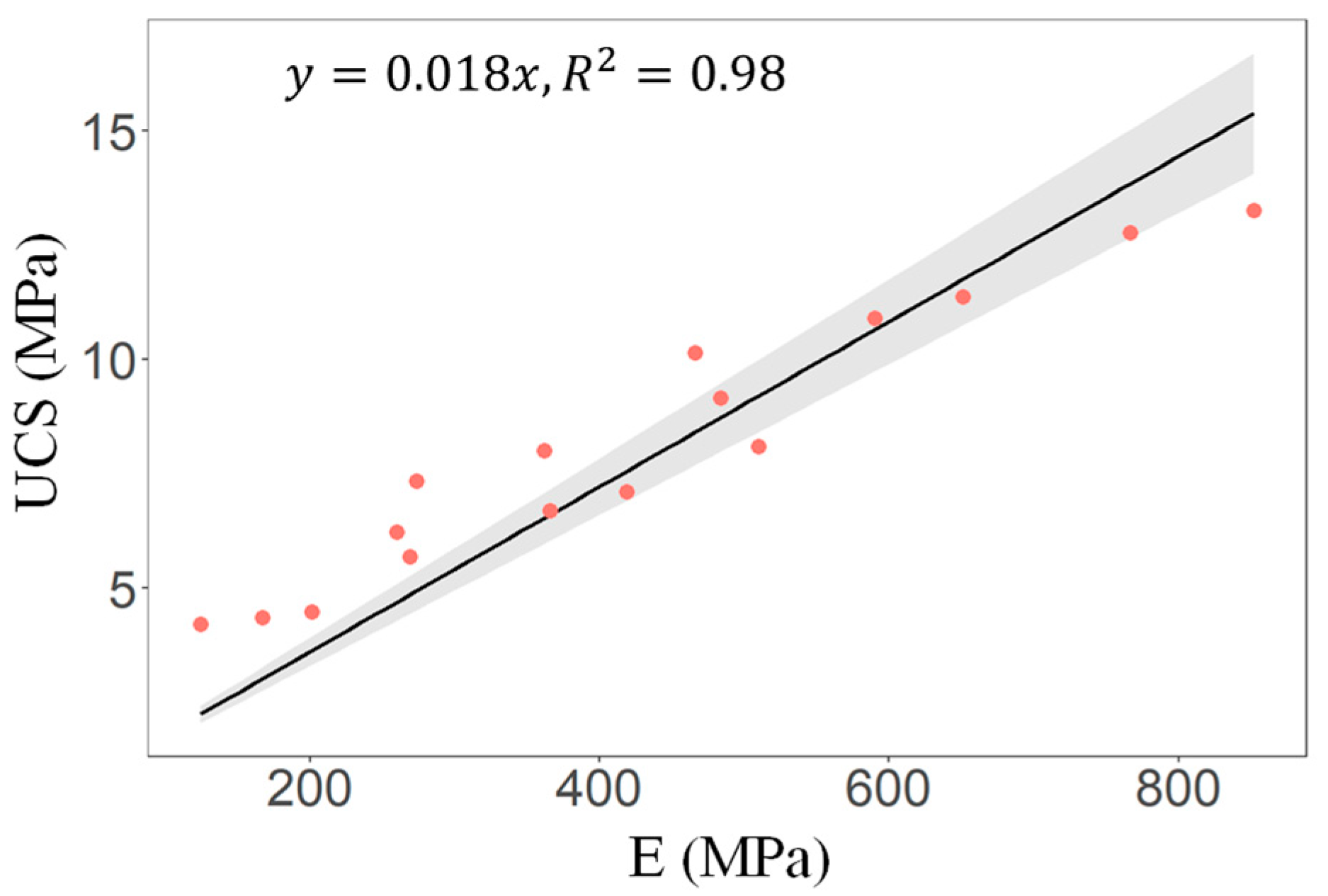
- Multiple linear regression models incorporating six key variables achieved excellent predictive accuracy (R2 = 0.99 for UCS; R2 = 0.98 for E), confirming the effectiveness of microstructure-based modeling in predicting CTRB mechanical behavior;
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, J.; Wu, C.; Huang, N.; Deng, L.; Zhu, D. Utilization of Waste Rock from a Low-Carbon Perspective: Mechanical Performance Analysis of Waste Rock-Cemented Tailings Backfill. J. CO2 Util. 2025, 94, 103058. [Google Scholar] [CrossRef]
- Li, J.; Cao, S.; Song, W.; Sun, L. Visualization and Quantification of Pore Structure in Cement Tailings Waste Rock Composites Using X-Ray Computed Tomography and Deep Learning. Constr. Build. Mater. 2025, 476, 141341. [Google Scholar] [CrossRef]
- Zhu, T.; Chen, Z.; Wang, Z.; Cao, J.; Hao, J.; Zhou, Z. Energy Damage Evolution and Mesoscopic Failure Mechanism of Cemented Waste Rock Tailing Backfill under Axial Compression. Structures 2025, 71, 108057. [Google Scholar] [CrossRef]
- Gao, T.; Wu, A.; Wang, S.; Ruan, Z.; Chen, C.; Sun, W. Experimental and Numerical Investigations of Bending Mechanical Properties and Fracture Characteristics of Cemented Tailings-Waste Rock Backfill under Three-Point Bending. Constr. Build. Mater. 2024, 447, 138149. [Google Scholar] [CrossRef]
- Wang, B.; Kang, M.; Liu, C.; Yang, L.; Li, Q.; Zhou, S. Experimental Study on Mechanical and Microstructure Properties of Cemented Tailings-Waste Rock Backfill with Continuous Gradation. J. Build. Eng. 2024, 95, 110146. [Google Scholar] [CrossRef]
- Yin, S.; Zeng, J.; Yan, Z.; Wang, L.; Chen, W.; Chen, D.; Yang, J. Damage Constitutive Models and Damage Evolution of Cemented Tailings and Waste-Rock Backfill under Impact Loading. Constr. Build. Mater. 2025, 460, 139838. [Google Scholar] [CrossRef]
- Liu, S.; Wu, W.; Sun, X.; Tian, H.; Li, J.; Zhou, R.; Dembele, B.D.; Shen, X. Investigation of Temperature and Humidity Impact on Thermal Comfort in Deep Underground Tunnel during Construction in Hot Climate: A Case Study in an Underground Hydropower Station. Tunn. Undergr. Space Technol. 2025, 162, 106669. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y.; Lai, X.; Wang, G.; Sang, C. Investigation of Heat Stress and Thermal Response in Deep Hot-Humid Underground Environments: A Field and Experimental Study. Build. Environ. 2025, 270, 112506. [Google Scholar] [CrossRef]
- Yan, R.; Yin, S.; Zhang, H.; Wang, L.; Chen, D. Effect of Superplasticizer on the Setting Behaviors and Mechanical Properties of Tailings-Waste Rock Cemented Paste Backfills. Case Stud. Constr. Mater. 2023, 18, e01714. [Google Scholar] [CrossRef]
- Zhu, T.; Chen, Z.; Cao, J.; Nian, G.; Zhang, L.; Hao, J.; Zhou, Z. Investigation of the Fracture Behavior of Cemented Waste Rock-Tailing Backfill by Digital Image Correlation Technique and Discrete Element Modeling. Constr. Build. Mater. 2024, 428, 136367. [Google Scholar] [CrossRef]
- Zhu, T.; Chen, Z.; Wang, Z.; Cao, J.; Hao, J.; Zhou, Z. Experimental and DEM Analyses of Type I Fracture Characteristics of Waste Rock Aggregate Reinforced Cemented Tailing Backfill. Theor. Appl. Fract. Mech. 2025, 135, 104764. [Google Scholar] [CrossRef]
- Zhang, S.; Sun, W.; Hou, Z.; Wu, A.; Li, Z.; Wang, S.; Jiang, M.; Liu, Z. Research on Damage and Crack Evolution Mechanism of Backfill under the Coupling Effect of Layer-Inclined Angle-Pore Triple Defect Structure. Constr. Build. Mater. 2024, 444, 137793. [Google Scholar] [CrossRef]
- Li, Y.; Fu, J.; Wang, K.; He, Z. Influence of Shell Ash on Pore Structure and Mechanical Characteristics of Cemented Tailings Backfill. Constr. Build. Mater. 2024, 411, 134473. [Google Scholar] [CrossRef]
- Li, J.; Liu, H.; Ai, K.; Zhu, L. An NMR-Based Experimental Study on the Pore Structure of the Hydration Process of Mine Filling Slurry. Adv. Civ. Eng. 2018, 2018, 4720356. [Google Scholar] [CrossRef]
- Zhou, A.; Qian, R.; Miao, G.; Zhang, Y.; Xue, C.; Zhang, Y.; Qiao, H.; Shi, J. Gas Permeability Characteristics of Granite-Manufactured Sand Concrete and Its Numerical Simulation Using NMR-MIP Modified Method. Constr. Build. Mater. 2024, 431, 136520. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, H.; Chen, P.; Ju, Y.; Guo, P. Study on Freeze-Thaw Resistance and Pore Structure Deterioration of Fly Ash Reactive Powder Concrete Based on Low-Field NMR Relaxation. Case Stud. Constr. Mater. 2025, 22, e04334. [Google Scholar] [CrossRef]
- Gao, H.; Zhai, Y.; Wei, S. Research on Compressive Failure and Damage Mechanism of Concrete-Granite Composites with Different Roughness Coefficient by NMR and DIC Techniques. Eng. Fail. Anal. 2025, 170, 109291. [Google Scholar] [CrossRef]
- Abdo, S.; Phung, Q.T.; Caspeele, R.; Seetharam, S.C.; Wan-Wendner, R. Microstructure Evolution, Hydration Kinetics and Development of the Mechanical and Transport Properties of a Lining Concrete at Ambient Temperature. Constr. Build. Mater. 2025, 472, 140959. [Google Scholar] [CrossRef]
- Xu, W.; Zhang, Y.; Zhang, Y.; Wang, Q.; Li, Y. Prediction of Temperature Distribution in Manufactured Sand Concrete Based on Hydration-Temperature Coupling Model. J. Build. Eng. 2025, 101, 111961. [Google Scholar] [CrossRef]
- Zhao, Z.; Hu, Y.; Zhao, Z.; Liu, Y.; Xie, C.; Hu, Z. Effect of Curing Temperature on the Hydration Process of Carbon Nanotubes Modified Face Slab Concrete at the Ultra-Early Age. Mater. Lett. 2025, 394, 138633. [Google Scholar] [CrossRef]
- Aminossadati, S.M.; Mohammed, N.M.; Shemshad, J. Distributed Temperature Measurements Using Optical Fibre Technology in an Underground Mine Environment. Tunn. Undergr. Space Technol. 2010, 25, 220–229. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Dino, G.A.; Zhang, L.; Ruan, Z.; Zhang, M.; Li, J.; Wu, A. Degradation of Hemihydrate Phosphogypsum-Based Backfill in Underground Mining: Mechanical and Microstructural Insights on the Effects of pH and Temperature of Mine Water. Process Saf. Environ. Prot. 2025, 193, 272–285. [Google Scholar] [CrossRef]
- Gao, R.; Wang, W.; Xiong, X.; Li, J.; Xu, C. Effect of Curing Temperature on the Mechanical Properties and Pore Structure of Cemented Backfill Materials with Waste Rock-Tailings. Constr. Build. Mater. 2023, 409, 133850. [Google Scholar] [CrossRef]
- Zhang, P.; Gao, Z.; Shi, Y.; Lin, Y.; Li, J. Effect of Large Broken Stone Content on Properties of Roller Compacted Concrete Based on Fractal Theory. Constr. Build. Mater. 2020, 262, 120821. [Google Scholar] [CrossRef]
- Dong, W.; Wang, J. Research on Capillary Water Absorption Characteristics of Aeolian Sand Concrete under Sulfate Freeze-Thaw Coupling Based on Fractal Theory. Constr. Build. Mater. 2024, 455, 139184. [Google Scholar] [CrossRef]
- Su, H.; Zhu, Z.; Jia, W.; Li, T.; Cheng, Z.; Xiang, H. Analysis of Fractal and Energy Characteristics of Low-Temperature Concrete under an Impact Load. Cold Reg. Sci. Technol. 2025, 235, 104493. [Google Scholar] [CrossRef]
- Hu, J.; Ren, Q.; Yang, D.; Ma, S.; Shang, J.; Ding, X.; Luo, Z. Cross-Scale Characteristics of Backfill Material Using NMR and Fractal Theory. Trans. Nonferrous Met. Soc. China 2020, 30, 1347–1363. [Google Scholar] [CrossRef]
- GB/T 50123-2019; Standard for Soil Test Methods. China Institute of Water Resources and Hydropower Research and Design, Ministry of Water Resources. Nanjing Hydraulic Research Institute: Beijing, China, 2019.
- GB/T51450-2022; Technical Standard for Backfill Eengineering in Metal and Non-Metal Mines. China Planning Press Co., Ltd.: Beijing, China, 2022.
- Ren, Q.; Pacheco, J.; De Brito, J. Methods for the Modelling of Concrete Mesostructures: A Critical Review. Constr. Build. Mater. 2023, 408, 133570. [Google Scholar] [CrossRef]
- Fuller William, B.; Thompson Sanford, E. The Laws of Proportioning Concrete. Trans. Am. Soc. Civ. Eng. 1907, 59, 67–143. [Google Scholar] [CrossRef]
- Tashman, L.; Masad, E.; Peterson, B.; Saleh, H. Internal Structure Analysis of Asphalt Mixes to Improve the Simulation of Superpave Gyratory Compaction to Field Conditions. In Proceedings of the Journal of the Association of Asphalt Paving Technologists, Clearwater Beach, FL, USA, 19–20 March 2001; Volume 70. [Google Scholar]
- Talbot, A.N.; Richart, F.E. The Strength of Concrete, Its Relation to the Cement Aggregates and Water; University of Illinois, Engineering Experiment Station, Bulletin no. 137; University of Illinois at Urbana Champaign, College of Engineering. Engineering Experiment Station: Champaign, IL, USA, 1923. [Google Scholar]
- Wu, D.; Guo, W.; Luo, F.; Li, M. Simulation Experimental Investigations on Particle Breakage Mechanism and Fractal Characteristics of Mixed Size Gangue Backfill Materials. J. Mater. Res. Technol. 2023, 24, 125–142. [Google Scholar] [CrossRef]
- Hu, J.; Ding, X.; Ren, Q.; Luo, Z.; Jiang, Q. Effect of Incorporating Waste Limestone Powder into Solid Waste Cemented Paste Backfill Material. Appl. Sci. 2019, 9, 2076. [Google Scholar] [CrossRef]
- Hu, J.; Ren, Q.; Ding, X.; Jiang, Q. Trans-Scale Relationship Analysis between the Pore Structure and Macro Parameters of Backfill and Slurry. R. Soc. Open Sci. 2019, 6, 190389. [Google Scholar] [CrossRef] [PubMed]
- BS EN 12390-3; Testing Hardened Concrete—Compressive Strength of Test Specimens. BSI: London, UK, 2002.
- Li, B.; Zhang, W.; Xue, Y.; Li, Z.; Kong, F.; Kong, R.; Wang, G. Approach to Characterize Rock Fracture Surface: Insight from Roughness and Fractal Dimension. Eng. Geol. 2023, 325, 107302. [Google Scholar] [CrossRef]
- Yin, Y.; Ren, Q.; Lei, S.; Zhou, J.; Xu, L.; Wang, T. Mesoscopic Crack Pattern Fractal Dimension-Based Concrete Damage Identification. Eng. Fract. Mech. 2024, 296, 109829. [Google Scholar] [CrossRef]
- Zhou, S.; Wu, C.; Li, J.; Shi, Y.; Luo, M.; Guo, K. Study on the Influence of Fractal Dimension and Size Effect of Coarse Aggregate on the Frost Resistance of Hydraulic Concrete. Constr. Build. Mater. 2024, 431, 136526. [Google Scholar] [CrossRef]
- Luo, T.; Hua, C.; Li, L.; Zhang, T.; Lu, X.; Li, L.G.; Mostafa, S.A. The Effect of Micro Silica Fume (MSF) Content on Pore Fractal Dimension (PFD) and Mechanical Properties of Self-Consolidating Concrete. Case Stud. Constr. Mater. 2024, 21, e04065. [Google Scholar] [CrossRef]
- International Federation for Structural Concrete. Model Code Fib Model Code for Concrete Structures 2010; International Federation for Structural Concrete: Lausanne, Switzerland, 2010; ISBN 978-3-433-03061-5. Available online: https://www.ernst-und-sohn.de/index.php?q=en/fib-model-code-for-concrete-structures-2010 (accessed on 3 June 2025).
- Jiang, Z.; Cai, G.; Liu, Y.; Wang, P.; Yu, S. Pore Structure and Mechanical Characteristics of CRS Mortar Based on NMR and Fractal Theory. Constr. Build. Mater. 2024, 457, 139459. [Google Scholar] [CrossRef]


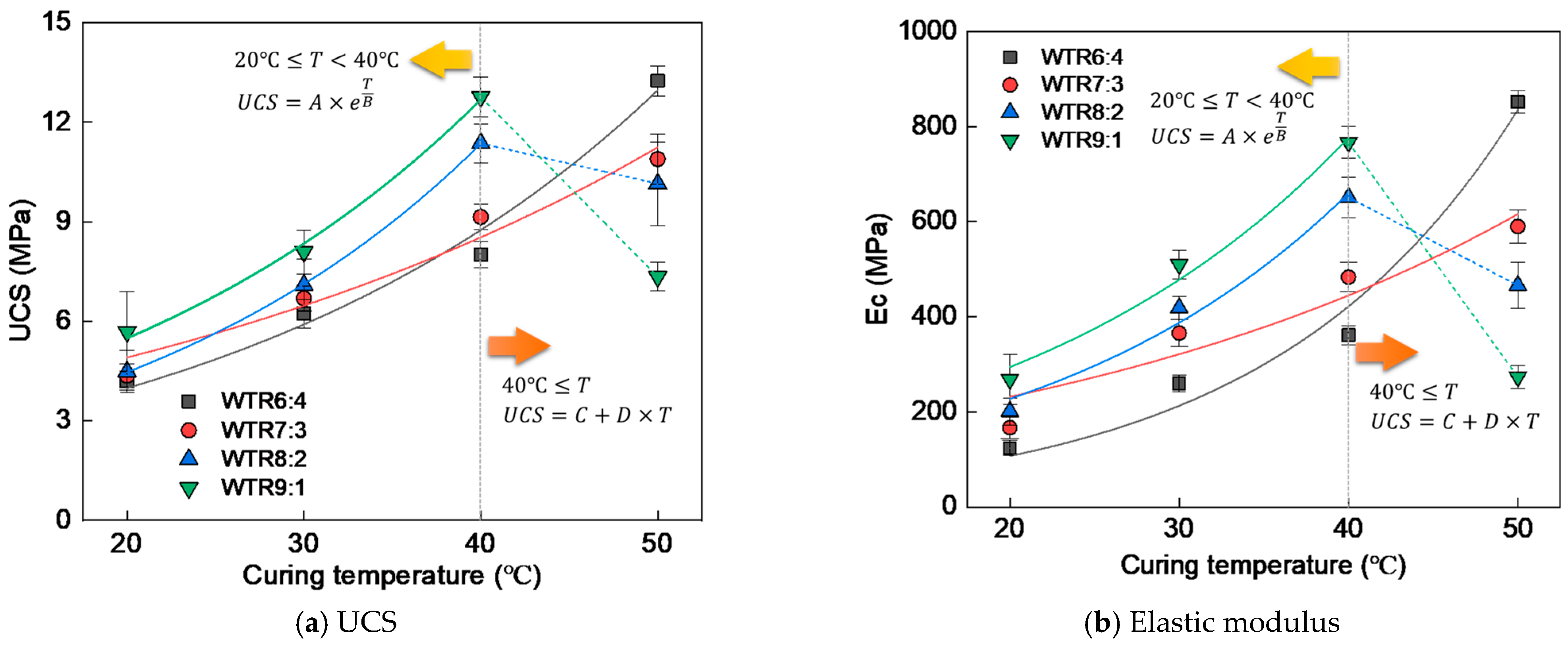



| WTR | ) | UCS (MPa) | Elastic Modulus (MPa) | |||
|---|---|---|---|---|---|---|
| Equation | Equation | |||||
| 6:4 | 20 ≤ T < 50 | 0.97 | 7.16 | 0.97 | ||
| 7:3 | 20 ≤ T < 50 | 0.95 | 4.99 | 0.87 | ||
| 8:2 | 20 ≤ T < 40 | 0.99 | 7.67 | 0.97 | ||
| 40 ≤ T | 1 | −1.07 | 1 | |||
| 9:1 | 20 ≤ T < 40 | 0.99 | 6.24 | 0.97 | ||
| 40 ≤ T | 1 | −4.25 | 1 | |||
| Groups | Micropores | Mesopores | Macropores | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
(ms) | (ms) | (ms) | |||||||||||||
| CTRB64_20 | 4.50 | −0.45 | 1.14 | 0.71 | 1.86 | 38.72 | −0.04 | 0.03 | 0.93 | 2.97 | 191.16 | −0.02 | 0.01 | 0.99 | 2.99 |
| CTRB64_30 | 9.66 | −0.59 | 0.91 | 0.64 | 2.09 | 83.10 | −0.04 | 0.02 | 0.93 | 2.98 | 289.94 | −0.01 | 0.01 | 0.93 | 2.99 |
| CTRB64_40 | 7.84 | −0.61 | 1.04 | 0.66 | 1.96 | 41.50 | −0.04 | 0.02 | 0.94 | 2.98 | 310.79 | −0.01 | 0.00 | 0.75 | 3.00 |
| CTRB64_50 | 1.70 | −0.05 | 1.53 | 0.78 | 1.47 | 13.67 | −0.04 | 0.03 | 0.98 | 2.97 | 102.34 | −0.01 | 0.01 | 0.98 | 2.99 |
| CTRB73_20 | 2.97 | −0.35 | 1.39 | 0.73 | 1.61 | 27.36 | −0.06 | 0.04 | 0.96 | 2.96 | 252.35 | −0.03 | 0.01 | 0.98 | 2.99 |
| CTRB73_30 | 4.82 | −0.47 | 1.12 | 0.69 | 1.88 | 27.36 | −0.05 | 0.03 | 0.94 | 2.97 | 191.16 | −0.02 | 0.01 | 0.98 | 2.99 |
| CTRB73_40 | 6.37 | −0.51 | 0.99 | 0.69 | 2.01 | 27.36 | −0.04 | 0.03 | 0.91 | 2.97 | 144.81 | −0.02 | 0.01 | 0.98 | 2.99 |
| CTRB73_50 | 1.70 | 0.00 | 1.49 | 0.74 | 1.51 | 11.90 | −0.06 | 0.06 | 0.98 | 2.94 | 83.10 | −0.02 | 0.01 | 0.98 | 2.99 |
| CTRB82_20 | 2.58 | −0.29 | 1.44 | 0.74 | 1.56 | 23.82 | −0.05 | 0.04 | 0.96 | 2.96 | 252.35 | −0.03 | 0.01 | 0.97 | 2.99 |
| CTRB82_30 | 3.18 | −0.39 | 1.38 | 0.73 | 1.62 | 27.36 | −0.04 | 0.03 | 0.97 | 2.97 | 191.16 | −0.02 | 0.01 | 0.98 | 2.99 |
| CTRB82_40 | 4.50 | −0.47 | 1.19 | 0.70 | 1.81 | 33.70 | −0.04 | 0.02 | 0.93 | 2.98 | 166.38 | −0.01 | 0.01 | 0.98 | 2.99 |
| CTRB82_50 | 2.10 | −0.09 | 1.32 | 0.73 | 1.68 | 11.90 | −0.06 | 0.05 | 0.98 | 2.95 | 77.53 | −0.01 | 0.01 | 0.85 | 2.99 |
| CTRB91_20 | 2.25 | −0.24 | 1.62 | 0.74 | 1.38 | 29.33 | −0.04 | 0.03 | 0.97 | 2.97 | 219.64 | −0.02 | 0.01 | 0.99 | 2.99 |
| CTRB91_30 | 2.97 | −0.38 | 1.42 | 0.74 | 1.58 | 27.36 | −0.04 | 0.03 | 0.96 | 2.97 | 155.22 | −0.02 | 0.01 | 0.98 | 2.99 |
| CTRB91_40 | 4.20 | −0.46 | 1.19 | 0.73 | 1.81 | 23.82 | −0.04 | 0.03 | 0.97 | 2.97 | 155.22 | −0.01 | 0.01 | 0.98 | 2.99 |
| CTRB91_50 | 5.94 | −0.53 | 1.07 | 0.71 | 1.93 | 47.69 | −0.04 | 0.02 | 0.94 | 2.98 | 166.38 | −0.02 | 0.01 | 0.99 | 2.99 |
| UCS | |||||
|---|---|---|---|---|---|
| Variable | Variable | ||||
| 35.00 | 11.55 | 35.00 | 11.55 | ||
| 2.99 | 0.00 | 31.00 | 17.07 | ||
| 184.35 | 68.34 | 184.35 | 68.34 | ||
| 5.02 | 1.04 | 5.02 | 1.04 | ||
| 0.26 | 0.07 | 0.26 | 0.07 | ||
| 0.07 | 0.04 | 0.07 | 0.04 | ||
| Parameters | UCS | Elastic Modulus | ||
|---|---|---|---|---|
| Values | 95% Confidence Interval | Values | 95% Confidence Interval | |
| 8.11 | [7.56, 8.66] | 422.58 | [373.92, 471.23] | |
| −0.27 | [−1.46, 0.92] | −5.08 | [−103.08, 92.92] | |
| 1.23 | [0.24, 2.23] | −180.07 | [−336.05, −24.08] | |
| −0.76 | [−1.89, 0.37] | 144.67 | [−45.28, [334.63] | |
| −2.07 | [−3.43, −0.71] | −22.61 | [−150.52, 105.31] | |
| −0.27 | [−1.23, 0.69] | −36.83 | [−125.88, 52.22] | |
| 0.10 | [−1.16, 1.37] | −216.51 | [−402.86, −30.16] | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, J.; Xiong, X.; Zhou, K. Fractal Characterization and NMR Analysis of Curing-Dependent Pore Structures in Cemented Tailings Waste RockBackfill. Fractal Fract. 2025, 9, 367. https://doi.org/10.3390/fractalfract9060367
Qiu J, Xiong X, Zhou K. Fractal Characterization and NMR Analysis of Curing-Dependent Pore Structures in Cemented Tailings Waste RockBackfill. Fractal and Fractional. 2025; 9(6):367. https://doi.org/10.3390/fractalfract9060367
Chicago/Turabian StyleQiu, Jianhui, Xin Xiong, and Keping Zhou. 2025. "Fractal Characterization and NMR Analysis of Curing-Dependent Pore Structures in Cemented Tailings Waste RockBackfill" Fractal and Fractional 9, no. 6: 367. https://doi.org/10.3390/fractalfract9060367
APA StyleQiu, J., Xiong, X., & Zhou, K. (2025). Fractal Characterization and NMR Analysis of Curing-Dependent Pore Structures in Cemented Tailings Waste RockBackfill. Fractal and Fractional, 9(6), 367. https://doi.org/10.3390/fractalfract9060367








