Sharp Bounds on Hankel Determinant of q-Starlike and q-Convex Functions Subordinate to Secant Hyperbolic Functions

Abstract

In the present paper, using the q-difference operator, we introduce two classes of q-starlike functions and q-convex functions subordinate to secant hyperbolic functions. As functions in these classes have unique characteristic of missing coefficients on the second term in their analytic expansions, we define a new functional to unify the Hankel determinants with entries of the original coefficients, inverse coefficients, logarithmic coefficients, and inverse logarithmic coefficients for these functions. We obtain the sharp bounds on the new functional for functions in the two classes, and as a consequence, the best results on Hankel determinant for the starlike and convex functions subordinate to secant hyperbolic functions are given. The outcomes include some existing findings as corollaries and may help to deepen the understanding the properties of q-analogue analytic functions.

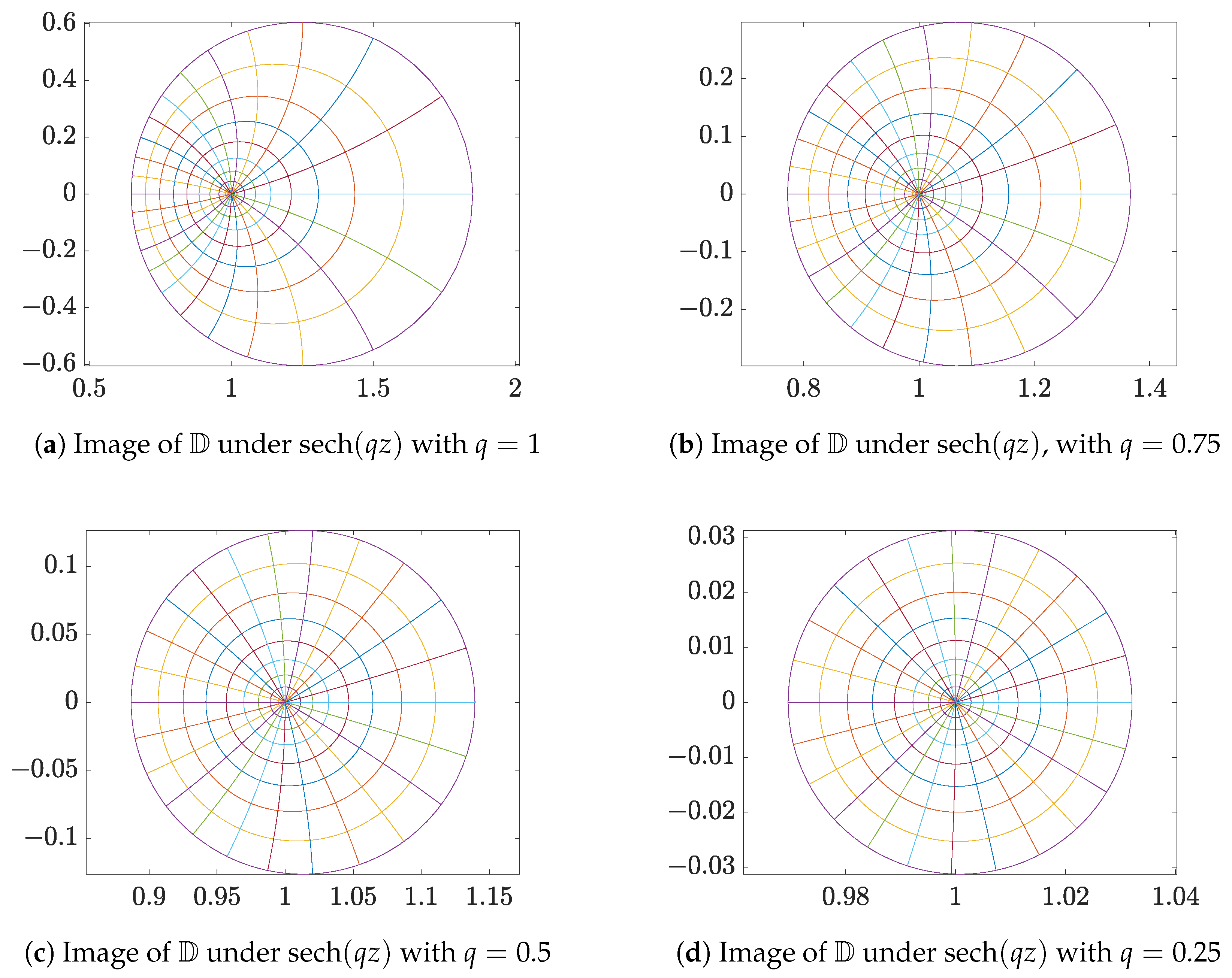
1. Introduction and Definitions

Let $\mathbb{D}=\left\{z\in \mathbb{C}:\left|z\right|<1\right\}$ be the unit disc and $\mathcal{A}$ be the group of analytic functions f in $\mathbb{D}$ with the normalization $f\left(0\right)=f^{\prime }\left(0\right)-1=0.$ For $f\in \mathcal{A}$, it can be written as

$$f\left(z\right)=z+\sum _{n=2}^{\infty }{a}_n{z}^n,z\in \mathbb{D}.$$

(1)

If a function never takes a value twice, it is called univalent. Traditionally, $\mathcal{S}$ is used to represent the set of such functions in geometric function theory. For an analytic function $\omega$ with $\omega \left(0\right)=0$ and $\left|\omega \left(z\right)\right|<1$ in $\mathbb{D}$, we call it a Schwarz function. Let $\mathcal{P}$ denote the class of functions $f\in \mathcal{A}$ with $\Re \left(p\left(z\right)\right)>0(z\in \mathbb{D})$ and normalized by

$$p\left(z\right)=1+\sum _{n=1}^{\infty }{p}_n{z}^n,z\in \mathbb{D}.$$

For $p\in \mathcal{P}$, it is often called a Carathéodory function [1].

For two given analytic functions f and g, $f\prec g$ means that f is subordinate to g, i.e., there exists a Schwarz function $\omega$ in the manner of

$$f\left(z\right)=g\left(\omega \left(z\right)\right),z\in \mathbb{D}.$$

To illustrate our main idea, the notions of q-calculus need to be addressed. Throughout this paper, q is fixed to be $(0,1)$. The q-number ${\left[\zeta \right]}_q$ is introduced as

$${\left[\zeta \right]}_q=\left\{\begin{array}{cc}{\displaystyle \frac{1-q^{\zeta }}{1-q}},\hfill & if\zeta \in \mathbb{C}\setminus \mathbb{N},\\ 1+q+\dots +q^{m-1},\hfill & if\zeta =m\in \mathbb{N}.\end{array}\right.$$

(2)

The q-factorial ${\left[m\right]}_q!$ is used to denote

$${\left[m\right]}_q!=\left\{\begin{array}{cc}1,\hfill & ifm=0,\\ {\left[m\right]}_q·{\left[m-1\right]}_q\dots {\left[2\right]}_q·{\left[1\right]}_q,\hfill & ifm\in \mathbb{N}.\end{array}\right.$$

(3)

In particular, ${lim}_{q\to 1^{-}}{\left[m\right]}_q=m$.

The q-difference operator of a function $\varphi$ is defined as

$$D_q\varphi \left(z\right)={\displaystyle \frac{\varphi \left(qz\right)-\varphi \left(z\right)}{\left(q-1\right)z}},z\in \mathbb{D}\setminus \left\{0\right\},$$

(4)

see [2]. Clearly, ${lim}_{q\to 1^{-}}{D}_q\varphi \left(z\right)={\varphi }^{\prime }\left(z\right)$, and $D_q{z}^m={\left[m\right]}_q{z}^{m-1}$. This operator is widely used in the theory of hypergeometric series and quantum physics and is also known as the Jackson q-difference operator; we refer to [3,4,5] for more details.

Using the q-difference operator, Ismail et al. [6] first proposed the concept of q-starlike functions. In [7], it is proved that the conditions of q-starlike functions can be equivalently characterized by $f\in \mathcal{A}$ and

$${\displaystyle \frac{z{D}_{q}f\left(z\right)}{f\left(z\right)}}\prec {\displaystyle \frac{1+z}{1-qz}},z\in \mathbb{D}.$$

(5)

For $0\le \alpha <1$, Seoudy and Aouf [8] introduced the subclasses ${\mathcal{S}}_q^{*}\left(\alpha \right)$ and ${\mathcal{K}}_q\left(\alpha \right)$ defined, respectively, by

$${\mathcal{S}}_q^{*}:=\left\{f\in \mathcal{A}:\Re \left({\displaystyle \frac{z{D}_{q}f\left(z\right)}{f\left(z\right)}}\right)>\alpha ,z\in \mathbb{D}\right\}$$

(6)

and

$${\mathcal{K}}_q:=\left\{f\in \mathcal{A}:\Re \left({\displaystyle \frac{D_q\left(z{D}_{q}f\left(z\right)\right)}{D_{q}f\left(z\right)}}\right)>\alpha ,z\in \mathbb{D}\right\}.$$

(7)

When $q\to 1^{-}$, ${\mathcal{S}}_q^{*}\left(\alpha \right)$ and ${\mathcal{K}}_q\left(\alpha \right)$ reduce to the class of starlike functions of order $\alpha$ and convex of order $\alpha$ in $\mathbb{D}$ (see Duren [9]). Afterwards, the research on q-starlike functions and q-convex functions continued to enrich, including the works on q-starlike functions associated with the Janowski functions [10], the q-exponential function [11], the q-Bernoulli numbers [12] and some others like [13,14,15].

In [16], Bano et al. introduced a novel class of starlike functions ${\mathcal{S}}^{*}\left(\mathrm{sech}\right)$ defined by

$${\mathcal{S}}^{*}\left(\mathrm{sech}\right):=\left\{f\in \mathcal{A}:{\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}\prec \mathrm{sech}\left(z\right),z\in \mathbb{D}\right\}.$$

We remark that the function $\mathrm{sech}\left(z\right)$ is not univalent in $\mathbb{D}$. By virtue of $\mathrm{sech}\left(z\right)={\displaystyle \frac{2}{e^z+e^{-z}}}$, it is clear that $\mathrm{sech}\left({\displaystyle \frac{1}{2}}\right)=\mathrm{sech}\left(-{\displaystyle \frac{1}{2}}\right)$. As $\Re \left(\mathrm{sech}\left(z\right)\right)>0$ in $\mathbb{D}$, functions in the class ${\mathcal{S}}^{*}\left(\mathrm{sech}\right)$ are starlike and thus univalent. Recently, the coefficient problems for this class were studied in [17,18] and an interesting observation is that $a_2\equiv 0$ when $f\in {\mathcal{S}}^{*}\left(\mathrm{sech}\right)$, with $a_2={\displaystyle \frac{f^{\prime \prime }\left(0\right)}{2!}}$.

Inspired by the mentioned works, we consider the classes ${\mathcal{S}}_q^{*}\left(\mathrm{sech}\right)$ and ${\mathcal{K}}_q\left(\mathrm{sech}\right)$ defined, respectively, by

$${\mathcal{S}}_q^{*}\left(\mathrm{sech}\right):=\left\{f\in \mathcal{A}:{\displaystyle \frac{z{D}_{q}f\left(z\right)}{f\left(z\right)}}\prec \mathrm{sech}\left(qz\right),z\in \mathbb{D}\right\}$$

(8)

and

$${\mathcal{K}}_q\left(\mathrm{sech}\right):=\left\{f\in \mathcal{A}:{\displaystyle \frac{D_q\left(z{D}_{q}f\left(z\right)\right)}{D_{q}f\left(z\right)}}\prec \mathrm{sech}\left(qz\right),z\in \mathbb{D}\right\}.$$

(9)

For different choices of q, the images domains of $\mathrm{sech}\left(qz\right)$ are presented in Figure 1a–d. Clearly, ${lim}_{q\to 1^{-}}{\mathcal{S}}_q^{*}\left(\mathrm{sech}\right)={\mathcal{S}}^{*}\left(\mathrm{sech}\right)$. Denote ${lim}_{q\to 1^{-}}{\mathcal{K}}_q\left(\mathrm{sech}\right)=\mathcal{K}\left(\mathrm{sech}\right)$. We remark that $\mathcal{K}\left(\mathrm{sech}\right)$ is a subclass of convex functions.

Hankel determinant is an important tool in the study of analytic functions. In [19,20], Pommerenke introduced the Hankel determinant ${\mathcal{H}}_{q,n}\left(f\right)$ with $a_1=1$ and $q,n\in \mathbb{N}$ for $f\in \mathcal{A}$. It is defined by the coefficients $a_n$ of f arranged in the form

$${\mathcal{H}}_{q,n}\left(f\right):=\left|\begin{array}{cccc}{a}_n\hfill & a_{n+1}\hfill & \dots \hfill & a_{n+q-1}\hfill \\ a_{n+1}\hfill & a_{n+2}\hfill & \dots \hfill & a_{n+q}\hfill \\ ⋮\hfill & ⋮\hfill & \dots \hfill & ⋮\hfill \\ a_{n+q-1}\hfill & a_{n+q}\hfill & \dots \hfill & a_{n+2q-2}\hfill \end{array}\right|.$$

Utilizing the initial coefficients $a_2$, $a_3$, $a_4$, and $a_5$ of f, we may write

$$\begin{array}{cc}\hfill {\mathcal{H}}_{2,3}\left(f\right)& =a_3{a}_5-a_4^2,\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill {\mathcal{H}}_{3,1}\left(f\right)& =2a_2{a}_3{a}_4-a_2^2{a}_5-a_4^2+a_3{a}_5-a_3^3.\hfill \end{array}$$

(11)

In recent years, the upper bounds of Hankel determinants for f belonging to various subfamilies of analytic functions were obtained. For example, the study on bounded turning functions [21,22], close-to-convex functions [23], bi-univalent functions [24], convex functions [25] and starlike functions [26,27]. The results are abundant enough, and those interested can also refer to [28,29,30].

If $f\in \mathcal{S}$ defined in $\mathbb{D},$ the inverse of f exists and is univalent at least in a disk of radius $1/4$. Denote

$$F\left(w\right):=f^{-1}\left(w\right)=w+A_2{w}^2+A_3{w}^3+\dots .$$

As $f\left(F\left(w\right)\right)=w$, the coefficients of F are closely related with f. Researchers endeavor to study the inverse functions from different perspectives; in particular, the Hankel determinant using the inverse coefficients is smoothly introduced [31,32,33,34]. We note that ${\mathcal{H}}_{2,3}\left(f^{-1}\right)$ and ${\mathcal{H}}_{3,1}\left(f^{-1}\right)$ are given by

$$\begin{array}{cc}\hfill {\mathcal{H}}_{2,3}\left(f^{-1}\right)& =A_3{A}_5-A_4^2,\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill {\mathcal{H}}_{3,1}\left(f^{-1}\right)& =2A_2{A}_3{A}_4-A_2^2{A}_5-A_4^2+A_3{A}_5-A_3^3.\hfill \end{array}$$

(13)

The logarithmic coefficients ${\gamma }_n$ of $f\in \mathcal{S}$ are well discussed for the reason of their connection with the Bieberbach conjecture. They are presented by

$$F_f:=log\left({\displaystyle \frac{f\left(z\right)}{z}}\right)=2\sum _{n=1}^{\infty }{\gamma }_n{z}^n,log1=0.$$

(14)

The idea of taking ${\gamma }_n$ as the entries of the Hankel determinant was first proposed in [35] and later widely accepted by researchers [36,37,38,39]. Based on existing representation methods, the second Hankel determinant of logarithmic coefficients is denoted by

$$\begin{array}{cc}\hfill {\mathcal{H}}_{2,1}\left(F_f/2\right)& ={\gamma }_1{\gamma }_3-{\gamma }_2^2,\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill {\mathcal{H}}_{2,2}\left(F_f/2\right)& ={\gamma }_2{\gamma }_4-{\gamma }_3^2.\hfill \end{array}$$

(16)

In [40], Ponnusamy et al. first introduced the concept of logarithmic coefficients of inverse functions. It is defined by

$$log\left({\displaystyle \frac{F\left(w\right)}{w}}\right)=2\sum _{n=1}^{\infty }{\varpi }_n{w}^n,\left|w\right|<{\displaystyle \frac{1}{4}}.$$

(17)

To broaden the fields on coefficient problems for univalent functions, it is bound to consider the Hankel determinant, with $a_n$ replaced by ${\varpi }_n$; see [41,42,43]. Using this idea, we have

$$\begin{array}{cc}\hfill {\mathcal{H}}_{2,1}\left(F_{f^{-1}}/2\right)& ={\varpi }_1{\varpi }_3-{\varpi }_3^2,\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill {\mathcal{H}}_{2,2}\left(F_{f^{-1}}/2\right)& ={\varpi }_2{\varpi }_4-{\varpi }_3^2.\hfill \end{array}$$

(19)

Taking $a_n$ to express the Hankel determinant ${\mathcal{H}}_{2,3}\left(f^{-1}\right)$ and ${\mathcal{H}}_{3,1}\left(f^{-1}\right)$, it is calculated that

$$\begin{gathered} {\mathcal{H}}_{2,3}\left(f^{-1}\right)=3a_2^6-6a_2^4{a}_3+2a_2^3{a}_4-2a_2^2{a}_5+2a_2^2{a}_3^2+4a_2{a}_3{a}_4 \\ +a_3{a}_5-a_4^2-3a_3^3, \end{gathered}$$

(20)

$$\begin{array}{cc}\hfill {\mathcal{H}}_{3,1}\left(f^{-1}\right)& =a_2^6-3a_2^4{a}_3+3a_2^2{a}_3^2-a_2^2{a}_5+2a_2{a}_3{a}_4+a_3{a}_5-a_4^2-2a_3^3.\hfill \end{array}$$

(21)

Differentiating (14) and using (1), we may obtain the correspondence between $a_n$ and ${\gamma }_n$ of f. Substituting ${\gamma }_n$ with $a_n$ leads to

$$\begin{array}{cc}\hfill {\mathcal{H}}_{2,2}\left(F_f/2\right)& ={\displaystyle \frac{1}{288}}{a}_2^6-{\displaystyle \frac{1}{48}}{a}_2^4{a}_3-{\displaystyle \frac{1}{24}}{a}_2^3{a}_4+{\displaystyle \frac{1}{16}}{a}_2^2{a}_3^2-{\displaystyle \frac{1}{8}}{a}_2^2{a}_5+{\displaystyle \frac{1}{4}}{a}_2{a}_3{a}_4\hfill \\ \hfill & +{\displaystyle \frac{1}{4}}{a}_3{a}_5-{\displaystyle \frac{1}{4}}{a}_2^4-{\displaystyle \frac{1}{8}}{a}_3^3.\hfill \end{array}$$

(22)

In [44], it is shown that

$$\begin{array}{cc}\hfill {\mathcal{H}}_{2,2}\left(F_{f^{-1}}/2\right)& ={\displaystyle \frac{145}{288}}{a}_2^6-{\displaystyle \frac{55}{48}}{a}_2^4{a}_3+{\displaystyle \frac{5}{24}}{a}_2^3{a}_4+{\displaystyle \frac{11}{16}}{a}_2^2{a}_3^2-{\displaystyle \frac{5}{8}}{a}_2^2{a}_5+{\displaystyle \frac{3}{4}}{a}_2{a}_3{a}_4\hfill \\ \hfill & +{\displaystyle \frac{1}{4}}{a}_3{a}_5-{\displaystyle \frac{1}{4}}{a}_2^4-{\displaystyle \frac{5}{8}}{a}_3^3.\hfill \end{array}$$

(23)

When $a_2=0$, it is noted that

$$\begin{array}{cc}\hfill {\mathcal{H}}_{2,3}\left(f\right)& =a_3{a}_5-a_4^2,\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill {\mathcal{H}}_{3,1}\left(f\right)& =a_3{a}_5-a_4^2-a_3^3,\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill {\mathcal{H}}_{2,3}\left(f^{-1}\right)& =a_3{a}_5-a_4^2-3a_3^3,\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill {\mathcal{H}}_{3,1}\left(f^{-1}\right)& =a_3{a}_5-a_4^2-2a_3^3,\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill {\mathcal{H}}_{2,2}\left(F_f/2\right)& ={\displaystyle \frac{1}{4}}\left(a_3{a}_5-a_4^2-{\displaystyle \frac{1}{2}}{a}_3^3\right),\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill {\mathcal{H}}_{2,2}\left(F_{f^{-1}}/2\right)& ={\displaystyle \frac{1}{4}}\left(a_3{a}_5-a_4^2-{\displaystyle \frac{5}{2}}{a}_3^3\right).\hfill \end{array}$$

(29)

It is interesting that they are all connected with $a_3{a}_5-a_4^2-\mu a_3^3$, where $\mu$ is a real number, and $\mu \ge 0$. Thus, we may expect this expression as a new functional of analytic functions.

Let $\mu \in \left[0,+\infty \right)$ and $f\in \mathcal{A}$ be of the form (1). Define

$${\mathcal{H}}_{\mu }\left(f\right)=a_3{a}_5-a_4^2-\mu a_3^3,$$

(30)

where $a_n:={\displaystyle \frac{f^{\left(n\right)}\left(0\right)}{n!}}$ for $n\ge 2$. For different choices of the parameter $\mu$, this functional may be used as a unified tool to give the upper bound of a certain Hankel determinant.

In this article, we aim to study the sharp bounds on the new functional ${\mathcal{H}}_{\mu }\left(f\right)$ for the functions in the classes ${\mathcal{S}}_q^{*}\left(\mathrm{sech}\right)$ and ${\mathcal{K}}_q\left(\mathrm{sech}\right)$. As a consequence, some useful results on the bounds of the second and third Hankel determinants with different entries are obtained.

2. Lemmas

In this section, we list two crucial lemmas that will be applied to investigate the main results of this work. As we know, an efficient way to solve coefficient problems for various classes of analytic functions is to associate them with the coefficients of Carathéodory functions. The first lemma is frequently used, as it provides a parametric representation of some initial coefficients for Carathéodory functions.

Lemma 1

(see [45]). Let $p\in \mathcal{P}$ be of the form (1), and let $c_1\ge 0$. Then, for some $x,\kappa \in \overline{\mathbb{D}}:=\left\{z\in \mathbb{C}:\left|z\right|\le 1\right\}$,

$$\begin{array}{cc}\hfill & 2c_2=c_1^2+\left(4-c_1^2\right)x,\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill & 4c_3=c_1^3+2\left(4-c_1^2\right)c_{1}x-c_1\left(4-c_1^2\right)x^2+2\left(4-c_1^2\right)\left(1-{\left|x\right|}^2\right)\kappa .\hfill \end{array}$$

(32)

Lemma 2

(see [46]). Let ${\tau }_1$, ${\tau }_2$, ${\tau }_3\in \mathbb{R}$, and be defined as

$$U\left({\tau }_1,{\tau }_2,{\tau }_3\right)=\underset{z\in \overline{\mathbb{D}}}{max}\left\{\left|{\tau }_1+{\tau }_{2}z+{\tau }_3{z}^2\right|+1-{\left|z\right|}^2\right\}.$$

(33)

If ${\tau }_1\le 0$ and ${\tau }_3<0$, then

$$U\left({\tau }_1,{\tau }_2,{\tau }_3\right)=\left\{\begin{array}{cc}-{\tau }_1+\left|{\tau }_2\right|-{\tau }_3,\hfill & if\left|{\tau }_2\right|\ge 2\left(1+{\tau }_3\right),\\ \\ 1-{\tau }_1+{\displaystyle \frac{{\tau }_2^2}{4\left(1+{\tau }_3\right)}},\hfill & if\left|{\tau }_2\right|<2\left(1+{\tau }_3\right).\end{array}\right.$$

If ${\tau }_1>0$ and ${\tau }_3<0$, then

$$U\left({\tau }_1,{\tau }_2,{\tau }_3\right)=\left\{\begin{array}{cc}1-{\tau }_1+{\displaystyle \frac{{\tau }_2^2}{4\left(1+{\tau }_3\right)}},\hfill & if{\tau }_2^2\ge -{\displaystyle \frac{4{\tau }_1{\tau }_3^3}{1-{\tau }_3^2}},\left|{\tau }_2\right|<2\left(1+{\tau }_3\right),\\ \\ 1+{\tau }_1+{\displaystyle \frac{{\tau }_2^2}{4\left(1-{\tau }_3\right)}},\hfill & if{\tau }_2^2<min\left\{4{\left(1-{\tau }_3\right)}^2,-{\displaystyle \frac{4{\tau }_1{\tau }_3^3}{1-{\tau }_3^2}}\right\},\\ \\ V\left({\tau }_1,{\tau }_2,{\tau }_3\right),\hfill & otherwise,\end{array}\right.$$

where

$$V\left({\tau }_1,{\tau }_2,{\tau }_3\right)=\left\{\begin{array}{cc}{\tau }_1+\left|{\tau }_2\right|+{\tau }_3,\hfill & if-{\tau }_3\left(4{\tau }_1+\left|{\tau }_2\right|\right)\le {\tau }_1\left|{\tau }_2\right|,\\ \\ -{\tau }_1+\left|{\tau }_2\right|-{\tau }_3,\hfill & if-{\tau }_3\left(-4{\tau }_1+\left|{\tau }_2\right|\right)\ge {\tau }_1\left|{\tau }_2\right|,\\ \\ \left({\tau }_1-{\tau }_3\right)\sqrt{1-{\displaystyle \frac{{\tau }_2^2}{4{\tau }_1{\tau }_3}}},\hfill & otherwise.\end{array}\right.$$

(34)

3. Main Results

At first, we will discuss the upper bound of ${\mathcal{H}}_{\mu }\left(f\right)$ for functions in the class ${\mathcal{S}}_q^{*}\left(\mathrm{sech}\right)$.

Theorem 1.

If $f\in {\mathcal{S}}_q^{*}\left(\mathrm{sech}\right)$, then

$$\left|{\mathcal{H}}_{\mu }\left(f\right)\right|\le \left\{\begin{array}{cc}{\displaystyle \frac{q^2}{3072{\left[2\right]}_q^3{\left[3\right]}_q^2{\left[4\right]}_q}}\underset{t\in [0,2]}{max}\left\{{\mathsf{\Lambda }}_0{t}^6+{\mathsf{\Lambda }}_2{t}^4+{\mathsf{\Lambda }}_3{t}^2\right\},\hfill & if\mu \in \left[0,{\displaystyle \frac{6{\left[2\right]}_q+5q{\left[2\right]}_q^2}{6{\left[4\right]}_q}}\right],\\ {\displaystyle \frac{q^2}{3072{\left[2\right]}_q^3{\left[3\right]}_q^2{\left[4\right]}_q}}\underset{t\in [0,2]}{max}\left\{{\mathsf{\Lambda }}_1{t}^6+{\mathsf{\Lambda }}_2{t}^4+{\mathsf{\Lambda }}_3{t}^2\right\},\hfill & if\mu \in \left({\displaystyle \frac{6{\left[2\right]}_q+5q{\left[2\right]}_q^2}{6{\left[4\right]}_q}},+\infty \right),\end{array}\right.$$

where

$$\begin{array}{cc}\hfill {\mathsf{\Lambda }}_0& =48{\left[2\right]}_q^3{\left[4\right]}_q-36{\left[2\right]}_q^2{\left[3\right]}_q^2+6q{\left[2\right]}_q{\left[3\right]}_q^2+5q^2{\left[2\right]}_q^2{\left[3\right]}_q^2-6\mu q{\left[3\right]}_q^2{\left[4\right]}_q,\hfill \\ \hfill {\mathsf{\Lambda }}_1& =48{\left[2\right]}_q^3{\left[4\right]}_q-36{\left[2\right]}_q^2{\left[3\right]}_q^2-6q{\left[2\right]}_q{\left[3\right]}_q^2-5q^2{\left[2\right]}_q^2{\left[3\right]}_q^2+6\mu q{\left[3\right]}_q^2{\left[4\right]}_q,\hfill \\ \hfill {\mathsf{\Lambda }}_2& =192{\left[2\right]}_q^2{\left[3\right]}_q^2-384{\left[2\right]}_q^3{\left[4\right]}_q,\hfill \\ \hfill {\mathsf{\Lambda }}_3& =768{\left[2\right]}_q^3{\left[4\right]}_q-192{\left[2\right]}_q^2{\left[3\right]}_q^2.\hfill \end{array}$$

Proof. 

Let $f\in {\mathcal{S}}_q^{*}\left(\mathrm{sech}\right)$. According to the subordination principle, there is a Schwarz function $\omega$ such that

$${\displaystyle \frac{z{D}_{q}f\left(z\right)}{f\left(z\right)}}=\mathrm{sech}\left(q\omega \left(z\right)\right),z\in \mathbb{D}.$$

Taking

$$p\left(z\right)={\displaystyle \frac{1+\omega \left(z\right)}{1-\omega \left(z\right)}}=1+c_{1}z+c_2{z}^2+c_3{z}^3+c_4{z}^4+\dots ,z\in \mathbb{D},$$

it is seen that $p\in \mathcal{P}$, and

$$\begin{array}{cc}\hfill \omega \left(z\right)& ={\displaystyle \frac{c_1}{2}}z+{\displaystyle \frac{2c_2-c_1^2}{4}}{z}^2+{\displaystyle \frac{4c_3-4c_2{c}_1+c_1^3}{8}}{z}^3\hfill \\ \hfill & +{\displaystyle \frac{8c_4-8c_3{c}_1-4c_2^2+6c_1^2{c}_2-c_1^4}{16}}{z}^4+\dots ,z\in \mathbb{D}.\hfill \end{array}$$

Then,

$$\begin{array}{cc}\hfill \mathrm{sech}\left(q\omega \left(z\right)\right)& =1-{\displaystyle \frac{1}{8}}{q}^2{c}_1^2{z}^2+{\displaystyle \frac{1}{8}}{q}^2\left(-2c_1{c}_2+c_1^3\right)z^3\hfill \\ \hfill & +{\displaystyle \frac{1}{384}}{q}^2\left[144c_1^2{c}_2-96c_1{c}_3-48c_2^2-\left(36-5q^2\right)c_1^4\right]z^4+\dots ,z\in \mathbb{D}.\hfill \end{array}$$

(35)

Using the form of (1), we obtain

$$\begin{array}{cc}\hfill {\displaystyle \frac{z{D}_{q}f\left(z\right)}{f\left(z\right)}}& =1+q{a}_{2}z+q\left({\left[2\right]}_q{a}_3-a_2^2\right)z^2+q\left[{\left[3\right]}_q{a}_4-\left(1+{\left[2\right]}_q\right)a_2{a}_3+a_2^3\right]z^3\hfill \\ \hfill & +q\left[{\left[4\right]}_q{a}_5-\left(1+{\left[3\right]}_q\right)a_2{a}_4-{\left[2\right]}_q{a}_3^2+\left(2+{\left[2\right]}_q\right)a_2^2{a}_3-a_2^4\right]z^4+\dots ,z\in \mathbb{D}.\hfill \end{array}$$

(36)

By comparing the coefficients on the right side of (35) and (36), we have

$$\begin{array}{cc}\hfill a_2& =0,\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill a_3& =-{\displaystyle \frac{q}{8{\left[2\right]}_q}}{c}_1^2,\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill a_4& =-{\displaystyle \frac{q}{8{\left[3\right]}_q}}\left(2c_1{c}_2-c_1^3\right),\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill a_5& ={\displaystyle \frac{q}{384{\left[4\right]}_q}}\left[-\left(36-5q^2-{\displaystyle \frac{6q}{{\left[2\right]}_q}}\right)c_1^4+144c_1^2{c}_2-96c_1{c}_3-48c_2^2\right].\hfill \end{array}$$

(40)

Let $f\in {\mathcal{S}}_q^{*}\left(\mathrm{sech}\right)$ and $f_{\theta }\left(z\right)=e^{-i\theta }f\left(e^{i\theta }z\right)$, with $\theta \in \mathbb{R}$. Noting that

$${\displaystyle \frac{z{D}_q{f}_{\theta }\left(z\right)}{f_{\theta }\left(z\right)}}={\displaystyle \frac{z·\frac{e^{-i\theta }f\left(e^{i\theta }qz\right)-e^{-i\theta }f\left(e^{i\theta }z\right)}{(q-1)z}}{e^{-i\theta }f\left(e^{i\theta }z\right)}}={\displaystyle \frac{e^{i\theta }z·\frac{f\left(e^{i\theta }qz\right)-f\left(e^{i\theta }z\right)}{e^{i\theta }(q-1)z}}{f\left(e^{i\theta }z\right)}}={\displaystyle \frac{e^{i\theta }z{D}_{q}f\left(e^{i\theta }z\right)}{f\left(e^{i\theta }z\right)}}\in {\mathcal{S}}_q^{*}\left(\mathrm{sech}\right)$$

and

$$H_{\mu }\left(f_{\theta }\right)=e^{4i\theta }{H}_{\mu }\left(f\right),$$

the functional $\left|{\mathcal{H}}_{\mu }\left(f_{\theta }\right)\right|=\left|{\mathcal{H}}_{\mu }\left(f\right)\right|$ for all $\theta \in \mathbb{R}$ and $f\in {\mathcal{S}}_q^{*}\left(\mathrm{sech}\right)$. Hence, we are able to assume $c_1=c\in [0,2]$ in estimating the upper bound of $\left|{\mathcal{H}}_{\mu }\left(f\right)\right|$ for $f\in {\mathcal{S}}_q^{*}\left(\mathrm{sech}\right)$. Using (38)–(40) and (30), we obtain

$${\mathcal{H}}_{\mu }\left(f\right)={\displaystyle \frac{q^2{c}^2}{3072{\left[2\right]}_q^3{\left[3\right]}_q^2{\left[4\right]}_q}}\left({\alpha }_1{c}^4+{\alpha }_2{c}^2{c}_2+{\alpha }_{3}c{c}_3+{\alpha }_4{c}_2^2\right),$$

(41)

where

$$\begin{array}{cc}\hfill {\alpha }_1& =6\mu q{\left[3\right]}_q^2{\left[4\right]}_q-48{\left[2\right]}_q^3{\left[4\right]}_q+36{\left[2\right]}_q^2{\left[3\right]}_q^2-6q{\left[2\right]}_q{\left[3\right]}_q^2-5q^2{\left[2\right]}_q^2{\left[3\right]}_q^2,\hfill \\ \hfill {\alpha }_2& =48{\left[2\right]}_q^2\left(4{\left[2\right]}_q{\left[4\right]}_q-3{\left[3\right]}_q^2\right),\hfill \\ \hfill {\alpha }_3& =96{\left[2\right]}_q^2{\left[3\right]}_q^2,\hfill \\ \hfill {\alpha }_4& =48{\left[2\right]}_q^2\left({\left[3\right]}_q^2-4{\left[2\right]}_q{\left[4\right]}_q\right).\hfill \end{array}$$

Using Lemma 1 and substituting $c_2$ and $c_3$ into (41) gives

$$H_{\mu }\left(f\right)={\displaystyle \frac{q^2{c}^2}{3072{\left[2\right]}_q^3{\left[3\right]}_q^2{\left[4\right]}_q}}\left[{\beta }_1+{\beta }_{2}x+{\beta }_3{x}^2+48{\left[2\right]}_q^2{\left[3\right]}_q^{2}c(4-c^2)\left(1-{\left|x\right|}^2\right)\kappa \right],$$

where $x,\kappa \in \overline{\mathbb{D}}$, and

$$\begin{array}{cc}\hfill {\beta }_1& =q{\left[3\right]}_q^2\left(6\mu {\left[4\right]}_q-6{\left[2\right]}_q-5q{\left[2\right]}_q^2\right)c^4,\hfill \\ \hfill {\beta }_2& =0,\hfill \\ \hfill {\beta }_3& =-12{\left[2\right]}_q^2\left(4-c^2\right)\left[4\left(4{\left[2\right]}_q{\left[4\right]}_q-{\left[3\right]}_q^2\right)+\left(3{\left[3\right]}_q^2-4{\left[2\right]}_q{\left[4\right]}_q\right)c^2\right].\hfill \end{array}$$

When $c=0$, it is clear that ${\mathcal{H}}_{\mu }\left(f\right)=0$. When $c=2$,

$${\mathcal{H}}_{\mu }\left(f\right)={\displaystyle \frac{q^3\left(6\mu {\left[4\right]}_q-6{\left[2\right]}_q-5q{\left[2\right]}_q^2\right)}{48{\left[2\right]}_q^3{\left[4\right]}_q}},c=2.$$

(42)

Now we assume that $c\in (0,2)$. By taking $\left|\kappa \right|\le 1,$ it is achieved that

$$\begin{array}{cc}\hfill \left|{\mathcal{H}}_{\mu }\left(f\right)\right|& \le {\displaystyle \frac{q^2{c}^3\left(4-c^2\right)}{64{\left[2\right]}_q{\left[4\right]}_q}}\left(\left|{\sigma }_1+{\sigma }_{2}x+{\sigma }_3{x}^2\right|+1-{\left|x\right|}^2\right)\hfill \\ \hfill & :={\displaystyle \frac{q^2{c}^3\left(4-c^2\right)}{64{\left[2\right]}_q{\left[4\right]}_q}}U\left({\sigma }_1,{\sigma }_2,{\sigma }_3\right),\hfill \end{array}$$

(43)

where U is defined in (33), and

$$\begin{array}{cc}\hfill {\sigma }_1& ={\displaystyle \frac{\left(6\mu {\left[4\right]}_q-6{\left[2\right]}_q-5q{\left[2\right]}_q^2\right)q{c}^3}{48{\left[2\right]}_q^2\left(4-c^2\right)}},\hfill \\ \hfill {\sigma }_2& =0,\hfill \\ \hfill {\sigma }_3& =-{\displaystyle \frac{16{\left[2\right]}_q{\left[4\right]}_q-4{\left[3\right]}_q^2+\left(3{\left[3\right]}_q^2-4{\left[2\right]}_q{\left[4\right]}_q\right)c^2}{4{\left[3\right]}_q^{2}c}}.\hfill \end{array}$$

Since

$$3{\left[3\right]}_q^2-4{\left[2\right]}_q{\left[4\right]}_q=-q^4-2q^3+q^2-2q-1<0$$

(44)

for all $q\in (0,1)$, we have

$$16{\left[2\right]}_q{\left[4\right]}_q-4{\left[3\right]}_q^2+\left(3{\left[3\right]}_q^2-4{\left[2\right]}_q{\left[4\right]}_q\right)c^2>16{\left[2\right]}_q{\left[4\right]}_q-4{\left[3\right]}_q^2+4\left(3{\left[3\right]}_q^2-4{\left[2\right]}_q{\left[4\right]}_q\right)=8{\left[3\right]}_q^2>0$$

for $c\in (0,2)$. Thus, ${\sigma }_3<0$. From (44), it is obvious that ${\left[3\right]}_q^2-4{\left[2\right]}_q{\left[4\right]}_q<0$. Hence,

$$1+{\sigma }_3={\displaystyle \frac{\left(2-c\right)\left[2\left({\left[3\right]}_q^2-4{\left[2\right]}_q{\left[4\right]}_q\right)+\left(3{\left[3\right]}_q^2-4{\left[2\right]}_q{\left[4\right]}_q\right)c\right]}{4{\left[3\right]}_q^{2}c}}<0,$$

which means that ${\sigma }_3<-1$.

When $\mu \le {\displaystyle \frac{6{\left[2\right]}_q+5q{\left[2\right]}_q^2}{6{\left[4\right]}_q}}$, ${\sigma }_1\le 0$. It is observed that ${\sigma }_1\le 0$, ${\sigma }_3<0$, and $\left|{\sigma }_2\right|\ge 2\left(1+{\sigma }_3\right)$; thus, an application of Lemma 2 yields

$$U\left({\sigma }_1,{\sigma }_2,{\sigma }_3\right)\le -{\sigma }_1+\left|{\sigma }_2\right|-{\sigma }_3={\displaystyle \frac{{\psi }_1{c}^4+{\psi }_2{c}^2+{\psi }_3}{48{\left[2\right]}_q^2{\left[3\right]}_q^{2}c\left(4-c^2\right)}},$$

(45)

where

$$\begin{array}{cc}\hfill {\psi }_1& =48{\left[2\right]}_q^3{\left[4\right]}_q-36{\left[2\right]}_q^2{\left[3\right]}_q^2+6q{\left[2\right]}_q{\left[3\right]}_q^2+5q^2{\left[2\right]}_q^2{\left[3\right]}_q^2-6\mu q{\left[3\right]}_q^2{\left[4\right]}_q,\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill {\psi }_2& =192{\left[2\right]}_q^2{\left[3\right]}_q^2-384{\left[2\right]}_q^3{\left[4\right]}_q,\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill {\psi }_3& =768{\left[2\right]}_q^3{\left[4\right]}_q-192{\left[2\right]}_q^2{\left[3\right]}_q^2.\hfill \end{array}$$

(48)

Combining (43) and (45), we conclude that

$$\left|{\mathcal{H}}_{\mu }\left(f\right)\right|\le {\displaystyle \frac{q^2}{3072{\left[2\right]}_q^3{\left[3\right]}_q^2{\left[4\right]}_q}}\left({\psi }_1{c}^6+{\psi }_2{c}^4+{\psi }_3{c}^2\right),c\in (0,2).$$

(49)

Let

$$\mathsf{\Phi }\left(t\right)={\displaystyle \frac{q^2}{3072{\left[2\right]}_q^3{\left[3\right]}_q^2{\left[4\right]}_q}}\left({\psi }_1{t}^6+{\psi }_2{t}^4+{\psi }_3{t}^2\right),t\in [0,2],$$

(50)

where ${\psi }_1$, ${\psi }_2$, and ${\psi }_3$ are given, respectively, by (46)–(48). Based on (42), (49), and

$$\mathsf{\Phi }\left(2\right)=-{\displaystyle \frac{q^3\left(6\mu {\left[4\right]}_q-6{\left[2\right]}_q-5q{\left[2\right]}_q^2\right)}{48{\left[2\right]}_q^3{\left[4\right]}_q}},$$

(51)

we obtain

$$\left|{\mathcal{H}}_{\mu }\left(f\right)\right|\le \underset{t\in [0,2]}{max}\left\{\mathsf{\Phi }\left(t\right)\right\},\mu \in \left[0,{\displaystyle \frac{6{\left[2\right]}_q+5q{\left[2\right]}_q^2}{6{\left[4\right]}_q}}\right],$$

(52)

where $\mathsf{\Phi }$ is defined in (50).

In the following, we consider $\mu >{\displaystyle \frac{6{\left[2\right]}_q+5q{\left[2\right]}_q^2}{6{\left[4\right]}_q}}$. In this case, ${\sigma }_1>0$, and ${\sigma }_3<0$. Furthermore, as ${\sigma }_3<-1$, it is known that $-{\displaystyle \frac{4{\sigma }_1{\sigma }_3^3}{1-{\sigma }_3^2}}<0$. Then, we have $\left|{\sigma }_2\right|\ge 2\left(1+{\sigma }_3\right)$ and ${\sigma }_2^2\ge -{\displaystyle \frac{4{\sigma }_1{\sigma }_3^3}{1-{\sigma }_3^2}}$. Applying Lemma 2, it is seen that

$$U\left({\sigma }_1,{\sigma }_2,{\sigma }_3\right)=V\left({\sigma }_1,{\sigma }_2,{\sigma }_3\right),$$

(53)

where V is defined in (34). Noting that $-{\sigma }_3\left(4{\sigma }_1+\left|{\sigma }_2\right|\right)=-4{\sigma }_1{\sigma }_3>0$ and $-{\sigma }_3\left(-4{\sigma }_1+\left|{\sigma }_2\right|\right)=4{\sigma }_1{\sigma }_3<0$, we have

$$V\left({\sigma }_1,{\sigma }_2,{\sigma }_3\right)\le \left({\sigma }_1-{\sigma }_3\right)\sqrt{1-{\displaystyle \frac{{\sigma }_2^2}{4{\sigma }_1{\sigma }_3}}}={\displaystyle \frac{{\xi }_1{c}^4+{\xi }_2{c}^2+{\xi }_3}{48{\left[2\right]}_q^2{\left[3\right]}_q^{2}c\left(4-c^2\right)}},$$

(54)

where

$$\begin{array}{cc}\hfill {\xi }_1& =48{\left[2\right]}_q^3{\left[4\right]}_q-36{\left[2\right]}_q^2{\left[3\right]}_q^2-6q{\left[2\right]}_q{\left[3\right]}_q^2-5q^2{\left[2\right]}_q^2{\left[3\right]}_q^2+6\mu q{\left[3\right]}_q^2{\left[4\right]}_q,\hfill \end{array}$$

(55)

$$\begin{array}{cc}\hfill {\xi }_2& =192{\left[2\right]}_q^2{\left[3\right]}_q^2-384{\left[2\right]}_q^3{\left[4\right]}_q,\hfill \end{array}$$

(56)

$$\begin{array}{cc}\hfill {\xi }_3& =768{\left[2\right]}_q^3{\left[4\right]}_q-192{\left[2\right]}_q^2{\left[3\right]}_q^2.\hfill \end{array}$$

(57)

From (43), (53), and (54), we obtain

$$\left|{\mathcal{H}}_{\mu }\left(f\right)\right|\le {\displaystyle \frac{q^2}{3072{\left[2\right]}_q^3{\left[3\right]}_q^2{\left[4\right]}_q}}\left({\xi }_1{c}^6+{\xi }_2{c}^4+{\xi }_3{c}^2\right),c\in (0,2).$$

(58)

Define

$$\mathsf{\Psi }\left(t\right)={\displaystyle \frac{q^2}{3072{\left[2\right]}_q^3{\left[3\right]}_q^2{\left[4\right]}_q}}\left({\xi }_1{t}^6+{\xi }_2{t}^4+{\xi }_3{t}^2\right),t\in [0,2],$$

(59)

where ${\xi }_1$, ${\xi }_2$, and ${\xi }_3$ are given by (55)–(57). As

$$\mathsf{\Psi }\left(2\right)={\displaystyle \frac{q^3\left(6\mu {\left[4\right]}_q-6{\left[2\right]}_q-5q{\left[2\right]}_q^2\right)}{48{\left[2\right]}_q^3{\left[4\right]}_q}},$$

using (42) and (58), we have

$$\left|{\mathcal{H}}_{\mu }\left(f\right)\right|\le \underset{t\in [0,2]}{max}\left\{\mathsf{\Psi }\left(t\right)\right\},\mu \in \left({\displaystyle \frac{6{\left[2\right]}_q+5q{\left[2\right]}_q^2}{6{\left[4\right]}_q}},+\infty \right),$$

(60)

where $\mathsf{\Psi }$ is defined in (59). Combining (52) and (60), we obtain the inequalities in Theorem 1. The proof is completed. □

Taking $q\to 1^{-}$ in Theorem 1, we obtain the upper bound of ${\mathcal{H}}_{\mu }\left(f\right)$ for $f\in {\mathcal{S}}^{*}\left(\mathrm{sech}\right)$.

Theorem 2.

If $f\in {\mathcal{S}}^{*}\left(\mathrm{sech}\right)$, then

$$\left|{\mathcal{H}}_{\mu }\left(f\right)\right|\le \left\{\begin{array}{cc}{\displaystyle \frac{1}{36864}}\underset{t\in [0,2]}{max}\left\{{\Gamma }_1\left(t\right)\right\},\hfill & if\mu \in \left[0,{\displaystyle \frac{4}{3}}\right],\\ \\ {\displaystyle \frac{1}{36864}}\underset{t\in [0,2]}{max}\left\{{\Gamma }_2\left(t\right)\right\},\hfill & if\mu \in \left({\displaystyle \frac{4}{3}},+\infty \right),\end{array}\right.$$

where ${\Gamma }_1$ and ${\Gamma }_2$ are defined, respectively, by

$$\begin{array}{cc}\hfill {\Gamma }_1\left(t\right)& =\left(22-9\mu \right)t^6-224t^4+736t^2,t\in \left[0,2\right],\hfill \\ \hfill {\Gamma }_2\left(t\right)& =\left(9\mu -2\right)t^6-224t^4+736t^2,t\in \left[0,2\right].\hfill \end{array}$$

Proof. 

Setting $q\to 1^{-}$ in Theorem 1, it is seen that ${\mathsf{\Lambda }}_0\to 528-216\mu$, ${\mathsf{\Lambda }}_1\to 216\mu -48$, ${\mathsf{\Lambda }}_2\to -5376$, and ${\mathsf{\Lambda }}_3\to 17664$. Also, ${\displaystyle \frac{q^2}{3072{\left[2\right]}_q^3{\left[3\right]}_q^2{\left[4\right]}_q}}\to {\displaystyle \frac{1}{884736}}$, and ${\displaystyle \frac{6{\left[2\right]}_q+5q{\left[2\right]}_q^2}{6{\left[4\right]}_q}}\to {\displaystyle \frac{4}{3}}$. Substituting these results, the assertion in Theorem 2 follows. □

By ${\mathcal{H}}_{2,3}\left(f\right)=a_3{a}_5-a_4^2$, taking $\mu =0$ in Theorem 2 yields the upper bound of the second Hankel determinant for $f\in {\mathcal{S}}^{*}\left(\mathrm{sech}\right)$.

Corollary 1.

Let $f\in {\mathcal{S}}^{*}\left(\mathrm{sech}\right)$. Then,

$$\left|{\mathcal{H}}_{2,3}\left(f\right)\right|\le {\displaystyle \frac{10051}{470448}}=0.021364\dots .$$

(61)

The bound is sharp, with the extremal functions $g_1$ given by

$$g_1\left(z\right)=zexp\left({\int }_0^z{\displaystyle \frac{\mathrm{sech}\left(\frac{p_1\left(s\right)-1}{p_1\left(s\right)+1}\right)-1}{s}}ds\right),z\in \mathbb{D},$$

(62)

where

$$p_1\left(z\right)={\displaystyle \frac{1+{\varrho }_{1}z+z^2}{1-z^2}},z\in \mathbb{D}$$

(63)

and ${\varrho }_1={\displaystyle \frac{2\sqrt{759}}{33}}\approx 1.669694$.

Proof. 

From the definition, we know that ${\mathcal{H}}_{2,3}\left(f\right)={\mathcal{H}}_0\left(f\right)$. Applying Theorem 2 yields

$$\left|{\mathcal{H}}_{2,3}\left(f\right)\right|\le \underset{t\in [0,2]}{max}{\displaystyle \frac{1}{36864}}\left(22t^6-224t^4+736t^2\right).$$

Let $r_0\left(t\right)={\displaystyle \frac{1}{36864}}\left(22t^6-224t^4+736t^2\right)$, with $t\in [0,2]$. Since $r_0$ has a maximum value ${\displaystyle \frac{10051}{470448}}$ attained at ${\varrho }_1={\displaystyle \frac{2\sqrt{759}}{33}}$, the inequality (61) in Corollary 1 is thus obtained. Now, we consider the sharpness. Taking the logarithmic derivative on both sides in (62), we obtain

$${\displaystyle \frac{z{g}_1^{\prime }\left(z\right)}{g_1\left(z\right)}}=\mathrm{sech}\left({\displaystyle \frac{p_1\left(z\right)-1}{p_1\left(z\right)+1}}\right),$$

where $p_1$ is defined by (63). As ${\varrho }_1\in [0,2]$, it is known that $p_1\in \mathcal{P}$, and $g_1\in {\mathcal{S}}^{*}\left(\mathrm{sech}\right)$. In view of

$$g_1\left(z\right)=z-{\displaystyle \frac{23}{132}}{z}^3-{\displaystyle \frac{10\sqrt{759}}{3267}}{z}^4+{\displaystyle \frac{1069}{13068}}{z}^5+\dots ,z\in \mathbb{D},$$

we conclude that

$$\left|{\mathcal{H}}_{2,3}\left(g_1\right)\right|={\displaystyle \frac{10051}{470448}}.$$

The proof of Corollary 1 is completed. □

Remark 1

(In [18], Theorem 2.7). It is asserted that the sharp bound of ${\mathcal{H}}_{2,3}\left(f\right)$ for $f\in {\mathcal{S}}^{*}\left(\mathrm{sech}\right)$ is ${\displaystyle \frac{1}{48}}$. Indeed, a minor mistake occurs in their proof.

Since $a_2\equiv 0$ for $f\in {\mathcal{S}}^{*}\left(\mathrm{sech}\right)$, we have ${\mathcal{H}}_{3,1}\left(f\right)=a_3{a}_5-a_4^2-a_3^3$. Choosing $\mu =1$ in Theorem 2 gives the known result on the third Hankel determinant for $f\in {\mathcal{S}}^{*}\left(\mathrm{sech}\right)$.

Corollary 2

([18], Theorem 2.6). Let $f\in {\mathcal{S}}^{*}\left(\mathrm{sech}\right)$. Then,

$$\left|H_{3,1}\left(f\right)\right|\le {\displaystyle \frac{671\sqrt{1342}-12460}{657072}}=0.018446\dots .$$

The inequality is sharp, with the extremal function $g_2$ presented by

$$g_2\left(z\right)=zexp\left({\int }_0^z{\displaystyle \frac{\mathrm{sech}\left(\frac{p_2\left(z\right)-1}{p_2\left(z\right)+1}\right)-1}{s}}ds\right),z\in \mathbb{D},$$

where

$$p_2\left(z\right)={\displaystyle \frac{1+{\varrho }_{2}z+z^2}{1-z^2}},z\in \mathbb{D}$$

and ${\varrho }_2={\displaystyle \frac{2}{39}}\sqrt{2184-39\sqrt{1342}}\approx 1.409371$.

Regarding the Hankel determinant with entry of the inverse coefficients, it is noted that ${\mathcal{H}}_{2,3}\left(f^{-1}\right)={\mathcal{H}}_3\left(f\right)$, and ${\mathcal{H}}_{3,1}\left(f^{-1}\right)={\mathcal{H}}_2\left(f\right)$ for $f\in {\mathcal{S}}^{*}\left(\mathrm{sech}\right)$. Hence, we may obtain the two existing outcomes by assigning $\mu =3$ and $\mu =2$ in Theorem 2, respectively.

Corollary 3

([18], Theorem 3.4). Suppose that $f\in {\mathcal{S}}^{*}\left(\mathrm{sech}\right)$. Then,

$$\left|{\mathcal{H}}_{2,3}\left(f^{-1}\right)\right|\le {\displaystyle \frac{5}{192}}.$$

The extremal function is given by

$$g_3\left(z\right)=zexp\left({\int }_0^z{\displaystyle \frac{\mathrm{sech}\left(s\right)-1}{s}}ds\right),z\in \mathbb{D}.$$

(64)

Corollary 4

([18], Theorem 3.3). Suppose that $f\in {\mathcal{S}}^{*}\left(\mathrm{sech}\right)$. Then,

$$\left|{\mathcal{H}}_{3,1}\left(f^{-1}\right)\right|\le {\displaystyle \frac{77+29\sqrt{58}}{15552}}=0.019152\dots .$$

Remark 2

(In [18], Theorem 3.3). The authors gave the upper bound of ${\mathcal{H}}_{2,3}\left(f^{-1}\right)$ for $f\in {\mathcal{S}}^{*}\left(\mathrm{sech}\right)$ while the extremal function is missing. In fact, the bound is sharp, with the function $g_4$ defined by

$$g_4\left(z\right)=zexp\left({\int }_0^z{\displaystyle \frac{\mathrm{sech}\left(i\frac{p_3\left(z\right)-1}{p_3\left(z\right)+1}\right)-1}{s}}ds\right),z\in \mathbb{D},$$

(65)

where

$$p_3\left(z\right)={\displaystyle \frac{1-z^2}{1+{\varrho }_{3}z+z^2}},z\in \mathbb{D}$$

and ${\varrho }_3=\sqrt{{\displaystyle \frac{14-\sqrt{58}}{3}}}\approx 1.458793$.

Regarding the Hankel determinant with elements of logarithmic coefficients for $f\in {\mathcal{S}}^{*}\left(\mathrm{sech}\right)$, we have ${\mathcal{H}}_{2,2}\left(F_f/2\right)={\displaystyle \frac{1}{4}}{\mathcal{H}}_{{\displaystyle \frac{1}{2}}}\left(f\right)$. Thus, an application of Theorem 2 leads to the new finding on the upper bound of the second Hankel determinant for logarithmic functions.

Corollary 5.

Suppose that $f\in {\mathcal{S}}^{*}\left(\mathrm{sech}\right)$. Then,

$$\left|{\mathcal{H}}_{2,2}\left(F_f/2\right)\right|\le {\displaystyle \frac{3892+103\sqrt{721}}{1360800}}=0.0048924\dots .$$

The result is sharp, with the extremal function $g_5$ presented by

$$g_5\left(z\right)=zexp\left({\int }_0^z{\displaystyle \frac{\mathrm{sech}\left(\frac{p_4\left(z\right)-1}{p_4\left(z\right)+1}\right)-1}{s}}ds\right),z\in \mathbb{D},$$

(66)

where

$$p_4\left(z\right)={\displaystyle \frac{1+{\varrho }_{4}z+z^2}{1-z^2}},z\in \mathbb{D}$$

and

$${\varrho }_4=\sqrt{{\displaystyle \frac{448-8\sqrt{721}}{105}}}\approx 1.490249.$$

(67)

Proof. 

Let $f\in {\mathcal{S}}^{*}\left(\mathrm{sech}\right)$. Taking $\mu ={\displaystyle \frac{1}{2}}$ in Theorem 2, we obtain

$$\left|{\mathcal{H}}_{2,2}\left(F_f/2\right)\right|=\left|{\displaystyle \frac{1}{4}}{\mathcal{H}}_{{\displaystyle \frac{1}{2}}}\left(f\right)\right|\le \underset{t\in [0,2]}{max}{\displaystyle \frac{1}{147456}}\left({\displaystyle \frac{35}{2}}{t}^6-224t^4+736t^2\right).$$

Let $r_1\left(t\right)={\displaystyle \frac{1}{147456}}\left({\displaystyle \frac{35}{2}}{t}^6-224t^4+736t^2\right)$, with $t\in [0,2]$. The only critical point of $r_1$ in $(0,2)$ is ${\varrho }_4$ given in (67) at which $r_1$ attains its maximum value ${\displaystyle \frac{3892+103\sqrt{721}}{1360800}}$.

For the sharpness, it is seen that $g_5$ defined in (66) has the form

$$g_5\left(z\right)=z-{\displaystyle \frac{{\varrho }_4^2}{16}}{z}^3-{\displaystyle \frac{{\varrho }_4\left(4-{\varrho }_4^2\right)}{24}}{z}^4-{\displaystyle \frac{7{\varrho }_4^4-48{\varrho }_4+48}{384}}{z}^5+\dots ,z\in \mathbb{D}$$

and

$$\left|{\mathcal{H}}_{2,2}\left(F_{g_5}/2\right)\right|=\left|-{\displaystyle \frac{1}{147456}}\left({\displaystyle \frac{35}{2}}{\varrho }_4^6-224{\varrho }_4^4+736{\varrho }_4^2\right)\right|={\displaystyle \frac{3892+103\sqrt{721}}{1360800}}.$$

The proof of Corollary 5 is completed. □

In view of ${\mathcal{H}}_{2,2}\left(F_{f^{-1}}/2\right)={\displaystyle \frac{1}{4}}{\mathcal{H}}_{{\displaystyle \frac{5}{2}}}\left(f\right)$ for $f\in {\mathcal{S}}^{*}\left(\mathrm{sech}\right)$, we are able to obtain the exact bound of the Hankel determinant with inverse logarithmic coefficients as input for functions in this group.

Corollary 6.

Suppose that $f\in {\mathcal{S}}^{*}\left(\mathrm{sech}\right)$. Then,

$$\left|{\mathcal{H}}_{2,2}\left(F_{f^{-1}}/2\right)\right|\le {\displaystyle \frac{62020+307\sqrt{307}}{13071456}}=0.005156\dots .$$

The equality is attained by the function $g_6$ given by

$$g_6\left(z\right)=zexp\left({\int }_0^z{\displaystyle \frac{\mathrm{sech}\left(i\frac{p\left(z\right)-1}{p\left(z\right)+1}\right)-1}{s}}ds\right),z\in \mathbb{D},$$

(68)

where

$$p\left(z\right)={\displaystyle \frac{1-z^2}{1+{\varrho }_{5}z+z^2}},z\in \mathbb{D}$$

and

$${\varrho }_5=\sqrt{{\displaystyle \frac{448-8\sqrt{307}}{123}}}\approx 1.581984.$$

(69)

Proof. 

Let $f\in {\mathcal{S}}^{*}\left(\mathrm{sech}\right)$. Using Theorem 2, we obtain

$$\left|{\mathcal{H}}_{2,2}\left(F_{f^{-1}}/2\right)\right|=\left|{\displaystyle \frac{1}{4}}{\mathcal{H}}_{{\displaystyle \frac{5}{2}}}\left(f\right)\right|\le \underset{t\in [0,2]}{max}{\displaystyle \frac{1}{147456}}\left({\displaystyle \frac{41}{2}}{t}^6-224t^4+736t^2\right).$$

Let $r_2\left(t\right)={\displaystyle \frac{1}{147456}}\left({\displaystyle \frac{41}{2}}{t}^6-224t^4+736t^2\right)$, with $t\in [0,2]$. The unique critical point of $r_2$ in $(0,2)$ is ${\varrho }_5$ given in (69) at which $r_2$ achieves its maximum value ${\displaystyle \frac{62020+307\sqrt{307}}{13071456}}$.

For the sharpness, we note that $g_6$ defined in (68) has the expansion of

$$g_6\left(z\right)=z+{\displaystyle \frac{{\varrho }_5^2}{16}}{z}^3+{\displaystyle \frac{{\varrho }_5\left(4-{\varrho }_5^2\right)}{24}}{z}^4+{\displaystyle \frac{11{\varrho }_5^4-48{\varrho }_5^2+48}{384}},z\in \mathbb{D}$$

and

$$\left|{\mathcal{H}}_{2,2}\left(F_{g_6^{-1}}/2\right)\right|=\left|-{\displaystyle \frac{1}{147456}}\left({\displaystyle \frac{41}{2}}{\varrho }_5^6-224{\varrho }_5^4+736{\varrho }_5^2\right)\right|={\displaystyle \frac{62020+307\sqrt{307}}{13071456}}.$$

The proof of Corollary 6 is then completed. □

Now, we aim to determine the bound of ${\mathcal{H}}_{\mu }\left(f\right)$ for $f\in {\mathcal{K}}_q\left(\mathrm{sech}\right)$.

Theorem 3.

Let $f\in {\mathcal{K}}_q\left(\mathrm{sech}\right)$. Then,

$$\left|{\mathcal{H}}_{\mu }\left(f\right)\right|\le \left\{\begin{array}{cc}{\displaystyle \frac{q^2}{3072{\left[2\right]}_q^3{\left[3\right]}_q^3{\left[4\right]}_q^2{\left[5\right]}_q}}\underset{t\in [0,2]}{max}\left\{{\mathsf{\Pi }}_0{t}^6+{\mathsf{\Pi }}_2{t}^4+{\mathsf{\Pi }}_3{t}^2\right\},\hfill & if\mu \in \left[0,{\displaystyle \frac{6{\left[2\right]}_q{\left[3\right]}_q^2+5q{\left[2\right]}_q^2{\left[3\right]}_q^2}{6{\left[4\right]}_q{\left[5\right]}_q}}\right],\\ \\ {\displaystyle \frac{q^2}{3072{\left[2\right]}_q^3{\left[3\right]}_q^3{\left[4\right]}_q^2{\left[5\right]}_q}}\underset{t\in [0,2]}{max}\left\{{\mathsf{\Pi }}_1{t}^6+{\mathsf{\Pi }}_2{t}^4+{\mathsf{\Pi }}_3{t}^2\right\},\hfill & if\mu \in \left({\displaystyle \frac{6{\left[2\right]}_q{\left[3\right]}_q^2+5q{\left[2\right]}_q^2{\left[3\right]}_q^2}{6{\left[4\right]}_q{\left[5\right]}_q}},+\infty \right),\end{array}\right.$$

where

$$\begin{array}{cc}\hfill {\mathsf{\Pi }}_0\left(t\right)& =48{\left[2\right]}_q^3{\left[3\right]}_q{\left[5\right]}_q-36{\left[2\right]}_q^2{\left[3\right]}_q^2{\left[4\right]}_q+6q{\left[2\right]}_q{\left[3\right]}_q^2{\left[4\right]}_q+5q^2{\left[2\right]}_q^2{\left[3\right]}_q^2{\left[4\right]}_q-6\mu q{\left[4\right]}_q^2{\left[5\right]}_q,\hfill \\ \hfill {\mathsf{\Pi }}_1\left(t\right)& =48{\left[2\right]}_q^3{\left[3\right]}_q{\left[5\right]}_q-36{\left[2\right]}_q^2{\left[3\right]}_q^2{\left[4\right]}_q-6q{\left[2\right]}_q{\left[3\right]}_q^2{\left[4\right]}_q-5q^2{\left[2\right]}_q^2{\left[3\right]}_q^2{\left[4\right]}_q+6\mu q{\left[4\right]}_q^2{\left[5\right]}_q,\hfill \\ \hfill {\mathsf{\Pi }}_2\left(t\right)& =192{\left[2\right]}_q^2{\left[3\right]}_q^2{\left[4\right]}_q-384{\left[2\right]}_q^3{\left[3\right]}_q{\left[5\right]}_q,\hfill \\ \hfill {\mathsf{\Pi }}_3\left(t\right)& =768{\left[2\right]}_q^3{\left[3\right]}_q{\left[5\right]}_q-192{\left[2\right]}_q^2{\left[3\right]}_q^2{\left[4\right]}_q.\hfill \end{array}$$

Proof. 

Suppose that $f\in {\mathcal{K}}_q\left(\mathrm{sech}\right)$ and

$$f\left(z\right)=z+b_2{z}^2+b_3{z}^3+b_4{z}^4+b_5{z}^5+\dots ,z\in \mathbb{D}.$$

Based on the relationship between the class ${\mathcal{S}}_q^{*}\left(\mathrm{sech}\right)$ and ${\mathcal{K}}_q\left(\mathrm{sech}\right)$, we know that $g\left(z\right)=z{D}_{q}f\left(z\right)\in {\mathcal{S}}_q^{*}\left(\mathrm{sech}\right)$. Thus, $b_n={\displaystyle \frac{a_n}{{\left[n\right]}_q}}(n\ge 2)$, where $a_n$ are the corresponding coefficients of $g\in {\mathcal{S}}_q^{*}\left(\mathrm{sech}\right)$. From the proof of Theorem 1, we can write

$$\begin{array}{cc}\hfill b_2& =0,\hfill \end{array}$$

(70)

$$\begin{array}{cc}\hfill b_3& =-{\displaystyle \frac{q}{8{\left[2\right]}_q{\left[3\right]}_q}}{d}_1^2,\hfill \end{array}$$

(71)

$$\begin{array}{cc}\hfill b_4& =-{\displaystyle \frac{q}{8{\left[3\right]}_q{\left[4\right]}_q}}\left(2d_1{d}_2-d_1^3\right),\hfill \end{array}$$

(72)

$$\begin{array}{cc}\hfill b_5& ={\displaystyle \frac{q}{384{\left[4\right]}_q{\left[5\right]}_q}}\left[-\left(36-5q^2-{\displaystyle \frac{6q}{{\left[2\right]}_q}}\right)d_1^4+144d_1^2{d}_2-96d_1{d}_3-48d_2^2\right]\hfill \end{array}$$

(73)

for some $p\in \mathcal{P}$, with

$$p\left(z\right)=1+d_{1}z+d_2{z}^2+d_3{z}^3+\dots ,z\in \mathbb{D}.$$

Let $f\in {\mathcal{K}}_q\left(\mathrm{sech}\right)$ and $f_{\theta }\left(z\right)=e^{-i\theta }f\left(e^{i\theta }z\right)$, with $\theta \in \mathbb{R}$. From the definition,

$$D_q{f}_{\theta }\left(z\right)={\displaystyle \frac{f_{\theta }\left(qz\right)-f_{\theta }\left(z\right)}{\left(q-1\right)z}}={\displaystyle \frac{e^{-i\theta }f\left(e^{i\theta }qz\right)-e^{-i\theta }f\left(e^{i\theta }z\right)}{\left(q-1\right)z}}=D_{q}f\left(e^{i\theta }z\right).$$

Setting $u=e^{i\theta }z$, it is noted that $D_q{f}_{\theta }\left(z\right)=D_{q}f\left(u\right)$, and thus, $D_q^2{f}_{\theta }\left(z\right)=e^{i\theta }{D}_q^{2}f\left(u\right)$. Using the basic property of the q-difference operator, we have

$${\displaystyle \frac{z{D}_q\left(z{D}_q{f}_{\theta }\left(z\right)\right)}{z{D}_q{f}_{\theta }\left(z\right)}}=z·{\displaystyle \frac{q{D}_q{f}_{\theta }\left(z\right)+z{D}_q^2{f}_{\theta }\left(qz\right)}{z{D}_q{f}_{\theta }\left(z\right)}}=z·{\displaystyle \frac{q{D}_{q}f\left(u\right)+u{D}_q^{2}f\left(u\right)}{z{D}_{q}f\left(u\right)}}={\displaystyle \frac{u{D}_q\left(u{D}_{q}f\left(u\right)\right)}{u{D}_{q}f\left(u\right)}}.$$

Thus, $f_{\theta }\in {\mathcal{K}}_q\left(\mathrm{sech}\right)$. As the class ${\mathcal{K}}_q\left(\mathrm{sech}\right)$ and the functional ${\mathcal{H}}_{\mu }\left(f\right)$ are rotation-invariant, we may assume that $d_1=d\in [0,2]$. Substituting (71)–(73) into ${\mathcal{H}}_{\mu }\left(f\right)$ defined in (30), we obtain

$${\mathcal{H}}_{\mu }\left(f\right)={\displaystyle \frac{q^2{d}^2}{3072{\left[2\right]}_q^3{\left[3\right]}_q^3{\left[4\right]}_q^2{\left[5\right]}_q}}\left({\nu }_1{d}^4+{\nu }_2{d}^2{d}_2+{\nu }_{3}d{d}_3+{\nu }_4{d}_2^2\right),$$

where

$$\begin{array}{cc}\hfill {\nu }_1& =36{\left[2\right]}_q^2{\left[3\right]}_q^2{\left[4\right]}_q-48{\left[2\right]}_q^3{\left[3\right]}_q{\left[5\right]}_q-6q{\left[2\right]}_q{\left[3\right]}_q^2{\left[4\right]}_q-5q^2{\left[2\right]}_q^2{\left[3\right]}_q^2{\left[4\right]}_q+6\mu q{\left[4\right]}_q^2{\left[5\right]}_q,\hfill \\ \hfill {\nu }_2& =-48{\left[2\right]}_q^2{\left[3\right]}_q\left(3{\left[3\right]}_q{\left[4\right]}_q-4{\left[2\right]}_q{\left[5\right]}_q\right),\hfill \\ \hfill {\nu }_3& =96{\left[2\right]}_q^2{\left[3\right]}_q^2{\left[4\right]}_q,\hfill \\ \hfill {\nu }_4& =48{\left[2\right]}_q^2{\left[3\right]}_q\left({\left[3\right]}_q{\left[4\right]}_q-4{\left[2\right]}_q{\left[5\right]}_q\right).\hfill \end{array}$$

Using (58) and (60) in Lemma 1, we obtain

$${\mathcal{H}}_{\mu }\left(f\right)={\displaystyle \frac{q^2{d}^2}{3072{\left[2\right]}_q^3{\left[3\right]}_q^3{\left[4\right]}_q^2{\left[5\right]}_q}}\left[{\lambda }_1+{\lambda }_{2}x+{\lambda }_3{x}^2+48{\left[2\right]}_q^2{\left[3\right]}_q^2{\left[4\right]}_{q}d\left(4-d^2\right)\left(1-{\left|x\right|}^2\right)\kappa \right]$$

for some $x,\kappa \in \overline{\mathbb{D}}$, with

$$\begin{array}{cc}\hfill {\lambda }_1& =q{\left[4\right]}_q\left(6\mu {\left[4\right]}_q{\left[5\right]}_q-6{\left[2\right]}_q{\left[3\right]}_q^2-5q{\left[2\right]}_q^2{\left[3\right]}_q^2\right)d^4,\hfill \\ \hfill {\lambda }_2& =0,\hfill \\ \hfill {\lambda }_3& =-12{\left[2\right]}_q^2{\left[3\right]}_q\left(4-d^2\right)\left[16{\left[2\right]}_q{\left[5\right]}_q-4{\left[3\right]}_q{\left[4\right]}_q-\left(4{\left[2\right]}_q{\left[5\right]}_q-3{\left[3\right]}_q{\left[4\right]}_q\right)d^2\right].\hfill \end{array}$$

When $d=0$, ${\mathcal{H}}_{\mu }\left(f\right)=0$. When $d=2$,

$${\mathcal{H}}_{\mu }\left(f\right)={\displaystyle \frac{\left(6\mu {\left[4\right]}_q{\left[5\right]}_q-6{\left[2\right]}_q{\left[3\right]}_q^2-5q{\left[2\right]}_q^2{\left[3\right]}_q^2\right)q^3}{48{\left[2\right]}_q^3{\left[3\right]}_q^3{\left[4\right]}_q{\left[5\right]}_q}},d=2.$$

(74)

Consider $d\in (0,2)$. From $\left|\kappa \right|\le 1$, we obtain

$$\begin{array}{cc}\hfill \left|{\mathcal{H}}_{\mu }\left(f\right)\right|& \le {\displaystyle \frac{q^2{d}^3\left(4-d^2\right)}{64{\left[2\right]}_q{\left[3\right]}_q{\left[4\right]}_q{\left[5\right]}_q}}\left(\left|{\varsigma }_1+{\varsigma }_{2}x+{\varsigma }_3{x}^2\right|+1-{\left|x\right|}^2\right)\hfill \\ \hfill & :={\displaystyle \frac{q^2{d}^3\left(4-d^2\right)}{64{\left[2\right]}_q{\left[3\right]}_q{\left[4\right]}_q{\left[5\right]}_q}}U\left({\varsigma }_1,{\varsigma }_2,{\varsigma }_3\right),\hfill \end{array}$$

where U is defined in (33), and

$$\begin{array}{cc}\hfill {\varsigma }_1& ={\displaystyle \frac{q\left(6\mu {\left[4\right]}_q{\left[5\right]}_q-6{\left[2\right]}_q{\left[3\right]}_q^2-5q{\left[2\right]}_q^2{\left[3\right]}_q^2\right)d^3}{48{\left[2\right]}_q^2{\left[3\right]}_q^2\left(4-d^2\right)}},\hfill \end{array}$$

(75)

$$\begin{array}{cc}\hfill {\varsigma }_2& =0,\hfill \end{array}$$

(76)

$$\begin{array}{cc}\hfill {\varsigma }_3& ={\displaystyle \frac{4{\left[3\right]}_q{\left[4\right]}_q-16{\left[2\right]}_q{\left[5\right]}_q+\left(4{\left[2\right]}_q{\left[5\right]}_q-3{\left[3\right]}_q{\left[4\right]}_q\right)d^2}{4{\left[3\right]}_q{\left[4\right]}_{q}d}}.\hfill \end{array}$$

(77)

It is easily seen that

$$4{\left[2\right]}_q{\left[5\right]}_q-3{\left[3\right]}_q{\left[4\right]}_q=1+2q-q^2-q^3+2q^4+q^5>0,q\in (0,1),$$

(78)

which leads to

$$4{\left[3\right]}_q{\left[4\right]}_q-16{\left[2\right]}_q{\left[5\right]}_q+\left(4{\left[2\right]}_q{\left[5\right]}_q-3{\left[3\right]}_q{\left[4\right]}_q\right)d^2<4{\left[3\right]}_q{\left[4\right]}_q-16{\left[2\right]}_q{\left[5\right]}_q+4\left(4{\left[2\right]}_q{\left[5\right]}_q-3{\left[3\right]}_q{\left[4\right]}_q\right)<0.$$

From (77), we have ${\varsigma }_3<0$. Indeed, using (78), it yields

$$2{\left[3\right]}_q{\left[4\right]}_q-8{\left[2\right]}_q{\left[5\right]}_q+\left(3{\left[3\right]}_q{\left[4\right]}_q-4{\left[2\right]}_q{\left[5\right]}_q\right)d<2{\left[3\right]}_q{\left[4\right]}_q-8{\left[2\right]}_q{\left[5\right]}_q<0,$$

which implies that

$$1+{\varsigma }_3={\displaystyle \frac{\left(2-d\right)\left[2{\left[3\right]}_q{\left[4\right]}_q-8{\left[2\right]}_q{\left[5\right]}_q+\left(3{\left[3\right]}_q{\left[4\right]}_q-4{\left[2\right]}_q{\left[5\right]}_q\right)d\right]}{4{\left[3\right]}_q{\left[4\right]}_{q}d}}<0,$$

i.e., ${\varsigma }_3<-1$.

When $\mu \le {\displaystyle \frac{6{\left[2\right]}_q{\left[3\right]}_q^2+5q{\left[2\right]}_q^2{\left[3\right]}_q^2}{6{\left[4\right]}_q{\left[5\right]}_q}}$, clearly, ${\varsigma }_1\le 0$. Since $\left|{\varsigma }_2\right|\ge 2\left(1+{\varsigma }_3\right)$, using Lemma 2, we obtain

$$\begin{array}{cc}\hfill U\left({\varsigma }_1,{\varsigma }_2,{\varsigma }_3\right)& \le -{\varsigma }_1+\left|{\varsigma }_2\right|-{\varsigma }_3={\displaystyle \frac{{\vartheta }_1{d}^4+{\vartheta }_2{d}^2+{\vartheta }_3}{48{\left[2\right]}_q^2{\left[3\right]}_q^2{\left[4\right]}_{q}d\left(4-d^2\right)}},\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill {\vartheta }_1& =48{\left[2\right]}_q^3{\left[3\right]}_q{\left[5\right]}_q-36{\left[2\right]}_q^2{\left[3\right]}_q^2{\left[4\right]}_q+6q{\left[2\right]}_q{\left[3\right]}_q^2{\left[4\right]}_q+5q^2{\left[2\right]}_q^2{\left[3\right]}_q^2{\left[4\right]}_q-6\mu q{\left[4\right]}_q^2{\left[5\right]}_q,\hfill \\ \hfill {\vartheta }_2& =192{\left[2\right]}_q^2{\left[3\right]}_q^2{\left[4\right]}_q-384{\left[2\right]}_q^3{\left[3\right]}_q{\left[5\right]}_q,\hfill \\ \hfill {\vartheta }_3& =768{\left[2\right]}_q^3{\left[3\right]}_q{\left[5\right]}_q-192{\left[2\right]}_q^2{\left[3\right]}_q^2{\left[4\right]}_q.\hfill \end{array}$$

Therefore,

$$\left|{\mathcal{H}}_{\mu }\left(f\right)\right|\le {\displaystyle \frac{q^2}{3072{\left[2\right]}_q^3{\left[3\right]}_q^3{\left[4\right]}_q^2{\left[5\right]}_q}}\left({\vartheta }_1{d}^6+{\vartheta }_2{d}^4+{\vartheta }_3{d}^2\right),d\in \left(0,2\right).$$

(79)

Define

$${\rm Y}\left(t\right)={\displaystyle \frac{q^2}{3072{\left[2\right]}_q^3{\left[3\right]}_q^3{\left[4\right]}_q^2{\left[5\right]}_q}}\left({\vartheta }_1{t}^6+{\vartheta }_2{t}^4+{\vartheta }_3{t}^2\right),t\in [0,2].$$

Clearly,

$${\rm Y}\left(2\right)=-{\displaystyle \frac{\left(6\mu {\left[4\right]}_q{\left[5\right]}_q-6{\left[2\right]}_q{\left[3\right]}_q^2-5q{\left[2\right]}_q^2{\left[3\right]}_q^2\right)q^3}{48{\left[2\right]}_q^3{\left[3\right]}_q^3{\left[4\right]}_q{\left[5\right]}_q}}.$$

Combining (74) and (79), we conclude that

$$\left|{\mathcal{H}}_{\mu }\left(f\right)\right|\le \underset{t\in [0,2]}{max}\left\{{\rm Y}\left(t\right)\right\},\mu \in \left[0,{\displaystyle \frac{6{\left[2\right]}_q{\left[3\right]}_q^2+5q{\left[2\right]}_q^2{\left[3\right]}_q^2}{6{\left[4\right]}_q{\left[5\right]}_q}}\right].$$

(80)

Now, we consider $\mu >{\displaystyle \frac{6{\left[2\right]}_q{\left[3\right]}_q^2+5q{\left[2\right]}_q^2{\left[3\right]}_q^2}{6{\left[4\right]}_q{\left[5\right]}_q}}$. Then, ${\varsigma }_1>0$, and ${\varsigma }_3<0$. As ${\varsigma }_3<-1$, we see that $1-{\varsigma }_3^2<0$, and thus, ${\displaystyle \frac{-4{\varsigma }_1{\varsigma }_3^3}{1-{\varsigma }_3^2}}<0.$ Combining the fact that $\left|{\varsigma }_2\right|\ge 2\left(1+{\varsigma }_3\right)$ and ${\varsigma }_2^2\ge {\displaystyle \frac{-4{\varsigma }_1{\varsigma }_3^3}{1-{\varsigma }_3^2}}$, an application of Lemma 2 leads to $U\left({\varsigma }_1,{\varsigma }_2,{\varsigma }_3\right)\le V\left({\varsigma }_1,{\varsigma }_2,{\varsigma }_3\right)$, where V is defined in (34). Obviously, $-{\varsigma }_3\left(4{\varsigma }_1+\left|{\varsigma }_2\right|\right)>{\varsigma }_1\left|{\varsigma }_2\right|$, and $-{\varsigma }_3\left(-4{\varsigma }_1+\left|{\varsigma }_2\right|\right)<{\varsigma }_1\left|{\varsigma }_2\right|$ because ${\varsigma }_1>0$, ${\varsigma }_2=0$, and ${\varsigma }_3<0$. Therefore, we may find that

$$V\left({\varsigma }_1,{\varsigma }_2,{\varsigma }_3\right)\le \left({\varsigma }_1-{\varsigma }_3\right)\sqrt{1-{\displaystyle \frac{{\varsigma }_2^2}{4{\varsigma }_1{\varsigma }_3}}}={\displaystyle \frac{{\iota }_1{d}^4+{\iota }_2{d}^2+{\iota }_3}{48{\left[2\right]}_q^2{]\left[3\right]}_q^2{\left[4\right]}_{q}d\left(4-d^2\right)}},$$

where

$$\begin{array}{cc}\hfill {\iota }_1& =48{\left[2\right]}_q^3{\left[3\right]}_q{\left[5\right]}_q-36{\left[2\right]}_q^2{\left[3\right]}_q^2{\left[4\right]}_q-6q{\left[2\right]}_q{\left[3\right]}_q^2{\left[4\right]}_q-5q^2{\left[2\right]}_q^2{\left[3\right]}_q^2{\left[4\right]}_q+6\mu q{\left[4\right]}_q^2{\left[5\right]}_q,\hfill \\ \hfill {\iota }_2& =192{\left[2\right]}_q^2{\left[3\right]}_q^2{\left[4\right]}_q-384{\left[2\right]}_q^3{\left[3\right]}_q{\left[5\right]}_q,\hfill \\ \hfill {\iota }_3& =768{\left[2\right]}_q^3{\left[3\right]}_q{\left[5\right]}_q-192{\left[2\right]}_q^2{\left[3\right]}_q^2{\left[4\right]}_q.\hfill \end{array}$$

It follows that

$$\left|{\mathcal{H}}_{\mu }\left(f\right)\right|\le {\displaystyle \frac{q^2}{3072{\left[2\right]}_q^3{\left[3\right]}_q^3{\left[4\right]}_q^2{\left[5\right]}_q}}\left({\iota }_1{d}^6+{\iota }_2{d}^4+{\iota }_3{d}^2\right),d\in \left(0,2\right).$$

(81)

Define

$$\Xi \left(t\right)={\displaystyle \frac{q^2}{3072{\left[2\right]}_q^3{\left[3\right]}_q^3{\left[4\right]}_q^2{\left[5\right]}_q}}\left({\iota }_1{d}^6+{\iota }_2{d}^4+{\iota }_3{d}^2\right),t\in [0,2].$$

By $\Xi \left(2\right)={\displaystyle \frac{\left(6\mu {\left[4\right]}_q{\left[5\right]}_q-6{\left[2\right]}_q{\left[3\right]}_q^2-5q{\left[2\right]}_q^2{\left[3\right]}_q^2\right)q^3}{48{\left[2\right]}_q^3{\left[3\right]}_q^3{\left[4\right]}_q{\left[5\right]}_q}}$, along with (74) and (81), we obtain

$$\left|{\mathcal{H}}_{\mu }\left(f\right)\right|\le \underset{t\in [0,2]}{max}\left\{\Xi \left(t\right)\right\},\mu \in \left({\displaystyle \frac{6{\left[2\right]}_q{\left[3\right]}_q^2+5q{\left[2\right]}_q^2{\left[3\right]}_q^2}{6{\left[4\right]}_q{\left[5\right]}_q}},+\infty \right].$$

(82)

Combining (80) and (82), the assertion in Theorem 3 follows. □

Let $q\to 1^{-}$; then, we obtain the estimation on the functional ${\mathcal{H}}_{\mu }\left(f\right)$ for functions in the class $\mathcal{K}\left(\mathrm{sech}\right)$, which is a subfamily of convex functions.

Theorem 4.

Let $f\in \mathcal{K}\left(\mathrm{sech}\right)$. Then,

$$\left|{\mathcal{H}}_{\mu }\left(f\right)\right|\le \left\{\begin{array}{cc}{\displaystyle \frac{1}{552960}}\underset{t\in [0,2]}{max}\left\{{\Gamma }_3\left(t\right)\right\},\hfill & if\mu \in \left[0,{\displaystyle \frac{12}{5}}\right],\\ \\ {\displaystyle \frac{1}{552960}}\underset{t\in [0,2]}{max}\left\{{\Gamma }_4\left(t\right)\right\},\hfill & if\mu \in \left({\displaystyle \frac{12}{5}},+\infty \right),\end{array}\right.$$

where ${\Gamma }_3$ and ${\Gamma }_4$ are defined, respectively, by

$$\begin{array}{cc}\hfill {\Gamma }_3\left(t\right)& =\left(18-5\mu \right)t^6-192t^4+672t^2,t\in \left[0,2\right],\hfill \\ \hfill {\Gamma }_4\left(t\right)& =\left(5\mu -6\right)t^6-192t^4+672t^2,t\in \left[0,2\right].\hfill \end{array}$$

Proof. 

Let $q\to 1^{-}$ in Theorem 3. Then, ${\mathsf{\Pi }}_0\to 1728-480\mu$, ${\mathsf{\Pi }}_1\to -576+480\mu$, ${\mathsf{\Pi }}_2\to -18432$, and ${\mathsf{\Pi }}_3\to 64512$. Also, ${\displaystyle \frac{q^2}{3072{\left[2\right]}_q^3{\left[3\right]}_q^3{\left[4\right]}_q^2{\left[5\right]}_q}}\to {\displaystyle \frac{1}{53084160}}$, and ${\displaystyle \frac{6{\left[2\right]}_q{\left[3\right]}_q^2+5q{\left[2\right]}_q^2{\left[3\right]}_q^2}{6{\left[4\right]}_q{\left[5\right]}_q}}\to {\displaystyle \frac{12}{5}}$. Substituting these results, the assertion in Theorem 4 follows. □

Taking $\mu =0,1,3,2,{\displaystyle \frac{1}{2}},{\displaystyle \frac{5}{2}}$ in Theorem 4, we obtain the sharp bounds of the Hankel determinant with the original coefficients, inverse coefficients, logarithmic coefficients, and inverse logarithmic coefficients, respectively, for functions in the class $\mathcal{K}\left(\mathrm{sech}\right)$.

Corollary 7.

Let $f\in \mathcal{K}\left(\mathrm{sech}\right)$. Then,

$$\left|{\mathcal{H}}_{2,3}\left(f\right)\right|\le {\displaystyle \frac{49}{34992}}=0.001400\dots .$$

(83)

The estimate is sharp with the extremal function $h_1$ expressed by

$$h_1\left(z\right)={\int }_0^{z}exp\left({\int }_0^u{\displaystyle \frac{\mathrm{sech}\left(\frac{{\widehat{p}}_1\left(u\right)-1}{{\widehat{p}}_1\left(u\right)+1}\right)-1}{u}}du\right)ds,z\in \mathbb{D},$$

(84)

where

$${\widehat{p}}_1\left(z\right)={\displaystyle \frac{1+\frac{2\sqrt{7}}{3}z+z^2}{1-z^2}},z\in \mathbb{D}.$$

Proof. 

Suppose that $f\in \mathcal{K}\left(\mathrm{sech}\right)$. From Theorem 4, we know that

$$\left|{\mathcal{H}}_{2,3}\left(f\right)\right|=\left|{\mathcal{H}}_0\left(f\right)\right|\le \underset{t\in [0,2]}{max}{\displaystyle \frac{1}{552960}}\left(18t^6-192t^4+672t^2\right).$$

Let $r_3\left(t\right)={\displaystyle \frac{1}{552960}}\left(18t^6-192t^4+672t^2\right)$, with $t\in [0,2]$. It is seen that $r_3$ has a maximum value ${\displaystyle \frac{49}{34992}}$ achieved at $\widetilde{t_0}={\displaystyle \frac{2\sqrt{7}}{3}}$. The inequality (83) in Corollary 7 is thus obtained.

For the sharpness, we observe that the function $h_1$ defined in (84), satisfying $z{h}_1^{\prime }\left(z\right)\in {\mathcal{S}}^{*}\left(\mathrm{sech}\right)$, which implies that $h_1\in \mathcal{K}\left(\mathrm{sech}\right)$ according to the Alexander relationship. We note that

$$h_1\left(z\right)=z-{\displaystyle \frac{7}{108}}{z}^3-{\displaystyle \frac{\sqrt{7}}{162}}{z}^4+{\displaystyle \frac{17}{972}}{z}^5+\dots ,z\in \mathbb{D}$$

and $\left|{\mathcal{H}}_{2,3}\left(h_1\right)\right|={\displaystyle \frac{49}{34992}}$. This completes the proof of Corollary 7. □

Corollary 8.

Let $f\in \mathcal{K}\left(\mathrm{sech}\right)$. Then,

$$\left|H_{3,1}\left(f\right)\right|\le {\displaystyle \frac{136+37\sqrt{74}}{365040}}=0.001244\dots .$$

(85)

The result is sharp, with the extremal function $h_2$ presented by

$$h_2\left(z\right)={\int }_0^{z}exp\left({\int }_0^u{\displaystyle \frac{\mathrm{sech}\left(\frac{{\widehat{p}}_2\left(u\right)-1}{{\widehat{p}}_2\left(u\right)+1}\right)-1}{u}}du\right)ds,z\in \mathbb{D},$$

(86)

where

$${\widehat{p}}_2\left(z\right)={\displaystyle \frac{1+{\chi }_{1}z+z^2}{1-z^2}},z\in \mathbb{D}$$

and

$${\chi }_1=\sqrt{{\displaystyle \frac{64-4\sqrt{74}}{13}}}\approx 1.508710.$$

(87)

Proof. 

Assume that $f\in \mathcal{K}\left(\mathrm{sech}\right)$. Utilizing Theorem 4, we obtain

$$\left|H_{3,1}\left(f\right)\right|=\left|H_1\left(f\right)\right|\le \underset{t\in [0,2]}{max}{\displaystyle \frac{1}{552960}}\left(13t^6-192t^4+62t^2\right).$$

Define $r_4\left(t\right)={\displaystyle \frac{1}{552960}}\left(13t^6-192t^4+62t^2\right)$ with $t\in [0,2]$. It is found that $r_4$ has a maximum value ${\displaystyle \frac{136+37\sqrt{74}}{365040}}$ attained at ${\chi }_1$, which is given in (87). The inequality (85) in Corollary 8 is thus obtained.

For the extremal function, clearly, $h_2$ defined in (86) belongs to the class $\mathcal{K}\left(\mathrm{sech}\right)$ by ${\widehat{p}}_2\in \mathcal{P}$. As

$$h_2\left(z\right)=z-{\displaystyle \frac{{\chi }_1^2}{48}}{z}^3-{\displaystyle \frac{{\chi }_1\left(4-{\chi }_1^2\right)}{96}}{z}^4-{\displaystyle \frac{7{\chi }_1^4-48{\chi }_1^2-48}{1920}}{z}^5+\dots ,z\in \mathbb{D},$$

we have

$$\left|H_{3,1}\left(h_2\right)\right|=\left|-{\displaystyle \frac{1}{552960}}\left(13{\chi }_1^6-192{\chi }_1^4+672{\chi }_1^2\right)\right|={\displaystyle \frac{136+37\sqrt{74}}{365040}}.$$

The proof of Corollary 8 is thus completed. □

Corollary 9.

Let $f\in \mathcal{K}\left(\mathrm{sech}\right)$. Then,

$$\left|{\mathcal{H}}_{2,3}\left(f^{-1}\right)\right|\le {\displaystyle \frac{65\sqrt{130}-536}{174960}}=0.001172\dots .$$

The equality is attained by the function $h_3$ given by

$$h_3\left(z\right)={\int }_0^{z}exp\left({\int }_0^u{\displaystyle \frac{\mathrm{sech}\left(i\frac{{\widehat{p}}_3\left(u\right)-1}{{\widehat{p}}_3\left(u\right)+1}\right)-1}{u}}du\right)ds,z\in \mathbb{D},$$

(88)

where

$${\widehat{p}}_3\left(z\right)={\displaystyle \frac{1-z^2}{1+{\chi }_{2}z+z^2}},z\in \mathbb{D}$$

and

$${\chi }_2={\displaystyle \frac{2\sqrt{16-\sqrt{130}}}{3}}\approx 1.429568.$$

(89)

Proof. 

Let $f\in \mathcal{K}\left(\mathrm{sech}\right)$. It is seen that

$$\left|{\mathcal{H}}_{2,3}\left(f^{-1}\right)\right|=\left|{\mathcal{H}}_3\left(f\right)\right|\le \underset{t\in [0,2]}{max}{\displaystyle \frac{1}{552960}}\left(9t^6-192t^4+672t^2\right).$$

Setting $r_5\left(t\right)={\displaystyle \frac{1}{552960}}\left(9t^6-192t^4+672t^2\right)$, with $t\in [0,2]$, it is calculated that $r_5$ has a maximum value ${\displaystyle \frac{65\sqrt{130}-536}{174960}}$ achieved at ${\chi }_2$, which is given in (89).

For the sharpness, we observe that $h_3$ presented in (88) belongs to the class $\mathcal{K}\left(\mathrm{sech}\right)$. In view of

$$h_3\left(z\right)=z+{\displaystyle \frac{{\chi }_2^2}{48}}{z}^3+{\displaystyle \frac{{\chi }_2\left(4-{\chi }_2^2\right)}{96}}{z}^4+{\displaystyle \frac{11{\chi }_2^4-48{\chi }_2^2+48}{1920}}{z}^5+\dots ,z\in \mathbb{D}$$

and

$$\left|H_{2,3}\left(h_3^{-1}\right)\right|=\left|-{\displaystyle \frac{1}{184320}}\left(3{\chi }_2^6-64{\chi }_1^4+224{\chi }_1^2\right)\right|={\displaystyle \frac{65\sqrt{130}-536}{174960}},$$

we complete the proof of Corollary 9. □

Corollary 10.

Suppose that $f\in \mathcal{K}\left(\mathrm{sech}\right)$. Then,

$$\left|{\mathcal{H}}_{3,1}\left(f^{-1}\right)\right|\le {\displaystyle \frac{1}{864}}=0.001157\dots .$$

The equality holds for the function $h_4$ defined as

$$h_4\left(z\right)={\int }_0^{z}exp\left({\int }_0^u{\displaystyle \frac{\mathrm{sech}\left(\frac{{\widehat{p}}_4\left(u\right)-1}{{\widehat{p}}_4\left(u\right)+1}\right)-1}{u}}du\right)ds,z\in \mathbb{D}$$

(90)

with

$${\widehat{p}}_4\left(z\right)={\displaystyle \frac{1+\sqrt{2}z+z^2}{1-z^2}},z\in \mathbb{D}.$$

Proof. 

Applying Theorem 4, we see that

$$\left|{\mathcal{H}}_{3,1}\left(f^{-1}\right)\right|=\left|{\mathcal{H}}_2\left(f\right)\right|\le \underset{t\in [0,2]}{max}{\displaystyle \frac{1}{552960}}\left(8t^6-192t^4+672t^2\right).$$

Let $r_6\left(t\right)={\displaystyle \frac{1}{552960}}\left(8t^6-192t^4+672t^2\right)$ with $t\in [0,2]$. The only critical point of $r_6$ in $(0,2)$ is $\sqrt{2}$, and $r_6\left(t\right)\le r_6\left(\sqrt{2}\right)={\displaystyle \frac{1}{864}}$ for all $t\in [0,2]$.

For the equality, it is easy to know that $h_4$ given in (90) belongs to the class $\mathcal{K}\left(\mathrm{sech}\right)$. Since

$$h_4\left(z\right)=z-{\displaystyle \frac{1}{24}}{z}^3-{\displaystyle \frac{\sqrt{2}}{48}}{z}^4+{\displaystyle \frac{1}{96}}{z}^5+\dots ,z\in \mathbb{D}$$

and

$$\left|H_{3,1}\left(h_4^{-1}\right)\right|={\displaystyle \frac{1}{864}},$$

we obtain the desired result in Corollary 10. □

Corollary 11.

Suppose that $f\in \mathcal{K}\left(\mathrm{sech}\right)$. Then,

$$\left|{\mathcal{H}}_{2,2}\left(F_f/2\right)\right|\le {\displaystyle \frac{1112+39\sqrt{39}}{4151520}}=0.000326\dots .$$

(91)

The result is sharp, with the extremal function $h_5$ presented by

$$h_5\left(z\right)={\int }_0^{z}exp\left({\int }_0^u{\displaystyle \frac{\mathrm{sech}\left(\frac{{\widehat{p}}_5\left(u\right)-1}{{\widehat{p}}_5\left(u\right)+1}\right)-1}{u}}du\right)ds,z\in \mathbb{D},$$

(92)

where

$${\widehat{p}}_5\left(z\right)={\displaystyle \frac{1+{\chi }_{3}z+z^2}{1-z^2}},z\in \mathbb{D}$$

and

$${\chi }_3=\sqrt{{\displaystyle \frac{128-8\sqrt{39}}{31}}}\approx 1.586638.$$

(93)

Proof. 

Utilizing Theorem 4, we have

$$\left|{\mathcal{H}}_{2,2}\left(F_f/2\right)\right|=\left|{\displaystyle \frac{1}{4}}{\mathcal{H}}_{{\displaystyle \frac{1}{2}}}\left(f\right)\right|\le \underset{t\in [0,2]}{max}{\displaystyle \frac{1}{2211840}}\left({\displaystyle \frac{31}{2}}{t}^6-192t^4+672t^2\right).$$

Define $r_7\left(t\right)={\displaystyle \frac{1}{2211840}}\left({\displaystyle \frac{31}{2}}{t}^6-192t^4+672t^2\right)$, with $t\in [0,2]$. We note that ${\chi }_3$ given in (93) is the unique critical point of $r_7$ in $(0,2)$, and $r_7\left(t\right)\le r_7\left({\chi }_3\right)={\displaystyle \frac{1112+39\sqrt{39}}{4151520}}$ for all $t\in [0,2]$. This yields the inequality (91) in Corollary 11.

To show the sharpness, we note that $h_5$ defined in (92) belongs to the class $\mathcal{K}\left(\mathrm{sech}\right)$. As

$$h_5\left(z\right)=z-{\displaystyle \frac{{\chi }_3^2}{48}}{z}^3-{\displaystyle \frac{{\chi }_3\left(4-{\chi }_3^2\right)}{96}}{z}^4-{\displaystyle \frac{7{\chi }_3^4-48{\chi }_3^2+48}{1920}}{z}^5+\dots ,z\in \mathbb{D}$$

and

$$\left|{\mathcal{H}}_{2,2}\left(F_f/2\right)\right|={\displaystyle \frac{1}{2211840}}\left({\displaystyle \frac{31}{2}}{\chi }_3^6-192{\chi }_3^4+672{\chi }_3^2\right)={\displaystyle \frac{1112+39\sqrt{39}}{4151520}},$$

we complete the proof of Corollary 11. □

Corollary 12.

Suppose that $f\in \mathcal{K}\left(\mathrm{sech}\right)$. Then,

$$\left|{\mathcal{H}}_{2,2}\left(F_{f^{-1}}/2\right)\right|\le {\displaystyle \frac{165\sqrt{165}-1912}{730080}}\approx 0.000284\dots .$$

(94)

The equality holds by function $h_6$ taking

$$h_6\left(z\right)={\int }_0^{z}exp\left({\int }_0^u{\displaystyle \frac{\mathrm{sech}\left(i\frac{{\widehat{p}}_6\left(u\right)-1}{{\widehat{p}}_6\left(u\right)+1}\right)-1}{u}}du\right)ds,z\in \mathbb{D},$$

(95)

where

$${\widehat{p}}_6\left(z\right)={\displaystyle \frac{1-z^2}{1+{\chi }_{4}z+z^2}},z\in \mathbb{D}$$

and

$${\chi }_4=\sqrt{{\displaystyle \frac{128-8\sqrt{165}}{13}}}\approx 1.393340.$$

(96)

Proof. 

From Theorem 4, we obtain

$$\left|{\mathcal{H}}_{2,2}\left(F_{f^{-1}}/2\right)\right|=\left|{\displaystyle \frac{1}{4}}{\mathcal{H}}_{{\displaystyle \frac{5}{2}}}\left(f\right)\right|\le \underset{t\in [0,2]}{max}{\displaystyle \frac{1}{2211840}}\left({\displaystyle \frac{13}{2}}{t}^6-192t^4+672t^2\right)={\displaystyle \frac{165\sqrt{165}-1912}{730080}}.$$

It is easy to check that $h_6$ defined in (95) belongs to the class $\mathcal{K}\left(\mathrm{sech}\right)$. Let ${\chi }_4$ be given in (96). As

$$h_6\left(z\right)=z+{\displaystyle \frac{{\chi }_4^2}{48}}{z}^3+{\displaystyle \frac{{\chi }_4\left(4-{\chi }_4^2\right)}{96}}{z}^4+{\displaystyle \frac{11{\chi }_4^4-48{\chi }_4^2+48}{1920}}{z}^5+\dots ,z\in \mathbb{D}$$

and

$$\left|{\mathcal{H}}_{2,2}\left(F_{f^{-1}}/2\right)\right|={\displaystyle \frac{1}{2211840}}\left({\displaystyle \frac{13}{2}}{\chi }_4^6-192{\chi }_4^4+672{\chi }_4^2\right)={\displaystyle \frac{165\sqrt{165}-1912}{730080}},$$

we know the equality in (94) of Corollary 12 holds. □

4. Conclusions

In the study of q-starlike and q-convex functions, we recall that the Fekete–Szegö problem has attracted a great deal of attention; see [47,48,49,50]. Its analytic representation is $a_3-\mu a_2^2$, where $a_2$ and $a_3$ are the initial coefficients of the considered functions, and $\mu$ is a constant. In the present paper, we define a new functional in the form of $a_3{a}_5-a_4^2-\mu a_3^3$, where $\mu \ge 0$. When $a_2=0$, it is found that some of the second and third Hankel determinants with different entries all take this form. Using this functional, we are able to give a unified expression of the desired coefficient problems. As an application, we introduce two classes q-starlike and q-convex functions subordinate to secant hyperbolic functions and calculate the sharp bounds on this functional. By $q\to 1^{-}$, we are able to obtain the bounds on this functional for functions in the families of starlike and convex functions. By taking $\mu =0,1,3,2,{\displaystyle \frac{1}{2}},{\displaystyle \frac{5}{2}}$, we obtain some known results and also new findings on the exact bounds of the Hankel determinant.

Although a significant amount of valuable work on q-analogue analytic functions has been done and the output is abundant, some important issues need to be addressed. An example includes what conditions guarantee functions in the q-analogue classes to be univalent. As $q\to 0$, the performances of the q-classes of analytic functions can be very complex.