Optimizing Optical Fiber Communications: Bifurcation Analysis and Soliton Dynamics in the Quintic Kundu–Eckhaus Model
Abstract
1. Introduction
2. Governing Model
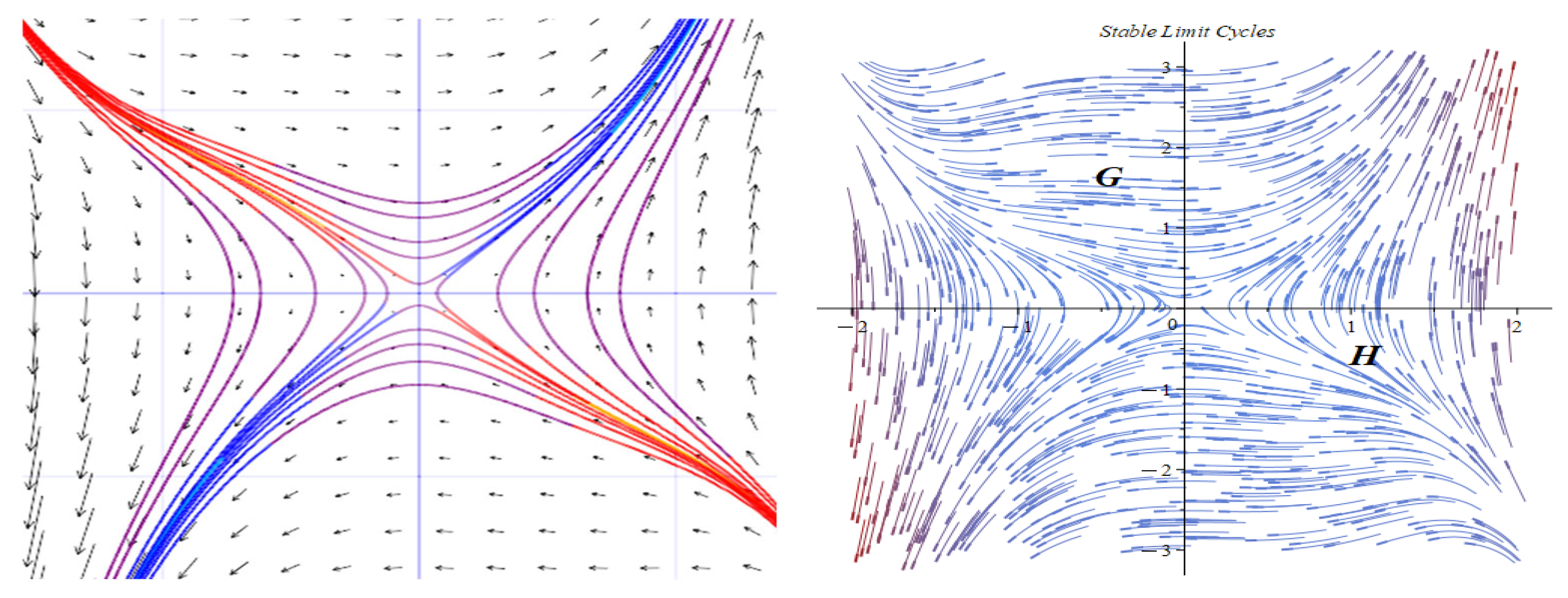
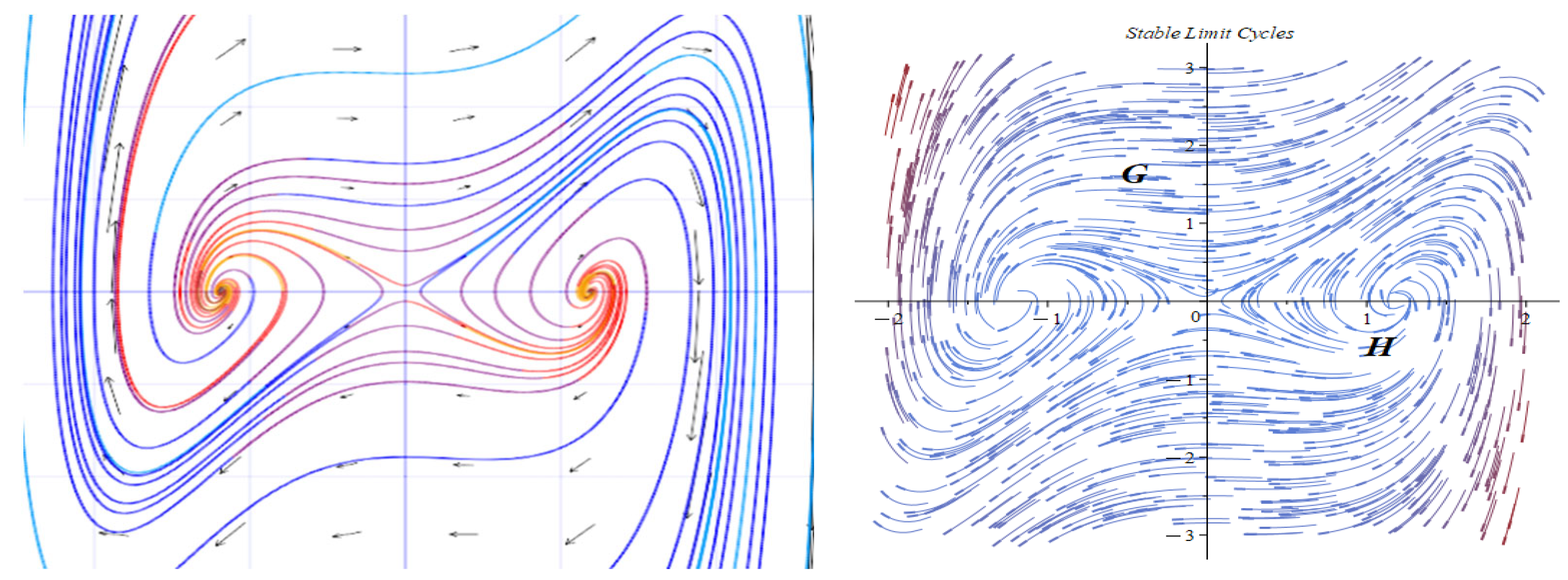
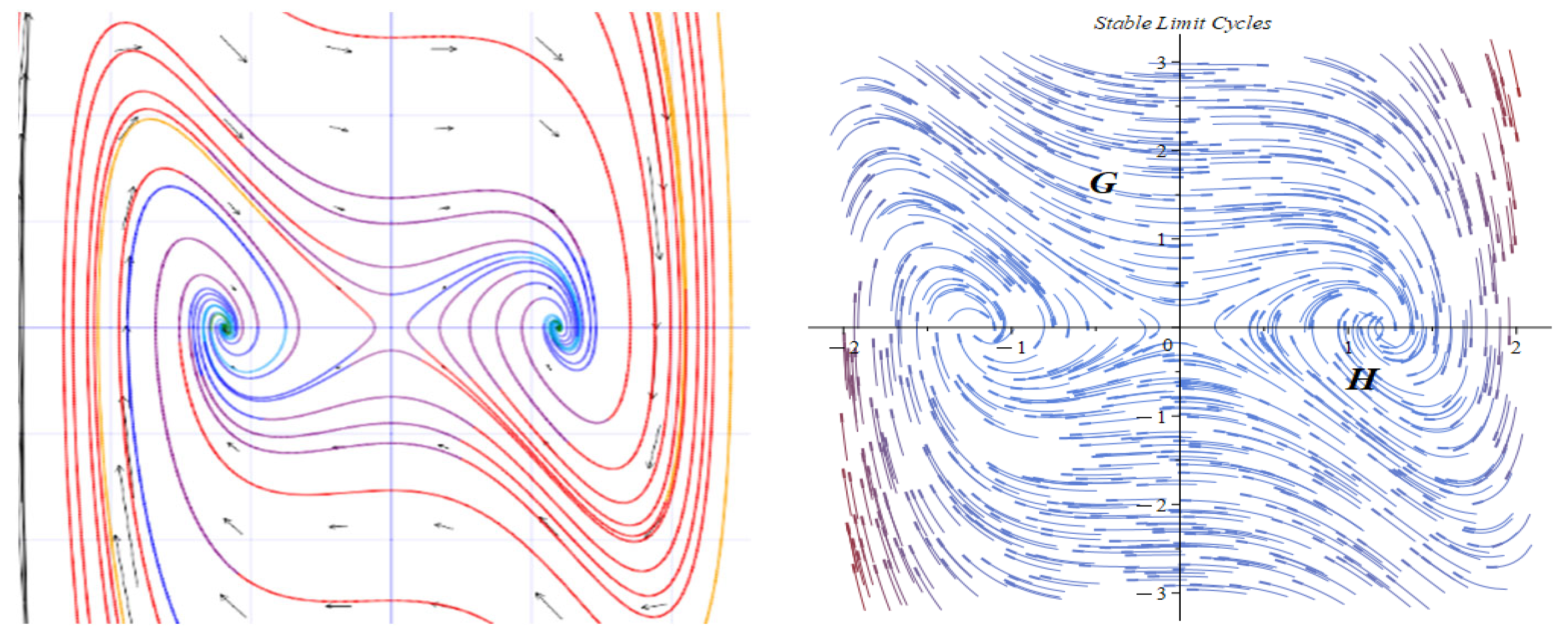
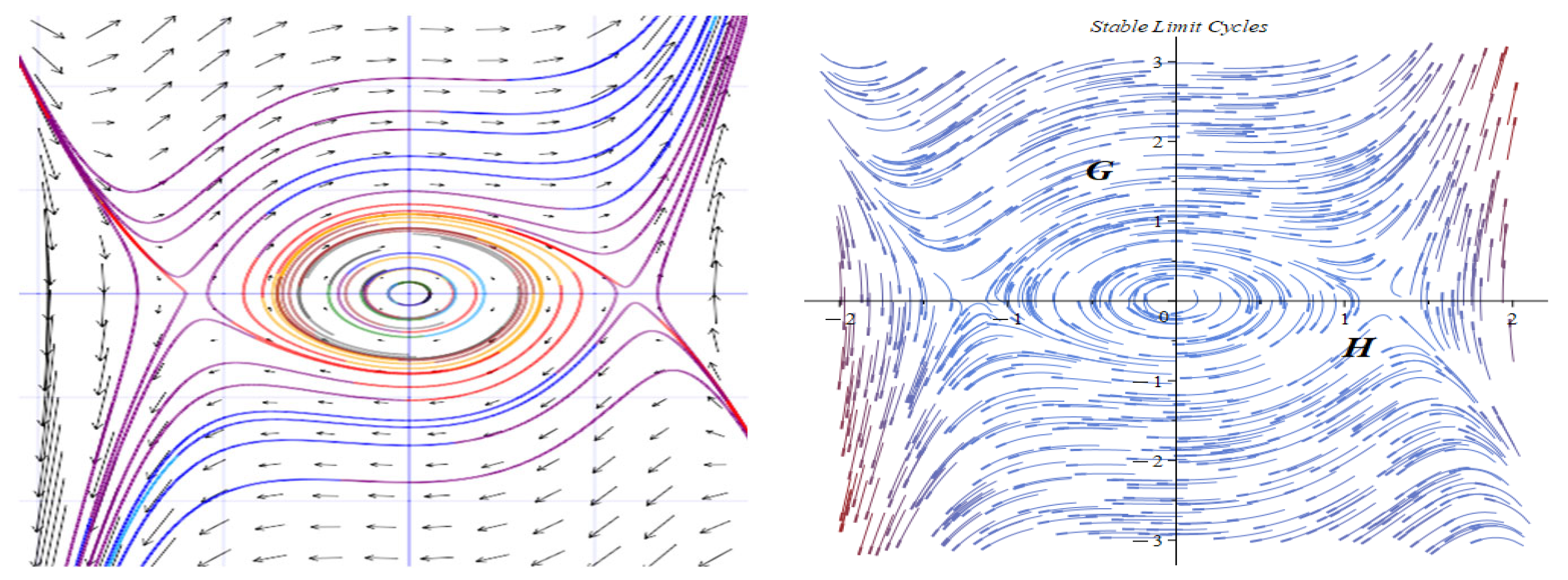
3. Dynamic Analysis
- Case 1: for .
- Subcase 1.1: For .
- Subcase 1.2: For .
- Case 2: for .
- Subcase 2.1: For .
- Subcase 2.2: For .
- Subcase 2.3: For .
- Subcase 2.4: For .
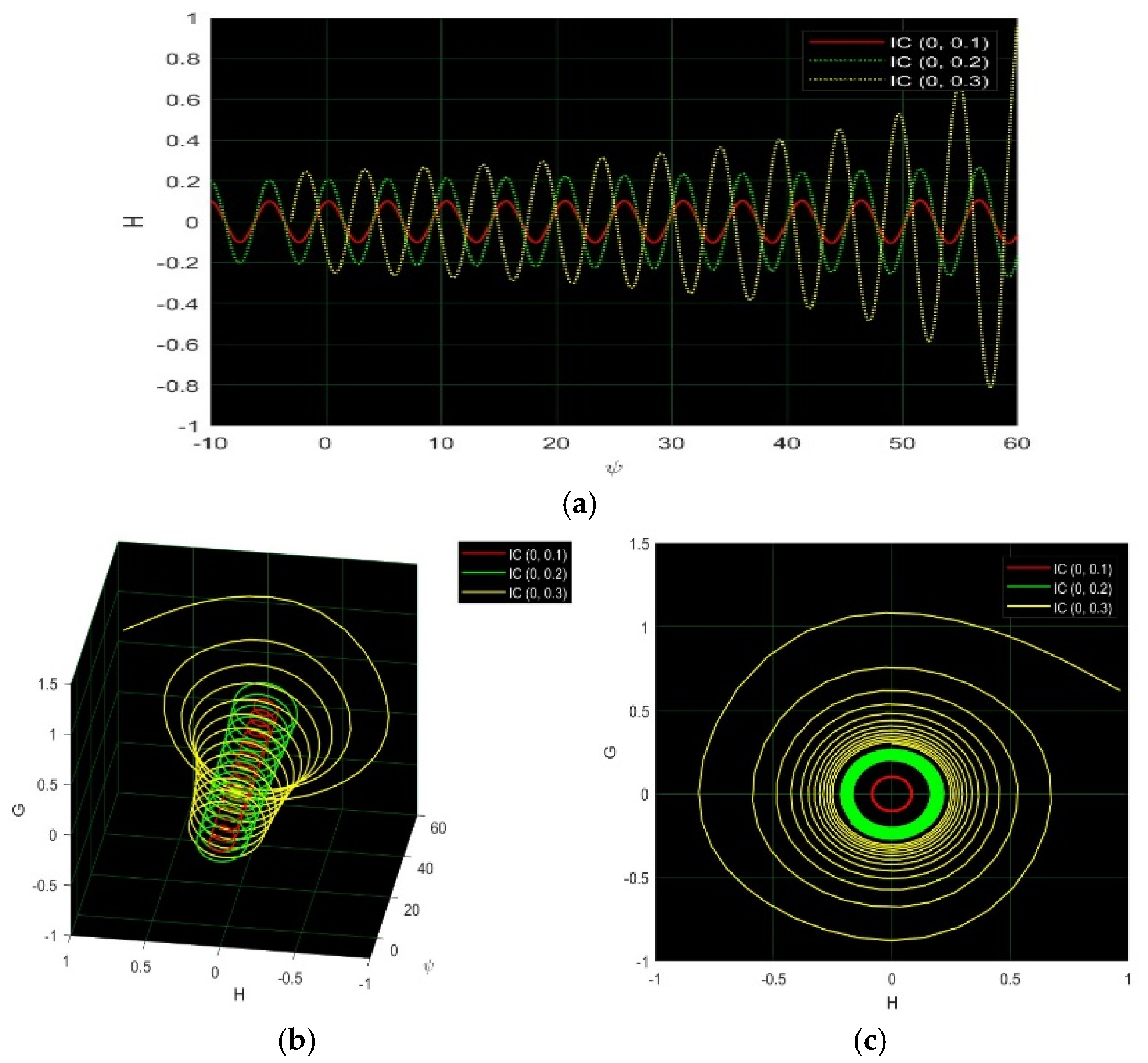
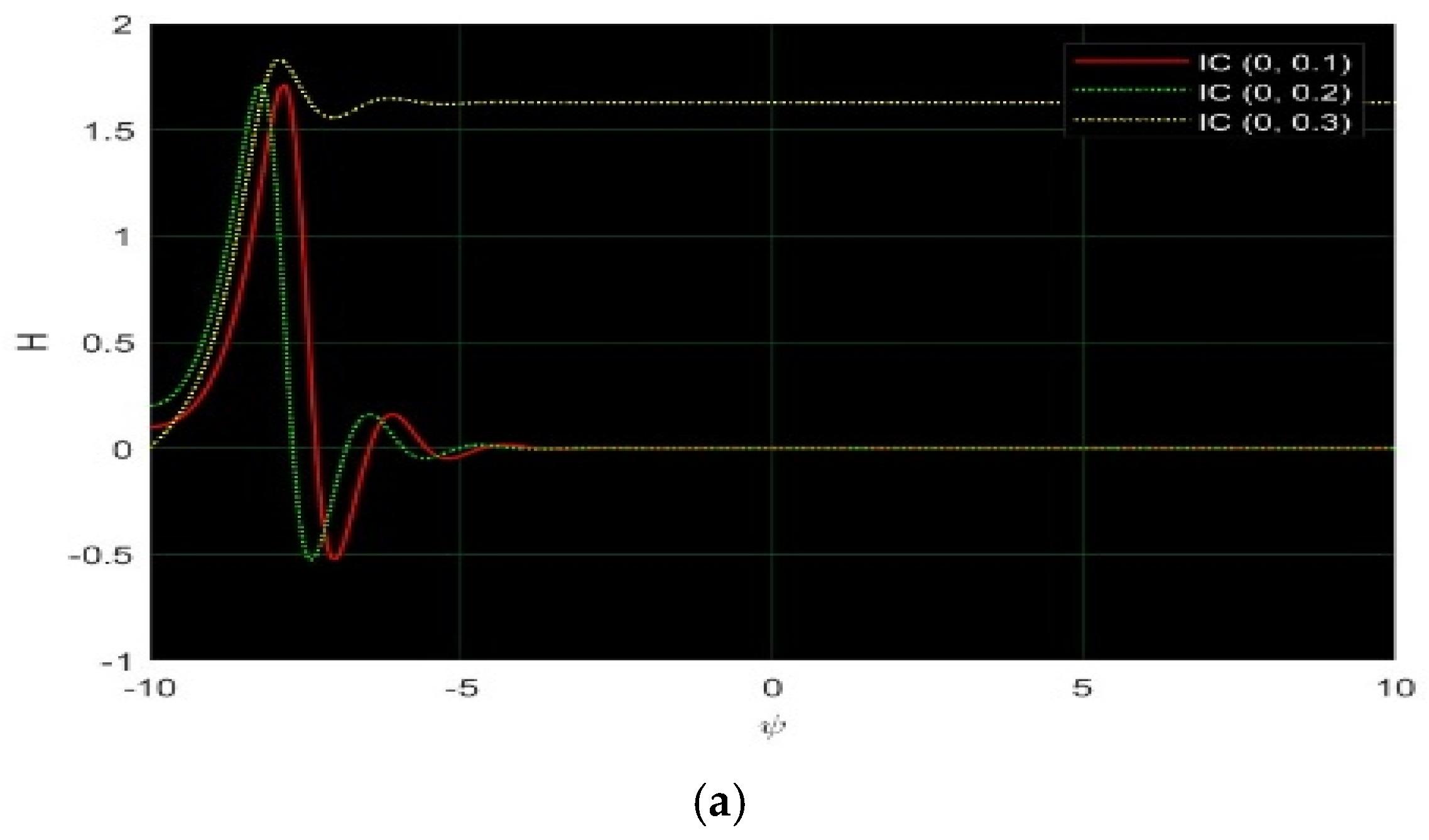
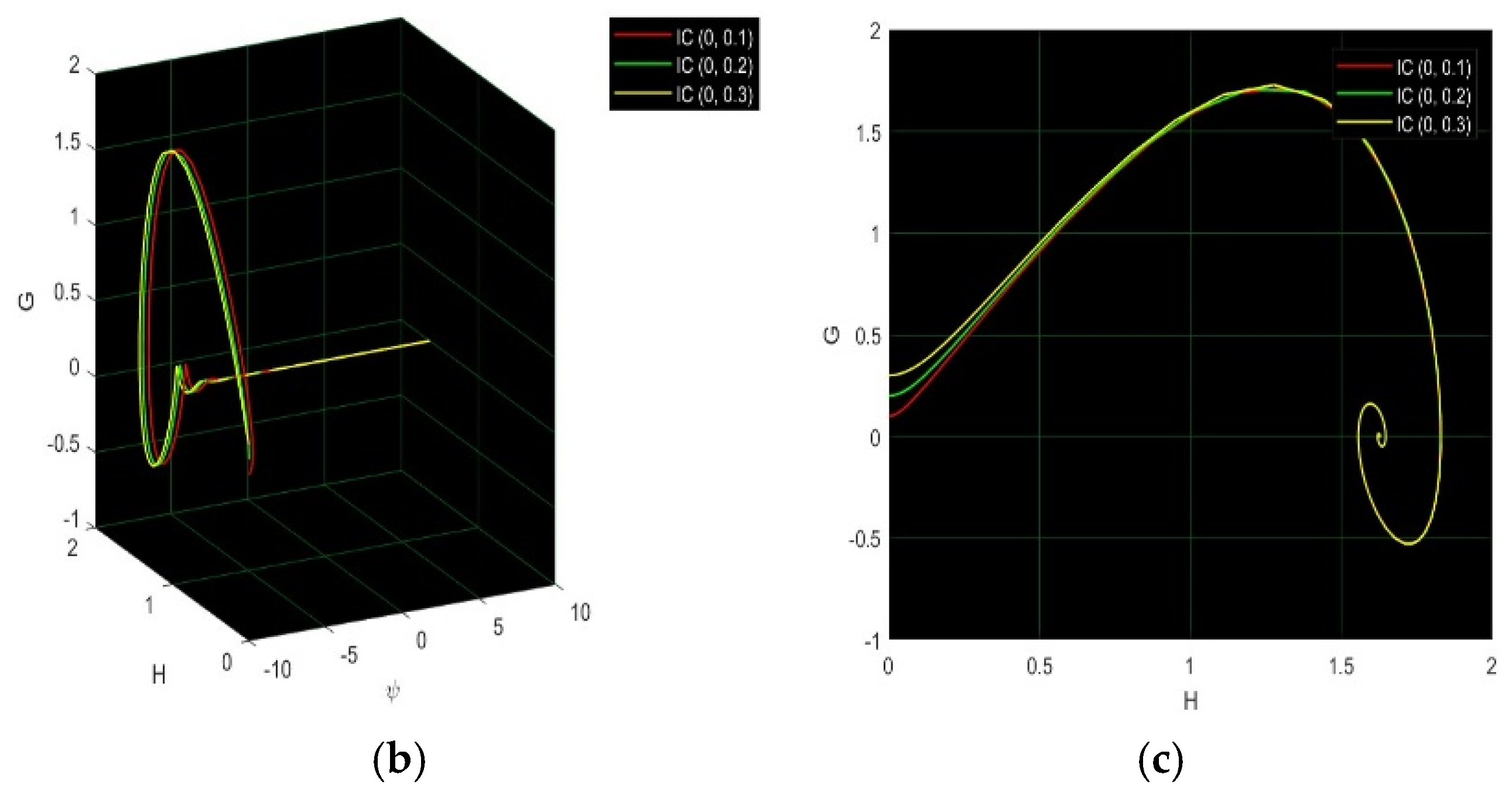
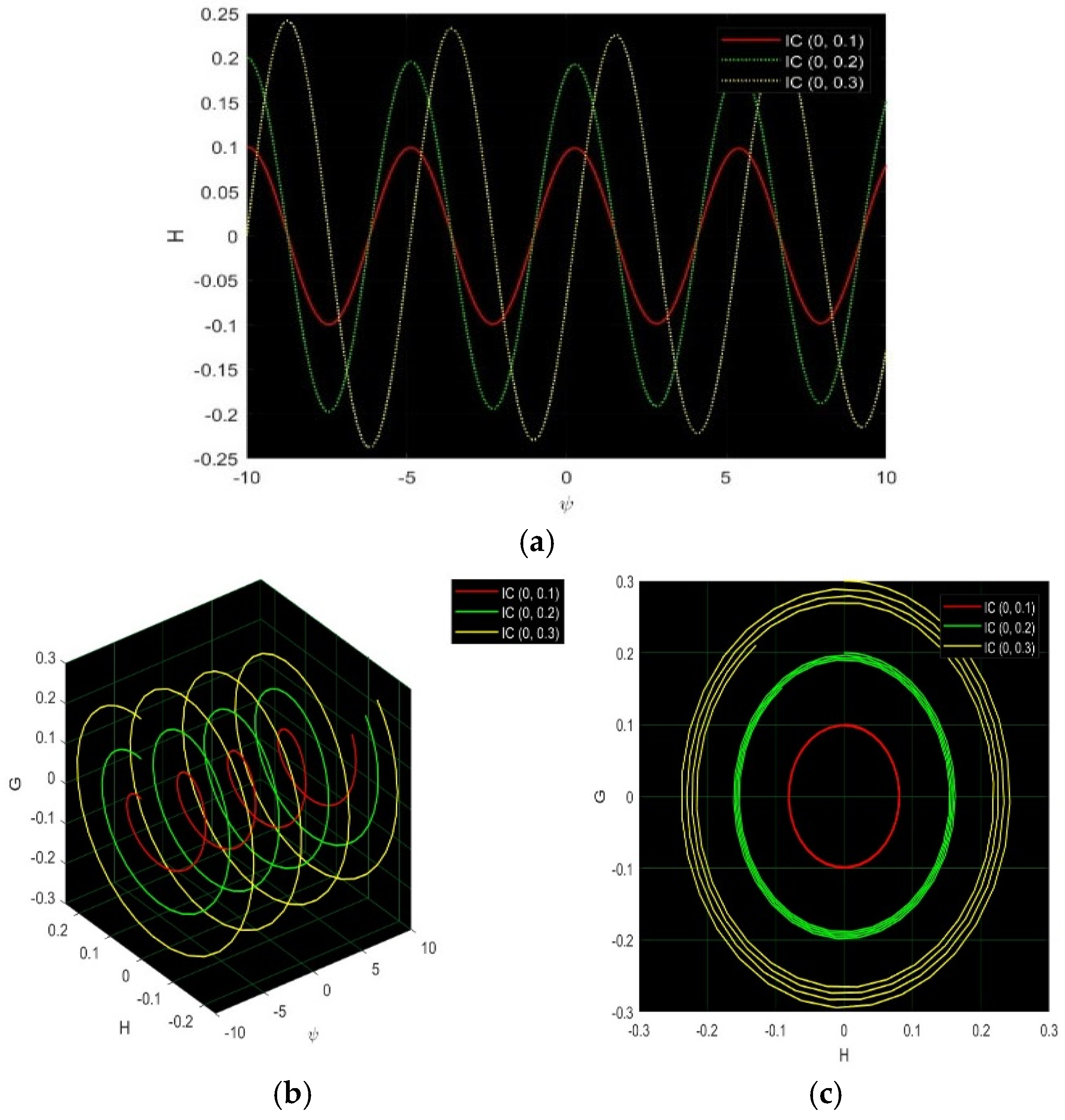
4. Sensitivity and Damping Effect
5. Methodology
5.1. Fundamental Stage of Modified Extended Tanh Method [41]
- For
5.2. Fundamental Stage of Simplest Equation Method [42,43]
6. Optical Soliton Solutions of Quintic M-Fractional Kundu–Eckhaus Equation
6.1. Application of the Modified Extended Tanh Method
- Set-02:
- For
6.2. Application of the Simplest Equation Method
- Set-01: .
- Set-02: .
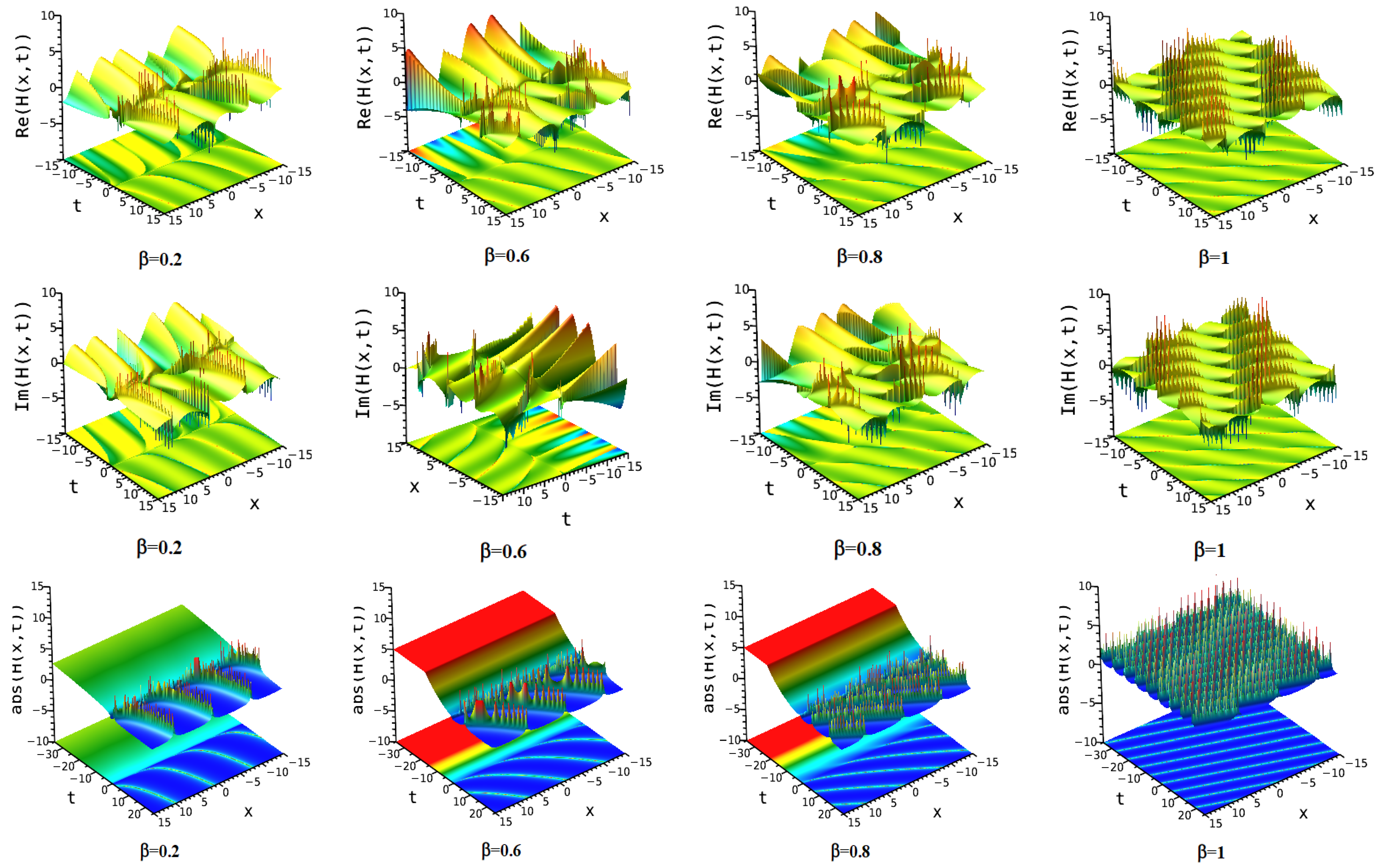
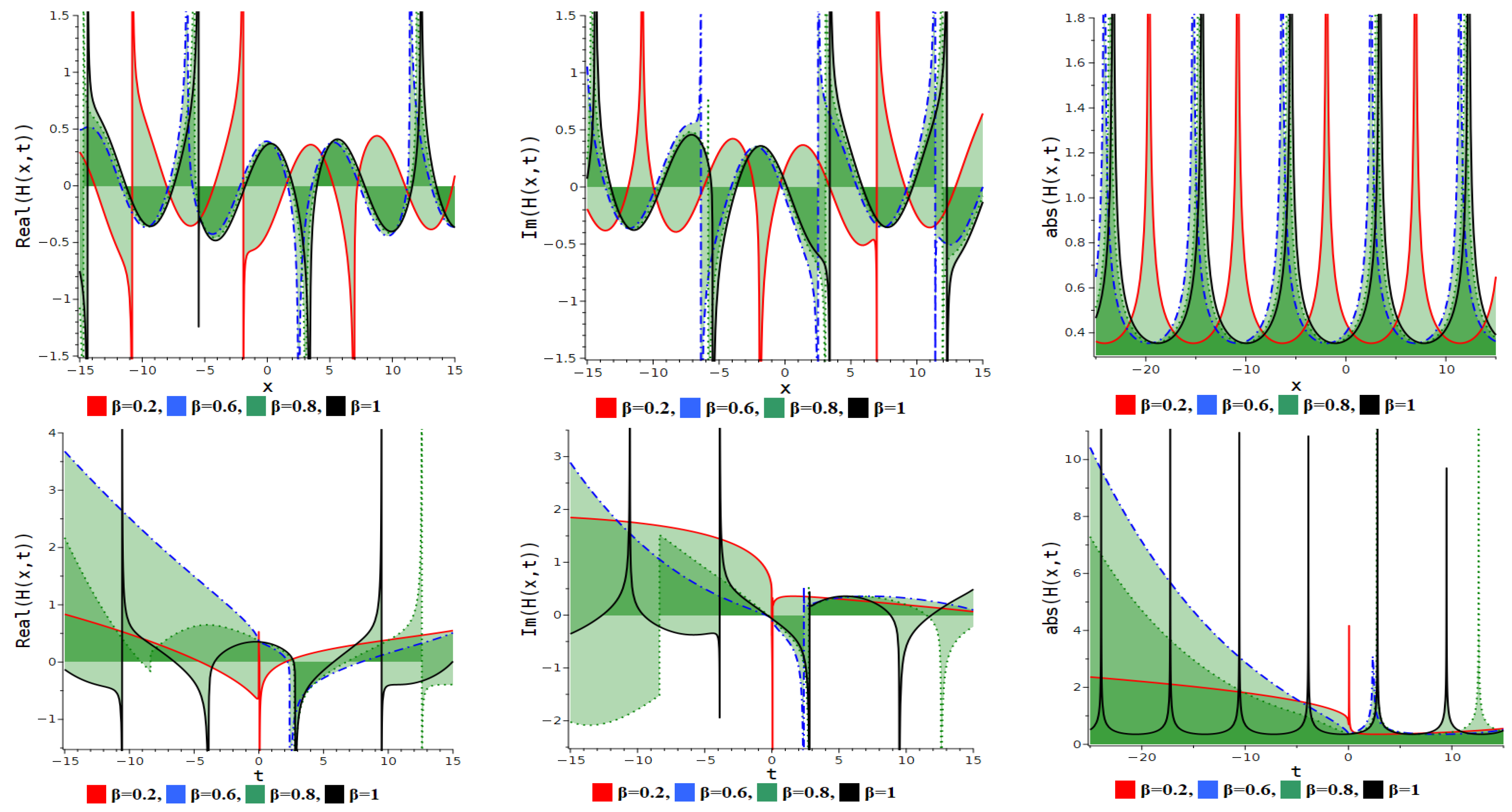
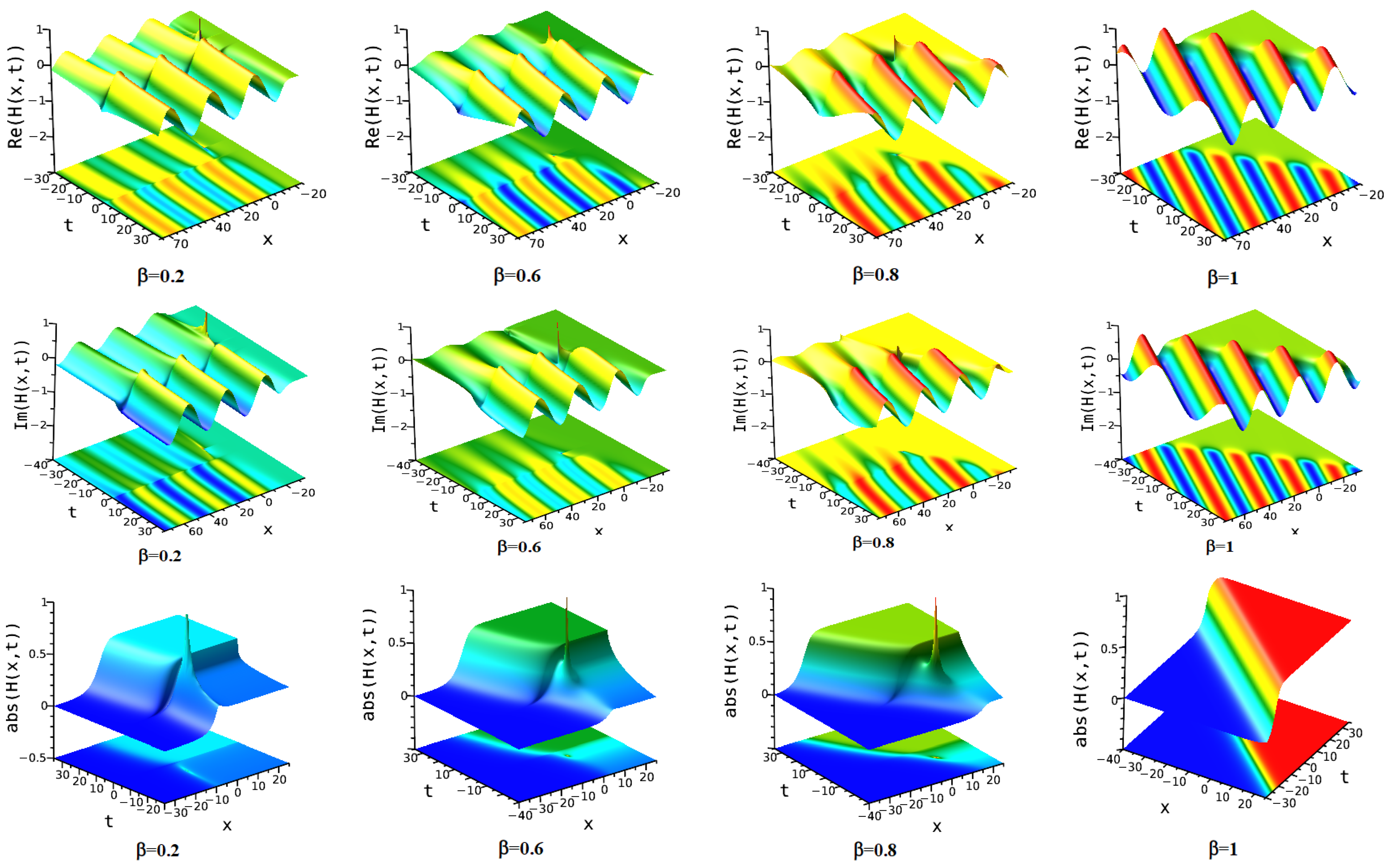
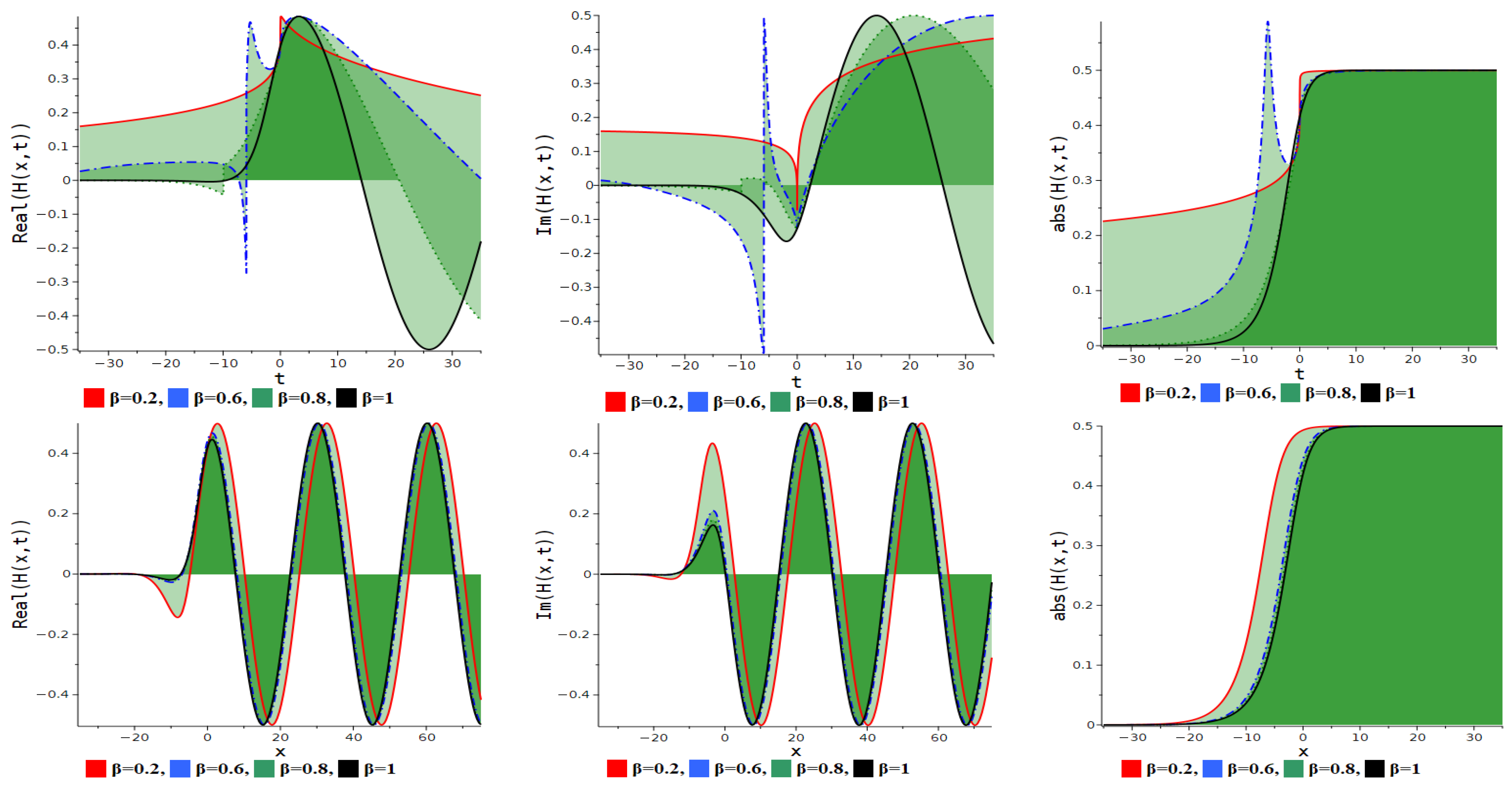
7. Numerical Discussion and Graphs
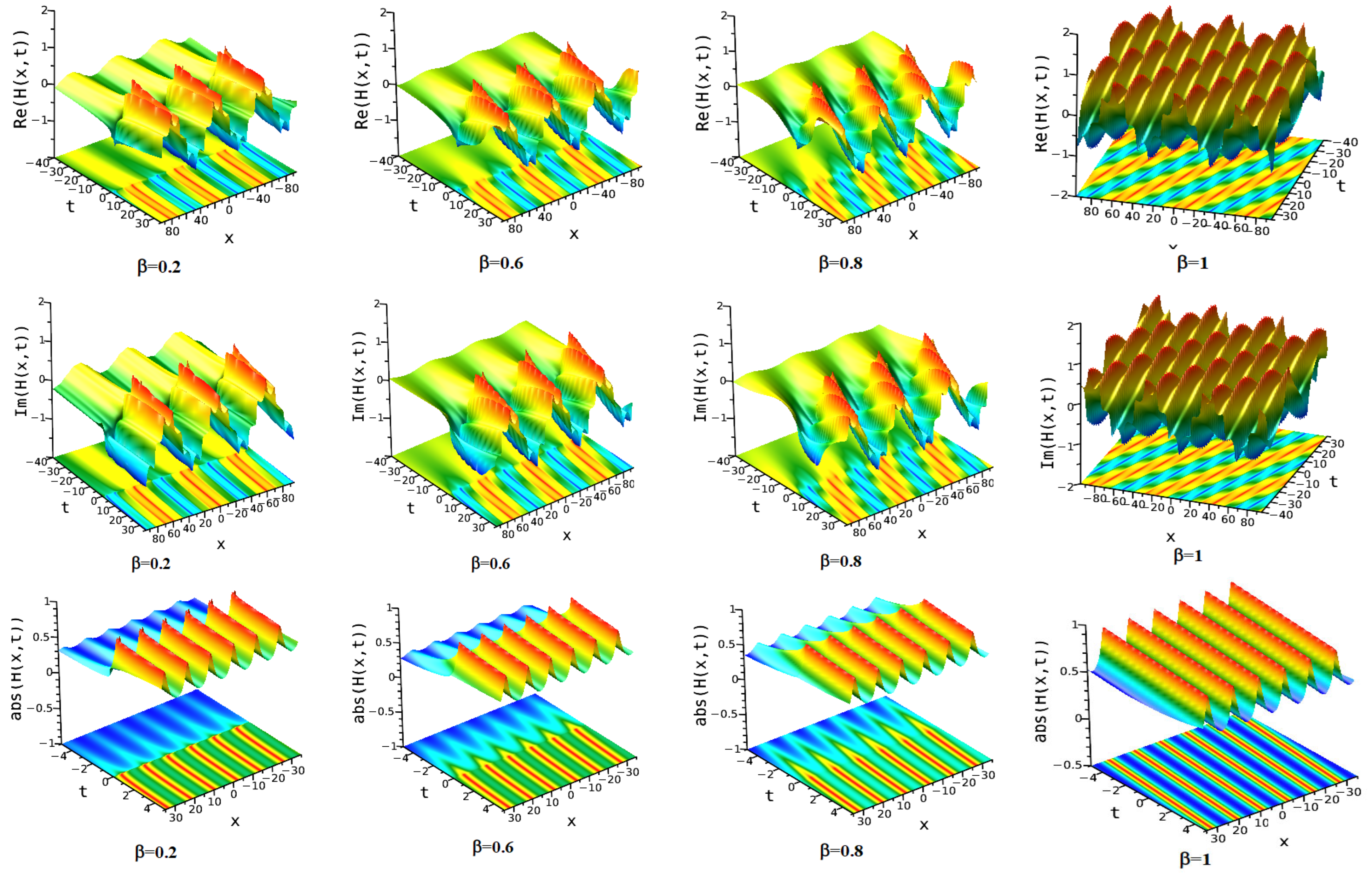
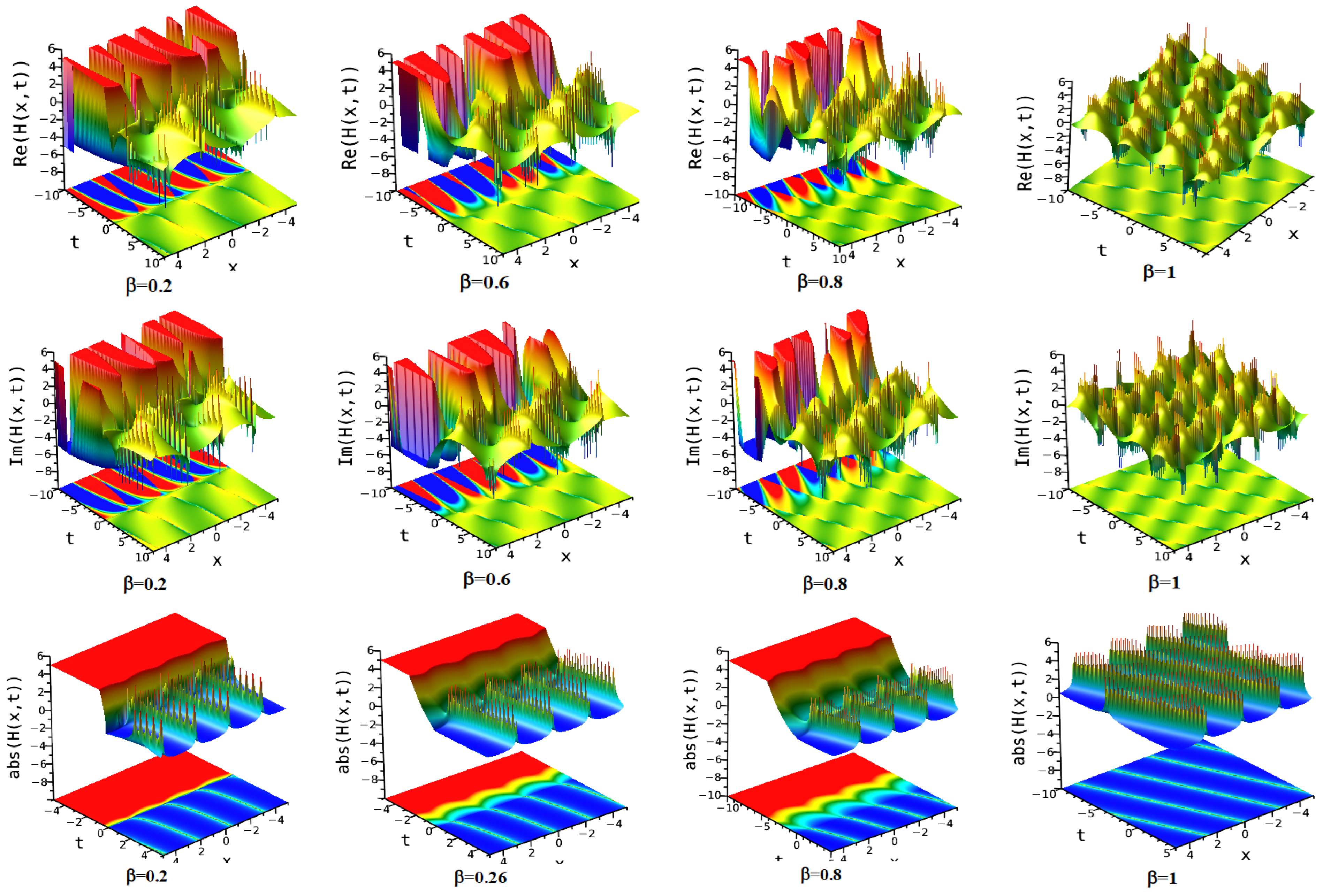
7.1. Modified Extended Tanh Method
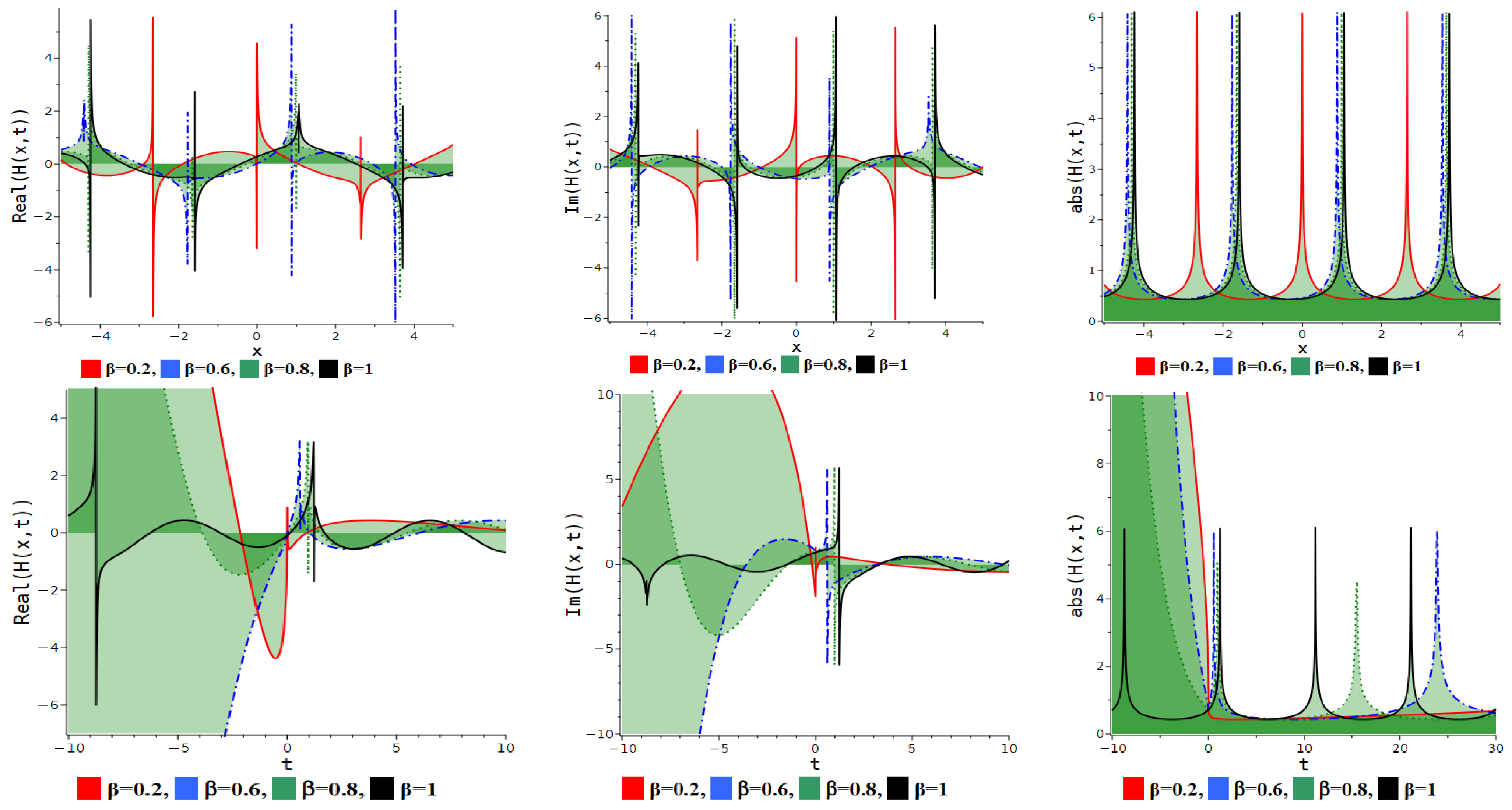
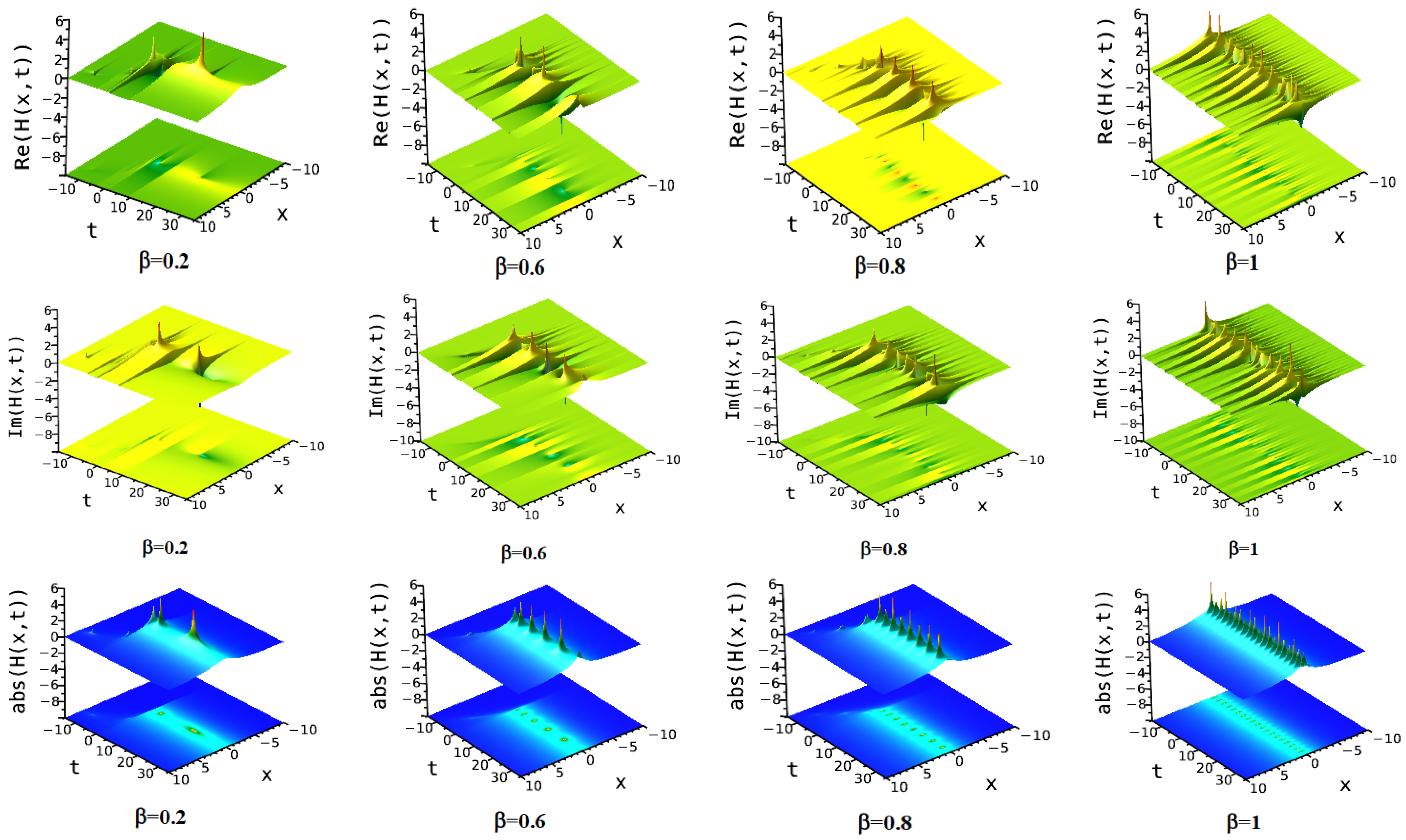
7.2. Simplest Equation Method
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gu, Y.; Chen, B.; Ye, F.; Aminakbari, N. Soliton Solutions of Nonlinear Schrödinger Equation with Variable Coefficients under the Influence of Woods–Saxon Potential. Results Phys. 2022, 42, 105979. [Google Scholar] [CrossRef]
- Chen, J.; Mihalache, D.; Belić, M.R.; Qin, W.; Zhu, D.; Zhu, X.; Zeng, L. Dark Gap Soliton Families in Coupled Nonlinear Schrödinger Equations with Linear Lattices. Nonlinear Dyn. 2024, 113, 10307–10318. [Google Scholar] [CrossRef]
- Roshid, M.M.; Rahman, M.; Sheikh, M.A.N.; Uddin, M.; Khatun, M.S.; Roshid, H.O. Dynamical Analysis of Multi-Soliton and Interaction of Soliton Solutions of Nonlinear Model Arising in Energy Particles of Physics. Indian J. Phys. 2025, 2025, 1–13. [Google Scholar]
- Ganie, A.H.; AlBaidani, M.M.; Wazwaz, A.M.; Ma, W.X.; Shamima, U.; Ullah, M.S. Soliton Dynamics and Chaotic Analysis of the Biswas–Arshed Model. Opt. Quant. Electron. 2024, 56, 1379. [Google Scholar] [CrossRef]
- Akter, M.; Ullah, M.S.; Wazwaz, A.M.; Seadawy, A.R. Unveiling Hirota–Maccari Model Dynamics via Diverse Elegant Methods. Opt. Quant. Electron. 2024, 56, 1127. [Google Scholar] [CrossRef]
- Akter, M.A.; Mostafa, G.; Uddin, M.; Roshid, M.M.; Roshid, H.O. Simulation of Optical Wave Propagation of Perturbed Nonlinear Schrödinger’s Equation with Truncated M-Fractional Derivative. Opt. Quant. Electron. 2024, 56, 1255. [Google Scholar] [CrossRef]
- Roshid, M.M. Exploring the Chaotic Behavior, and Ion Acoustic Wave of Generalized Perturbed Korteweg-de Vries Equation with a Fractional Operator. Partial Differ. Equ. Appl. Math. 2024, 13, 101042. [Google Scholar] [CrossRef]
- Shah, Z.; Raja, M.A.Z.; Shoaib, M.; Khan, I.; Kiani, A.K. Stochastic Supervised Networks for Numerical Treatment of Eyring–Powell Nanofluid Model with Darcy Forchheimer Slip Flow Involving Bioconvection and Nonlinear Thermal Radiation. Mod. Phys. Lett. B 2025, 39, 2450400. [Google Scholar] [CrossRef]
- Wazwaz, A.M.; Alhejaili, W.; El-Tantawy, S.A. Optical Solitons for Nonlinear Schrödinger Equation Formatted in the Absence of Chromatic Dispersion through Modified Exponential Rational Function Method and Other Distinct Schemes. Ukr. J. Phys. Opt. 2024, 25, 1049–1059. [Google Scholar] [CrossRef]
- Butler, S.; Joshi, N. An Inverse Scattering Transform for the Lattice Potential KdV Equation. Inverse Probl. 2010, 26, 115012. [Google Scholar] [CrossRef]
- Kazi Sazzad Hossain, A.K.M.; Kamrul Islam, M.; Akter, H.; Ali Akbar, M. Exact and Soliton Solutions of Nonlinear Evolution Equations in Mathematical Physics Using the Generalized (G′/G)-Expansion Approach. Phys. Scr. 2024, 99, 015269. [Google Scholar] [CrossRef]
- Seadawy, A.R. Fractional Solitary Wave Solutions of the Nonlinear Higher-Order Extended KdV Equation in a Stratified Shear Flow: Part I. Comput. Math. Appl. 2015, 70, 345–352. [Google Scholar] [CrossRef]
- Biswas, A.; Yıldırım, Y.; Yaşar, E. Optical Soliton Perturbation with Quadratic-Cubic Nonlinearity by Extended Trial Function Method. Optik 2019, 176, 542–548. [Google Scholar] [CrossRef]
- Wang, K.-J.; Liu, X.-L.; Shi, F.; Li, G. Bifurcation and Sensitivity Analysis, Chaotic Behaviors, Variational Principle, Hamiltonian and Diverse Wave Solutions of the New Extended Integrable Kadomtsev–Petviashvili Equation. Phys. Lett. A 2025, 534, 130246. [Google Scholar] [CrossRef]
- Ahmed, S.; Rehman, U.; Fei, J.; Khalid, M.I.; Chen, X. Shallow-Water Wave Dynamics: Butterfly Waves, X-Waves, Multiple-Lump Waves, Rogue Waves, Stripe Soliton Interactions, Generalized Breathers, and Kuznetsov–Ma Breathers. Fractal Fract. 2025, 9, 31. [Google Scholar] [CrossRef]
- Arnous, A.H.; Murad, M.A.S.; Biswas, A.; Yildirim, Y.; Georgescu, P.L.; Moraru, L.; Jawad, A.J.M.; Hussein, L. Optical Solitons for the Concatenation Model with Fractional Temporal Evolution. Ain Shams Eng. J. 2025, 16, 103243. [Google Scholar] [CrossRef]
- Iqbal, M.A.; Gepreel, K.A.; Akbar, M.A.; Osman, M.S. The Compatibility and Dynamics of Optical Soliton Solutions for Higher-Order Nonlinear Schrödinger Model. Mod. Phys. Lett. B 2024, 39, 2550086. [Google Scholar] [CrossRef]
- Chou, D.; Boulaaras, S.M.; Rehman, H.U.; Iqbal, I.; Ma, W.-X. Multiple Soliton and Singular Wave Solutions with Bifurcation Analysis for a Strain Wave Equation Arising in Microcrystalline Materials. Mod. Phys. Lett. B 2025, 39, 2150031. [Google Scholar] [CrossRef]
- Alhejaili, W.; Wazwaz, A.-M.; El-Tantawy, S.A. Extended New Painlevé Integrable KdV–CBS Equation: Multiple Shocks, Lump, Breathers, and Other Physical Wave Solutions. Phys. Scr. 2024, 99, 015269. [Google Scholar] [CrossRef]
- Abbagari, S.; Houwe, A.; Akinyemi, L.; Serge, D.Y.; Crépin, K.T. Multi-Hump Soliton and Rogue Waves of the Coupled Nonlinear Schrödinger Equations in Nonlinear Left-Handed Transmission Line. Nonlinear Dyn. 2024, 98, 2024. [Google Scholar] [CrossRef]
- Jawaz, M.; Macías-Díaz, J.E.; Aqeel, S.A.; Ahmed, N.; Baber, M.Z.; Medina-Guevara, M.G. On Some Explicit Solitary Wave Patterns for a Generalized Nonlinear Reaction–Diffusion Equation with Conformable Temporal Fractional Derivative. Partial Differ. Equ. Appl. Math. 2025, 13, 101036. [Google Scholar] [CrossRef]
- Ma, W.X.; Geng, X. New Completely Integrable Neumann Systems Related to the Perturbation KdV Hierarchy. Phys. Lett. B 2024, 475, 56–62. [Google Scholar] [CrossRef]
- Ma, W.X.; Zhou, R. On Inverse Recursion Operator and Tri-Hamiltonian Formulation for a Kaup-Newell System of DNLS Equations. J. Phys. A Math. Gen. 2024, 32, L239. [Google Scholar] [CrossRef]
- Islam, M.S.; Roshid, M.M.; Uddin, M.; Ahmed, A. Modulation Instability and Dynamical Analysis of New Abundant Closed-Form Solutions of the Modified Korteweg–de Vries–Zakharov–Kuznetsov Model With Truncated M-Fractional Derivative. J. Appl. Math. 2024, 2024, 1754782. [Google Scholar] [CrossRef]
- Djaouti, A.M.; Roshid, M.M.; Abdeljabbar, A.; Al-Quran, A. Bifurcation Analysis and Solitary Wave Solution of Fractional Longitudinal Wave Equation in Magneto-Electro-Elastic (MEE) Circular Rod. Results Phys. 2024, 64, 107918. [Google Scholar] [CrossRef]
- Wazwaz, A.M. New Solitary Wave Solutions to the Kuramoto-Sivashinsky and the Kawahara Equations. Appl. Math. Comput. 2024, 182, 1642–1650. [Google Scholar] [CrossRef]
- Liu, W.; Wazwaz, A.M.; Zheng, X. High-Order Breathers, Lumps, and Semi-Rational Solutions to the (2+1)-Dimensional Hirota–Satsuma–Ito Equation. Phys. Scr. 2024, 94, 075203. [Google Scholar] [CrossRef]
- Chakrabarty, A.K.; Akter, S.; Uddin, M.; Roshid, M.M.; Abdeljabbar, A.; Or-Roshid, H. Modulation Instability Analysis, and Characterize Time-Dependent Variable Coefficient Solutions in Electromagnetic Transmission and Biological Field. Partial Differ. Equ. Appl. Math. 2024, 11, 100765. [Google Scholar] [CrossRef]
- Ma, W.; Zhou, R. Binary Nonlinearization of Spectral Problems of the Perturbation AKNS Systems. Chaos Solitons Fractals 2002, 13, 1451–1463. [Google Scholar] [CrossRef]
- Li, B.; Zhu, L. Turing Instability Analysis of a Reaction–Diffusion System for Rumor Propagation in Continuous Space and Complex Networks. Inf. Process. Manag. 2024, 61, 103621. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, D.; Li, N. Predator Invasion in a Spatially Heterogeneous Predator-Prey Model with Group Defense and Prey-Taxis. Math. Comput. Simul. 2024, 226, 270–282. [Google Scholar] [CrossRef]
- Yuan, T.; Guan, G.; Shen, S.; Zhu, L. Stability Analysis and Optimal Control of Epidemic-Like Transmission Model with Nonlinear Inhibition Mechanism and Time Delay in Both Homogeneous and Heterogeneous Networks. J. Math. Anal. Appl. 2023, 526, 127273. [Google Scholar] [CrossRef]
- Ahmed, K.K.; Badra, N.M.; Ahmed, H.M.; Rabie, W.B. Soliton Solutions and Other Solutions for Kundu–Eckhaus Equation with Quintic Nonlinearity and Raman Effect Using the Improved Modified Extended Tanh-Function Method. Mathematics 2022, 10, 4203. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Oldham, K.B.; Spanier, J. The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order; Academic Press: Cambridge, MA, USA, 1974. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers: London, UK, 1993. [Google Scholar]
- Biswas, A.; Salah, M.B.H.; Zerrad, E. Optical Solitons in Fractional Domains. Appl. Math. Comput. 2016, 274, 208–213. [Google Scholar] [CrossRef]
- Jumarie, G. Modified Riemann–Liouville Derivative and Fractional Taylor Series of Nondifferentiable Functions: Further Results. Math. Comput. Model. 2009, 51, 16–26. [Google Scholar] [CrossRef]
- Alhejaili, W.; Shah, R.; Salas, A.H.; Raut, S.; Roy, S.; Roy, A.; El-Tantawy, S.A. Unearthing the Existence of Intermode Soliton-Like Solutions within Integrable Quintic Kundu–Eckhaus Equation. Rend. Lincei Sci. Fis. Nat. 2024, 36, 233–255. [Google Scholar] [CrossRef]
- Roshid, H.-O.; Roshid, M.M.; Abdeljabbar, A.; Begum, M.; Basher, H. Abundant Dynamical Solitary Waves through Kelvin-Voigt Fluid via the Truncated M-Fractional Oskolkov Model. Results Phys. 2023, 55, 107128. [Google Scholar] [CrossRef]
- Roshid, M.M.; Rahman, M.M.; Bashar, M.H.; Hossain, M.M.; Mannaf, M.A. Dynamical Simulation of Wave Solutions for the M-Fractional Lonngren-Wave Equation Using Two Distinct Methods. Alex. Eng. J. 2024, 81, 460–468. [Google Scholar] [CrossRef]
- Roshid, M.M.; Uddin, M.; Hossain, M.M.; Roshid, H.-O. Investigation of Rogue Wave and Dynamic Solitary Wave Propagations of the M-Fractional (1+1)-Dimensional Longitudinal Wave Equation in a Magnetic-Electro-Elastic Circular Rod. Indian J. Phys. 2024, 99, 1787–1803. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Djaouti, A.M.; Roshid, M.M.; Roshid, H.-O.; Al-Quran, A. Optimizing Optical Fiber Communications: Bifurcation Analysis and Soliton Dynamics in the Quintic Kundu–Eckhaus Model. Fractal Fract. 2025, 9, 334. https://doi.org/10.3390/fractalfract9060334
Djaouti AM, Roshid MM, Roshid H-O, Al-Quran A. Optimizing Optical Fiber Communications: Bifurcation Analysis and Soliton Dynamics in the Quintic Kundu–Eckhaus Model. Fractal and Fractional. 2025; 9(6):334. https://doi.org/10.3390/fractalfract9060334
Chicago/Turabian StyleDjaouti, Abdelhamid Mohammed, Md. Mamunur Roshid, Harun-Or Roshid, and Ashraf Al-Quran. 2025. "Optimizing Optical Fiber Communications: Bifurcation Analysis and Soliton Dynamics in the Quintic Kundu–Eckhaus Model" Fractal and Fractional 9, no. 6: 334. https://doi.org/10.3390/fractalfract9060334
APA StyleDjaouti, A. M., Roshid, M. M., Roshid, H.-O., & Al-Quran, A. (2025). Optimizing Optical Fiber Communications: Bifurcation Analysis and Soliton Dynamics in the Quintic Kundu–Eckhaus Model. Fractal and Fractional, 9(6), 334. https://doi.org/10.3390/fractalfract9060334






