Exploring Multifractal Asymmetric Detrended Cross-Correlation Behavior in Semiconductor Stocks
Abstract
1. Introduction
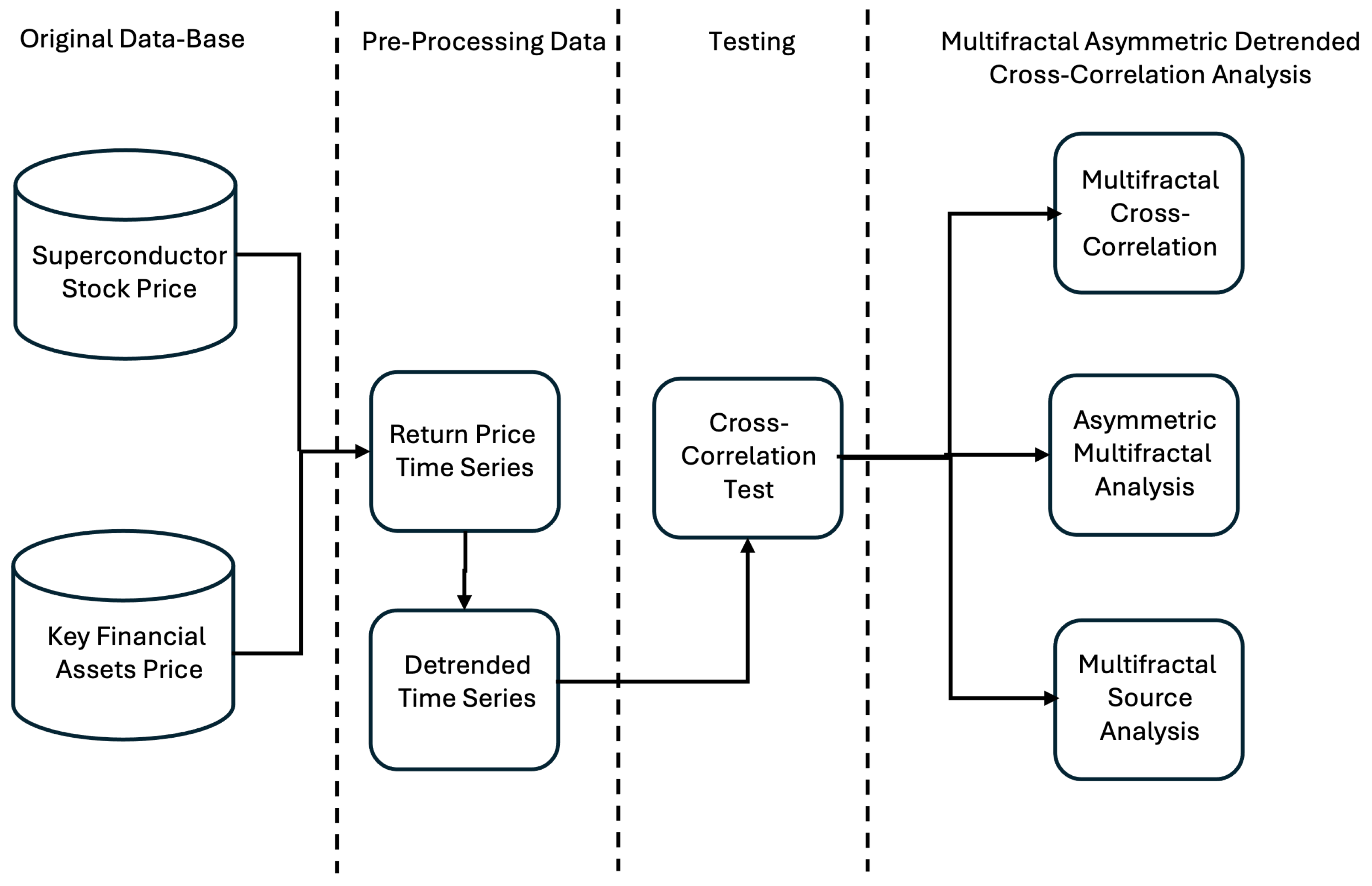
2. Materials and Methods
- 1.
- Profile ConstructionGiven a time series and , both of length N, the profiles are computed as:where and represent the mean of each time series.
- 2.
- Segmentation of the ProfilesThe profiles and are divided into non-overlapping segments of equal length s. To ensure that all data points are included—since N is not necessarily an exact multiple of s—the same segmentation procedure is repeated from the end of each series. As a result, a total of segments are obtained for each time series.
- 3.
- Local Trend RemovalFor each segment, the local trend or , depending on the time series, is estimated using a least-squares polynomial fit. The detrended variance is then calculated as: forand for
- 4.
- Computation of the Fluctuation FunctionThe fluctuation function of order q is computed as:
- 5.
- Determination of Scaling BehaviorThe fluctuation function follows a power-law relationship:where is the generalized Hurst exponent. The series exhibits multifractal properties if varies with q.
- 6.
- Determination of asymmetric multifractal behaviorFurthermore, the asymmetric multifractal behavior is analyzed by comparing scaling properties for the positive and negative trends of the main financial assets separately. This approach helps identify whether trends behave differently in upward versus downward market conditions. The trend is adjusted for each segment . The direction or trend is the sign of the slope , indicating an upward or downward price trend.andwhere and denote the total number of segments with positive and negative trends, respectively.
- 7.
- Determination of Multifractal spectra and singularity exponentThe singularity exponent () is determined using Equation (12) in conjunction with the Legendre transformation (Equation (13)). This transformation plays a crucial role in characterizing the local scaling properties of a time series by relating the multifractal spectrum to the generalized Hurst exponent. Once the singularity exponent is obtained, the Rényi exponent () and the multifractal spectrum can be computed using Equation (14). The multifractal spectrum provides a comprehensive representation of the complexity and heterogeneity of the analyzed financial time series.Furthermore, the formulation of the multifractal spectrum can be rewritten in an equivalent form, as shown in Equation (15), which facilitates a more intuitive interpretation of the results.
3. Data Selection and Description
- 1.
- Dow Jones Industrial Average (DJI)—representing the main stock index.
- 2.
- Gold (XAU)—a low-risk, safe-haven commodity.
- 3.
- EUR/USD (EUR)—the primary exchange rate.
- 4.
- Crude oil (WTI)—a key energy commodity.
- 5.
- Bitcoin (BTC)—the dominant cryptocurrency.
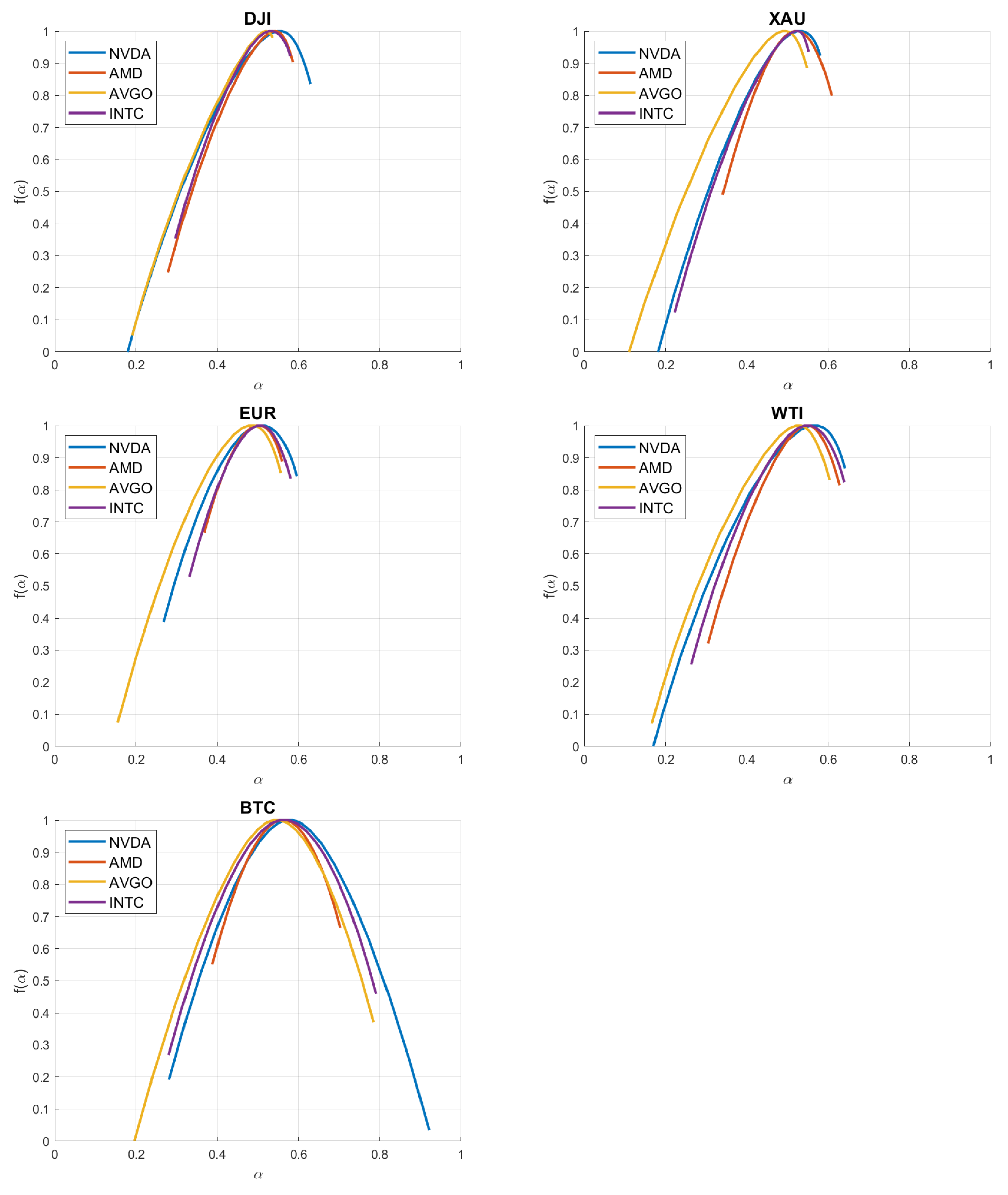
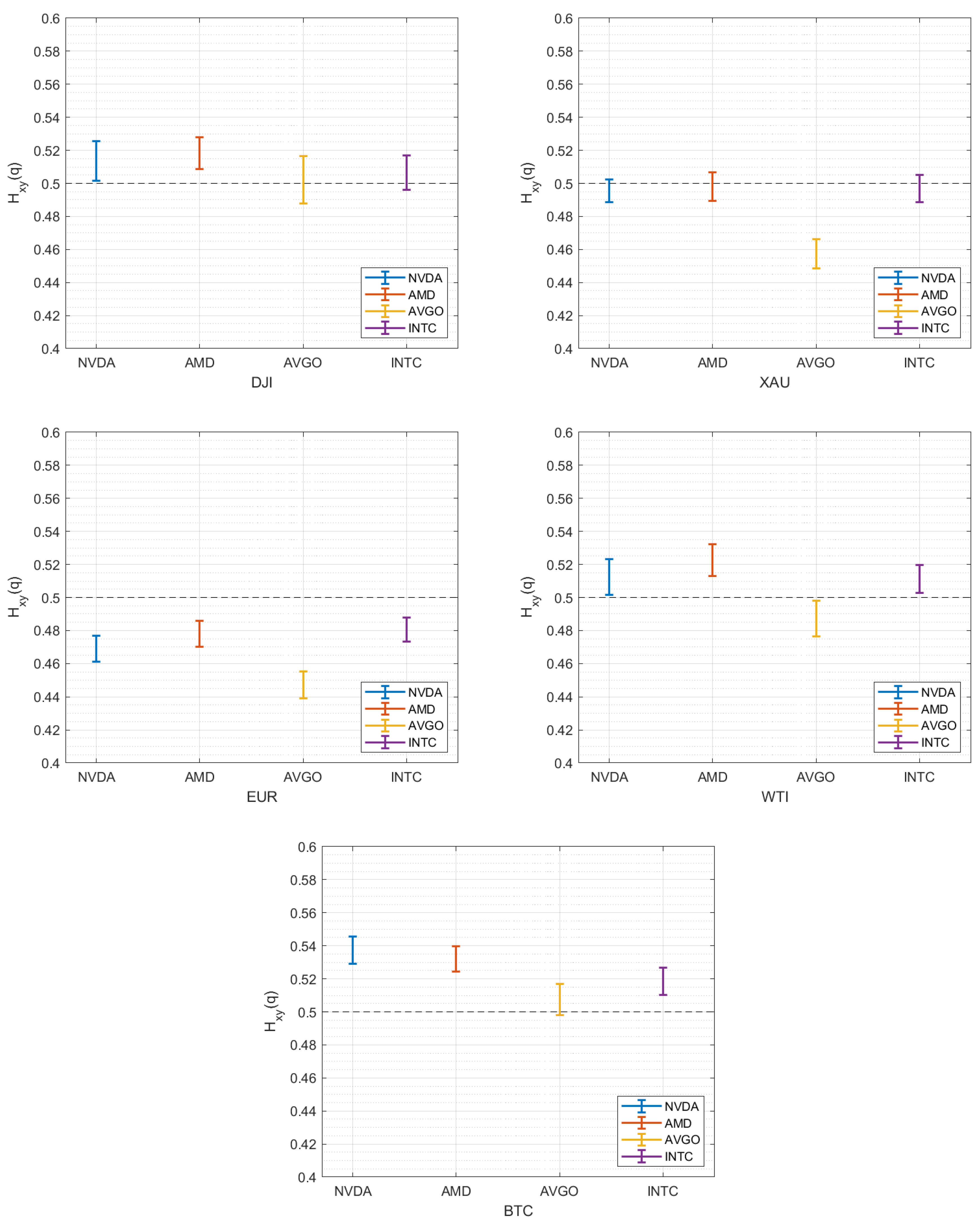
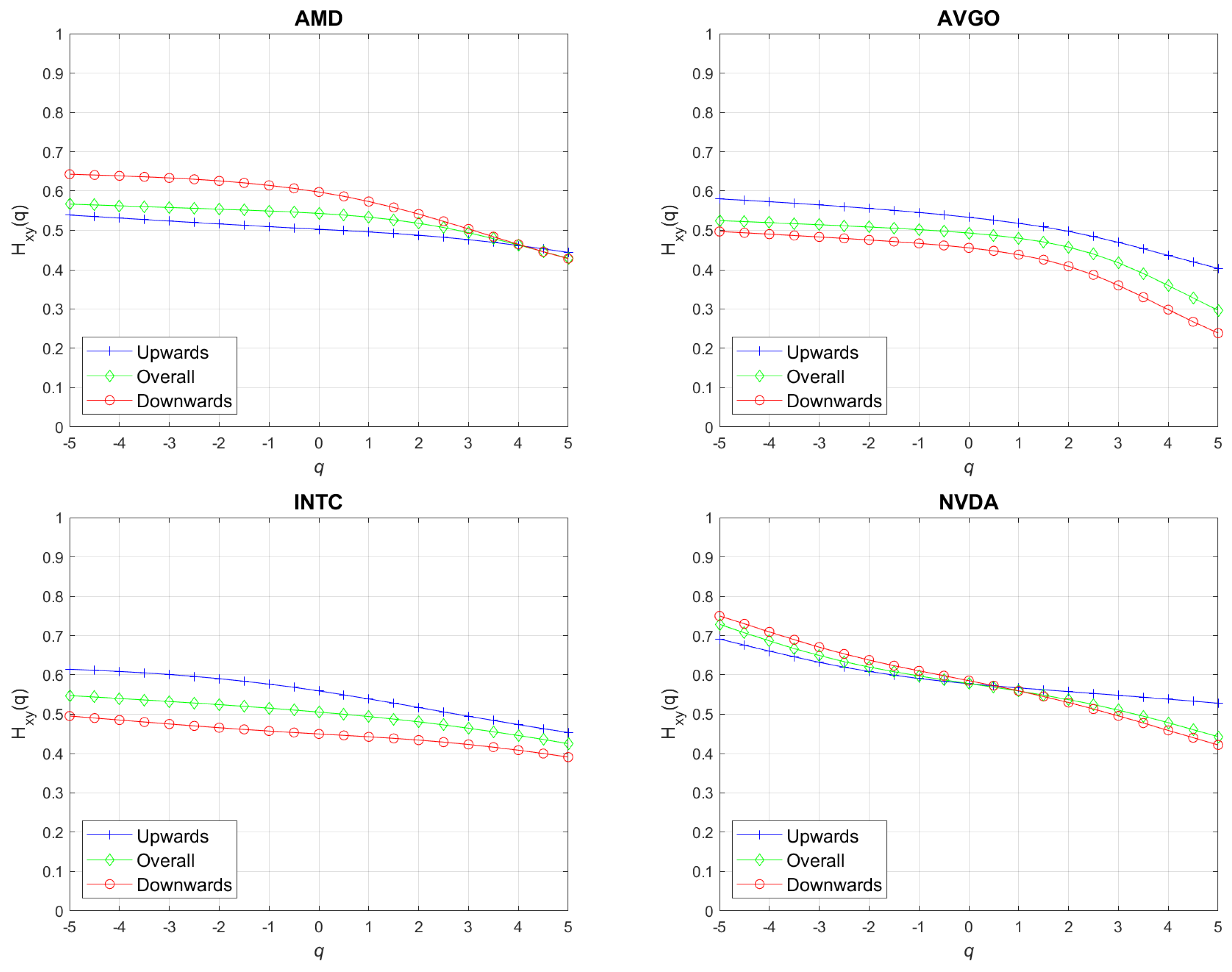
4. Analysis of Results
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rasheed, M.Q.; Zhao, Y.; Nazir, M.; Ahmed, Z.; Yu, X. How do semiconductors, artificial intelligence, geopolitical risk, and their moderating effects shape renewable energy production in leading semiconductor manufacturing countries? Technol. Soc. 2025, 80, 102761. [Google Scholar] [CrossRef]
- Zhang, K. 1.1 semiconductor industry: Present & future. In Proceedings of the 2024 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 18–22 February 2024; Volume 67, pp. 10–15. [Google Scholar]
- Richard, C. The Semiconductor Industry—Past, Present, and Future. In Understanding Semiconductors: A Technical Guide for Non-Technical People; Apress: Berkeley, CA, USA, 2022; pp. 175–210. [Google Scholar]
- Fama, E.F. Efficient capital markets. J. Financ. 1970, 25, 383–417. [Google Scholar] [CrossRef]
- Caginalp, G.; DeSantis, M. Nonlinear price dynamics of S&P 100 stocks. Phys. A Stat. Mech. Appl. 2020, 547, 122067. [Google Scholar]
- Bucur, C.; Tudorică, B.G.; Bâra, A.; Oprea, S.V. Multifractal analysis of Bitcoin price dynamics. J. Bus. Econ. Manag. 2025, 26, 21–48. [Google Scholar] [CrossRef]
- Zhuang, X.; Wei, D. Asymmetric multifractality, comparative efficiency analysis of green finance markets: A dynamic study by index-based model. Phys. Stat. Mech. Appl. 2022, 604, 127949. [Google Scholar] [CrossRef]
- Mensi, W.; Vo, X.V.; Kang, S.H. Upward/downward multifractality and efficiency in metals futures markets: The impacts of financial and oil crises. Resour. Policy 2022, 76, 102645. [Google Scholar] [CrossRef]
- Lee, M.; Song, J.W.; Park, J.H.; Chang, W. Asymmetric multi-fractality in the US stock indices using index-based model of A-MFDFA. Chaos Solitons Fractals 2017, 97, 28–38. [Google Scholar] [CrossRef]
- Stosic, D.; Stosic, D.; Vodenska, I.; Stanley, H.E.; Stosic, T. A New Look at Calendar Anomalies: Multifractality and Day-of-the-Week Effect. Entropy 2022, 24, 562. [Google Scholar] [CrossRef]
- Kristjanpoller, W.; Tabak, B.M. Day of the week effect on the cryptomarket: A high-frequency asymmetric multifractal analysis. Phys. A Stat. Mech. Appl. 2025, 658, 130306. [Google Scholar] [CrossRef]
- Zhang, S.; Fang, W. Multifractal behaviors of stock indices and their ability to improve forecasting in a volatility clustering period. Entropy 2021, 23, 1018. [Google Scholar] [CrossRef]
- Kristjanpoller, W.; Miranda Tabak, B. Day of the Week Effect on the World Exchange Rates through Fractal Analysis. Fractal Fract. 2024, 8, 340. [Google Scholar] [CrossRef]
- Wang, F.; Chang, J.; Zuo, W.; Zhou, W. Research on Efficiency and Multifractality of Gold Market under Major Events. Fractal Fract. 2024, 8, 488. [Google Scholar] [CrossRef]
- Orlando, G.; Lampart, M. Expecting the unexpected: Entropy and multifractal systems in finance. Entropy 2023, 25, 1527. [Google Scholar] [CrossRef]
- Fernandes, L.H.; Silva, J.W.; de Araujo, F.H. Multifractal risk measures by macroeconophysics perspective: The case of brazilian inflation dynamics. Chaos Solitons Fractals 2022, 158, 112052. [Google Scholar] [CrossRef]
- Kristjanpoller, W.; Minutolo, M.C. Asymmetric multi-fractal cross-correlations of the price of electricity in the US with crude oil and the natural gas. Phys. A Stat. Mech. Appl. 2021, 572, 125830. [Google Scholar] [CrossRef]
- Gajardo, G.; Kristjanpoller, W. Asymmetric multifractal cross-correlations and time varying features between Latin-American stock market indices and crude oil market. Chaos Solitons Fractals 2017, 104, 121–128. [Google Scholar] [CrossRef]
- Gao, X.L.; Shao, Y.H.; Yang, Y.H.; Zhou, W.X. Do the global grain spot markets exhibit multifractal nature? Chaos Solitons Fractals 2022, 164, 112663. [Google Scholar] [CrossRef]
- Gaio, L.E.; Capitani, D.H.D. Multifractal cross-correlation analysis between crude oil and agricultural futures markets: Evidence from Russia–Ukraine conflict. J. Agribus. Dev. Emerg. Econ. 2025, 15, 19–42. [Google Scholar] [CrossRef]
- Wang, H.Y.; Wang, T.T. Multifractal analysis of the Chinese stock, bond and fund markets. Phys. A Stat. Mech. Appl. 2018, 512, 280–292. [Google Scholar] [CrossRef]
- Wang, Z.; Yan, Y.; Chen, X. Multifractal properties of interest rates in bond market. Procedia Comput. Sci. 2016, 91, 432–441. [Google Scholar] [CrossRef]
- Naeem, M.A.; Farid, S.; Ferrer, R.; Shahzad, S.J.H. Comparative efficiency of green and conventional bonds pre-and during COVID-19: An asymmetric multifractal detrended fluctuation analysis. Energy Policy 2021, 153, 112285. [Google Scholar] [CrossRef]
- Fernandes, L.H.; Silva, J.W.; de Araujo, F.H.; Tabak, B.M. Multifractal cross-correlations between green bonds and financial assets. Financ. Res. Lett. 2023, 53, 103603. [Google Scholar] [CrossRef]
- Kristjanpoller, W.; Tabak, B.M. Comparison of the asymmetric multifractal behavior of green and US bonds against benchmark financial assets. Financ. Innov. 2025, 11, 57. [Google Scholar] [CrossRef]
- Stosic, D.; Stosic, D.; Ludermir, T.B.; Stosic, T. Multifractal behavior of price and volume changes in the cryptocurrency market. Phys. A Stat. Mech. Appl. 2019, 520, 54–61. [Google Scholar] [CrossRef]
- Derbentsev, V.; Kibalnyk, L.; Radzihovska, Y. Modelling multifractal properties of cryptocurrency market. Period. Eng. Nat. Sci. (PEN) 2019, 7, 690–701. [Google Scholar] [CrossRef]
- Bariviera, A.F. One model is not enough: Heterogeneity in cryptocurrencies’ multifractal profiles. Financ. Res. Lett. 2021, 39, 101649. [Google Scholar] [CrossRef]
- da Silva Filho, A.C.; Maganini, N.D.; de Almeida, E.F. Multifractal analysis of Bitcoin market. Phys. A Stat. Mech. Appl. 2018, 512, 954–967. [Google Scholar] [CrossRef]
- Kristjanpoller, W.; Bouri, E. Asymmetric multifractal cross-correlations between the main world currencies and the main cryptocurrencies. Phys. A Stat. Mech. Appl. 2019, 523, 1057–1071. [Google Scholar] [CrossRef]
- Kristjanpoller, W.; Bouri, E.; Takaishi, T. Cryptocurrencies and equity funds: Evidence from an asymmetric multifractal analysis. Phys. A Stat. Mech. Appl. 2020, 545, 123711. [Google Scholar] [CrossRef]
- Stavroyiannis, S.; Babalos, V.; Bekiros, S.; Lahmiri, S.; Uddin, G.S. The high frequency multifractal properties of Bitcoin. Phys. A Stat. Mech. Appl. 2019, 520, 62–71. [Google Scholar] [CrossRef]
- Lahmiri, S.; Bekiros, S. Big data analytics using multi-fractal wavelet leaders in high-frequency Bitcoin markets. Chaos Solitons Fractals 2020, 131, 109472. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhuang, X.-t.; Jin, X. Measuring multifractality of stock price fluctuation using multifractal detrended fluctuation analysis. Phys. A Stat. Mech. Appl. 2009, 388, 2189–2197. [Google Scholar] [CrossRef]
- Dewandaru, G.; Masih, R.; Bacha, O.I.; Masih, A.M.M. Developing trading strategies based on fractal finance: An application of MF-DFA in the context of Islamic equities. Phys. A Stat. Mech. Appl. 2015, 438, 223–235. [Google Scholar] [CrossRef]
- de Oliveira, A.S.; Ceretta, P.S.; Albrecht, P. Performance comparison of multifractal techniques and artificial neural networks in the construction of investment portfolios. Financ. Res. Lett. 2023, 55, 103814. [Google Scholar] [CrossRef]
- Wang, F.; Ye, X.; Chen, H.; Wu, C. A portfolio strategy of stock market based on mean-MF-X-DMA model. Chaos Solitons Fractals 2021, 143, 110645. [Google Scholar] [CrossRef]
- Muzy, J.F.; Sornette, D.; Delour, J.; Arneodo, A. Multifractal returns and hierarchical portfolio theory. Quant. Financ. 2001, 1, 131. [Google Scholar] [CrossRef]
- Wu, X.; Wang, P.; Yang, C.; Xiao, Y. A Study of Fractal Dual Momentum Investment Strategy Under the Constraint of Multi-Fractal Characteristics of Stock Market. Fractals 2024, 32, 2450041. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Q.; Zhang, Z.; Chen, L. A risk measure of the stock market that is based on multifractality. Phys. A Stat. Mech. Appl. 2022, 596, 127203. [Google Scholar] [CrossRef]
- Batten, J.A.; Kinateder, H.; Wagner, N. Multifractality and value-at-risk forecasting of exchange rates. Phys. A Stat. Mech. Appl. 2014, 401, 71–81. [Google Scholar] [CrossRef]
- Brandi, G.; Di Matteo, T. On the statistics of scaling exponents and the multiscaling value at risk. Eur. J. Financ. 2022, 28, 1361–1382. [Google Scholar] [CrossRef]
- Wei, Y.; Chen, W.; Lin, Y. Measuring daily Value-at-Risk of SSEC index: A new approach based on multifractal analysis and extreme value theory. Phys. A Stat. Mech. Appl. 2013, 392, 2163–2174. [Google Scholar] [CrossRef]
- Cho, P.; Lee, M. Forecasting the volatility of the stock index with deep learning using asymmetric Hurst exponents. Fractal Fract. 2022, 6, 394. [Google Scholar] [CrossRef]
- Li, H.; Chun, W.; Wu, X.; Luo, L. Multi-asset portfolio model optimization based on mean multifractal detrended cross correlation analysis. Math. Comput. Model. Dyn. Syst. 2024, 30, 736–757. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, X.; Zhang, L.; Chen, Z. The evaluation of mean-detrended cross-correlation analysis portfolio strategy for multiple risk assets. Eval. Rev. 2022, 46, 138–164. [Google Scholar] [CrossRef]
- Chun, W.; Li, H.; Wu, X. Portfolio model under fractal market based on mean-DCCA. Fractals 2020, 28, 2050142. [Google Scholar] [CrossRef]
- Cho, P.; Lee, M. Dynamic Black–Litterman Portfolios Incorporating Asymmetric Fractal Uncertainty. Fractal Fract. 2024, 8, 642. [Google Scholar] [CrossRef]
- Lux, T.; Morales-Arias, L.; Sattarhoff, C. Forecasting daily variations of stock index returns with a multifractal model of realized volatility. J. Forecast. 2014, 33, 532–541. [Google Scholar] [CrossRef]
- Kojić, M.; Mitić, P.; Minović, J. Gold and Sustainable stocks in the US and EU: Nonlinear analysis based on multifractal detrended Cross-Correlation analysis and Granger Causality. Fractal Fract. 2023, 7, 738. [Google Scholar] [CrossRef]
- Zhou, W.X. Multifractal detrended cross-correlation analysis for two nonstationary signals. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2008, 77, 066211. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Podobnik, B.; Stanley, H.E. Detrended Cross-Correlation Analysis: A New Method for Analyzing Two Nonstationary Time Series. Phys. Rev. Lett. 2008, 100, 084102. [Google Scholar] [CrossRef] [PubMed]
- Alvarez-Ramirez, J.; Rodriguez, E.; Echeverria, J.C. A DFA approach for assessing asymmetric correlations. Phys. A Stat. Mech. Its Appl. 2009, 388, 2263–2270. [Google Scholar] [CrossRef]
- Podobnik, B.; Grosse, I.; Horvatić, D.; Ilic, S.; Ivanov, P.C.; Stanley, H.E. Quantifying cross-correlations using local and global detrending approaches. Eur. Phys. J. B 2009, 71, 243–250. [Google Scholar] [CrossRef]
- Zebende, G.F. DCCA cross-correlation coefficient: Quantifying level of cross-correlation. Phys. A Stat. Mech. Its Appl. 2011, 390, 614–618. [Google Scholar] [CrossRef]
- Theiler, J.; Eubank, S.; Longtin, A.; Galdrikian, B.; Farmer, J.D. Testing for nonlinearity in time series: The method of surrogate data. Phys. D Nonlinear Phenom. 1992, 58, 77–94. [Google Scholar] [CrossRef]
- Schreiber, T.; Schmitz, A. Improved surrogate data for nonlinearity tests. Phys. Rev. Lett. 1996, 77, 635. [Google Scholar] [CrossRef]
- Barunik, J.; Aste, T.; Di Matteo, T.; Liu, R. Understanding the source of multifractality in financial markets. Phys. A Stat. Mech. Appl. 2012, 391, 4234–4251. [Google Scholar] [CrossRef]
- Podobnik, B.; Fu, D.; Stanley, H.E.; Ivanov, P.C. Power-law autocorrelated stochastic processes with long-range cross-correlations. Eur. Phys. J. B 2007, 56, 47–52. [Google Scholar] [CrossRef]






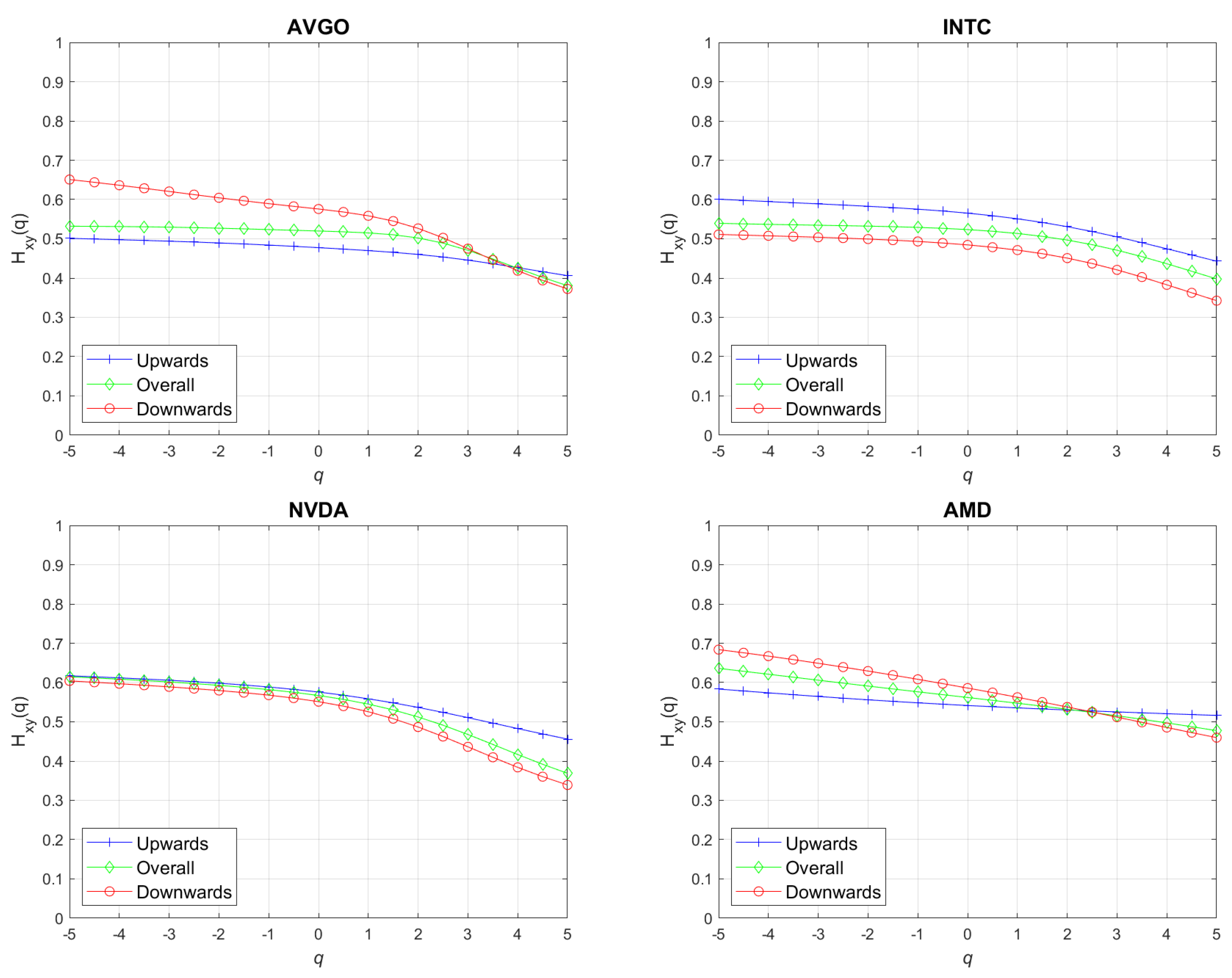
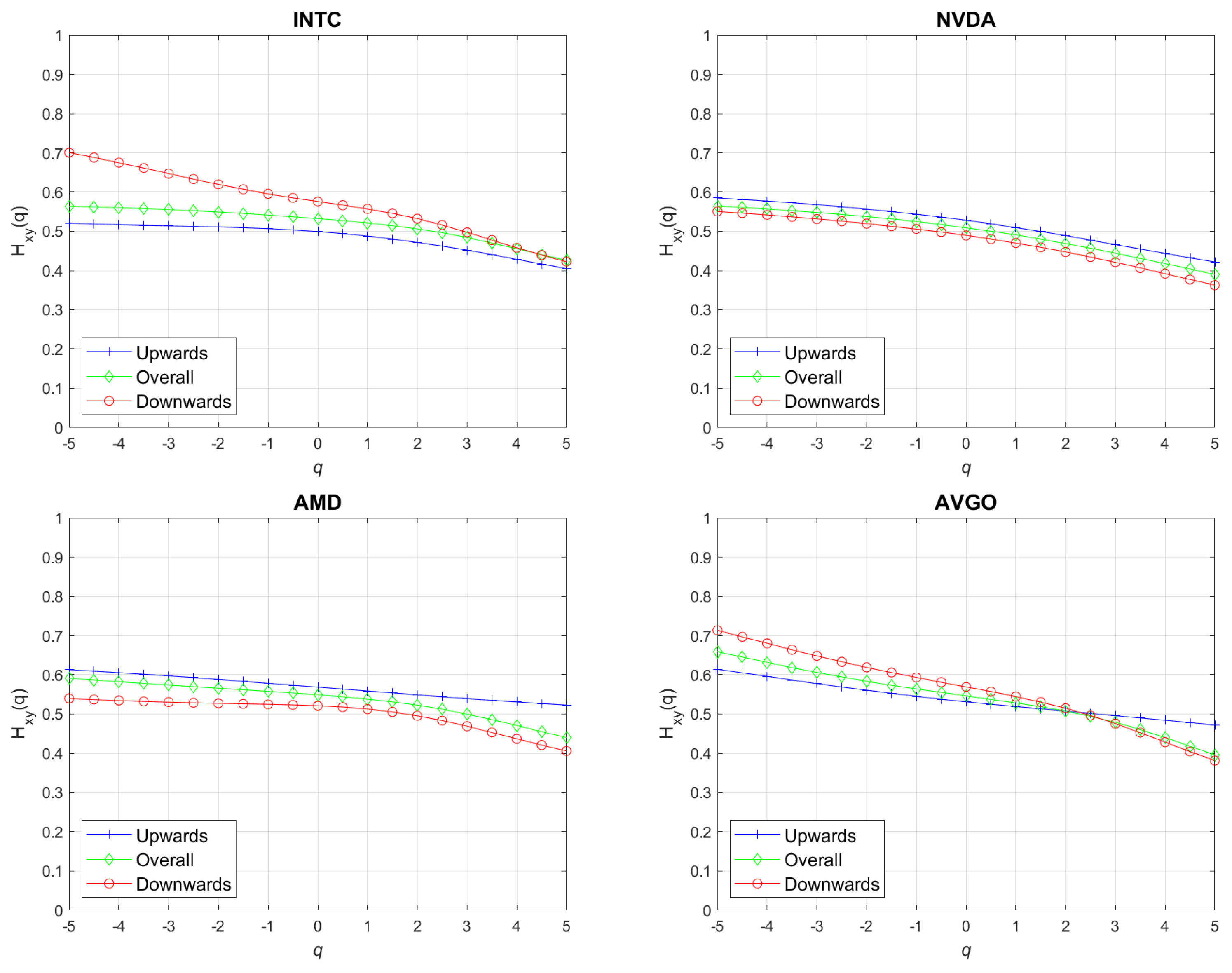

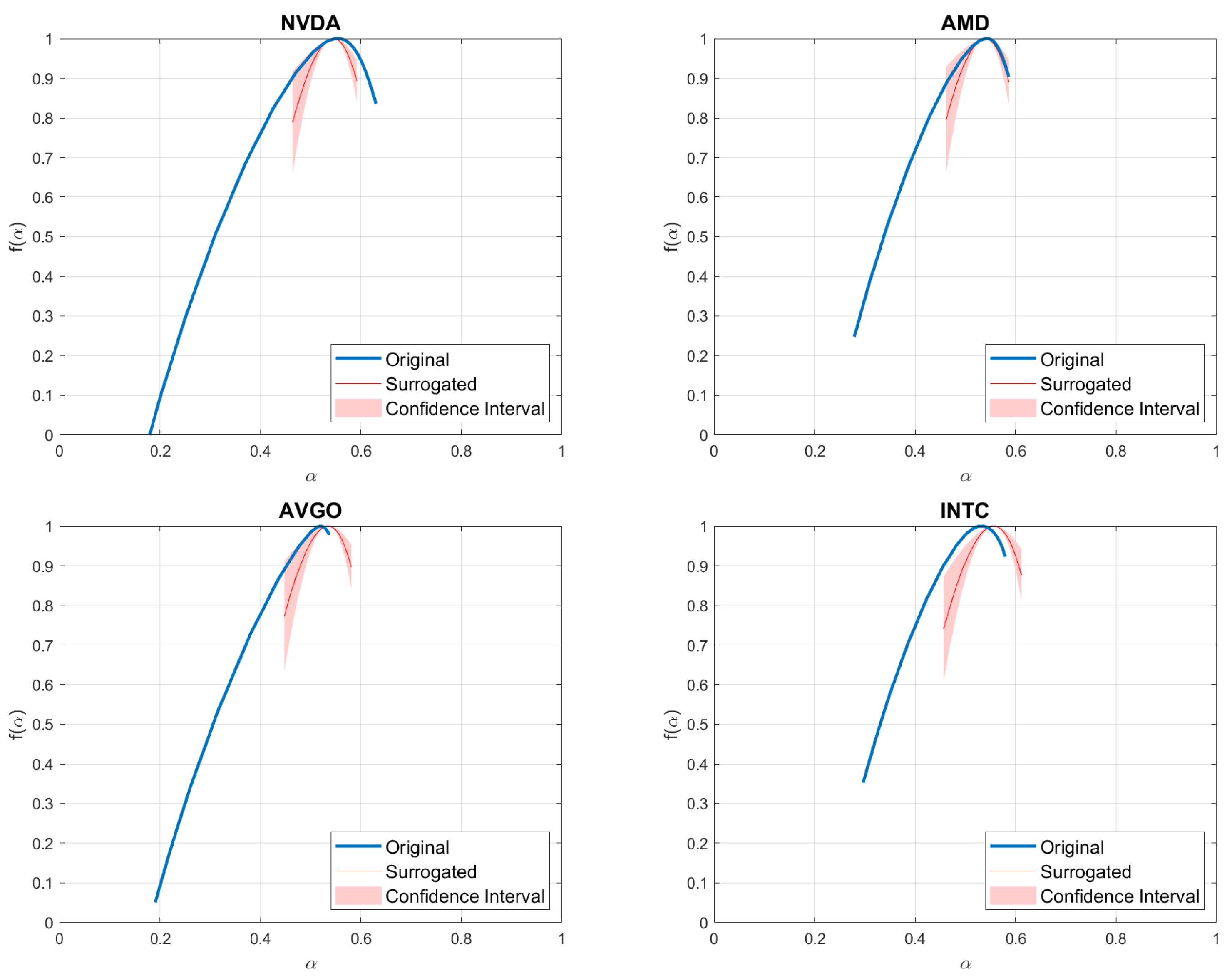

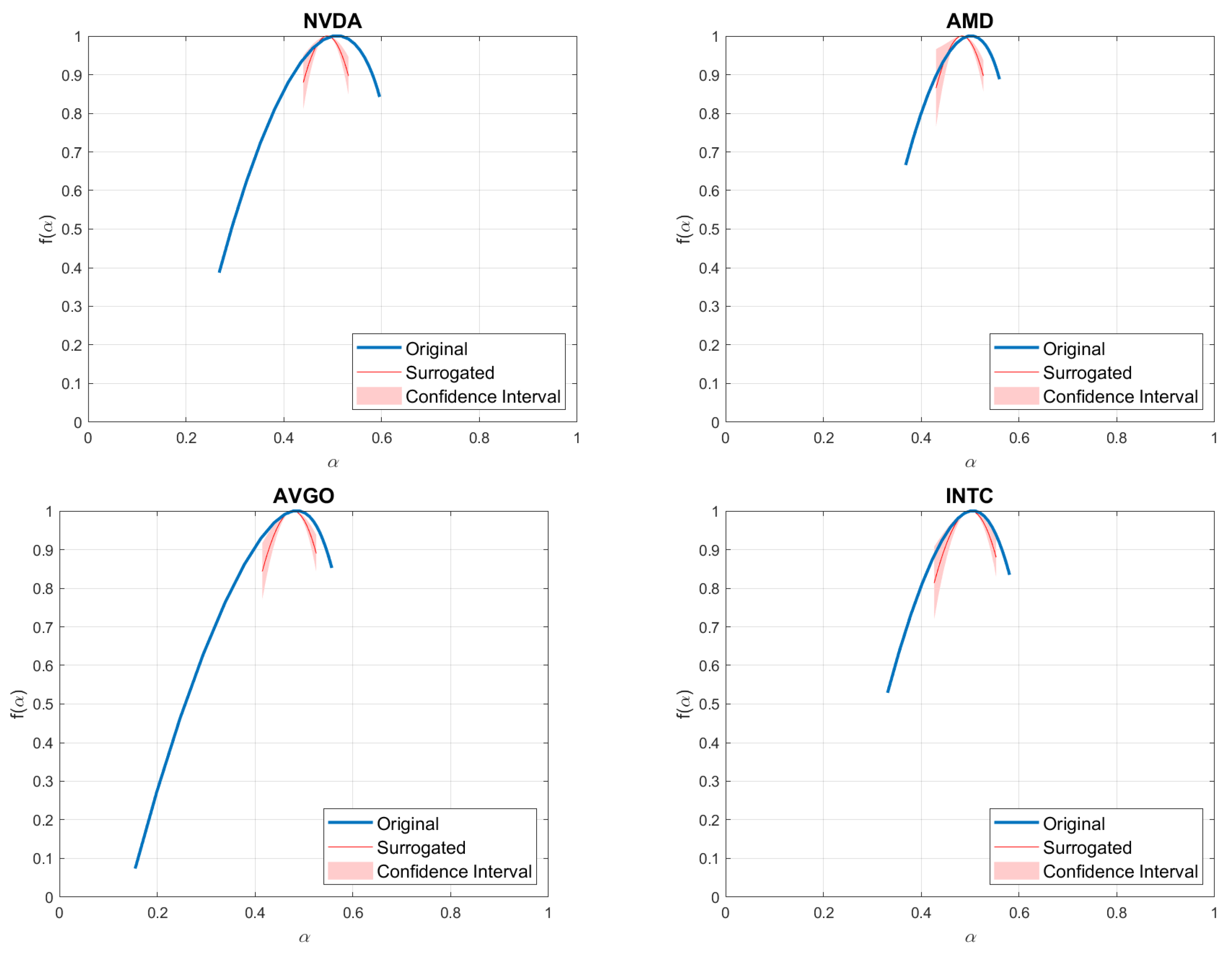

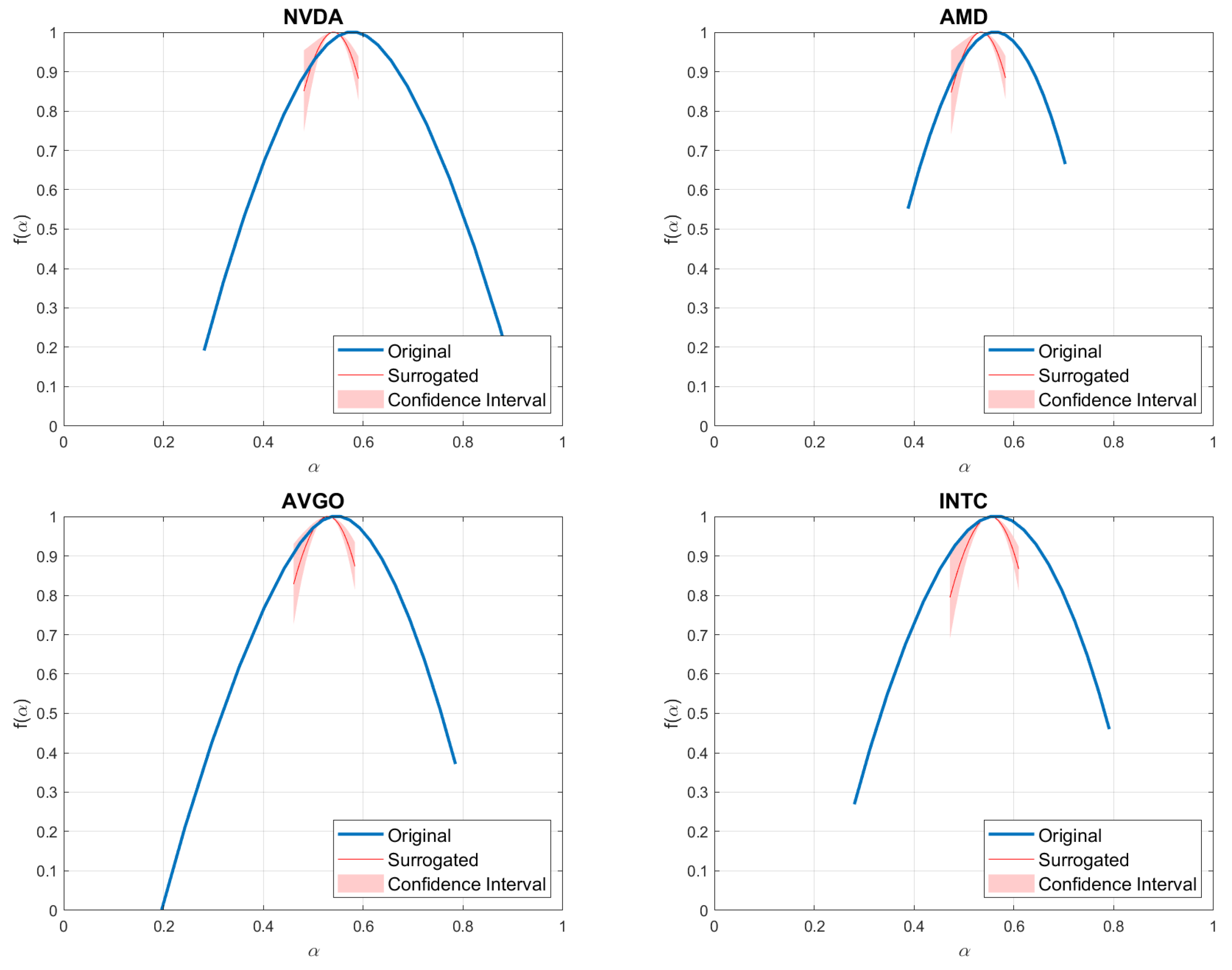
| NVDA | AMD | AVGO | INTC | DJI | XAU | EUR | WTI | BTC | |
|---|---|---|---|---|---|---|---|---|---|
| Mean | 0.22% | 0.15% | 0.12% | −0.02% | 0.03% | 0.03% | −0.01% | 0.01% | 0.23 |
| St. Dev. | 3.08% | 3.63% | 2.38% | 2.28% | 1.10% | 0.89% | 0.50% | 2.89% | 4.39 |
| Min | −20.79% | −27.75% | −22.19% | −30.19% | −13.09% | −5.90% | −2.40% | −41.77% | −49.73 |
| Max | 26.37% | 42.06% | 21.86% | 17.83% | 10.83% | 4.69% | 3.04% | 40.35% | 24.08 |
| NVDA | AMD | AVGO | INTC | DJI | XAU | EUR | WTI | BTC | |
|---|---|---|---|---|---|---|---|---|---|
| NVDA | 1.00 | ||||||||
| AMD | 0.03 | 1.00 | |||||||
| AVGO | 0.09 | 0.37 | 1.00 | ||||||
| INTC | 0.27 | 0.08 | 0.04 | 1.00 | |||||
| DJI | 0.20 | 0.08 | 0.06 | 0.06 | 1.00 | ||||
| XAU | 0.50 | 0.01 | 0.04 | 0.12 | 0.20 | 1.00 | |||
| EUR | 0.41 | 0.03 | 0.07 | 0.12 | 0.14 | 0.59 | 1.00 | ||
| WTI | 0.56 | 0.03 | 0.05 | 0.18 | 0.16 | 0.60 | 0.45 | 1.00 | |
| BTC | 0.57 | 0.05 | 0.03 | 0.16 | 0.16 | 0.47 | 0.38 | 0.50 | 1.00 |
| Stock | DJI | XAU | EUR | WTI | BTC |
|---|---|---|---|---|---|
| NVDA | 0.2190 | 0.1860 | 0.1740 | 0.2459 | 0.2857 |
| AMD | 0.1376 | 0.1268 | 0.1027 | 0.1507 | 0.1585 |
| AVGO | 0.1513 | 0.2279 | 0.1873 | 0.2176 | 0.2630 |
| INTC | 0.1376 | 0.1416 | 0.1223 | 0.1931 | 0.2565 |
| Stock | DJI | XAU | EUR | WTI | BTC | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| NVDA | 0.4646 | 0.5536 | 0.4150 | 0.5307 | 0.3281 | 0.5088 | 0.4803 | 0.5661 | 0.6403 | 0.5781 |
| AMD | 0.3075 | 0.5426 | 0.2691 | 0.5212 | 0.1919 | 0.5018 | 0.3237 | 0.5487 | 0.3151 | 0.5619 |
| AVGO | 0.3451 | 0.5198 | 0.5306 | 0.4927 | 0.4020 | 0.4846 | 0.4371 | 0.5271 | 0.5884 | 0.5463 |
| INTC | 0.2825 | 0.5320 | 0.3296 | 0.5229 | 0.2495 | 0.5054 | 0.3771 | 0.5494 | 0.5106 | 0.5642 |
| Stock | DJI | XAU | EUR | WTI | BTC | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Upward | Downward | Upward | Downward | Upward | Downward | Upward | Downward | Upward | Downward | |
| NVDA | 0.1790 | 0.2441 | 0.1791 | 0.1727 | 0.1629 | 0.1881 | 0.1610 | 0.2649 | 0.1631 | 0.3279 |
| AMD | 0.0947 | 0.2146 | 0.1019 | 0.1383 | 0.1305 | 0.0906 | 0.0905 | 0.1337 | 0.0671 | 0.2241 |
| AVGO | 0.0950 | 0.2785 | 0.1763 | 0.2583 | 0.1680 | 0.1978 | 0.1135 | 0.2254 | 0.1424 | 0.3320 |
| INTC | 0.1162 | 0.2780 | 0.1577 | 0.1685 | 0.1605 | 0.1045 | 0.1142 | 0.2160 | 0.1349 | 0.3494 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kristjanpoller, W. Exploring Multifractal Asymmetric Detrended Cross-Correlation Behavior in Semiconductor Stocks. Fractal Fract. 2025, 9, 292. https://doi.org/10.3390/fractalfract9050292
Kristjanpoller W. Exploring Multifractal Asymmetric Detrended Cross-Correlation Behavior in Semiconductor Stocks. Fractal and Fractional. 2025; 9(5):292. https://doi.org/10.3390/fractalfract9050292
Chicago/Turabian StyleKristjanpoller, Werner. 2025. "Exploring Multifractal Asymmetric Detrended Cross-Correlation Behavior in Semiconductor Stocks" Fractal and Fractional 9, no. 5: 292. https://doi.org/10.3390/fractalfract9050292
APA StyleKristjanpoller, W. (2025). Exploring Multifractal Asymmetric Detrended Cross-Correlation Behavior in Semiconductor Stocks. Fractal and Fractional, 9(5), 292. https://doi.org/10.3390/fractalfract9050292






