Abstract
The first step in investigating fractional difference maps, which do not have periodic points except fixed points, is to find asymptotically periodic and bifurcation points and draw asymptotic bifurcation diagrams. Recently derived equations that allow calculations of asymptotically periodic and bifurcation points contain coefficients defined as slowly converging infinite sums. In this paper, I derive analytic expressions for coefficients of the equations that allow calculations of asymptotically periodic and bifurcation points in fractional difference maps.
PACS:
05.45.Pq; 45.10.Hj
1. Introduction
Fractional difference maps are particular forms of generalized fractional maps, which are Volterra difference equations of convolution type, with the falling factorial kernels. Volterra difference equations of convolution type were investigated even before fractional maps were first introduced in [1] and investigated in [2]. The established results of investigations into Volterra difference convolution equations may be found in a textbook (see Section 6.3 of [3]) and in monographs (see Section 17 of [4,5]). The problems addressed in these books and in [6] are related to the stability of solutions (of fixed points) and existence of periodic solutions. The results, in most cases, are presented in abstract mathematical form. Conditions of the asymptotic stability of generalized fractional maps obtained in [7] depend on the map generating functions (K is a map parameter) and slowly converging sums , . The main objective of this paper is to obtain analytic expressions that define values of for any positive values of l and . Fractional difference maps are generalizations of regular maps obtained as solutions of fractional generalizations of the corresponding difference equations , where the map generating function is . For example, in fractional generalizations of the logistic map (), the map generating function is .
Fractional difference maps are investigated and used in applications in hundreds of papers. They are used to model biological (see, e.g., [8,9]) and socio-economic (see, e.g., [10,11]) systems, memristors (see, e.g., [12]), in image and signal encryption (see, e.g., [13,14]), control systems (see, e.g., [15,16]), etc. Their popularity may be represented by the fact that the paper given in [17], titled “Discrete fractional logistic map and its chaos”, according to the Web of Science, at the moment I am writing this sentence, has been cited 438 times, even though it is known that the fractional difference map introduced in this paper is not a fractional generalization of the logistic map, and all bifurcations diagrams in this paper are incorrect (see [18,19]).
The two main problems that appear when dealing with fractional maps are their complicated finite-time behavior and the asymptotic behavior of the corresponding systems. It is known that continuous and discrete fractional systems may not have periodic solutions except fixed points (see, for example, [20,21]). It has been proven in [22] (see, e.g., Theorem 4 in that paper) that the convergence of trajectories to stable fixed points in fractional difference maps of the orders follows the power law . In [23], the authors showed that in some cases of multidimensional systems of linear fractional difference maps of the orders , convergence to fixed points may follow the power law . It was numerically demonstrated in many papers (see, e.g., [24]) that the convergence of nonlinear fractional difference maps of any positive () orders to any periodic points (stable, or for some limited time, unstable, as in Figure 6.8 from [8]) also may follow the power law. This law could be for as in Figure 10 from [25]. First noticed in [2], cascade of bifurcations type trajectories (CBTTs) represent even more complicated, typical for the fractional and fractional difference maps, behavior. In CBTT, cascades of bifurcations or inverse cascades of bifurcations occur on single trajectories (see [24]). This complexity of evolution on single trajectories also leads to the complexity of approximations of asymptotic bifurcation diagrams (there are no finite-time bifurcation diagrams because there are no finite-time periodic points) based on simulations of single trajectories. These approximations depend on the numbers of iterations and on the initial conditions of the used trajectories. The explanation of this phenomenon is discussed in Section 4 of [26]. This complexity is also used in applications to explain finite-time stable behavior and the breaking of unstable systems with memory (see, e.g., [8,27]).
Although the finite-time behavior of discrete fractional systems is more complicated than the finite-time behavior of regular systems, their asymptotic behavior seems to be similar to the asymptotic behavior of regular systems (see, e.g., review [28]). The structure of bifurcation diagrams, the way in which systems approach the transition to chaos, and asymptotic attractors seem to be similar (no proofs yet). It is also important that asymptotic behavior is important for applications. For example, if we consider live species (which are systems with power law memory) and their organ tissues (which are viscoelastic and may be described by equations with power law memory), as well as the time step which corresponds to a single heartbeat, and investigate their life-time evolution, then the appropriate number of iterations could be of the order . A comparison of an asymptotic bifurcation diagram in the fractional difference logistic map with a bifurcation diagram obtained after iterations may be found in Figure 1 from [26].
Almost all of the hundreds of above-mentioned papers on fractional difference maps contain bifurcation diagrams, which are approximations to the asymptotic bifurcation diagrams. These approximations depend on the initial conditions and the number of iterations. But the asymptotically periodic solutions of fractional difference equations do exist, and the equations for finding these points in generalized fractional maps were derived in [29,30,31]. These equations contain coefficients (l is a period and ), which are slowly converging series. The numerical evaluation of these series, in the case of fractional and fractional difference maps, requires calculations of finite sums of tens of thousands of terms and calculations of the Riemann -function. It is also known, from the stability analysis of discrete fractional systems (see [7]), that, in the case of fractional difference maps, the corresponding series may be summable. These series could be written as sums of fractional binomial coefficients and, in some cases, the analytic expressions for their totals were obtained (see, e.g., calculations in [22,32,33,34]). The equations that define bifurcation points of fractional difference maps [26] also depend on the same coefficients (sums) . This encouraged the author of the present publication to find a way to express as totals of terms containing fractional binomial coefficients and to find their analytic expressions. This is the main objective of the present paper.
Following this introduction, in the preliminaries (Section 2), based on well-known results, we show that all aspects of the asymptotic theory of generalized fractional maps, such as periodic points, bifurcation points, and conditions of stability, strongly depend on the values of (see also a recent review [28]). Then, in Section 3, using a recently derived combinatorial identity (see [35]), we derive analytic expressions for the coefficients (sums) of the equations defining asymptotically periodic and bifurcation points in the case of fractional difference maps. In Section 4, we discuss the validity of our results, their fundamental significance, computational aspects of calculations of asymptotically periodic and bifurcation points of fractional difference maps, and possible applications. Concluding remarks are presented in Section 5. Appendix A contains C-codes for calculations of sums based the analytic formulae derived in this paper and on the numerical algorithm proposed in [29] (Equation (35) in that paper).
2. Preliminaries
For , the generalized universal -family of maps is defined as follows (see [29,30]):
where , is the initial condition, h is the time step of the map, is the order of the map, is a nonlinear function depending on the parameter K, for , and , where . The space for is defined as follows (see [30]):
where is a forward difference operator defined as
In the case of Caputo fractional difference maps, which are defined as solutions of the Caputo h-difference equation [25,36,37],
where , with the initial conditions
the kernel is the falling factorial function:
The definition of the falling factorial is
The falling factorial is asymptotically a power function—i.e.,
The h-falling factorial is defined as
The majority of the introduced, investigated, and used in applications maps are Caputo fractional difference maps.
The following equations define period-l points in generalized fractional maps of the orders [29]:
where
It is easy to see that
In the case of p-dimensional maps () (see [31]),
the periodic points are defined as solutions of the following system of equations:
and additional p equations
Bifurcation points in the maps of the order are defined by the Theorem 1 from [26]:
Theorem 1.
The – bifurcation points, values of with , and the value of the nonlinear parameter of a fractional generalization of a nonlinear one-dimensional map written as the Volterra difference equations of convolution type
where , is the initial condition, h is the time step of the map, α is the order of the map, , for , , and
are defined by the following system of equations:
where
and the elements of the -dimensional matrix A are
3. Sums for -Cycles of Fractional Difference Maps
As one may see from Section 2, all aspects of the asymptotic theory of fractional difference maps depend on the values of the slowly converging sums . As shown in [7], the stability conditions of the map’s fixed points also depend on . This is why obtaining analytic expressions for is an important part of the asymptotic theory of fractional difference maps.
The definition of from [29] for fractional difference maps may be rewritten using the following chain of transformations:
Using absolute convergence of series and the identity (see [35])
where and , for the even and odd periods, we obtain
It follows from the conditions of the validity of Equation (25) that for any integer , Equations (26) and (27) defining are valid only if . The values of for p beyond this interval are defined not by Equation (24) but by the condition of periodicity Equation (22) with period l. It is remarkable that Equations (26) and (27) define as a periodic function with the period l, and thus they correctly define for any integer values of p ().
4. Numerical Simulations and Discussion
Although in [35], Equation (25) is proven for integer values of , it is valid for any real values . To verify this, we can calculate the values of () using Equation (26) for and . A C-code used in these calculations is the second code presented in Appendix A. In Table 1 and Table 2, the output of this code is compared with the output of the first code from the appendix, which is a numerical realization of the formula for an accelerated direct calculation of sums as given in Equation (12) with the kernel Equation (6) derived in [29]—i.e.,
where
and a fast numerical method was used to calculate the values of the Riemann -function.


The computational time on a single processor of one of Courant’s computers is less than s for both C-codes. The relative accuracy of the calculations, in the case of exact calculations, is and it is in the case of approximate calculations. The last row in the tables represents the total , whose theoretical value is zero. This row is added to demonstrate the accuracy of the calculations. An increase in the value of N in the first C-code from Appendix A (approximate calculations according to Equation (29)) does not reduce the values in this row. This means that the error is a rounding computational error resulting from performing hundreds of thousands of operations. It is obvious that both algorithms provide sufficient speed and accuracy for most practical cases.
The computation of the coefficients is a part of the algorithm of the computation of periodic and bifurcation points used in [26,29], where it was applied to investigate the fractional logistic maps (fractional extensions of the map ). It took less than a second to calculate numerically all values. Computations of the periodic points were significantly more time-consuming. They required solving systems of thousands of second-order equations using standard Mathematica and Matlab algorithms. To calculate the data for the bifurcation diagram Figure 1 from [26], the authors used Mathematica’s built-in function FindRoot [38] to solve the system of equations given by Equations (10) and (11). To calculate the bifurcation points for Tables 1 and 2 from [26], the authors used MATLAB’s function fsolve [39] to solve the system of Equations (19)–(21). These algorithms converge only when the initial approximations to the solutions are very close to the real solutions. To draw the bifurcation diagrams, the calculations were performed with a small step in the nonlinear parameter K using the solutions from the previous step as the initial conditions for the next step. An additional time-consuming task was the separation of the stable periodic points from unstable lower-period points. It took a couple of months to calculate the data for the bifurcation diagram Figure 1 and Table 1 from [26]. So, one may see that the analytic formulae for are important but they do not play a critical role in drawing the bifurcation diagrams.
The objective of the present paper is to derive the formulae defining sums . For an example of how to use analytic equations to draw bifurcation diagrams, we refer readers to Figure 1a–f from [26], which represent a detailed comparison of a bifurcation diagram obtained by using Equations (10) and (11) with a bifurcation diagram obtained by performing iterations on single trajectories. Figure 1 in the present paper is an illustration of a simplified version of Figure 1 from [26] to compare bifurcation diagrams of the fractional difference logistic map of the order obtained using analytic equations (we used the same data as in [26]) with a bifurcation diagram obtained by performing 200 iterations on single trajectories.
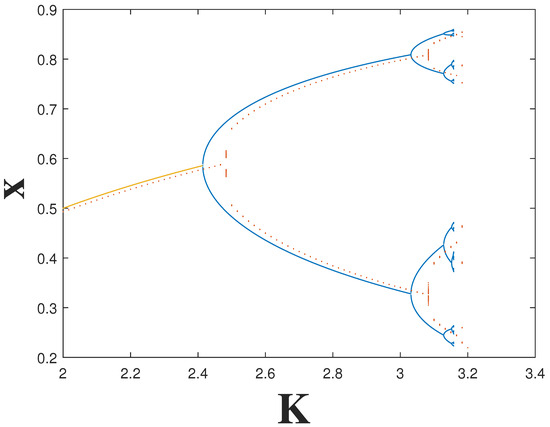
Figure 1.
A bifurcation diagram of the Caputo fractional difference logistic map () of the order . The solid line is a part of the bifurcation diagram from (fixed point) to approximately ( periodic point) obtained by solving Equations (10) and (11). Dots represent points of the initial part of the bifurcation diagram obtained by performing 200 iterations on single trajectories with the initial condition .
The analytic expressions for obtained in this paper may be used to obtain analytic expressions for low-period periodic and bifurcation points where possible. This may be important for the analysis of the low-period behavior of various discrete systems.
Another area of application of the results obtained in this paper is the analysis of the universality in fractional dynamics (for the universality in regular dynamics, see, e.g., [40,41]). The results of the computations presented in Tables 1 and 2 from [26] show that the ratios of the parameter intervals between the consecutive asymptotic bifurcations in fractional maps converge to the Feigenbaum constant [42] but much slower than in the integer case. A proof of universality in the fractional case is more complicated for the following reasons: (a) the periodicity in the fractional case exists only in the asymptotic sense, and the universality should only be the asymptotic universality; (b) fractional maps are maps with memory, and their Poincaré plots (graphs vs. ) used by Feigenbaum in his analysis of universality are less significant because depends on all previous values , . Obtaining analytic expressions for the coefficients of the equations defining asymptotic bifurcation points is a small but important step in the proof of the asymptotic universality in fractional difference maps (discrete systems with the falling factorial memory).
5. Conclusions
In this paper, I derived the analytic expressions for the coefficients of the equations that define periodic and bifurcation points in fractional difference maps of the orders (Equations (26) and (27)). The purpose of this publication was not to investigate any particular fractional difference map, but rather to provide a framework that will enable researchers to investigate maps with fractional factorial memory. The results will allow researchers to draw asymptotic bifurcation diagrams of fractional difference maps by solving Equations (10) and (11) in the case of maps of the orders , or Equations (15) and (16) in the case of multidimensional fractional maps. Calculations of coefficients (sums) of these equations should be a part of the corresponding numerical algorithms.
Using analytic expressions derived in this paper instead of adding tens of thousands of terms based on Equation (35) from [29] will make calculations of the coefficients thousands of times faster, more accurate, and will make it unnecessary to use Tables 2 and 4 from [29] for finding .
I should note two outstanding problems related to this paper to be addressed in further publications:
- •
- In this paper, the validity of the identity given in Equation (25) for fractional values of is demonstrated numerically, but the theoretical proof is still lacking.
- •
- Based on the results of numerical simulations, in [26], the authors made a conjecture that the Feigenbaum number exists in fractional difference maps and has the same value as in regular maps. Derivation of the analytic expression for in this paper is a small step which, in conjunction with Theorem 1 from [26] defining bifurcation points, may lead to a theoretical proof of this conjecture.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the author.
Acknowledgments
The author acknowledges support from Yeshiva University and expresses his gratitude to the administration of the Courant Institute of Mathematical Sciences at NYU for the opportunity to complete all computations at Courant.
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A
C-codes used to calculate based on Equation (35) from [29]:
#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#define NIter 19999.1
#define l 4
double Zeta(double s);
double gamma(double xx);
main(int argc, char *argv[])
{
double x, sum, S[l], SZ[l], St, S1, S2, S3, alp, beta, Z2, Z3, Z4, g1, Ssum;
int j, k, m;
FILE *in, *out;
if(argc > 2) {
if( (in = fopen(argv[1],"r")) == NULL) {
printf("Can’t open file %s\n", argv[1]);
exit(1); }
fscanf(in, "%le", &alp);
fclose(in); }
if( (out = fopen(argv[2],"w")) == NULL) {
printf("Can’t open file %s\n", argv[2]);
exit(1); }
k=0;
Ssum=0;
S1=S2=S3=0.;
while(k<NIter)
{
k++;
S1+=exp((alp-2.)*log(k));
S2+=exp((alp-3.)*log(k));
S3+=exp((alp-4.)*log(k));
}
Z2=Zeta(2-alp)-S1;
Z3=Zeta(3-alp)-S2;
Z4=Zeta(4-alp)-S3;
beta=1.-alp;
g1=gamma(alp-1.);
for(j=0; j<l; j++)
{
St=g1;
for(k=0; k<j; k++)
St=St*(alp+k-1)/(k+1);
S[j]=St;
k=0.;
while(k<NIter)
{
k++;
for(m=0; m<l; m++)
St=St*(l*(k-1)+j+alp-1+m)/(l*(k-1)+j+1+m);
S[j]+=St;
}
S[j]=beta*(S[j]+ exp((alp-2.)*log(l))*(Z2 +0.5*(alp-2.)/l*((2*j+alp-1.)*Z3+
(alp-3.)*(3.*(2*j+alp-1)*(2*j+alp-1)-alp+1.)*Z4/(12.*l))));
fprintf(out, "%17.15f \n", S[j]);
Ssum=Ssum+S[j];
}
fprintf(out, "%le, %17.15f \n", alp, Ssum);
fclose(out);
}
and on Equation (26) derived in this paper:
#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#define n 2
double gamma(double xx);
main(int argc, char *argv[])
{
double x, sum, S[2*n], alp, g1, Ssum;
int i, j, m;
FILE *in, *out;
if(argc > 2) {
if( (in = fopen(argv[1],"r")) == NULL) {
printf("Can’t open file %s\n", argv[1]);
exit(1); }
fscanf(in, "%le", &alp);
fclose(in); }
if( (out = fopen(argv[2],"w")) == NULL) {
printf("Can’t open file %s\n", argv[2]);
exit(1); }
g1=gamma(alp)* exp((-alp)*log(2.))/n;
j=1;
Ssum=0;
for(i=0; i<2*n; i++)
{
j=-j;
S[i]=1;
for(m=1; m<n; m++)
{
S[i]=S[i]+2.0*exp((1.-alp)*log(cos(3.141592653589793*m/2.0/n)))
*cos(3.141592653589793*m*(2.0*(i+1)+alp-3)/2.0/n);
}
S[i]=g1*j*S[i];
fprintf(out, "%17.15f \n", S[i]);
}
Ssum=Ssum+S[i];
fprintf(out, "%le, %17.15f \n", alp, Ssum);
fclose(out);
}
Here, Zeta(double s) and gamma(double xx) are some standard algorithms for calculations of the Riemann -function and the Gamma function freely available on the Internet. They are also available on request from the author.
References
- Tarasov, V.E.; Zaslavsky, G.M. Fractional equations of kicked systems and discrete maps. J. Phys. A 2008, 41, 435101. [Google Scholar] [CrossRef]
- Edelman, M.; Tarasov, V.E. Fractional standard map. Phys. Lett. A 2009, 374, 279–285. [Google Scholar] [CrossRef]
- Elaydi, S. An Introduction to Difference Equations, 3rd ed.; Springer: New York, NY, USA, 2005; Undergraduate Texts in Mathematics. [Google Scholar]
- Gil, M.I. Difference Equations in Normed Spaces: Stability and Oscillation; Elsevier: Amsterdam, The Netherlands, 2007; Volume 206, North Holland Mathematics Studies. [Google Scholar]
- Kostić, M. Almost Periodic Type Solutions to Integro-Differential-Difference Equations; W. de Gruyter: Berlin, Germany, 2025. [Google Scholar]
- Minh, N.V. On the asymptotic behaviour of Volterra difference equations. J. Differ. Equ. Appl. 2013, 19, 1317–1330. [Google Scholar] [CrossRef]
- Edelman, M. Stability of Fixed Points in Generalized Fractional Maps of the Orders 0 < α < 1. Nonlin. Dyn. 2023, 111, 10247–10254. [Google Scholar] [CrossRef]
- Edelman, M. Evolution of systems with power-law memory: Do we have to die? (Dedicated to the Memory of Valentin Afraimovich). In Demography of Population Health, Aging and Health Expenditures; Skiadas, C.H., Skiadas, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; pp. 65–85. [Google Scholar]
- Selvam, A.G.M.; Vianny, D.A. Discrete fractional order SIR epidemic model of childhood diseases with constant vaccination and its stability. Int. J. Tech. Innova. Mod. Engin. Sci. 2018, 4, 405–410. [Google Scholar]
- Tarasov, V.E.; Tarasova, V.V. Economic Dynamics with Memory: Fractional Calculus Approach; De Gruyter: Berlin, Germany; Boston, MA, USA, 2021. [Google Scholar]
- Tarasov, V.E.; Tarasova, V.V. Logistic map with memory from economic model. Chaos. Soliton. Fract. 2017, 95, 84–91. [Google Scholar] [CrossRef]
- He, S.; Sun, K.; Peng, Y.; Wang, L. Modeling of discrete fracmemristor and its application. AIP Adv. 2020, 10, 015332. [Google Scholar] [CrossRef]
- Huang, L.-L.; Baleanu, D.; Wu, G.-C.; Zeng, S.-D. A new application of the fractional logistic map. Rom. J. Phys. 2016, 61, 1172–1179. [Google Scholar]
- Ding, D.; Wang, J.; Wang, M.; Yang, Z.; Wang, W.; Niu, Y.; Xu, X. Controllable multistability of fractional-order memristive coupled chaotic map and its application in medical image encryption. Eur. Phys. J. Plus 2023, 138, 908. [Google Scholar] [CrossRef]
- Ostalczyk, P. Discrete Fractional Calculus: Applications in Control and Image Processing; World Scientific: River Edge, NJ, USA, 2016. [Google Scholar]
- Ortigueira, M. Discrete-time fractional difference calculus: Origins, evolutions, and new formalisms. Fractal Fract. 2023, 7, 502. [Google Scholar] [CrossRef]
- Wu, G.-C.; Baleanu, D. Discrete fractional logistic map and its chaos. Nonlin. Dyn. 2014, 75, 283–287. [Google Scholar]
- Edelman, M. Fractional maps and fractional attractors. Part ii: Fractional difference α-families of maps. Discont. Nonlinearit. Complex 2015, 4, 391–402. [Google Scholar]
- Peng, Y.; Sun, K.; He, S.; Wang, L. Comments on discrete fractional logistic map and its chaos. Nonlin. Dyn. 2019, 97, 897–901. [Google Scholar]
- Jagan Mohan, J. Quasi-periodic solutions of fractional nabla difference systems. Fract. Differ. Calc. 2017, 7, 339–355. [Google Scholar]
- Kaslik, E.; Sivasundaram, S. Nonexistence of periodic solutions in fractional order dynamical systems and a remarkable difference between integer and fractional order derivatives of periodic functions. Nonlinear Anal. Real World Appl. 2012, 13, 1489–1497. [Google Scholar]
- Anh, P.T.; Babiarz, A.; Czornik, A.; Niezabitowski, M.; Siegmund, S. Asymptotic properties of discrete linear fractional equations. B. Pol. Acad. Sci.-Tech. 2019, 67, 749–759. [Google Scholar]
- Cermák, J.; Kisela, T.; Nechvátal, L. Stability regions for linear fractional differential systems and their discretizations. Appl. Math. Comput. 2013, 219, 7012–7022. [Google Scholar]
- Edelman, M. Dynamics of nonlinear systems with power-law memory. In Handbook of Fractional Calculus with Applications: Applications in Physics; Tarasov, V.E., Ed.; De Gruyter: Berlin, Germany, 2019; Volume 4, pp. 103–132. [Google Scholar]
- Edelman, M. Caputo standard α-family of maps: Fractional difference vs. fractional. Chaos 2014, 24, 023137. [Google Scholar]
- Edelman, M.; Helman, A.B.; Smidtaite, R. Bifurcations and transition to chaos in generalized fractional maps of the orders 0 < α < 1. Chaos 2023, 33, 063123. [Google Scholar] [CrossRef]
- Uzdila, E.; Telksniene, I.; Telksnys, T.; Ragulskis, M. Finite-Time Stabilization of Unstable Orbits in the Fractional Difference Logistic Map. Fractal. Fract. 2023, 7, 570. [Google Scholar] [CrossRef]
- Edelman, M. Periodic Points, Stability, Bifurcations, and Transition to Chaos in Generalized Fractional Maps. IFAC-PapersOnLine 2024, 58, 131–142. [Google Scholar] [CrossRef]
- Edelman, M. Cycles in asymptotically stable and chaotic fractional maps. Nonlin. Dyn. 2021, 104, 2829–2841. [Google Scholar] [CrossRef]
- Edelman, M.; Helman, A.B. Asymptotic cycles in fractional maps of arbitrary positive orders. Fract. Calc. Appl. Anal. 2022, 25, 181–206. [Google Scholar] [CrossRef]
- Edelman, M. Asymptotic cycles in fractional generalizations of Multidimensional maps. Fract. Calc. Appl. Anal. 2025, 28, 24–37. [Google Scholar] [CrossRef]
- Abu-Saris, R.; Al-Mdallal, Q. On the asymptotic stability of linear system of fractional-order difference equations. Fract. Calc. Appl. Anal. 2013, 16, 613–629. [Google Scholar] [CrossRef]
- Čermák, J.; Győri, I.; Nechvátal, L. On explicit stability conditions for a linear fractional difference system. Fract. Calc. Appl. Anal. 2015, 18, 651–672. [Google Scholar]
- Mozyrska, D.; Wyrwas, M. The z-transform method and delta type fractional difference operators. Discret. Dyn. Nat. Soc. 2015, 2015, 852734. [Google Scholar] [CrossRef]
- Benjamin, A.T.; Chen, B.; Kindred, K. Sums of evenly spaced binomial coefficients. Maths. Mag. 2010, 83, 370–373. [Google Scholar]
- Chen, F.; Luo, X.; Zhou, Y. Existence Results for Nonlinear Fractional Difference Equation. Adv. Differ. Eq. 2011, 2011, 713201. [Google Scholar] [CrossRef]
- Wu, G.-C.; Baleanu, D.; Zeng, S.-D. Discrete chaos in fractional sine and standard maps. Phys. Lett. A 2014, 378, 484–487. [Google Scholar] [CrossRef]
- Wolfram Language & System Documentation Center. FindRoot. Available online: https://reference.wolfram.com/language/ref/FindRoot.html (accessed on 31 March 2025).
- MATLAB Help Center. fsolve. Available online: https://www.mathworks.com/help/optim/ug/fsolve.html (accessed on 31 March 2025).
- Cvitanovic, P. Universality in Chaos; Taylor & Francis Group: New York, NY, USA, 1989. [Google Scholar]
- Feigenbaum, M.J. Quantitative universality for a class of nonlinear transformations. J. Stat. Phys. 1978, 19, 25–52. [Google Scholar] [CrossRef]
- Feigenbaum Constants. Wikipedia. Available online: https://en.wikipedia.org/wiki/Feigenbaum_constants (accessed on 31 March 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).