Abstract
The fractal characteristics of soil microstructures, including the size, distribution, and dynamic evolution process of soil particles, cracks, and intergranular pores, are important factors influencing the macroscopic physical properties of soils. Quantitative characterization, qualitative analysis, and the impact of fractal characteristics on macroscopic properties have been important research directions in recent years. This paper summarizes the research status on soil microstructure fractal characteristics, elaborating on the kinds of soil fractal characteristics, the calculation methods of fractal characteristic parameters, and the influence of fractal characteristics on macroscopic properties. Based on existing research results, this paper proposes that future research on soil microstructure fractal characteristics should focus on the following aspects: (1) advancing fractal characteristic research towards higher precision and multi-dimensionality to reveal the internal relations between soil fractal characteristics and macroscopic physical properties; (2) strengthening interdisciplinary collaboration to promote theoretical innovation in fractal analysis and build a more comprehensive system for studying the evolution of soil fractal characteristics; and (3) a close integration with engineering tests to promote the application and transformation of research results, providing valuable references for optimizing construction schemes and improving the service performance of engineering structures.
1. Introduction
As an essential component of the earth’s surface in nature, soil has a complex composition and structure. It is a typical porous medium material with discontinuous and heterogeneous properties. The size, composition, and dynamic evolution of soil particles, cracks, and intergranular pores directly influence the macroscopic physical and mechanical properties of soil [1,2]. Fractal geometry provides an effective means to describe the complex and irregular shapes found in nature. The existing research has found that the size and distribution of particles, cracks, and intergranular pores in soil reveal fractal characteristics, and fractal characteristics at different scales exhibit self-similarity, meaning that the local and overall structures present similar geometrical forms statistically [3]. In addition, under the influence of primary sedimentary, stress history, and environmental factors, differences in particle size, arrangement, and pore morphology emerge within the soil’s internal spatial distribution, exhibiting heterogeneity and anisotropy [4,5]. Through a comprehensive analysis of self-similarity, heterogeneity, and anisotropy based on fractal theory, the complexity of particles and pores can be qualitatively described and quantitatively characterized, revealing the intrinsic relationship between the microstructure and macroscopic properties of soil. Since the 1980s, in order to solve the difficulties and challenges encountered by soil in terms of strength, deformation, and long-term service performance [6], domestic and foreign researchers have adopted the theories of fractal geometry, fractal measurement, and fractal mechanics [7,8]. Through theoretical research, laboratory tests, and modeling analysis, quantitative and qualitative studies have been carried out on the size, shape, and contact mode of soil particles, as well as the size, quantity, area, and connectivity of pores and pore diameters [9,10,11], revealing the self-similarity of soil microstructures and opening up new approaches and methods to reveal the evolution law and influence mechanism of soil macroscopic physical, mechanical, and chemical properties from the micro-perspective [12].
Li et al. [13] found that after F1 reinforcement, the fractal dimension of pore structure distribution in loess decreased from 1.244 to 1.076, the total pore area and pore quantity decreased significantly, and the density and carrying capacity increased significantly. Xu et al. [3] found that the fractal dimension of pore distribution in saturated soft soil particles decreased as porosity decreased, and the fractal dimension of particle distribution increased as the soil became denser. Kong et al. [14] found that an increase in the fractal dimension of soil can enhance its strength at low freezing temperatures. He et al. [15] found that both the cohesion and internal friction angle of gravelly soil decreased as the fractal dimension increased. Sun et al. [16] found that the unconfined compressive strength of cement-reinforced frozen clay increased as the fractal dimension of pore area decreased but decreased as the fractal dimension of pore volume increased. In current research, the quantitative characterization of the relationship between soil microstructures and macroscopic properties using fractal dimensions remains insufficient. For instance, a decrease in the fractal dimension of loess and soft soil enhances compactness and bearing capacity, while an increase in the fractal dimension of frozen soil improves strength. Conversely, gravel soil exhibits reduced strength with increasing fractal dimension. Despite these findings, the contradictions between different soil types lack thorough analysis and comparison of their underlying microscopic mechanisms. Moreover, most studies rely on static tests, failing to address how dynamic processes, such as loading and freeze–thaw cycles, influence the evolution of fractal characteristics in practical engineering scenarios. For example, changes in fractal dimensions may result from multiple factors, including pore compression and particle reorganization.
Xu et al. [7] developed a fractal model incorporating spatial heterogeneity and anisotropy to quantify the relationship between soil microstructural fractal features and macro-mechanical properties. Their results demonstrated significant correlations between fractal dimensions and key parameters, including the water characteristic curve, permeability, diffusion coefficients, and shear strength. Notably, the inflection points of the water characteristic curve aligned with dominant pore size intervals, while the nonlinear shear strength behavior was closely tied to the scale effects of pore fractal characteristics. Zhang et al. [8] discovered that the fractal characteristics of soil pores determine the mobility of water in the soil and affect its actual infiltration capacity; the larger the particle size of the soil, the coarser the pore aperture distribution, and the greater the allowable infiltration capacity of the soil. Wang et al. [17] studied the pore fractal dimension of expansive soil using mercury penetration experiment parameters and the Menger sponge model and found that there is a correlation between the pore fractal dimension of expansive soil and the pore characteristic parameters. Zhu et al. [18] revealed the relationship between the fractal characteristics, cementation degrees, and shear strength of rudstone and found that rudstone has good double fractal characteristics; the cementation degrees significantly affect its shear strength. Kong et al. [10] found that when the confining pressure increased, the cyclic dynamic stress ratio of soft soil increased, while the fractal dimension decreased. In recent years, with the development of high-precision digital image processing technology, researchers have further revealed the heterogeneity and anisotropy of particle contact modes and pore space distribution, establishing the quantitative relationship between the evolution laws of microstructural fractal features and macroproperties of soil. Future research should focus on combining high-resolution imaging techniques to conduct multi-scale analysis of the soil microstructure, providing more accurate theoretical support for engineering practices such as underground projects, soil property improvement, and infrastructure construction.
The existing research has found a correlation between the microstructure of soil and its macroscopic physical and mechanical properties. Fractal theory has attracted widespread attention from researchers studying the soil microstructure. However, research on the fractal characteristics of the soil microstructure is still in its preliminary stage, and the relationship and interaction mechanism between fractal characteristics and macroscopic properties are not yet clear. In view of this, this paper summarizes and analyzes existing research from the perspectives of the fractal characteristics of the soil microstructure, the methods for calculating fractal dimensions, and the influence of fractal characteristics on macroscopic properties. Based on the existing problems and deficiencies in current research, this paper explores the focus and future trends in this field. It provides a valuable reference for studying the fractal characteristics of the soil microstructure and their influence on macroscopic physical and mechanical properties.
2. Fractal Characteristics of Soil
2.1. Soil Particle Fractal Characteristics
Fractal characteristics of soil particles refer to the geometric characteristics shown by the size, shape, and spatial distribution of soil particles, which are mainly characterized by the mass, area, volume distribution, and particle shape parameters [19,20]. The fractal characteristic parameters of particles include the length–diameter ratio, circularity, fractal dimension of particle mass, volume, or surface roughness [21]. The methods for calculating the fractal characteristics of soil particles include Tyler and Wheatcraft model fitting, laser particle analysis technology, computer image analysis, and so on [22,23]. The Tyler and Wheatcraft models calculate the fractal dimensions of soil particle distribution at different scales through linear fitting. Laser particle analysis technology and computer image analysis are used to determine the equivalent diameters and distribution patterns of soil particles, providing data support for the calculation of particle fractal dimensions [22,23,24].
Dong et al. [25] analyzed the particle volume fractal characteristics of 31 loess specimens and found that the fractal dimension of loess particle volume ranged from 2.28 to 2.47, and the relationship between the fractal dimension of clay, silt, and sand was Dclay < Dsilt < Dsand. Moreover, the fragmentation probability P corresponding to Dclay, Dsilt, and Dsand showed scale dependency, decreasing as particle size decreased. Zuo et al. [26] found that the particle fractal dimension of Guiyang red clay was 2.83, and it gradually increased with the increase in soil dry density. Huang et al. [21] used fractal characteristic identification methods (FCIMs) to study soil particle characteristic parameters. The identification process includes microstructure photography, ovality recognition, roughness recognition, particle area calculation, gradation, and major axis inclination statistics. Here, ovality and roughness represent the shape and surface characteristics of soil particles, respectively, while gradation, the porosity ratio, and major axis inclination parameters represent the size, area content, and anisotropy of soil particles, as shown in Figure 1. Additionally, the remolded soil microstructure model was combined with finite element analysis to predict soil permeability using statistically significant soil particle characteristic parameters.
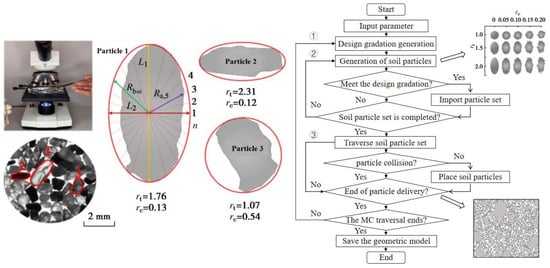
Figure 1.
Characteristic parameter identification algorithm (rt is ovality. rc is roughness. L1 and L2 are the long and short axis lengths; the unit is m. Rb,i and Ra,i are the solid length of the soil particle and the radius length of the ellipse on the same line segment; the unit is m) [21].
The analysis of the soil microstructure using fractal characteristic parameters of particles can not only quantitatively describe the complex microstructure of soil particles and reveal the statistical self-similarity of particle size, shape, and spatial distribution but also qualitatively characterize the heterogeneity and anisotropy of soil. This is of great significance for predicting the macroscopic physical and mechanical properties as well as the evolution laws of soil. Most existing research adopts the traditional single fractal analysis method, which fails to effectively integrate the local fractal characteristics of soil with the study of overall microstructure and soil properties. Therefore, it is necessary to further improve the fractal characteristic calculation methods and observation techniques to advance the in-depth understanding of fractal characteristics in the soil microstructure.
2.2. Pore Fractal Characteristics
The fractal characteristics of soil pores refer to the complex and irregular geometric properties exhibited by the size, quantity, and spatial distribution of pores. These characteristics can be quantitatively described using the fractal dimension, which captures the distribution and complexity of pore structures through parameters such as pore size distribution, quantity, area, volume, and surface area [2,27]. The pore profile of soil can be analyzed using various techniques, including the mercury intrusion method, adsorption method, light scattering method, scanning electron microscopy (SEM), and computed tomography (CT) scanning. The fractal dimension of pores can then be calculated using the box-counting method [28,29].
Yang et al. [30] studied the changing characteristics of effective seepage channel structures in coal under different confining and water pressures. They found that the volume of large pores in the coal specimens changed significantly under varying water and confining pressures, and pores with radii larger than 0.27 μm were identified as effective seepage pores. As shown in Figure 2, in the process of coal seam water injection, the influence of the change of coal internal microstructure caused by the change of water pressure and confining pressure on the seepage characteristics is mainly concentrated in the aperture range of large pore, middle pore, and transition pore. Tao et al. [31] investigated the pore distribution characteristics of Wuhan clay using mercury intrusion porosimetry tests. They found that small pores in the clay exhibit relatively strong fractal characteristics, and their fractal dimensions are unaffected by dry density. Compaction primarily causes the volume compression of large pores, and the overall fractal characteristics of the pores are enhanced, tending toward inherent fractal properties. Mao et al. [32] discovered that the pore distribution and shapes in soft soil exhibit fractal characteristics. After reinforcement, the pore distribution area in soft soil decreases, and the pore size distribution becomes more uniform. The fractal dimension can be used to evaluate the reinforcement effect and mechanical properties of the soil.
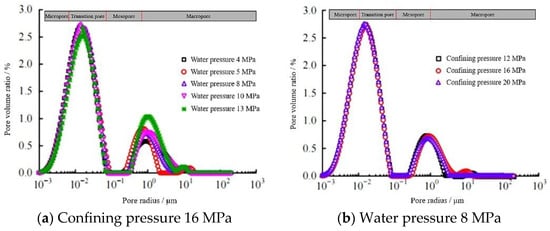
Figure 2.
Variation of pore radius distribution under fixed confining and water pressure conditions [30].
The pore fractal dimension can be used to qualitatively and quantitatively characterize the microstructure of porous materials, and it has been preliminarily applied in soil science and material science. Existing research has found that a single pore fractal dimension cannot fully reflect the multi-scale effects of soil pore structure, leading to the segmentation of pore fractal dimensions within different pore size ranges. Therefore, it is urgent to further optimize the observation and calculation methods of pore characteristic parameters. For example, when the microscopic pores of clay soil are analyzed using the mercury intrusion method, the bottleneck effect of this method results in a higher distribution density of small pores and a lower distribution density of large pores. Consequently, the study of soil pore fractal dimensions should focus on the multi-scale structure effects and advance the development of observation and calculation methods toward higher precision.
2.3. Multi-Fractal Characteristics
Multi-fractal characteristics refer to the self-similarity and heterogeneity of the soil microstructure at different scales, which cannot be quantitatively characterized by a single fractal dimension. It is necessary to consider the variation of fractal dimensions at different scales and establish a quantitative relationship between them and the macroscopic physical and mechanical parameters of soil [33,34]. The multi-fractal characteristic parameters of soil include the generalized fractal dimension spectrum, multi-fractal spectrum function, multi-fractal singularity index, multi-fractal spectrum width, and multi-fractal parameter ratio [35,36,37]. The equivalent diameters and distribution law of soil particles can be measured by a laser particle size analyzer, the fractal dimension D, the multi-fractal singularity index α, the corresponding spectrum function f(α), D1/D0, and Δα, which can be calculated to reflect the heterogeneous level of soil particle size distribution [36,37].
Zhang et al. [38] conducted a three-dimensional multi-fractal analysis to quantitatively characterize soil in a coal mine dump. They found a strong correlation between multi-fractal parameters, which effectively reflected the three-dimensional spatial characteristics of reconstructed soil pores. Ju et al. [39] used CT technology to establish a multiple regression model between the saturated permeability coefficient and the porosity of loess. Their results indicated that multi-fractal characteristics were significantly correlated with soil properties and large pore structures. Bai et al. [40] employed both single and multiple fractal analysis methods to study the particle size distribution (PSD) of loess. As shown in Table 1, when the clay volume fraction varied within a narrow range, the variation in D1 was also limited. The ratio D1/D0 was used to characterize the heterogeneity of PSD; the closer the ratio is to 1, the more uniform the particle distribution.

Table 1.
Correlation analysis between soil texture, fractal, and multi-fractal parameters [40].
Multi-fractal characteristic analysis can calculate the full-scale fractal dimension to a certain extent and reveal the evolution law of microstructure fractal characteristics as the physical and mechanical properties of soil change. However, its essence lies in adopting different calculation models for different test methods, and it lacks a relevant methodological basis and applied research. In the future, research on the applicability of calculation methods and models should be conducted in combination with test principles and calculation models.
3. Calculation Method of Soil Fractal Dimension
3.1. Fractal Dimension of Particle (Pore) Quantity–Particle (Pore) Size Distribution
In 1986, Turcotte [41] proposed a fractal model to describe the relationship between particle quantity and particle size distribution. Building on this foundational work, subsequent researchers extended the model to include both particles and pores, establishing a generalized fractal model for quantity-size distribution based on Turcotte’s principles as follows:
* N(r > R) is the number of particles (pores) whose particle (pore) size is larger than R. D is the fractal dimension of the particle (pore) quantity–particle (pore) size distribution.
Zhang et al. [24] found that the larger the fractal dimension of particle quantity–particle size distribution, the smaller the particle size of soils and the higher the content of particles of a single size. Li [42] studied the fractal dimension of soil particle distribution and the spatial variability of soil physical and mechanical parameters. By calculating the particle quantity fractal dimension, it was found that this dimension was significantly negatively correlated with the content of sand particles, and the finer the soil texture, the smaller the particle quantity fractal dimension. Yang et al. [43] found that with an increase in slag micro-powder content, the fractal dimension of solidified loess first decreased and then increased, indicating that an optimal amount of slag micro-powder can effectively reduce the fractal dimension of loess, resulting in a smoother and more uniform pore structure and improved mechanical properties of loess.
The fractal dimension of particle quantity–particle size distribution (pore quantity–pore size distribution) can quantitatively or qualitatively characterize the complexity of soil particles (pores), which provides effective support for studying the evolution of macroscopic physical and mechanical properties of soil. The quantity of particles (pores) cannot be obtained directly, and the approximate calculation method is usually affected by the assumed conditions and the degree of conformity to reality. In addition, when the quantity of particles (pores) is obtained by the sieving method or SEM, it is difficult to accurately predict the particles (pores) with small diameters, and due to the limited quantity of particles (pores), usually only 4–6 particle levels of data can be obtained. Such a discrete classification method will significantly affect the calculation accuracy of the fractal dimension. The particle mass distribution can reflect the actual composition characteristics of soil more accurately by considering the difference in the specific gravity of soil particles of different particle sizes and avoid the systematic error caused by ignoring the difference of specific gravity in the particle quantity method. In addition, the mass distribution method is less dependent on experimental data and can still obtain more reliable fractal dimension calculation results, even under the condition of incomplete particle size distribution data. Therefore, in the study of the fractal dimension of particle quantity-size distribution, it is recommended to prioritize the particle mass distribution method, and at the same time, combine a variety of experimental methods (such as laser particle size analysis, mercury intrusion method, etc.) to obtain more comprehensive particle size distribution data so as to improve the accuracy and reliability of the calculation of shape dimension.
3.2. Fractal Dimension of Particle Mass–Particle Size Distribution
It is easier to obtain particle mass than particle quantity. Tyler et al. [44] deduced the fractal model of particle mass–particle size distribution, assuming the particle density is the same as follows:
* M(r < R) is the particle mass with a particle size of less than R. MT is the total mass of particles. RL is the maximum particle size. D is the fractal dimension of particle mass.
Yang et al. [45] established the fractal relationship between particle mass distribution and average particle size and found that clay content and the concentration ratio of single-sized particles significantly affect the fractal characteristics of soil particle size distribution. The larger the fractal dimension, the denser the soil structure and the weaker the permeability. Hu et al. [46] found that the fractal dimension of soil particle size distribution was positively correlated with the content of fine soil particles, and the more fine particles present, the larger the fractal dimension. Huang et al. [19] found that the value of the fractal dimension can reflect the composition of soil particles, and the fractal dimension increases with the increase in clay content and decreases with the increase in sand content. These findings collectively highlight the importance of fractal dimensions in characterizing soil properties.
Compared with other fractal dimension calculation methods, Formula (2), which is widely adopted in most existing studies both domestically and internationally, has the advantages of a simple calculation process and easy acquisition of measured data on particle mass–particle size distribution. However, this method usually requires the assumption of uniformity of particle density in the calculation process, which has obvious limitations in practical application, especially when calculating the fractal dimension of fine soil particle mass. The results are often low, and it is difficult to accurately reflect the complexity of the soil microstructure. In addition, the method ignores the spatial variability of particle density when dealing with heterogeneous soils, which may lead to systematic deviation of the fractal dimension calculation results. In future studies, the calculation method should be further optimized to adopt more reasonable and realistic assumptions, such as introducing the spatial distribution function of particle density or considering the influence of particle shape. At the same time, for different soil properties, more precise calculation models should be established, combined with experimental data and numerical simulation, to improve the accuracy and applicability of the fractal dimension calculation results. In addition, the application of multi-scale fractal theory can be explored to describe the complex characteristics of the soil microstructure more comprehensively and provide a more reliable theoretical basis for engineering practice.
3.3. Fractal Dimension of Particle (Pore) Volume–Particle (Pore) Size Distribution
Tyler and Wheatcraft [47] assumed that the density of soil particles is constant and all particles are spherical in shape. Wang and Tao et al. [48,49] optimized the assumption and derived the fractal model of the particle (pore) volume–particle (pore) size distribution as follows:
* V(r ˂ R) is the volume of particles (pores) whose particle (pore) size is less than R. VT is the total volume of particles (pores). λv is the maximum size of the particle (pore). D is the fractal dimension of the particle (pore) volume–particle (pore) size distribution.
Wang et al. [48] analyzed the volume fractal dimension of 178 soil specimens and found that the calculation results were more reasonable when the assumption of particle density uniformity was not made. They also discovered a significant logarithmic correlation between the volume fractal dimension of soil particles and the volume content of particles. Dang et al. [50] observed that the fractal dimension of particle volume in Chinese loess gradually decreased from south to north, with minimal variation at different depths within the same location. Zhang et al. [51] analyzed the fractal dimension of particle distribution and the maximum or minimum pore size of clay and eco-materials, proposing a calculation formula for consolidation deformation based on the microscopic pore structure of soil. Wang et al. [52] studied the fractal dimension of pore volume distribution in soft clay before and after freeze–thaw and compression. They found that as the fractal dimension of pore volume distribution increased, the distribution trend became more nonhomogeneous, with a significant increase in the volume of micro- and small pores.
The fractal dimension of particle volume offers the advantage of characterizing the size, composition, and texture uniformity of soil particles without assuming uniform particle density. Future research endeavors should concentrate on elucidating the influence mechanisms by which spatial variability in soil formation and storage environments impacts particle fractal characteristics. Additionally, it is imperative to delve into the evolutionary patterns of soil texture and particle fractal characteristics across varying geological ages, depositional environments, and stress history conditions. It is recommended to employ multi-scale analysis methods to systematically evaluate the volume fractal dimension across different particle size ranges and establish quantitative relationship models between fractal dimensions and the physical–mechanical properties of soil, mineral composition, and structural features. Furthermore, classification variables, such as soil engineering categories and usage, should be integrated into the research framework to develop a comprehensive evaluation method for soil microstructure macroproperties based on fractal theory. This approach will not only enhance our understanding of the distribution characteristics of soil particle (pore) volume–particle size (pore) but also provide a novel theoretical foundation for predicting and controlling soil engineering properties, thereby promoting innovative applications of fractal theory in geotechnical engineering.
3.4. Fractal Dimension of Undisturbed Area (Volume) Distribution of Particles (Pores)
When calculating the quantity and volume fractal dimensions of particles or pores, measurements must be taken after dispersion. However, this process can destroy the original microstructure of the soil. To obtain a fractal dimension that reflects the undisturbed characteristics of the soil, researchers should use the undisturbed area or volume of soil particles or pores to address this issue [53].
The box-counting method is extensively utilized in the investigation of the soil microstructure owing to its simplicity. However, it exhibits notable limitations in terms of accuracy and precision, with the selection of box size significantly influencing the calculation outcomes. Advances in digital image processing technology, high-resolution microscopic imaging techniques, and intelligent algorithms have enabled computer programs not only to automate the box-counting process and handle large-scale data but also to optimize box size selection through adaptive algorithms, thereby enhancing computational efficiency and accuracy. For instance, integrating edge detection and image enhancement techniques allows for more precise identification of boundary characteristics in the soil microstructure. The incorporation of intelligent algorithms can automatically determine the optimal range of box sizes, thereby minimizing errors associated with human intervention. Nonetheless, despite significant technological advancements, the box-counting method still faces challenges when dealing with complex microstructures and remains inadequate in characterizing multi-fractal features [54,55,56]. When applying the area or volume fractal model of particles or pores to calculate the fractal dimension, it is crucial to consider the limitations of the calculation model and the accuracy of data acquisition and processing. Currently, the application of fractal models for calculating fractal dimensions is limited. Future research should focus on improving the rationality of the assumptions underlying fractal models and enhancing the accuracy of the calculation results. See Table 2.

Table 2.
Fractal dimension of undisturbed area (volume) distribution of particles (pores).
3.5. Fractal Dimension of Particle (Pore) Surface Distribution
3.5.1. Fractal Dimension of Particle Surface Distribution
Qin et al. [58] studied the fractal characteristics of silt particle size distribution using the yardstick method. They found that the fractal dimension could effectively characterize the uniformity of silt particle size distribution, with a smaller fractal dimension indicating a more uniform particle distribution. Xia et al. [59] obtained the Hurst index and fractal dimension of loess specimens using the rescaled range analysis (R/S) method. They found that the Hurst index could reflect the evolution trend of the soil erosion process, with a larger Hurst index corresponding to a smaller fractal dimension. Wang et al. [60] used the structure function method to quantitatively analyze the three-dimensional distribution and fractal dimension of clay particle surfaces. They found that the surface area-volume combined quantitative characterization method could better reflect the three-dimensional characteristics of soil. Hou et al. [61] used the W-M function in the spectral dimension method to quantitatively analyze the distribution characteristics of soil surfaces. They found that the fractal dimension is an intrinsic property of rough surfaces, independent of the resolution ratio of the measuring instrument and sampling length. They also proposed that the W-M function analysis method has high accuracy for simulating measured soil surfaces. See Table 3.

Table 3.
Fractal dimension of particle surface distribution.
When calculating the fractal dimension of the particle (pore) surface distribution, the structure function method has the highest calculation accuracy because of its full use of logarithmic data and accurate capture of local details; especially, when dealing with complex microstructures, it can effectively avoid the impact of scale effect. In contrast, the sizing method is highly sensitive to the selection of the scale and the scale interval, so it is easy to introduce large errors; especially, in the case of an unreasonable division of the scale interval or an uneven distribution of data points, the calculation results of fractal dimensions will have significant deviations. The structure function method can better reflect the nonlinear characteristics of the particle (pore) surface, but the size rule is easily affected by the artificial scale division, which leads to a large error in the calculation result of the fractal dimension. To address this, future research should establish consistent data acquisition and processing standards, thereby improving both the objectivity of calculations and the accuracy of fractal characteristics for particle or pore surfaces.
3.5.2. Fractal Dimension of Pore Surface Distribution
Liu et al. [68] derived the functional relationship between the cumulative mass curve of soil particles and the fractal dimension of the pore surface and obtained the cumulative volume of soil particles with a radius ≤ R (assuming that the minimum radius of the particles is 0), as shown in Formula (4). Taking logarithms on both sides, the fractal dimension Ds of the soil pore surface can be obtained as follows:
* V(≤R) is the cumulative volume. R is the particle size. Ds is the fractal dimension of the pore surface. c is a constant term.
By analyzing the relationship between mercury injection and pore surface energy in the mercury intrusion test, the fractal dimension calculation model of the pore surface can be established [69] as follows:
* Pi and ΔVn are the pressure and volume of the ith mercury injection. rn and Vn are the nth mercury injection and nth cumulative mercury injection.
Zhang et al. [70] used a low-temperature nitrogen adsorption test and an FHH fractal model to study the fractal dimension of earthen site specimens and found that the smaller the pore fractal dimension, the lower the pore wall roughness and the greater the likelihood of producing weathering diseases. Cui et al. [71] found that the fractal dimension of the pore surface, the pore diameter, and the volume in the micropore and mesoporous regions of the freeze-dried samples were all larger than those of the dried samples.
4. Analysis of the Influence of Soil Fractal Characteristics on Macroscopic Properties
4.1. Permeability
The existing research has revealed that microstructure irregularity directly impacts soil permeability, whereas particle gradation heterogeneity influences pore channel geometry [21]. Specifically, a smaller fractal dimension indicates a more concentrated particle size distribution, which enhances pore structure regularity and stabilizes seepage channel width and tortuosity [72]. In contrast, a larger fractal dimension increases pore space network heterogeneity, leading to detoured seepage paths with increased resistance from both detour angles and extension lengths [72,73]. Yang et al. [74] discovered that tight sandstone exhibits significant three-level fractal characteristics in its pore structure—large, medium, and small pores—with large pores showing the strongest heterogeneity. The medium pore volume and its fractal dimension are crucial determinants of tight sandstone permeability. Deng et al. [75] found that sand and clay content significantly influences particle fractal dimensions; higher sand content correlates with lower clay content, resulting in smaller fractal dimensions and greater soil permeability. Huang et al. [21] constructed a microscopic seepage pore channel model of soil based on soil particle fractal characteristics and the fractal reconstruction algorithm (FCRM). The test parameters and modeling parameters of the model are shown in Table 4, where the modeling parameters are obtained by image recognition and empirical estimation. As shown in Figure 3, gradation and porosity mainly affect the width and tortuosity of seepage channels, while the ovality, roughness, and dip angle of the major axis mainly affect the angle and length of seepage channels’ detour.

Table 4.
Parameters for model validation [21].
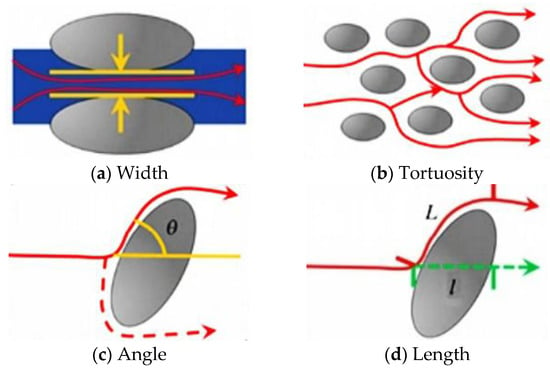
Figure 3.
Influence mechanism of soil permeability [21].
4.2. Shear Strength
The influence of soil particles and pore fractal characteristics on shear strength is mainly embodied in the parameters of microstructure characteristics, such as the fractal dimension of soil particles and pores, which can reflect their contact and arrangement state. The larger the fractal dimension of soil particles, the more irregular their shape becomes and the higher their surface roughness, resulting in stronger mechanical interlocking between soil particles and an increase in soil shear strength. The larger fractal dimension of soil pores leads to a more complex and fragmented pore structure, resulting in smaller effective contact areas between particles, reduced friction between soil particles, and decreased shear strength [76]. In research, it is essential to consider the coupling effect of particle and pore fractal characteristics to accurately predict and evaluate the shear strength properties of soil [76,77]. Yi et al. [78] found that when the fractal dimension of fracture structures increased, the cohesion and internal friction angle of expansive soils decreased. Wang et al. [79] discovered that the fractal dimension of particle distribution significantly influenced the internal friction angle in soil, while the fractal dimension of pore distribution had the least impact on it. When the fractal dimension of particle distribution was reduced, cohesion and internal friction angles could be increased to prevent soil shear failure. Chai et al. [80] investigated the evolution law of compressed shear failure particles and the fractal characteristics of fractured block distribution in mudstone samples. As shown in Table 5, with an increase in shear angle, fractured blocks tend to become larger, and the fractal dimension of fractured block distribution decreases logarithmically.

Table 5.
Fractal dimension of the compressive shear fracture particle in mudstone [80].
4.3. Compression Characteristics
Interaction between particles and pore evolution are the key factors affecting the compression characteristics of soil. The fractal characteristics of particles and pores can characterize the arrangement of particles, pore distribution, and evolution law of soil under external forces [31]. The friction, extrusion, and cementation between particles can cause particles to rearrange and spall, strengthen the connection strength between particles, change the compression modulus of soil, and affect the stress–strain relationship of soil [81]. During the compression process, the loss of large pores will lead to an increase in soil density and a decrease in permeability coefficient, while the formation of small pores will affect the water holding and gas migration characteristics of soil [81,82]; the changes in the soil microstructure during consolidation and shear are shown in Figure 4a [83]. Moreover, as shown in Figure 4b [83], intergranular pores of compacted soil are sensitive to consolidation, and the dominant pore size decreases with the increase in consolidation pressure. Before the arrangement of aggregates is changed, the structure of aggregates will not be destroyed and the pores within the aggregates will not be compressed. Zhou et al. [84] conducted triaxial compression tests on mudstone samples and found that higher confining pressure results in a slower growth rate of crack fractal dimension. Tao et al. [31] discovered that the soil compression process forces large pores to constantly adjust towards a stronger fractal distribution, and the inherent fractal characteristics of small pores can serve as a benchmark index for clay compression.
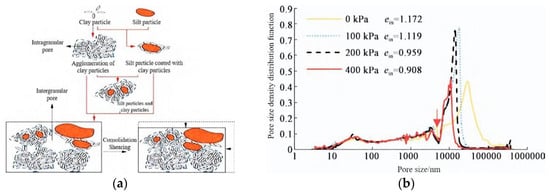
Figure 4.
(a) Schematic diagram of microstructure changes during soil consolidation and shear [83]. (b) PSDD under different consolidation pressures (ein is the cumulative pore ratio. PSDD is pore size density distribution) [83].
The existing research has shown that the theory of porous medium seepage and the fractal model of pores can accurately predict the permeability of soils. However, the influence of fractal characteristics on shear strength is mainly focused on specific soils (such as clay and sand). Moreover, the existing research results on the fractal characteristics of pores and particles cannot fully reflect the evolution characteristics of the soil microstructure and their impact on macroscopic properties, such as soil particle spallation, particle contact, and pore self-organization. Additionally, the physical and chemical properties of soil vary significantly across different regions, along with differences in specimen preparation and test environments, which results in the existing research findings not being universally applicable. Therefore, future research should enhance the qualitative and quantitative characterization of the fractal dimension of particle (pore) distribution, further clarify the influence of fractal characteristics on variations in the macroscopic physical and chemical properties of soils, advance the development of fractal characteristic analysis and calculation methods toward higher precision, and transition from two-dimensional image analysis to three-dimensional structural evolution research.
5. Conclusions and Prospects
Research on the fractal characteristics of the soil microstructure provides new ideas and methods for revealing the mechanisms of microstructural evolution and the variation of macroscopic physical properties. This paper summarizes and analyzes the types of fractal characteristics in soil, methods for calculating fractal characteristic parameters, and the impact of fractal characteristics on macroscopic properties. It is found that future research in this field should focus on the following aspects:
(1) Research on fractal characteristics is evolving towards higher precision and multi-dimensionality. The existing two-dimensional fractal analysis methods fail to adequately account for the pronounced non-uniformity and spatial heterogeneity inherent in the soil microstructures. Future research should prioritize the integration of high-resolution three-dimensional imaging technologies, such as X-ray computed tomography and focused ion beam scanning electron microscopy, with advanced digital image processing techniques. Such methodological advancements are crucial for elucidating the intrinsic relationships between soil fractal characteristics and their macroscopic physicochemical properties.
(2) Strengthen interdisciplinarity and promote theoretical innovation of fractal analysis. Future research should integrate advances in geological morphology, computational modeling, and micromechanical analysis from materials science. By incorporating deep learning algorithms, a predictive model for the soil microstructure based on fractal characteristics can be developed. This integrated approach will enable systematic analysis of microstructural evolution and fractal feature development under varying formation and environmental conditions, thereby building a more comprehensive system for the study of soil fractal characteristics evolution.
(3) Close contact with engineering tests to promote the application and transformation of research results in underground engineering, soil property improvement, and infrastructure construction. Current research on soil fractal characteristics primarily emphasizes theoretical analysis and laboratory investigations. Future studies should integrate fractal analysis of soil with complex engineering conditions to develop macroscopic physical–mechanical models based on microscopic fractal characteristics. For instance, fractal analysis can optimize grouting material particle size distribution to enhance grouting efficiency, while fractal dimensions can predict surrounding rock crack propagation to inform support design. These models will enable the prediction and analysis of soil physical and mechanical properties, as well as engineering behaviors under varying conditions, accurately assessing soil strength, deformation, and long-term stability.
Funding
This research was funded by the National Natural Science Foundation of China, grant numbers 42362033 and 52268058, the project supported by the Industrial Support Plan of Gansu province (2023CYZC-34), the project supported by the Gansu Provincial Department of Education Youth Doctor Support Project (2024QB-053), and the Patent Transformation Guide Foundation of Lanzhou Jiaotong University (ZH2023008).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Tan, L.R.; Zhang, M.Y.; Shao, W.M.; Hua, L.L. Microstructure Characteristics and Engineering Properties of Expansive Soil. Chin. J. Geotech. Eng. 1994, 16, 48–57. [Google Scholar]
- Liu, S.Y.; Zhang, J.W. Fractal Approach to Measuring Soil Porosity. J. Southeast Univ. (Nat. Sci. Ed.) 1997, 27, 129–132. [Google Scholar]
- Xu, Y.; Zhang, J.C.; Li, W.P. Research on microstructure fractal features of the saturation soft soil. Rock Soil Mech. 2007, 28, 49–52. [Google Scholar]
- Zhang, K.Y.; Yin, Z.Z.; Mei, G.X. Development of soil’s anisotropy study. Rock Soil Mech. 2004, 9, 1503–1509. [Google Scholar]
- Qian, J.G.; Huang, M.S. Micro-macro mechanismic analysis of plastic anisotropy in soil. Rock Soil Mech. 2011, 32, 88–93. [Google Scholar]
- Lin, P.Y.; Tang, L.S.; Sang, H.T.; Deng, X.B.; Wu, K.; Deng, Z.W. Fractal Geometry in the Past, Present and Future Research of Rock and Soil Mechanics. China Earthq. Eng. J. 2011, 33, 24–29. [Google Scholar]
- Xu, Y.F.; Huang, Y.C. Fractal-textured soils and their unsaturated mechanical properties. Chin. J. Geotech. Eng. 2006, 28, 635–638. [Google Scholar]
- Zhang, X.D.; Lu, Z.J.; Liu, M.; Yang, F.; Zhao, L.H. Analysis of infiltration and stability of shallow slopes under heavy rainfall conditions with fractal theory corrections. J. Harbin Inst. Technol. 2024, 56, 1–14. [Google Scholar]
- Wang, Y.; Duan, X.; Gu, Y.; Wang, S. Fractal Characteristics of the Seepage Erosion Process in Porous Soil. Geofluids 2022, 2022, 3383773. [Google Scholar]
- Kong, B.; Dai, C.X.; Hu, H.; Xia, J.; He, S.H. The Fractal Characteristics of Soft Soil Under Cyclic Loading Based on SEM. Fractal Fract. 2022, 6, 423. [Google Scholar] [CrossRef]
- Torres-Guerrero, C.A.; Álvarez, D.; Preusser, F.; Olarieta, J.R.; Poch, R.M. Evolution of soil porosity in loess-palaeosol sequences of the Ebro Valley, NE Iberia. Catena 2023, 230, 107244. [Google Scholar]
- Liu, X.R.; Tu, Y.L.; Wang, L.F.; Feng, H.; Zhong, Z.L.; Lei, X.D.; Wang, L. Fractal characteristics of shear failure surface and mechanism of strength generation of soil-rock aggregate. Chin. J. Rock Mech. Eng. 2017, 36, 2260–2274. [Google Scholar]
- Li, J.D.; Wang, X.; Zhang, Y.J.; Jiang, D.J.; Liu, D.R.; Ma, X.N.; Wang, J.L. Experimental study on strength and microstructure of loess reinforced with F1 ionic soil stabilizer. J. Southeast Univ. (Nat. Sci. Ed.) 2021, 51, 618–624. [Google Scholar]
- Kong, B.; Yan, Y.; He, H.; Yu, J.; Zou, B.; Chen, Q. Strength and Fractal Characteristics of Artificial Frozen-Thawed Sandy Soft Soil. Fractal Fract. 2024, 8, 393. [Google Scholar] [CrossRef]
- Na, H.; Tao, L.; Wei, Z.; Cosgrove, T.; Mei, Z. Analysis of the Correlation Between Strength and Fractal Dimension of Gravelly Soil in Debris-Flow Source Areas. Open Civ. Eng. J. 2016, 10, 866–876. [Google Scholar]
- Sun, G.C.; Zhang, J.M.; Dang, Y.S.; Ding, C. Microstructure and strength features of warm and ice-rich frozen soil treated with high-performance cements. J. Mt. Sci. 2019, 16, 1470–1482. [Google Scholar]
- Wang, M.L.; Zhang, Y.; Yin, X.X. Microstructure characteristics of expansive soil with coal gangue based on Menger sponge model. Trans. Chin. Soc. Agric. Eng. 2020, 36, 124–130. [Google Scholar]
- Zhu, J.; Qiao, C.S.; Song, Y.; Han, Z.M.; Tu, H.L. Effect of particle characteristics on shear strength of weakly cemented conglomerate in tertiary. J. Harbin Inst. Technol. 2019, 5, 100–109. [Google Scholar]
- Huang, G.H.; Zhan, W.H. Fractal property of soil particle size distribution and its application. Acta Pedol. Sin. 2002, 39, 490–497. [Google Scholar]
- Wang, X.K.; Li, D.J.; Zhu, Y.T.; Zhang, J.Y.; Yuan, F.L. Particle shape analysis of clay based on digital image technology. Chin. J. Geotech. Eng. 2020, 42, 168–171. [Google Scholar]
- Huang, X.W.; Jiang, P.M.; Zhou, A.Z.; Wang, W.; Tang, C.X. Prediction model for soil permeability based on fractal characteristics of particles. Chin. J. Geotech. Eng. 2023, 45, 1907–1915. [Google Scholar]
- Yang, C.; Wu, J.; Li, P.; Wang, Y.; Yang, N. Evaluation of Soil-Water Characteristic Curves for Different Textural Soils Using Fractal Analysis. Water 2023, 15, 772. [Google Scholar] [CrossRef]
- Su, W.; Gao, Y.; Gao, P.; Dong, X.; Wang, G.; Dun, X.; Xu, J. Effects of Different Vegetation Restoration Types on the Fractal Characteristics of Soil Particles in Earthy-Rocky Mountain Area of Northern China. Forests 2022, 13, 1246. [Google Scholar] [CrossRef]
- Zhang, J.R.; Zhu, R.G.; Zhu, W.H. Fractal features of soils characterized by grain size distribution. J. Hydraul. Eng. 2004, 12, 67–71+79. [Google Scholar]
- Dong, L.L.; Zheng, F.L. Fractal Characteristics of Soil Particle Size Distributions in Gully-Hilly Regions of the Loess Plateau, North of Shaanxi, China. Soils 2010, 42, 302–308. [Google Scholar]
- Zuo, S.Y.; Zhang, Y.Z.; Zhao, R.; Zhang, J. Study on fractal characteristics of meso-microstructure of red clay in Guiyang. J. Beijing Jiaotong Univ. 2019, 43, 122–129. [Google Scholar]
- Zhang, P.; Han, X.; Guo, J.; Zhang, H. Fractal Characteristics of Geopolymer Mortar Containing Municipal Solid Waste Incineration Fly Ash and Its Correlations to Pore Structure and Strength. Fractal Fract. 2022, 6, 676. [Google Scholar] [CrossRef]
- Sun, G. Study on crack structure and fractal characteristics of expansive rock and soil body based on microscopic CT scan. Ind. Miner. Process. 2018, 47, 48–51+55. [Google Scholar]
- He, J.; Liu, J.L.; Lv, F. Characterizing Fractal Characteristics of Soil Pores Based on High-Resolution Digital CT Images. Soils 2008, 40, 662–666. [Google Scholar]
- Yang, H.; Cheng, W.M.; Liu, Z.; Wang, W.Y.; Zhao, D.W.; Wang, W.D. Fractal characteristics of effective seepage channel structure of water infusion coal based on NMR experiment. Rock Soil Mech. 2020, 41, 1279–1286. [Google Scholar]
- Tao, G.L.; Zhu, X.L.; Hu, Q.Z.; Zhuang, X.S.; He, J.; Chen, Y. Critical pore-size phenomenon and intrinsic fractal characteristic of clay in process of compression. Rock Soil Mech. 2019, 40, 81–90. [Google Scholar]
- Mao, L.T.; Xue, R.; Yuan, Z.X. Fractal approach on soft soil subgrade microstructure SEM image. J. Chang. Univ. (Nat. Sci. Ed.) 2007, 2, 30–33. [Google Scholar]
- Li, Y.Y.; Wei, Z.; Tong, Y.W.; Zhang, Q.F. Multifractal Characteristics of Water Erosion Factors in Typical Watershed of the Loess Plateau. Res. Soil Water Conserv. 2024, 31, 122–129. [Google Scholar]
- Meng, F.D.; Zhai, Y.; Zhang, Y.S.; Li, Y.B.; Dong, Q. Multifractal Characteristics of Sandstone Microstructure after Freeze-Thaw Damage. Chin. J. Undergr. Space Eng. 2023, 19, 1791–1799. [Google Scholar]
- Wang, J.M.; Zhang, M.; Bai, Z.K.; Yang, R.X.; Guo, L.L. Multi-fractal characteristics of reconstructed soil particle in opencast coal mine dump in loess area. Trans. Chin. Soc. Agric. Eng. 2014, 30, 230–238. [Google Scholar]
- Guan, X.Y.; Yang, P.L.; Ren, S.M.; Li, X.Y.; Lv, Y. Heterogeneity Analysis of Particle Size Distribution for Loamy Soil Based on Multifractal Theory. J. Basic Sci. Eng. 2009, 2, 196–205. [Google Scholar]
- Guan, X.Y.; Yang, P.L.; Lv, Y. Relationships Between Soil Particle Size Distribution and Soil Physical Properties Based on Multifractal. Trans. Chin. Soc. Agric. Mach. 2011, 42, 44–50. [Google Scholar]
- Zhang, J.R.; Wang, J.M.; Qin, Q.; Bai, Z.K. Three-dimensional Multi-fractal Characteristics of Reconstruction Soil Pore at Opencast Coal Mine Dump based on CT Scanning. Chin. J. Soil Sci. 2017, 48, 786–793. [Google Scholar]
- Ju, X.; Jia, Y.; Li, T.; Gao, L.; Gan, M. Morphology and multifractal characteristics of soil pores and their functional implication. Catena 2021, 196, 104822. [Google Scholar]
- Bai, Y.R.; Wang, Y.K. Monofractal and Multifractal Analysis on Soil Particle Distribution in Hilly and Gully Areas of the Loess Plateau. Trans. Chin. Soc. Agric. Mach. 2012, 43, 43–48+42. [Google Scholar]
- Turcotte, D.L. Fractals and fragmentation. J Geophys Res B 1986, 91, 1921–1926. [Google Scholar] [CrossRef]
- Li, Y.; Li, M.; Cao, W.; Zhang, J. Spatial Variability of Fractal Dimensions for Soil Particle Size Distributions and Physical Properties. Trans. Chin. Soc. Agric. Eng. 2010, 26, 94–102. [Google Scholar]
- Yang, G.H.; Li, C.; Shang, Y.; Zhang, Z.G.; Gao, Y.; Li, S.H. Experimental study on improving loess pore properties by slag powder based on CT scanning technology. Water Resour. Hydropower Eng. 2023, 54, 201–209. [Google Scholar]
- Tyler, S.W.; Wheatcraft, S.W. Fractal scaling of soil particle size distributions: Analysis and limitations. Soil Sci. Soc. Am. J. 1992, 56, 362–369. [Google Scholar] [CrossRef]
- Yang, P.L.; Luo, Y.P.; Shi, Y.C. Soil fractal characteristics characterized by weight distribution of particle size. Chin. Sci. Bull. 1993, 20, 1896–1899. [Google Scholar]
- Hu, Y.F.; Liu, J.Y.; Zhuang, D.F.; Cao, H.X.; Yan, H.M. Fractal dimension of soil particle size distribution under different land use/land coverage. Acta Pedol. Sin. 2005, 2, 336–339. [Google Scholar]
- Tyler, S.W.; Wheatcraft, S.W. Application of fractal mathematics to soil water retention estimation. Soil Sci. Soc. Am. J. 1989, 53, 987–996. [Google Scholar] [CrossRef]
- Wang, G.L.; Zhou, S.L.; Zhao, Q.G. Volume fractal dimension of soil particles and its applications to land use. Acta Pedol. Sin. 2005, 42, 545–550. [Google Scholar]
- Tao, G.L.; Zhang, J.R. Two kinds of fractal models characterizing the volume and scale distribution of pores and particles. Chin. Sci. Bull. 2009, 54, 838–846. [Google Scholar] [CrossRef]
- Dang, Y.A.; Li, S.Q.; Wang, G.D.; Zhao, K. Fractal characteristics of soil particle composition for typical types of soil profile on Loess Plateau. Trans. Chin. Soc. Agric. Eng. 2009, 25, 74–78. [Google Scholar]
- Zhang, J.R.; Tao, G.L.; Huang, L.; Yuan, L. The porosity model of rock and soil mass characterizing pore size distribution and its application. Chin. Sci. Bull. 2010, 55, 2661–2670. [Google Scholar]
- Wang, S.F.; Yang, P.; Liu, G.R.; Fan, W.H. Micro pore change and fractal characteristics of artificial freeze thaw soft clay. Chin. J. Geotech. Eng. 2016, 38, 1254–1261. [Google Scholar]
- Tao, G.L.; Zhang, J.R. Fractal theory and its applications in geotechnical engineering. China Sci. 2009, 4, 493–497. [Google Scholar]
- Ding, J.; Sun, H.Q. Comparative analysis of fractal dimension determination methods. Eng. Constr. 2010, 42, 10–13+25. [Google Scholar]
- Cao, J.X.; Song, C.L. Calculation and improvement of the fractal dimension. Inf. Technol. Informatiz. 2017, 10, 19–23. [Google Scholar]
- Liu, H.Y. A method for calculating the box dimension of computer images. Electron. Technol. Softw. Eng. 2015, 20, 87–88. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman: San Francisco, CA, USA, 1983. [Google Scholar]
- Qin, W.; Sha, A.M. Fractal features of silt particle size distribution. J. Chang. Univ. (Nat. Sci. Ed.) 2009, 29, 10–14. [Google Scholar]
- Xia, J.D.; Wu, F.Q.; Zhang, Q.F.; Wang, J.; Xia, H.J. Study on Micro Topography Fractal Characteristics of Rainfall Erosion in Loess Area. Yellow River 2016, 38, 78–81. [Google Scholar]
- Wang, B.J.; Shi, B.; Tang, C.S. Study on 3D fractal dimension of clayey soil by use of GIS. Chin. J. Geotech. Eng. 2007, 29, 309–312. [Google Scholar]
- Hou, Z.F.; Xue, J.; Yan, J.G.; Zhu, L.Z.; Chen, Z. Fractional model applicable to characterization of soil surface. J. Inn. Mong. Agric. Univ. (Nat. Sci. Ed.) 2014, 35, 96–99. [Google Scholar]
- Mandelbrot, B. How long is the coast of Britain? statistical self-similarity and fractional dimension. Science 1967, 156, 636–638. [Google Scholar] [PubMed]
- Hurst, H.E. Long-term storage capacity of reservoirs: An experimental study. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–808. [Google Scholar]
- Liang, Z.; Feng, Z.; Guangxiang, X. Comparison of Fractal Dimension Calculation Methods for Channel Bed Profiles. Procedia Eng. 2012, 28, 252–257. [Google Scholar]
- Yuan, C.Q.; Li, J.; Yan, X.P.; Peng, Z. The use of the fractal description to characterize engineering surfaces and wear particles. Wear 2003, 255, 315–326. [Google Scholar]
- Majumdar, A.; Bhushan, B. Fractal Model of Elastic-Plastic Contact Between Rough Surfaces. J. Tribol. 1991, 1–11. [Google Scholar] [CrossRef]
- Itzhak, G. Exact Spectral Moments and Differentiability of the Weierstrass-Mandelbrot Fractal Function. J. Tribol. 2020, 142, 041501. [Google Scholar]
- Liu, Y.L.; Liang, X.; Zhu, C.K.; Li, J. Prediction of soil water retention curve by surface fractal dimensions. Hydrogeol. Eng. Geol. 2014, 3, 125–130. [Google Scholar]
- Zhang, B.; Li, S. Determination of the Surface Fractal Dimension for Porous Media by Mercury Porosimetry. Ind. Eng. Chem. Res. 1995, 34, 1383–1386. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Yi, Q.; Liu, H.L.; Li, X.Y.; Yu, H.L. Research on the pore structure and fractal characteristics of the Suoyang earthen site. Sci. Conserv. Archaeol. 2024, 36, 19–31. [Google Scholar]
- Cui, D.S.; Xiang, W.; Chen, Q.; Liu, Q.B.; Lang, L.Z.; Wu, Y.P. Pore Characteristics of Sliding Zone Soils of Huangtupo Landslide by Vacuum Freeze-Dried and Dried Methods. Earth Sci. 2014, 39, 1531–1537. [Google Scholar]
- Peng, J.Y.; Zhang, J.F.; Shen, Z.Z.; Ye, J.B. Effect of grain shape on pore characteristics and permeability of coarse-grained soil. Rock Soil Mech. 2020, 41, 592–600. [Google Scholar]
- Wei, H.H. Study on the microscopic mechanism and permeability model of granular soils considering the particle size distribution. Zhejiang Univ. 2023, 17–90. [Google Scholar] [CrossRef]
- Yang, Y.; Wen, Z.; Tian, W.; Fan, Y.; Gao, H. A New Model for Predicting Permeability of Chang 7 Tight Sandstone Based on Fractal Characteristics from High-Pressure Mercury Injection. Energies 2024, 17, 821. [Google Scholar] [CrossRef]
- Deng, Y.S.; Li, S.X.; Ding, S.W.; Cai, C.F.; Xia, D.; Liu, D.L. Research on different soil layers of collapsing gully fractal characteristics and erosion characteristics in Tongcheng. Resour. Environ. Yangtze Basin 2016, 25, 63–70. [Google Scholar]
- Feng, D.L.; Fang, Y.G. Theoretical and experimental research on particle size effect of direct shear mechanical properties of soil. Chin. J. Rock Mech. Eng. 2015, 34, 4307–4319. [Google Scholar]
- Pan, Y.Y. Study on the influence of particle morphology on shear fracture mechanical properties of coarse grained soils. Chengdu Univ. Technol. 2020, 30–97. [Google Scholar] [CrossRef]
- Yi, S.M.; Li, Z.H.; Zhang, Y.Z. The fractal characteristics of fractures in expansion soil and its significance. Chin. J. Geotech. Eng. 1999, 21, 294–298. [Google Scholar]
- Wang, Y.Q.; Wang, Y.J.; Zhang, H.J.; Xiao, J.W.; Wu, Y.; Chen, L. Impacts of soil structure on shear-resistantance of soil under different land uses in Jinyun Mountain of Chongqing City. Trans. Chin. Soc. Agric. Eng. 2006, 22, 40–45. [Google Scholar]
- Chai, Z.Y.; Kang, T.H.; Chen, W.Y.; Yang, Y.K. Fracture evolutionary rules of mudstone under coupled compression and shear and its fractal characteristics. Chin. J. Rock Mech. Eng. 2011, 2, 3844–3850. [Google Scholar]
- Zhang, X.W.; Kong, L.W.; Guo, A.G.; Tuo, Y.F. Evolution of microscopic pore of structured clay in compression process based on SEM and MIP test. Chin. J. Rock Mech. Eng. 2012, 31, 406–412. [Google Scholar]
- Tang, S.L.; Wang, X.Y. Study on the Internal Mechanics and Energy Characteristics of Soil under Different Failure Modes. Appl. Sci. 2023, 13, 8648. [Google Scholar] [CrossRef]
- Xiao, T.; Li, P.; Shao, S.J. Microstructural evolution of compacted loess during consolidation and shearing. Chin. J. Geotech. Eng. 2021, 43, 99–104. [Google Scholar]
- Zhou, C.Y.; Liang, N.; Liu, Z. Fractal characteristics of compression failure of red soft rock and cascading failure process. Rock Soil Mech. 2019, 40, 21–31. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).