Evolution Characteristics of Pore–Fractures and Mechanical Response of Dehydrated Lignite Based on In Situ Computed Tomography (CT) Scanning
Abstract
1. Introduction
2. Experiments and Methods
2.1. Sample Preparation
2.2. Experimental Procedure
2.2.1. Dehydration Treatment
2.2.2. Uniaxial Compression Tests
2.2.3. In Situ CT Scanning Experiments
2.3. Methods
2.3.1. Image Processing
2.3.2. Quantitative Analysis of Pore–Fracture Volume and Area
2.3.3. Quantitative Analysis of Fractal Dimension
3. Results
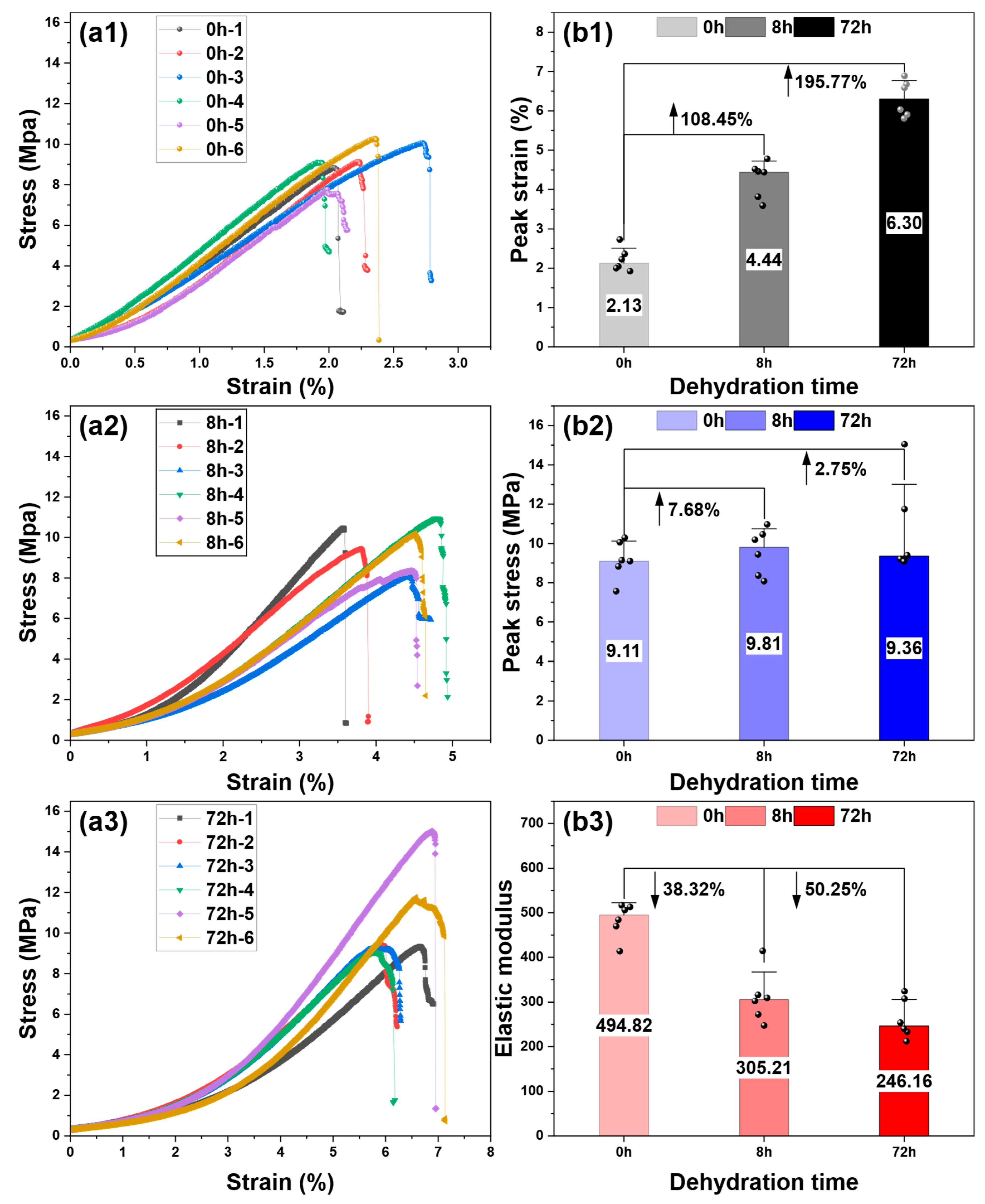
3.1. Macro-Mechanical Property Changes of the Dehydrated Lignite
3.1.1. Overall Mechanical Property Evolution of the Dehydrated Lignite
3.1.2. Stage-by-Stage Mechanical Property Changes of the Dehydrated Lignite
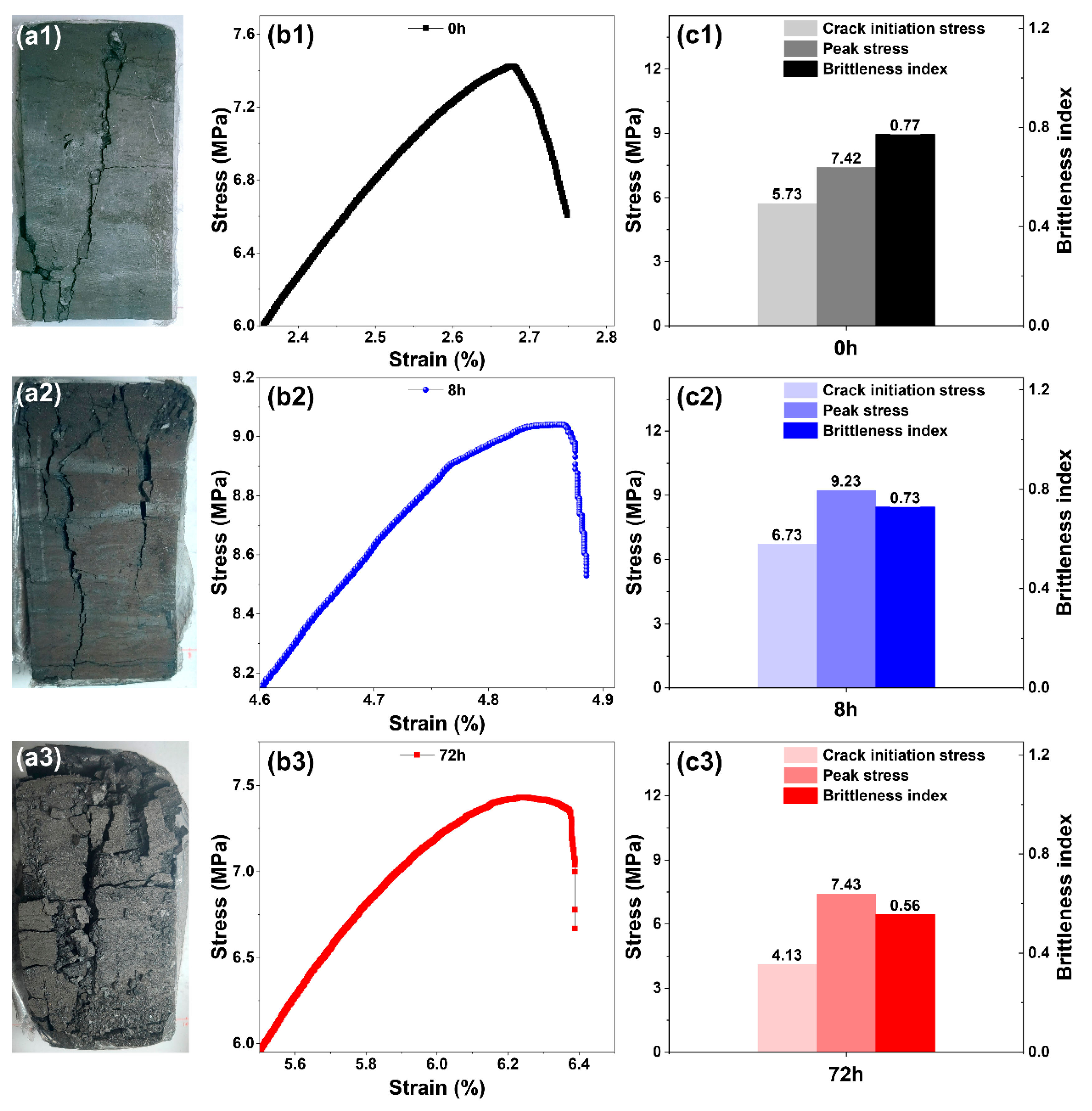
3.1.3. Influence of the Dehydration Effect on the Failure Mode of the Lignite
3.2. Dynamic Evolution of 2D Pore–Fractures in Dehydrated Lignite
3.2.1. Qualitative Analysis of 2D Pore–Fracture Dynamic Evolution in Dehydrated Lignite
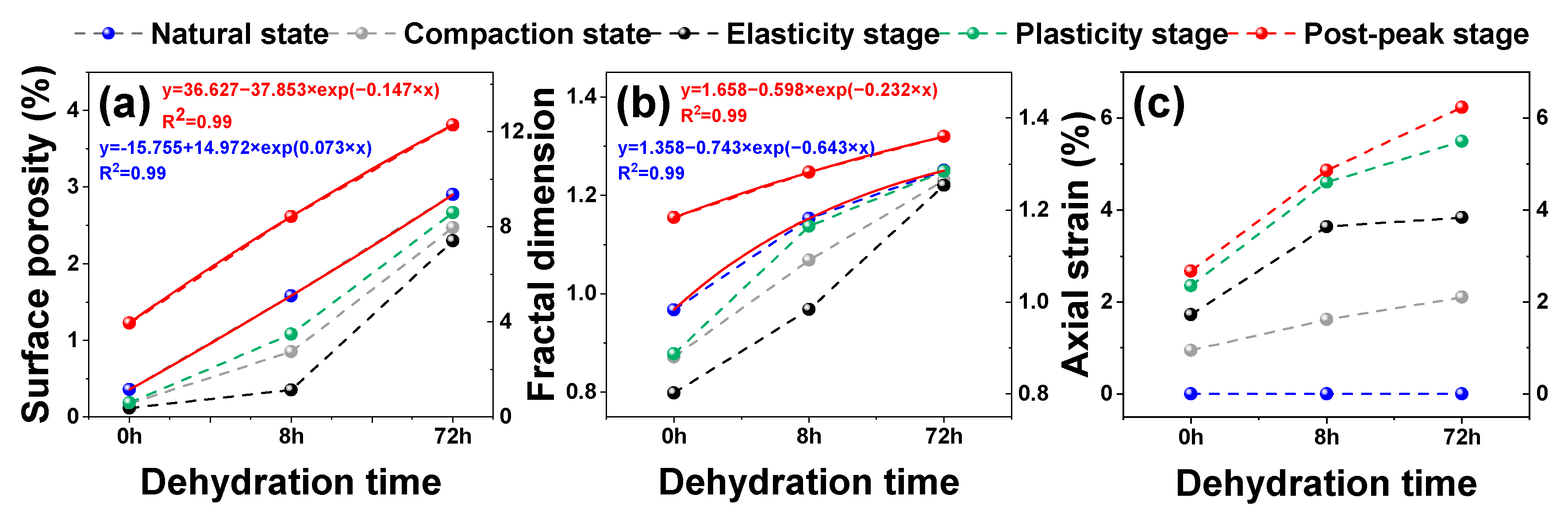
3.2.2. Quantitative Analysis of 2D Pore–Fracture Dynamic Evolution in Dehydrated Lignite
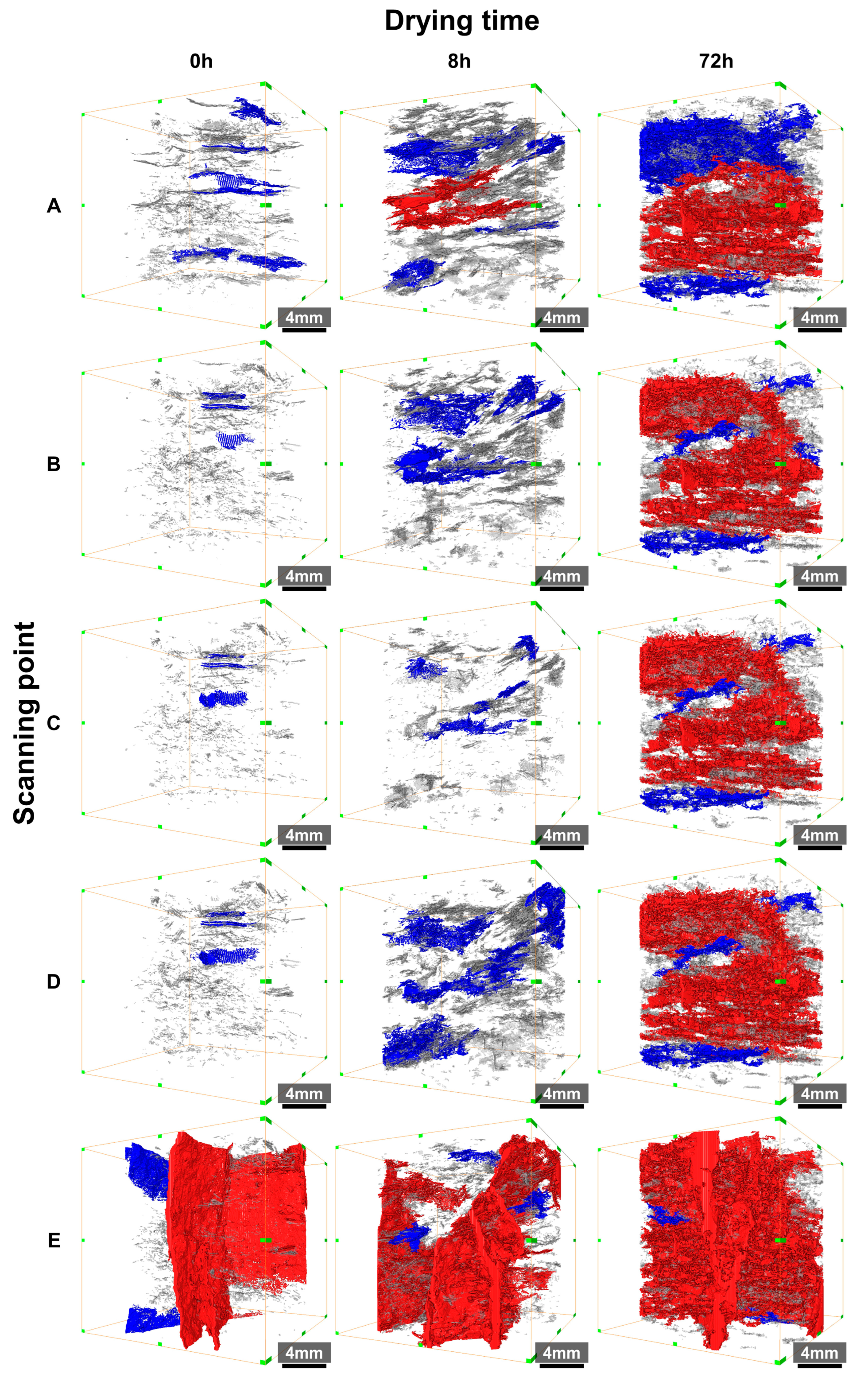
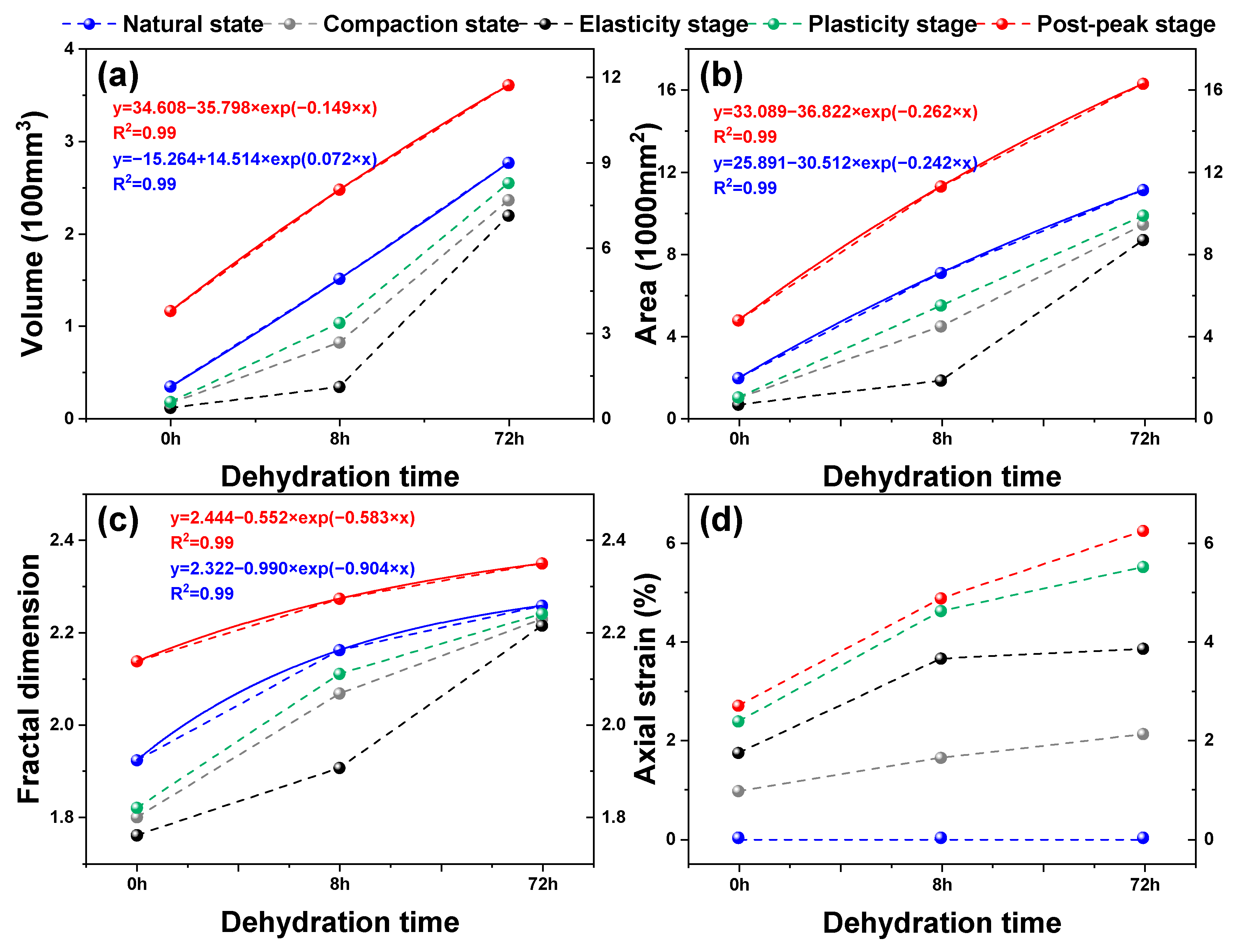
3.3. Dynamic Evolution of 3D Pore–Fractures in Dehydrated Lignite
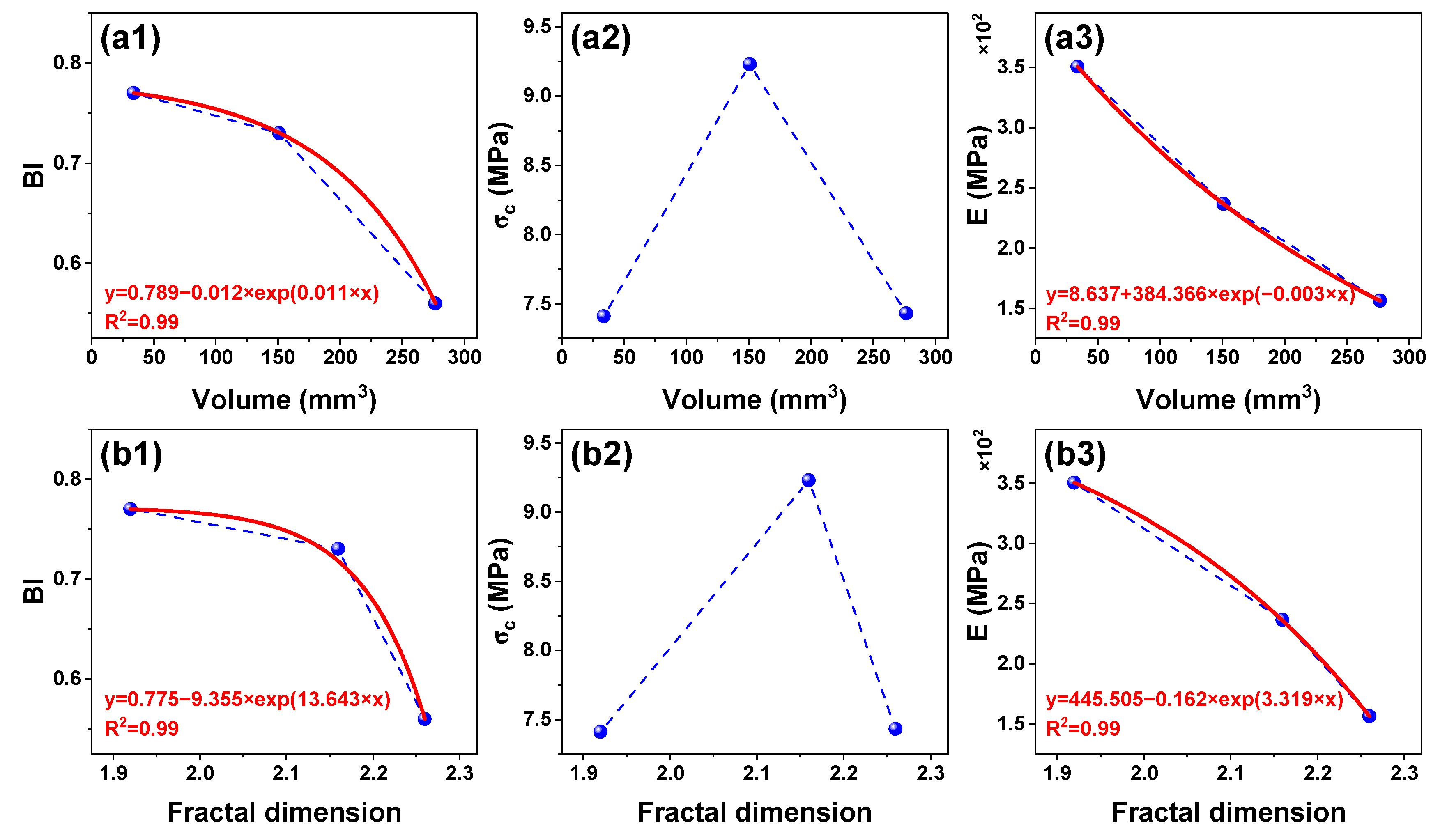
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gao, M.; Cheng, C.; Miao, Z.; Zhou, Y.; Wan, K.; He, Q. The non-isothermal drying characteristics of lignite and prevention strategies for structure damage. Energy 2023, 284, 129258. [Google Scholar] [CrossRef]
- Liu, X.; Yu, H.; Wei, L. Experimental study on the dehydration characteristics and evolution of the physicochemical structure of XilinGol lignite during the dehydration process. Fuel 2021, 291, 120241. [Google Scholar] [CrossRef]
- Cheng, C.; Gao, M.; Miao, Z.; Wan, K.; He, Q. Structural changes mechanism of lignite during drying: Correlation between macroscopic and microscopic. Fuel 2023, 339, 126955. [Google Scholar] [CrossRef]
- Zhou, Y.; Gao, M.; Miao, Z.; Cheng, C.; Wan, K.; He, Q. Physicochemical properties and combustion kinetics of dried lignite. Energy 2024, 289, 129928. [Google Scholar] [CrossRef]
- Liu, W.; Niu, S.; Tang, H. Structural characteristics of pores and fractures during lignite pyrolysis obtained from X-ray computed tomography. J. Pet. Sci. Eng. 2023, 220, 111150. [Google Scholar] [CrossRef]
- Zhang, T.; Lou, C.; Teng, D.; Li, G.; Li, P.; Yun, Q.; Zhou, G. Hot-air drying behavior of lignite and quantitative characterization for its surface damage. Dry. Technol. 2023, 41, 2171–2188. [Google Scholar] [CrossRef]
- Xin, F.; Xu, H.; Tang, D.; Chen, Y.; Cao, L.; Yuan, Y. Experimental study on the change of reservoir characteristics of different lithotypes of lignite after dehydration and improvement of seepage capacity. Fuel 2020, 277, 118196. [Google Scholar] [CrossRef]
- Lu, Y.; Pu, H.; Wang, L.; Li, Z.; Meng, X.; Wang, B.; Zhang, K. Fracture evolution in mudstone specimens containing a pre-existing flaw under true triaxial compression. Int. J. Rock Mech. Min. Sci. 2021, 138, 104594. [Google Scholar] [CrossRef]
- Yu, Y.; Ni, C.; Cui, W.; Cheng, W.; Chen, Y. Progressive failure characteristics of coal under uniaxial compression: A comprehensive application of micro-ct and digital volume correlation. Bull. Eng. Geol. Environ. 2024, 83, 419. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, D.; Wang, L.; Shang, Z.; Zhu, C.; Wei, J.; Yuan, A.; Zhang, H.; Zeng, F. An analysis of the meso-structural damage evolution of coal using X-ray CT and a gray-scale level co-occurrence matrix method. Int. J. Rock Mech. Min. Sci. 2022, 152, 105062. [Google Scholar] [CrossRef]
- Tutluoğlu, L.; Öge, İ.F.; Karpuz, C. Relationship Between Pre-failure and Post-failure Mechanical Properties of Rock Material of Different Origin. Rock Mech. Rock Eng. 2015, 48, 121–141. [Google Scholar] [CrossRef]
- Wen, J.; Tang, Z.; Dyson, A.P.; Tolooiyan, A. The mechanical behaviour of pre-existing transverse cracks in lignite under uniaxial compression. Geomech. Geophys. Geo-Energy Geo-Resour. 2020, 7, 6. [Google Scholar] [CrossRef]
- Wu, H.; Bai, H.; Chen, Y.; Pu, H.; Zhang, K. Mechanical Properties and Damage in Lignite under Combined Cyclic Compression and Shear Loading. Sustainability 2020, 12, 8393. [Google Scholar] [CrossRef]
- Song, Y.; Ma, H.; Yang, J.; Zheng, J.; Yang, J.; Bao, W. Dynamic Mechanical Behaviors and Failure Mechanism of Lignite under SHPB Compression Test. Sustainability 2022, 14, 10528. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, T.; Lin, B. Micromechanical Properties of Different Rank Coal and Their Impact on Fracture Compressibility. Energy Fuels 2024, 38, 9515–9528. [Google Scholar] [CrossRef]
- Yang, N.; Hu, G.; Zhu, J.; Duan, H.; Wang, T.; Li, Y. Evolution of pore-fracture structure and permeability of coal by microwave irradiation under uniaxial compression. J. Nat. Gas Sci. Eng. 2022, 107, 104759. [Google Scholar] [CrossRef]
- Xin, F.; Fang, C.; Wang, S.; Xiong, B.; Cao, C.; Liu, D.; Tang, D.; Xu, H. Influence of Composition on Differential Evolution of Pore–Fracture Systems and Micro-mechanical Properties of Lignite During Drying-Wetting Cycles. Nat. Resour. Res. 2024, 33, 365–388. [Google Scholar] [CrossRef]
- Ma, H.; Song, Y.; Yang, J.; Zheng, J.; Shen, F.; Shao, Z. Experimental investigation on acoustic emission and damage characteristics of dehydrated lignite in uniaxial compression test. Bull. Eng. Geol. Environ. 2023, 82, 292. [Google Scholar] [CrossRef]
- Ma, H.; Song, Y.; Yang, J.; Zheng, J.; Shen, F.; Shao, Z.; Xia, Z. Experimental Investigation on Physical–Mechanical Behaviors and Macro–Micro-structural Responses of Lignite Subjected to Freeze–Thaw Cycles. Nat. Resour. Res. 2023, 32, 543–566. [Google Scholar] [CrossRef]
- Wang, G.; Qin, X.; Shen, J.; Zhang, Z.; Han, D.; Jiang, C. Quantitative analysis of microscopic structure and gas seepage characteristics of low-rank coal based on CT three-dimensional reconstruction of CT images and fractal theory. Fuel 2019, 256, 115900. [Google Scholar] [CrossRef]
- Han, L.; Shen, J.; Wang, J.; Shabbiri, K. Characteristics of Pore Evolution and Its Maceral Contributions in the Huolinhe Lignite during Coal Pyrolysis. Nat. Resour. Res. 2021, 30, 2195–2210. [Google Scholar] [CrossRef]
- Liu, W.; Wang, G.; Han, D.; Xu, H.; Chu, X. Accurate characterization of coal pore and fissure structure based on CT 3D reconstruction and NMR. J. Nat. Gas Sci. Eng. 2021, 96, 104242. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, C.; Wang, G.; Huang, Q.; Shi, Q. Research on the evolution of pore and fracture structures during spontaneous combustion of coal based on CT 3D reconstruction. Energy 2022, 260, 125033. [Google Scholar] [CrossRef]
- Wu, Y.; Tao, S.; Bi, C.; Tang, S.; Men, X. Pore-fracture and permeability heterogeneity of different marcolithotypes of medium-rank coals in Jixi Basin, China. Geoenergy Sci. Eng. 2023, 231, 212395. [Google Scholar] [CrossRef]
- Chen, S.; Dou, L.; Cai, W.; Zhang, L.; Tian, M.; Han, Z. Evolution of Coal Microfracture by Cyclic Fracturing of Liquid Nitrogen Based on μCT and Convolutional Neural Networks. Rock Mech. Rock Eng. 2024, 57, 2103–2124. [Google Scholar] [CrossRef]
- Hou, C.; Jiang, B.; Li, M.; Song, Y.; Cheng, G. Micro-deformation and fracture evolution of in-situ coal affected by temperature, confining pressure, and differential stress. J. Nat. Gas Sci. Eng. 2022, 100, 104455. [Google Scholar] [CrossRef]
- Zhou, Z.; Sheng, M.; Ge, Z.; Li, R.; Gong, S.; Zhang, H. Mechanical properties and failure characteristics of supercritical carbon dioxide soak in water-bearing coal rocks. Energy 2024, 286, 129599. [Google Scholar] [CrossRef]
- Shi, X.; Pan, J.; Hou, Q.; Jin, Y.; Wang, Z.; Niu, Q.; Li, M. Micrometer-scale fractures in coal related to coal rank based on micro-CT scanning and fractal theory. Fuel 2018, 212, 162–172. [Google Scholar] [CrossRef]
- Liu, Y.; Yin, G.; Li, M.; Zhang, D.; Deng, B.; Liu, C.; Lu, J. Anisotropic Mechanical Properties and the Permeability Evolution of Cubic Coal Under True Triaxial Stress Paths. Rock Mech. Rock Eng. 2019, 52, 2505–2521. [Google Scholar] [CrossRef]
- Kou, M.-M.; Liu, X.-R.; Wang, Z.-Q.; Nowruzpour, M. Mechanical properties, failure behaviors and permeability evolutions of fissured rock-like materials under coupled hydro-mechanical unloading. Eng. Fract. Mech. 2021, 254, 107929. [Google Scholar] [CrossRef]
- Lu, Q.; Guo, J.; Liu, Z.; Ren, Y.; Wang, X.; Guan, B.; Chen, C.; He, L. Investigation of thermal induced damage of deep shale considering in-situ thermal shock effects. Geoenergy Sci. Eng. 2023, 222, 211439. [Google Scholar] [CrossRef]
- Zhu, J.; Qi, T.; Li, J.; Cheng, Z.; Zhang, Y. The Effects of High Temperature on Crack Propagation and Failure Characteristics of Sandstone. Rock Mech. Rock Eng. 2023, 56, 5753–5779. [Google Scholar] [CrossRef]
- Shan, C.; Yao, Q.; Cao, S.; Xu, Q.; Zheng, C.; Xia, Z.; Li, Y.; Yan, L. Fracture Development Patterns and Micro–Macrostructural Fractal Characteristics of Acid–Base Coal Samples. Nat. Resour. Res. 2024, 33, 831–865. [Google Scholar] [CrossRef]
- Wei, G.; Zhang, R.; Yu, C.; Zhang, K.; Wang, K. Coupled relationships between overburden stress and ultra-deep sandstone brittle deformation properties based on in situ CT scanning. J. Struct. Geol. 2023, 173, 104905. [Google Scholar] [CrossRef]
- Wu, K.; Meng, Q.; Li, R.; Wang, C.; Shen, T. In-situ CT scan-based analysis of damage evolution of coral reef limestone under cyclic loads. J. Build. Eng. 2024, 96, 110596. [Google Scholar] [CrossRef]
- Wang, D.; Zeng, F.; Wei, J.; Zhang, H.; Wu, Y.; Wei, Q. Quantitative analysis of fracture dynamic evolution in coal subjected to uniaxial and triaxial compression loads based on industrial CT and fractal theory. J. Pet. Sci. Eng. 2021, 196, 108051. [Google Scholar] [CrossRef]
- Yu, Y.; Qiu, Z.; Cheng, W.; Yang, Q.; Cui, W.; Rong, K.; Li, Y. Fracture and porosity evolution of coal under uniaxial compression: An in-situ X-ray tomography study. Geomech. Energy Environ. 2023, 36, 100499. [Google Scholar] [CrossRef]
- Li, X.; Wang, Q.; Wu, K.; Wang, J.; Qi, Q. Microscopic fracture evolution and propagation mechanism of coal with high coal burst liability. Theor. Appl. Fract. Mech. 2024, 130, 104331. [Google Scholar] [CrossRef]
- Liu, H.; Mao, L.; Ju, Y.; Hild, F. Damage evolution in coal under different loading modes using advanced digital volume correlation based on X-ray computed tomography. Energy 2023, 275, 127447. [Google Scholar] [CrossRef]
- Li, G.; Qin, Y.; Yao, H.; Qu, J.; Zhang, H.; Fang, X.; Shang, F.; Zhang, L. 3D pore structure characterization and permeability anisotropy visualization simulation of fusain. Energy 2024, 291, 130422. [Google Scholar] [CrossRef]
- GB/T 50266-2013; Standard for Test Methods of Engineering Rock Mass. China Planning Press: Beijing, China, 2013.
- Wen, Y.; Ni, G.; Zhang, X.; Zheng, Y.; Wang, G.; Wang, Z.; Huang, Q. Fine characterization of pore structure of acidified anthracite based on liquid intrusion method and Micro-CT. Energy 2023, 263, 125639. [Google Scholar] [CrossRef]
- Sun, X.; Shi, F.; Ding, J.; Tao, Z.; Zhang, Y.; Miao, C.; Cui, L. Study on Microscopic Mechanism and Failure Mode of Water–Rock Coupling in Fine Sandstone Under Uniaxial Compression. Rock Mech. Rock Eng. 2023, 56, 6823–6842. [Google Scholar] [CrossRef]
- Zhao, G.; Guo, Y.; Wang, L.; Chang, X.; Yang, H.; Guo, W.; Wu, X.; Yang, C. Experimental Study on Mechanical, Brittleness, and Fracture Behavior of Deep Shales Subjected to Fracturing Fluid-Shale Interactions at Reservoir Temperature and In-Situ Stress Conditions. Rock Mech. Rock Eng. 2024, 57, 27–44. [Google Scholar] [CrossRef]






| Properties | Wujianfang Lignite | |
|---|---|---|
| Proximate analysis, % | Mad | 17.40 |
| Aad | 16.94 | |
| Vad | 28.51 | |
| FCad | 37.15 | |
| Maceral composition (%) | Huminite | 51.81 |
| Inertinite | 45.46 | |
| Liptinite | 2.74 | |
| Ro (%) | Vitrinite reflectance | 0.28 |
| Sample | Scan 1 | Scan 2 | Scan 3 | Scan 4 | Scan 5 | Scan 6 |
|---|---|---|---|---|---|---|
| S-0h | Initial state | Compaction state | Elasticity stage | Plasticity stage | Post-peak stage | None |
| S-8h | Initial state | Compaction state | Elasticity stage | Elasticity stage | Plasticity stage | Post-peak stage |
| S-72h | Initial state | Compaction state | Elasticity stage | Plasticity stage | Post-peak stage | None |
| Sample | Scanning Point | Surface Porosity | 2D Fractal Dimension | ||
|---|---|---|---|---|---|
| (%) | σp | σf | |||
| S-0h | A | 0.36 | 0.31 | 0.97 | 0.14 |
| C | 0.12 | 0.13 | 0.80 | 0.19 | |
| D | 0.18 | 0.18 | 0.88 | 0.17 | |
| E | 3.95 | 1.31 | 1.18 | 0.04 | |
| S-8h | A | 1.58 | 0.85 | 1.15 | 0.09 |
| C | 0.35 | 0.22 | 0.97 | 0.11 | |
| D | 1.08 | 0.47 | 1.14 | 0.07 | |
| E | 8.42 | 3.55 | 1.28 | 0.05 | |
| S-72h | A | 2.90 | 1.28 | 1.25 | 0.08 |
| C | 2.30 | 1.13 | 1.22 | 0.09 | |
| D | 2.67 | 1.21 | 1.25 | 0.08 | |
| E | 12.28 | 2.57 | 1.36 | 0.04 | |
| Sample | Scanning Point | ε1 (%) | Volume (mm3) | Area (mm2) | DF,3D |
|---|---|---|---|---|---|
| S-0h | A | 0 | 33.96 | 1936.77 | 1.92 |
| B | 0.94 | 16.36 | 970.70 | 1.80 | |
| C | 1.72 | 11.18 | 651.46 | 1.76 | |
| D | 2.36 | 17.52 | 1011.44 | 1.82 | |
| E | 2.68 | 377.13 | 4758.84 | 2.14 | |
| S-8h | A | 0 | 150.99 | 7084.84 | 2.16 |
| B | 1.62 | 81.73 | 4476.68 | 2.07 | |
| C | 3.63 | 33.71 | 1818.89 | 1.90 | |
| D | 4.60 | 103.31 | 5497.56 | 2.11 | |
| E | 4.86 | 804.48 | 11,292.50 | 2.27 | |
| S-72h | A | 0 | 276.80 | 11,126.54 | 2.26 |
| B | 2.10 | 236.12 | 9439.16 | 2.23 | |
| C | 3.84 | 219.71 | 8689.06 | 2.21 | |
| D | 5.50 | 254.74 | 9886.99 | 2.24 | |
| E | 6.24 | 1172.61 | 16,319.31 | 2.35 |
| Sample | Scanning Point | Pore–Fracture Parameters | Mechanical Parameters | |||||
|---|---|---|---|---|---|---|---|---|
| Volume (mm3) | Area (mm2) | DF,3D | ε1 (%) | Estage (MPa) | σc (MPa) | BI | ||
| S-0h | A | 33.96 | 1936.77 | 1.92 | 0 | 7.41 | 0.77 | |
| B | 16.36 | 970.70 | 1.80 | 0.94 | 177.09 | |||
| C | 11.18 | 651.46 | 1.76 | 1.72 | 350.42 | |||
| D | 17.52 | 1011.44 | 1.82 | 2.36 | 444.79 | |||
| E | 377.13 | 4758.84 | 2.14 | 2.68 | ||||
| S-8h | A | 150.99 | 7084.84 | 2.16 | 0 | 9.23 | 0.73 | |
| B | 81.73 | 4476.68 | 2.07 | 1.62 | 107.06 | |||
| C | 33.71 | 1818.89 | 1.90 | 3.63 | 236.62 | |||
| D | 103.31 | 5497.56 | 2.11 | 4.60 | 319.40 | |||
| E | 804.48 | 11,292.50 | 2.27 | 4.86 | ||||
| S-72h | A | 276.80 | 11,126.54 | 2.26 | 0 | 7.43 | 0.56 | |
| B | 236.12 | 9439.16 | 2.23 | 2.10 | 77.19 | |||
| C | 219.71 | 8689.06 | 2.21 | 3.84 | 156.23 | |||
| D | 254.74 | 9886.99 | 2.24 | 5.50 | 173.36 | |||
| E | 1172.61 | 16,319.31 | 2.35 | 6.24 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, S.; Han, L.; Zhang, S.; Zhao, W.; Meng, L. Evolution Characteristics of Pore–Fractures and Mechanical Response of Dehydrated Lignite Based on In Situ Computed Tomography (CT) Scanning. Fractal Fract. 2025, 9, 220. https://doi.org/10.3390/fractalfract9040220
Yan S, Han L, Zhang S, Zhao W, Meng L. Evolution Characteristics of Pore–Fractures and Mechanical Response of Dehydrated Lignite Based on In Situ Computed Tomography (CT) Scanning. Fractal and Fractional. 2025; 9(4):220. https://doi.org/10.3390/fractalfract9040220
Chicago/Turabian StyleYan, Shuai, Lijun Han, Shasha Zhang, Weisheng Zhao, and Lingdong Meng. 2025. "Evolution Characteristics of Pore–Fractures and Mechanical Response of Dehydrated Lignite Based on In Situ Computed Tomography (CT) Scanning" Fractal and Fractional 9, no. 4: 220. https://doi.org/10.3390/fractalfract9040220
APA StyleYan, S., Han, L., Zhang, S., Zhao, W., & Meng, L. (2025). Evolution Characteristics of Pore–Fractures and Mechanical Response of Dehydrated Lignite Based on In Situ Computed Tomography (CT) Scanning. Fractal and Fractional, 9(4), 220. https://doi.org/10.3390/fractalfract9040220








