Fractal, Spectral, and Topological Analysis of the Reservoir-Induced Seismicity of Pertusillo Area (Southern Italy)
Abstract
1. Introduction
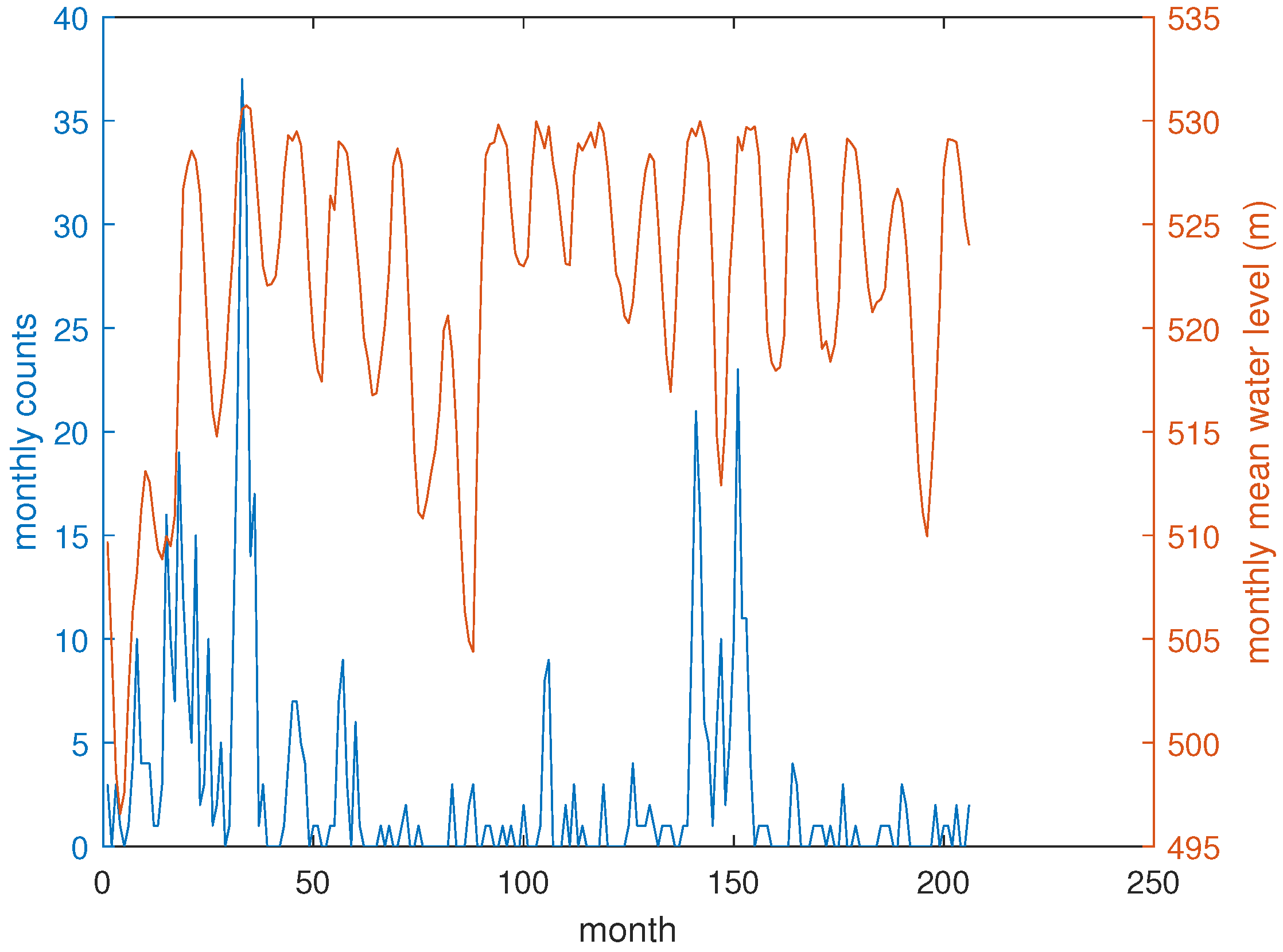
2. Seismotectonics of the High Agri Valley and Dataset Description
3. The Frequency–Magnitude Distribution
4. Methods
4.1. The Global and Local Coefficient of Variation
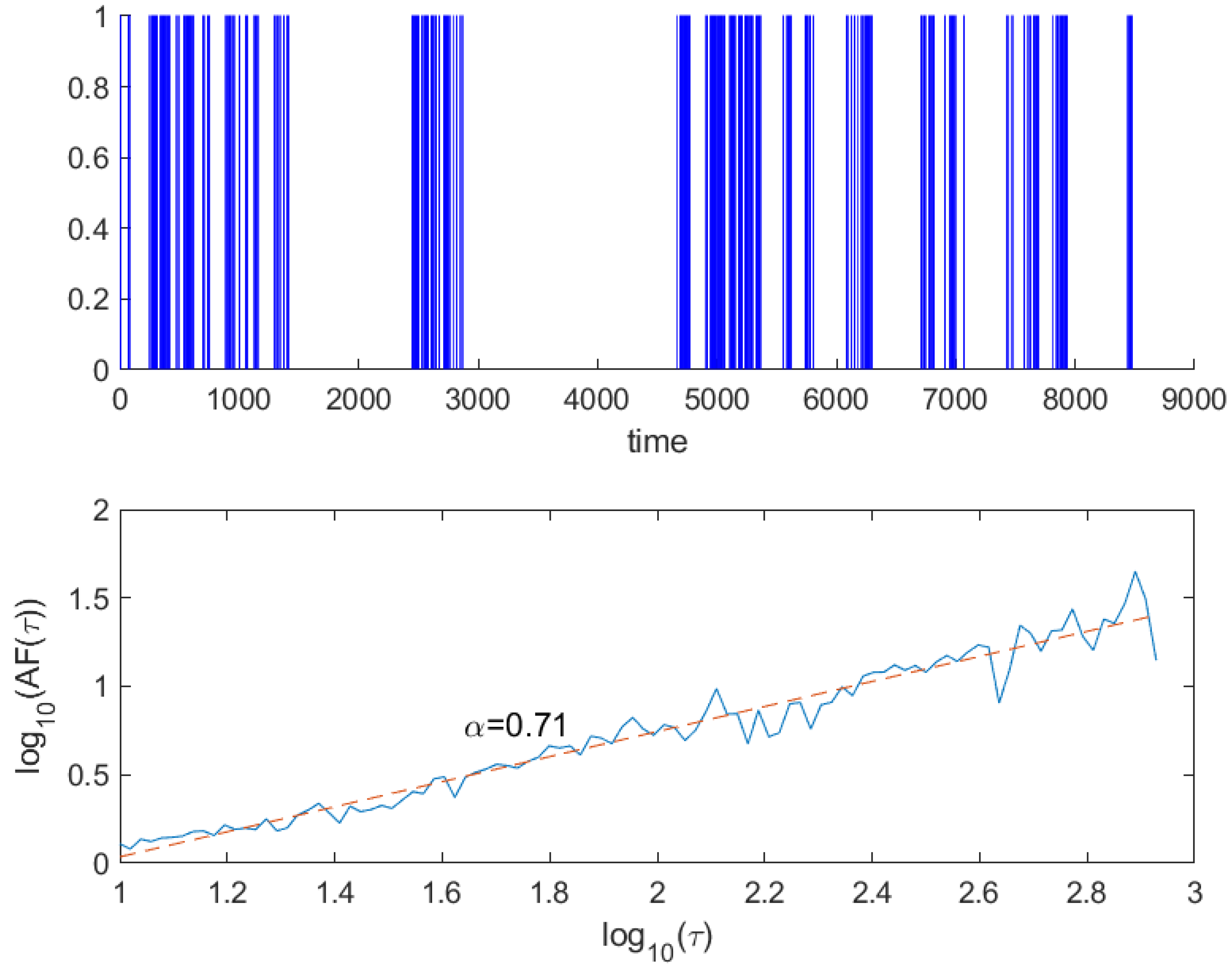
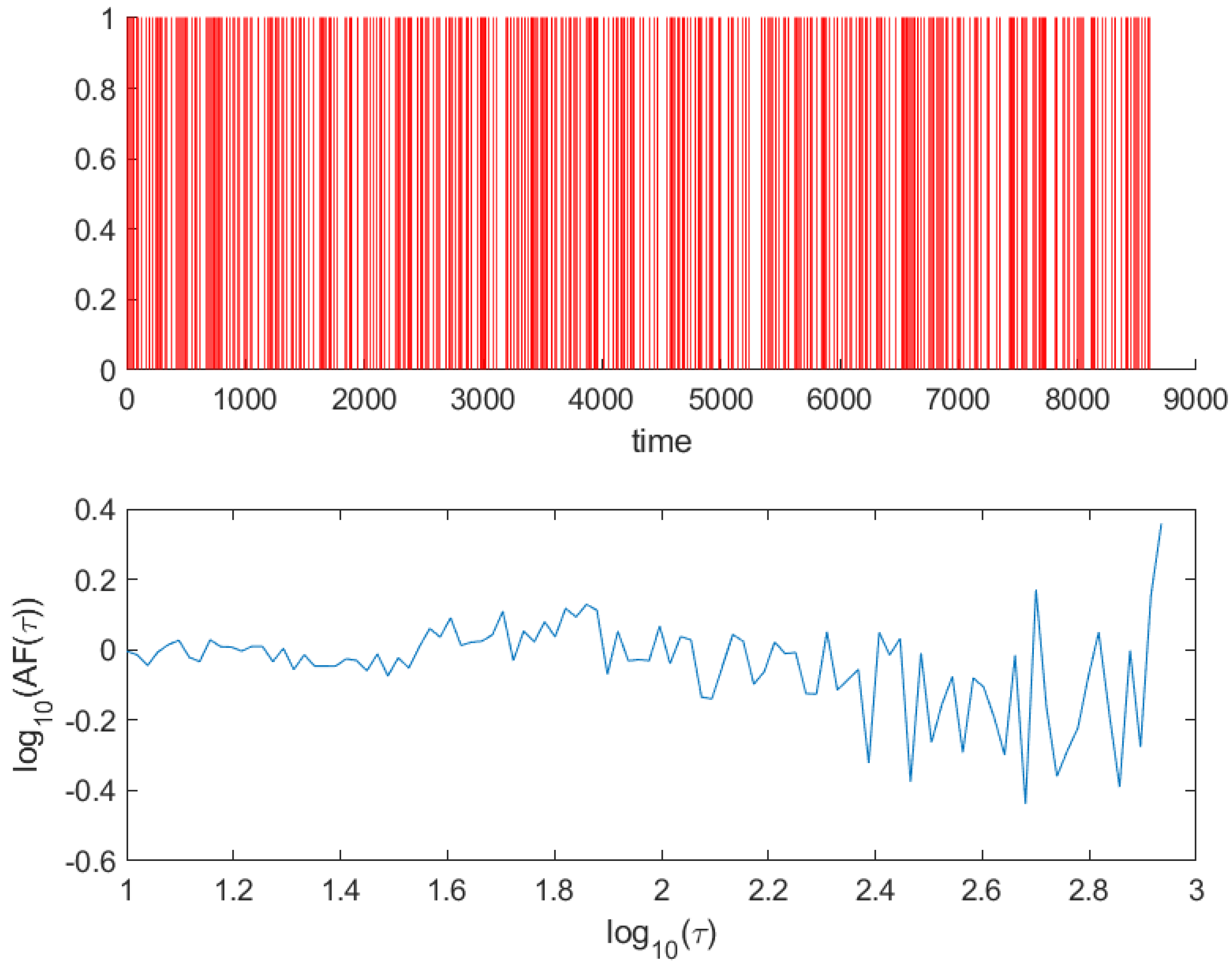
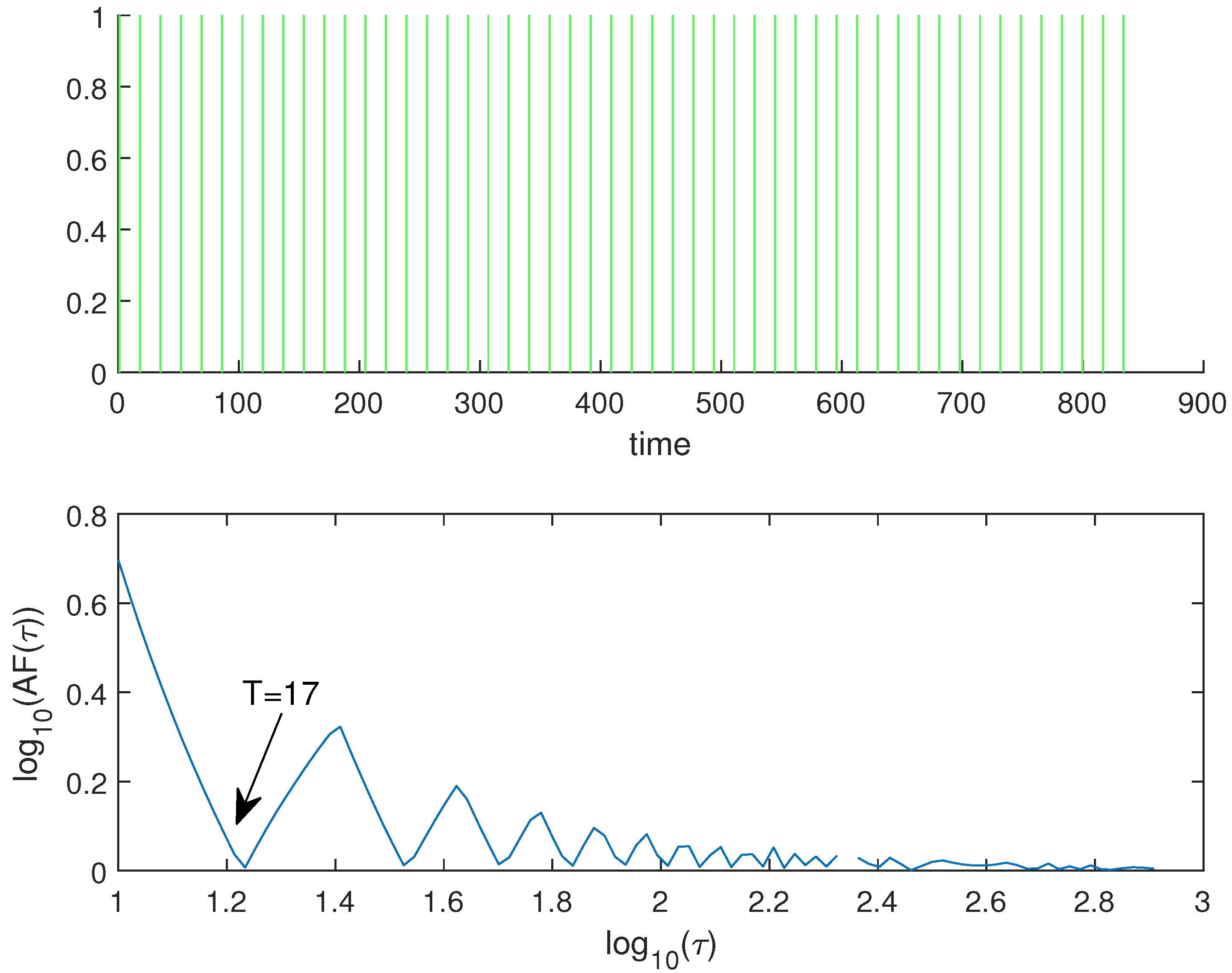
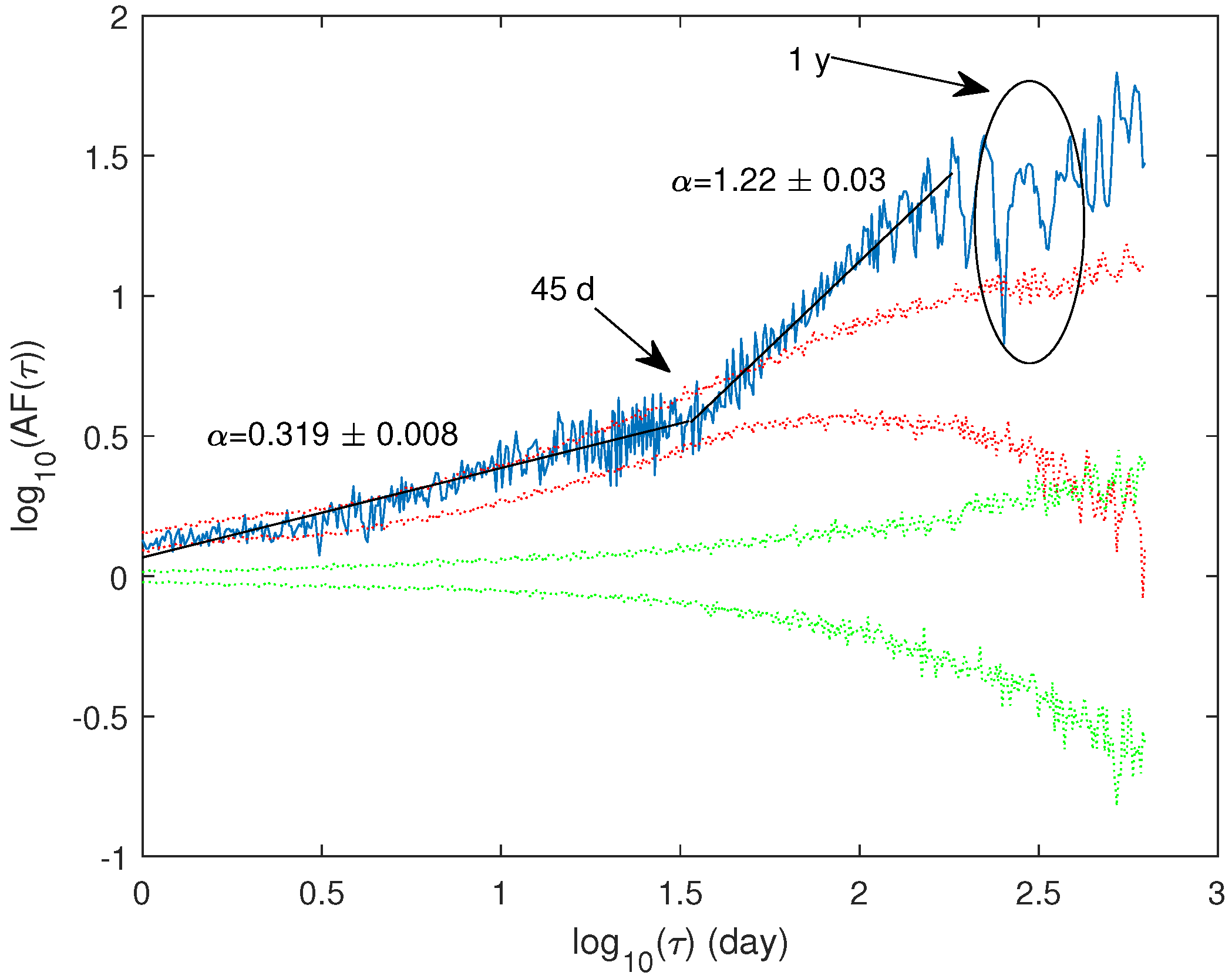
4.2. The Allan Factor
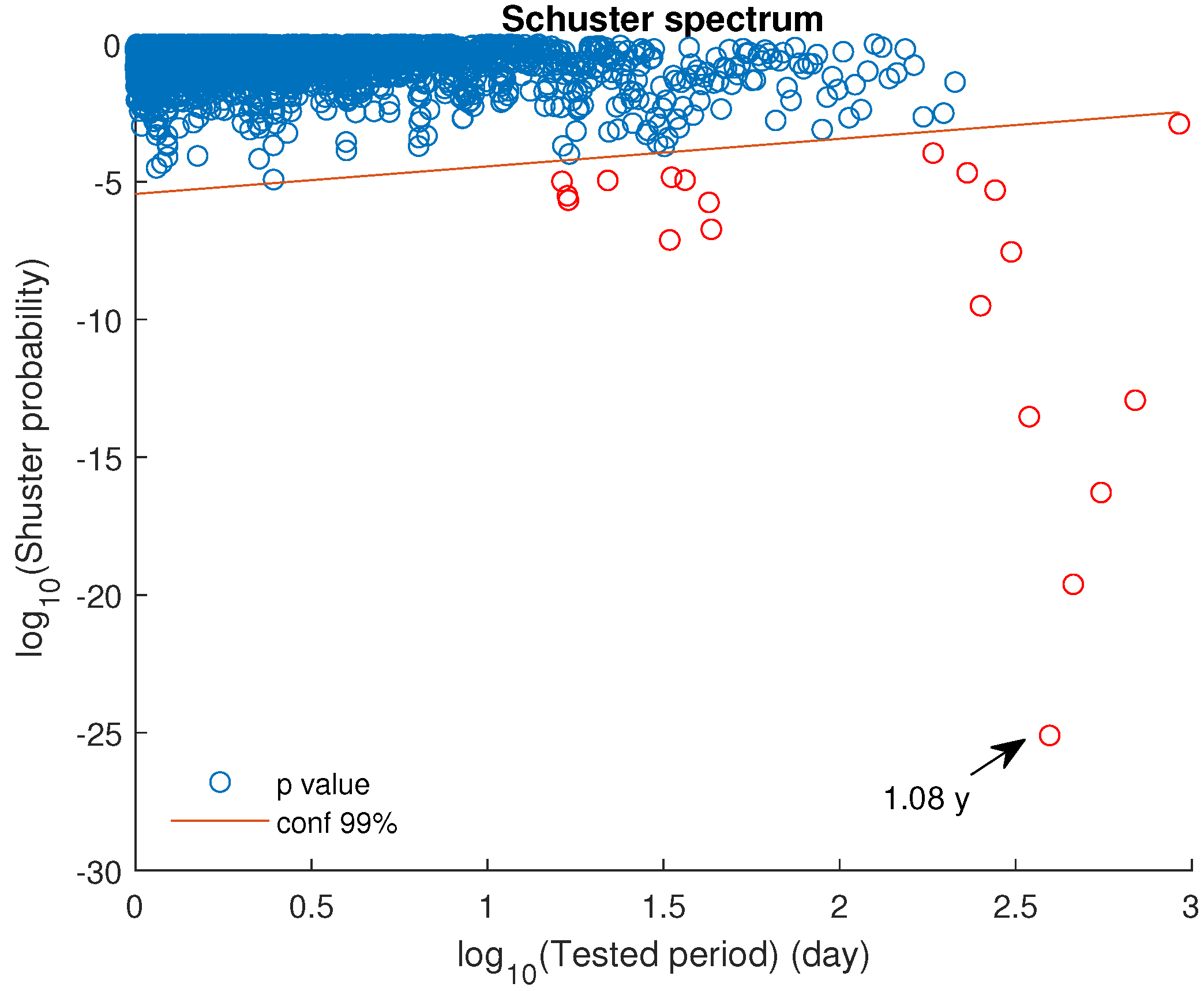
4.3. The Schuster’s Spectrum
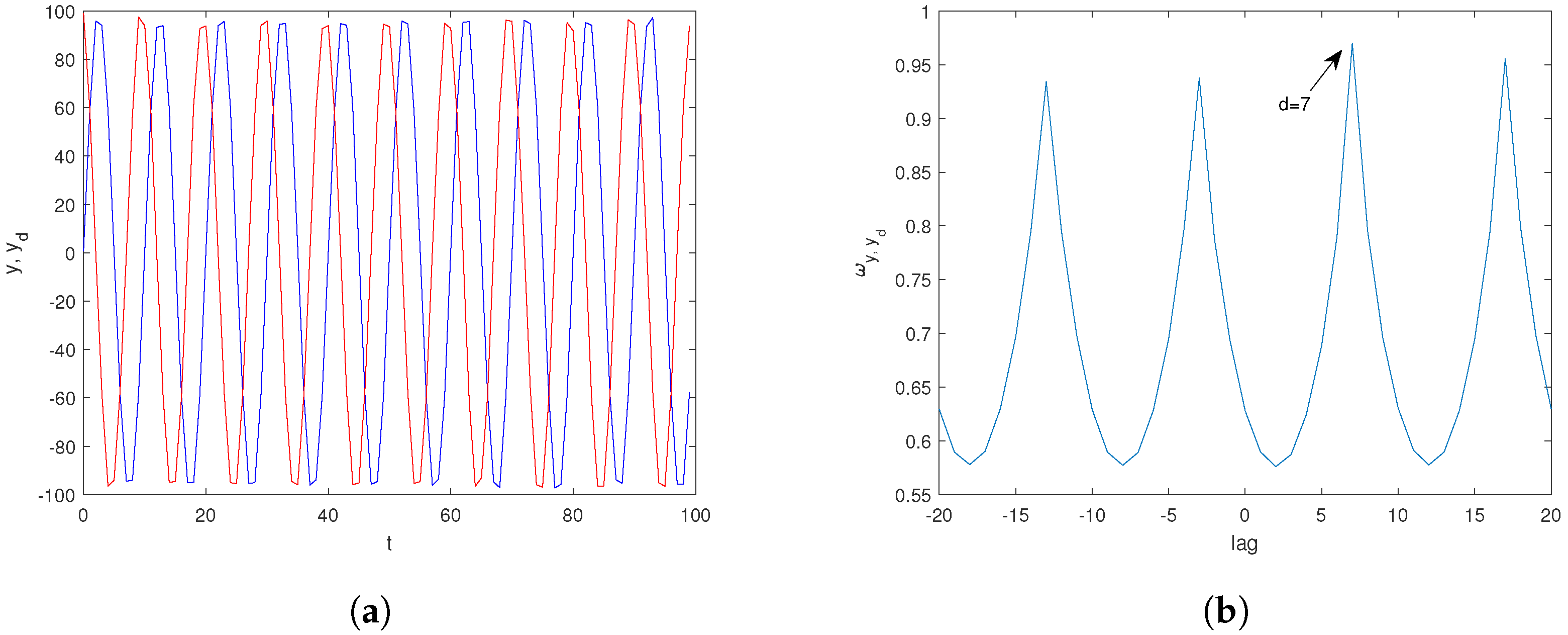
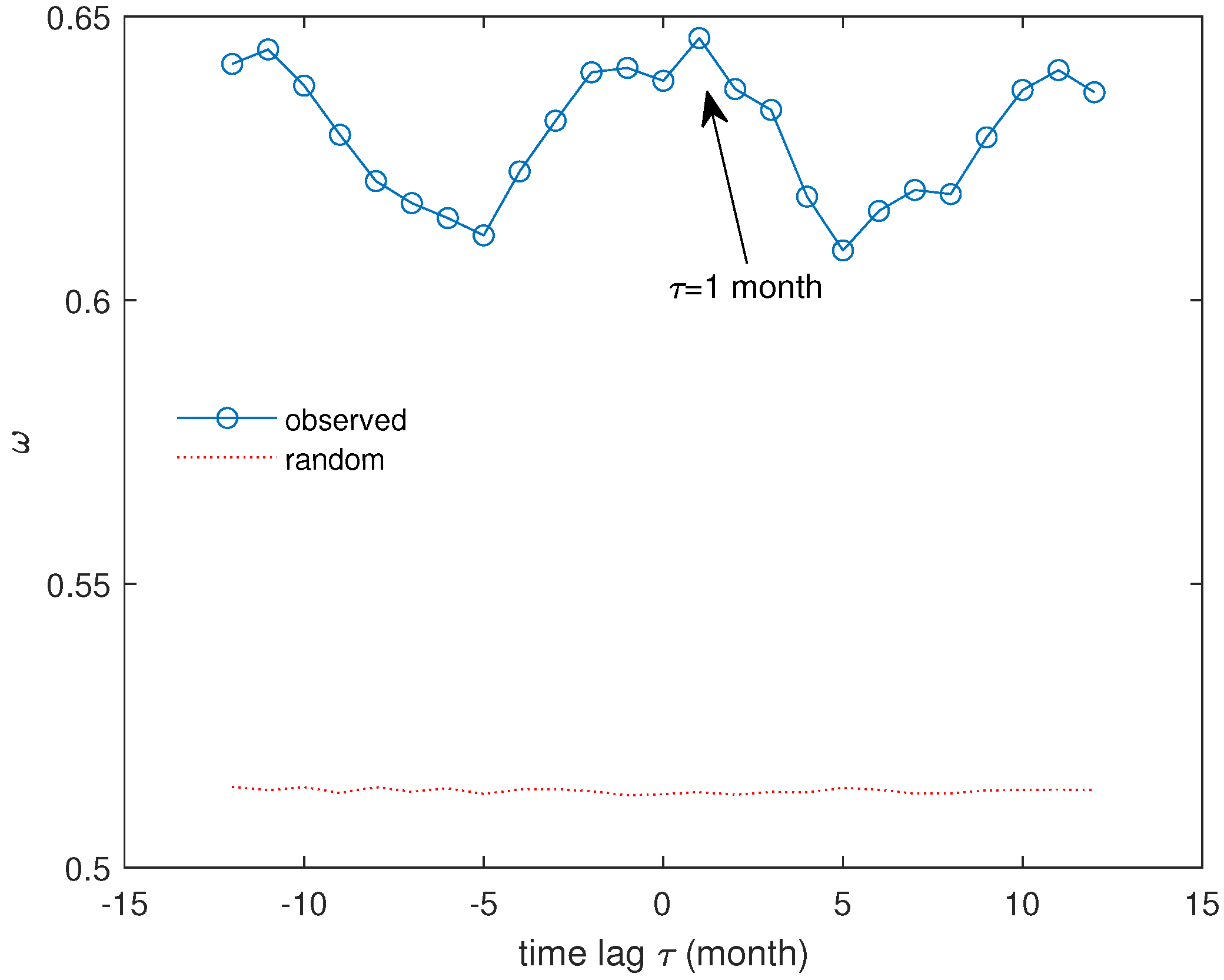
4.4. The Correlogram-Based Periodogram
4.5. The Visibility Graph
5. Results and Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Moein, M.; Langenbruch, C.; Schultz, R.; Grigoli, F.; Ellsworth, W.; Wang, R.; Rinaldi, A.; Shapiro, S. The physical mechanisms of induced earthquakes. Nat. Rev. Earth Environ. 2023, 4, 847–863. [Google Scholar] [CrossRef]
- Saar, M.; Manga, M. Seismicity induced by seasonal groundwater recharge at Mt. Hood, Oregon. Earth Planet. Sci. Lett. 2003, 214, 605–618. [Google Scholar] [CrossRef]
- Shapiro, S.A. Fluid-Induced Seismicity; Cambridge University Press: Cambridge, UK, 2015; p. 298. [Google Scholar]
- King, G.; Stein, R.; Lin, J. Static stress changes and the triggering of earthquakes. Bull. Seismol. Soc. Am. 1994, 84, 935–953. [Google Scholar]
- Harris, R. Introduction to special section: Stress triggers, stress shadows, and implications for seismic hazard. J. Geophys. Res. 1998, 103, 24347–24358. [Google Scholar] [CrossRef]
- Stokes, S.M.; Ge, S.; Brown, M.R.M.; Menezes, E.A.; Sheehan, A.F.; Tiampo, K.F. Pore pressure diffusion and onset of induced seismicity. J. Geophys. Res. 2023, 128, e2022JB026012. [Google Scholar] [CrossRef]
- Gupta, H.K.; Rastogi, B.K. Dams and Earthquakes; Elsevier: Amsterdam, The Netherlands, 1976; p. 229. [Google Scholar]
- Tao, W.; Masterlark, T.; Shen, Z.K.; Ronchin, E. Impoundment of the Zipingpu reservoir and triggering of the 2008 Mw 7.9 Wenchuan earthquake, China. J. Geophys. Res. Solid Earth 2015, 120, 7033–7047. [Google Scholar] [CrossRef]
- Wilson, M.P.; Foulger, G.R.; Gluyas, J.G.; Davies, R.J.; Julian, B.R. HiQuake: The human-induced earthquake database. Seismol. Res. Lett. 2017, 88, 1560–1565. [Google Scholar] [CrossRef]
- Wilkinson, M.; Mhana, N.; Wilson, M.P.; Foulger, G.R.; Tezel, T.; Gluyas, J.G. The plausibility of claimed induced seismicity. Sci. Rep. 2024, 14, 30846. [Google Scholar] [CrossRef]
- Chen, R.; Zhu, J.; Li, S.; Zhang, S.; Chen, X.; Li, Q.; Wang, P.; Zhang, J.; Dai, L.; Jia, Y. Characteristics and mechanisms of human-induced earthquakes in China from the QuakeQuake database. Geol. J. 2023, 58, 2099–2131. [Google Scholar] [CrossRef]
- Roeloffs, E.A. Fault stability changes induced beneath a reservoir with cyclic variations in water level. J. Geophys. Res. 1988, 93, 2107–2124. [Google Scholar]
- Bell, M.L.; Nur, A. Strength changes due to reservoir-induced pore pressure and stresses and application to Lake Oroville. J. Geophys. Res. 1978, 83, 4469–4483. [Google Scholar] [CrossRef]
- Simpson, D.W.; Leith, W.S.; Scholz, C.H. Two types of reservoir-induced seismicity. Bull. Seismol. Soc. Am. 1988, 78, 2025–2040. [Google Scholar]
- Carder, D. Seismic investigations in the Boulder Dam area, 1940–1944, and the influence of reservoir loading on earthquake activity. Bull. Seismol. Soc. Am. 1945, 35, 175–192. [Google Scholar] [CrossRef]
- Stabile, T.A.; Fat-Helbary, E.R.; Serlenga, V.; Panebianco, S.; Tizzani, P.; Castaldo, R.; Telesca, L.; El-Amin, E.M.; Hamed, A. Fault structure and earthquake clustering in Aswan region (Egypt) revealed by high-precision earthquake location from 35 years of recorded natural and induced seismicity. Earth Planet. Sci. Lett. 2024, 642, 118881. [Google Scholar] [CrossRef]
- Dura-Gomez, I.; Talwani, P. Hydromechanics of the Koyna-Warna region, India. Pure Appl. Geophys. 2010, 167, 183–213. [Google Scholar] [CrossRef]
- Goswami, D.; Akkiraju, V.V.; Roy, S. Heat flow and thermal structure in the Koyna seismic zone, western India: Implications for recurrent reservoir triggered seismicity. Tectonophysics 2024, 873, 230216. [Google Scholar] [CrossRef]
- Simpson, D.; Negmatullaev, S. Induced seismicity at Nurek Reservoir, Tadjikistan, USSR. Bull. Seismol. Soc. Am. 1981, 71, 1561–1586. [Google Scholar] [CrossRef]
- Talwani, P. On the nature of reservoir-induced seismicity. Pure Appl. Geophys. 1997, 150, 473–492. [Google Scholar] [CrossRef]
- Gupta, H. A review of recent studies of triggered earthquakes by artificial water reservoirs with special emphasis on earthquakes in Koyna, India. Earth Sci. Rev. 2002, 58, 279–310. [Google Scholar] [CrossRef]
- Valoroso, L.; Improta, L.; Chiaraluce, L.; DiStefano, R.; Ferranti, L.; Govoni, A.; Chiarabba, C. Active faults and induced seismicity in the Val d’Agri area (southern Apennines, Italy). Geophys. J. Int. 2009, 178, 488–502. [Google Scholar] [CrossRef]
- Stabile, T.A.; Giocoli, A.; Perrone, A.; Piscitelli, S.; Lapenna, V. Fluid injection induced seismicity reveals a NE dipping fault in the southeastern sector of the High Agri Valley (southern Italy). Geophys. Res. Lett. 2014, 41, 5847–5854. [Google Scholar] [CrossRef]
- Stabile, T.A.; Giocoli, A.; Perrone, A.; Piscitelli, S.; Telesca, L.; Lapenna, V. Relationship between seismicity and water level of the Pertusillo reservoir (southern Italy). Boll. Geofis. Teor. Appl. 2015, 56, 505–517. [Google Scholar] [CrossRef]
- Telesca, L.; Giocoli, A.; Lapenna, V.; Stabile, T.A. Robust identification of periodic behavior in the time dynamics of short seismic series: The case of seismicity induced by Pertusillo Lake, southern Italy. Stoch. Environ. Res. Risk Assess. 2015, 29, 1437–1446. [Google Scholar] [CrossRef]
- Vlček, J.; Eisner, L.; Stabile, T.A.; Telesca, L. Temporal Relationship Between Injection Rates and Induced Seismicity. Pure Appl. Geophys. 2018, 175, 2821–2835. [Google Scholar] [CrossRef]
- Rinaldi, A.; Improta, L.; Hainzl, S.; Catalli, F.; Urpi, L.; Wiemer, S. Combined approach of poroelastic and earthquake nucleation applied to the reservoir-induced seismic activity in the Val d’Agri area, Italy. J. Rock Mech. Geotech. Eng. 2020, 12, 802–810. [Google Scholar] [CrossRef]
- Picozzi, M.; Serlenga, V.; Stabile, T.A. Spatio-temporal evolution of ground motion intensity caused by reservoir-induced seismicity at the Pertusillo artificial lake (southern Italy). Front. Earth Sci. 2022, 10, 1048196. [Google Scholar] [CrossRef]
- Barkat, A.; Tan, Y.J.; Madson, A. Deciphering the Interplay between Reservoir Loading and Dynamic Stresses at the Pertusillo Reservoir. Seismol. Res. Lett. 2024, 96, 461–472. [Google Scholar] [CrossRef]
- Lavecchia, A.; Serlenga, V.; Filippucci, M.; Stabile, T.A.; Prosser, G.; Tallarico, A. Fault (re)activation and fluid-induced seismicity: An example from the Val d’Agri intermontane basin (southern Italy). J. Geophys. Res. Solid Earth 2024, 129, e2024JB028710. [Google Scholar] [CrossRef]
- Mazzoli, S.; Barkham, S.; Cello, G.; Gambini, R.; Mattioni, L.; Shiner, P.; Tondi, E. Reconstruction of continental margin architecture deformed by the contraction of Lagonegro Basin, southern Apennines, Italy. J. Geol. Soc. 2001, 158, 309–319. [Google Scholar]
- Shiner, P.; Beccaccini, A.; Mazzoli, S. Thin-skinned versus thick-skinned structural models for Apulian carbonate reservoirs: Constraints from the Val d’Agri Fields, S Apennines, Italy. Mar. Petrol. Geol. 2004, 21, 805–827. [Google Scholar]
- Mallet, R. Great Neapolitan Earthquake of 1857. The First Principles of Observational Seismology; Traduzione italiana in Ferrari G.: London, UK, 1862. [Google Scholar]
- Rovida, A.; Antonucci, A. EPICA-European PreInstrumental Earthquake Catalogue, Version 1.1; Istituto Nazionale di Geofisica e Vulcanologia (INGV): Roma, Italy, 2021. [Google Scholar] [CrossRef]
- Panebianco, S.; Serlenga, V.; Satriano, C.; Cavalcante, F.; Stabile, T.A. Semi-automated template matching and machine-learning based analysis of the August 2020 Castelsaraceno microearthquake sequence (southern Italy). Geomat. Nat. Hazards Risk 2023, 14, 2207715. [Google Scholar] [CrossRef]
- Stabile, T.A.; Vlček, J.; Wcisło, M.; Serlenga, V. Analysis of the 2016–2018 fluid-injection induced seismicity in the High Agri Valley (Southern Italy) from improved detections using template matching. Sci. Rep. 2021, 11, 20630. [Google Scholar] [CrossRef]
- Stabile, T.A.; Giocoli, A.; Lapenna, V.; Perrone, A.; Piscitelli, S.; Telesca, L. Evidence of low-magnitude continued reservoir-induced seismicity associated with the Pertusillo artificial lake (southern Italy). Bull Seism. Soc. Am. 2014, 104, 1820–1828. [Google Scholar] [CrossRef]
- Serlenga, V.; Stabile, T.A. How do local earthquake tomography and inverted dataset affect earthquake locations? The case study of High Agri Valley (Southern Italy). Geomat. Nat. Hazards Risk 2019, 10, 49–78. [Google Scholar] [CrossRef]
- Eni spa. VAL D’AGRI NETWORK. [Data Set]. 2001. Available online: https://www.fdsn.org/networks/detail/VA/ (accessed on 31 January 2025).
- INGV. Rete Sismica Nazionale (RSN); Istituto Nazionale di Geofisica e Vulcanologia (INGV): Roma, Italy, 2005. [Google Scholar] [CrossRef]
- Stabile, T.A.; Serlenga, V.; Satriano, C.; Romanelli, M.; Gueguen, E.; Gallipoli, M.R.; Ripepi, E.; Saurel, J.M.; Panebianco, S.; Bellanova, J.; et al. The INSIEME seismic network: A research infrastructure for studying induced seismicity in the high Agri Valley (southern Italy). Earth Syst. Sci. Data 2020, 12, 519–538. [Google Scholar] [CrossRef]
- GEOFON Data Centre. GEOFON Seismic Network; GFZ Data Services: Potsdam, Germany, 1993. [Google Scholar] [CrossRef]
- Lomax, A.; Virieux, J.; Volant, P.; Berge, C. Probabilistic earthquake location in 3D and layered models: Introduction of a Metropolis-Gibbs method and comparison with linear locations. In Advances in Seismic Event Location; Thurber, C.H., Rabinowitz, N., Eds.; Kluwer: Amsterdam, The Netherlands, 2000; pp. 101–134. [Google Scholar]
- Hutton, L.; Boore, D.M. The ML scale in southern California. Bull. Seismol. Soc. Am. 1987, 77, 2074–2094. [Google Scholar]
- Gutenberg, R.; Richter, C. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188. [Google Scholar]
- Scholz, C.H. The frequency-magnitude relation of microfracturing in rock and its relation to earthquakes. Bull. Seismol. Soc. Am. 1968, 58, 399–415. [Google Scholar]
- Wyss, M. Towards a physical understanding of the earthquake frequency distribution. Geophys. J. R. Astron. Soc. 1973, 31, 341–359. [Google Scholar]
- Amitrano, D. Brittle-ductile transition and associated seismicity: Experimental and numerical studies and relationship with the b value. J. Geophys. Res. 2003, 108, 2044. [Google Scholar] [CrossRef]
- Gulia, L.; Wiemer, S. The influence of tectonic regimes on the earthquake size distribution: A case study for Italy. Geophys. Res. Lett. 2010, 37, 10305. [Google Scholar] [CrossRef]
- Godano, C.; Petrillo, G. Estimating the Completeness Magnitude m and the b-Values in a Snap. Earth Space Sci. 2023, 10, e2022EA002540. [Google Scholar] [CrossRef]
- Rydelek, P.A.; Sacks, I.S. Testing the completeness of Earthquake catalogs and the hypothesis of self-similarity. Nature 1989, 337, 251–253. [Google Scholar] [CrossRef]
- Wiemer, S.; Wyss, M. Minimum magnitude of completeness in earthquake catalogs: Examples from Alaska, the Western United States, and Japan. Bull. Seismol. Soc. Am. 2000, 90, 859–869. [Google Scholar]
- Cao, A.; Gao, S.S. Temporal variation of seismic b-values beneath northeastern Japan island arc. Geophys. Res. Lett. 2002, 29, 48-1–48-3. [Google Scholar] [CrossRef]
- Ogata, Y.; Katsura, K. Analysis of temporal and spatial heterogeneity of magnitude frequency distribution inferred from earthquake catalogues. Geophys. J. Int. 1993, 113, 727–738. [Google Scholar] [CrossRef]
- Godano, C. A new method for the estimation of the completeness magnitude. Phys. Earth Planet. Inter. 2017, 263, 7–11. [Google Scholar] [CrossRef]
- Woessner, J.; Wiemer, S. Assessing the Quality of Earthquake Catalogues: Estimating the Magnitude of Completeness and Its Uncertainty. Bull. Seismol. Soc. Am. 2005, 95, 684–698. [Google Scholar] [CrossRef]
- Kařník, V.; Klíma, K. Magnitude-frequency distribution in the European-Mediterranean earthquake regions. Tectonophysics 1993, 220, 309–323. [Google Scholar] [CrossRef]
- Aki, K. Maximum likelihood estimate of b in the formula log(N) = a − bM and its confidence limits. Bull. Earthq. Res. Inst. Univ. Tokyo 1965, 43, 237–239. [Google Scholar]
- Mignan, A.; Woessner, J. Estimating the magnitude of completeness for earthquake catalogs. Community Online Resour. Stat. Seism. Anal. 2012, 1–45. [Google Scholar] [CrossRef]
- Kagan, Y.Y.; Jackson, D.D. Long-Term Earthquake Clustering. Geophys. J. Int. 1991, 104, 117–134. [Google Scholar] [CrossRef]
- Shinomoto, S.; Miura, K.; Koyama, S. A measure of local variation of inter-spike intervals. Biosystems 2005, 79, 67–72. [Google Scholar] [CrossRef] [PubMed]
- Thurner, S.; Lowen, S.B.; Feurstein, M.C.; Heneghan, C.; Feichtinger, H.G.; Teich, M.C. Analysis, synthesis, and estimation of fractal-rate stochastic point processes. Fractals 1997, 5, 565–596. [Google Scholar] [CrossRef]
- Telesca, L.; Cuomo, V.; Lapenna, V.; Macchiato, M. Statistical analysis of fractal properties of point processes modelling seismic sequences. Phys. Earth Planet. Int. 2001, 125, 65–83. [Google Scholar] [CrossRef]
- Telesca, L.; Amatulli, G.; Lasaponara, R.; Lovallo, M.; Santulli, A. Time-scaling properties in forest-fire sequences observed in Gargano area (southern Italy). Ecol. Model. 2005, 185, 531–544. [Google Scholar] [CrossRef]
- Telesca, L.; ElShafey Fat ElBary, R.; Amin Mohamed, A.E.E.; ElGabry, M. Analysis of the cross-correlation between seismicity and water level in the Aswan area (Egypt) from 1982 to 2010. Nat. Hazards Earth Syst. Sci. 2012, 12, 2203–2207. [Google Scholar] [CrossRef]
- Gebber, G.L.; Orer, H.S.; Barman, S.M. Fractal Noises and Motions in Time Series of Presympathetic and Sympathetic Neural Activities. J. Neurophysiol. 2006, 95, 1176–1184. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G. On the sampling distribution of Allan factor estimator for a homogeneous Poisson process and its use to test inhomogeneities at multiple scales. Phys. A Stat. Mech. Its Appl. 2013, 392, 1080–1089. [Google Scholar] [CrossRef]
- Tanaka, S.; Sato, H.; Matsumura, S.; Ohtake, M. Tidal triggering of earthquakes in the subducting Philippine Sea plate beneath the locked zone of the plate interface in the Tokai region, Japan. Tectonophysics 2006, 417, 69–80. [Google Scholar] [CrossRef]
- Telesca, L.; Tsereteli, N.; Chelidze, T.; Lapenna, V. Spectral Investigation of the Relationship between Seismicity and Water Level in the Enguri High Dam Area (Georgia). Geosciences 2024, 14, 22. [Google Scholar] [CrossRef]
- Ader, T.J.; Avouac, J.P. Detecting periodicities and declustering in earthquake catalogs using the Schuster spectrum, application to Himalayan seismicity. Earth Planet. Sci. Lett. 2013, 377–378, 97–105. [Google Scholar] [CrossRef]
- Ader, T.J.; Lapusta, N.; Avouac, J.P.; Ampuero, J.P. Response of rate-and-state seismogenic faults to harmonic shear-stress perturbations. Geophys. J. Int. 2014, 198, 385–413. [Google Scholar] [CrossRef]
- Priestley, M.B. Spectral Analysis and Time Series; Academic Press: London, UK; New York, NY, USA, 1981; p. 890. [Google Scholar]
- Ahdesmäki, M.; Lähdesmäki, H.; Pearson, R.; Huttunen, H.; Yli-Harja, O. Robust detection of periodic time series measured from biological systems. BMC Bioinform. 2005, 6, 117. [Google Scholar]
- Lacasa, L.; Luque, B.; Ballesteros, F.; Luque, J.; Nuno, J.C. From time series to complex networks: The visibility graph. Proc. Natl. Acad. Sci. USA 2008, 105, 4972–4975. [Google Scholar] [PubMed]
- Zhang, R.; Ashuri, B.; Shyr, Y.; Deng, Y. Forecasting construction cost index based on visibility graph: A network approach. Phys. A Stat. Mech. Its Appl. 2018, 493, 239–252. [Google Scholar]
- Long, Y. Visibility graph network analysis of gold price time series. Phys. A Stat. Mech. Its Appl. 2013, 392, 3374–3384. [Google Scholar]
- Wang, N.; Li, D.; Wang, Q. Visibility graph analysis on quarterly macroeconomic series of China based on complex network theory. Phys. A Stat. Mech. Its Appl. 2012, 391, 6543–6555. [Google Scholar] [CrossRef]
- Jiang, W.; Wei, B.; Zhan, J.; Xie, C.; Zhou, D. A visibility graph power averaging aggregation operator: A methodology based on network analysis. Comput. Ind. Eng. 2016, 101, 260–268. [Google Scholar]
- Chen, S.; Hu, Y.; Mahadevan, S.; Deng, Y. A visibility graph averaging aggregation operator. Phys. A Stat. Mech. Its Appl. 2014, 403, 1–12. [Google Scholar]
- Yu, M.; Hillebrand, A.; Gouw, A.A.; Stam, C.J. Horizontal visibility graph transfer entropy (HVG-TE): A novel metric to characterize directed connectivity in large-scale brain networks. NeuroImage 2017, 156, 249–264. [Google Scholar] [CrossRef] [PubMed]
- Telesca, L.; Lovallo, M.; Pierini, J.O. Visibility graph approach to the analysis of ocean tidal records. Chaos. Solit. Fractals. 2012, 45, 1087–1091. [Google Scholar] [CrossRef]
- Lacasa, L.; Nicosia, V.; Latora, V. Network structure of multivariate time series. Sci. Rep. 2015, 5, 15508. [Google Scholar] [PubMed]
- Bianchi, F.M.; Livi, L.; Alippi, C.; Jenssen, R. Multiplex visibility graphs to investigate recurrent neural network dynamics. Sci. Rep. 2017, 7, 44037. [Google Scholar] [CrossRef]
- Carmona-Cabezas, R.; Gómez-Gómez, J.; Ariza-Villaverde, A.B.; Gutiérrez de Ravé, E.; Jiménez-Hornero, F.J. Multiplex Visibility Graphs as a complementary tool for describing the relation between ground level O3 and NO2. Atmos. Pollut. Res. 2020, 11, 205–212. [Google Scholar]

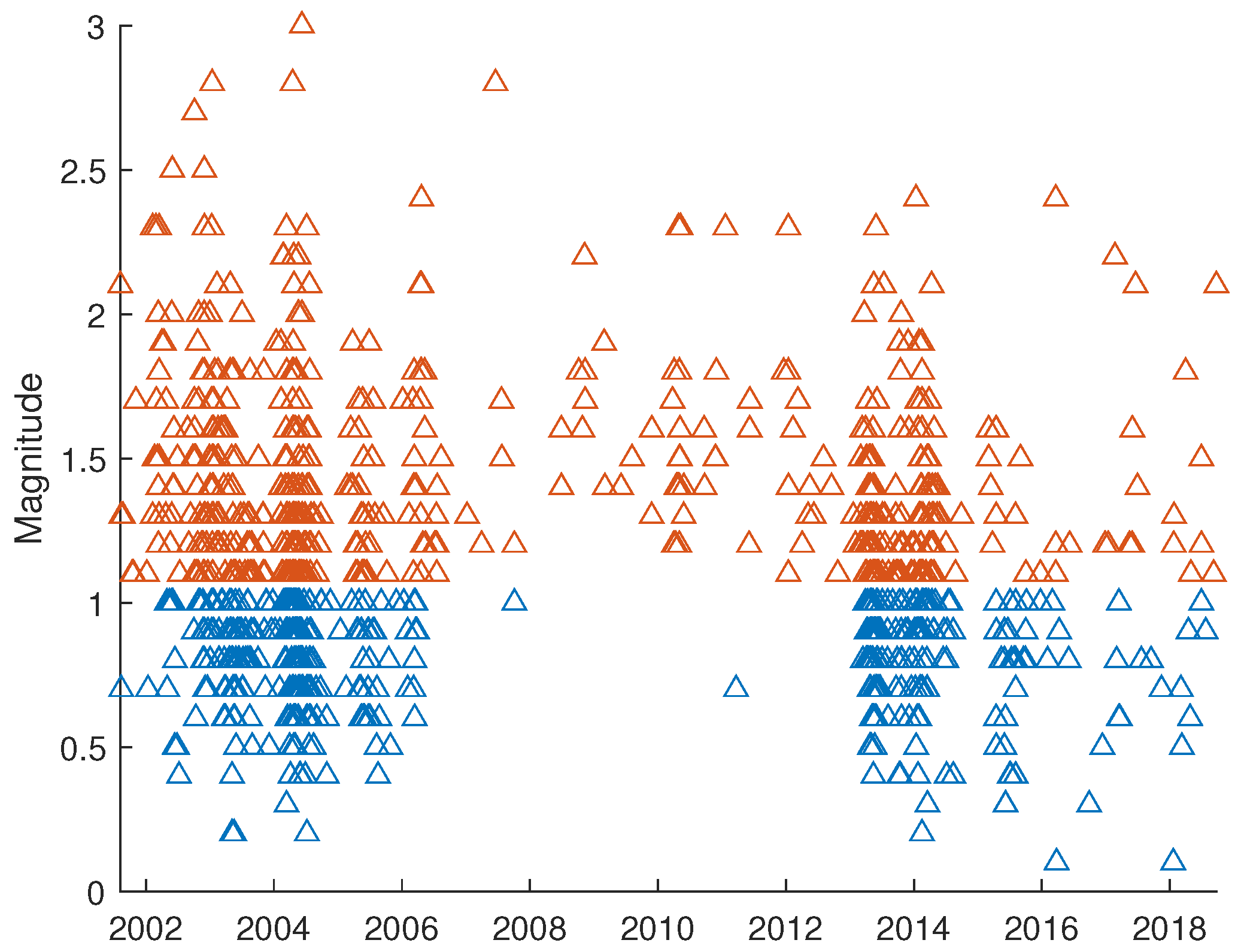
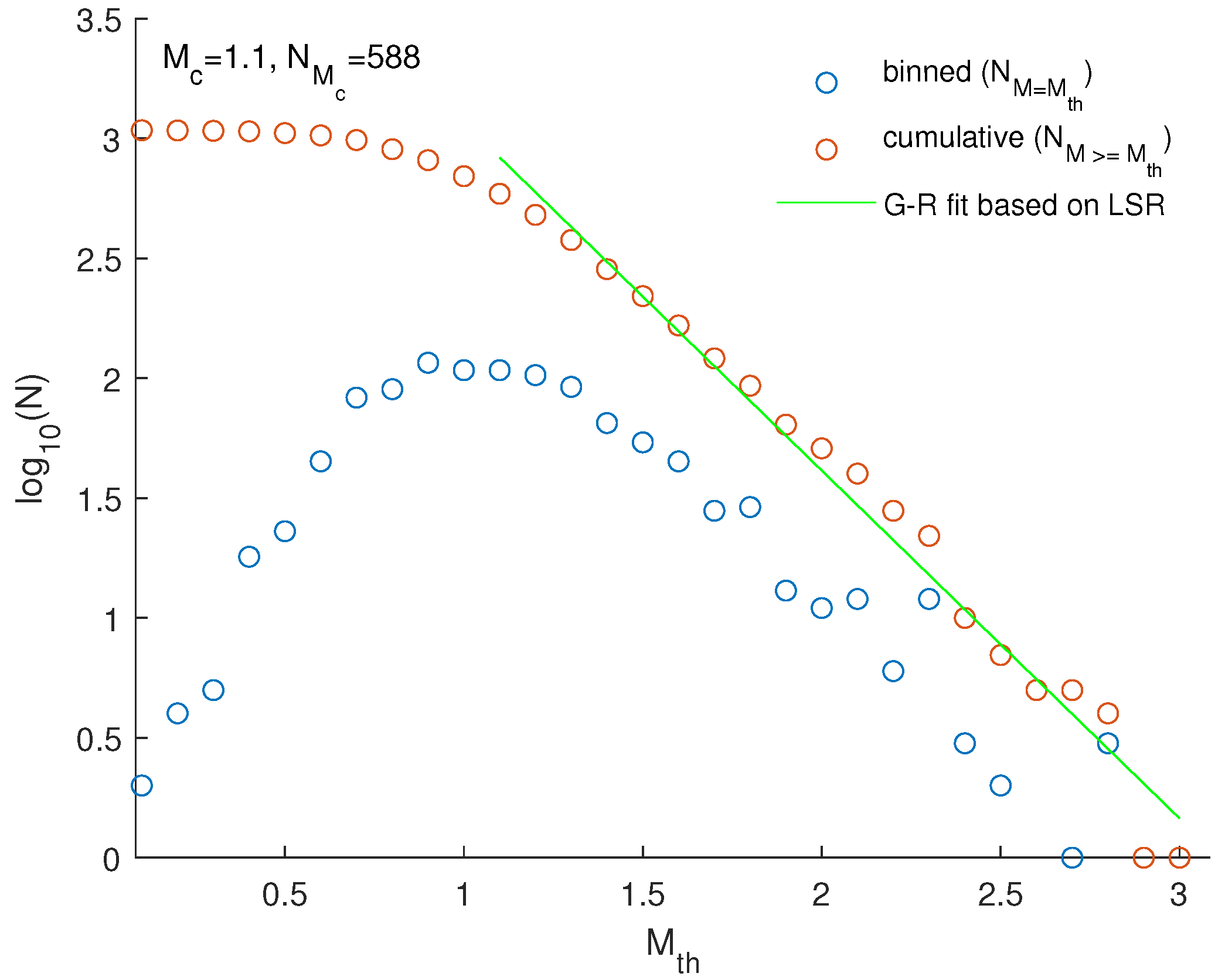

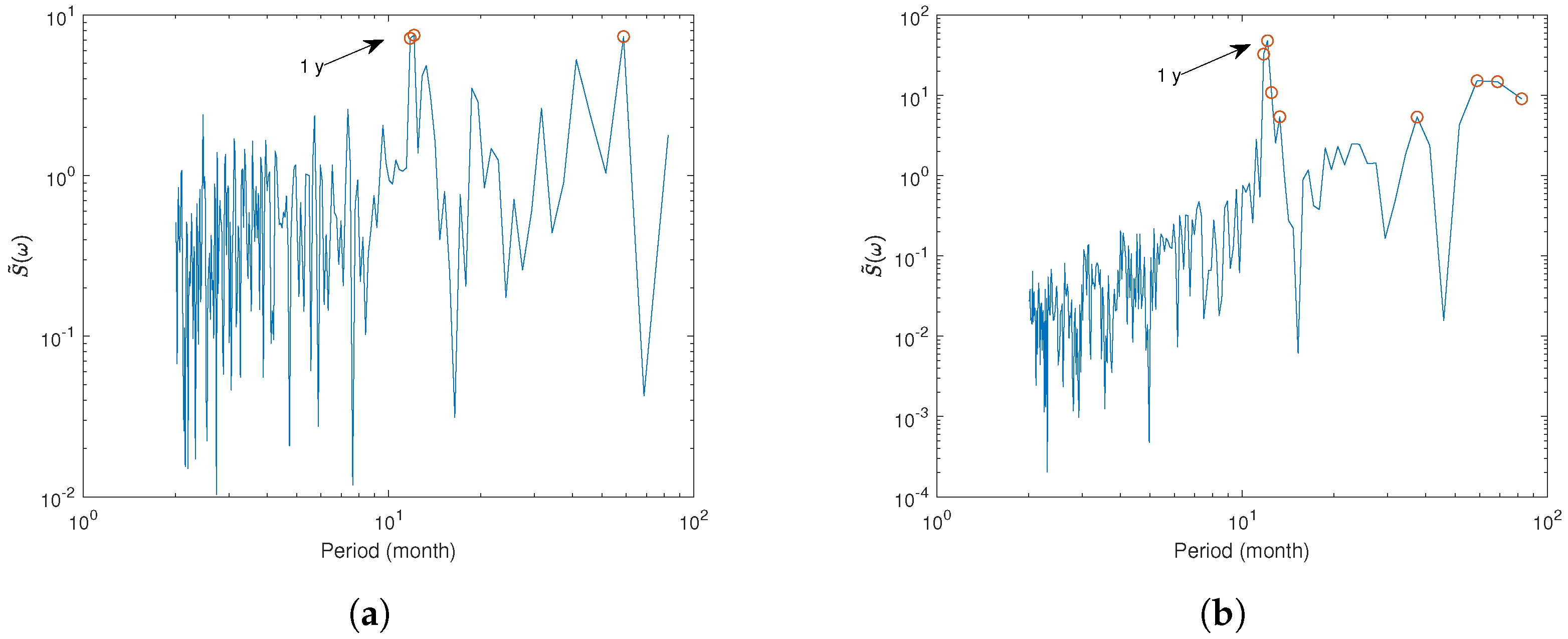
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Telesca, L.; Panebianco, S.; Serlenga, V.; Stabile, T.A. Fractal, Spectral, and Topological Analysis of the Reservoir-Induced Seismicity of Pertusillo Area (Southern Italy). Fractal Fract. 2025, 9, 208. https://doi.org/10.3390/fractalfract9040208
Telesca L, Panebianco S, Serlenga V, Stabile TA. Fractal, Spectral, and Topological Analysis of the Reservoir-Induced Seismicity of Pertusillo Area (Southern Italy). Fractal and Fractional. 2025; 9(4):208. https://doi.org/10.3390/fractalfract9040208
Chicago/Turabian StyleTelesca, Luciano, Serena Panebianco, Vincenzo Serlenga, and Tony Alfredo Stabile. 2025. "Fractal, Spectral, and Topological Analysis of the Reservoir-Induced Seismicity of Pertusillo Area (Southern Italy)" Fractal and Fractional 9, no. 4: 208. https://doi.org/10.3390/fractalfract9040208
APA StyleTelesca, L., Panebianco, S., Serlenga, V., & Stabile, T. A. (2025). Fractal, Spectral, and Topological Analysis of the Reservoir-Induced Seismicity of Pertusillo Area (Southern Italy). Fractal and Fractional, 9(4), 208. https://doi.org/10.3390/fractalfract9040208






