Parameter Estimation of Fractional Uncertain Differential Equations
Abstract
1. Introduction
- (1)
- A novel approach for estimating parameters of FUDEs is introduced. In particular, the rectangular and trapezoidal methods are utilized for the numerical approximation of optimization problems.
- (2)
- The prediction–correction technique is employed to solve fractional-order uncertain differential equations, with expected values being derived through the -path method. Numerical simulations are carried out along various -paths, yielding corresponding numerical solutions.
- (3)
- Finally, the proposed method is applied to practical models for prediction, demonstrating its applicability and robustness.
2. Preliminaries
- (A1) Normality axiom. for the universal set Γ.
- (A2) Duality axiom. for any event Λ.
- (A3) Subadditivity axiom. For every countable sequence of events , we have
- (A4) Product axiom. Let be uncertain spaces for . Then, the product uncertain measure satisfieswhere is an arbitrarily chosen event from for , respectively.
- (i)
- , and almost all simple paths are Lipschitz continuous;
- (ii)
- has stationary and independent increments;
- (iii)
- The increment has a normal uncertain distribution
- (H1)
- Lipschitz condition ,
- (H2)
- linear growth condition ,
3. Parameter Estimation
3.1. Discretization Model of the Fractional-Order Rectangular Method
| Algorithm 1 Parameter Estimation for FUDE (1) Using the Fractional-Order Rectangular Method |
|
3.2. The Discretization Model of Fractional Stepwise Normal Method
| Algorithm 2 Parameter Estimation for FUDE (1) Using the Fractional-Order Trapezoidal Method |
|
3.3. Some Example
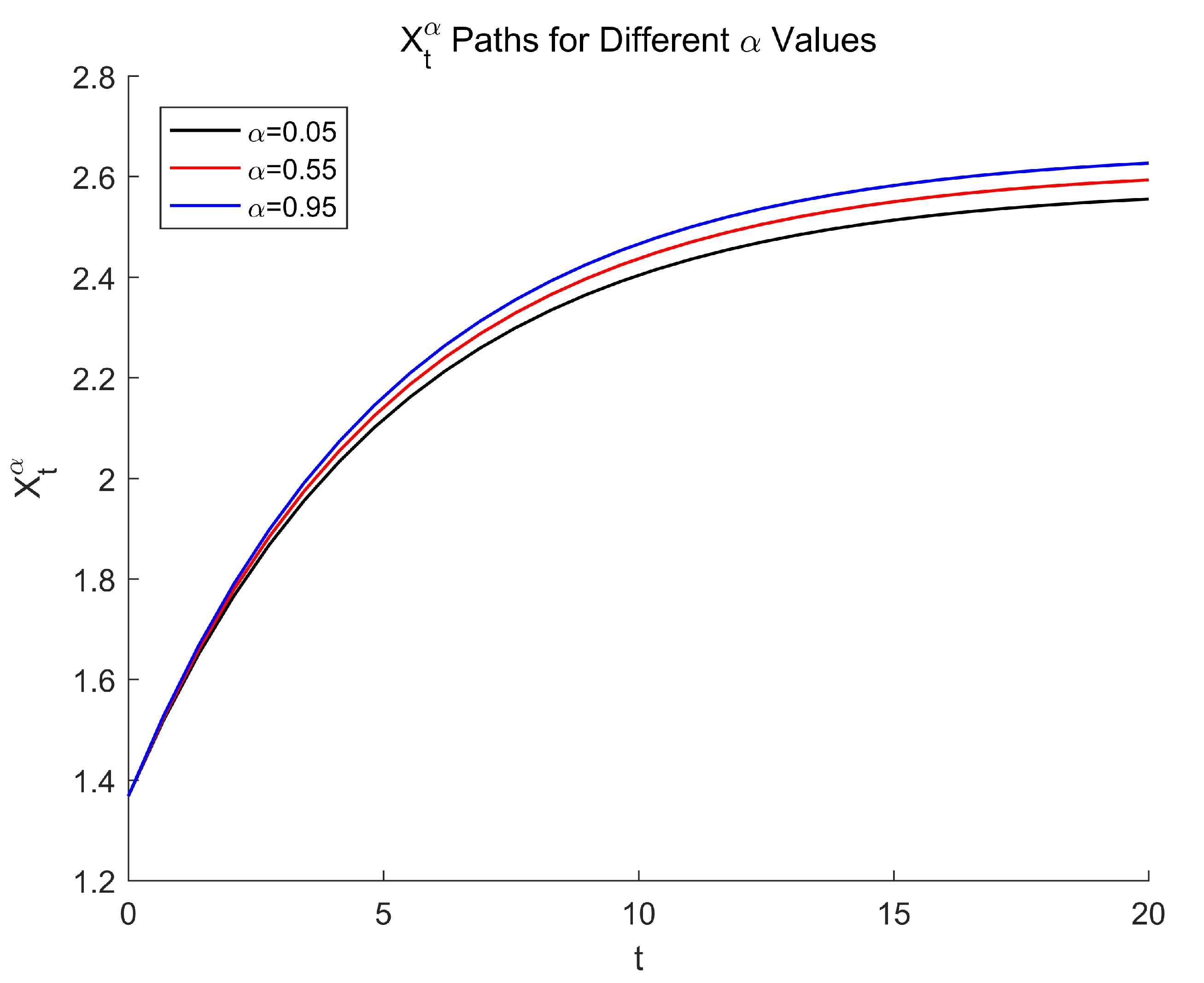
4. -Path Solutions of Fractional Uncertain Differential Equation
4.1. Theoretical Explanation
4.2. Example 3
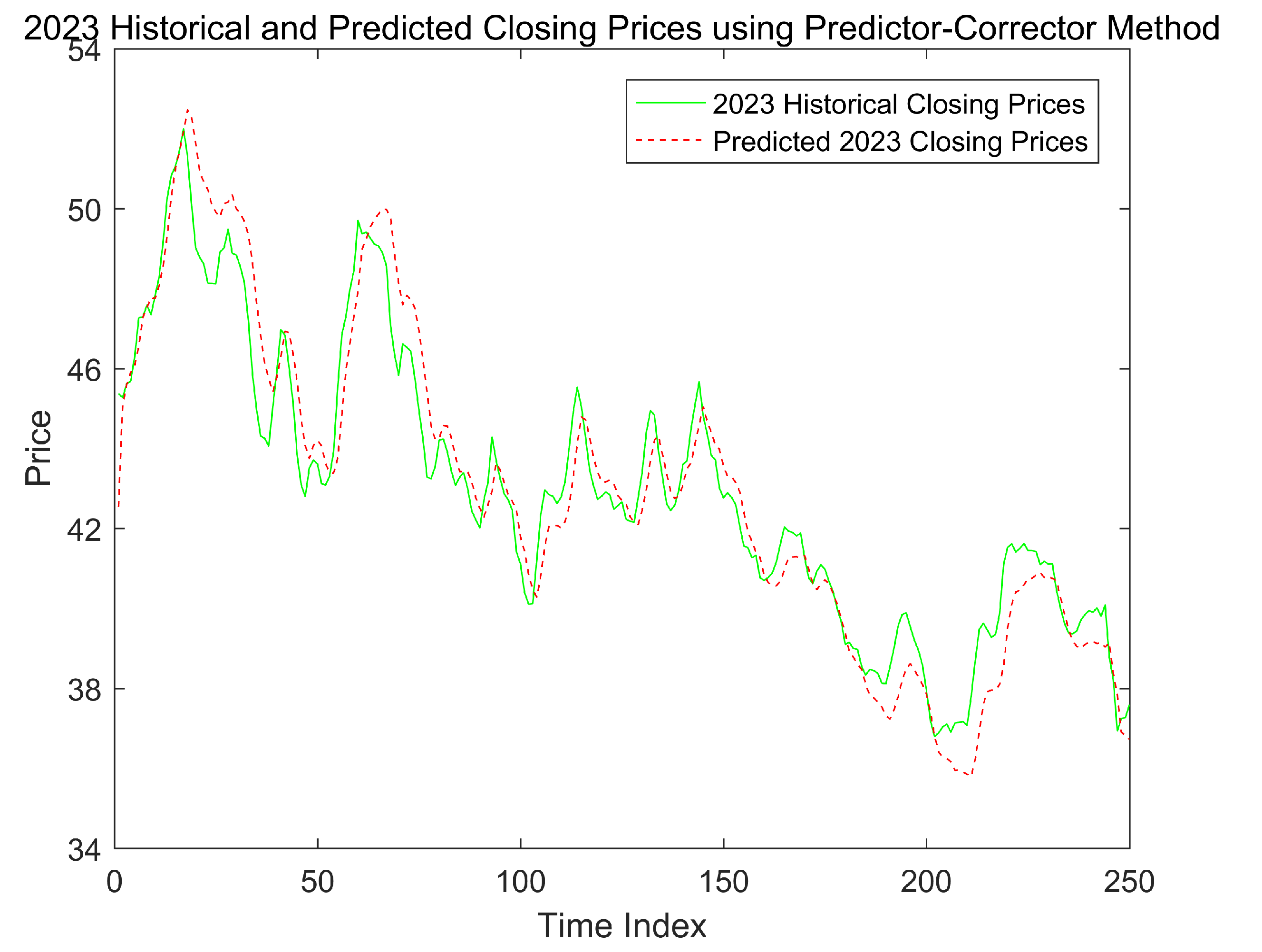
5. An Example: Tencent Holdings Ltd. Stock
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets Syst. 1978, 1, 3–28. [Google Scholar] [CrossRef]
- Liu, B. Uncertainty Theory, 2nd ed.; Springer: Berlin, Germany, 2007. [Google Scholar]
- Chen, X.; Liu, B. Existence and uniqueness theorem for uncertain differential equations. Fuzzy Optim. Decis. Mak. 2010, 9, 69–81. [Google Scholar] [CrossRef]
- Gao, Y. Existence and uniqueness theorem on uncertain differential equations with local Lipschitz condition. J. Uncertain Syst. 2012, 6, 223–232. [Google Scholar]
- Ge, X.T.; Zhu, Y.G. Existence and uniqueness theorem for uncertain delay differential equations. J. Comput. Inf. Syst. 2012, 20, 8341–8347. [Google Scholar]
- Lu, Z.; Zhu, Y. Nonlinear impulsive problems for uncertain fractional differential equations. Chaos Solitons Fractals 2022, 157, 111958. [Google Scholar] [CrossRef]
- Shu, Y.; Li, B. Existence and uniqueness of solutions to uncertain fractional switched systems with an uncertain stock model. Chaos Solitons Fractals 2022, 155, 111746. [Google Scholar] [CrossRef]
- Li, Z.; Wen, X.; Xu, L. Exponential stability of uncertain functional differential equations. Appl. Soft Comput. 2023, 147, 110816. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Y.; Ning, J.; Xu, L. Doubly perturbed uncertain differential equations. Commun. Nonlinear Sci. Numer. Simul. 2024, 138, 108228. [Google Scholar] [CrossRef]
- Tang, H.; Yang, X. Moment estimation in uncertain differential equations based on the Milstein scheme. Appl. Math. Comput. 2022, 418, 126825. [Google Scholar] [CrossRef]
- Yao, K.; Chen, X.W. A numerical method for solving uncertain differential equations. J. Intell. Fuzzy Syst. 2013, 25, 825–832. [Google Scholar] [CrossRef]
- Ge, X.T.; Zhu, Y.G. A necessary condition of optimality for uncertain optimal control problem. Fuzzy Optim. Decis. Mak. 2013, 12, 41–51. [Google Scholar] [CrossRef]
- Li, B.; Zhang, R.; Jin, T.; Shu, Y. Parametric approximate optimal control of uncertain differential game with application to counter terror. Chaos Solitons Fractals 2021, 146, 110940. [Google Scholar] [CrossRef]
- Gao, R. Milne method for solving uncertain differential equations. Appl. Math. Comput. 2016, 274, 774–785. [Google Scholar] [CrossRef]
- Ji, X.Y.; Zhou, J. Solving high-order uncertain differential equations via Runge-Kutta method. IEEE Trans. Fuzzy Syst. 2018, 26, 1379–1386. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Nain, A.K.; Vats, R.K.; Das, P. A theoretical study of the fractional-order p-Laplacian nonlinear Hadamard type turbulent flow models having the Ulam-Hyers stability. Rev. Real Acad. Cienc. Exactas Fis. Nat. Ser. A-Mat. 2023, 117, 160. [Google Scholar] [CrossRef]
- Yang, X.F.; Shen, Y.Y. Runge-Kutta method for solving uncertain differential equations. J. Uncertain. Anal. Appl. 2015, 17, 5337. [Google Scholar] [CrossRef]
- Zhang, X.; Mao, C.; Liu, L.; Wu, Y. Exact iterative solution for an abstract fractional dynamic system model for bioprocess. Qual. Theory Dyn. Syst. 2017, 16, 205–222. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, X.; Liu, L.; Wu, Y.; Cui, Y. Convergence analysis of iterative scheme and error estimation of positive solution for a fractional differential equation. Math. Model. Anal. 2018, 23, 611–626. [Google Scholar]
- He, J.; Zhang, X.; Liu, L.; Wu, Y.; Cui, Y. A singular fractional Kelvin–Voigt model involving a nonlinear operator and their convergence properties. Bound. Value Probl. 2019, 2019, 112. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Thabet, S.T.M.; Kedim, I.; Vivas-Cortez, M. On a new structure of multi-term Hilfer fractional impulsive neutral Levin-Nohel integrodifferential system with variable time delay. AIMS Math. 2024, 9, 7372–7395. [Google Scholar] [CrossRef]
- Boutiara, A.; Etemad, S.; Thabet, S.T.M.; Ntouyas, S.K.; Rezapour, S.; Tariboon, J. A mathematical theoretical study of a coupled fully hybrid (k, Φ)-fractional order system of BVPs in generalized Banach spaces. Symmetry 2023, 15, 1041. [Google Scholar] [CrossRef]
- Rafeeq, A.S.; Thabet, S.T.M.; Mohammed, M.O.; Kedim, I.; Vivas-Cortez, M. On Caputo-Hadamard fractional pantograph problem of two different orders with Dirichlet boundary conditions. Alex. Eng. J. 2024, 86, 386–398. [Google Scholar] [CrossRef]
- Yao, K.; Liu, B. Parameter estimation in uncertain differential equations. Fuzzy Optim. Decis. Mak. 2020, 19, 1–12. [Google Scholar] [CrossRef]
- Liu, Z.; Jia, L.F. Moment estimations for parameters in uncertain delay differential equations. J. Intell. Fuzzy Syst. 2020, 39, 841–849. [Google Scholar] [CrossRef]
- Liu, Z. Generalized moment estimation for uncertain differential equations. Appl. Math. Comput. 2021, 392, 125724. [Google Scholar] [CrossRef]
- Sheng, Y.; Yao, K.; Chen, W. Least squares estimation in uncertain differential equations. IEEE Trans. Fuzzy Syst. 2020, 28, 2651–2655. [Google Scholar] [CrossRef]
- Grigoriu, M. Stochastic Calculus: Applications in Science and Engineering; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Yang, X.; Liu, Y.; Park, G.K. Parameter estimation of uncertain differential equation with application to financial market. Chaos Solitons Fractals 2020, 139, 110026. [Google Scholar] [CrossRef]
- Lu, Z.Q.; Zhu, Y.G. Numerical approach for solution to an uncertain fractional differential equation. Appl. Math. Comput. 2019, 343, 137–148. [Google Scholar] [CrossRef]
- Yao, K.; Ke, H.; Sheng, Y. Stability in mean for uncertain differential equation. Fuzzy Optim. Decis. Mak. 2015, 14, 365–379. [Google Scholar] [CrossRef]
- Zhu, Y.G. Uncertain optimal control with application to a portfolio selection model. Cybern. Syst. Int. J. 2010, 41, 535–547. [Google Scholar] [CrossRef]
- Wu, G.C. Parameter estimation of fractional uncertain differential equations via Adams method. Nonlinear Anal. Model. Control 2022, 27, 413–427. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach: Yverdon, Switzerland, 1993. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
| 0.0333 | 0.2673 | 0.3000 | 0.6757 | 0.5667 | 0.8316 | 0.8333 | 1.0767 |
| 0.0667 | 0.3383 | 0.3333 | 0.6709 | 0.6000 | 0.8287 | 0.8667 | 0.9615 |
| 0.1000 | 0.4051 | 0.3667 | 0.6738 | 0.6333 | 0.8575 | 0.9000 | 0.9844 |
| 0.1333 | 0.5149 | 0.4000 | 0.6922 | 0.6667 | 0.9440 | 0.9333 | 1.0370 |
| 0.1667 | 0.3382 | 0.4333 | 0.8186 | 0.7000 | 0.9088 | 0.9667 | 1.0895 |
| 0.2000 | 0.5763 | 0.4667 | 0.7060 | 0.7333 | 0.9489 | 1.0000 | 1.0381 |
| 0.2333 | 0.5676 | 0.5000 | 0.7738 | 0.7667 | 0.9622 | ||
| 0.2667 | 0.4241 | 0.5333 | 0.7627 | 0.8000 | 0.8669 |
| 0.0333 | 1.3678 | 0.3000 | 2.3468 | 0.5667 | 4.1754 | 0.8333 | 6.3859 |
| 0.0667 | 1.5076 | 0.3333 | 2.7597 | 0.6000 | 3.3747 | 0.8667 | 5.5457 |
| 0.1000 | 1.8188 | 0.3667 | 2.8815 | 0.6333 | 3.8666 | 0.9000 | 6.3509 |
| 0.1333 | 1.7297 | 0.4000 | 2.5305 | 0.6667 | 3.8233 | 0.9333 | 4.4128 |
| 0.1667 | 1.9184 | 0.4333 | 3.1536 | 0.7000 | 3.7180 | 0.9667 | 5.1034 |
| 0.2000 | 1.9780 | 0.4667 | 2.9979 | 0.7333 | 3.9068 | 1.0000 | 7.1114 |
| 0.2333 | 2.2190 | 0.5000 | 3.4912 | 0.7667 | 4.8796 | ||
| 0.2667 | 2.2190 | 0.5333 | 3.3200 | 0.8000 | 4.6056 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ning, J.; Li, Z.; Xu, L. Parameter Estimation of Fractional Uncertain Differential Equations. Fractal Fract. 2025, 9, 138. https://doi.org/10.3390/fractalfract9030138
Ning J, Li Z, Xu L. Parameter Estimation of Fractional Uncertain Differential Equations. Fractal and Fractional. 2025; 9(3):138. https://doi.org/10.3390/fractalfract9030138
Chicago/Turabian StyleNing, Jing, Zhi Li, and Liping Xu. 2025. "Parameter Estimation of Fractional Uncertain Differential Equations" Fractal and Fractional 9, no. 3: 138. https://doi.org/10.3390/fractalfract9030138
APA StyleNing, J., Li, Z., & Xu, L. (2025). Parameter Estimation of Fractional Uncertain Differential Equations. Fractal and Fractional, 9(3), 138. https://doi.org/10.3390/fractalfract9030138






