Entropies and Degree-Based Topological Indices of Coronene Fractal Structures
Abstract
1. Introduction
2. Degree-Based Entropy
- Entropy related to the reciprocal Randić index
- Entropy related to the reduced second Zagreb index
- Entropy related to the Balaban index
- Entropy related to the -Zagreb index
- Entropy related to the elliptic sombor index
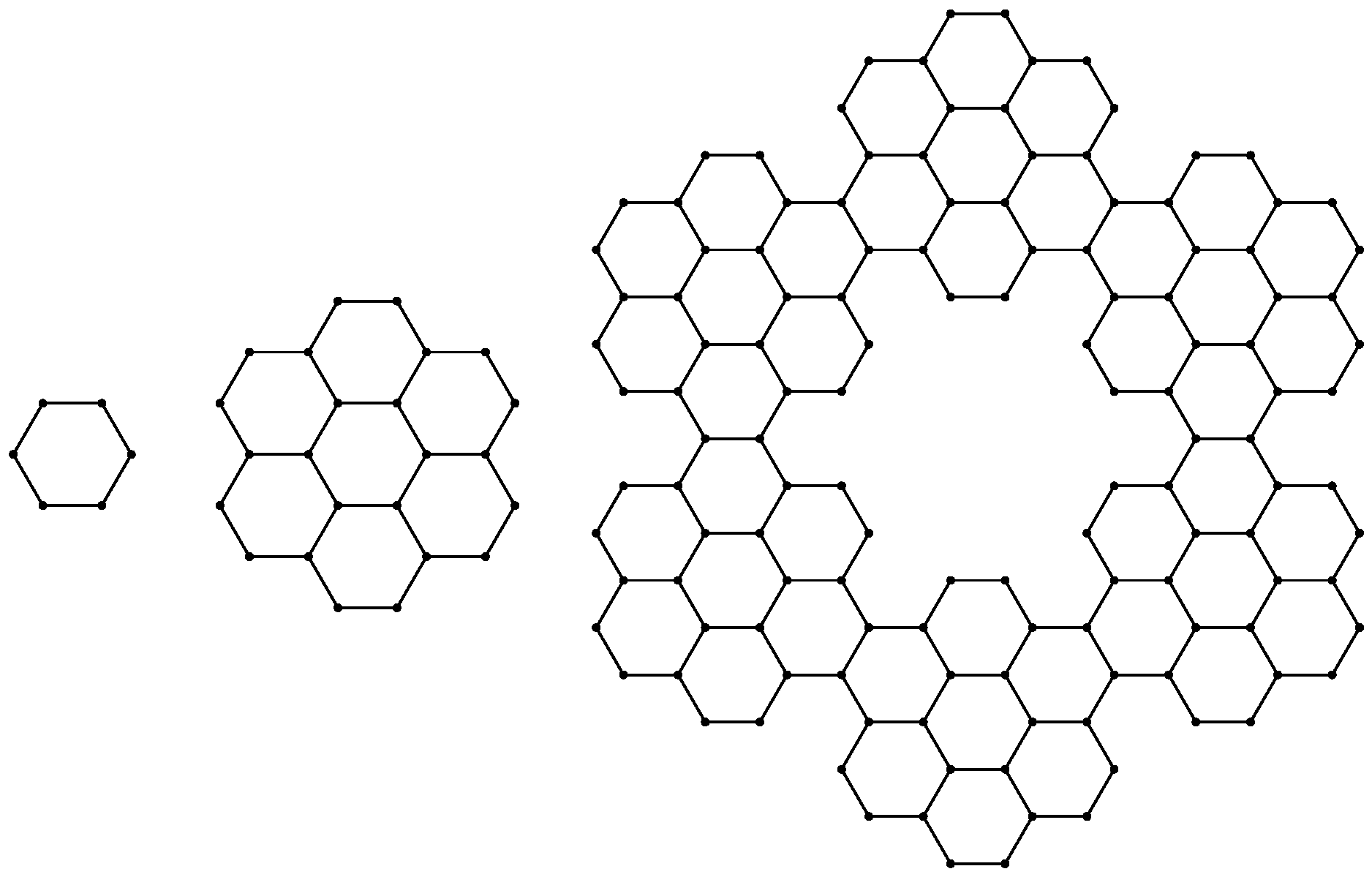
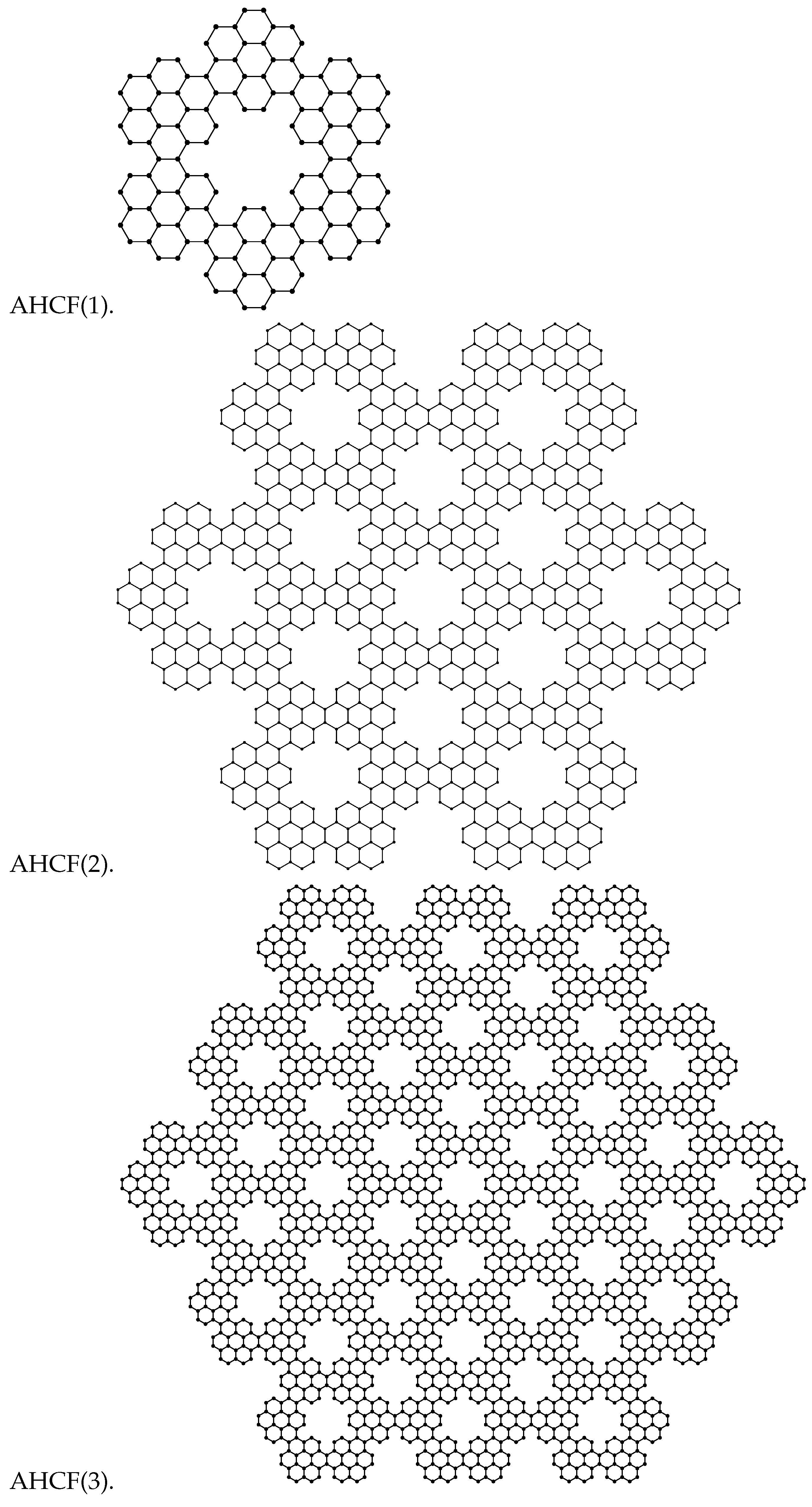
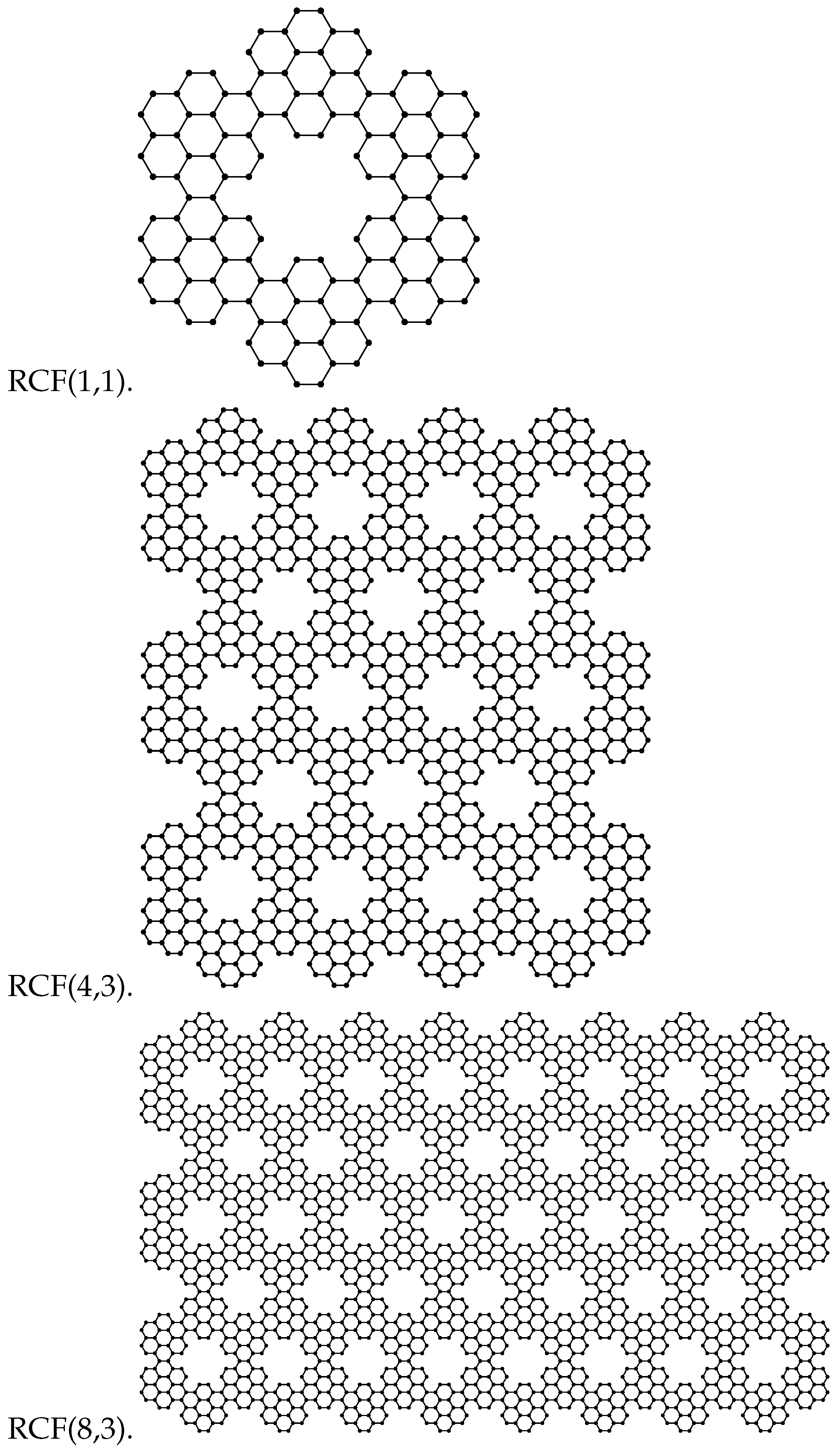
3. Topological Indices and Entropies of ZHCF, AHCF, and RCF
- 1.
- ;
- 2.
- ;
- 3.
- ;
- 4.
- ;
- 5.
- .
- 1.
- ;
- 2.
- ;
- 3.
- 4.
- 5.
- 1.
- ;
- 2.
- ;
- 3.
- ;
- 4.
- ;
- 5.
- .
- 1.
- 2.
- ;
- 3.
- 4.
- 5.
- 1.
- ;
- 2.
- ;
- 3.
- ;
- 4.
- ;
- 5.
- .
- 1.
- 2.
- ;
- 3.
- 4.
- 5.
4. Comparison
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Klein, D.; Cravey, M.; Hite, G. Fractal benzenoids. Polycyclic Aromat. Compd. 1991, 2, 163–182. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The fractal geometry of nature. Earth Surf. Process. Landf. 1983, 8, 406. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Frame, M. Fractals. Encycl. Phys. Sci. Technol. 1987, 5, 579–593. [Google Scholar]
- Uahabi, K.L.; Atounti, M. Applications of fractals in medicine. Ann. Univ. Craiova Math. Comput. Sci. Ser. 2015, 42, 167–174. [Google Scholar]
- Wornell, G. Signal Processing with Fractals: A Wavelet-Based Approach; Prentice Hall Press: Hoboken, NJ, USA, 1996. [Google Scholar]
- Lee, J.S.; Chang, K.S. Applications of chaos and fractals in process systems engineering. J. Process Control 1996, 6, 71–87. [Google Scholar] [CrossRef]
- Diab, H.; Abboud, N. The engineering applications of fractals. Simulation 1991, 57, 89–97. [Google Scholar] [CrossRef]
- Gutman, I.; Cyvin, S.J. Introduction to the Theory of Benzenoid Hydrocarbons; Springer: Berlin, Germany, 1989. [Google Scholar]
- Ciesielski, A.; Krygowski, T.M.; Cyrański, M.K. How to find the fries structures for benzenoid hydrocarbons. Symmetry 2010, 2, 1390–1400. [Google Scholar] [CrossRef]
- Clar, E.; Schoental, R. Polycyclic Hydrocarbons; Academic Press: London, UK, 1964; Volume 1. [Google Scholar]
- Dias, J.R. Handbook of Polycyclic Hydrocarbons. Part A: Benzenoid Hydrocarbons; Elsevier: Philadelphia, PA, USA, 1987. [Google Scholar]
- Arockiaraj, M.; Clement, J.; Balasubramanian, K. Analytical expressions for topological properties of polycyclic benzenoid networks. J. Chemom. 2016, 30, 682–697. [Google Scholar] [CrossRef]
- Julietraja, K.; Venugopal, P.; Prabhu, S.; Deepa, S.; Muhammad Kamran, S. Molecular structural descriptors of donut benzenoid systems. Polycycl. Aromat. Compd. 2022, 42, 4146–4172. [Google Scholar]
- Arockiaraj, M.; Clement, J.; Balasubramanian, K. Topological indices and their applications to circumcised donut benzenoid systems, kekulenes and drugs. Polycycl. Aromat. Compd. 2020, 40, 280–303. [Google Scholar] [CrossRef]
- Plavšić, D.; Trinajstić, N.; Klein, D.J. Clar structures in fractal benzenoids. Croat. Chem. Acta 1992, 65, 279–284. [Google Scholar]
- El-Basil, S. Fractal properties of homologous series of structures. J. Chem. Soc. Faraday Trans. 1994, 90, 2201–2210. [Google Scholar] [CrossRef]
- Bondy, J.A.; Murty, U. Graph Theory; Springer: London, UK, 2008. [Google Scholar]
- Chen, H.; Wu, R.; Deng, H. The extremal values of some topological indices in bipartite graphs with a given matching number. Appl. Math. Comput. 2016, 280, 103–109. [Google Scholar] [CrossRef]
- Deng, H.; Huang, G.; Jiang, X. A unified linear-programming modeling of some topological indices. J. Comb. Optim. 2015, 30, 826–837. [Google Scholar] [CrossRef]
- Liu, J.B.; Pan, X.F. Minimizing Kirchhoff index among graphs with a given vertex bipartiteness. Appl. Math. Comput. 2016, 291, 84–88. [Google Scholar] [CrossRef]
- Gutman, I.; Furtula, B.; Elphick, C. Three new/old vertex-degree-based topological indices. MATCH Commun. Math. Comput. Chem. 2014, 72, 617–632. [Google Scholar]
- Shigehalli, V.; Dsouza, A.M. Quantitative structure property relationship (QSPR) analysis of general randić index. J. Algebr. Stat. 2022, 13, 1957–1967. [Google Scholar]
- Furtula, B.; Gutman, I.; Ediz, S. On difference of Zagreb indices. Discret. Appl. Math. 2014, 178, 83–88. [Google Scholar] [CrossRef]
- Mahboob, A.; Rasheed, M.W.; Dhiaa, A.M.; Hanif, I.; Amin, L. On quantitative structure-property relationship (QSPR) analysis of physicochemical properties and anti-hepatitis prescription drugs using a linear regression model. Heliyon 2024, 10, e25908. [Google Scholar] [CrossRef]
- Balaban, A.T. Highly discriminating distance-based topological index. Chem. Phys. Lett. 1982, 89, 399–404. [Google Scholar] [CrossRef]
- Balaban, A.T.; Quintas, L. The smallest graphs, trees, and 4-trees with degenerate topological index. J. Math. Chem. 1983, 14, 213–233. [Google Scholar]
- Thakur, A.; Thakur, M.; Khadikar, P.V.; Supuran, C.T.; Sudele, P. QSAR study on benzenesulphonamide carbonic anhydrase inhibitors: Topological approach using Balaban index. Bioorgan. Med. Chem. 2004, 12, 789–793. [Google Scholar] [CrossRef] [PubMed]
- Azari, M.; Iranmanesh, A. Generalized Zagreb index of graphs. Studia Univ. Babes-Bolyai Chem. 2011, 56, 59–71. [Google Scholar]
- Gutman, I.; Furtula, B.; Oz, M.S. Geometric approach to vertex-degree-based topological indices–elliptic sombor index, theory and application. Int. J. Quantum Chem. 2024, 124, e27346. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Ashraful Alam, M.; Ghani, M.U.; Kamran, M.; Shazib Hameed, M.; Hussain Khan, R.; Baig, A. Degree-based entropy for a non-kekulean benzenoid graph. J. Math. 2022, 2022, 2288207. [Google Scholar] [CrossRef]
- Rashid, T.; Faizi, S.; Zafar, S. Distance based entropy measure of interval-valued intuitionistic fuzzy sets and its application in multicriteria decision making. Adv. Fuzzy Syst. 2018, 2018, 3637897. [Google Scholar] [CrossRef]
- Hayat, S. Computing distance-based topological descriptors of complex chemical networks: New theoretical techniques. Chem. Phys. Lett. 2017, 688, 51–58. [Google Scholar] [CrossRef]
- Hu, M.; Ali, H.; Binyamin, M.A.; Ali, B.; Liu, J.B.; Fan, C. On Distance-Based Topological Descriptors of Chemical Interconnection Networks. J. Math. 2021, 2021, 5520619. [Google Scholar] [CrossRef]
- Manzoor, S.; Siddiqui, M.K.; Ahmad, S. On entropy measures of molecular graphs using topological indices. Arab. J. Chem. 2020, 13, 6285–6298. [Google Scholar] [CrossRef]
- Ghani, M.U.; Sultan, F.; Tag El Din, E.S.M.; Khan, A.R.; Liu, J.B.; Cancan, M. A paradigmatic approach to find the valency-based K-banhatti and redefined Zagreb entropy for niobium oxide and a metal–organic framework. Molecules 2022, 27, 6975. [Google Scholar] [CrossRef] [PubMed]
- Ghani, M.U.; Campena, F.J.H.; Ali, S.; Dehraj, S.; Cancan, M.; Alharbi, F.M.; Galal, A.M. Characterizations of chemical networks entropies by K-banhatii topological indices. Symmetry 2023, 15, 143. [Google Scholar] [CrossRef]
- Arockiaraj, M.; Raza, Z.; Maaran, A.; Abraham, J.; Balasubramanian, K. Comparative analysis of scaled entropies and topological properties of triphenylene-based metal and covalent organic frameworks. Chem. Pap. 2024, 78, 4095–4118. [Google Scholar] [CrossRef]
- Raza, Z.; Arockiaraj, M.; Maaran, A.; Kavitha, S.R.J.; Balasubramanian, K. Topological entropy characterization, NMR and ESR spectral patterns of coronene-based transition metal organic frameworks. ACS Omega 2023, 8, 13371–13383. [Google Scholar] [CrossRef]
- Yang, J.; Konsalraj, J.; Raja S., A. A. Neighbourhood sum degree-based indices and entropy measures for certain family of graphene molecules. Molecules 2022, 28, 168. [Google Scholar] [CrossRef]
- Ghani, M.U.; Campena, F.J.H.; Maqbool, M.K.; Liu, J.B.; Dehraj, S.; Cancan, M.; Alharbi, F.M. Entropy related to K-Banhatti indices via valency based on the presence of C6H6 in various molecules. Molecules 2023, 28, 452. [Google Scholar] [CrossRef]
- Arockiaraj, M.; Jency, J.; Abraham, J.; Ruth Julie Kavitha, S.; Balasubramanian, K. Two-dimensional coronene fractal structures: Topological entropy measures, energetics, NMR and ESR spectroscopic patterns and existence of isentropic structures. Mol. Phys. 2022, 120, e2079568. [Google Scholar] [CrossRef]
- Zhao, X.; Siddiqui, M.K.; Manzoor, S.; Ahmad, S.; Muhammad, M.H.; Liu, J.B. On computation and analysis of entropy measures for metal-insulator transition super lattice. IETE J. Res. 2024, 70, 1911–1922. [Google Scholar] [CrossRef]
- Abraham, J.; Arockiaraj, M.; Jency, J.; Kavitha, S.R.J.; Balasubramanian, K. Graph entropies, enumeration of circuits, walks and topological properties of three classes of isoreticular metal organic frameworks. J. Math. Chem. 2022, 60, 695–732. [Google Scholar] [CrossRef]
- Manzoor, S.; Chu, Y.M.; Siddiqui, M.K.; Ahmad, S. On topological aspects of degree based entropy for two carbon nanosheets. Main Group Met. Chem. 2020, 43, 205–218. [Google Scholar] [CrossRef]
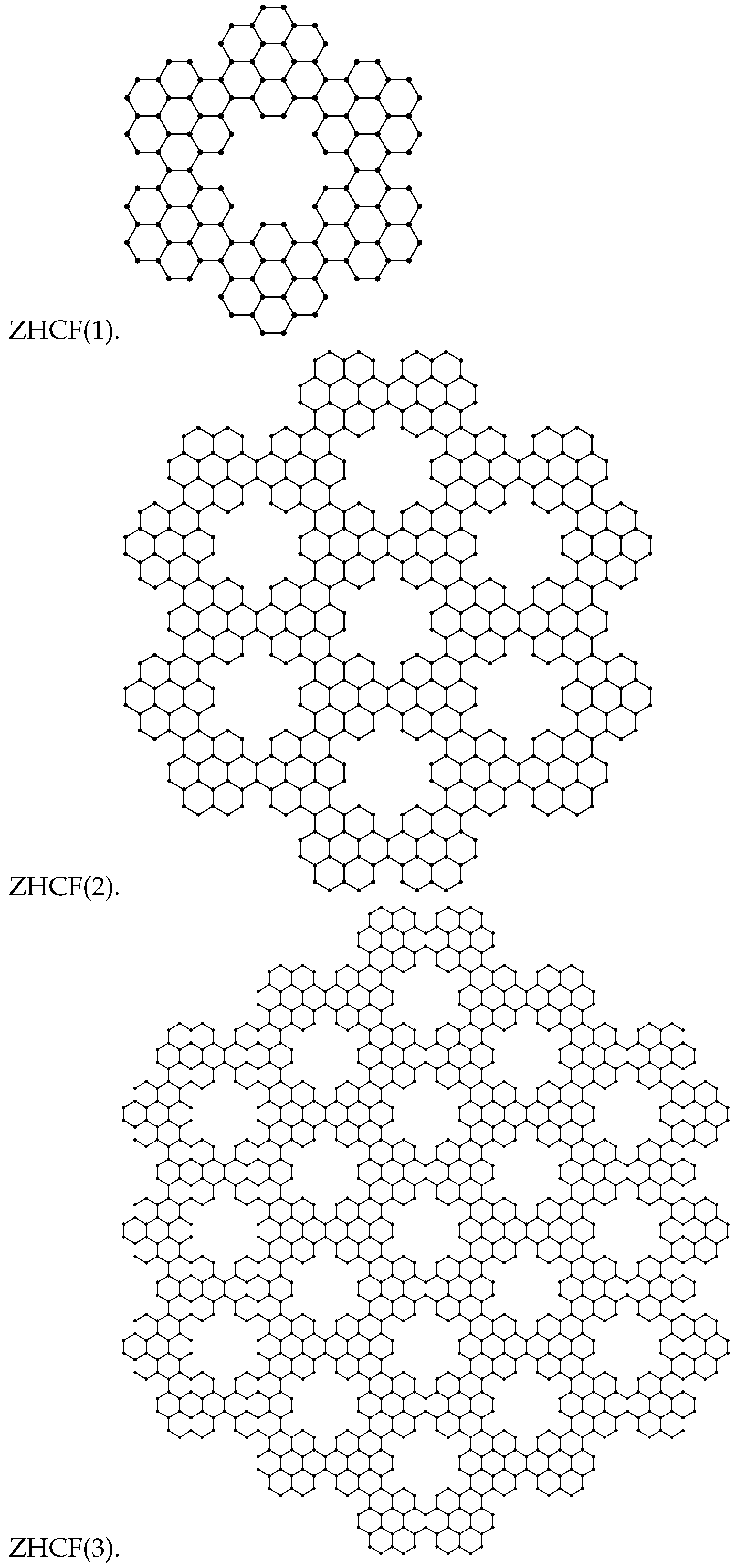



| Number of Edges | |
|---|---|
| Number of Edges | |
|---|---|
| Number of Edges | |
|---|---|
| f | t = 1 | t = 2 | t = 3 | t = 4 | t = 5 | t = 6 | t = 7 | t = 8 | t = 9 | t = 10 |
|---|---|---|---|---|---|---|---|---|---|---|
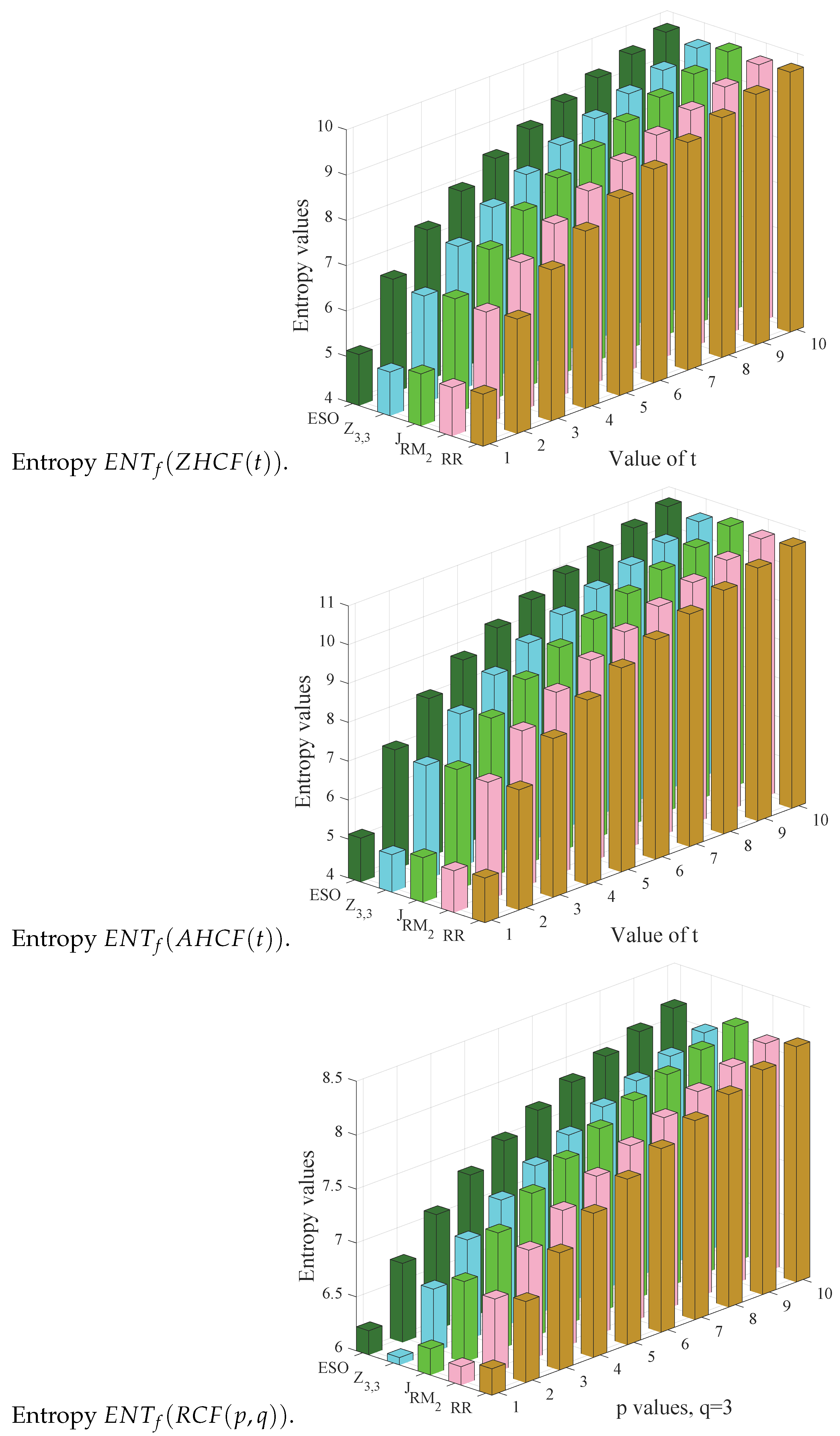
| 5.1493 | 6.5276 | 7.3359 | 7.91 | 8.3554 | 8.7196 | 9.0275 | 9.2943 | 9.5296 | 9.7402 | |
| 5.0718 | 6.458 | 7.269 | 7.8444 | 8.2908 | 8.6555 | 8.9638 | 9.2309 | 9.4665 | 9.6772 | |
| J | 5.1474 | 6.5255 | 7.3338 | 7.9078 | 8.3533 | 8.7174 | 9.0253 | 9.2921 | 9.5274 | 9.738 |
| 4.963 | 6.3634 | 7.1792 | 7.757 | 8.2048 | 8.5704 | 8.8794 | 9.147 | 9.383 | 9.594 | |
| 5.1271 | 6.5074 | 7.3164 | 7.8909 | 8.3366 | 8.7009 | 9.0089 | 9.2758 | 9.5112 | 9.7218 |
| f | t = 1 | t = 2 | t = 3 | t = 4 | t = 5 | t = 6 | t = 7 | t = 8 | t = 9 | t = 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 5.1493 | 7.0861 | 8.082 | 8.7473 | 9.2466 | 9.6462 | 9.9792 | 10.2647 | 10.5146 | 10.7366 | |
| 5.0718 | 7.0176 | 8.0163 | 8.6828 | 9.1829 | 9.5829 | 9.9162 | 10.202 | 10.452 | 10.6742 | |
| J | 5.1474 | 7.084 | 8.0798 | 8.7451 | 9.2444 | 9.644 | 9.977 | 10.2625 | 10.5123 | 10.7344 |
| 4.963 | 6.9251 | 7.9284 | 8.5971 | 9.0983 | 9.4991 | 9.833 | 10.1191 | 10.3694 | 10.5919 | |
| 5.1271 | 7.0662 | 8.0629 | 8.7285 | 9.228 | 9.6277 | 9.9608 | 10.2464 | 10.4962 | 10.7184 |
| f | t = 1 | t = 2 | t = 3 | t = 4 | t = 5 | t = 6 | t = 7 | t = 8 | t = 9 | t = 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 6.2443 | 6.7513 | 7.0861 | 7.3365 | 7.5366 | 7.7032 | 7.846 | 7.971 | 8.082 | 8.1819 | |
| 6.1703 | 6.6811 | 7.0176 | 7.269 | 7.4697 | 7.6367 | 7.7799 | 7.905 | 8.0163 | 8.1164 | |
| J | 6.2424 | 6.7492 | 7.084 | 7.3344 | 7.5344 | 7.7011 | 7.8439 | 7.9688 | 8.0798 | 8.1798 |
| 6.0678 | 6.5856 | 6.9251 | 7.1781 | 7.3798 | 7.5476 | 7.6913 | 7.8169 | 7.9284 | 8.0288 | |
| 6.223 | 6.7309 | 7.0662 | 7.3169 | 7.5171 | 7.6839 | 7.8268 | 7.9518 | 8.0629 | 8.1628 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, S.-A.; Liu, J.-B. Entropies and Degree-Based Topological Indices of Coronene Fractal Structures. Fractal Fract. 2025, 9, 133. https://doi.org/10.3390/fractalfract9030133
Xu S-A, Liu J-B. Entropies and Degree-Based Topological Indices of Coronene Fractal Structures. Fractal and Fractional. 2025; 9(3):133. https://doi.org/10.3390/fractalfract9030133
Chicago/Turabian StyleXu, Si-Ao, and Jia-Bao Liu. 2025. "Entropies and Degree-Based Topological Indices of Coronene Fractal Structures" Fractal and Fractional 9, no. 3: 133. https://doi.org/10.3390/fractalfract9030133
APA StyleXu, S.-A., & Liu, J.-B. (2025). Entropies and Degree-Based Topological Indices of Coronene Fractal Structures. Fractal and Fractional, 9(3), 133. https://doi.org/10.3390/fractalfract9030133







