Generalized Fractional Integral Inequalities Derived from Convexity Properties of Twice-Differentiable Functions
Abstract
1. Introduction and Preliminaries
- For , the operators reduce to the classical Riemann integral.
- For with , the operators correspond to Riemann–Liouville fractional integrals and [27], where is defined as
- For , the operators become k-Riemann–Liouville fractional integrals and , where is the k-Gamma function, defined as
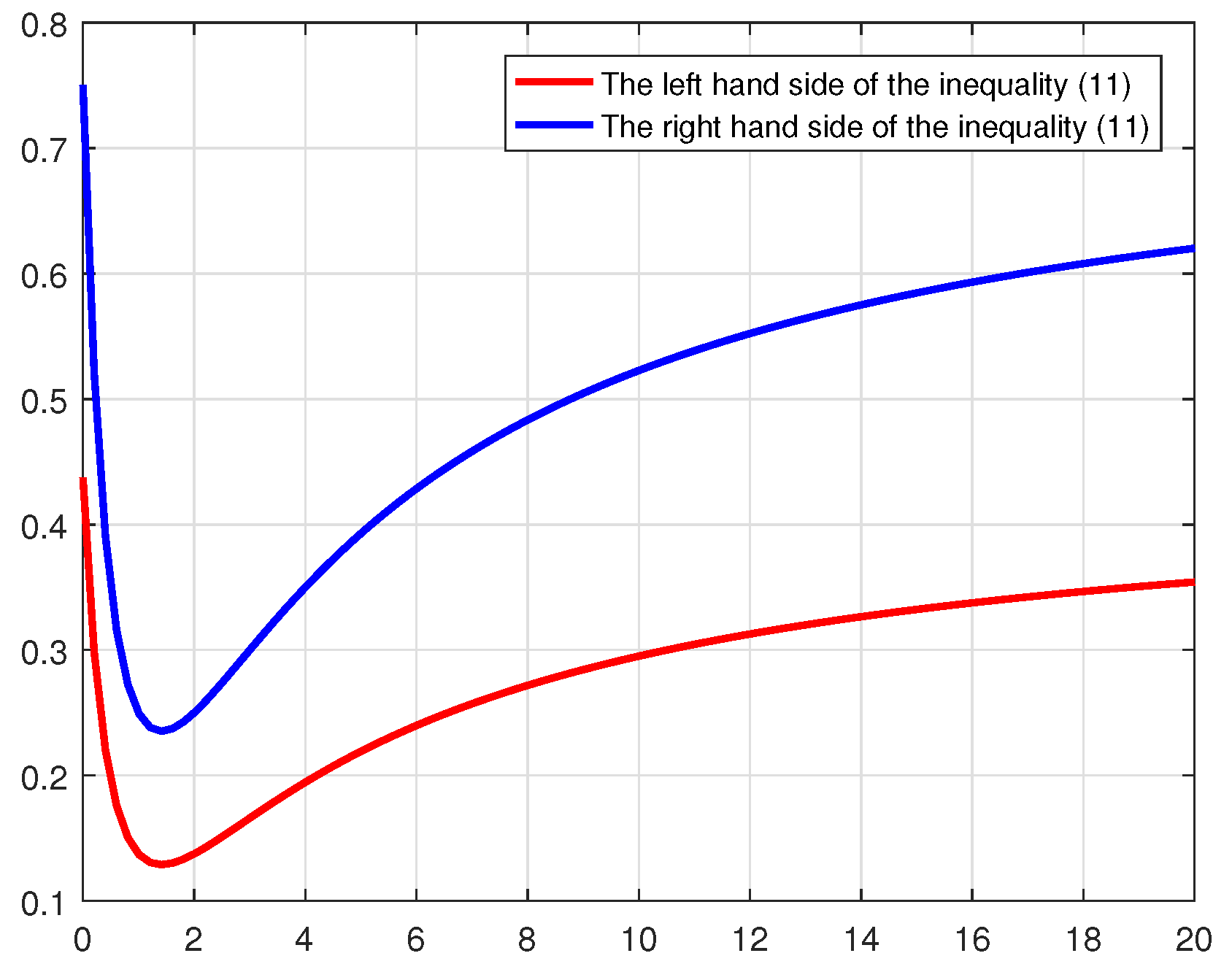
2. Main Results
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Denton, Z.; Vatsala, A.S. Fractional integral inequalities and applications. Comput. Math. Appl. 2010, 59, 1087–1094. [Google Scholar] [CrossRef]
- Mihai, M.V.; Awan, M.U.; Noor, M.A.; Kim, J.K.; Noor, K.I. Hermite–Hadamard inequalities and their applications. J. Inequalities Appl. 2018, 2018, 309. [Google Scholar] [CrossRef]
- Dragomir, S.S. Operator Inequalities of Ostrowski and Trapezoidal Type; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Hyder, A.A.; Budak, H.; Almoneef, A.A. Further midpoint inequalities via generalized fractional operators in Riemann–Liouville sense. Fractal Fract. 2022, 6, 496. [Google Scholar] [CrossRef]
- Jin, S.; Aying, W.; Guo, B.N. Some new integral inequalities of the Simpson type for MT-convex functions. Adv. Theory Nonlinear Anal. Its Appl. 2022, 6, 168–172. [Google Scholar] [CrossRef]
- Constantin, P. Niculescu, L.E.P. Convex Functions and Their Applications, 2nd ed.; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Dragomir, S.; Agarwal, R. Two inequalities for differentiable mappings and applications to special means of real numbers and to trapezoidal formula. Appl. Math. Lett. 1998, 11, 91–95. [Google Scholar] [CrossRef]
- Kirmaci, U. Inequalities for differentiable mappings and applications to special means of real numbers to midpoint formula. Appl. Math. Comput. 2004, 147, 137–146. [Google Scholar] [CrossRef]
- Iqbal, M.; Bhatti, M.; Nazeer, K. Generalization of inequalities analogous to Hermite–Hadamard inequality via fractional integrals. Bull. Korean Math. Soc. 2015, 52, 707–716. [Google Scholar] [CrossRef]
- Sarikaya, M.; Set, E.; Yaldiz, H.; Basak, N. Hermite–Hadamard’s inequalities for fractional integrals and related fractional inequalities. Math. Comput. Model. 2013, 57, 2403–2407. [Google Scholar] [CrossRef]
- Dragomir, S. On Hadamard’s inequality for convex functions on the co–ordinates in a rectangle from the plane. Taiwan J. Math. 2001, 4, 775–788. [Google Scholar]
- Latif, M.; Dragomir, S. On some new inequalities for differentiable co–ordinated convex functions. J. Inequalities Appl. 2012, 2012, 28. [Google Scholar] [CrossRef]
- Sarikaya, M.; Set, E.; Ozdemir, M.; Dragomir, S. New some Hadamard’s type inequalities for coordinated convex functions. Tamsui Oxf. J. Inf. Math. Sci. 2012, 28, 137–152. [Google Scholar]
- Sarikaya, M.; Ertugral, F. On the generalized Hermite–Hadamard inequalities. Ann. Univ. Craiova Math. Comput. Sci. Ser. 2020, 47, 193–213. [Google Scholar]
- Chen, F. A note on the Hermite–Hadamard inequality for convex functions on the co–ordinates. J. Math. Inequalities 2014, 8, 915–923. [Google Scholar] [CrossRef]
- Kavurmaci, H.; Avci, M.; Ozdemir, M. New inequalities of Hermite-Hadamard type for convex functions with applications. J. Inequalities Appl. 2011, 2011, 86. [Google Scholar] [CrossRef]
- Budak, H.; Hezenci, F.; Kara, H. On generalized Ostrowski, Simpson and Trapezoidal type inequalities for co–ordinated convex functions via generalized fractional integrals. Adv. Differ. Equ. 2021, 2021, 312. [Google Scholar] [CrossRef]
- Rahman, G.; Samraiz, M.; Shah, K.; Abdeljawad, T.; Elmasry, Y. Advancements in integral inequalities of Ostrowski type via modified Atangana-Baleanu fractional integral operator. Heliyon 2025, 11, e41525. [Google Scholar] [CrossRef]
- Barani, A.; Barani, S.; Dragomir, S. Refinements of Hermite-Hadamard type inequality for functions whose second derivatives absolute values are quasi convex. J. Appl. Math. 2012, 2012, 615737. [Google Scholar] [CrossRef]
- Mohammed, P.; Sarikaya, M. On generalized fractional integral inequalities for twice differentiable convex functions. J. Comput. Appl. Math. 2020, 372, 112740. [Google Scholar] [CrossRef]
- Sarikaya, M.; Aktan, N. On the generalization of some integral inequalities and their applications. Math. Comput. Model. 2011, 54, 2175–2182. [Google Scholar] [CrossRef]
- Budak, H.; Ertugral, F.; Pehlivan, E. Hermite-Hadamard type inequalities for twice differentiable functions via generalized fractional integrals. Filomat 2019, 33, 4967–4979. [Google Scholar] [CrossRef]
- Park, J. On Some Integral Inequalities for Twice Differentiable Quasi–Convex and Convex Functions via Fractional Integrals. Appl. Math. Sci. 2015, 9, 3057–3069. [Google Scholar] [CrossRef]
- Hezenci, F.; Budak, H.; Kara, H. New version of Fractional Simpson type inequalities for twice differentiable functions. Adv. Differ. Equ. 2021, 2021, 460. [Google Scholar] [CrossRef]
- Sarikaya, M.; Saglam, A.; Yildirim, H. New inequalities of Hermite-Hadamard type for functions whose second derivatives absolute values are convex and quasi–convex. Int. J. Open Probl. Comput. Sci. Math. 2012, 5, 2074–2827. [Google Scholar] [CrossRef]
- Saleh, W.; Boulares, H.; Moumen, A.; Albala, H.; Meftah, B. New Approaches to Fractal–Fractional Bullen’s Inequalities Through Generalized Convexity. Fractal Fract. 2025, 9, 25. [Google Scholar] [CrossRef]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies, Elsevier Sci. B.V.: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Sarikaya, M. On the Hermite-Hadamard-type inequalities for co-ordinated convex function via fractional integrals. Integral Transform. Spec. Funct. 2014, 25, 134–147. [Google Scholar] [CrossRef]
- Gorenflo, R.; Mainardi, F. Fractional Calculus: Integral and Differential Equations of Fractional Order; Springer: Vienna, Austria, 1997; pp. 223–276. [Google Scholar]
- Miller, S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Agarwal, P.; Tariboon, J.; Ntouyas, S.K. Some generalized Riemann–Liouville k–fractional integral inequalities. J. Inequalities Appl. 2016, 2016, 122. [Google Scholar] [CrossRef]
- Ozdemir, M.; Avci, M.; Kavurmaci, H. Hermite-Hadamard-type inequalities via (α,m)-convexity. Comput. Math. Appl. 2011, 61, 2614–2620. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almoneef, A.A.; Hyder, A.-A.; Hezenci, F.; Budak, H. Generalized Fractional Integral Inequalities Derived from Convexity Properties of Twice-Differentiable Functions. Fractal Fract. 2025, 9, 97. https://doi.org/10.3390/fractalfract9020097
Almoneef AA, Hyder A-A, Hezenci F, Budak H. Generalized Fractional Integral Inequalities Derived from Convexity Properties of Twice-Differentiable Functions. Fractal and Fractional. 2025; 9(2):97. https://doi.org/10.3390/fractalfract9020097
Chicago/Turabian StyleAlmoneef, Areej A., Abd-Allah Hyder, Fatih Hezenci, and Hüseyin Budak. 2025. "Generalized Fractional Integral Inequalities Derived from Convexity Properties of Twice-Differentiable Functions" Fractal and Fractional 9, no. 2: 97. https://doi.org/10.3390/fractalfract9020097
APA StyleAlmoneef, A. A., Hyder, A.-A., Hezenci, F., & Budak, H. (2025). Generalized Fractional Integral Inequalities Derived from Convexity Properties of Twice-Differentiable Functions. Fractal and Fractional, 9(2), 97. https://doi.org/10.3390/fractalfract9020097






