Enhancing Banking Transaction Security with Fractal-Based Image Steganography Using Fibonacci Sequences and Discrete Wavelet Transform

Abstract

The growing reliance on digital banking and financial transactions has brought significant security challenges, including data breaches and unauthorized access. This paper proposes a robust method for enhancing the security of banking and financial transactions. In this context, steganography—hiding information within digital media—is valuable for improving data protection. This approach combines biometric authentication, using face and voice recognition, with image steganography to secure communication channels. A novel application of Fibonacci sequences is introduced within a direct-sequence spread-spectrum (DSSS) system for encryption, along with a discrete wavelet transform (DWT) for embedding data. The secret message, encrypted through Fibonacci sequences, is concealed within an image and tested for effectiveness using the Mean Square Error (MSE) and Peak Signal-to-Noise Ratio (PSNR). The experimental results demonstrate that the proposed method achieves a high PSNR, particularly for grayscale images, enhancing the robustness of security measures in mobile and online banking environments.

1. Introduction

The rapid growth of digital technologies has significantly transformed the landscape of banking and financial transactions. As mobile banking, online payment systems, and financial applications have become increasingly popular, the risk of cyber-attacks, data breaches, and unauthorized access have also escalated. To mitigate these risks, enhancing transaction security has become paramount for financial institutions. Effective security measures are critical for protecting sensitive data, ensuring the integrity of economic systems, and maintaining user trust [1,2].

In particular, financial transactions are vulnerable to various types of attacks, including phishing, man-in-the-middle attacks, and unauthorized access to personal information. A comprehensive security system must protect against these threats using multi-layered encryption, biometric verification, and secure communication channels. Steganography, which involves concealing messages or information within digital media, offers a promising solution for enhancing the confidentiality of transaction data. By embedding hidden messages in images or other digital files, steganography can provide an additional layer of security, making it difficult for attackers to detect or access critical information [3].

Security plays a fundamental role in the stability and trustworthiness of financial systems. Banking institutions handle vast amounts of sensitive information, such as customer data, transaction records, and account details, which are prime targets for cyber-attacks [4]. Implementing robust security measures is essential for safeguarding this information, complying with regulatory standards, and avoiding financial penalties. With financial services increasingly moving to online platforms, maintaining a secure environment for mobile banking and online payments is crucial. Using biometric authentication, such as facial and voice recognition, has proven effective for enhancing security by requiring additional layers of user verification.

In digital contexts, steganography involves embedding information within computer files. This can include encoding hidden data in various formats, such as document files, image files, or network protocols [5,6]. Due to their size, media files are particularly suited for steganographic purposes. For instance, an innocuous image file might have subtle changes in pixel color, where the color of every 100th pixel represents a letter in the alphabet. Such slight alterations would likely go unnoticed without specific scrutiny.

Image compression and noise reduction are significant in digital image processing and steganography. Transform domains are essential to these processes, as they provide an alternative representation of the data, making the key features more distinguishable for further manipulation [7]. Image compression aims to reduce the number of bits necessary for image representation while minimizing quality loss. However, the noise from acquisition systems or environmental factors often degrades images, making transparent marking more challenging. In such cases, noise reduction techniques help to improve image quality, making it easier to conceal messages while maintaining accuracy.

Signal compression and noise reduction are closely related processes, particularly in transformed domains like the wavelet domain. These two processes often overlap in their applications, as both aim to improve the overall quality of images. There are instances where noise interference reduces the compression efficiency, as noise is also compressed alongside an image. In contrast, some images compressed at low bit rates may have reduced quality but can be enhanced using noise reduction algorithms.

Steganographic methods allow financial institutions to embed critical data—such as authentication credentials, encryption keys, or transaction details—within digital files, like images or audio, ensuring an additional layer of security that is difficult to detect or intercept. This covert approach addresses the growing challenges posed by cyber threats, offering a mechanism to enhance confidentiality and mitigate the risks associated with data breaches or unauthorized access. While promising, the adoption of steganography in finance demands a careful balance between imperceptibility, robustness, and resilience to manipulations, such as compression or noise, ensuring its effectiveness in real-world applications.

Financial steganography encompasses a diverse array of techniques designed to safeguard sensitive information in innovative ways. Text-based methods leverage the manipulation of textual attributes—such as line spacing, font style, or punctuation—within financial documents, reports, or emails to encode hidden messages imperceptibly. Image and audio steganography involve embedding confidential data within digital media by altering pixel values or audio frequencies, often employing techniques like the least significant bit (LSB) modification or spread-spectrum encoding. These methods are particularly effective for embedding data without visibly compromising the host media. Network traffic steganography, another advanced approach, encodes hidden messages within the timing or structure of network packets, enabling secure and inconspicuous communication over financial systems. Emerging in the field is blockchain-based steganography, which integrates the immutability and distributed nature of blockchain technology to conceal data within transactional records, offering unparalleled security and resistance to tampering. Together, these techniques provide robust solutions for maintaining confidentiality and enhancing data security in a dynamic financial landscape.

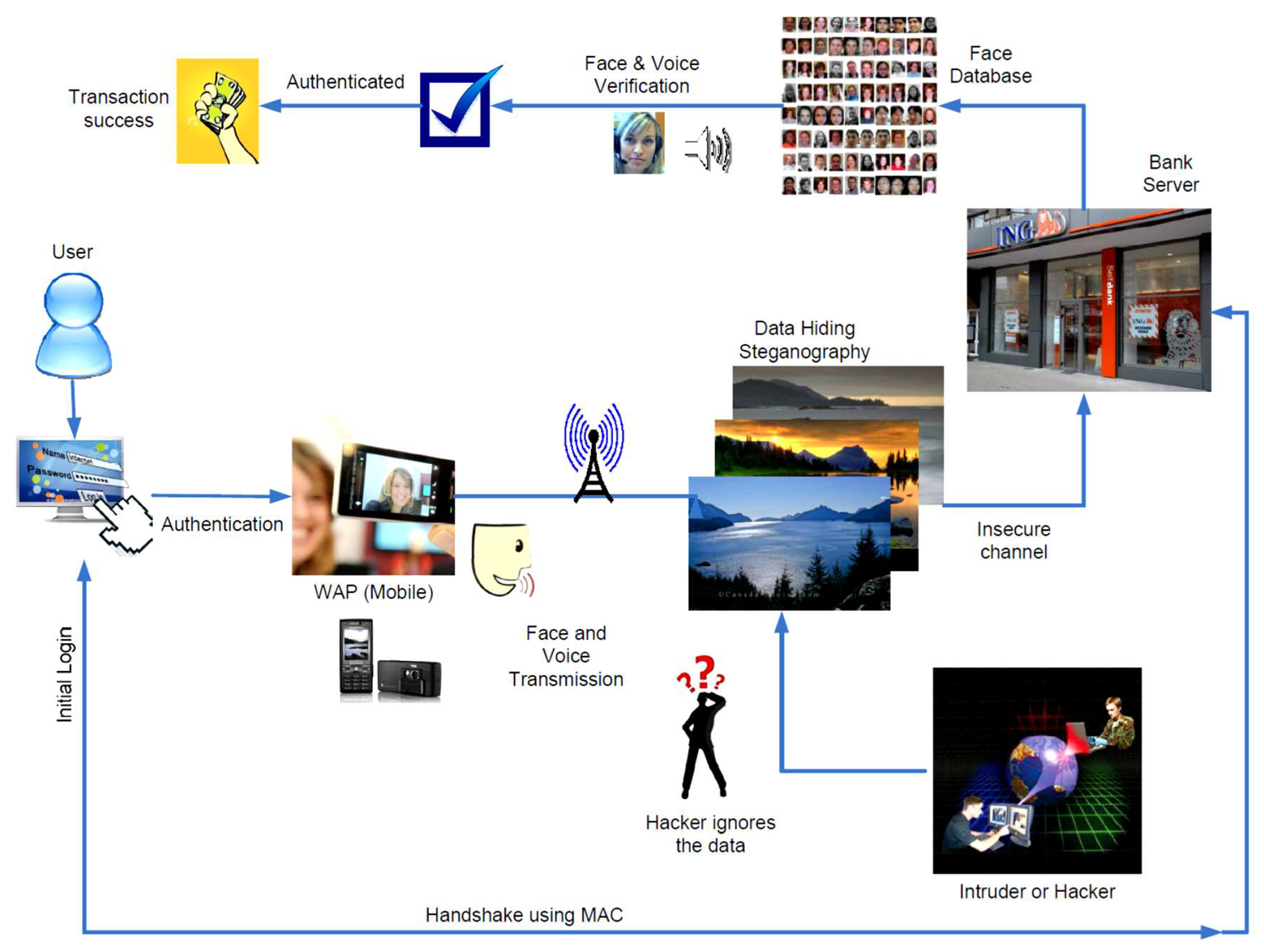
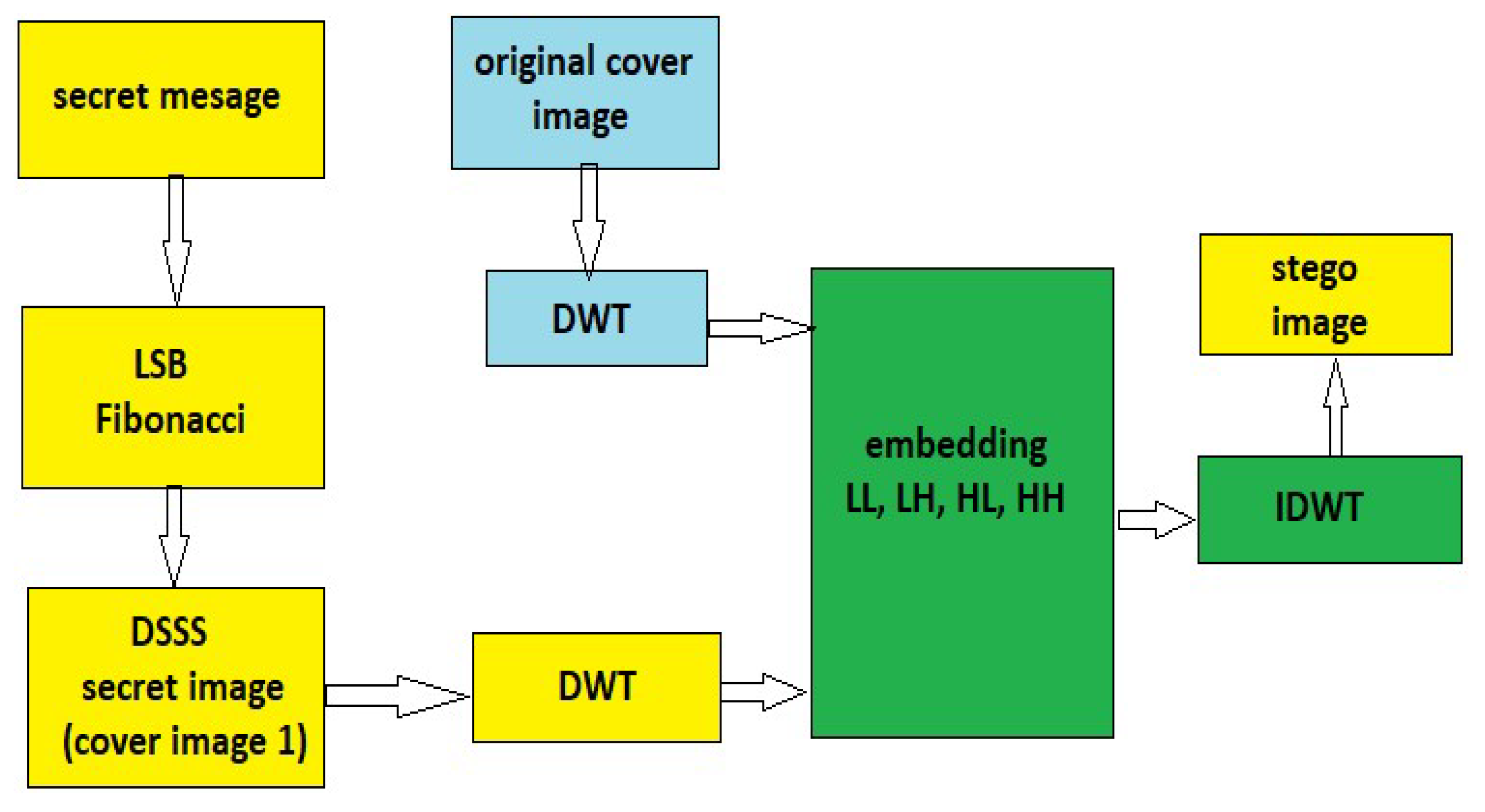
The algorithm proposed in this paper operates in two stages. In the first stage, a secret message of up to 10,000 characters is embedded in an image using Fibonacci sequences with LSB embedding for data security, and a hash function is generated. In the second stage, the resulting stego image is further hidden within a cover image using multiresolution discrete wavelet transform (DWT) decomposition, effectively embedding the secret message and secret pictures within a single cover image.

This paper also proposes a novel approach that combines biometric authentication with steganography to ensure secure communication channels for banking transactions. Using Fibonacci sequences for encryption within a DWT framework provides a highly robust method for concealing sensitive data within digital images. This dual-layered approach addresses the vulnerabilities of traditional security methods by integrating cryptography and biometric-based user verification into a unified security model (Figure 1).

The remainder of this paper is organized as follows. Section 2 presents the materials and methods, detailing the algorithms and techniques used in the proposed steganography system, including the application of Fibonacci sequences and DWT. Section 3 provides the results for the experimental tests conducted, focusing on the system’s performance with respect to the Peak Signal-to-Noise Ratio (PSNR) and security robustness. Section 4 discusses the implications of these findings and compares them to existing methods. Finally, Section 5 concludes the paper by summarizing the contributions of this study and outlining potential future research directions.

2. Materials and Methods

This study proposes a method for perceptual marking that operates within the wavelet domain, leveraging the spread-spectrum technique in combination with Fibonacci sequences. The proposed perceptual mask considers noise, texture, and luminance sensitivity across all sub-bands. An improved perceptual mask is introduced, where the texture content is estimated using the local standard deviation of the original image, compressed in the DWT domain to match the size of the inserted marker [8].

An essential requirement for any marking system is imperceptibility. This can be achieved through various approaches, including using statistical characteristics of the wavelet coefficients of the original image. The variance in these coefficients can be estimated at different resolution levels, with coefficients of high absolute value identified using a threshold detector. When markings are inserted into these coefficients, particularly within the first three levels of resolution, the system achieves robust marking. The robustness of this approach is directly proportional to the threshold value [9].

This method aligns with other solutions, which enhance robustness by inserting multiple labels across specific sub-bands [10,11,12]. In this approach, all marker bits are embedded with uniform intensity. High-value coefficients correspond to image contours, medium-value coefficients to textures, and low-value coefficients to homogeneous areas. However, this technique faces challenges: embedding longer messages (which introduce a higher load) may require lowering the threshold value, resulting in markings inserted into the textures [13].

The stated method effectively employs perceptual masking, but analyzing its robustness becomes complex, especially with increased marking repetitions. While robustness improves with repeated markings, it decreases when threshold values are reduced. Not all coefficients are suitable for embedding; thus, the marking process involves varying intensities. Coefficients in contours are embedded with higher intensity, those in textures with medium intensity, and those in homogeneous areas with low intensity. This approach is consistent with the analogy between water-filling and watermarking, as described in previous research [14,15].

2.1. Perceptual Marking

Building on the methodology outlined above, the process of perceptual marking is further detailed. The proposed approach incorporates a novel implementation strategy where the characteristics of the human visual system guide the marking process. This ensures that the embedded data remain imperceptible while maintaining robustness against potential distortions [16].

The process of perceptual marking leverages the wavelet domain to embed information that aligns with the perceptual characteristics of the human visual system, ensuring imperceptibility and robustness [17]. Figure 2 illustrates the architecture of the proposed method, highlighting the step-by-step process of applying the perceptual mask and embedding the marking within the wavelet domain.

An image I, with size 2M × 2N, is decomposed into four levels of resolution using the discrete wavelet transform, Daubechies-6, where $I_l^{\theta }$ is the sub-band of level l ∈ {0, 1, 2, 3} and the orientation θ ∈ {0, 1, 2, 3}. A binary marker $x_l^{\theta }\left(i,j\right)$ of length 3MN/2^l is inserted into all the coefficients of the detail sub-bands at level l = 0 (high frequency/high resolution) by addition:

$$I_l^{\theta }=I_l^{\theta }\left(i,j\right)+\alpha w_l^{\theta }\left(i,j\right)x_l^{\theta }\left(i,j\right)$$

(1)

where α is the marking intensity and $w_l^{\theta }\left(i,j\right)$ is a weighting function, the value of which is equal to half the quantization step, $q_l^{\theta }\left(i,j\right)$. The quantization step is calculated by [17] as the weighted product of three factors:

$$q_l^{\theta }\left(i,j\right)=\vartheta \left(l,\theta \right)\mathsf{\Lambda }\left(l,i,j\right)\mathsf{\Xi }{\left(l,i,j\right)}^{0.2}$$

(2)

and insertion occurs only in the first level of decomposition, l = 0 (high frequency).

The first factor is the sensitivity to noise, depending on the orientation and the level of resolution:

$$\vartheta \left(l,\theta \right)=\left\{\begin{array}{c}\sqrt{2}, \theta =1\\ 1,otherwise\end{array}\right\}.\left\{\begin{array}{c}1.00, l=0\\ 0.32. l=1\\ 0.16, l=2\\ 0.10, l=3\end{array}\right\}$$

(3)

The second factor considers the local brightness, based on the grey levels of the low-pass version of the image (i.e., the sub-image of the level 4 approximation obtained after calculating the wavelet transformation):

$$\mathsf{\Lambda }\left(l,i,j\right)=1+L^{,}\left(l,i,j\right)$$

(4)

where

$$L^{,}\left(l,i,j\right)=\left\{\begin{array}{c}1-L\left(l,i,j\right), L\left(l,i,j\right)<0.4\\ L\left(l,i,j\right),otherwise \end{array}\right\}$$

(5)

and

$$L\left(l,i,j\right)={\displaystyle \frac{1}{256}}{I}_3^3\left(1+⌊{\displaystyle \frac{i}{2^{3-l}}}⌋,1+⌊{\displaystyle \frac{j}{2^{3-l}}}⌋\right)$$

(6)

The third factor is

$$\begin{gathered} \mathsf{\Phi }\left(l,i,j\right)={\displaystyle {\sum }_{k=0}^{3-i}}{\displaystyle \frac{1}{{16}^k}}{\displaystyle {\sum }_{\theta =0}^2}{\displaystyle {\sum }_{x=0}^1}{\displaystyle {\sum }_{y=0}^1}{\left[I_{k+1}^{\theta }\left(y+{\displaystyle \frac{i}{2^k}},x+{\displaystyle \frac{j}{2^k}}\right)\right]}^2.Var \\ \left\{I_3^3{I}_{k+1}^{\theta }\left(1+y+{\displaystyle \frac{i}{2^{3-l}}},1+x+{\displaystyle \frac{j}{2^{3-l}}}\right)\right\} \end{gathered}$$

(7)

where x = (0, 1) and y = (0, 1).

The texture in the vicinity of a pixel is determined by the product of two key factors. The first factor is the local square mean of the wavelet coefficients derived from all the detailed sub-images. The second factor represents the local dispersion of the approximation sub-band. Both factors are computed within a 2 × 2 window centered on the pixel located at (i, j). The first factor can be interpreted as the distance from the edges, while the second factor correlates with the texture. It is important to note that this estimate of local dispersion lacks precision, as it is derived at a low resolution. Consequently, a new method for more accurately estimating both texture and luminance is proposed.

2.2. Enhanced Perceptual Mask

An alternative method for generating the third factor in the quantization step involves segmenting the original image to identify its contours, textures, and homogeneous regions. The segmentation criterion applied is the standard deviation value for each pixel in the original image. Within a square sliding window W(i, j), which encompasses WS ⋅ WS pixels and is centered on each pixel I(m, n) of the host image, the local average is calculated by the formula

$$\mu \left(i,j\right)={\displaystyle \frac{1}{W_S.W_S}}{\sum }_{I(m,n)\in W(i,j)}I(m,n)$$

(8)

and the local dispersion is

$${\sigma }^2\left(i,j\right)={\displaystyle \frac{1}{W_S.W_S}}{\sum }_{I(m,n)\in W(i,j)}{\left(I\left(m,n\right)-\mu (i,j)\right)}^2$$

(9)

The estimated local standard deviation derives from the local dispersion. For example, the Lena image can be segmented into classes where each class’s elements have the value of the normalized standard deviation, belonging to possible intervals I_p = (α_p, α_p+1), where p takes the values 1, …, 6, and α₁ = 0, α₂ = 0.025, α₃ = 0.05, α₄ = 0.075, α₅ = 0.1, α₆ = 0.25, and α₇ = 1. This image is chosen for its rich content of contours, textures, and homogeneous areas. The results are represented by the class corresponding to the interval I_p, p = 1, …, 6, with the other elements being ignored (represented in white). It should be noted that the grey levels represent contours and textures, and the white color represents the insignificant areas.

These images illustrate the high quality of segmentation achieved through the values of the local standard deviation. Such images can serve as effective perceptual masking when applying a marking. The quantization step for a wavelet coefficient is determined by a value that is directly proportional to the local standard deviation of the corresponding pixel in the original image.

To achieve perceptual masking, the dimensions of the various details in the sub-images must match the dimensions of their corresponding masks. As a result, the local deviation image is subject to compression. The compression factor required for a mask corresponding to resolution level l is 4(l + 1), for l = 0, …, 3. This compression can be performed in the DWT range.

The discrete wavelet transform of the local standard deviation image is calculated to generate the mask used to insert the marking into resolution level l, making l + 1 iterations. The approximate image produced reflects the outcome of the compression, essentially serving as the desired mask. This method of compression and noise reduction is illustrated in Figure 3a.

The main difference between the marking system proposed by other research [18] and the system presented here is given by calculating the local dispersion—the second factor—in relation (7). To obtain the new texture values, the local variance in the image is calculated using the relations (8)–(9), with a sliding window size W_S = 7. The local standard deviation is analyzed in the wavelet domain, preserving only its approximation image, which is subsequently normalized to its average. Relationship (7) is replaced by:

$$\begin{gathered} \mathsf{\Phi }\left(l,i,j\right)=\sum _{k=0}^{3-i}{\displaystyle \frac{1}{{16}^k}}\sum _{\theta =0}^2\sum _{x=0}^1\sum _{y=0}^1{\left[I_{k+1}^{\theta }\left(y+{\displaystyle \frac{i}{2^k}},x+{\displaystyle \frac{j}{2^k}}\right)\right]}^2.{DWT}_l^3 \\ \left\{Std{\left(I\right)}_{x,y=0.7}\right\} \end{gathered}$$

(10)

For the introduction of digital watermarking, the Lena image is used, which has been improved by the noise reduction algorithm proposed and the obtained image is presented in Figure 3b.

2.3. Fibonacci Sequences Using LSB

The LSB approach offers several advantages for steganographic applications, particularly for embedding data within digital media. Its simplicity and efficiency make it easy to implement while maintaining a low computational cost. By altering only the least significant bits of pixel values or audio samples, the method ensures minimal distortion, preserving the visual or auditory quality of the host media. This imperceptibility makes the hidden data virtually undetectable to human perception [19]. Additionally, the LSB technique supports high data-embedding capacity, making it suitable for applications requiring the concealment of substantial amounts of information. Its compatibility with various media types, such as images, audio, and video, further enhances its versatility in practical applications [20].

The fundamental principle of LSB substitution involves embedding confidential data into the rightmost bits (the bits with the least significance) of pixel values. This technique ensures that the embedding process does not significantly alter the original pixel values. The mathematical representation for LSB embedding is as follows:

X_i′ = x_i − x_i mod 2k + m

(11)

The ith pixel value of the stego image and x_i represent that of the original cover image. The variable M_i indicates the decimal value of the ith block of confidential data, and k refers to the number of LSBs that are substituted. During the extraction process, the k rightmost bits are directly copied. The mathematical representation of the extracted message can be expressed by Equation (12).

m_i = x_i mod 2k

(12)

Thus, a simple permutation of the extracted LSB allows us to retrieve the original confidential data. While this method is straightforward, it is vulnerable to signal processing and noise interference. Additionally, secret information can be easily compromised by extracting the entire LSB plane.

The Fibonacci sequence is a recursive series defined by the sum of the two preceding numbers, with 0 and 1 serving as the base reference points. Therefore, if the reference values are considered to be a = 0 and b = 1, the Fibonacci sequence can be represented mathematically by Equation (13), where F_ab(n) is the nth Fibonacci number, a is the first number from the reference base, and n is the second number from the reference base.

$$F_{ab}\left(n\right)=\left\{\begin{array}{c}a, for n=1\\ b, for n=2\\ F\left(n-1\right)+F\left(n-2\right),else\end{array}\right.$$

(13)

where a ≠ b ≠ 0.

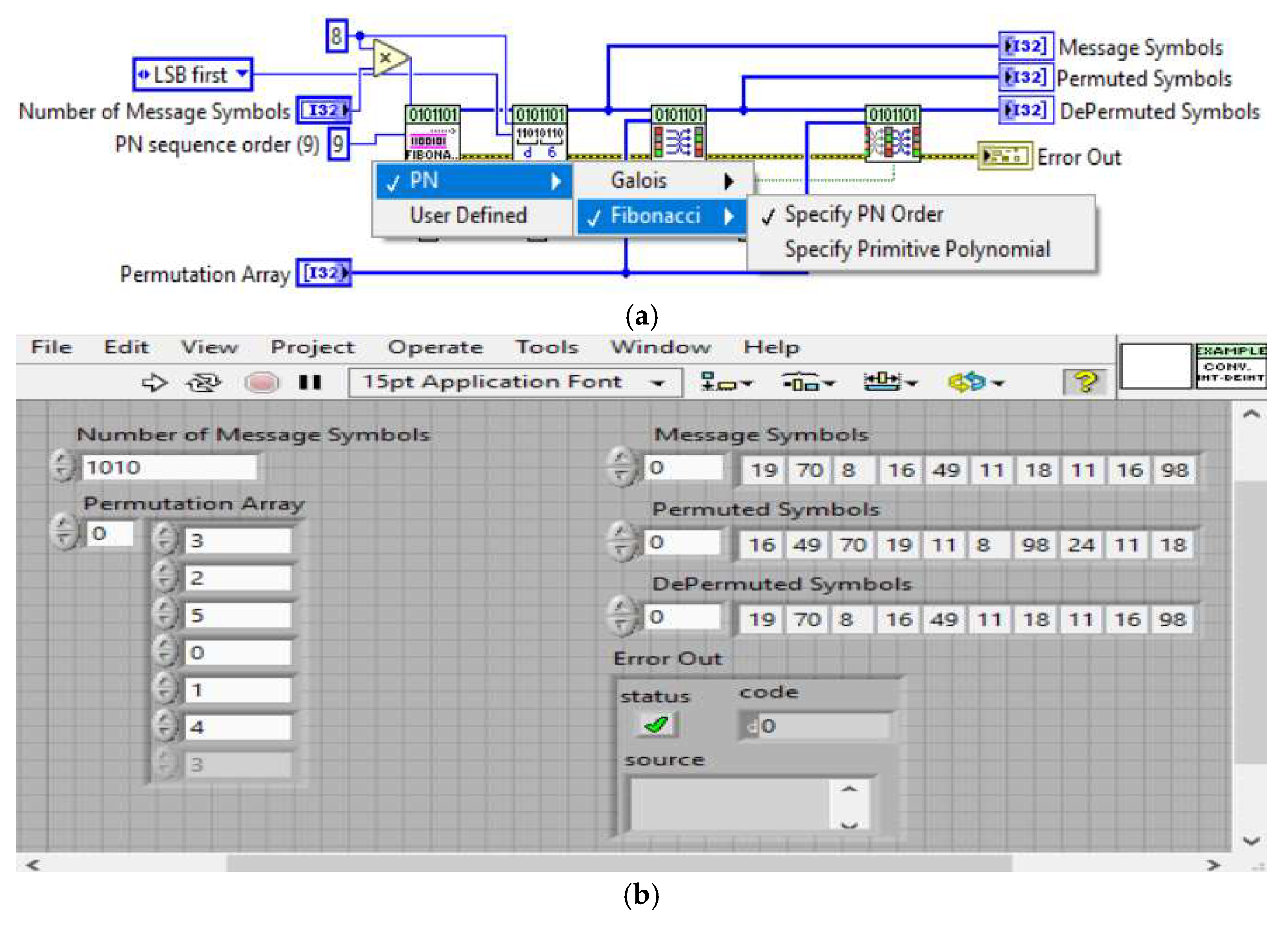
Figure 4 shows the code for generating the Fibonacci sequence using LSB.

Figure 4a illustrates the software code implementation for generating Fibonacci sequences, which are used in the LSB substitution technique for data hiding. The code leverages the recursive properties of the Fibonacci sequence to provide a predictable yet complex basis for embedding secret data by replacing the least significant bits of digital media. Figure 4b displays the results of this implementation through a GUI, showcasing how the Fibonacci sequence is generated and used to encrypt and embed data within host files. This visualization highlights the seamless integration of hidden data with minimal impact on the host’s original values, demonstrating the method’s effectiveness.

2.4. Direct-Sequence Spread Spectrum (DSSS)

Spread codes are essential in the DSSS system. M sequences, the golden sequences, have traditionally been used to spread codes in DSSS. These sequences are generated by shift registers, which are periodic in nature. This paper proposes the use of alternative types of sequences, called Fibonacci sequences, for the DSSS system for image encryption using pseudo-random code generators with Fibonacci sequences. 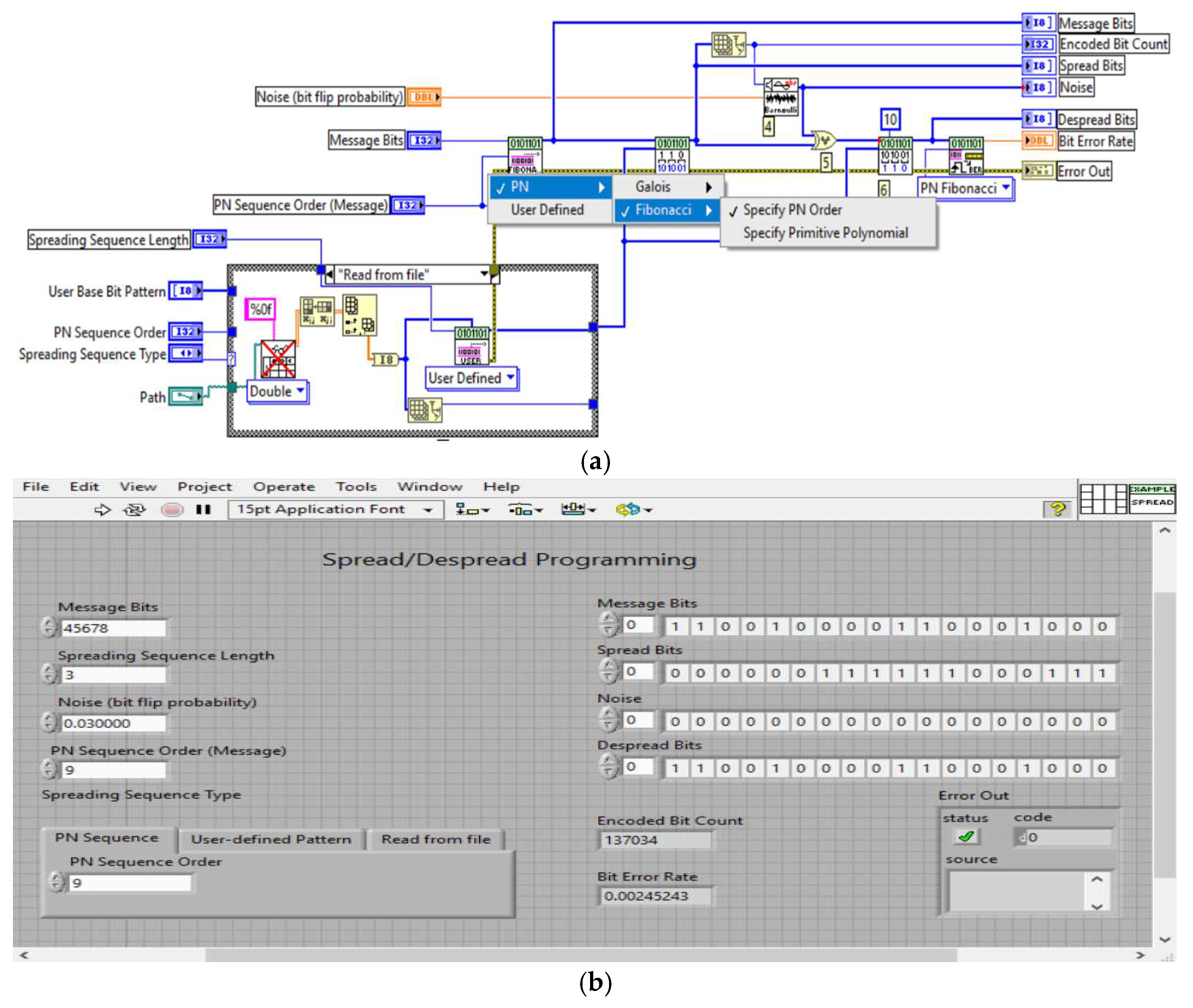Figure 5 shows the code for generating the direct-sequence spread spectrum using a Fibonacci sequence.

Figure 5a shows the implementation of the code for generating a direct sequence-spread-spectrum (DSSS) system based on Fibonacci sequences. The code creates pseudo-random sequences used to encrypt and spread hidden data across multiple frequencies, enhancing resistance to interception and detection. Figure 5b presents the GUI results of this DSSS system, illustrating the encryption and integration of data into a host file. The GUI visualization emphasizes how Fibonacci sequences are used to securely disperse data within digital media, providing robust protection against tampering and ensuring secure communication.

3. Results

The proposed method was evaluated through experiments to measure its effectiveness at embedding and retrieving hidden information within digital images. Key performance metrics, including the PSNR and MSE, were used to assess the imperceptibility and robustness of the steganographic technique. The method demonstrated significant improvements in security and image quality preservation by embedding secret messages using Fibonacci sequences and a DWT. The following results detail the system’s performance under varying conditions, including different marking intensities, compression rates, and noise levels, comprehensively analyzing its capabilities and limitations.

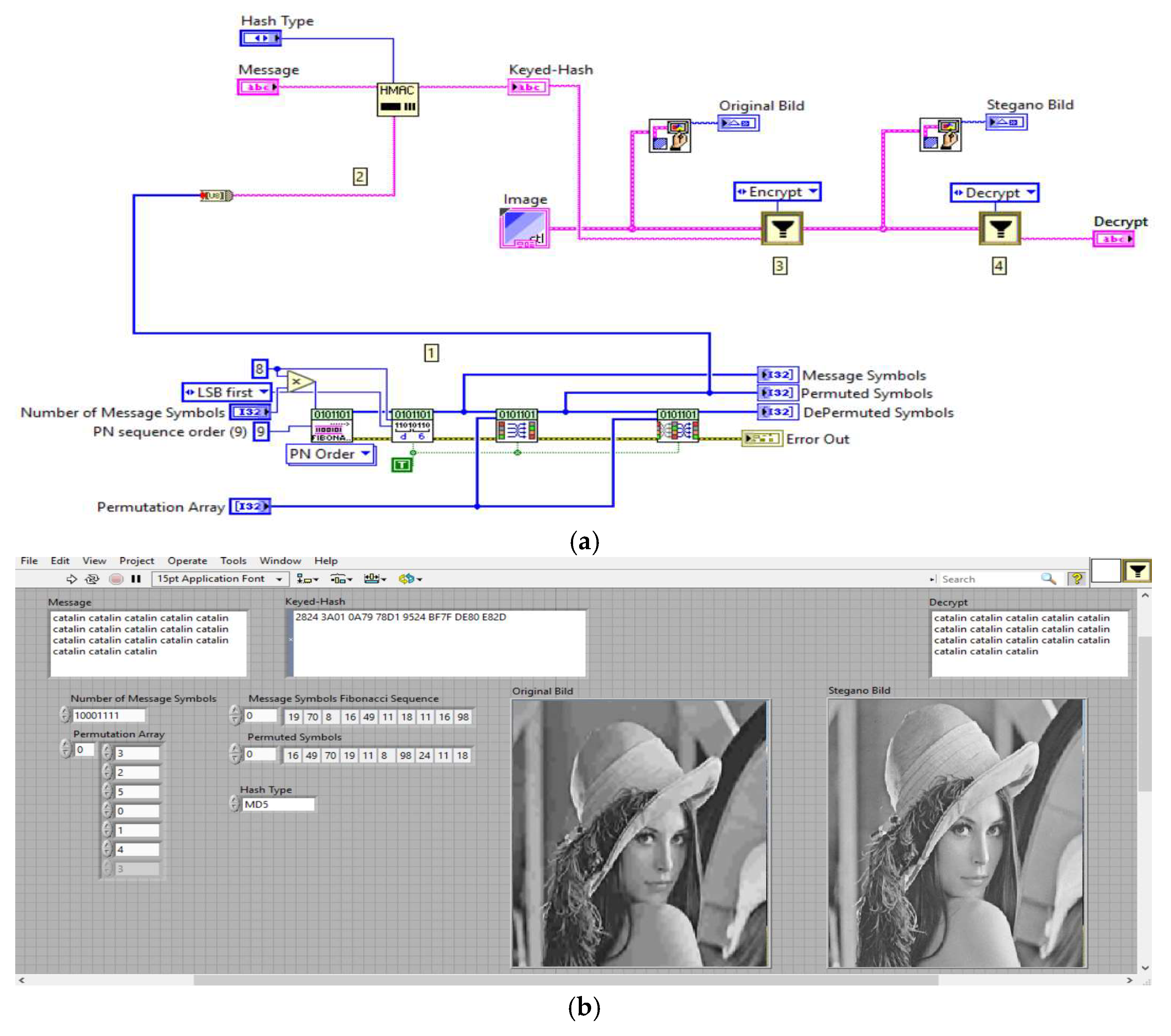
The following software code was created to test the proposed algorithm. This is presented in Figure 6.

According to Figure 6a, the proposed algorithm performs the following steps:

• The hash function employs the generation of Fibonacci sequences alongside a permutation process that alters the position of the input data elements according to the values specified in the permutation array. These methods enhance encryption security.
• The hash function is generated using the MD5 algorithm, a cryptographic hash function that accepts input messages of any length and transforms them into a fixed-length output of 16 bytes. MD5 stands for message-digest algorithm.
• The message is embedded within the cover image using multiresolution DWT decompositions.
• The deciphering of the message from the stegano cover image.

In Figure 6b, you can analyze the obtained results: the image on the left is the original Lena image with PSNR 32 dB, and the image on the right is the stegano image (marked image) with PSNR 63 dB. This PSNR increase is due to the Fibonacci sequences combined with the multiresolution DWT transform. The results of the multiresolution DWT transform are presented below.

The binary marking is embedded in all the detailed sub-images from the first wavelet resolution level, using relations (1)–(5). The Lena image is marked with different α-mark intensities, between 0.1 and 1.5. The Lena image marked with α = 1.5 is shown in Figure 7. As can be seen, there is no noticeable difference between the original image and the marked one, the value of the PSNR for this second image being 47 dB. Each tagged image is JPEG compressed using various quality factors 5, 10, 15, 20, 25, 50.

To evaluate the performance of the algorithm, the results for the JPEG compression are illustrated in Figure 8 for only the Q/T ratio, as a function of the PSNR between the marked (unattached) image and the original one, respectively, as a function of α. For each PSNR value and quality factor Q, the correlation ρ and the threshold T are calculated. The probability of a false-positive detection is set at 10⁻⁸. The efficiency of the proposed marking system can be measured using the Q/T ratio. If Q/T > 1, the marking is detected.

The analysis of the results of the images presented in Figure 9, Figure 10 and Figure 11 indicates that the marking is detectable across a wide range of PSNR values and Q quality factors. Specifically, for PSNR values exceeding 50 dB, the marking becomes invisible. In contrast, for Q factors of 25 or higher, the distortion caused by the JPEG compression remains acceptable. Notably, for PSNR values between 60 dB and 65 dB, which hold practical significance, the marking can be successfully extracted for all relevant quality factors (Q ≥ 25). Thus, the proposed system demonstrates its viability.

These figures collectively demonstrate the trade-off between marking power (α), PSNR, and resistance to JPEG compression. A higher marking intensity leads to improved robustness at the cost of a lower PSNR, while images with PSNR values above 50 dB achieve an ideal balance between invisibility and detectability. The results confirm the effectiveness of the proposed method for secure data embedding in practical applications, even under challenging compression conditions.

In Figure 9, the marked image demonstrates excellent visual fidelity with a PSNR value of 58 dB, indicating that the embedded data remain invisible to the human eye while maintaining high robustness against potential distortions.

Figure 10 shows the marking’s performance when the intensity is adjusted, resulting in a PSNR of 63 dB. The results confirm that higher PSNR values improve imperceptibility while preserving the embedded information.

Figure 11 highlights the impact of extreme compression (PSNR = 20 dB) on the marked image, revealing the lower limit of the method’s robustness under aggressive compression.

The results in Figure 12 show the dependence of the Q/T ratio upon the marking power, α, in the context of a JPEG compression. As the marking power increases, the PSNR values of the marked images decrease, leading to an increase in the Q/T ratio. The Q/T ratio exhibits an inverse relationship with α, a direct relationship with the PSNR, and an inverse relationship with the compression rate. The label remains detectable at minimal values of α. For a quality factor Q = 5 (or a compression rate CR = 32), the marking is identifiable even at low values of α, specifically at 0.5.

Table 1. Comparison between the old method and the proposed method.

CR=46, JPEG Compression	New Method	Old Method
φ	0.3289	0.021
T	0.0734	0.035
φ2	0.0418	0.02

Source: author’s results.

presents a comparison between the method proposed in this study and an earlier method detailed in previous research [21]. For this evaluation, the algorithm was applied to the Lena image with α set to 1.5 and a quality factor Q of 5, which corresponded to a JPEG compression rate of 46. The value of Pf was set at 10⁻⁸, and the detector’s response was evaluated using 1000 markings.

Table 1 presents the detector’s response for the original marking, φ; the detection threshold, T; and the second magnitude response, φ². The detector’s response is noticeably improved compared to the previous method. The new perceptual mask effectively conceals the data more efficiently, thanks to a more precise estimation of the texture, which leverages the local standard deviation of the compressed image in the wavelet domain. The next step will be extending this method in the future, whereby the marking can be hidden imperceptibly in lower-frequency sub-bands. This will bring an increased level of robustness.

Figure 13 presents the original and watermarked images at a marking power of α = 0.05, achieving a PSNR value of 66.60 dB. This high PSNR value reflects minimal distortion, indicating that the embedded data does not compromise the visual quality of the host image.

In Figure 14, the marking power is increased to α = 0.05, resulting in a PSNR value of 67.21 dB. Despite the higher marking intensity, the image quality remains excellent, demonstrating the algorithm’s capacity to embed robust watermarks without affecting the visual integrity. Also, it compares the proposed algorithm’s performance against a benchmark method, showcasing its superior ability to preserve image quality even under higher marking loads and compression scenarios.

Based on these figures, Figure 15 demonstrates the visual results of the encryption process using the proposed algorithm. Panels (a) and (b) represent the original plaintext images before encryption, showcasing their unaltered appearance. Panels (c) and (d) display the corresponding ciphertext images, where the encryption algorithm has transformed the original images into an encrypted format. The ciphertext images appear visually scrambled, ensuring that the embedded data and original content are indecipherable without the decryption key. This visual contrast highlights the algorithm’s effectiveness at securely encrypting sensitive data while maintaining its robustness against unauthorized access or tampering.

For testing the RGB images, the Lena image was used with different extensions, tiff, png, bmp, and gif, using DWT–Fibonacci LSB and DWT–Fibonacci DSSS. The stegano results for the Lena.tiff image with DWT–Fibonacci LSB and with DWT–Fibonacci DSSS are presented in Figure 16.

Four images, each with a unique extension, were processed visually using two DWT steganography techniques: Fibonacci LSB and DWT–Fibonacci DSSS. Whether treated with the Fibonacci LSB or Fibonacci DSSS, the original image and the stego image appear indistinguishable to the human eye.

The test for Lena.tiff was repeated for the Lena png, bmp, and gif images. The MSE and PSNR results are presented in

Table 2. MSE and PSNR values for the test RGB images.

Image	Stegano DWT– Fibonacci LSB MSE	Stegano DWT– Fibonacci DSSS MSE	Stegano DWT– Fibonacci LSB PSNR [dB]	Stegano DWT– Fibonacci DSSS PSNR [dB]
Lena.tiff	0.00019	0.00015	87	86.5
Lena.png	0.0002	0.0002	85	85
Lena.bmp	0.00018	0.0001	88	86
Lena.gif	0.0006	0.0005	82	80

Source: author’s results.

.

According to the findings presented in Table 2, three out of the four test images show an increase in the PSNR. Notably, the images with the “.png” extension exhibit identical MSE and PSNR values. However, as the calculations do not involve an “inf,” the difference must be attributed to a small decimal variation. The lowest PSNR value is recorded for the images with the “.gif” extension.

To substantiate the proposed algorithm, Figure 17 also presents the Structural Similarity Index (SSIM), which is relevant to the robustness against different types of attacks (e.g., noise, cropping), and the cryptographic strength of the analysis.

Figure 18 presents the SSIM analysis for the stegano image. Assessing the quality of imperceptibility of steganography methods is essential for evaluating the effectiveness of a proposed approach. Various measurement tools have been employed to evaluate imperceptibility, including the PSNR, SSIM, and MSE. Of these, the PSNR is the most commonly utilized measurement tool, due to its straightforward calculation and established validity, given its widespread use in various image processing research worldwide. However, the PSNR has notable limitations for assessing signal fidelity, which is closely linked to the imperceptibility of steganographic images. According to the findings of this research, the SSIM demonstrates superior sensitivity for detecting distortions caused by message embedding in steganographic grayscale images, compared to the PSNR. This advantage arises from the SSIM’s design, which is based on the principles of the human visual system. The SSIM calculations take into account the brightness, contrast, and structure of both the original container image and the stego image. The SSIM results presented in Figure 18 highlight the measurement of imperceptibility in the steganographic images.

The hash function identifies users and their devices through a shared secret and subsequently stores their data to enhance security. The data are irrevocably encrypted using Hashed Message Authentication Code (HMAC) functions, which incorporate algebraic modifications. In cryptography, the primary purpose of hash functions is to ensure message integrity. The hash function generates a unique fingerprint for the uploaded communication, confirming that the text has not been altered by external sources, such as viruses or other forms of tampering. Given the minimal likelihood that two distinct plaintexts will yield the same hash result, hash algorithms are highly efficient. We introduce an HMAC-LSB method along with Fibonacci algorithms, refining an adaptive DWT approach for secure steganography that offers greater protection compared to other variants currently employed for concealing information in data communications.

Figure 19 shows the software development for the application proposed in this article, and Figure 20 shows the encryption–decryption result for a text message.

According to Figure 19, the steps for encrypting–decrypting (encoding–decoding) a text message are as follows:

• Plaintext: enter the text message that must be encrypted and transmitted.
• Keyed hash: The message is encrypted using a hash-based message authentication code (HMAC), as defined in RFC 2104. The hash-type function is a Fibonacci sequence based on the encryption key (stego key).
• Stegano in RGB image: the encrypted message is inserted into the cover image (original image) using DWT decompositions, performing the adaptive process of hiding the text message in the cover image, resulting in the ciphertext image and the stegano image (stegano image).
• Decrypt text: the transmitted text message is recovered by entering the encryption key used in point 2 and IDWT, thus extracting the original message.

To test the proposed algorithm for transmitting and receiving a secret message through the proposed steganography method shown in Figure 20, we performed a communication simulation with a 64QAM modulation. This modulation is used for WiFi 5 (IEEE 802.11 ac) communication. The simulation result is presented in Figure 20.

To enhance the encryption framework for real-time applications, minimizing the computation time is essential. This research conducted computational analyses on images of varying sizes, specifically 256 × 256 and 512 × 512. In addition to assessing the computation time for image encryption, the analysis also covered the key generation process and the decryption process. Although the key generation process is distinct from encryption, it is vital, as the generated keys are integral to the proposed encryption framework. The computation time for encryption, decryption, and key generation was evaluated using an application developed in LabVIEW. As shown in

Table 3. Computational complexity analysis (sec).

Key Generation Process	Size	Images	Encryption Process	Decryption Process
0.0001	256 × 256	Lena	0.0020	0.0021
		Building	0.0021	0.0022
		Vegetables	0.0020	0.0021
0.0002	512 × 512	Cameraman	0.0030	0.0032
		Building	0.0031	0.0033
		Flower	0.0040	0.0041

Source: author’s results.

, the proposed encryption framework successfully encrypts images of sizes 256 × 256 and 512 × 512 in under one second, demonstrating its suitability for real-time applications. Furthermore, it is clear that the execution times for both the encryption and decryption processes are roughly equivalent. This consistency is due to the decryption process involving the same number of mathematical steps as the encryption, executed in reverse order, along with the reversal of each individual step.

These results confirm that the proposed adaptive filtering and digital watermarking algorithms display a robust performance at securely embedding data, including images, text, and sound, within multimedia carriers. Achieving high PSNR values across various marking intensities ensures that the hidden data remain imperceptible while maintaining the robustness required for practical applications, such as digital rights management and secure communications.

4. Discussion

The proposed algorithm presents an innovative approach to digital watermarking by integrating Fibonacci sequences with DWT to achieve both imperceptibility and robustness. The findings demonstrate the method’s capability to securely embed data within images while preserving high image quality, as indicated by the PSNR values exceeding 50 dB. This exceptional performance ensures that the embedded data remain invisible to the naked eye, even in the presence of compression or noise distortion [22].

Adaptive and non-adaptive steganography methods are categorized into two types based on how the embedding capacity of each pixel is determined. In non-adaptive approaches, the number of bytes per pixel remains constant and does not consider neighboring regions. To select the embedding sites, these methods typically utilize a pseudo-random number generator. They do not take neighboring pixels into account, allowing for a substantial amount of data to be embedded in the smooth areas of an image, making it difficult for the human visual system to detect changes in those regions. In contrast, adaptive approaches focus on greater embedding in the edge regions of an image, while minimizing it in the smoother areas. The proposed algorithm introduces an efficient adaptive strategy by employing the LSB and DWT–Fibonacci techniques. Additionally, adaptive filtering enhances stability against potential image alterations, particularly in the presence of noise.

Two methods for spatial steganography are mentioned in the literature, namely the conventional non-adaptive method and the adaptive method. The non-adaptive method refers to steganography techniques that embed secret data in images without considering the disturbance of the content of neighboring pixels by changing the pixel value. Typical methods include LSB, LSB matching, quantization index modulation, and stochastic modulation steganography. Adaptive embedding adaptively selects the hiding areas where changes in pixel values are difficult for steganalysis software applications to detect.

To highlight the efficiency of the adaptive method proposed in

Table 4. The results using MSE and PSNR parameters for non-adaptive and adaptive methods for RGB images.

No	Image (512 × 512 Pixels)	Adaptive Methods Proposed RGB Images		Non-Adaptive RGB Images
		MSE	PSNR	MSE	PSNR
1	Lenna	4.70	41.38	5.77	40.32
2	Boat	5.82	41.43	8.56	37.56
3	Goldhill	5.72	40.53	7.03	37.59
4	House	4.67	41.43	5.33	40.35
5	Congress	4.61	41.49	6.45	40.68

Source: author’s results.

, we compare the two, the non-adaptive and adaptive methods, using the MSE and PSNR parameters. They are difficult for steganalysis software applications to detect.

The comparison between the non-adaptive steganography method and the proposed adaptive method based on the MSE and PSNR for the analyzed RGB images shows that the MSE is higher and the PSNR has a lower value for the non-adaptive steganography method compared to the adaptive steganography method. To increase the performance of the steganography method, the MSE values must be lower and the PSNR values must be higher. The proposed adaptive steganography method meets the conditions for the MSE and PSNR values, being a good choice for RGB images.

The main methods identified are summarized in

Table 5. Comparison of method with those from specialized literature.

Research	Year	Methods Domain	Real-Word Performance	Robustness Attacks	Disadvantages
Yadollahi et al. [23]	2020	DNA and RNA	Not specified	Not specified	Lack of real-world performance data
Abbasi et al. [24]	2021	Chaotic evolutionary model	Not specified	Not specified	Requires performance evaluation
Zhong and Li [25]	2022	Random number generation	Enhanced security	Improved security	Real-world implementation challenges
Begum et al. [26]	2022	Image watermarking	Security watermark	Hybrid approach	Potential for complexity in the process
Benaissi et al. [27]	2023	Image encryption	Efficacious	Resilient to attack	Limited to 1D chaotic maps
Liu and Wang [28]	2023	Chaotic maps	Theoretical validation	Topological conjunction	Requires further validation
Shraida et al. [29]	2023	Color image encryption	Robust	Resistant to cyberattacks	Complexity in diffusion method
Zhang et al. [30]	2023	Image encryption	Scrambling images	Matrix-based encryption	Limited explanation of practical use
Biban et al. [31]	2023	Image encryption	Enhanced security	Robust against attacks	Potential for Computational overhead
Ganavi and Prabhudeva [32]	2023	Image encryption	Data confidentiality	Data integrity	Practical verification required
This Research	2024	DWT and Fibonacci sequences—DSSS for encryption	Enhanced security	Robust against attacks/Data integrity	Limited testing in the banking sector

Source: author’s results.

to compare the results obtained here with similar results from the literature.

Furthermore, this watermarking algorithm has significant potential for enhancing the security of banking transactions, particularly for protecting sensitive information during digital communications. In banking systems, where customer data and transaction details are prime targets for cyberattacks, the ability to embed critical security elements, such as authentication keys or encrypted information within digital media, adds an extra layer of protection [33]. The imperceptibility and robustness of this method guarantee that the embedded information remains concealed and secure, even amidst common distortions like compression or noise. This makes the algorithm an invaluable tool for establishing secure communication channels for mobile banking and online financial transactions, effectively addressing the vulnerabilities that traditional encryption methods may not fully mitigate [34].

A key strength of this approach lies in its adaptability to different marking intensities and compression rates. The results demonstrate that the watermark remains detectable even under aggressive JPEG compression without compromising the image’s integrity. This robustness positions the method as a reliable tool for real-world applications, such as protecting sensitive data during transmission or embedding metadata in multimedia content for copyright purposes [35].

Furthermore, using Fibonacci sequences enhances security by introducing unique and complex embedding patterns, reducing the risk of tampering or unauthorized access. The DWT framework further optimizes the spatial and frequency domains, ensuring the marking remains resistant to scaling and noise addition transformations [36].

The algorithm’s imperceptibility and resilience suit several practical scenarios, including banking transaction security. It is particularly effective for digital rights management, as it can embed copyright information or identifiers directly into images without affecting usability. This method can safeguard sensitive data during transmission over public or insecure networks for secure communications [37]. Its ability to maintain data integrity under compression makes it suitable for modern digital ecosystems, such as social media and cloud storage platforms, where images and multimedia content are frequently shared and resized.

While the algorithm achieves solid results for grayscale images, its scalability to color images and other multimedia formats, such as video or audio, warrants further investigation. This could extend its utility to broader domains, such as streaming services or secure video conferencing systems. Future advancements could also explore dynamic parameter adjustments for optimized performance based on varying content or security requirements.

This study’s findings demonstrate the proposed algorithm’s utility for enhancing banking transaction security by providing a robust and imperceptible mechanism for embedding sensitive data. This approach could be applied to secure banking applications by embedding biometric authentication data or transaction verification codes within images exchanged between users and financial institutions. Combining the security benefits of Fibonacci sequences with the DWT framework’s efficiency could strengthen existing banking security measures and reduce the risk of data breaches. Future developments could expand its application to real-time banking scenarios, offering an advanced solution for protecting financial data in increasingly digital and interconnected systems.

The implementation of an adaptive DWT-HMAC Fibonacci steganography for IEEE 802.11 MAC Layer Covert Channel Based will be addressed in the next stage of development. This new proposal for advancing research focuses on concealing information within the MAC layer of the 802.15.4 protocol. Our primary objective will be to implement a steganographic method that can withstand steganalysis in this protocol. Future outcomes will demonstrate that employing steganography with the 802.15.4 protocol offers an energy-efficient and low-latency solution for securing and concealing data in wireless sensor networks.

The proposed algorithm signifies a notable advancement in digital watermarking, offering a resilient and secure solution to contemporary challenges in multimedia security. Its strong performance, coupled with its potential for scalability and further refinement, positions it as a valuable asset for a range of applications, including secure data transmission and copyright protection.

5. Conclusions

This study presents a novel method for digital watermarking that successfully integrates Fibonacci sequences with DWT to achieve robust and imperceptible data embedding. The algorithm demonstrates high PSNR values and impressive resilience to noise and compression, confirming its effectiveness at securely embedding data while maintaining the visual quality of the host images. By utilizing Fibonacci sequences, this method adds an extra layer of complexity, which enhances security and minimizes the risk of tampering or unauthorized extraction.

This research demonstrates the algorithm’s versatility at embedding various data types, including text, images, and audio, making it applicable to multiple multimedia applications. Its ability to remain imperceptible under challenging conditions, such as low-quality compression or high embedding intensities, makes it a viable solution for digital rights management and secure communication systems.

While the current implementation focuses on grayscale images, extending the method to color images, video, and other multimedia formats offers a promising avenue for further research. Additionally, integrating advanced techniques, like machine learning, could enhance the algorithm’s adaptability and efficiency, allowing for dynamic parameter adjustments based on content characteristics or security requirements.