Fractional Calculus for Type 2 Interval-Valued Functions

Abstract

This paper presents a contemporary introduction of fractional calculus for Type 2 interval-valued functions. Type 2 interval uncertainty involves interval uncertainty with the goal of more assembled perception with reference to impreciseness. In this paper, a Riemann–Liouville fractional-order integral is constructed in Type 2 interval delineated vague encompassment. The exploration of fractional calculus is continued with the manifestation of Riemann–Liouville and Caputo fractional derivatives in the cited phenomenon. In addition, Type 2 interval Laplace transformation is proposed in this text. Conclusively, a mathematical model regarding economic lot maintenance is analyzed as a conceivable implementation of this theoretical advancement.

1. Introduction

The term “memory” is very crucial in several contexts of physical phenomena and decision-making scenarios. For instance, the current deformation pattern of a viscoelastic material due to the response to stress or strain is influenced by its past. The impacts of past happenings are also associated with current and voltage in electrical circuits. Neuronal activities in human brain are also controlled by experiences from previous communications. In the arena of economic transitions and dealing, memory has a significant influence. The managerial decision involves demand prediction, pricing, and purchasing patterns, and customers’ sentiments must be impacted by the experiences gained by the strategy makers. A mathematical model can be useful for analyzing physical phenomena with the references of mathematical tools and making an overall perception approximating occurrences in reality. Differential equations of both partial and ordinary types are conventionally used for describing dynamical systems representing numerous natural phenomena. However, integer-order calculus has limitations to its local characteristics. The hereditary nature involved in several real phenomena mentioned earlier cannot be represented accurately by conventional texts of integer-order calculus. In this context, the theory of fractional calculus becomes an adequate substitute for its integer counterpart. A prominent colloquy between two legends, L’ Hospital and Leibnitz, was the inceptive move towards fractional calculus as a generalized means of celebrated Newtonian calculus. So, the root of the fractional calculus theory is age-old. However, it has remained unpopular throughout many centuries due to the undiscovered physical significance and understanding of fractional derivatives and integration. It is to be noted that the fractional calculus corresponds a non-local attribute involving iterated kernels in its mathematical formation, distancing the nature of Newtonian calculus. The non-local behavior has been interpreted as memory of the dynamical systems [1,2,3,4,5]. Several researchers [6,7,8,9] have conducted insightful studies on the memory using mathematical correspondence of fractional calculus. Thus, fractional calculus, including differential and integral equations of non-integer orders, has been used in many perspectives of modeling in engineering and managerial circumstances [10,11,12,13].

The cumulative process of model formulation and managerial decision making concerning real-world management sectors and applied sciences cannot avoid impreciseness. Vague information makes decision-making procedures imprecise, leading towards an uncertain conclusion. The notion of probability is one of the celebrated approaches dealing with uncertainty regarding the likelihood of outcomes. Zadeh [14] introduced the Fuzzy set, another popular notion of impreciseness, where the vagueness in definitions is quantified by membership values. In this context, the lack of precise information may be dealt with using interval number theory, in which information is available between bounds. The interval number theory [15,16] is prevalent in the existing literature regarding decision making and modeling under uncertainty. It is to be noted that the upper and lower bounds of the interval are fixed. However, it is evident that many engineering and management phenomena may be comprehended by intervals where bounds are uncertain. For instance, the impreciseness regarding prediction of temperature for a day in certain locality is described as follows: The lowest temperature of the day may be between 18 °C and 20 °C. Also, the highest temperature of the day may be between 28 °C and 30 °C. Therefore, the strategic phenomena may exist where the bounds are not deterministic, but given in a generalized manner. In this context, the theory of Type 2 interval numbers [17] came into relevance. According to Rahman et al. [17], the imprecise phenomena can be represented mathematically by an interval [18,19,20,21,22] called a Type 2 interval. This added a second layer of uncertainty, as the ends of the interval were considered to be imprecise. This concept can be useful for economic models, where demand prediction and optimal pricing include two layered uncertainties without randomness or fuzziness.

Now, this paper presents an introductory study regarding the following fundamental queries:

(i)

What can be a fitting mathematical framework for dealing with decision-making problems under joint influences of memory and non-random, non-fuzzy, two-layered impreciseness?

(ii)

Is there any existing literature addressing memory and two-layered interval uncertainty together for effective managerial policies?

With the mentioned research questions, the existing literatures related to fractional calculus, interval number, interval-valued fractional calculus, and type interval-valued calculus were reviewed. The summary of the literature survey is given in the subsequent subsections.

1.1. Literature on Fuzzy Arithmetic and Calculus

After almost four decades since the introduction of fuzzy set theory by Zadeh [14], Dubois and Prade [18] contributed the L-R fuzzy model for a formal representation of fuzzy mathematics with associated formulae and operations. Fuzzy arithmetic operations are distinctive compared to crisp correspondences. The arithmetic properties can be approached in the context of membership grades using the Zadeh extension principle. Alternatively, it can be viewed in the context of level cut representation [23]. Later, fuzzy valued calculus was advanced based on either of the mentioned approaches. In this context, the notion of fuzzy derivatives in the literature was contributed by Chang and Zadeh [19]. Kaleva [24] followed the approach to define fuzzy differential equations. Later, the concepts of Hukuhara and generalized Hukuhara derivatives became popular for dealing with fuzzy differential equations [25,26,27,28]. Alternatively, fuzzy differential equations were solved using the Zadeh extension principle [29,30]. Fuzzy ruled arithmetic has become popular in the field of operation research and, more specially, in the domain of multi-criteria group decision making (MCDM). Fuzzy MCDM models are currently used for tracing alternatives in predetermined criteria by a panel of decision makers, where the fitness criteria of the alternatives are given in linguistic terms [20]. In this context, an impactive study on fuzzy decision making was conducted by Saha et al. [21]. They addressed an optimization approach with a linear combination of both subjective and objective weights of expertise to obtain an ultimate optimal decision using the Dombi operator and Maclaurin symmetric mean. Ala et al. [22] framed a fuzzy MCDM model for a sustainable supply chain network associated with healthcare facilities. Interval correspondences of such a fuzzy theory were also advanced in a parallel manner. In next subsection, the literature on interval arithmetic and calculus is summarized.

1.2. Literature Associated with Interval-Valued Calculus

Regardless of the celebrated exercises involving interval numbers and their optimization-oriented perspectives, the notion was not implemented to describe dynamical systems under uncertainty before the concepts of Hukuhara difference and differentiability, proposed by Stefanini and Bede [31], arose. Subsequently, differential equations integrating the mentioned senses of distance and difference was discussed by Malinowski [32]. Hukuhara difference and differentiability possessed some lacunas, which were removed by modifying definitions, namely those of generalized Hukuhara difference and differentiability, respectively. Following this notion, Stefanini and Bede [31] shared a categorical study on interval-valued differential equations. More studies with interval-valued calculus [33,34,35,36,37,38,39,40,41] were performed in this regard. In a recent study, Chalco-Cano et al. [42] discussed the switching point associated with the differentiability of interval-valued function subjects and the generalized Hukuhara derivative approach. Later, fractional calculus was also introduced for interval-valued functions. Lupulescu [43] was among the first who considered the definitions of fractional derivatives in the Riemann–Liouville’s and Caputo’s sense related to the interval phenomena, resulting in the introduction of interval-valued fractional calculus. Subsequently, more theoretical advancements [44,45,46,47,48,49] were carried out in this domain of research with distinctive perspectives. In this present paper, we place interval-valued fractional calculus in a more generalized landscape pertaining to Type 2 interval uncertainty. Thus, in the immediate subsection, we present an exhaustive survey on the literature of Type 2 interval numbers and functions to date.

1.3. Literature of Type 2 Interval Numbers and Functions

Interval number describes the vagueness regarding information lying between bounds. Therefore, the interval numbers are usually represented by closed intervals. It is to be noted that the bounds of both ends are fixed. Also, there is no such sense of the degree of membership in the definition of interval numbers. The functions whose ranges include interval numbers are called interval-valued functions. Rahman et al. [17] extended the notion of interval numbers by making the bounds flexible instead of deterministic. Insights on the uncertainty regarding the bounds introduced Type 2 interval uncertainty. In subsequent literature, the strategic decision for an inventory management problem was also predicted by Rahman et al. [50]. Later, Rahman et al. [51] manifested some intriguing characteristics of Type 2 interval arithmetic, emphasizing the scoring and ordering of Type 2 interval numbers. In another study, Rahman et al. [52] considered constrained and unconstrained optimization methods associated with Type 2 interval-valued functions. Smart warehousing technology was also addressed in the Type 2 interval setting [53]. A worthy study of unconstrained nonlinear optimization was performed by Das et al. [54]. In above-mentioned studies, the primary targets were limited to elementary arithmetic, optimization techniques, and possible application to inventory problems. However, a theory of Type 2 interval calculus was needed in order to utilize the innovative notion of Type 2 interval uncertainty for other dynamical problems involving differential equations. Use of the crisp differential equation and imprecise Type 2 data cannot fulfill the need to create a mathematical model ruled by Type 2 interval analysis. Thus, a separate study of Type 2 interval-valued calculus was needed. Rahaman et al. [55] introduced conformable calculus for Type 2 interval-valued functions. It is a matter of debate whether conformable calculus is a fractional or Newtonian calculus. Rahaman et al. [56] contributed an introductory study on Type 2 interval-valued functions emphasizing metric space and differential and integral calculus in detail. Also, existence and uniqueness results for an uncertain differential equation involving Type 2 interval variables were established by Rahaman et al. [57]. To date, the author has not found any document which exhibits exercises on fractional calculus for a Type 2 interval-valued function. This paper attempts a novel introduction of Type 2 interval-valued fractional calculus. To achieve this, we needed some conceptual pockets from the literature on fuzzy fractional calculus, as it is analogous to the interval fractional calculus discussed in the earlier subsection. Thus, in the subsequent subsection, we provide a brief review of the existing literature on fuzzy fractional calculus.

1.4. Literature of Fuzzy Fractional Calculus

The senses of difference and derivatives of fuzzy valued functions were developed analogously. Agarwal et al. [58] was the first who described fractional differential equation under fuzzy uncertainty. The pioneering work was succeeded by two insightful investigations [59,60] regarding the existence and uniqueness of the solution for fuzzy fractional differential equations. Mukherjee et al. [61] introduced a numerical simulation approach for fuzzy fractional differential equations. Introduction of fuzzy Laplace transformation by Allahviranloo and Ahmadi [62] became an instrumental development associating the theory of fuzzy fractional calculus. Babakordi et al. [63] studied a fuzzy fractional economic model based on market equilibrium using fuzzy Laplace transformation as the key tool. Ahmad et al. [64] studied the same model using the Zadeh extension principle. Later, distinctive definitions of fractional derivatives [47,65,66,67,68,69,70,71] were taken into consideration for the fuzzy framework. Different solution approaches, including Taylor series expansion [72,73] and Adomian decomposition [74], were engaged for the purpose of solving fractional differential equations under fuzzy uncertainty. Van and Ho [75] summarized the impacts of Riemann–Liouville, Caputo, and Hadamard fuzzy fractional derivatives to obtain solutions to implicit fractional differential equations under fuzzy phenomena. Van Ngo et al. [76] discussed the necessary conditions for equivalence of fuzzy fractional differential and integral equations. An et al. [77] explained the short-term memory phenomena with a mathematical representation of non-instantaneous impulsive fuzzy differential equations incurring the Caputo fractional derivative. The senses of memory and uncertainty in the economic lot size model were addressed by Pakhira et al. [78].

1.5. Research Gaps and Motivations

An out-and-out assessment of the convenient literature involves the following points:

(i)

Type 2 interval uncertainty is a mathematical structure for defining he uncertainty of data due to belongingness in given intervals. A type 2 interval extends the sense of uncertainty represented by the traditional interval number, making both ends uncertain. Thus, the newly defined uncertain phenomena may have several suitable applications in decision scenarios associated with mathematical modeling and optimization, as discussed earlier.

(ii)

The theory of Type 2 interval-valued calculus become instrumental when the dynamical models are taken into consideration for Type 2 interval uncertainty. We found only few documents addressing Type 2 interval-valued calculus.

(iii)

Fractional calculus has undergone advancement compared to Newtonian calculus in that it can address the non-local nature, and, more precisely, the memory-carrying characteristic, in dynamical procedures.

(iv)

Therefore, the memory-concerned dynamical model is taken under Type 2 interval-driven uncertainty, and the obligation of Type 2 interval-valued fractional calculus becomes acute.

(v)

To date, the theory of fractional calculus for Type 2 interval-valued functions has not been identified in the existing literature.

1.6. Contribution of This Paper

With the aforementioned scope, this paper defines and analyses the following issues with a novel introduction in this context:

(i)

The fractional integral calculus is introduced using Riemann–Liouville definition of a fractional integral for Type 2 interval-valued functions.

(ii)

The fractional differential calculus is introduced with both Riemann–Liouville’s and Caputo’s approaches to derivatives in Type 2 interval uncertainty.

(iii)

A brief introduction to Laplace transformation for Type 2 interval-valued function is added in this text, which would be instrumental for dealing with systems involving Type 2 interval-valued fractional differential equations.

(iv)

Furthermore, an inventory model is analyzed, and memory and uncertain driven phenomena are involved as suitable consequences of the proposed theory.

2. Mathematical Prerequisite

Definition 1 

([17]). Let us consider interval number $\Theta =\left[\left[{\underset{\_}{\theta }}_1,{\overline{\theta }}_1\right],\left[{\underset{\_}{\theta }}_2,{\overline{\theta }}_2\right]\right]$ in which ${\underset{\_}{\theta }}_1\le {\overline{\theta }}_1\le {\underset{\_}{\theta }}_2\le {\overline{\theta }}_2$. Then, $\Theta$ is called Type 2 interval number.

Definition 2 

([17]). We consider two Type 2 interval numbers, $\Theta =\left[\left[{\underset{\_}{\theta }}_1,{\overline{\theta }}_1\right],\left[{\underset{\_}{\theta }}_2,{\overline{\theta }}_2\right]\right]$ and $\Omega =\left[\left[{\underset{\_}{\omega }}_1,{\overline{\omega }}_1\right],\left[{\underset{\_}{\omega }}_2,{\overline{\omega }}_2\right]\right]$, and $\kappa$ is the scalar number. Then, addition between Type 2 interval numbers and scalar multiplication are performed as follows:

$$\Theta ⊞\Omega =\left[[{\underset{\_}{\theta }}_1+{\underset{\_}{\omega }}_1,{\overline{\theta }}_1+{\overline{\omega }}_1],[{\underset{\_}{\theta }}_2+{\underset{\_}{\omega }}_2{,\overline{\theta }}_2+{\overline{\omega }}_2]\right]$$

and

$$\kappa ⊡\Theta =\left\{\begin{array}{c}\left[[\kappa {\underset{\_}{\theta }}_1,\kappa {\overline{\theta }}_1],\left[\kappa {\underset{\_}{\theta }}_2{,\kappa \overline{\theta }}_2\right]\right]for \kappa \ge 0,\\ \left[[\kappa {\overline{\theta }}_2,\kappa {\underset{\_}{\theta }}_2],[\kappa {\overline{l}}_1,\kappa {\underset{\_}{\theta }}_1]\right] for \kappa <0.\end{array}\right.$$

Definition 3 

([55]). The interval width of $\Theta =\left[\left[{\underset{\_}{\theta }}_1,{\overline{\theta }}_1\right],\left[{\underset{\_}{\theta }}_2,{\overline{\theta }}_2\right]\right]$ is defined as $\mathcal{W}\left(\Theta \right)=[{\underset{\_}{\theta }}_2-{\overline{\theta }}_1{,\overline{\theta }}_2-{\underset{\_}{\theta }}_1]$.

Definition 4 

([55]). We consider two Type 2 interval numbers $\Theta =\left[\left[{\underset{\_}{\theta }}_1,{\overline{\theta }}_1\right],\left[{\underset{\_}{\theta }}_2,{\overline{\theta }}_2\right]\right]$ and $\Omega =\left[\left[{\underset{\_}{\omega }}_1,{\overline{\omega }}_1\right],\left[{\underset{\_}{\omega }}_2,{\overline{\omega }}_2\right]\right]$. Then, comparison in term of interval widths is defined as follows: $\mathcal{W}\left(\Theta \right){\succcurlyeq }_{in}\mathcal{W}\left(\Omega \right)$ if and only if ${\underset{\_}{\theta }}_2-{\overline{\theta }}_1\ge {\underset{\_}{\omega }}_2-{\overline{\omega }}_1$, and ${\overline{\theta }}_2-{\underset{\_}{\theta }}_1\ge {\overline{\omega }}_2-{\underset{\_}{\omega }}_1$.

Remark 1. 

For two Type 2 interval numbesr $\Theta =\left[\left[{\underset{\_}{\theta }}_1,{\overline{\theta }}_1\right],\left[{\underset{\_}{\theta }}_2,{\overline{\theta }}_2\right]\right]$ and $\Omega =\left[\left[{\underset{\_}{\omega }}_1,{\overline{\omega }}_1\right],\left[{\underset{\_}{\omega }}_2,{\overline{\omega }}_2\right]\right]$, it does not follow that either $\mathcal{W}\left(\Theta \right){\succcurlyeq }_{in}\mathcal{W}\left(\Omega \right)$ or $\mathcal{W}\left(\Omega \right){\succcurlyeq }_{in}\mathcal{W}\left(\Theta \right)$. For understanding the matter, we take $\Theta =\left[\left[1,2\right],\left[4,5\right]\right]$ and $\Omega =\left[\left[1,3\right],\left[4,5\right]\right]$. Then, $\mathcal{W}\left(\Theta \right)=[2,4]$ and $\mathcal{W}\left(\Omega \right)=[1,5]$.

Definition 5 

([17]). The generalized Hukuhara difference between $\Theta =\left[\left[{\underset{\_}{\theta }}_1,{\overline{\theta }}_1\right],\left[{\underset{\_}{\theta }}_2,{\overline{\theta }}_2\right]\right]$, and $\Omega =\left[\left[{\underset{\_}{\omega }}_1,{\overline{\omega }}_1\right],\left[{\underset{\_}{\omega }}_2,{\overline{\omega }}_2\right]\right]$, is defined as follows

$$\Theta {\boxminus }_g\Omega =\left[\left[A,B\right],\left[C,D\right]\right]$$

, where

$$A=\mathit{min}\left\{{\underset{\_}{\theta }}_1-{\underset{\_}{\omega }}_1,{\overline{\theta }}_2-{\overline{\omega }}_2\right\}, B=min\left\{{\underset{\_}{\theta }}_2-{\underset{\_}{\omega }}_2,{\overline{\theta }}_1-{\overline{\omega }}_1\right\},C=max\left\{{\underset{\_}{\theta }}_1-{\underset{\_}{\omega }}_1,{\overline{\theta }}_2-{\overline{\omega }}_2\right\}$$

and

$$D=\mathit{max}\left\{{\underset{\_}{\theta }}_2-{\underset{\_}{\omega }}_2,{\overline{\theta }}_1-{\overline{\omega }}_1\right\}$$

Lemma 1 

([55]). The generalized Hukuhara difference between $\Theta =\left[\left[{\underset{\_}{\theta }}_1,{\overline{\theta }}_1\right],\left[{\underset{\_}{\theta }}_2,{\overline{\theta }}_2\right]\right]$ and $\Omega =\left[\left[{\underset{\_}{\omega }}_1,{\overline{\omega }}_1\right],\left[{\underset{\_}{\omega }}_2,{\overline{\omega }}_2\right]\right]$ depends on interval widths as follows.

$$\Theta {\boxminus }_g\Omega =\left[\begin{array}{c}\left[[{\underset{\_}{\theta }}_1-{\underset{\_}{\omega }}_1,{\overline{\theta }}_1-{\overline{\omega }}_1],[{\underset{\_}{\theta }}_2-{\underset{\_}{\omega }}_2,{\overline{\theta }}_2-{\overline{\omega }}_2]\right], when \mathcal{W}\left(\Theta \right){\succcurlyeq }_{in}\mathcal{W}\left(\Omega \right),\\ \left[[{\overline{\theta }}_2-{\overline{\omega }}_2,{\underset{\_}{\theta }}_2-{\underset{\_}{\omega }}_2],[{\overline{\theta }}_1-{\overline{\omega }}_1,{\underset{\_}{\theta }}_1-{\underset{\_}{\omega }}_1]\right], when \mathcal{W}\left(\Omega \right){\succcurlyeq }_{in}\mathcal{W}\left(\Theta \right).\end{array}\right.$$

Remark 2. 

The existence of $\Theta {\boxminus }_g\Omega$ is the most significant condition in Lemma 1. It may occur that either $\mathcal{W}\left(\Theta \right){\succcurlyeq }_{in}\mathcal{W}\left(\Omega \right)$ or $\mathcal{W}\left(\Omega \right){\succcurlyeq }_{in}\mathcal{W}\left(\Theta \right)$; however, $\Theta {\boxminus }_g\Omega$ does not exist. For better understanding, let $\Theta =\left[\left[-1,2\right],\left[3,4\right]\right]$ and $\Omega =\left[\left[1,2\right],\left[3,5\right]\right]$. In that case, $\mathcal{W}\left(\Theta \right)=[1,5]$ and $\mathcal{W}\left(\Omega \right)=[1,4]$. Clearly, here, $\mathcal{W}\left(\Theta \right){\succcurlyeq }_{in}\mathcal{W}\left(\Omega \right)$. But $\Theta {\boxminus }_g\Omega$ does not exist. Because, if we claim that $\Theta {\boxminus }_g\Omega$ exists, then it will be $\left[[-2,0],[0,-1]\right]$, which is not a Type 2 interval number.

3. R-L Fractional Integral of Type 2 Interval-Valued Functions

Definition 6. 

Let $\mathcal{F}$ be a Lebesgue integrable T2IF defined on $[a,b]$. Then, each of the four components describing $\mathcal{F}$ is a Lebesgue integrable real-valued function defined on $[a,b]$. This follows that ${\left(x-u\right)}^{\beta -1}{\underset{\_}{f}}_1\left(u\right), {\left(x-u\right)}^{\beta -1}{\overline{f}}_1\left(u\right),{\left(x-u\right)}^{\beta -1}{\underset{\_}{f}}_2\left(u\right), {\left(x-u\right)}^{\beta -1}{\overline{f}}_2\left(u\right)$ are all Lebesgue integrable real-valued functions defined on $[a,b]$ for all $\beta >0$. Consequently,

$${\left(x-u\right)}^{\beta -1}\mathcal{F}\left(u\right)=\left[\left[{\left(x-u\right)}^{\beta -1}{\underset{\_}{f}}_1\left(u\right), {\left(x-u\right)}^{\beta -1}{\overline{f}}_1\left(u\right)\right],\left[{\left(x-u\right)}^{\beta -1}{\underset{\_}{f}}_2\left(u\right), {\left(x-u\right)}^{\beta -1}{\overline{f}}_2\left(u\right)\right]\right]$$

is a Lebesgue integrable T2IF defined on $[a,b]$. This implies the existence of the following integral.

$${I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{\beta }={\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{\beta -1}\mathcal{F}\left(u\right)du}{\mathsf{\Gamma }\left(\beta \right)}}, \mathrm{for} \mathrm{all} x\in [a,b].$$

${I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{\beta }$ is called the Type 2 interval-valued Riemann–Liouville fractional integral of order $\beta >0$ of the T2IF$\mathcal{F}$, and it can be drawn that

$$\begin{gathered} {\mathrm{I}2\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left(\mathcal{F}\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\beta }}=\left[\left[{\displaystyle \frac{{\int }_{\mathrm{a}}^{\mathrm{x}}{\left(\mathrm{x}-\mathrm{u}\right)}^{\mathsf{\beta }-1}{\underset{\_}{\mathrm{f}}}_1\left(\mathrm{u}\right)\mathrm{d}\mathrm{u}}{\mathsf{\Gamma }\left(\mathsf{\beta }\right)}},{\displaystyle \frac{{\int }_{\mathrm{a}}^{\mathrm{x}}{\left(\mathrm{x}-\mathrm{u}\right)}^{\mathsf{\beta }-1}{\overline{\mathrm{f}}}_1\left(\mathrm{u}\right)\mathrm{d}\mathrm{u}}{\mathsf{\Gamma }\left(\mathsf{\beta }\right)}}\right],\left[{\displaystyle \frac{{\int }_{\mathrm{a}}^{\mathrm{x}}{\left(\mathrm{x}-\mathrm{u}\right)}^{\mathsf{\beta }-1}{\underset{\_}{\mathrm{f}}}_2\left(\mathrm{u}\right)\mathrm{d}\mathrm{u}}{\mathsf{\Gamma }\left(\mathsf{\beta }\right)}},{\displaystyle \frac{{\int }_{\mathrm{a}}^{\mathrm{x}}{\left(\mathrm{x}-\mathrm{u}\right)}^{\mathsf{\beta }-1}{\overline{\mathrm{f}}}_2\left(\mathrm{u}\right)\mathrm{d}\mathrm{u}}{\mathsf{\Gamma }\left(\mathsf{\beta }\right)}}\right]\right] \\ =\left[\left[{\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left({\underset{\_}{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\beta }},{\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left({\overline{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\beta }}\right],\left[{\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left({\underset{\_}{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\beta }},{\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left({\overline{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\beta }}\right]\right], \end{gathered}$$

where ${RLFI\left(\phi \left(x\right)\right)}_a^{\beta }={\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{\beta -1}\phi \left(u\right)du}{\Gamma \left(\beta \right)}}$ is the Riemann–Liouville fractional integral of order $\beta >0$ of the crisp valued function $\phi$.

Lemma 2. 

Let $\mathcal{F}$ be a Lebesgue integrable T2IF defined on $[a,b]$. If $\mathcal{F}$ is positive and $\mathcal{W}$- increasing, then ${I2RLFI\left(\mathcal{F}\right)}_a^{\beta }$ and ${I2RLFI\left(\mathcal{F}\right)}_a^{1-\beta }$ are also $\mathcal{W}$-increasing functions on $[a,b]$.

Proof. 

Since $\mathcal{F}$ is positive and $\mathcal{W}$- increasing on $[a,b]$ then for $x>y$,

$$\mathcal{W}\left(\mathcal{F}\left(\mathrm{x}\right)\right){\succcurlyeq }_{in}\mathcal{W}\left(\mathcal{F}\left(\mathrm{y}\right)\right)$$

where

$$\mathcal{F}\left(x\right)=\left[\left[{\underset{\_}{\mathrm{f}}}_1\right(\mathrm{x}),{\overline{\mathrm{f}}}_1(\mathrm{x}\left)\right],\left[{\underset{\_}{\mathrm{f}}}_2\left(\mathrm{x}\right){,\overline{\mathrm{f}}}_2\right(\mathrm{x}\left)\right]\right], \mathrm{and} \mathcal{F}\left(y\right)=\left[\left[{\underset{\_}{\mathrm{f}}}_1\right(\mathrm{y}),{\overline{\mathrm{f}}}_1(\mathrm{y}\left)\right],\left[{\underset{\_}{\mathrm{f}}}_2\left(\mathrm{y}\right){,\overline{\mathrm{f}}}_2\right(\mathrm{y}\left)\right]\right]$$

Therefore, we have

$$\left\{\begin{array}{c}{\underset{\_}{\mathrm{f}}}_2\left(\mathrm{x}\right)-{\overline{\mathrm{f}}}_1\left(\mathrm{x}\right)\ge {\underset{\_}{\mathrm{f}}}_2\left(\mathrm{y}\right)-{\overline{\mathrm{f}}}_1\left(\mathrm{y}\right),\\ {\overline{\mathrm{f}}}_2\left(\mathrm{x}\right)-{\underset{\_}{\mathrm{f}}}_1\left(\mathrm{x}\right)\ge {\overline{\mathrm{f}}}_2\left(\mathrm{y}\right)-{\underset{\_}{\mathrm{f}}}_1\left(\mathrm{y}\right).\end{array}\right.$$

We write ${\underset{\_}{\mathrm{f}}}_2-{\overline{\mathrm{f}}}_1=\rho$ and ${\overline{\mathrm{f}}}_2-{\underset{\_}{\mathrm{f}}}_1=\mathsf{\sigma }$. Then, $\rho$ and $\mathsf{\sigma }$ are both real-valued positive and increasing functions.

Therefore, by Lemma 1 in [43], ${\int }_a^x{\left(x-u\right)}^{-\beta }\rho \left(u\right)du$ and ${\int }_a^x{\left(x-u\right)}^{-\beta }\mathsf{\sigma }\left(u\right)du$ are increasing functions on $\left[a,b\right]$. Consequently, ${RLFI\left(\rho \left(x\right)\right)}_a^{1-\beta }={\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{-\beta }\rho \left(u\right)du}{\mathsf{\Gamma }\left(1-\beta \right)}}$, and

$${RLFI\left(\mathsf{\sigma }\left(x\right)\right)}_a^{1-\beta }={\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{-\beta }\mathsf{\sigma }\left(u\right)du}{\mathsf{\Gamma }\left(1-\beta \right)}}$$

are increasing functions on $[a,b]$. That is,

$$\left\{\begin{array}{c}{RLFI\left(\rho \left(x\right)\right)}_a^{1-\beta }\ge {RLFI\left(\rho \left(y\right)\right)}_a^{1-\beta },\\ {RLFI\left(\mathsf{\sigma }\left(x\right)\right)}_a^{1-\beta }\ge {RLFI\left(\mathsf{\sigma }\left(y\right)\right)}_a^{1-\beta }.\end{array}\right.$$

which is equivalent to the following inequalities:

$$\left\{\begin{array}{c}{RLFI\left({\underset{\_}{\mathrm{f}}}_2\left(x\right)\right)}_a^{1-\beta }-{RLFI\left({\overline{\mathrm{f}}}_1\left(x\right)\right)}_a^{1-\beta }\ge {RLFI\left({\underset{\_}{\mathrm{f}}}_2\left(y\right)\right)}_a^{1-\beta }-{RLFI\left({\overline{\mathrm{f}}}_1\left(y\right)\right)}_a^{1-\beta },\\ {RLFI\left({\overline{\mathrm{f}}}_2\left(x\right)\right)}_a^{1-\beta }-{RLFI\left({\underset{\_}{\mathrm{f}}}_1\left(x\right)\right)}_a^{1-\beta }\ge {RLFI\left({\overline{\mathrm{f}}}_2\left(y\right)\right)}_a^{1-\beta }-{RLFI\left({\underset{\_}{\mathrm{f}}}_1\left(y\right)\right)}_a^{1-\beta }.\end{array}\right.$$

Therefore, ${I2RLFI\left(\mathcal{F}\right)}_a^{1-\beta }$ is a $\mathcal{W}$-increasing function on $[a,b]$. Since $0<\beta <1$, then $0<1-\beta <1$, and thus, ${I2RLFI\left(\mathcal{F}\right)}_a^{\beta }$ is also a $\mathcal{W}$-increasing function on $[a,b]$. □

Example 1. 

Suppose a function $\mathcal{F}\left(x\right)=\left[\left[x,2x\right],\left[4x,5x\right]\right]$. Then, the interval width of the function is $\mathcal{W}\left(\mathcal{F} \left(x\right)\right)=\left[2x, 4x\right]$, and thus, $\mathcal{F}$ is $\mathcal{W}$-increasing and positive on $[0,1]$. The Type 2 interval-valued Riemann–Liouville integral of order $1-\beta$ is obtained as follows:

$$\begin{gathered} {I2RLFI\left(\mathcal{F}\right(x\left)\right)}_0^{1-\beta }={\displaystyle \frac{{\int }_0^x{\left(x-u\right)}^{-\beta }\mathcal{F}\left(u\right)du}{\mathsf{\Gamma }\left(1-\beta \right)}} \\ =\left[\left[1,2\right],\left[4,5\right]\right]{\displaystyle \frac{{\int }_0^x{\left(x-u\right)}^{-\beta }udu}{\mathsf{\Gamma }\left(1-\beta \right)}} \\ ={\displaystyle \frac{\left[\left[\mathrm{1,2}\right],\left[\mathrm{4,5}\right]\right]x^{2-\beta }}{\left(1-\beta \right)\left(2-\beta \right)\mathsf{\Gamma }\left(1-\beta \right)}} \end{gathered}$$

The interval width of ${I2RLFI\left(\mathcal{F}\left(x\right)\right)}_0^{1-\beta }$ is

$$\mathcal{W}\left({I2RLFI\left(\mathcal{F}\left(x\right)\right)}_0^{1-\beta }\right)=\left[{\displaystyle \frac{2x^{2-\beta }}{\left(1-\beta \right)\left(2-\beta \right)\mathsf{\Gamma }\left(1-\beta \right)}},{\displaystyle \frac{4x^{2-\beta }}{\left(1-\beta \right)\left(2-\beta \right)\mathsf{\Gamma }\left(1-\beta \right)}}\right]$$

Therefore, ${\mathrm{I}2\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left(\mathcal{F}\left(\mathrm{x}\right)\right)}_0^{1-\mathsf{\beta }}$ is $\mathcal{W}$-increasing on $[0,1]$. The Type 2 interval-valued function, its $\mathcal{W}$-increasing nature, Type 2 interval-valued Riemann–Liouville integral of order $(1-\mathsf{\beta })$ of the function, and $\mathcal{W}$-increasing property of that fractional integral are depicted in Figure 1, Figure 2, Figure 3, and Figure 4, respectively.

In Figure 2, $\beta =0.5$, and $a=0$. The plotting in Figure 2 depicts the fact that $\mathcal{F}\left(x\right)$ is $\mathcal{W}$-increasing on $\left[\mathrm{0,1}\right]$.

In Figure 3, $\beta =0.5$ and $a=0$. The plotting in Figure 3 depicts the fact that ${I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{1-\beta }$ is $\mathcal{W}$-increasing on $[0, 1]$.

In Figure 4, blue, blue-dashed, red-dashed, and red colored curves represent ${RLFI\left({\underset{\_}{\mathrm{f}}}_1\left(x\right)\right)}_a^{1-\beta }$, ${RLFI\left({\overline{\mathrm{f}}}_1\left(x\right)\right)}_a^{1-\beta }$, ${RLFI\left({\underset{\_}{\mathrm{f}}}_2\left(x\right)\right)}_a^{1-\beta }$, and ${RLFI\left({\overline{\mathrm{f}}}_2\left(x\right)\right)}_a^{1-\beta }$, respectively. Here, $\beta =0.5$ and $a=0$. Each of the curves is monotone, increasing on $[0,1]$.

Remark 3. 

Suppose a function $\mathcal{F}\left(x\right)=[\left[(1-x),2(1-x)\right],[4(1-x),5(1-x)\left]\right]$. Then, the interval width of the function is $\mathcal{W}\left(\mathcal{F} \left(x\right)\right)=[2\left(1-x\right), 4(1-x\left)\right]$, and thus, $\mathcal{F}$ is $\mathcal{W}$-decreasing and positive on $[0,1]$. The Type 2 interval-valued Riemann–Liouville integral of order $1-\beta$ is obtained as follows:

$$\begin{gathered} {I2RLFI\left(\mathcal{F}\right(x\left)\right)}_0^{1-\beta }={\displaystyle \frac{{\int }_0^x{\left(x-u\right)}^{-\beta }\mathcal{F}\left(u\right)du}{\mathsf{\Gamma }\left(1-\beta \right)}} \\ =\left[\left[1,2\right],\left[4,5\right]\right]{\displaystyle \frac{{\int }_0^x{\left(x-u\right)}^{-\beta }\left(1-u\right)du}{\mathsf{\Gamma }\left(1-\beta \right)}} \\ ={\displaystyle \frac{\left[\left[1,2\right],\left[4,5\right]\right]x^{1-\beta }}{\left(1-\beta \right)\mathsf{\Gamma }\left(1-\beta \right)}}\left(1-{\displaystyle \frac{x}{2-\beta }}\right) \end{gathered}$$

The interval width of ${I2RLFI\left(\mathcal{F}\left(x\right)\right)}_0^{1-\beta }$ is

$$\mathcal{W}\left({I2RLFI\left(\mathcal{F}\left(x\right)\right)}_0^{1-\beta }\right)=\left[{\displaystyle \frac{2x^{1-\beta }}{\left(1-\beta \right)\mathsf{\Gamma }\left(1-\beta \right)}}\left(1-{\displaystyle \frac{x}{2-\beta }}\right),{\displaystyle \frac{4x^{1-\beta }}{\left(1-\beta \right)\mathsf{\Gamma }\left(1-\beta \right)}}\left(1-{\displaystyle \frac{x}{2-\beta }}\right)\right]$$

Therefore, ${I2RLFI\left(\mathcal{F}\left(x\right)\right)}_0^{1-\beta }$ is $\mathcal{W}$-increasing on $[0,1-\beta ]$ and $\mathcal{W}$-decreasing on $[1-\beta ,1]$. The Type 2 interval-valued function, its $\mathcal{W}$-decreasing nature, Type 2 interval-valued Riemann–Liouville integral of order $(1-\beta )$ of the function, and $\mathcal{W}$-increasing/decreasing property of that fractional integral are depicted in Figure 5, Figure 6, Figure 7 and Figure 8, respectively.

In Figure 6, $\beta =0.5$ and $a=0$. The plotting in Figure 6 depicts the fact that $\mathcal{F}\left(x\right)$ is $\mathcal{W}$-decreasing on $[0,1]$.

In Figure 7, $\beta =0.5$, and $a=0$. The plotting in Figure 7 depicts the fact that ${I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{1-\beta }$ is $\mathcal{W}$-increasing on $[0.1-0.5]$ and $\mathcal{W}$-decreasing on $[1-0.5,1]$.

In Figure 8, blue, blue-dashed, red-dashed, and red-colored curves represent ${RLFI\left({\underset{\_}{\mathrm{f}}}_1\left(x\right)\right)}_a^{1-\beta }$, ${RLFI\left({\overline{\mathrm{f}}}_1\left(x\right)\right)}_a^{1-\beta }$, ${RLFI\left({\underset{\_}{\mathrm{f}}}_2\left(x\right)\right)}_a^{1-\beta }$, and ${RLFI\left({\overline{\mathrm{f}}}_2\left(x\right)\right)}_a^{1-\beta }$, respectively. Here, $\beta =0.5$ and $a=0$. Each of the curves is monotone increasing on $[0.1-0.5]$ and monotone decreasing on $[1-\mathrm{0.5,1}]$.

Lemma 3. 

${I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{{\beta }_1}$ and ${I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{{\beta }_2}$ represent Type 2 interval-valued Riemann–Liouville fractional integrals of $\mathcal{F}\left(x\right)$ of order ${\beta }_1$ and ${\beta }_2$, respectively, where $0<{\beta }_1,{\beta }_2<1$ are real fractions. Then, ${I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{{\beta }_1+{\beta }_2}={I2RLFI\left({I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{{\beta }_2}\right)}_a^{{\beta }_1}$.

Proof. 

By Definition 6,

$$\begin{gathered} {I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{{\beta }_1+{\beta }_2}=\left[\left[{RLFI\left({\underset{\_}{f}}_1\left(x\right)\right)}_a^{{\beta }_1+{\beta }_2},{RLFI\left({\overline{f}}_1\left(x\right)\right)}_a^{{\beta }_1+{\beta }_2}\right],\left[{RLFI\left({\underset{\_}{f}}_2\left(x\right)\right)}_a^{{\beta }_1+{\beta }_2}, {RLFI\left({\overline{f}}_2\left(x\right)\right)}_a^{{\beta }_1+{\beta }_2}\right]\right] \\ \left[\left[{RLFI\left({RLFI\left({\underset{\_}{f}}_1\left(x\right)\right)}_a^{{\beta }_2}\right)}_a^{{\beta }_1},{RLFI\left({RLFI\left({\overline{f}}_1\left(x\right)\right)}_a^{{\beta }_2}\right)}_a^{{\beta }_1}\right],\left[{RLFI\left({RLFI\left({\underset{\_}{f}}_2\left(x\right)\right)}_a^{{\beta }_2}\right)}_a^{{\beta }_1}, {RLFI\left({RLFI\left({\overline{f}}_2\left(x\right)\right)}_a^{{\beta }_2}\right)}_a^{{\beta }_1}\right]\right] \end{gathered}$$

(1)

almost everywhere on $[a,b]$, provided ${\beta }_1+{\beta }_2<1$, (see Lemma 2.3, page no. 73 in Kilbas et al. [79]).

$$={I2RLFI\left({I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{{\beta }_2}\right)}_a^{{\beta }_1}$$

In case of ${\beta }_1+{\beta }_2>1$, the result is true for all points on $[a,b]$. □

Lemma 4. 

Let ${I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{\beta }$ and ${I2RLFI\left(\mathcal{G}\left(x\right)\right)}_a^{\beta }$ be Type 2 interval-valued Riemann–Liouville fractional integrals of order $\beta$ for the function $\mathcal{F}\left(x\right)$ and $\mathcal{G}\left(x\right)$, respectively. Then,

$${I2RLFI(\mathcal{F}\left(x\right)⊞\mathcal{G}\left(x\right))}_a^{\beta }={I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{\beta }⊞{I2RLFI\left(\mathcal{G}\left(x\right)\right)}_a^{\beta }$$

Proof. 

The proof is straightforward. Therefore, we omit the proof. □

Lemma 5. 

$\mathcal{W}\left({I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{\beta }\right)={I1RLFI\left(\mathcal{W}\left(\mathcal{F}\left(x\right)\right)\right)}_a^{\beta }$, where ${I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{\beta }$ is a Type 2 interval-valued Riemann–Liouville fractional integral of order $\beta$ for the function $\mathcal{F}\left(x\right)$. ${I1RLFI\left(\mathcal{W}\left(\mathcal{F}\left(x\right)\right)\right)}_a^{\beta }$ is an interval-valued Riemann–Liouville fractional integral of order $\beta$ for the function $\mathcal{W}\left(\mathcal{F}\left(x\right)\right)$.

Proof. 

We have:

$${I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{\beta }=\left[\left[{RLFI\left({\underset{\_}{f}}_1\left(x\right)\right)}_a^{\beta },{RLFI\left({\overline{f}}_1\left(x\right)\right)}_a^{\beta }\right],\left[{RLFI\left({\underset{\_}{f}}_2\left(x\right)\right)}_a^{\beta }, {RLFI\left({\overline{f}}_2\left(x\right)\right)}_a^{\beta }\right]\right]$$

Then,

$$\begin{gathered} \mathcal{W}\left({I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{\beta }\right) \\ =\left[{RLFI\left({\overline{f}}_2\left(x\right)\right)}_a^{\beta }-{RLFI\left({\underset{\_}{f}}_1\left(x\right)\right)}_a^{\beta }, {RLFI\left({\underset{\_}{f}}_2\left(x\right)\right)}_a^{\beta }-{RLFI\left({\overline{f}}_1\left(x\right)\right)}_a^{\beta }\right] \\ =\left[{RLFI\left({\overline{f}}_2\left(x\right)-{\underset{\_}{f}}_1\left(x\right)\right)}_a^{\beta }, {RLFI\left({\underset{\_}{f}}_2\left(x\right)-{\overline{f}}_1\left(x\right)\right)}_a^{\beta }\right] \\ ={I1RLFI\left(\left[{\overline{f}}_2\left(x\right)-{\underset{\_}{f}}_1\left(x\right),{\underset{\_}{f}}_2\left(x\right)-{\overline{f}}_1\left(x\right)\right]\right)}_a^{\beta } \\ ={I1RLFI\left(\mathcal{W}\left(\mathcal{F}\left(x\right)\right)\right)}_a^{\beta }. \end{gathered}$$

□

Theorem 1. 

Let $\mathcal{F}$ and $\mathcal{G}$ be a Lebesgue integrable T2IF defined on $[a,b]$ and $\beta >0$. Then, $\mathcal{W}({I2RLFI\left(\mathcal{F}\left(x\right){\boxminus }_g\mathcal{G}\left(x\right)\right)}_a^{\beta }{\succcurlyeq }_{in}\mathcal{W}\left({I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{\beta }{\boxminus }_g{I2RLFI\left(\mathcal{G}\left(x\right)\right)}_a^{\beta }\right)$, for all $x\in [a,b]$. Furthermore, ${I2RLFI\left(\mathcal{F}\left(x\right){\boxminus }_g\mathcal{G}\left(x\right)\right)}_a^{\beta }={I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{\beta }{\boxminus }_g{I2RLFI\left(\mathcal{G}\left(x\right)\right)}_a^{\beta }$ when either $\mathcal{W}\left(\mathcal{F}\left(x\right)\right){\succcurlyeq }_{in}\mathcal{W}\left(\mathcal{G}\left(x\right)\right)$, for all $x\in [a,b]$ or $\mathcal{W}\left(\mathcal{G}\left(x\right)\right){\succcurlyeq }_{in}\mathcal{W}\left(\mathcal{F}\left(x\right)\right)$, for all $x\in [a,b]$.

Proof. 

Let $\mathcal{F}\left(\mathrm{x}\right)=\left[\left[{\underset{\_}{\mathrm{f}}}_1\right(\mathrm{x}),{\overline{\mathrm{f}}}_1(\mathrm{x}\left)\right],\left[{\underset{\_}{\mathrm{f}}}_2\left(\mathrm{x}\right){,\overline{\mathrm{f}}}_2\right(\mathrm{x}\left)\right]\right]$ and $\mathcal{G}\left(\mathrm{x}\right)=\left[\left[{\underset{\_}{\mathrm{g}}}_1\right(\mathrm{x}),{\overline{\mathrm{g}}}_1(\mathrm{x}\left)\right],\left[{\underset{\_}{\mathrm{g}}}_2\left(\mathrm{x}\right){,\overline{\mathrm{g}}}_2\right(\mathrm{x}\left)\right]\right]$. We consider the following:

$$\left\{\begin{array}{c}\begin{array}{c}{\underset{\_}{\mathsf{\tau }}}_1\left(\mathrm{x}\right)={\underset{\_}{\mathrm{f}}}_1\left(\mathrm{x}\right)-{\underset{\_}{\mathrm{g}}}_1\left(\mathrm{x}\right),\\ {\overline{\tau }}_1\left(\mathrm{x}\right)={\overline{\mathrm{f}}}_1\left(\mathrm{x}\right)-{\overline{\mathrm{g}}}_1\left(\mathrm{x}\right),\end{array}\\ \begin{array}{c}{\underset{\_}{\mathsf{\tau }}}_2\left(\mathrm{x}\right)={\underset{\_}{\mathrm{f}}}_2\left(\mathrm{x}\right)-{\underset{\_}{\mathrm{g}}}_2\left(\mathrm{x}\right),\\ {\overline{\mathsf{\tau }}}_2\left(\mathrm{x}\right)={\overline{\mathrm{f}}}_2\left(\mathrm{x}\right)-{\overline{\mathrm{g}}}_2\left(\mathrm{x}\right).\end{array}\end{array}\right.$$

Then, we have:

$$\begin{gathered} {\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{\beta -1}\min \left\{{\overline{\mathsf{\tau }}}_2\left(\mathrm{u}\right),{\underset{\_}{\mathsf{\tau }}}_1\left(\mathrm{u}\right)\right\}du}{\mathsf{\Gamma }\left(\beta \right)}} \\ \le \min \left\{{\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{\beta -1}{\underset{\_}{\mathsf{\tau }}}_1\left(\mathrm{u}\right)du}{\mathsf{\Gamma }\left(\beta \right)}},{\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{\beta -1}{\overline{\mathsf{\tau }}}_2\left(\mathrm{u}\right)du}{\mathsf{\Gamma }\left(\beta \right)}}\right\} \\ \le \max \left\{{\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{\beta -1}{\underset{\_}{\mathsf{\tau }}}_1\left(\mathrm{u}\right)du}{\mathsf{\Gamma }\left(\beta \right)}},{\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{\beta -1}{\overline{\mathsf{\tau }}}_2\left(\mathrm{u}\right)du}{\mathsf{\Gamma }\left(\beta \right)}}\right\} \\ \le {\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{\beta -1}\max \left\{{\overline{\mathsf{\tau }}}_2\left(\mathrm{u}\right),{\underset{\_}{\mathsf{\tau }}}_1\left(\mathrm{u}\right)\right\}du}{\mathsf{\Gamma }\left(\beta \right)}} \end{gathered}$$

That is,

$$\begin{gathered} \max \left\{{\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{\beta -1}{\underset{\_}{\mathsf{\tau }}}_1\left(\mathrm{u}\right)du}{\mathsf{\Gamma }\left(\beta \right)}},{\displaystyle \frac{\underset{a}{\overset{x}{\int }}{\left(x-u\right)}^{\beta -1}{\overline{\mathsf{\tau }}}_2\left(\mathrm{u}\right)du}{\mathsf{\Gamma }\left(\beta \right)}}\right\}-\min \left\{{\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{\beta -1}{\underset{\_}{\mathsf{\tau }}}_1\left(\mathrm{u}\right)du}{\mathsf{\Gamma }\left(\beta \right)}},{\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{\beta -1}{\overline{\mathsf{\tau }}}_2\left(\mathrm{u}\right)du}{\mathsf{\Gamma }\left(\beta \right)}}\right\} \\ \le {\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{\beta -1}\max \left\{{\overline{\mathsf{\tau }}}_2\left(\mathrm{u}\right),{\underset{\_}{\mathsf{\tau }}}_1\left(\mathrm{u}\right)\right\}du}{\mathsf{\Gamma }\left(\beta \right)}}-{\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{\beta -1}\min \left\{{\overline{\mathsf{\tau }}}_2\left(\mathrm{u}\right),{\underset{\_}{\mathsf{\tau }}}_1\left(\mathrm{u}\right)\right\}du}{\mathsf{\Gamma }\left(\beta \right)}} \end{gathered}$$

Similarly,

$$\begin{gathered} \max \left\{{\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{\beta -1}{\underset{\_}{\mathsf{\tau }}}_2\left(\mathrm{u}\right)du}{\mathsf{\Gamma }\left(\beta \right)}},{\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{\beta -1}{\overline{\mathsf{\tau }}}_1\left(\mathrm{u}\right)du}{\mathsf{\Gamma }\left(\beta \right)}}\right\}-\min \left\{{\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{\beta -1}{\underset{\_}{\mathsf{\tau }}}_2\left(\mathrm{u}\right)du}{\mathsf{\Gamma }\left(\beta \right)}},{\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{\beta -1}{\overline{\mathsf{\tau }}}_1\left(\mathrm{u}\right)du}{\mathsf{\Gamma }\left(\beta \right)}}\right\} \\ \le {\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{\beta -1}\max \left\{{\overline{\mathsf{\tau }}}_1\left(\mathrm{u}\right),{\underset{\_}{\mathsf{\tau }}}_2\left(\mathrm{u}\right)\right\}du}{\mathsf{\Gamma }\left(\beta \right)}}-{\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{\beta -1}\min \left\{{\overline{\mathsf{\tau }}}_1\left(\mathrm{u}\right),{\underset{\_}{\mathsf{\tau }}}_2\left(\mathrm{u}\right)\right\}du}{\mathsf{\Gamma }\left(\beta \right)}} \end{gathered}$$

In standard notation, the inequalities can be written as follows.

$$\begin{gathered} \max \left\{{RLFI\left({\underset{\_}{\mathsf{\tau }}}_1\left(x\right)\right)}_a^{\beta },{RLFI\left({\overline{\mathsf{\tau }}}_2\left(x\right)\right)}_a^{\beta }\right\}-\min \left\{{RLFI\left({\underset{\_}{\mathsf{\tau }}}_1\left(x\right)\right)}_a^{\beta }, {RLFI\left({\overline{\mathsf{\tau }}}_2\left(x\right)\right)}_a^{\beta }\right\} \\ \le {RLFI\left(\max \left\{{\overline{\mathsf{\tau }}}_2\left(\mathrm{x}\right),{\underset{\_}{\mathsf{\tau }}}_1\left(\mathrm{x}\right)\right\}\right)}_a^{\beta }-{RLFI\left(\min \left\{{\overline{\mathsf{\tau }}}_2\left(\mathrm{x}\right),{\underset{\_}{\mathsf{\tau }}}_1\left(\mathrm{x}\right)\right\}\right)}_a^{\beta } \end{gathered}$$

and

$$\begin{gathered} \max \left\{{RLFI\left({\underset{\_}{\mathsf{\tau }}}_2\left(x\right)\right)}_a^{\beta },{RLFI\left({\overline{\mathsf{\tau }}}_1\left(x\right)\right)}_a^{\beta }\right\}-\min \left\{{RLFI\left({\underset{\_}{\mathsf{\tau }}}_2\left(x\right)\right)}_a^{\beta },{RLFI\left({\overline{\mathsf{\tau }}}_1\left(x\right)\right)}_a^{\beta }\right\} \\ \le {RLFI\left(\max \left\{{\overline{\mathsf{\tau }}}_1\left(\mathrm{x}\right),{\underset{\_}{\mathsf{\tau }}}_2\left(\mathrm{x}\right)\right\}\right)}_a^{\beta }-{RLFI\left(\min \left\{{\overline{\mathsf{\tau }}}_1\left(\mathrm{x}\right),{\underset{\_}{\mathsf{\tau }}}_2\left(\mathrm{x}\right)\right\}\right)}_a^{\beta } \\ \mathcal{W}\left(\left[\left[{RLFI\left(\min \left\{{\overline{\mathsf{\tau }}}_2\left(\mathrm{x}\right),{\underset{\_}{\mathsf{\tau }}}_1\left(\mathrm{x}\right)\right\}\right)}_a^{\beta },{RLFI\left(\min \left\{{\overline{\mathsf{\tau }}}_1\left(\mathrm{x}\right),{\underset{\_}{\mathsf{\tau }}}_2\left(\mathrm{x}\right)\right\}\right)}_a^{\beta }\right],\left[{RLFI\left(\max \left\{{\overline{\mathsf{\tau }}}_1\left(\mathrm{x}\right),{\underset{\_}{\mathsf{\tau }}}_2\left(\mathrm{x}\right)\right\}\right)}_a^{\beta },{RLFI\left(\max \left\{{\overline{\mathsf{\tau }}}_2\left(\mathrm{x}\right),{\underset{\_}{\mathsf{\tau }}}_1\left(\mathrm{x}\right)\right\}\right)}_a^{\beta }\right]\right]\right) \\ {\succcurlyeq }_{in}\mathcal{W}\left(\begin{array}{c}[\left[\min \left\{{RLFI\left({\underset{\_}{\mathsf{\tau }}}_1\left(x\right)\right)}_a^{\beta },{RLFI\left({\overline{\mathsf{\tau }}}_2\left(x\right)\right)}_a^{\beta }\right\},\min \left\{{RLFI\left({\underset{\_}{\mathsf{\tau }}}_2\left(x\right)\right)}_a^{\beta },{RLFI\left({\overline{\mathsf{\tau }}}_1\left(x\right)\right)}_a^{\beta }\right\}\right],\\ \left[\max \left\{{RLFI\left({\underset{\_}{\mathsf{\tau }}}_2\left(x\right)\right)}_a^{\beta },{RLFI\left({\overline{\mathsf{\tau }}}_1\left(x\right)\right)}_a^{\beta }\right\} ,\max \left\{{RLFI\left({\underset{\_}{\mathsf{\tau }}}_1\left(x\right)\right)}_a^{\beta },{RLFI\left({\overline{\mathsf{\tau }}}_2\left(x\right)\right)}_a^{\beta }\right\}\right]] \end{array}\right) \end{gathered}$$

This implies that

$$\begin{gathered} \mathcal{W}\left({I2RLFI\left(\left[\left[\min \left\{{\overline{\mathsf{\tau }}}_2\left(\mathrm{x}\right),{\underset{\_}{\mathsf{\tau }}}_1\left(\mathrm{x}\right)\right\},\min \left\{{\overline{\mathsf{\tau }}}_1\left(\mathrm{x}\right),{\underset{\_}{\mathsf{\tau }}}_2\left(\mathrm{x}\right)\right\}\right],\left[\max \left\{{\overline{\mathsf{\tau }}}_1\left(\mathrm{x}\right),{\underset{\_}{\mathsf{\tau }}}_2\left(\mathrm{x}\right)\right\}\right],\max \left\{{\overline{\mathsf{\tau }}}_2\left(\mathrm{x}\right),{\underset{\_}{\mathsf{\tau }}}_1\left(\mathrm{x}\right)\right\}\right]\right)}_a^{\beta }\right) \\ {\succcurlyeq }_{in}\mathcal{W}\left({I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{\beta }{\boxminus }_g{I2RLFI\left(\mathcal{G}\left(x\right)\right)}_a^{\beta }\right) \end{gathered}$$

That is

$$\mathcal{W}\left({I2RLFI\left(\mathcal{F}\left(x\right){\boxminus }_g\mathcal{G}\left(x\right)\right)}_a^{\beta }\right){\succcurlyeq }_{in}\mathcal{W}\left({I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{\beta }{\boxminus }_g{I2RLFI\left(\mathcal{G}\left(x\right)\right)}_a^{\beta }\right)$$

Suppose $\mathcal{W}\left(\mathcal{F}\left(x\right)\right){\succcurlyeq }_{in}\mathcal{W}\left(\mathcal{G}\left(x\right)\right)$ for all $x\in [a,b]$. Then,

$$\begin{gathered} \mathcal{F}\left(x\right){\boxminus }_g\mathcal{G}\left(x\right) \\ =\left[\left[\min \left\{{\overline{\mathsf{\tau }}}_2\left(\mathrm{x}\right),{\underset{\_}{\mathsf{\tau }}}_1\left(\mathrm{x}\right)\right\},\min \left\{{\overline{\mathsf{\tau }}}_1\left(\mathrm{x}\right),{\underset{\_}{\mathsf{\tau }}}_2\left(\mathrm{x}\right)\right\}\right],\left[\max \left\{{\overline{\mathsf{\tau }}}_1\left(\mathrm{x}\right),{\underset{\_}{\mathsf{\tau }}}_2\left(\mathrm{x}\right)\right\},\max \left\{{\overline{\mathsf{\tau }}}_2\left(\mathrm{x}\right),{\underset{\_}{\mathsf{\tau }}}_1\left(\mathrm{x}\right)\right\}\right]\right] \\ =\left[\left[{\underset{\_}{\mathsf{\tau }}}_1\left(\mathrm{x}\right),{\overline{\mathsf{\tau }}}_1\left(\mathrm{x}\right)\right],\left[{\underset{\_}{\mathsf{\tau }}}_2\left(\mathrm{x}\right),{\overline{\mathsf{\tau }}}_2\left(\mathrm{x}\right)\right]\right] \end{gathered}$$

Therefore,

$$\begin{gathered} {I2RLFI\left(\mathcal{F}\left(x\right){\boxminus }_g\mathcal{G}\left(x\right)\right)}_a^{\beta }={I2RLFI\left(\left[\left[{\underset{\_}{\mathsf{\tau }}}_1\left(\mathrm{x}\right),{\overline{\mathsf{\tau }}}_1\left(\mathrm{x}\right)\right],\left[{\underset{\_}{\mathsf{\tau }}}_2\left(\mathrm{x}\right),{\overline{\mathsf{\tau }}}_2\left(\mathrm{x}\right)\right]\right]\right)}_a^{\beta } \\ =\left[\left[{RLFI\left({\underset{\_}{\mathsf{\tau }}}_1\left(\mathrm{x}\right)\right)}_a^{\beta },{RLFI\left({\overline{\mathsf{\tau }}}_1\left(\mathrm{x}\right)\right)}_a^{\beta }\right],\left[{RLFI\left({\underset{\_}{\mathsf{\tau }}}_2\left(\mathrm{x}\right)\right)}_a^{\beta },{RLFI\left({\overline{\mathsf{\tau }}}_2\left(\mathrm{x}\right)\right)}_a^{\beta }\right]\right] \\ =\left[\begin{array}{c}\left[{RLFI\left({\underset{\_}{\mathrm{f}}}_1\left(\mathrm{x}\right)-{\underset{\_}{\mathrm{g}}}_1\left(\mathrm{x}\right)\right)}_a^{\beta },{RLFI\left({\overline{\mathrm{f}}}_1\left(\mathrm{x}\right)-{\overline{\mathrm{g}}}_1\left(\mathrm{x}\right)\right)}_a^{\beta }\right],\\ \left[{RLFI\left({\underset{\_}{\mathrm{f}}}_2\left(\mathrm{x}\right)-{\underset{\_}{\mathrm{g}}}_2\left(\mathrm{x}\right)\right)}_a^{\beta },{RLFI\left({\overline{\mathrm{f}}}_2\left(\mathrm{x}\right)-{\overline{\mathrm{g}}}_2\left(\mathrm{x}\right)\right)}_a^{\beta }\right]\end{array}\right] \end{gathered}$$

Since $0<{\underset{\_}{\mathsf{\tau }}}_1\left(x\right)\le {\overline{\mathsf{\tau }}}_1\left(\mathrm{x}\right)\le {\underset{\_}{\mathsf{\tau }}}_2\left(\mathrm{x}\right)\le {\overline{\mathsf{\tau }}}_2\left(\mathrm{x}\right)$ are all real functions on $[a,b]$, the consequence is that $0\le {RLFI\left({\underset{\_}{\mathsf{\tau }}}_1\left(x\right)\right)}_a^{\beta }\le RLFI\left({\overline{\mathsf{\tau }}}_1\left(x\right)\right)\le {RLFI\left({\underset{\_}{\mathsf{\tau }}}_2\left(x\right)\right)}_a^{\beta }\le {RLFI\left({\overline{\mathsf{\tau }}}_2\left(x\right)\right)}_a^{\beta }$, and then

$$\begin{gathered} {I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{\beta }{\boxminus }_g{I2RLFI\left(\mathcal{G}\left(x\right)\right)}_a^{\beta } \\ =\left[\begin{array}{c}\left[\min \left\{{RLFI\left({\underset{\_}{\mathsf{\tau }}}_1\left(x\right)\right)}_a^{\beta },{RLFI\left({\overline{\mathsf{\tau }}}_2\left(x\right)\right)}_a^{\beta }\right\},\min \left\{{RLFI\left({\underset{\_}{\mathsf{\tau }}}_2\left(x\right)\right)}_a^{\beta },{RLFI\left({\overline{\mathsf{\tau }}}_1\left(x\right)\right)}_a^{\beta }\right\}\right],\\ \left[\max \left\{{RLFI\left({\underset{\_}{\mathsf{\tau }}}_2\left(x\right)\right)}_a^{\beta },{RLFI\left({\overline{\mathsf{\tau }}}_1\left(x\right)\right)}_a^{\beta }\right\},\max \left\{{RLFI\left({\underset{\_}{\mathsf{\tau }}}_1\left(x\right)\right)}_a^{\beta },{RLFI\left({\overline{\mathsf{\tau }}}_2\left(x\right)\right)}_a^{\beta }\right\}\right]\end{array}\right] \\ =\left[\left[{RLFI\left({\underset{\_}{\mathsf{\tau }}}_1\left(\mathrm{x}\right)\right)}_a^{\beta },{RLFI\left({\overline{\mathsf{\tau }}}_1\left(\mathrm{x}\right)\right)}_a^{\beta }\right],\left[{RLFI\left({\underset{\_}{\mathsf{\tau }}}_2\left(\mathrm{x}\right)\right)}_a^{\beta },{RLFI\left({\overline{\mathsf{\tau }}}_2\left(\mathrm{x}\right)\right)}_a^{\beta }\right]\right] \\ =\left[\begin{array}{c}\left[{RLFI\left({\underset{\_}{\mathrm{f}}}_1\left(\mathrm{x}\right)-{\underset{\_}{\mathrm{g}}}_1\left(\mathrm{x}\right)\right)}_a^{\beta },{RLFI\left({\overline{\mathrm{f}}}_1\left(\mathrm{x}\right)-{\overline{\mathrm{g}}}_1\left(\mathrm{x}\right)\right)}_a^{\beta }\right],\\ \left[{RLFI\left({\underset{\_}{\mathrm{f}}}_2\left(\mathrm{x}\right)-{\underset{\_}{\mathrm{g}}}_2\left(\mathrm{x}\right)\right)}_a^{\beta },{RLFI\left({\overline{\mathrm{f}}}_2\left(\mathrm{x}\right)-{\overline{\mathrm{g}}}_2\left(\mathrm{x}\right)\right)}_a^{\beta }\right]\end{array}\right]. \end{gathered}$$

Therefore, ${I2RLFI\left(\mathcal{F}\left(x\right){\boxminus }_g\mathcal{G}\left(x\right)\right)}_a^{\beta }={I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{\beta }{\boxminus }_g{I2RLFI\left(\mathcal{G}\left(x\right)\right)}_a^{\beta }$ for all $\mathcal{W}\left(\mathcal{F}\left(x\right)\right){\succcurlyeq }_{in}\mathcal{W}\left(\mathcal{G}\left(x\right)\right)$ □

4. R-L Fractional Derivative of Type 2 Interval-Valued Functions

Definition 7. 

Let $\mathcal{F}$ be a T2IF defined on $[a,b]$ and let $\mathcal{F}$ be absolutely continuous on $[a,b]$. Then, each of the four components describing $\mathcal{F}$ is a Lebesgue integrable real-valued function defined on $[a,b]$. Consequently,

$${\left(x-u\right)}^{-\alpha }\mathcal{F}\left(u\right)=\left[\left[{\left(x-u\right)}^{-\alpha }{\underset{\_}{f}}_1\left(u\right), {\left(x-u\right)}^{-\alpha }{\overline{f}}_1\left(u\right)\right],\left[{\left(x-u\right)}^{-\alpha }{\underset{\_}{f}}_2\left(u\right), {\left(x-u\right)}^{-\alpha }{\overline{f}}_2\left(u\right)\right]\right]$$

is a Lebesgue integrable T2IF defined on $[a,b]$. This implies the existence of the following Type 2 interval-valued Riemann–Liouville fractional integral of order $(1-\alpha )$.

$${\mathrm{I}2\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left(\mathcal{F}\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{1-\mathsf{\alpha }}={\displaystyle \frac{{\int }_{\mathrm{a}}^{\mathrm{x}}{\left(\mathrm{x}-\mathrm{u}\right)}^{-\mathsf{\alpha }}\mathcal{F}\left(\mathrm{u}\right)\mathrm{d}\mathrm{u}}{\mathsf{\Gamma }(1-\mathsf{\alpha })}}, \mathrm{for} \mathrm{all} \mathrm{x}\in [\mathrm{a},\mathrm{b}]$$

If the T2IF ${\mathrm{I}2\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left(\mathcal{F}\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{1-\mathsf{\alpha }}$ is generalized Hukuhara differentiable, then its generalized Hukuhara derivative ${\displaystyle \frac{\mathrm{d}\left({\mathrm{I}2\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left(\mathcal{F}\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{1-\mathsf{\alpha }}\right)}{\mathrm{d}\mathrm{x}}}$ is called the Type 2 interval-valued Riemann–Liouville gH fractional derivative of order $\mathsf{\alpha }>0$, and it is denoted as ${\mathrm{I}2\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{D}\left(\mathcal{F}\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}$. Therefore,

$${\mathrm{I}2\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{D}\left(\mathcal{F}\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}={\displaystyle \frac{1}{\mathsf{\Gamma }(1-\mathsf{\alpha })}}{\displaystyle \frac{\mathrm{d}\left({\int }_{\mathrm{a}}^{\mathrm{x}}{\left(\mathrm{x}-\mathrm{u}\right)}^{-\mathsf{\alpha }}\mathcal{F}\left(\mathrm{u}\right)\mathrm{d}\mathrm{u}\right)}{\mathrm{d}\mathrm{x}}}$$

Theorem 2. 

Let $\mathcal{F}$ be a T2IF defined on $[a,b]$ and let $\mathcal{F}$ be absolutely continuous on $[a,b]$. Then,${I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{1-\alpha }$ is absolutely continuous on $[a,b]$, and ${I2RLFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }$can be obtained as

$${\mathrm{I}2\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{D}\left(\mathcal{F}\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}=\left[\begin{array}{c}\left[\mathrm{m}\mathrm{i}\mathrm{n}\left\{{\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{D}\left({\underset{\_}{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }},{\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{D}\left({\overline{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}\right\},\mathrm{m}\mathrm{i}\mathrm{n}\left\{{\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{D}\left({\overline{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }},{\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{D}\left({\underset{\_}{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}\right\}\right]\\ \left[\max \left\{{\mathrm{RLFD}\left({\overline{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }},{\mathrm{RLFD}\left({\underset{\_}{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}\right\},\mathrm{m}\mathrm{a}\mathrm{x}\left\{{\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{D}\left({\underset{\_}{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }},{\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{D}\left({\overline{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}\right\}\right]\end{array},\right]$$

(2)

almost everywhere in $[a,b]$. In the above equation, ${RLFD\left(\phi \left(x\right)\right)}_a^{\alpha }={\displaystyle \frac{1}{\Gamma (1-\alpha )}}{\displaystyle \frac{d\left({\int }_a^x{\left(x-u\right)}^{-\alpha }\phi \left(u\right)du\right)}{dx}}$ is the Riemann–Liouville fractional derivative of order $\alpha >0$ of the crisp valued function $\phi$.

Proof. 

$\mathcal{F}$ is a T2IF defined on $[\mathrm{a},\mathrm{b}]$ and $\mathcal{F}$ is absolutely continuous on $[\mathrm{a},\mathrm{b}]$. Then, ${\mathrm{I}2\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left(\mathcal{F}\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{1-\mathsf{\alpha }}$ is absolutely continuous on $[\mathrm{a},\mathrm{b}]$, and therefore, ${\mathrm{I}2\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left(\mathcal{F}\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{1-\mathsf{\alpha }}$ is gH differentiable almost everywhere on $[\mathrm{a},\mathrm{b}]$ (Theorem 4.4, Theorem 4.5, and Theorem 4.6 in [56]). Then, by Theorem 1, Type 2 interval-valued Riemann–Liouville gH fractional derivative of order $\mathsf{\alpha }>0$ is obtained as Equation (2).□

Theorem 3. 

Let $\mathcal{F}$ be a T2IF defined on $[a,b]$ and let $\mathcal{F}$ be absolutely continuous on $[a,b]$. Then,

(i) 

${I2RLFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }=\left[\left[{RLFD\left({\underset{\_}{f}}_1\left(x\right)\right)}_a^{\alpha },{RLFD\left({\overline{f}}_1\left(x\right)\right)}_a^{\alpha }\right],\left[{RLFD\left({\underset{\_}{f}}_2\left(x\right)\right)}_a^{\alpha }, {RLFD\left({\overline{f}}_2\left(x\right)\right)}_a^{\alpha }\right]\right]$, when ${I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{1-\alpha }$ is $\mathcal{W}$-increasing for almost everywhere on $[a,b]$.

(ii) 

${I2RLFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }=\left[\left[{RLFD\left({\overline{f}}_2\left(x\right)\right)}_a^{\alpha },{RLFD\left({\underset{\_}{f}}_2\left(x\right)\right)}_a^{\alpha }\right],\left[{RLFD\left({\overline{f}}_1\left(x\right)\right)}_a^{\alpha },{RLFD\left({\underset{\_}{f}}_1\left(x\right)\right)}_a^{\alpha }\right]\right]$, when ${I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{1-\alpha }$ is $\mathcal{W}$-decreasing for almost everywhere on $[a,b]$

Proof. 

The proof of the above statement shows the consequences of Theorem 3.2 in [56] and Theorem 2 in this present paper.□

Theorem 4. 

Let two T2IFs $\mathcal{F}$ and $\mathcal{G}$ given by $\mathcal{F}\left(x\right)=\left[\left[{\underset{\_}{f}}_1\right(x),{\overline{f}}_1(x\left)\right],\left[{\underset{\_}{f}}_2\left(x\right){,\overline{f}}_2\right(x\left)\right]\right]$ and $\mathcal{G}\left(x\right)=\left[\left[{\underset{\_}{g}}_1\right(x),{\overline{g}}_1(x\left)\right],\left[{\underset{\_}{g}}_2\left(x\right){,\overline{g}}_2\right(x\left)\right]\right]$ be absolutely continuous on $[a,b]$. Also, $\mathcal{F}$ and $\mathcal{G}$ are either $\mathcal{W}$-increasing or $\mathcal{W}$-decreasing on $[a,b]$. Then, the following results are true.

(i) 

If both ${I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{1-\alpha }$ and ${I2RLFI\left(\mathcal{G}\left(x\right)\right)}_a^{1-\alpha }$ are either $\mathcal{W}$-increasing or $\mathcal{W}$-decreasing, then $\mathcal{F}⊞\mathcal{G}$ is Type 2 interval-valued Riemann–Liouville gH fractional differentiable almost everywhere on $[a,b]$ and

$${I2RLFD\left((\mathcal{F}⊞\mathcal{G})\left(x\right)\right)}_a^{\alpha }={I2RLFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }⊞{I2RLFD\left(\mathcal{G}\left(x\right)\right)}_a^{\alpha }$$

(ii) 

If both ${I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{1-\alpha }$ and ${I2RLFI\left(\mathcal{G}\left(x\right)\right)}_a^{1-\alpha }$ are either $\mathcal{W}$-increasing or $\mathcal{W}$-decreasing, then $\mathcal{F}{\boxminus }_g\mathcal{G}$ is Type 2 interval-valued Riemann–Liouville gH fractional differentiable almost everywhere on $[a,b]$ and

$${I2RLFD\left(\left(\mathcal{F}{\boxminus }_g\mathcal{G}\right)\left(x\right)\right)}_a^{\alpha }={I2RLFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }{\boxminus }_g{I2RLFD\left(\mathcal{G}\left(x\right)\right)}_a^{\alpha }$$

(iii) 

If ${I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{1-\alpha }$ is $\mathcal{W}$-increasing and ${I2RLFI\left(\mathcal{G}\left(x\right)\right)}_a^{1-\alpha }$ is $\mathcal{W}$-decreasing (or ${I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{1-\alpha }$ is $\mathcal{W}$-decreasing and ${I2RLFI\left(\mathcal{G}\left(x\right)\right)}_a^{1-\alpha }$ is $\mathcal{W}$-increasing), then

$${I2RLFD\left((\mathcal{F}⊞\mathcal{G})\left(x\right)\right)}_a^{\alpha }={I2RLFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }{\boxminus }_g(-1)⊡{I2RLFD\left(\mathcal{G}\left(x\right)\right)}_a^{\alpha }$$

and

$${I2RLFD\left(\left(\mathcal{F}{\boxminus }_g\mathcal{G}\right)\left(x\right)\right)}_a^{\alpha }={I2RLFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }⊞(-1)⊡{I2RLFD\left(\mathcal{G}\left(x\right)\right)}_a^{\alpha }$$

Proof. 

The proof of the above statement is the consequences of Theorem 2 and Theorem 3 of this paper and Theorem 3.3 in [56]. □

Remark 4. 

It is to be noted that the above results regarding Type 2 interval-valued Riemann–Liouville gH fractional differentiability of $\mathcal{F}$ are influenced by the $\mathcal{W}$-increasing or $\mathcal{W}$-decreasing nature of ${I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{1-\alpha }$ instead that of $\mathcal{F}$. This is one of the fundamental distinctions between generalized Hukuhra differentiability and Riemann–Liouville gH fractional differentiability of type 2 interval-valued functions.

Theorem 5. 

Let $\mathcal{F}$ be a T2IF defined on $[a,b]$ and $\mathcal{F}$ be Lebesgue integrable $[a,b]$. Then, ${I2RLFD\left({I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }\right)}_a^{\alpha }=\mathcal{F}\left(x\right)$ almost everywhere on $[a,b]$.

Proof. 

We have

$$\begin{gathered} {I2RLFD\left({I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }\right)}_a^{\alpha } \\ ={\displaystyle \frac{d\left({I2RLFI\left({I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }\right)}_a^{1-\alpha }\right)}{dx}} \\ ={\displaystyle \frac{d\left({I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{\text{'}}\right)}{dx}, \mathrm{using} \mathrm{Lemma} 5} \\ ={\displaystyle \frac{d\left({\int }_a^x\mathcal{F}\left(u\right)du\right)}{dx}}=\mathcal{F}(x) \end{gathered}$$

almost everywhere on $[a,b]$.□

Theorem 6. 

Let $\mathcal{F}$ be a T2IF defined on $[a,b]$ and $\mathcal{F}$ be Lebesgue integrable $[a,b]$. Furthermore, there exists a Lebesgue integrable T2IF $\mathcal{G}$ on $[a,b]$ such that $\mathcal{F}\left(x\right)={I2RLFI\left(\mathcal{G}\left(x\right)\right)}_a^{\alpha }={\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{\alpha -1}\mathcal{G}\left(u\right)du}{\Gamma \left(\alpha \right)}}$. Then, ${I2RLFI\left({I2RLFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }\right)}_a^{\alpha }=\mathcal{F}\left(x\right)$ almost everywhere on $[a,b]$.

Proof. 

We have

$$\begin{gathered} {I2RLFI\left({I2RLFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }\right)}_a^{\alpha } \\ ={I2RLFI\left({\displaystyle \frac{d{\left(I2RLFI\right({I2RLFI\left(\mathcal{G}\left(x\right)\right)}_a^{\alpha })}_a^{1-\alpha })}{dx}}\right)}_a^{\alpha } \\ ={I2RLFI\left({\displaystyle \frac{d{\left(I2RLFI\right(\mathcal{G}\left(x\right))}_a^{\text{'}})}{dx}}\right)}_a^{\alpha } \\ ={I2RLFI\left(\mathcal{G}\left(x\right)\right)}_a^{\alpha }=\mathcal{F}\left(x\right) \end{gathered}$$

almost everywhere on $[a,b]$. □

5. Type 2 Interval-Valued Caputo gH Fractional Derivative

Definition 8. 

Let $\mathcal{F}$ be a T2IF defined on $[a,b]$ and $\mathcal{F}$ be absolutely continuous on $[a,b]$. Then, its generalized Hukuhara derivative ${\displaystyle \frac{d\left(\mathcal{F}\left(u\right)\right)}{du}}$ is Lebesgue integrable on $[a,b]$. This implies the existence of the following Type 2 interval-valued Caputo gH fractional derivative of order $\alpha >0$ almost everywhere in $[a,b]$. Then, it is denoted by ${I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }$ and is defined as

$${I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }={\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{-\alpha }\frac{d\left(\mathcal{F}\left(u\right)\right)}{du}du}{\Gamma (1-\alpha )}}$$

for almost everywhere in $[a,b]$.

Theorem 7. 

Let $\mathcal{F}$ be a T2IF defined on $[a,b]$ and $\mathcal{F}$ be absolutely continuous on $[a,b]$. Then, the Type 2 interval-valued Caputo gH fractional derivative ${I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }$ of order $\alpha >0$ can be obtained as

$${I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }=\left[\begin{array}{c}\left[min\left\{{CFD\left({\underset{\_}{f}}_1\left(x\right)\right)}_a^{\alpha },{CFD\left({\overline{f}}_2\left(x\right)\right)}_a^{\alpha }\right\},min\left\{{CFD\left({\overline{f}}_1\left(x\right)\right)}_a^{\alpha },{CFD\left({\underset{\_}{f}}_2\left(x\right)\right)}_a^{\alpha }\right\}\right]\\ \left[\mathit{max}\left\{{\mathit{CFD}\left({\overline{f}}_1\left(x\right)\right)}_a^{\alpha },{\mathit{CFD}\left({\underset{\_}{f}}_2\left(x\right)\right)}_a^{\alpha }\right\}, max\left\{{CFD\left({\underset{\_}{f}}_1\left(x\right)\right)}_a^{\alpha },{CFD\left({\overline{f}}_2\left(x\right)\right)}_a^{\alpha }\right\}\right]\end{array},\right]$$

almost everywhere in $[a,b]$. In the above equation, ${CFD\left(\phi \left(x\right)\right)}_a^{\alpha }={\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{-\alpha }\frac{d\left(\phi \left(u\right)\right)}{du}du}{\Gamma (1-\alpha )}}$ is the Caputo fractional derivative of order $\alpha >0$ of the crisp valued function $\phi$.

Proof. 

$\mathcal{F}$ is a T2IF defined on $\left[\mathrm{a},\mathrm{b}\right]$ and is given by $\mathcal{F}\left(\mathrm{x}\right)=\left[\left[{\underset{\_}{\mathrm{f}}}_1\left(\mathrm{x}\right),{\overline{\mathrm{f}}}_1\left(\mathrm{x}\right)\right],\left[{\underset{\_}{\mathrm{f}}}_2\left(\mathrm{x}\right),{\overline{\mathrm{f}}}_2\left(\mathrm{x}\right)\right]\right]$. Then, the generalized Hukuhara derivative of $\mathcal{F}$ is given by

$$\begin{gathered} {\displaystyle \frac{\mathrm{d}\left(\mathcal{F}\left(\mathrm{u}\right)\right)}{\mathrm{d}\mathrm{u}}} \\ =\left[\left[\mathrm{m}\mathrm{i}\mathrm{n}\left\{{\displaystyle \frac{\mathrm{d}\left({\underset{\_}{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}{\mathrm{d}\mathrm{x}}},{\displaystyle \frac{\mathrm{d}\left({\overline{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}{\mathrm{d}\mathrm{x}}}\right\},\mathrm{m}\mathrm{i}\mathrm{n}\left\{{\displaystyle \frac{\mathrm{d}\left({\overline{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}{\mathrm{d}\mathrm{x}}},{\displaystyle \frac{\mathrm{d}\left({\underset{\_}{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}{\mathrm{d}\mathrm{x}}}\right\}\right],\left[\max \left\{{\displaystyle \frac{\mathrm{d}\left({\overline{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}{\mathrm{dx}}},{\displaystyle \frac{\mathrm{d}\left({\underset{\_}{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}{\mathrm{dx}}}\right\},\mathrm{m}\mathrm{a}\mathrm{x}\left\{{\displaystyle \frac{\mathrm{d}\left({\underset{\_}{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}{\mathrm{d}\mathrm{x}}},{\displaystyle \frac{\mathrm{d}\left({\overline{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}{\mathrm{d}\mathrm{x}}}\right\}\right]\right] \\ =\left[\left[{\underset{\_}{\mathrm{g}}}_1\right(\mathrm{x}),{\overline{\mathrm{g}}}_1(\mathrm{x}\left)\right],\left[{\underset{\_}{\mathrm{g}}}_2\left(\mathrm{x}\right){,\overline{\mathrm{g}}}_2\right(\mathrm{x}\left)\right]\right] \end{gathered}$$

where

$${\underset{\_}{\mathrm{g}}}_1\left(\mathrm{x}\right)=\mathrm{m}\mathrm{i}\mathrm{n}\left\{{\displaystyle \frac{\mathrm{d}\left({\underset{\_}{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}{\mathrm{d}\mathrm{x}}},{\displaystyle \frac{\mathrm{d}\left({\overline{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}{\mathrm{d}\mathrm{x}}}\right\}, {\overline{\mathrm{g}}}_1\left(\mathrm{x}\right)=\mathrm{m}\mathrm{i}\mathrm{n}\left\{{\displaystyle \frac{\mathrm{d}\left({\overline{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}{\mathrm{d}\mathrm{x}}},{\displaystyle \frac{\mathrm{d}\left({\underset{\_}{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}{\mathrm{d}\mathrm{x}}}\right\}, {\underset{\_}{\mathrm{g}}}_2\left(\mathrm{x}\right)=\mathrm{m}\mathrm{a}\mathrm{x}\left\{{\displaystyle \frac{\mathrm{d}\left({\overline{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}{\mathrm{d}\mathrm{x}}},{\displaystyle \frac{\mathrm{d}\left({\underset{\_}{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}{\mathrm{d}\mathrm{x}}}\right\}, \mathrm{and} {\overline{\mathrm{g}}}_2\left(\mathrm{x}\right)=\mathrm{m}\mathrm{a}\mathrm{x}\left\{{\displaystyle \frac{\mathrm{d}\left({\underset{\_}{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}{\mathrm{d}\mathrm{x}}},{\displaystyle \frac{\mathrm{d}\left({\overline{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}{\mathrm{d}\mathrm{x}}}\right\}$$

Then, we have

$$\begin{gathered} {\displaystyle \frac{{\int }_{\mathrm{a}}^{\mathrm{x}}{\left(\mathrm{x}-\mathrm{u}\right)}^{-\mathsf{\alpha }}{\underset{\_}{\mathrm{g}}}_1\left(\mathrm{u}\right)\mathrm{d}\mathrm{u}}{\mathsf{\Gamma }(1-\mathsf{\alpha })}}={\displaystyle \frac{{\int }_{\mathrm{a}}^{\mathrm{x}}{\left(\mathrm{x}-\mathrm{u}\right)}^{-\mathsf{\alpha }}\left(\mathrm{m}\mathrm{i}\mathrm{n}\left\{\frac{\mathrm{d}\left({\underset{\_}{\mathrm{f}}}_1\left(\mathrm{u}\right)\right)}{\mathrm{d}\mathrm{u}},\frac{\mathrm{d}\left({\overline{\mathrm{f}}}_2\left(\mathrm{u}\right)\right)}{\mathrm{d}\mathrm{u}}\right\}\right)\mathrm{d}\mathrm{u}}{\mathsf{\Gamma }(1-\mathsf{\alpha })}}=\mathrm{m}\mathrm{i}\mathrm{n}\left\{{\mathrm{C}\mathrm{F}\mathrm{D}\left({\underset{\_}{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }},{\mathrm{C}\mathrm{F}\mathrm{D}\left({\overline{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}\right\} \\ {\displaystyle \frac{{\int }_{\mathrm{a}}^{\mathrm{x}}{\left(\mathrm{x}-\mathrm{u}\right)}^{-\mathsf{\alpha }}{\overline{\mathrm{g}}}_1\left(\mathrm{u}\right)\mathrm{d}\mathrm{u}}{\mathsf{\Gamma }(1-\mathsf{\alpha })}}={\displaystyle \frac{{\int }_{\mathrm{a}}^{\mathrm{x}}{\left(\mathrm{x}-\mathrm{u}\right)}^{-\mathsf{\alpha }}\left(\mathrm{m}\mathrm{i}\mathrm{n}\left\{\frac{\mathrm{d}\left({\overline{\mathrm{f}}}_1\left(\mathrm{u}\right)\right)}{\mathrm{d}\mathrm{u}},\frac{\mathrm{d}\left({\underset{\_}{\mathrm{f}}}_2\left(\mathrm{u}\right)\right)}{\mathrm{d}\mathrm{u}}\right\}\right)\mathrm{d}\mathrm{u}}{\mathsf{\Gamma }(1-\mathsf{\alpha })}}=\mathrm{m}\mathrm{i}\mathrm{n}\left\{{\mathrm{C}\mathrm{F}\mathrm{D}\left({\overline{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }},{\mathrm{C}\mathrm{F}\mathrm{D}\left({\underset{\_}{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}\right\} \\ {\displaystyle \frac{{\int }_{\mathrm{a}}^{\mathrm{x}}{\left(\mathrm{x}-\mathrm{u}\right)}^{-\mathsf{\alpha }}{\underset{\_}{\mathrm{g}}}_2\left(\mathrm{u}\right)\mathrm{d}\mathrm{u}}{\mathsf{\Gamma }(1-\mathsf{\alpha })}}={\displaystyle \frac{{\int }_{\mathrm{a}}^{\mathrm{x}}{\left(\mathrm{x}-\mathrm{u}\right)}^{-\mathsf{\alpha }}\left(\mathrm{m}\mathrm{a}\mathrm{x}\left\{\frac{\mathrm{d}\left({\overline{\mathrm{f}}}_1\left(\mathrm{u}\right)\right)}{\mathrm{d}\mathrm{u}},\frac{\mathrm{d}\left({\underset{\_}{\mathrm{f}}}_2\left(\mathrm{u}\right)\right)}{\mathrm{d}\mathrm{u}}\right\}\right)\mathrm{d}\mathrm{u}}{\mathsf{\Gamma }(1-\mathsf{\alpha })}}=\mathrm{m}\mathrm{a}\mathrm{x}\left\{{\mathrm{C}\mathrm{F}\mathrm{D}\left({\overline{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }},{\mathrm{C}\mathrm{F}\mathrm{D}\left({\underset{\_}{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}\right\},\mathrm{and} \\ {\displaystyle \frac{{\int }_{\mathrm{a}}^{\mathrm{x}}{\left(\mathrm{x}-\mathrm{u}\right)}^{-\mathsf{\alpha }}{\overline{\mathrm{g}}}_2\left(\mathrm{u}\right)\mathrm{d}\mathrm{u}}{\mathsf{\Gamma }(1-\mathsf{\alpha })}}={\displaystyle \frac{{\int }_{\mathrm{a}}^{\mathrm{x}}{\left(\mathrm{x}-\mathrm{u}\right)}^{-\mathsf{\alpha }}\left(\mathrm{m}\mathrm{a}\mathrm{x}\left\{\frac{\mathrm{d}\left({\underset{\_}{\mathrm{f}}}_1\left(\mathrm{u}\right)\right)}{\mathrm{d}\mathrm{u}},\frac{\mathrm{d}\left({\overline{\mathrm{f}}}_2\left(\mathrm{u}\right)\right)}{\mathrm{d}\mathrm{u}}\right\}\right)\mathrm{d}\mathrm{u}}{\mathsf{\Gamma }(1-\mathsf{\alpha })}}=\mathrm{m}\mathrm{a}\mathrm{x}\left\{{\mathrm{C}\mathrm{F}\mathrm{D}\left({\underset{\_}{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }},{\mathrm{C}\mathrm{F}\mathrm{D}\left({\overline{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}\right\} \end{gathered}$$

We have the following result.

$$\begin{gathered} {\mathrm{I}2\mathrm{C}\mathrm{F}\mathrm{D}\left(\mathcal{F}\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}={\displaystyle \frac{{\int }_{\mathrm{a}}^{\mathrm{x}}{\left(\mathrm{x}-\mathrm{u}\right)}^{-\mathsf{\alpha }}\frac{\mathrm{d}\left(\mathcal{F}\left(\mathrm{u}\right)\right)}{\mathrm{d}\mathrm{u}}\mathrm{d}\mathrm{u}}{\mathsf{\Gamma }(1-\mathsf{\alpha })}} \\ ={\displaystyle \frac{{\int }_{\mathrm{a}}^{\mathrm{x}}{\left(\mathrm{x}-\mathrm{u}\right)}^{-\mathsf{\alpha }}\left(\left[\left[{\underset{\_}{\mathrm{g}}}_1\right(\mathrm{u}),{\overline{\mathrm{g}}}_1(\mathrm{u}\left)\right],\left[{\underset{\_}{\mathrm{g}}}_2\left(\mathrm{u}\right){,\overline{\mathrm{g}}}_2\right(\mathrm{u}\left)\right]\right]\right)\mathrm{d}\mathrm{u}}{\mathsf{\Gamma }(1-\mathsf{\alpha })}} \\ =\left[\left[{\displaystyle \frac{{\int }_{\mathrm{a}}^{\mathrm{x}}{\left(\mathrm{x}-\mathrm{u}\right)}^{-\mathsf{\alpha }}{\underset{\_}{\mathrm{g}}}_1\left(\mathrm{u}\right)\mathrm{d}\mathrm{u}}{\mathsf{\Gamma }(1-\mathsf{\alpha })}},{\displaystyle \frac{{\int }_{\mathrm{a}}^{\mathrm{x}}{\left(\mathrm{x}-\mathrm{u}\right)}^{-\mathsf{\alpha }}{\overline{\mathrm{g}}}_1\left(\mathrm{u}\right)\mathrm{d}\mathrm{u}}{\mathsf{\Gamma }(1-\mathsf{\alpha })}}\right],\left[{\displaystyle \frac{{\int }_{\mathrm{a}}^{\mathrm{x}}{\left(\mathrm{x}-\mathrm{u}\right)}^{-\mathsf{\alpha }}{\underset{\_}{\mathrm{g}}}_2\left(\mathrm{u}\right)\mathrm{d}\mathrm{u}}{\mathsf{\Gamma }(1-\mathsf{\alpha })}},{\displaystyle \frac{{\int }_{\mathrm{a}}^{\mathrm{x}}{\left(\mathrm{x}-\mathrm{u}\right)}^{-\mathsf{\alpha }}{\overline{\mathrm{g}}}_2\left(\mathrm{u}\right)\mathrm{d}\mathrm{u}}{\mathsf{\Gamma }(1-\mathsf{\alpha })}}\right]\right] \\ =\left[\begin{array}{c}\left[\mathrm{m}\mathrm{i}\mathrm{n}\left\{{\mathrm{C}\mathrm{F}\mathrm{D}\left({\underset{\_}{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }},{\mathrm{C}\mathrm{F}\mathrm{D}\left({\overline{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}\right\},\mathrm{m}\mathrm{i}\mathrm{n}\left\{{\mathrm{C}\mathrm{F}\mathrm{D}\left({\overline{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }},{\mathrm{C}\mathrm{F}\mathrm{D}\left({\underset{\_}{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}\right\}\right]\\ \left[\max \left\{{\mathrm{CFD}\left({\overline{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }},{\mathrm{CFD}\left({\underset{\_}{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}\right\},\mathrm{m}\mathrm{a}\mathrm{x}\left\{{\mathrm{C}\mathrm{F}\mathrm{D}\left({\underset{\_}{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }},{\mathrm{C}\mathrm{F}\mathrm{D}\left({\overline{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}\right\}\right]\end{array},\right]. \end{gathered}$$

□

Theorem 8. 

Let $\mathcal{F}$ be a T2IF defined on $[a,b]$ and $\mathcal{F}$ be absolutely continuous on $[a,b]$. Then,

(i) 

${I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }=\left[\left[{CFD\left({\underset{\_}{f}}_1\left(x\right)\right)}_a^{\alpha },{CFD\left({\overline{f}}_1\left(x\right)\right)}_a^{\alpha }\right],\left[{CFD\left({\underset{\_}{f}}_2\left(x\right)\right)}_a^{\alpha }, {CFD\left({\overline{f}}_2\left(x\right)\right)}_a^{\alpha }\right]\right]$, when $\mathcal{F}$ is $\mathcal{W}$-increasing for almost everywhere on $[a,b]$.

(ii) 

${I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }=\left[\left[{CFD\left({\overline{f}}_2\left(x\right)\right)}_a^{\alpha },{CFD\left({\underset{\_}{f}}_2\left(x\right)\right)}_a^{\alpha }\right],\left[{CFD\left({\overline{f}}_1\left(x\right)\right)}_a^{\alpha },{CFD\left({\underset{\_}{f}}_1\left(x\right)\right)}_a^{\alpha }\right]\right]$, when $\mathcal{F}$ is $\mathcal{W}$-decreasing for almost everywhere on $[a,b]$.

Proof. 

Since $\mathcal{F}$ is a T2IF defined on $[a,b]$ and $\mathcal{F}$ is absolutely continuous on $[a,b]$, then ${I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }$ exists. Now, we consider the following two cases.

Case 1: when $\mathcal{F}$ is $\mathcal{W}$-increasing for almost everywhere on $[a,b]$.

Then, by Theorem 3.2 in [56],

$$\begin{gathered} {\displaystyle \frac{d\left(\mathcal{F}\left(u\right)\right)}{du}} \\ =\left[\left[min\left\{{\displaystyle \frac{d\left({\underset{\_}{f}}_1\left(x\right)\right)}{dx}},{\displaystyle \frac{d\left({\overline{f}}_2\left(x\right)\right)}{dx}}\right\},min\left\{{\displaystyle \frac{d\left({\overline{f}}_1\left(x\right)\right)}{dx}},{\displaystyle \frac{d\left({\underset{\_}{f}}_2\left(x\right)\right)}{dx}}\right\}\right],\left[\max \left\{{\displaystyle \frac{d\left({\overline{f}}_1\left(x\right)\right)}{\mathit{dx}}},{\displaystyle \frac{d\left({\underset{\_}{f}}_2\left(x\right)\right)}{\mathit{dx}}}\right\}, max\left\{{\displaystyle \frac{d\left({\underset{\_}{f}}_1\left(x\right)\right)}{dx}},{\displaystyle \frac{d\left({\overline{f}}_2\left(x\right)\right)}{dx}}\right\}\right]\right] \\ =\left[\left[{\displaystyle \frac{d\left({\underset{\_}{f}}_1\left(x\right)\right)}{dx}},{\displaystyle \frac{d\left({\overline{f}}_1\left(x\right)\right)}{dx}}\right],\left[{\displaystyle \frac{d\left({\underset{\_}{f}}_2\left(x\right)\right)}{dx}},{\displaystyle \frac{d\left({\overline{f}}_2\left(x\right)\right)}{dx}}\right]\right] \end{gathered}$$

Then,

$$\begin{gathered} {I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }={\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{-\alpha }\frac{d\left(\mathcal{F}\left(u\right)\right)}{du}du}{\mathsf{\Gamma }(1-\alpha )}} \\ ={\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{-\alpha }\left(\left[\left[\frac{d\left({\underset{\_}{f}}_1\left(x\right)\right)}{dx},\frac{d\left({\overline{f}}_1\left(x\right)\right)}{dx}\right],\left[\frac{d\left({\underset{\_}{f}}_2\left(x\right)\right)}{dx},\frac{d\left({\overline{f}}_2\left(x\right)\right)}{dx}\right]\right]\right)du}{\mathsf{\Gamma }(1-\alpha )}} \\ =\left[\left[{\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{-\alpha }\frac{d\left({\underset{\_}{f}}_1\left(u\right)\right)}{du}du}{\mathsf{\Gamma }(1-\alpha )}},{\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{-\alpha }\frac{d\left({\overline{f}}_1\left(u\right)\right)}{du}du}{\mathsf{\Gamma }(1-\alpha )}}\right],\left[{\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{-\alpha }\frac{d\left({\underset{\_}{f}}_2\left(u\right)\right)}{du}du}{\mathsf{\Gamma }(1-\alpha )}},{\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{-\alpha }\frac{d\left({\overline{f}}_2\left(u\right)\right)}{du}du}{\mathsf{\Gamma }(1-\alpha )}}\right]\right] \\ =\left[\left[{CFD\left({\underset{\_}{f}}_1\left(x\right)\right)}_a^{\alpha },{CFD\left({\overline{f}}_1\left(x\right)\right)}_a^{\alpha }\right],\left[{CFD\left({\underset{\_}{f}}_2\left(x\right)\right)}_a^{\alpha }, {CFD\left({\overline{f}}_2\left(x\right)\right)}_a^{\alpha }\right]\right] \end{gathered}$$

Case 2: when $\mathcal{F}$ is $\mathcal{W}$-decreasing for almost everywhere on $[a,b]$

Then, by Theorem 3.2 in [56],

$$\begin{gathered} {\displaystyle \frac{d\left(\mathcal{F}\left(u\right)\right)}{du}} \\ =\left[\left[min\left\{{\displaystyle \frac{d\left({\underset{\_}{f}}_1\left(x\right)\right)}{dx}},{\displaystyle \frac{d\left({\overline{f}}_2\left(x\right)\right)}{dx}}\right\},min\left\{{\displaystyle \frac{d\left({\overline{f}}_1\left(x\right)\right)}{dx}},{\displaystyle \frac{d\left({\underset{\_}{f}}_2\left(x\right)\right)}{dx}}\right\}\right],\left[\max \left\{{\displaystyle \frac{d\left({\overline{f}}_1\left(x\right)\right)}{\mathit{dx}}},{\displaystyle \frac{d\left({\underset{\_}{f}}_2\left(x\right)\right)}{\mathit{dx}}}\right\}, max\left\{{\displaystyle \frac{d\left({\underset{\_}{f}}_1\left(x\right)\right)}{dx}},{\displaystyle \frac{d\left({\overline{f}}_2\left(x\right)\right)}{dx}}\right\}\right]\right] \\ =\left[\left[{\displaystyle \frac{d\left({\overline{f}}_2\left(x\right)\right)}{dx}},{\displaystyle \frac{d\left({\underset{\_}{f}}_2\left(x\right)\right)}{dx}}\right],\left[{\displaystyle \frac{d\left({\overline{f}}_1\left(x\right)\right)}{dx}},{\displaystyle \frac{d\left({\underset{\_}{f}}_1\left(x\right)\right)}{dx}}\right]\right] \end{gathered}$$

Then,

$$\begin{gathered} {I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }={\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{-\alpha }\frac{d\left(\mathcal{F}\left(u\right)\right)}{du}du}{\mathsf{\Gamma }(1-\alpha )}} \\ ={\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{-\alpha }\left(\left[\left[\frac{d\left({\overline{f}}_2\left(x\right)\right)}{dx},\frac{d\left({\underset{\_}{f}}_2\left(x\right)\right)}{dx}\right],\left[\frac{d\left({\overline{f}}_1\left(x\right)\right)}{dx},\frac{d\left({\underset{\_}{f}}_1\left(x\right)\right)}{dx}\right]\right]\right)du}{\mathsf{\Gamma }(1-\alpha )}} \\ =\left[\left[{\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{-\alpha }\frac{d\left({\overline{f}}_2\left(u\right)\right)}{du}du}{\mathsf{\Gamma }(1-\alpha )}},{\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{-\alpha }\frac{d\left({\underset{\_}{f}}_2\left(u\right)\right)}{du}du}{\mathsf{\Gamma }(1-\alpha )}}\right],\left[{\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{-\alpha }\frac{d\left({\overline{f}}_1\left(u\right)\right)}{du}du}{\mathsf{\Gamma }(1-\alpha )}},{\displaystyle \frac{{\int }_a^x{\left(x-u\right)}^{-\alpha }\frac{d\left({\underset{\_}{f}}_1\left(u\right)\right)}{du}du}{\mathsf{\Gamma }(1-\alpha )}}\right]\right] \\ =\left[\left[{CFD\left({\overline{f}}_2\left(x\right)\right)}_a^{\alpha },{CFD\left({\underset{\_}{f}}_2\left(x\right)\right)}_a^{\alpha }\right],\left[{CFD\left({\overline{f}}_1\left(x\right)\right)}_a^{\alpha },{CFD\left({\underset{\_}{f}}_1\left(x\right)\right)}_a^{\alpha }\right]\right] \end{gathered}$$

□

Remark 5. 

${I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }$ is said to be a Type 2 interval-valued Caputo gH fractional derivative of the first type when

$${I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }=\left[\left[{CFD\left({\underset{\_}{f}}_1\left(x\right)\right)}_a^{\alpha },{CFD\left({\overline{f}}_1\left(x\right)\right)}_a^{\alpha }\right],\left[{CFD\left({\underset{\_}{f}}_2\left(x\right)\right)}_a^{\alpha }, {CFD\left({\overline{f}}_2\left(x\right)\right)}_a^{\alpha }\right]\right]and$$

of second type when

$${\mathrm{I}2\mathrm{C}\mathrm{F}\mathrm{D}\left(\mathcal{F}\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}=\left[\left[{\mathrm{C}\mathrm{F}\mathrm{D}\left({\overline{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }},{\mathrm{C}\mathrm{F}\mathrm{D}\left({\underset{\_}{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}\right],\left[{\mathrm{C}\mathrm{F}\mathrm{D}\left({\overline{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }},{\mathrm{C}\mathrm{F}\mathrm{D}\left({\underset{\_}{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}\right]\right]$$

Theorem 9. 

Let two T2IFs $\mathcal{F}$ and $\mathcal{G}$ given by $\mathcal{F}\left(x\right)=\left[\left[{\underset{\_}{f}}_1\right(x),{\overline{f}}_1(x\left)\right],\left[{\underset{\_}{f}}_2\left(x\right){,\overline{f}}_2\right(x\left)\right]\right]$ and $\mathcal{G}\left(x\right)=\left[\left[{\underset{\_}{g}}_1\right(x),{\overline{g}}_1(x\left)\right],\left[{\underset{\_}{g}}_2\left(x\right){,\overline{g}}_2\right(x\left)\right]\right]$ be absolutely continuous on $[a,b]$. Also, $\mathcal{F}$ and $\mathcal{G}$ are either $\mathcal{W}$-increasing or $\mathcal{W}$-decreasing on $[a,b]$. Then, the following results are true.

(i) 

If both $\mathcal{F}$ and $\mathcal{G}$ are either $\mathcal{W}$-increasing or $\mathcal{W}$-decreasing simultaneously, then $\mathcal{F}⊞\mathcal{G}$ is Type 2 interval-valued Caputo gH fractional differentiable almost everywhere on $\left[a,b\right],$ and

$${I2CFD\left((\mathcal{F}⊞\mathcal{G})\left(x\right)\right)}_a^{\alpha }={I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }⊞{I2CFD\left(\mathcal{G}\left(x\right)\right)}_a^{\alpha }$$

(ii) 

If both $\mathcal{F}$ and $\mathcal{G}$ are either $\mathcal{W}$-increasing or $\mathcal{W}$-decreasing, then $\mathcal{F}{\boxminus }_g\mathcal{G}$ is Type 2 interval-valued Caputo gH fractional differentiable almost everywhere on $[a,b]$, and

$$\mathcal{W}({I2CFD\left(\mathcal{F}\left(x\right){\boxminus }_g\mathcal{G}\left(x\right)\right)}_a^{\alpha }{\succcurlyeq }_{in}\mathcal{W}\left({I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }{\boxminus }_g{I2CFD\left(\mathcal{G}\left(x\right)\right)}_a^{\alpha }\right)$$

Furthermore, ${ I2CFD\left(\mathcal{F}\left(x\right){\boxminus }_g\mathcal{G}\left(x\right)\right)}_a^{\alpha }={I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }{\boxminus }_g{I2CFD\left(\mathcal{G}\left(x\right)\right)}_a^{\alpha }$ when either $\mathcal{W}\left(\mathcal{F}\left(x\right)\right){\succcurlyeq }_{in}\mathcal{W}\left(\mathcal{G}\left(x\right)\right)$ for almost everywhere $[a,b]$ or $\mathcal{W}\left(\mathcal{G}\left(x\right)\right){\succcurlyeq }_{in}\mathcal{W}\left(\mathcal{F}\left(x\right)\right)$ for almost everywhere $[a,b]$.

(iii) 

If $\mathcal{F}$ is $\mathcal{W}$-increasing and $\mathcal{G}$ is $\mathcal{W}$-decreasing (or $\mathcal{F}$ is $\mathcal{W}$-decreasing and $\mathcal{G}$ is $\mathcal{W}$-increasing), then

$${I2CFD\left(\left(\mathcal{F}{\boxminus }_g\mathcal{G}\right)\left(x\right)\right)}_a^{\alpha }={I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }⊞\left(-1\right)⊡{I2CFD\left(\mathcal{G}\left(x\right)\right)}_a^{\alpha },$$

for almost everywhere $[a,b]$.

(iv) 

If $\mathcal{F}$ is $\mathcal{W}$-increasing and $\mathcal{G}$ is $\mathcal{W}$-decreasing (or $\mathcal{F}$ is $\mathcal{W}$-decreasing and $\mathcal{G}$ is $\mathcal{W}$-increasing), then

$$\mathcal{W}({I2CFD\left(\mathcal{F}\left(x\right)⊞\mathcal{G}\left(x\right)\right)}_a^{\alpha }{\succcurlyeq }_{in}\mathcal{W}\left({I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }{\boxminus }_g(-1) {I2CFD\left(\mathcal{G}\left(x\right)\right)}_a^{\alpha }\right)$$

Furthermore,${ I2CFD(\mathcal{F}\left(x\right)⊞\mathcal{G}\left(x\right))}_a^{\alpha }={I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }{\boxminus }_g(-1) {I2CFD\left(\mathcal{G}\left(x\right)\right)}_a^{\alpha }$, when either $\mathcal{W}\left(\mathcal{F}\left(x\right)\right){\succcurlyeq }_{in}\mathcal{W}\left(\mathcal{G}\left(x\right)\right)$ for almost everywhere $[a,b]$ or $\mathcal{W}\left(\mathcal{G}\left(x\right)\right){\succcurlyeq }_{in}\mathcal{W}\left(\mathcal{F}\left(x\right)\right)$ for almost everywhere $[a,b]$.

Proof. 

The proof of (i) is straightforward and is skipped. If both $\mathcal{F}$ and $\mathcal{G}$ are either $\mathcal{W}$-increasing or $\mathcal{W}$-decreasing, then by Theorem 3.3 in [56], $\mathcal{F}{\boxminus }_{\mathrm{g}}\mathcal{G}$ is gH differentiable at $\mathrm{x}\in [\mathrm{a},\mathrm{b}]$ and ${\left(\mathcal{F}{\boxminus }_{\mathrm{g}}\mathcal{G}\right)}^{\text{'}}\left(\mathrm{x}\right)={\mathcal{F}}^{\text{'}}\left(\mathrm{x}\right){\boxminus }_{\mathrm{g}}{\mathcal{G}}^{\text{'}}\left(\mathrm{x}\right)$, where ${\mathcal{F}}^{\text{'}}$ implies the generalized Hukuhara derivative of the T2IF $\mathcal{F}$. Therefore, using Theorem 1 in this paper, we obtain:

$$\begin{gathered} \mathcal{W}({\mathrm{I}2\mathrm{C}\mathrm{F}\mathrm{D}\left(\mathcal{F}\left(\mathrm{x}\right){\boxminus }_{\mathrm{g}}\mathcal{G}\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }} \\ =\mathcal{W}({\mathrm{I}2\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left({\left(\mathcal{F}{\boxminus }_{\mathrm{g}}\mathcal{G}\right)}^{\text{'}}\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{1-\mathsf{\alpha }} \\ =\mathcal{W}({\mathrm{I}2\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left({\mathcal{F}}^{\text{'}}\left(\mathrm{x}\right){\boxminus }_{\mathrm{g}}{\mathcal{G}}^{\text{'}}\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{1-\mathsf{\alpha }} \\ {\succcurlyeq }_{\mathrm{i}\mathrm{n}}\mathcal{W}\left({\mathrm{I}2\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left({\mathcal{F}}^{\text{'}}\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{1-\mathsf{\alpha }}{\boxminus }_{\mathrm{g}}{\mathrm{I}2\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left({\mathcal{G}}^{\text{'}}\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{1-\mathsf{\alpha }}\right) \\ =\mathcal{W}\left({\mathrm{I}2\mathrm{C}\mathrm{F}\mathrm{D}\left(\mathcal{F}\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}{\boxminus }_{\mathrm{g}}{\mathrm{I}2\mathrm{C}\mathrm{F}\mathrm{D}\left(\mathcal{G}\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}\right) \end{gathered}$$

Furthermore, $\mathcal{W}({\mathrm{I}2\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left({\mathcal{F}}^{\text{'}}\left(\mathrm{x}\right){\boxminus }_{\mathrm{g}}{\mathcal{G}}^{\text{'}}\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{1-\mathsf{\alpha }}=\mathcal{W}\left({\mathrm{I}2\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left({\mathcal{F}}^{\text{'}}\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{1-\mathsf{\alpha }}{\boxminus }_{\mathrm{g}}{\mathrm{I}2\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left({\mathcal{G}}^{\text{'}}\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{1-\mathsf{\alpha }}\right)$, when either $\mathcal{W}\left(\mathcal{F}\left(\mathrm{x}\right)\right){\succcurlyeq }_{\mathrm{i}\mathrm{n}}\mathcal{W}\left(\mathcal{G}\left(\mathrm{x}\right)\right)$ or $\mathcal{W}\left(\mathcal{G}\left(\mathrm{x}\right)\right){\succcurlyeq }_{\mathrm{i}\mathrm{n}}\mathcal{W}\left(\mathcal{F}\left(\mathrm{x}\right)\right)$, for almost everywhere in $[\mathrm{a},\mathrm{b}]$. This preserves the equality regarding the properties (ii) in this theorem.

By Theorem 3.3 in [56], if $\mathcal{F}$ is $\mathcal{W}$-increasing and $\mathcal{G}$ is $\mathcal{W}$-decreasing (or $\mathcal{F}$ is $\mathcal{W}$-decreasing and $\mathcal{G}$ is $\mathcal{W}$-increasing), then ${(\mathcal{F}⊞\mathcal{G})}^{\text{'}}\left(\mathrm{x}\right)={\mathcal{F}}^{\text{'}}\left(\mathrm{x}\right){\boxminus }_{\mathrm{g}}(-1)⊡{\mathcal{G}}^{\text{'}}\left(\mathrm{x}\right)$ and ${\left(\mathcal{F}{\boxminus }_{\mathrm{g}}\mathcal{G}\right)}^{\text{'}}\left(\mathrm{x}\right)={\mathcal{F}}^{\text{'}}\left(\mathrm{x}\right)⊞(-1)⊡{\mathcal{G}}^{\text{'}}\left(\mathrm{x}\right)$. Then, proceeding similarly as the proof for the property (ii), the proofs for the properties (iii) and (iv) can be made. □

Theorem 10. 

Let $\mathcal{F}$ be a T2IF that is defined and absolutely continuous on $[a,b]$. Also, $\mathcal{F}$ is either $\mathcal{W}$-increasing or $\mathcal{W}$-decreasing almost everywhere in $[a,b]$. Then, ${I2RLFI\left({I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }\right)}_a^{\alpha }=\mathcal{F}\left(x\right)$ almost everywhere on $[a,b]$.

Proof. 

F is absolutely continuous and $\mathcal{F}$ is either $\mathcal{W}$-increasing or $\mathcal{W}$-decreasing almost everywhere in $[a,b]$. Then,

$$\begin{gathered} {I2RLFI\left({I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }\right)}_a^{\alpha }={I2RLFI\left({I2RLFI\left({\mathcal{F}}^{\text{'}}\left(x\right)\right)}_a^{1-\alpha }\right)}_a^{\alpha }={I2RLFI\left({\mathcal{F}}^{\text{'}}\left(x\right)\right)}_a^{\text{'}} \\ ={\int }_a^x{\mathcal{F}}^{\text{'}}\left(u\right)du=\mathcal{F}\left(x\right){\boxminus }_g\mathcal{F}\left(a\right) \end{gathered}$$

almost everywhere on $[a,b]$. Also, $\mathcal{F}$ is either $\mathcal{W}$-increasing or $\mathcal{W}$-decreasing almost everywhere in $[a,b]$. □

Theorem 11. 

Let $\mathcal{F}$ be a T2IF such that $\mathcal{F}$ is either $\mathcal{W}$-increasing or $\mathcal{W}$-decreasing in $[a,b]$ and ${I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }$ is $\mathcal{W}$-increasing in $[a,b]$. Then, ${I2CFD\left({I2RLFI\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }\right)}_a^{\alpha }=\mathcal{F}\left(x\right)$, almost everywhere on $[a,b]$.

Proof. 

F is a T2IF such that $\mathcal{F}$ is either $\mathcal{W}$-increasing or $\mathcal{W}$-decreasing in $\left[\mathrm{a},\mathrm{b}\right]$. Then, ${\mathrm{I}2\mathrm{C}\mathrm{F}\mathrm{D}\left({\mathrm{I}2\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left(\mathcal{F}\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}\right)}_{\mathrm{a}}^{\mathsf{\alpha }}$ exists almost everywhere on $\left[\mathrm{a},\mathrm{b}\right]$. Then,

$$\begin{gathered} {\mathrm{I}2\mathrm{C}\mathrm{F}\mathrm{D}\left({\mathrm{I}2\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left(\mathcal{F}\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}\right)}_{\mathrm{a}}^{\mathsf{\alpha }} \\ ={\mathrm{I}2\mathrm{C}\mathrm{F}\mathrm{D}\left(\left[\left[{\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left({\underset{\_}{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }},{\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left({\overline{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}\right],\left[{\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left({\underset{\_}{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }},{\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left({\overline{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}\right]\right]\right)}_{\mathrm{a}}^{\mathsf{\alpha }} \\ =\left[\left[{\mathrm{C}\mathrm{F}\mathrm{D}\left({\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left({\underset{\_}{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}\right)}_{\mathrm{a}}^{\mathsf{\alpha }},{\mathrm{C}\mathrm{F}\mathrm{D}\left({\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left({\overline{\mathrm{f}}}_1\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}\right)}_{\mathrm{a}}^{\mathsf{\alpha }}\right],\left[{\mathrm{C}\mathrm{F}\mathrm{D}\left({\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left({\underset{\_}{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}\right)}_{\mathrm{a}}^{\mathsf{\alpha }},{\mathrm{C}\mathrm{F}\mathrm{D}\left({\mathrm{R}\mathrm{L}\mathrm{F}\mathrm{I}\left({\overline{\mathrm{f}}}_2\left(\mathrm{x}\right)\right)}_{\mathrm{a}}^{\mathsf{\alpha }}\right)}_{\mathrm{a}}^{\mathsf{\alpha }}\right]\right] \\ =\left[\left[{\underset{\_}{\mathrm{f}}}_1\left(\mathrm{x}\right),{\overline{\mathrm{f}}}_1\left(\mathrm{x}\right)\right],\left[{\underset{\_}{\mathrm{f}}}_2\left(\mathrm{x}\right),{\overline{\mathrm{f}}}_2\left(\mathrm{x}\right)\right]\right]=\mathcal{F}\left(\mathrm{x}\right) \end{gathered}$$

□

6. Type 2 Interval-Valued Laplace Transformations

Definition 9. 

Let $\mathcal{F}$ be a Type 2 interval-valued function given by $\mathcal{F}\left(x\right)=\left[\left[{\underset{\_}{f}}_1\right(x),{\overline{f}}_1(x\left)\right],\left[{\underset{\_}{f}}_2\left(x\right){,\overline{f}}_2\right(x\left)\right]\right]$, which is continuous on $[0,\infty )$. Then, the Type 2 interval Laplace transformation $\mathcal{L}\left[\mathcal{F}\left(x\right)\right]$ of $\mathcal{F}$ is defined as

$$\mathcal{L}\left[\mathcal{F}\left(x\right);s\right]={\int }_0^{\infty }\mathcal{F}\left(x\right)⊡e^{-sx}dx$$

Then,

$$\begin{gathered} \mathcal{L}\left[\mathcal{F}\left(x\right);s\right]={\int }_0^{\infty }\mathcal{F}\left(x\right)⊡e^{-sx}dx={\int }_0^{\infty }\left[\left[{\underset{\_}{f}}_1\right(x),{\overline{f}}_1(x\left)\right],\left[{\underset{\_}{f}}_2\left(x\right){,\overline{f}}_2\right(x\left)\right]\right]⊡e^{-sx}dx \\ =\left[\left[{\int }_0^{\infty }{\underset{\_}{f}}_1\left(x\right)e^{-sx}dx,{\int }_0^{\infty }{\overline{f}}_1\left(x\right)e^{-sx}dx\right],\left[{\int }_0^{\infty }{\underset{\_}{f}}_2\left(x\right)e^{-sx}dx,{\int }_0^{\infty }{\overline{f}}_2\left(x\right)e^{-sx}dx\right]\right] \\ =\left[\left[\mathit{l}\left[{\underset{\_}{f}}_1\left(x\right);s\right], \mathit{l}\left[{\overline{f}}_1\left(x\right);s\right]\right],\left[\mathit{l}\left[{\underset{\_}{f}}_2\left(x\right);s\right], \mathit{l}\left[{\overline{f}}_2\left(x\right);s\right]\right]\right] \end{gathered}$$

Definition 10. 

Let $\mathcal{F}$ be a Type 2 interval-valued function given by $\mathcal{F}\left(x\right)=\left[\left[{\underset{\_}{f}}_1\right(x),{\overline{f}}_1(x\left)\right],\left[{\underset{\_}{f}}_2\left(x\right){,\overline{f}}_2\left(x\right)\right]\right]$. $\mathcal{F}$ is said to be of exponential order $\rho$ if there exist real numbers $M,x_1>0$ such that

$${‖\mathcal{F}‖}_{4,Sup}=\underset{a\le x\le b}{\mathit{sup}}max\{\left|{\underset{\_}{f}}_1\left(x\right)\right|,\left|{\overline{f}}_1\left(x\right)\right|,\left|{\underset{\_}{f}}_2\left(x\right)\right|,\left|{\overline{f}}_2\left(x\right)\right|\}<M{e}^{\rho x_1}$$

Remark 6. 

It is easy to verify that $\mathcal{F}$ is of some exponential order if and only if the four crisp components ${\underset{\_}{f}}_1$, ${\overline{f}}_1$, ${\underset{\_}{f}}_2$, and ${\overline{f}}_2$ are of some exponential order.

Remark 7. 

It is noted that the Laplace transformation $\mathit{l}\left[\phi \left(x\right);s\right]$ of the crisp function $\phi \left(x\right)$ exists when $\phi \left(x\right)$ is piecewise continuous on the positive half on the real line and is of some exponential order. Therefore, it is to be concluded that $\mathcal{L}\left[\mathcal{F}\right(x\left)\right]$ exists if and only if each of $\mathit{l}\left[{\underset{\_}{f}}_1\left(x\right);s\right], \mathit{l}\left[{\overline{f}}_1\left(x\right);s\right], \mathit{l}\left[{\underset{\_}{f}}_2\left(x\right);s\right]$, and $\mathit{l}\left[{\overline{f}}_2\left(x\right);s\right]$ exists.

Theorem 12. 

Let $\mathcal{F}$ be a Type 2 interval-valued function defined as $[0,\infty )$, and Type 2 interval Laplace transformation $\mathcal{L}\left[\mathcal{F}\right(x\left)\right]$ of $\mathcal{F}$ exists. Then, the following results are true.

(i) 

When $\mathcal{F}$ is Type 2 interval-valued Riemann–Liouville gH fractional differentiable of the first type, then

$$\mathcal{L}\left[{I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha };s\right]=s^{\alpha }\mathcal{L}\left[\mathcal{F}\left(x\right)\right]{\boxminus }_H{I2RLFD\left(\mathcal{F}\left(0\right)\right)}_a^{\alpha -1}$$

(ii) 

When $\mathcal{F}$ is Type 2 interval-valued Riemann–Liouville gH fractional differentiable of the second type, then

$$\mathcal{L}\left[{I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha };s\right]=(-1)⊡{I2RLFD\left(\mathcal{F}\left(0\right)\right)}_a^{\alpha -1}{\boxminus }_H(-1)⊡s^{\alpha }\mathcal{L}\left[\mathcal{F}\right(x\left)\right]$$

Proof. 

Let $\mathcal{F}$ be a Type 2 interval-valued function given by $\mathcal{F}\left(x\right)=\left[\left[{\underset{\_}{f}}_1\right(x),{\overline{f}}_1(x\left)\right],\left[{\underset{\_}{f}}_2\left(x\right){,\overline{f}}_2\right(x\left)\right]\right]$. We consider the following two cases.

(i)

When $\mathcal{F}$ is a Type 2 interval-valued Riemann–Liouville gH fractional differentiable of the first type, then,

$${I2RLFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }=\left[\left[{RLFD\left({\underset{\_}{f}}_1\left(x\right)\right)}_a^{\alpha },{RLFD\left({\overline{f}}_1\left(x\right)\right)}_a^{\alpha }\right],\left[{RLFD\left({\underset{\_}{f}}_2\left(x\right)\right)}_a^{\alpha }, {RLFD\left({\overline{f}}_2\left(x\right)\right)}_a^{\alpha }\right]\right]$$

Then, we have

$$\begin{gathered} s^{\alpha }\mathcal{L}\left[\mathcal{F}\left(x\right)\right]{\boxminus }_H{I2RLFD\left(\mathcal{F}\left(0\right)\right)}_a^{\alpha -1} \\ =\left[\left[s^{\alpha }l\left[{\underset{\_}{f}}_1\left(x\right);s\right]-{RLFD\left({\underset{\_}{f}}_1\left(0\right)\right)}_a^{\alpha -1},s^{\alpha }l\left[{\overline{f}}_1\left(x\right);s\right]-{RLFD\left({\overline{f}}_1\left(0\right)\right)}_a^{\alpha -1}\right],\left[s^{\alpha }l\left[{\underset{\_}{f}}_2\left(x\right);s\right]-{RLFD\left({\underset{\_}{f}}_2\left(0\right)\right)}_a^{\alpha -1},s^{\alpha }l\left[{\overline{f}}_2\left(x\right);s\right]-{RLFD\left({\overline{f}}_2\left(0\right)\right)}_a^{\alpha -1}\right]\right] \\ =\left[\left[\mathit{l}\left[{RLFD\left({\underset{\_}{f}}_1\left(x\right)\right)}_a^{\alpha };s\right], \mathit{l}\left[{RLFD\left({\overline{f}}_1\left(x\right)\right)}_a^{\alpha };s\right]\right],\left[\mathit{l}\left[{RLFD\left({\underset{\_}{f}}_2\left(x\right)\right)}_a^{\alpha };s\right], \mathit{l}\left[{RLFD\left({\overline{f}}_2\left(x\right)\right)}_a^{\alpha };s\right]\right]\right] \\ =\mathcal{L}\left[{I2RLFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha };s\right] \end{gathered}$$

(ii)

When $\mathcal{F}$ is Type 2 interval-valued Riemann–Liouville gH fractional differentiable of the second type, then,

$${I2RLFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }=\left[\left[{RLFD\left({\overline{f}}_2\left(x\right)\right)}_a^{\alpha },{RLFD\left({\underset{\_}{f}}_2\left(x\right)\right)}_a^{\alpha }\right],\left[{RLFD\left({\overline{f}}_1\left(x\right)\right)}_a^{\alpha }, {RlFD\left({\underset{\_}{f}}_1\left(x\right)\right)}_a^{\alpha }\right]\right]$$

Then, we have

$$\begin{gathered} (-1)⊡{I2RLFD\left(\mathcal{F}\left(0\right)\right)}_a^{\alpha -1}{\boxminus }_H(-1)⊡s^{\alpha }\mathcal{L}\left[\mathcal{F}\right(x\left)\right] \\ =\left[\left[s^{\alpha }l\left[{\overline{f}}_2\left(x\right);s\right]-{RLFD\left({\overline{f}}_2\left(0\right)\right)}_a^{\alpha -1},s^{\alpha }l\left[{\underset{\_}{f}}_2\left(x\right);s\right]-{RLFD\left({\underset{\_}{f}}_2\left(0\right)\right)}_a^{\alpha -1}\right],\left[s^{\alpha }l\left[{\overline{f}}_1\left(x\right);s\right]-{RLFD\left({\overline{f}}_1\left(0\right)\right)}_a^{\alpha -1},s^{\alpha }l\left[{\underset{\_}{f}}_1\left(x\right);s\right]-{RLFD\left({\underset{\_}{f}}_1\left(0\right)\right)}_a^{\alpha -1}\right]\right] \\ =\left[\left[\mathit{l}\left[{RLFD\left({\overline{f}}_2\left(x\right)\right)}_a^{\alpha };s\right], \right]\mathit{l}\left[{RLFD\left({\underset{\_}{f}}_2\left(x\right)\right)}_a^{\alpha };s\right],\left[\mathit{l}\left[{RLFD\left({\overline{f}}_1\left(x\right)\right)}_a^{\alpha };s\right],\mathit{l}\left[{RLFD\left({\underset{\_}{f}}_1\left(x\right)\right)}_a^{\alpha };s\right]\right]\right] \\ =\mathcal{L}\left[{I2RLFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha };s\right] \end{gathered}$$

□

Theorem 13. 

Let $\mathcal{F}$ be a Type 2 interval-valued function defined $[0,\infty )$, and Type 2 interval conformable Laplace transformation $\mathcal{L}\left[\mathcal{F}\right(x\left)\right]$ of $\mathcal{F}$ exists. Then, the following results are true.

(i) 

When $\mathcal{F}$ is Type 2 interval-valued Caputo gH fractional differentiable of the first type, then

$$\mathcal{L}\left[{I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha };s\right]=s^{\alpha }\mathcal{L}\left[\mathcal{F}\left(x\right)\right]{\boxminus }_H{s}^{\alpha -1}\mathcal{F}\left(0\right)$$

(ii) 

When $\mathcal{F}$ is Type 2 interval-valued Caputo gH fractional differentiable of the second type, then

$$\mathcal{L}\left[{I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha };s\right]=(-1)⊡s^{\alpha -1}\mathcal{F}\left(0\right){\boxminus }_H(-1)⊡s^{\alpha }\mathcal{L}\left[\mathcal{F}\right(x\left)\right]$$

Proof. 

Let $\mathcal{F}$ be a Type 2 interval-valued function given by $\mathcal{F}\left(x\right)=\left[\left[{\underset{\_}{f}}_1\right(x),{\overline{f}}_1(x\left)\right],\left[{\underset{\_}{f}}_2\left(x\right){,\overline{f}}_2\right(x\left)\right]\right]$. We consider the following two cases.

(i)

When $\mathcal{F}$ is Type 2 interval-valued Caputo gH fractional differentiable of the first type, then,

$${I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }=\left[\left[{CFD\left({\underset{\_}{f}}_1\left(x\right)\right)}_a^{\alpha },{CFD\left({\overline{f}}_1\left(x\right)\right)}_a^{\alpha }\right],\left[{CFD\left({\underset{\_}{f}}_2\left(x\right)\right)}_a^{\alpha }, {CFD\left({\overline{f}}_2\left(x\right)\right)}_a^{\alpha }\right]\right]$$

Then, we have

$$\begin{gathered} s^{\alpha }\mathcal{L}\left[\mathcal{F}\left(x\right)\right]{\boxminus }_H{s}^{\alpha -1}\mathcal{F}\left(0\right) \\ =\left[\left[s^{\alpha }l\left[{\underset{\_}{f}}_1\left(x\right);s\right]-s^{\alpha -1}{\underset{\_}{f}}_1\left(0\right),s^{\alpha }l\left[{\overline{f}}_1\left(x\right);s\right]-s^{\alpha -1}{\overline{f}}_1\left(0\right)\right],\left[s^{\alpha }l\left[{\underset{\_}{f}}_2\left(x\right);s\right]-s^{\alpha -1}{\underset{\_}{f}}_2\left(0\right),s^{\alpha }l\left[{\overline{f}}_2\left(x\right);s\right]-s^{\alpha -1}{\overline{f}}_2\left(0\right)\right]\right] \\ =\left[\left[\mathit{l}\left[{CFD\left({\underset{\_}{f}}_1\left(x\right)\right)}_a^{\alpha };s\right], \mathit{l}\left[{CFD\left({\overline{f}}_1\left(x\right)\right)}_a^{\alpha };s\right]\right],\left[\mathit{l}\left[{CFD\left({\underset{\_}{f}}_2\left(x\right)\right)}_a^{\alpha };s\right], \mathit{l}\left[{CFD\left({\overline{f}}_2\left(x\right)\right)}_a^{\alpha };s\right]\right]\right] \\ =\mathcal{L}\left[{I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha };s\right] \end{gathered}$$

(ii)

When $\mathcal{F}$ is Type 2 interval-valued Caputo gH fractional differentiable of the second type, then,

$${I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha }=\left[\left[{CFD\left({\overline{f}}_2\left(x\right)\right)}_a^{\alpha },{CFD\left({\underset{\_}{f}}_2\left(x\right)\right)}_a^{\alpha }\right],\left[{CFD\left({\overline{f}}_1\left(x\right)\right)}_a^{\alpha }, {CFD\left({\underset{\_}{f}}_1\left(x\right)\right)}_a^{\alpha }\right]\right]$$

Then, we have

$$\begin{gathered} (-1)⊡s^{\alpha -1}\mathcal{F}\left(0\right){\boxminus }_H(-1)⊡s^{\alpha }\mathcal{L}\left[\mathcal{F}\right(x\left)\right] \\ =\left[\left[s^{\alpha }l\left[{\overline{f}}_2\left(x\right);s\right]-s^{\alpha -1}{\overline{f}}_2\left(0\right),s^{\alpha }l\left[{\underset{\_}{f}}_2\left(x\right);s\right]-s^{\alpha -1}{\underset{\_}{f}}_2\left(0\right)\right],\left[s^{\alpha }l\left[{\overline{f}}_1\left(x\right);s\right]-s^{\alpha -1}{\overline{f}}_1\left(0\right),s^{\alpha }l\left[{\underset{\_}{f}}_1\left(x\right);s\right]-s^{\alpha -1}{\underset{\_}{f}}_1\left(0\right)\right]\right] \\ =\left[\left[\mathit{l}\left[{CFD\left({\overline{f}}_2\left(x\right)\right)}_a^{\alpha };s\right], \right]\mathit{l}\left[{CFD\left({\underset{\_}{f}}_2\left(x\right)\right)}_a^{\alpha };s\right],\left[\mathit{l}\left[{CFD\left({\overline{f}}_1\left(x\right)\right)}_a^{\alpha };s\right],\mathit{l}\left[{CFD\left({\underset{\_}{f}}_1\left(x\right)\right)}_a^{\alpha };s\right]\right]\right] \\ =\mathcal{L}\left[{I2CFD\left(\mathcal{F}\left(x\right)\right)}_a^{\alpha };s\right] \end{gathered}$$

□

Theorem 14. 

Let $\mathcal{F}$ and $\mathcal{G}$ be two continuous Type 2 interval-valued functions defined as $[0,\infty )$; $\mathcal{A}$ and $\mathcal{B}$ are two Type 2 interval numbers. Also, let Type 2 interval conformable Laplace transformations $\mathcal{L}\left[\mathcal{F}\left(x\right);s\right]$ and $\mathcal{L}\left[\mathcal{G}\left(x\right);s\right]$ exist. Then, $\mathcal{L}\left[\left\{\mathcal{A}⊡\mathcal{F}\left(x\right)\right\}⊞\left\{\mathcal{B}⊡\mathcal{G}\left(x\right)\right\};s\right]=\{\mathcal{A}⊡\mathcal{L}[\mathcal{F}\left(x\right);s\left]\right\}⊞\left\{\mathcal{B}⊡\mathcal{L}\left[\mathcal{G}\left(x\right);s\right]\right\}$.

Proof. 

The proof is straightforward and is omitted. □

7. Application of the Proposed Theory in Memory-Controlled Lot Sizing Policy

7.1. Notations and Hypothesis

The proposed EOQ model is developed under the following assumptions:

(i)

The demand during the retail process can be boosted by lowering the retail price. Then, the pricing and associated demand may go through two-layered interval uncertainty. Therefore, the demand ($D_2$) is dependent on the selling price, i.e., $D_2=l-k{p}_2$, where $l$ and $k$ are two positive crisp constants and $p_2=\left[\left[{\underset{\_}{p}}_1,{\overline{p}}_1\right],\left[{\underset{\_}{p}}_2,{\overline{p}}_2\right]\right]$ is a T2IN.

(ii)

Production is instantaneous and the lead time is zero. For the sake of simplicity, this hypothesis assumes that the replenishment will be executed as soon as the order is placed.

(iii)

The decision cycle ends when the inventory level reaches zero. The total consumption of production is equal to the lot size, and therefore, shortages are not allowed.

(iv)

The EOQ model is memory-sensitive, i.e., the demand depends on the customer’s memory of the previous experience with the shopkeeper’s behavior, the product’s quality, etc.

Table 1. Notations used in the EOQ model and their meanings.

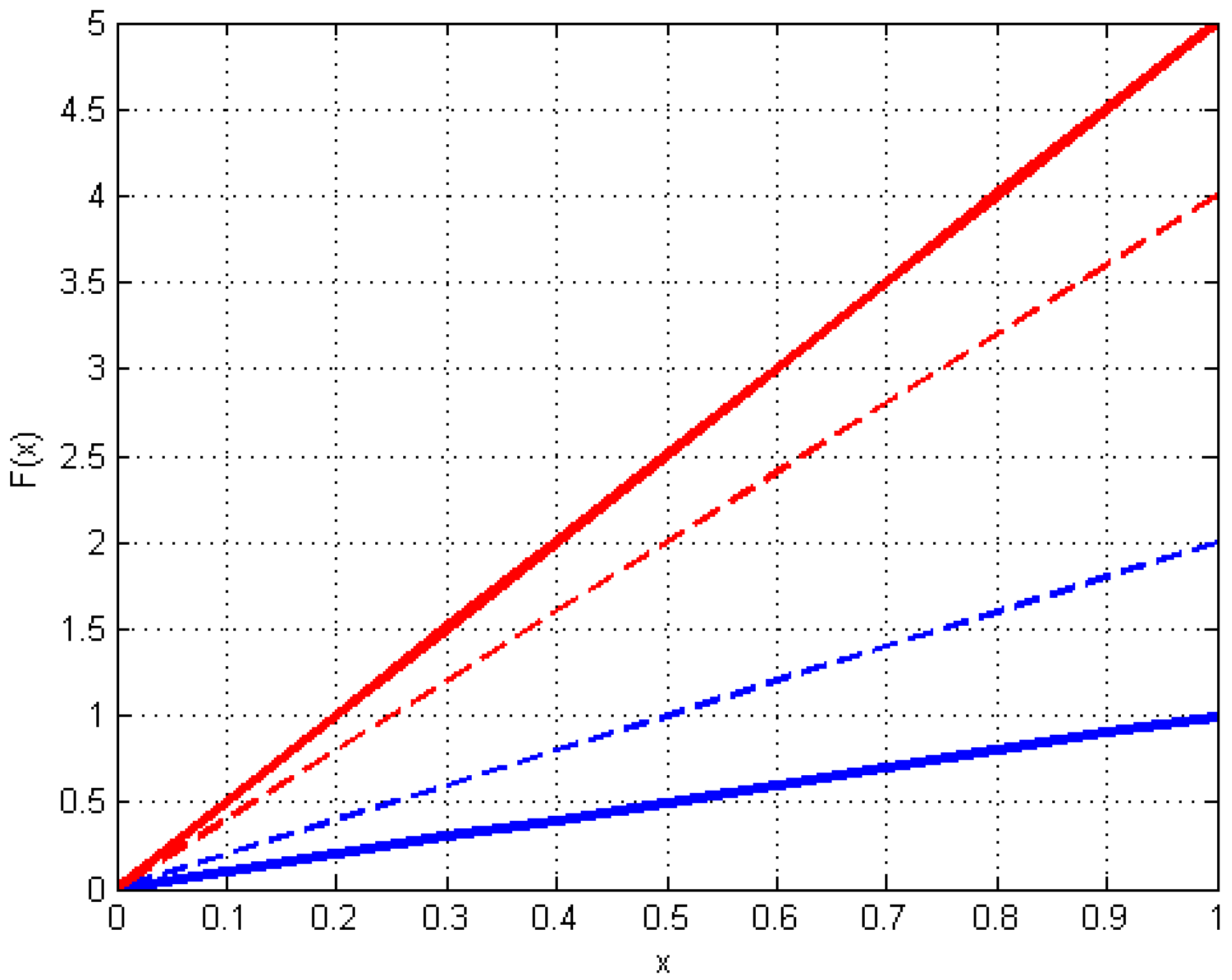
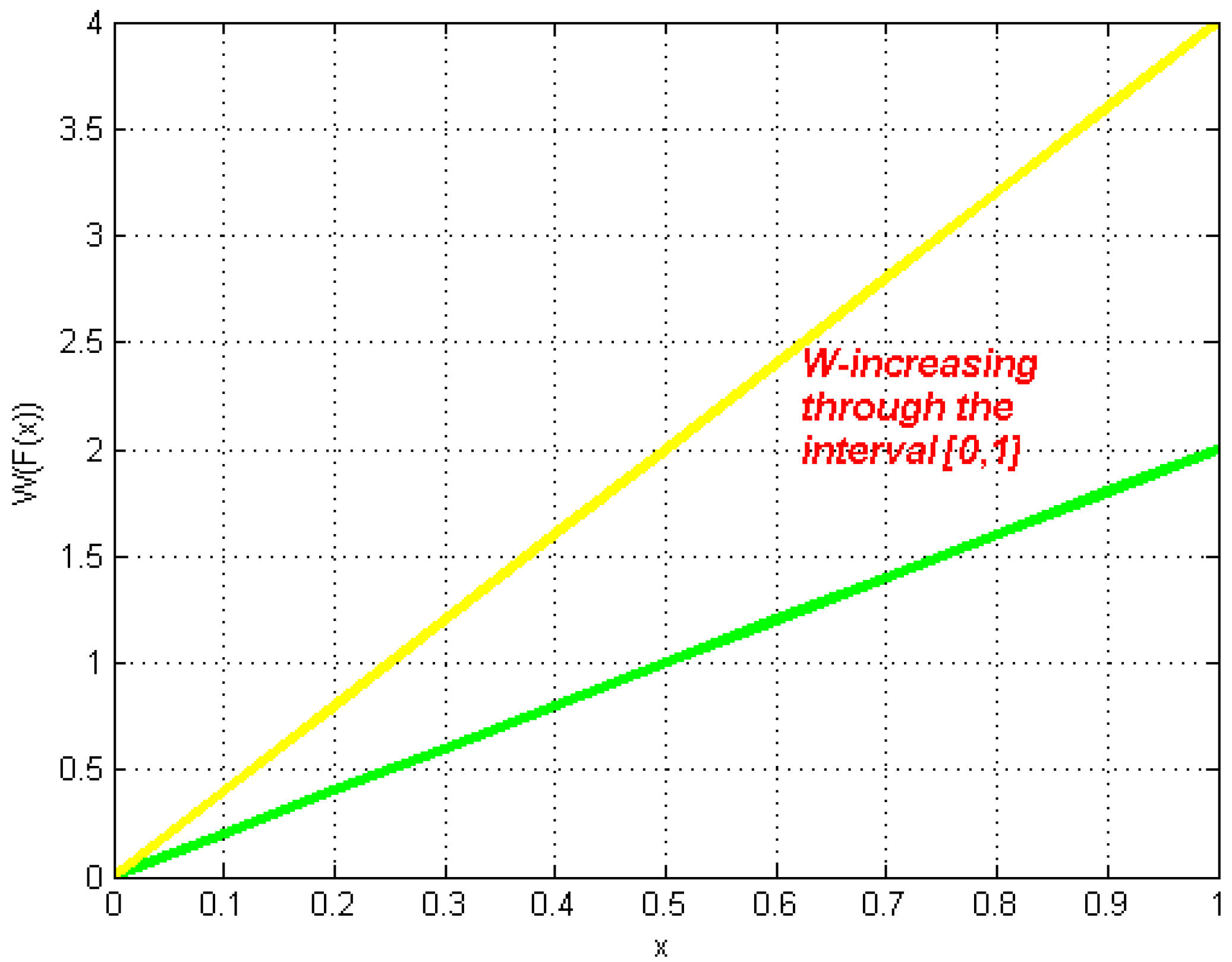
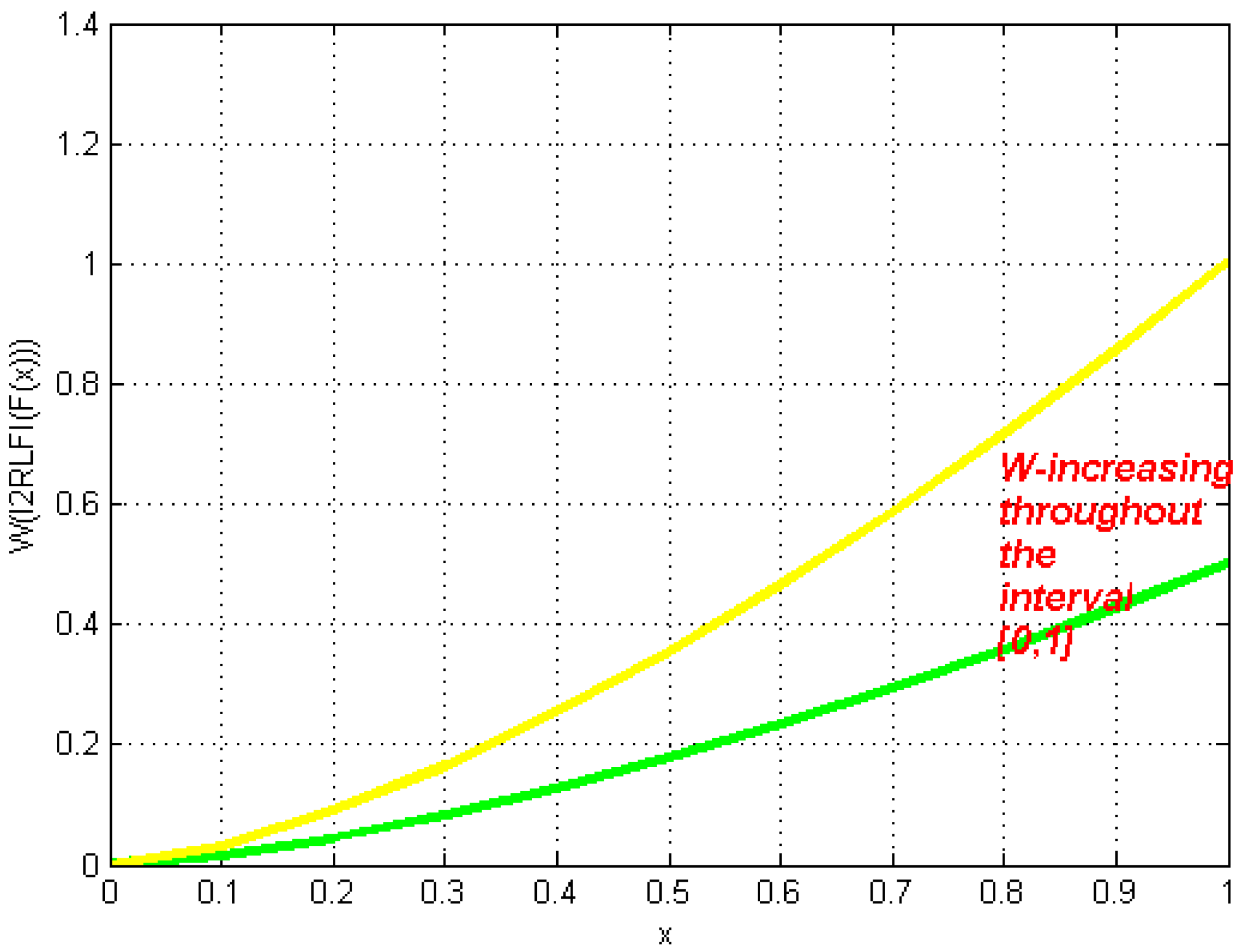
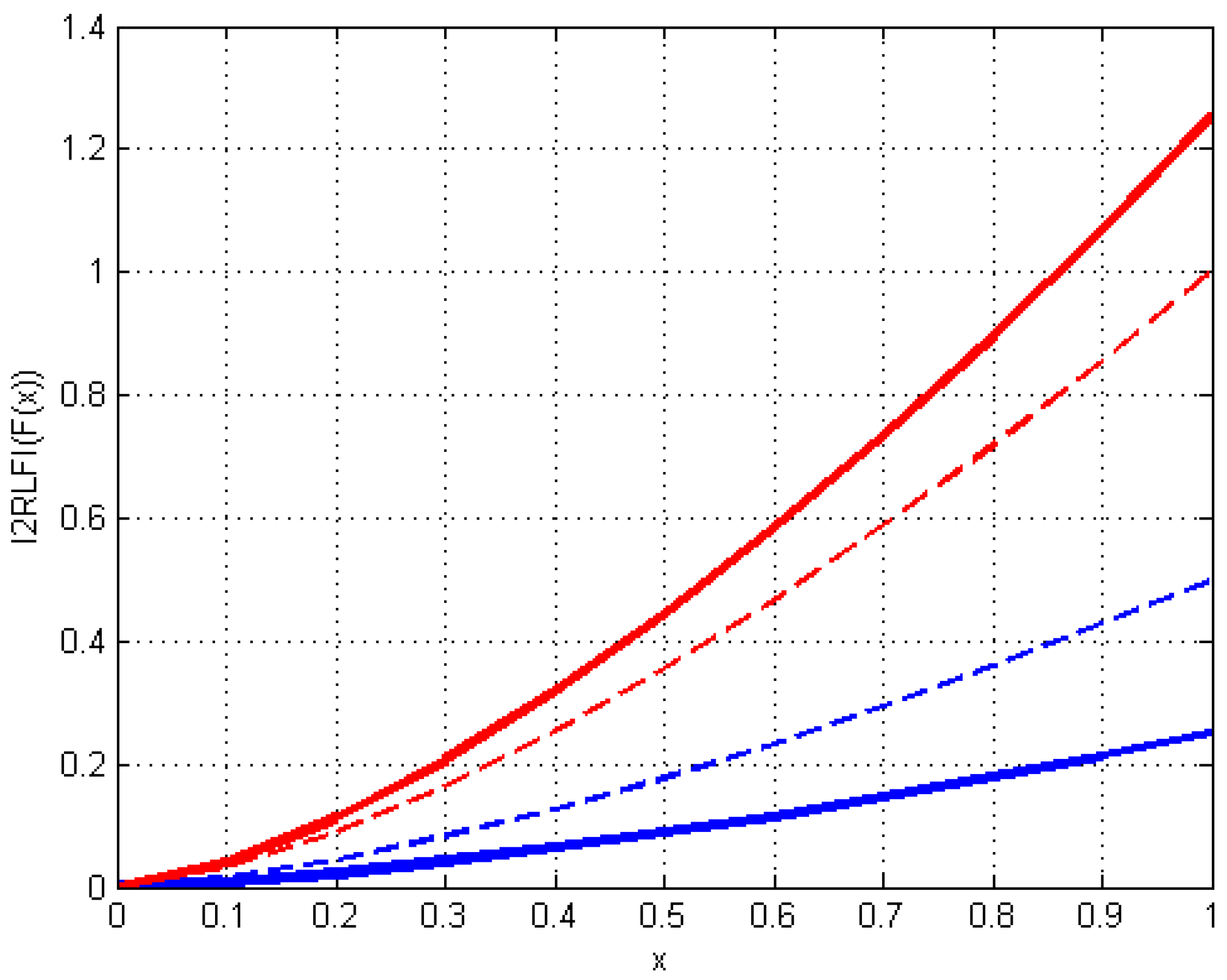
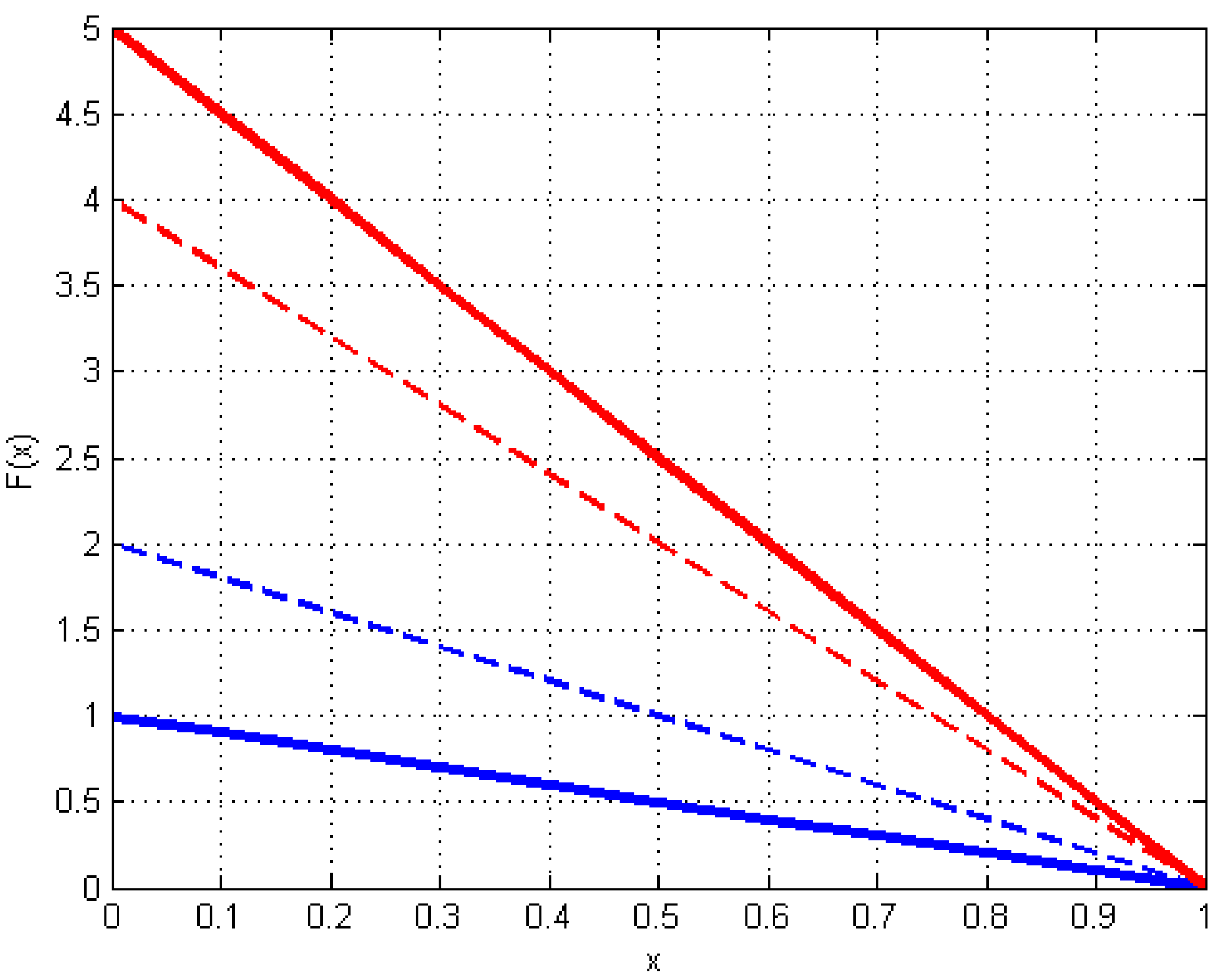
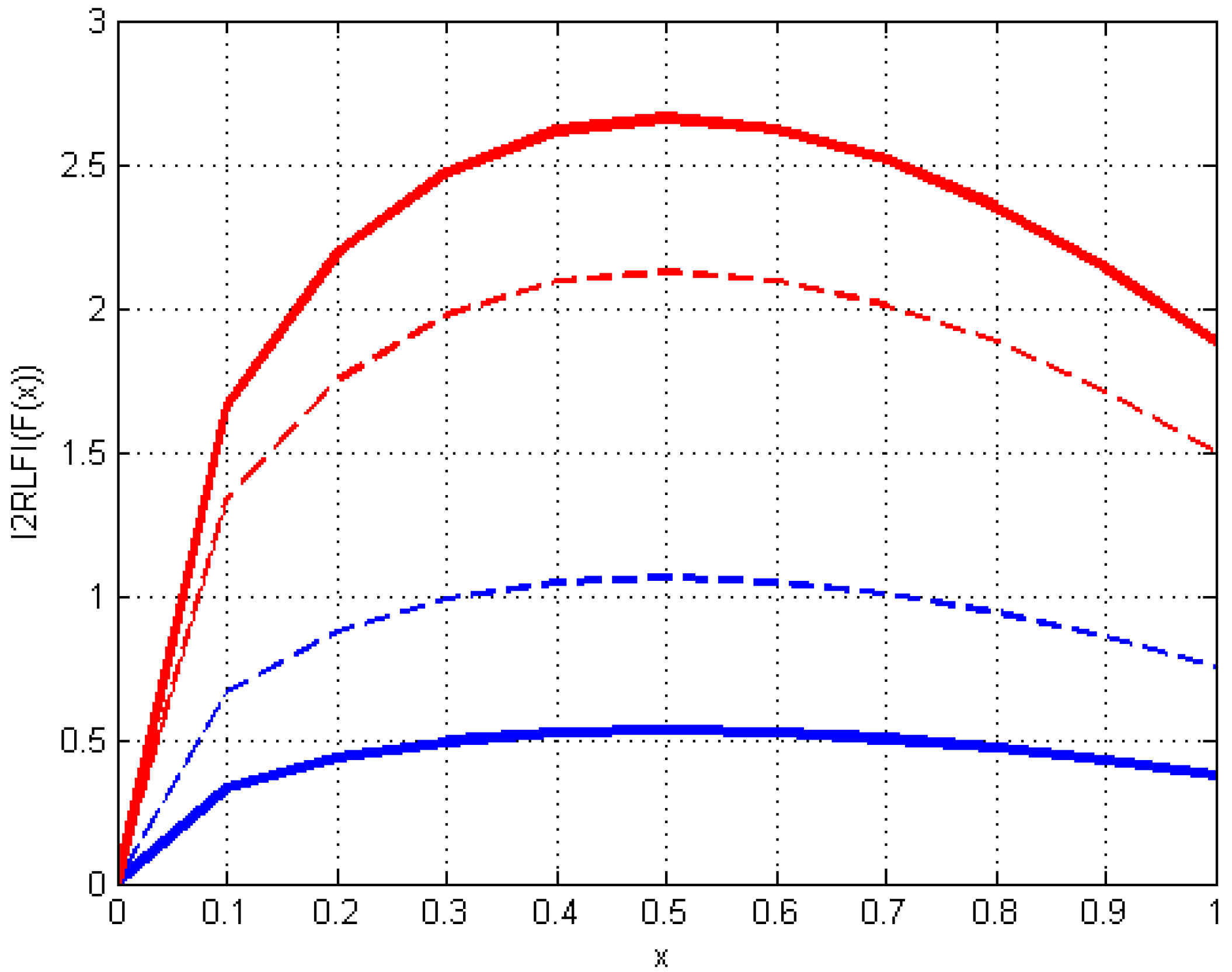
Notation	Meaning
$D_2=\left[\left[{\underset{\_}{d}}_1,{\overline{d}}_1\right],\left[{\underset{\_}{d}}_2,{\overline{d}}_2\right]\right]$	Demand (units)
$p_2=\left[\left[{\underset{\_}{p}}_1,{\overline{p}}_1\right],\left[{\underset{\_}{p}}_2,{\overline{p}}_2\right]\right]$	Selling price (USD/units)
$I_2\left(t\right)=\left[\left[{\underset{\_}{i}}_1\left(t\right),{\overline{i}}_1\left(t\right)\right],\left[{\underset{\_}{i}}_2\left(t\right),{\overline{i}}_2\left(t\right)\right]\right]$	Inventory level at time $t$
$Q_2=\left[\left[{\underset{\_}{Q}}_1,{\overline{Q}}_1\right],\left[{\underset{\_}{Q}}_2,{\overline{Q}}_2\right]\right]$	Lot size (units)
$T$	Total time cycle (month) (decision variable)
$\alpha$	Differential memory index (decision variables)
$\beta$	Integral memory index (decision variables)
$hc$	Holding cost (per unit per unit time)
$pc$	Purchasing cost (per unit per unit time)
$C$	Ordering cost (per complete cycle)
${AP}_2=\left[\left[{\underset{\_}{AP}}_1,{\overline{AP}}_1\right],\left[{\underset{\_}{AP}}_2,{\overline{AP}}_2\right]\right]$	Average profit (USD) (objective function)

describes the notations that are used to denote the parameters, decision variables, and objective functions involved in developing and optimizing the model:

7.2. Description of Model

The retail lot management scenario starts with a lot size $Q_2=\left[\left[{\underset{\_}{Q}}_1,{\overline{Q}}_1\right],\left[{\underset{\_}{Q}}_2,{\overline{Q}}_2\right]\right]$ at time $t=0$. The inventory level decreases as time progresses, meeting the demand at the rate of $D_2=\left[\left[{\underset{\_}{d}}_1,{\overline{d}}_1\right],\left[{\underset{\_}{d}}_2,{\overline{d}}_2\right]\right]$. The retail cycle and whole decision cycle are terminated $t=T$, reaching the zero level of inventory. The memory of the system can be interpreted by a fractional differential equation. In this model, the Type 2 interval uncertainty and memory are considered simultaneously. Therefore, a Type 2 interval-valued Caputo fractional differential equation can describe the memory-impacted uncertain retail process as follows:

$${I2CFD\left(I_2\left(t\right)\right)}_a^{\alpha }=-D_2$$

(3)

Since the inventory management scenario starts with lot size $Q_2$ and reaches the zero level upon completing the decision cycle, the boundary conditions regarding the stock level can be written as follows:

$$\left\{\begin{array}{c}{I}_2\left(0\right)=Q_{2,}\\ I_2\left(T\right)=0.\end{array}\right.$$

(4)

The demand becomes uncertain with the Type 2 interval due to the uncertain pricing, and the relation is obtained as $D_2=l-k{p}_2$. Therefore, Equation (3) can be rewritten as follows:

$${I2CFD\left(I_2\left(t\right)\right)}_a^{\alpha }=-(l-k{p}_2)$$

(5)

There is no conventional approach to solving Type 2 interval-valued fraction differential Equation (5) in the existing literature. We will use the Laplace transformation for the Type 2 interval-valued function defined in the previous section in this paper. Taking Type 2 interval-valued Laplace transformation of (5), we obtain:

$$\mathcal{L}\left[{I2CFD\left(I_2\left(t\right)\right)}_a^{\alpha };s\right]=-\mathcal{L}\left[\left(l-k{p}_2\right);s\right]$$

(6)

We consider the following two cases regarding the differentiability of the time-dependent inventory function.

Case 1: $I_2\left(t\right)$ is a Type 2 interval-valued Caputo gH fractional differentiable of the first type.

In the context of differentiability of the first type, Equation (6) provides the following system:

$$\left\{\begin{array}{c}\begin{array}{c}l\left[{\underset{\_}{i}}_1\left(t\right);s\right]={\displaystyle \frac{{\underset{\_}{Q}}_1}{s}}-{\displaystyle \frac{\left(l-k{\underset{\_}{p}}_1\right)}{s^{\alpha +1}}},\\ l\left[{\overline{i}}_1\left(t\right);s\right]={\displaystyle \frac{{\overline{Q}}_1}{s}}-{\displaystyle \frac{\left(l-k{\overline{p}}_1\right)}{s^{\alpha +1}}},\end{array}\\ \begin{array}{c}l\left[{\underset{\_}{i}}_2\left(t\right);s\right]={\displaystyle \frac{{\underset{\_}{Q}}_2}{s}}-{\displaystyle \frac{\left(l-k{\underset{\_}{p}}_2\right)}{s^{\alpha +1}}},\\ l\left[{\overline{i}}_2\left(t\right);s\right]={\displaystyle \frac{{\overline{Q}}_2}{s}}-{\displaystyle \frac{\left(l-k{\overline{p}}_2\right)}{s^{\alpha +1}}}.\end{array}\end{array}\right.$$

(7)

In Equation (7), $l\left[{\underset{\_}{i}}_1\left(t\right);s\right]$, $l\left[{\overline{i}}_1\left(t\right);s\right]$, $l\left[{\underset{\_}{i}}_2\left(t\right);s\right],$ and $l\left[{\overline{i}}_2\left(t\right);s\right]$ are Laplace transformations of ${\underset{\_}{i}}_1\left(t\right)$, ${\overline{i}}_1\left(t\right)$,${\underset{\_}{i}}_2\left(t\right)$, and ${\overline{i}}_2\left(t\right)$, respectively, in a crisp environment. Taking the inverse Laplace transformation of the equations in (7), the inventory level at $t$ is obtained as follows:

$$\left\{\begin{array}{c}\begin{array}{c}{\underset{\_}{i}}_1\left(t\right)={\displaystyle \frac{\left(l-k{\underset{\_}{p}}_1\right){(T^{\alpha }-t}^{\alpha })}{\mathsf{\Gamma }\left(\alpha +1\right)}},\\ {\overline{i}}_1\left(t\right)={\displaystyle \frac{\left(l-k{\overline{p}}_1\right)\left(T^{\alpha }-t^{\alpha }\right)}{\mathsf{\Gamma }\left(\alpha +1\right)}},\end{array}\\ \begin{array}{c}{\underset{\_}{i}}_2\left(t\right)={\displaystyle \frac{\left(l-k{\underset{\_}{p}}_2\right){(T^{\alpha }-t}^{\alpha })}{\mathsf{\Gamma }\left(\alpha +1\right)}},\\ {\overline{i}}_2\left(t\right)={\displaystyle \frac{\left(l-k{\overline{p}}_2\right)\left(T^{\alpha }-t^{\alpha }\right)}{\mathsf{\Gamma }\left(\alpha +1\right)}}.\end{array}\end{array}\right.$$

(8)

${Q_2}^1$ represents the lot size $Q_2$ for Case 1. Using the initial condition $I_2\left(0\right)=Q_2$, the lot size ${Q_2}^1=\left[\left[{{\underset{\_}{Q}}_1}^1,{{\overline{Q}}_1}^1\right],\left[{{\underset{\_}{Q}}_2}^1,{{\overline{Q}}_2}^1\right]\right]$ is obtained as follows.

$$\left\{\begin{array}{c}\begin{array}{c}{{\underset{\_}{Q}}_1}^1={\displaystyle \frac{\left(l-k{\underset{\_}{p}}_1\right)T^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}},\\ {{\overline{Q}}_1}^1={\displaystyle \frac{\left(l-k{\overline{p}}_1\right)T^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}},\end{array}\\ \begin{array}{c}{{\underset{\_}{Q}}_2}^1={\displaystyle \frac{\left(l-k{\underset{\_}{p}}_2\right)T^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}},\\ {{\overline{Q}}_2}^1={\displaystyle \frac{\left(l-k{\overline{p}}_2\right)T^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}}.\end{array}\end{array}\right.$$

(9)

Purchasing cost: Since the purchasing cost per unit item is $pc$, the total purchasing cost can be obtained by taking product of $pc$ with the lot size ${Q_2}^1$. Hence, the total purchasing cost ${PC}_2=\left[\left[{\underset{\_}{PC}}_1,{\overline{PC}}_1\right],\left[{\underset{\_}{PC}}_2,{\overline{PC}}_2\right]\right]$ can be obtained as below:

$$\left\{\begin{array}{c}\begin{array}{c}{\underset{\_}{PC}}_1={\displaystyle \frac{\left(l-k{\underset{\_}{p}}_1\right)pc{T}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}},\\ {\overline{PC}}_1={\displaystyle \frac{\left(l-k{\overline{p}}_1\right)pc{T}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}},\end{array}\\ \begin{array}{c}{\underset{\_}{PC}}_2={\displaystyle \frac{\left(l-k{\underset{\_}{p}}_2\right)pc{T}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}},\\ {\overline{PC}}_2={\displaystyle \frac{\left(l-k{\overline{p}}_2\right)pc{T}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}}.\end{array}\end{array}\right.$$

(10)

Holding cost: Since the holding cost per unit item is $hc$, the total holding cost can be obtained by taking product of $hc$ with the total accumulated stock in store during the span $[0,T]$. Therefore, the total holding cost, ${HC}_2=\left[\left[{\underset{\_}{HC}}_1,{\overline{HC}}_1\right],\left[{\underset{\_}{HC}}_2,{\overline{HC}}_2\right]\right]$, can be obtained as below:

$$\left\{\begin{array}{c}\begin{array}{c}{\underset{\_}{HC}}_1={\displaystyle \frac{hc}{\mathsf{\Gamma }\left(\beta \right)}}{\int }_0^T{\left(T-t\right)}^{\beta -1}{\underset{\_}{i}}_1\left(t\right)dt=\phi \left(\alpha ,\beta ,T\right)\left(l-k{\underset{\_}{p}}_1\right),\\ {\overline{HC}}_1={\displaystyle \frac{hc}{\mathsf{\Gamma }\left(\beta \right)}}{\int }_0^T{\left(T-t\right)}^{\beta -1}{\overline{i}}_1\left(t\right)dt=\phi \left(\alpha ,\beta ,T\right)\left(l-k{\overline{p}}_1\right),\end{array}\\ \begin{array}{c}{\underset{\_}{HC}}_2={\displaystyle \frac{hc}{\mathsf{\Gamma }\left(\beta \right)}}{\int }_0^T{\left(T-t\right)}^{\beta -1}{\underset{\_}{i}}_2\left(t\right)dt=\phi \left(\alpha ,\beta ,T\right)\left(l-k{\underset{\_}{p}}_2\right),\\ {\overline{HC}}_2={\displaystyle \frac{hc}{\mathsf{\Gamma }\left(\beta \right)}}{\int }_0^T{\left(T-t\right)}^{\beta -1}{\overline{i}}_2\left(t\right)dt=\phi \left(\alpha ,\beta ,T\right)\left(l-k{\overline{p}}_2\right).\end{array}\end{array}\right.$$

(11)

where

$$\left[{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\beta +1\right)\mathsf{\Gamma }\left(\alpha +1\right)}}-{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha +\beta +1\right)}}\right]hc{T}^{\alpha +\beta }=\phi (\alpha ,\beta ,T)$$

(12)

Earned revenue: Since the two-layered uncertain selling price per unit item is $p_2=\left[\left[{\underset{\_}{p}}_1,{\overline{p}}_1\right],\left[{\underset{\_}{p}}_2,{\overline{p}}_2\right]\right]$, then the earned revenue can be obtained by taking product of $p_2$ with the cumulative supply for consumption during the span $[0,T]$. Then, the total earned revenue, ${ER}_2=\left[\left[{\underset{\_}{ER}}_1,{\overline{ER}}_1\right],\left[{\underset{\_}{ER}}_2,{\overline{ER}}_2\right]\right]$, can be obtained as below:

$$\left\{\begin{array}{c}\begin{array}{c}{\underset{\_}{ER}}_1={\displaystyle \frac{{\underset{\_}{p}}_1}{\mathsf{\Gamma }\left(\beta \right)}}{\int }_0^T{\left(T-t\right)}^{\beta -1}\left(l-k{\overline{p}}_2\right)dt={\underset{\_}{p}}_1\left(l-k{\overline{p}}_2\right)\omega \left(\beta ,T\right),\\ {\overline{ER}}_1={\displaystyle \frac{{\overline{p}}_1}{\mathsf{\Gamma }\left(\beta \right)}}{\int }_0^T{\left(T-t\right)}^{\beta -1}\left(l-k{\underset{\_}{p}}_2\right)dt={\overline{p}}_1\left(l-k{\underset{\_}{p}}_2\right)\omega \left(\beta ,T\right),\end{array}\\ \begin{array}{c}{\underset{\_}{ER}}_2={\displaystyle \frac{{\underset{\_}{p}}_2}{\mathsf{\Gamma }\left(\beta \right)}}{\int }_0^T{\left(T-t\right)}^{\beta -1}\left(l-k{\overline{p}}_1\right)dt={\underset{\_}{p}}_2\left(l-k{\overline{p}}_1\right)\omega \left(\beta ,T\right),\\ {\overline{ER}}_2={\displaystyle \frac{{\overline{p}}_2}{\mathsf{\Gamma }\left(\beta \right)}}{\int }_0^T{\left(T-t\right)}^{\beta -1}\left(l-k{\underset{\_}{p}}_2\right)dt={\overline{p}}_2\left(l-k{\underset{\_}{p}}_1\right)\omega \left(\beta ,T\right).\end{array}\end{array}\right.$$

(13)

where

$${\displaystyle \frac{T^{\beta }}{\mathsf{\Gamma }(\beta +1)}}=\omega (\beta ,T)$$

(14)

Average profit: ${{AP}_2}^1$ represents the average profit ${AP}_2$ for Case 1. We know that $Average profit={\displaystyle \frac{Earned revenue-total cost}{Time duration}}$. Since all costs and earned revenue have been obtained as Type 2 interval-valued functions, the average profit, ${{AP}_2}^1=\left[\left[{{\underset{\_}{AP}}_1}^1,{{\overline{AP}}_1}^1\right],\left[{{\underset{\_}{AP}}_2}^1,{{\overline{AP}}_2}^1\right]\right]$, can be obtained as below:

$$\left\{\begin{array}{c}\begin{array}{c}{{\underset{\_}{AP}}_1}^1={\displaystyle \frac{{\underset{\_}{p}}_1\left(l-k{\overline{p}}_2\right)\omega \left(\beta ,T\right)-C-\frac{\left(l-k{\overline{p}}_2\right)pc{T}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}-\phi (\alpha ,\beta ,T)\left(l-k{\overline{p}}_2\right)}{T}},\\ {{\overline{AP}}_1}^1={\displaystyle \frac{{\overline{p}}_1\left(l-k{\underset{\_}{p}}_2\right)\omega \left(\beta ,T\right)-C-\frac{\left(l-k{\underset{\_}{p}}_2\right)pc{T}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}-\phi (\alpha ,\beta ,T)\left(l-k{\underset{\_}{p}}_2\right)}{T}},\end{array}\\ \begin{array}{c}{{\underset{\_}{AP}}_2}^1={\displaystyle \frac{{\underset{\_}{p}}_2\left(l-k{\overline{p}}_1\right)\omega \left(\beta ,T\right)-C-\frac{\left(l-k{\overline{p}}_1\right)pc{T}^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}-\phi (\alpha ,\beta ,T)\left(l-k{\overline{p}}_1\right)}{T}},\\ {{\overline{AP}}_2}^1={\displaystyle \frac{{\overline{p}}_2\left(l-k{\underset{\_}{p}}_1\right)\omega \left(\beta ,T\right)-C-\frac{\left(l-k{\underset{\_}{p}}_1\right)pc{T}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}-\phi (\alpha ,\beta ,T)\left(l-k{\underset{\_}{p}}_1\right)}{T}}.\end{array}\end{array}\right.$$

(15)

Therefore, the optimization problem for the proposed model can be written mathematically in the following form:

$$\left\{\begin{array}{c}\begin{array}{c}Max{{\underset{\_}{AP}}_1}^1\\ Max{{\overline{AP}}_1}^1\\ Max{{\underset{\_}{AP}}_2}^1\end{array}\\ \begin{array}{c}Max{{\overline{AP}}_2}^1\\ \mathrm{S}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t} \mathrm{t}\mathrm{o} 0\le \alpha ,\beta <1 \mathrm{a}\mathrm{n}\mathrm{d} T>0,\\ {{\underset{\_}{Q}}_1}^1={\displaystyle \frac{\left(l-k{\underset{\_}{p}}_1\right)T^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}},\end{array}\\ \begin{array}{c}{{\overline{Q}}_1}^1={\displaystyle \frac{\left(l-k{\overline{p}}_1\right)T^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}},\\ {{\underset{\_}{Q}}_2}^1={\displaystyle \frac{\left(l-k{\underset{\_}{p}}_2\right)T^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}},\\ {{\overline{Q}}_2}^1={\displaystyle \frac{\left(l-k{\overline{p}}_2\right)T^{\alpha }}{\mathsf{\Gamma }\left(\alpha +1\right)}}.\end{array}\end{array}\right.$$

(16)

Case 2: $I_2\left(t\right)$ is a Type 2 interval-valued Caputo gH fractional differentiable of the second type. ${Q_2}^2$ represents the lot size $Q_2$ for Case 2. Proceeding similarly to Case 1, we obtain the lot size ${Q_2}^2=\left[\left[{{\underset{\_}{Q}}_1}^2,{{\overline{Q}}_1}^2\right],\left[{{\underset{\_}{Q}}_2}^2,{{\overline{Q}}_2}^2\right]\right]$ as follows:

$$\left\{\begin{array}{c}\begin{array}{c}{{\underset{\_}{Q}}_1}^2={\displaystyle \frac{\left(l-k{\overline{p}}_2\right)T^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}},\\ {{\overline{Q}}_1}^2={\displaystyle \frac{\left(l-k{\underset{\_}{p}}_2\right)T^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}},\end{array}\\ \begin{array}{c}{{\underset{\_}{Q}}_2}^2={\displaystyle \frac{\left(l-k{\overline{p}}_1\right)T^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}},\\ {{\overline{Q}}_2}^2={\displaystyle \frac{\left(l-k{\underset{\_}{p}}_1\right)T^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}}.\end{array}\end{array}\right.$$

(17)

Average profit: ${{AP}_2}^1$ represents the average profit ${AP}_2$ for Case 1. Therefore, the total average profit, ${{AP}_2}^2=\left[\left[{{\underset{\_}{AP}}_1}^2,{{\overline{AP}}_1}^2\right],\left[{{\underset{\_}{AP}}_2}^2,{{\overline{AP}}_2}^2\right]\right]$, can be obtained as follows:

$$\left\{\begin{array}{c}\begin{array}{c}{{\underset{\_}{AP}}_1}^2={\displaystyle \frac{{\underset{\_}{p}}_1\left(l-k{\overline{p}}_2\right)\omega \left(\beta ,T\right)-C-\frac{\left(l-k{\underset{\_}{p}}_1\right)pc{T}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}-\phi (\alpha ,\beta ,T)\left(l-k{\underset{\_}{p}}_1\right)}{T}},\\ {{\overline{AP}}_1}^2={\displaystyle \frac{{\overline{p}}_1\left(l-k{\underset{\_}{p}}_2\right)\omega \left(\beta ,T\right)-C-\frac{\left(l-k{\overline{p}}_1\right)pc{T}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}-\phi (\alpha ,\beta ,T)\left(l-k{\overline{p}}_1\right)}{T}},\end{array}\\ \begin{array}{c}{{\underset{\_}{AP}}_2}^2={\displaystyle \frac{{\underset{\_}{p}}_2\left(l-k{\overline{p}}_1\right)\omega \left(\beta ,T\right)-C-\frac{\left(l-k{\underset{\_}{p}}_2\right)pc{T}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}-\phi (\alpha ,\beta ,T)\left(l-k{\underset{\_}{p}}_2\right)}{T}},\\ {{\overline{AP}}_2}^2={\displaystyle \frac{{\overline{p}}_2\left(l-k{\underset{\_}{p}}_1\right)\omega \left(\beta ,T\right)-C-\frac{\left(l-k{\overline{p}}_2\right)pc{T}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}-\phi (\alpha ,\beta ,T)\left(l-k{\overline{p}}_2\right)}{T}}.\end{array}\end{array}\right.$$

(18)

Therefore, the optimization problem for the proposed model can be written mathematically in the following form:

$$\left\{\begin{array}{c}\begin{array}{c}Max{{\underset{\_}{AP}}_1}^2\\ Max{{\overline{AP}}_1}^2\\ Max{{\underset{\_}{AP}}_2}^2\end{array}\\ \begin{array}{c}Max{{\overline{AP}}_2}^2\\ \mathrm{S}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t} \mathrm{t}\mathrm{o} 0\le \alpha ,\beta <1 \mathrm{a}\mathrm{n}\mathrm{d} T>0,\\ {{\underset{\_}{Q}}_1}^2={\displaystyle \frac{\left(l-k{\overline{p}}_2\right)T^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}},\end{array}\\ \begin{array}{c}{{\overline{Q}}_1}^2={\displaystyle \frac{\left(l-k{\underset{\_}{p}}_2\right)T^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}},\\ {{\underset{\_}{Q}}_2}^2={\displaystyle \frac{\left(l-k{\overline{p}}_1\right)T^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}}\\ {{\overline{Q}}_2}^2={\displaystyle \frac{\left(l-k{\underset{\_}{p}}_1\right)T^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}}.\end{array},\end{array}\right.$$

(19)

7.3. Numerical Result

The following numerical inputs are considered when executing the numerical optimization of the proposed inventory scenario in both cases: $pc=7$; $hc=2.5$; $p_2=\left[\left[17,18\right],\left[20,21\right]\right]$; $l=300$; $b=0.5$; $S=3000$. The systems given by Equations (16) and (19) are numerically optimized using the Mathematica software. In both cases, the classical memory-free scenarios correspond to the unity values of the integral and differential index. Thus, for the Type 2 interval-valued Caputo gH fractional differentiable of the first type with $\mathsf{\alpha }=\mathsf{\beta }=1$, the optimal average profit (${AP}_2$) is obtained as a Type 2 interval number [[−636.39, −345.68], [827.15, 1122.86]] where the best lot size ($Q_2$) is [[837.85, 836.42], [830.69, 829.26]] and the optimal lot cycle ($T$) is 2.864. We notice that the obtained best lot size inverts and violates the rule for being a Type 2 interval number. In such a case, we need to correct the result. Thus, the corrected optimal lot size will be [[829.26, 830.69], [836.42, 837.85]], a Type 2 interval number. After obtaining the best results corresponding to the memory-free case, we address the impacts of memory on the proposed model in the aforementioned cases. The results regarding the memory sensitivity of the model for Case 1 are displayed in

Table 2. Optimal solution for different differential memory index in Case 1 of EOQ.

α	$\mathit{T}$	${\mathit{Q}}_2$	${\mathit{A}\mathit{P}}_2$
1	2.864	[[837.85, 836.42], [830.69, 829.26]]	[[−636.39, −345.68], [827.15, 1122.86]]
0.9	3.753	[[1000.01, 998.30], [991.46, 989.75]]	[[−266.11, 24.81], [1198.50, 1494.42]]
0.8	5.147	[[1164.84, 1162.85], [1154.89, 1152.89]]	[[238.92, 530.34], [1706.02, 2002.44]]
0.7	7.361	[[1301.94, 1299.71], [1290.81, 1288.59]]	[[857.90, 1150.09], [2328.83, 2626.02]]
0.6	10.98	[[1378.45, 1376.09], [1366.67, 1364.31]]	[[1547.72, 1840.87], [3023.45, 3321.59]]
0.5	17.252	[[1370.89, 1368.54], [1359.17, 1356.83]]	[[2251.45, 2545.64], [3732.39, 4031.58]]
0.4	29.254	[[1272.17, 1269.99], [1261.30, 1259.12]]	[[2910.16, 3205.36], [4396.18, 4696.38]]
0.3	56.315	[[1092.18, 1090.31], [1082.84,1080.97]]	[[3473.64, 3769.73], [4964.09, 5265.19]]
0.2	138.171	[[853.66, 852.20], [846.37, 844.91]]	[[3907.59, 4204.38], [5401.53, 5703.31]]
0.1	621.65	[[584.98, 583.98], [579.98, 578.78]]	[[4196.77, 4494.03], [5693.06, 5995.31]]

,

Table 3. Optimal solution for different integral memory index in Case 1 of EOQ.

β	$\mathit{T}$	${\mathit{Q}}_2$	${\mathit{A}\mathit{P}}_2$
1	2.864	[[837.85, 836.42], [830.69, 839.26]]	[[−636.39, −345.68], [827.15, 1122.86]]
0.9	2.338	[[$684.00, 682.83$], [$678.15, 676.98$]]	[[−796.16, −518.34], [602.46, 885.04]]
0.8	1.849	[[540.71, 539.79], [536.09, 535.17]]	[[−959.19, −682.68], [432.84, 714.09]]
0.7	1.413	[[413.17, 412.46], [409.64, 408.93]]	[[−1127.79, −838.33], [329.45, 623.87]]
0.6	1.034	[[302.48, 301.96], [299.89, 299.37]]	[[−1310.72, −987.74], [315.23, 643.73]]
0.5	0.709	[[207.36, 207.01], [205.59, 205.24]]	[[−1536.33, −1143.03], [443.56, 843.56]]
0.4	0.433	[[126.54, 126.32], [125.46, 125.24]]	[[−1904.85, −1355.79], [859.05, 1417.42]]
0.3	0.208	[[60.94, 60.84], [60.42, 60.32]]	[[−2903.67, −1915.02], [2072.97, 3078.33]]
0.2	0.055	[[16.16, 16.14], [16.03, 16.00]]	[[−9295.04, −6014.63], [7217.44, 10553.10]]
0.1	0.001	[[0.39, 0.39], [0.39, 0.39]]	[[−481333.57, −361310.14], [122818.13, 244858.84]]

and

Table 4. Optimal solution for memory index in Case 1 of EOQ.

$\mathit{\alpha }=\mathit{\beta }$	$\mathit{T}$	${\mathit{Q}}_2$	${\mathit{A}\mathit{P}}_2$
1	2.684	[[837.85, 836.42], [830.69, 829.26]]	[[−636.39, −345.68], [827.15, 1122.86]]
0.9	3.035	[[826.04, 824.62], [818.98, 817.56]]	[[−494.09, −223.39], [868.70, 1144.05]]
0.8	3.171	[[790.65, 789.30], [783.89, 782.54]]	[[−367.89, −119.17], [881.55, 1134.00]]
0.7	3.196	[[725.99, 724.75], [719.78, 718.54]]	[[−282.39, −56.02], [857.23, 1087.48]]
0.6	3.043	[[638.24, 637.14], [632.78, 631.69]]	[[−259.81, −50.59], [793.46, 1006.26]]
0.5	2.731	[[545.45, 544.52], [540.79, 539.86]]	[[−307.85, −108.48], [695.82, 898.61]]
0.4	2.339	[[463.14, 462.35], [459.18, 458.39]]	[[−422.70, −224.93], [572.91, 774.06]]
0.3	1.922	[[296.49, 395.81], [393.10, 392.42]]	[[−608.19, −402.02], [429.72, 639.42]]
0.2	1.476	[[344.35, 343.77], [341.41, 340.82]]	[[−912.02, −678.73], [262.39, 499.66]]
0.1	0.891	[[303.94, 303.42], [301.34, 300.82]]	[[−1690.78, −1349.80], [25.76, 372.57]]

.

For the Type 2 interval-valued Caputo gH fractional differentiable of the second type with $\mathsf{\alpha }=\mathsf{\beta }=1$, the optimal average profit (${AP}_2$) as Type 2 interval number [[−677.16, −372.86], [854.33, 1163.63]] is obtained where the best lot size ($Q_2$) is [[833.55, 834.99], [840.74, 842.18]] and the optimal lot cycle ($T$) is 2.879. In this case, we notice that the obtained best lot size satisfies the rule for being a Type 2 interval number. After receiving the best results corresponding to the memory-free case, we address the impacts of memory on the proposed model in the aforementioned cases. The results regarding the memory sensitivity of the model for Case 2 are displayed in

Table 5. Optimal solution for different differential memory index in Case 2 of EOQ.

$\mathit{\alpha }$	$\mathit{T}$	${\mathit{Q}}_2$	${\mathit{A}\mathit{P}}_2$
1	2.879	[[833.55, 834.99], [840.74, 842.18]]	[[−677.16, −372.86], [854.33, 1163.63]]
0.9	3.77	[[993.87, 995.59], [1002.46, 1004.17]]	[[−305.60, −1.51], [1224.83, 1533.91]]
0.8	5.168	[[1156.59, 1158.59], [1166.58, 1168.58]]	[[202.42, 506.01], [1730.35, 2038.93]]
0.7	7.386	[[1291.69, 1293.92], [1302.85, 1205.08]]	[[826.01, 1128.83], [2350.09, 2657.91]]
0.6	11.013	[[1366.77, 1369.13], [1378.57, 1380.13]]	[[1521.59, 1823.45], [3040.87, 3347.73]]
0.5	17.299	[[1358.68, 1361.03], [1370.41, 1372.76]]	[[2231.58, 2532.39], [3745.64, 4051.45]]
0.4	29.33	[[1260.44, 1262.62], [1271.33, 1273.50]]	[[2896.38, 3196.18], [4405.36, 4710.16]]
0.3	56.466	[[1081.85, 1083.71], [1091.19, 1093.06]]	[[3465.18, 3764.09], [4969.73, 5273.64]]
0.2	138.583	[[845.41, 846.87], [852.71,854.17]]	[[3903.31,4201.52], [5404.38, 5707.59]]
0.1	623.905	[[579.19, 580.19], [584.19, 585.19]]	[[4195.31, 4493.06], [5694.03, 5996.77]]

,

Table 6. Optimal solution for different integral memory index in Case 2 of EOQ.

$\mathit{\beta }$	$\mathit{T}$	${\mathit{Q}}_2$	${\mathit{A}\mathit{P}}_2$
1	2.879	[[833.55, 834.99], [840.74, 842.18]]	[[−677.16, −372.86], [854.33, 1163.63]]
0.9	2.348	[[679.61, 680.78], [685.48, 686.65]]	[[−833.44, −543.09], [627.87, 922.99]]
0.8	1.854	[[536.60, 537.53], [541.24, 542.16]]	[[−994.13, −705.82], [456.90, 749.95]]
0.7	1.415	[[409.63, 410.34], [413.17, 413.87]]	[[−1161.21, −860.45], [352.49, 658.20]]
0.6	1.035	[[299.67, 300.19], [302.26, 302.78]]	[[−1343.14, −1009.22], [337.51, 676.95]]
0.5	0.709	[[205.34, 205.70], [207.12, 207.47]]	[[−1568.06, −1164.08], [465.25, 875.94]]
0.4	0.433	[[125.27, 125.49], [126.35, 126.57]]	[[−1936.08, −1376.54], [880.29, 1449.15]]
0.3	0.208	[[60.32, 60.42], [60.84, 60.95]]	[[−2934.52, −1945.53], [2093.84, 3109.53]]
0.2	0.055	[[16.00, 16.03], [16.14, 16.17]]	[[−9325.58, −6034.95], [7237.99, 10583.83]]
0.1	0.001	[[0.39, 0.39], [0.39,0.39]]	[[−481363.83, −361330.30], [122838.39, 244889.21]]

and

Table 7. Optimal solution for different memory index in Case 2 of EOQ.

$\mathit{\alpha }=\mathit{\beta }$	$\mathit{T}$	${\mathit{Q}}_2$	${\mathit{A}\mathit{P}}_2$
1	2.879	[[833.55, 834.99], [840.74, 842.18]]	[[−677.16, −372.86], [854.33, 1163.63]]
0.9	3.044	[[819.66, 8221.08], [826.74, 828.15]]	[[−530.27, −247.50], [893.29, 1180.81]]
0.8	3.168	[[781.94, 783.29], [788.69, 790.04]]	[[−400.55, −141.53], [903.08, 1166.36]]
0.7	3.175	[[715.33, 716.56], [721.51, 722.74]]	[[−313.24, −77.03], [875.55, 1115.65]]
0.6	3.005	[[626.93, 628.01], [632.34, 633.42]]	[[−291.14, −72.57], [808.89, 1031.06]]
0.5	2.681	[[534.87, 535.80], [539.49, 540.42]]	[[−241.94, −133.13], [708.98, 921.24]]
0.4	2.283	[[453.91, 454.69], [457.83, 458.61]]	[[−462.50, −254.50], [584.33, 795.76]]
0.3	1.86	[[388.60, 389.27], [391.95, 392.63]]	[[−659.65, −441.25], [439.53, 661.53]]
0.2	1.407	[[337.58, 338.16], [340.49, 341.07]]	[[−992.82, −742.02], [269.47, 524.42]]
0.1	0.812	[[298.02, 298.53], [300.59, 301.11]]	[[−1912.01, −1528.32], [19.16, 409.20]]

.

7.4. Discussions and Managerial Insights

We summarize the results obtained in six tables, including the following major points.

(i)

We consider both cases of Type 2 interval-valued Caputo gH fractional differentiability for the inventory-level function. The most significant distinguishing fact is that the first case produces an uncorrected lot size, but the latter does not, irrespective of the variable memory indices. The obtained lot sizes in the first case must be corrected in order to obtain a Type 2 interval number.

(ii)

Table 2 describes the sensitivity of the optimal solution concerning the differential memory index for a fixed integral memory index as unity for Case 1. Table 2 shows that diminishing the differential memory index can enhance the average profit. Table 3 describes the sensitivity of the optimal solution with respect to the integral memory index for a fixed differential memory index as unity for Case 1. Table 3 establishes that the average profit deviates more from the Type 2 interval number as the integral memory index is lowered. That strong integral memory contributes to more imprecision regarding the average profit. Table 4 describes the sensitivity of the optimal solution with respect to both memory indexes for Case 1. Table 4 does not follow any specific pattern in the first three rows. However, the remaining row in that table shows that the average profit decreases as the memory index is lowered simultaneously.

(iii)

Table 5 describes the sensitivity of the optimal solution with respect to the differential memory index for a fixed integral memory index as unity for Case 2. Table 5 shows that diminishing the differential memory index can enhance the average profit. Table 6 describes the sensitivity of the optimal solution with respect to the integral memory index for a fixed differential memory index as unity for Case 2. Table 6 establishes that the average profit deviates more from the Type 2 interval number as the integral memory index is lowered. That is, strong integral memory contributes to more imprecision regarding the average profit. Table 7 describes the sensitivity of the optimal solution with respect to both memory indexes for Case 2. The first five rows of Table 7 do not follow any specific pattern. However, the remaining row in that table shows that the average profit decreases as the memory index is lowered simultaneously.

(iv)

The second case does not need any correction in the obtained solution. In this sense, the case is preferable to the first for the order quantity model. The smaller values of the memory indices imply stronger memory sense. Thus, the proposed inventory model faces profit reductions due to the presence of hard memory sense.

8. Conclusions

This paper introduced fractional calculus for Type 2 interval-valued functions. Riemann–Liouville fractional integration and derivative, Caputo fractional derivative, and Laplace transformation are proposed for the case of a Type 2 interval. The significant aspects of this introductory theory concerning Type 2 interval calculus are as follows:

• Human-involved communications in a dynamical decision environment cannot be memory-free.
• Numerous physical phenomena exist, where uncertainties are involved in two-layer senses.
• Fractional calculus can represent the memory of the dynamical system. On the other hand, Type 2 intervals are an adequate mathematical framework to describe two-layered, non-random, and non-fuzzy impreciseness.
• In several engineering and managerial situations, senses of memory and two-layer uncertainties may co-exist. For model formulation and analysis of such managerial phenomena, there is no single theory available in the existing literature. This necessitates the introduction of Type 2 interval-valued fractional calculus.

Although the central objective of this paper was to make theoretical advancements in uncertain fractional calculus, an economic order quantity model has been discussed as an application of the proposed theory. The inventory management scenarios in retail business may be memory-concerned due to the involvement of human resources. Also, decision-making strategies may experience impreciseness due to vague demand and pricing anticipations. Thus, Type 2 interval-valued fractional differential equations, as a consequence of the proposed theory, can be applicable to such managerial situations. Lower memory index values signify stronger memory senses. From a numerical simulation of the EOQ model, we perceived that stronger memory does not favor the profit maximization goal of the retailer. It also causes dispersions in Type 2 intervals representing profit.

Despite the novel introduction of Type 2 interval-valued fractional calculus in the literature, this paper has a few limitations, as mentioned below:

• A single application in inventory management policy is discussed where memory impact is well addressed. However, the impact of two-layer impreciseness would be made more understandable by adding a sense of scoring and ordering of the obtained numerical data.
• In the proposed application, hypothetical data were used for the numerical simulation. Original data from industries and the management sector would provide better insights into the validation of the proposed theory.

This paper can be extended in the following direction in the future:

• A research gap exists for the direct use of this theory in dynamical models of diverging perspectives. It necessitates a fresh analytical theory of Type 2 interval-valued fractional differential equations to be used in mathematical modeling in the future.
• As an immediate application of the proposed theory, a simple EOQ model has been discussed. Following this pathway, more insightful inventory and supply chain models and other engineering problems may be considered in the mathematical framework of Type 2 interval-valued fractional calculus.
• On the contrary, other definitions of fractional derivatives, like those of Atangana–Baleanu, Atangana–Baleanu–Caputo, and Caputo–Katugampola, may be analyzed in a Type 2 interval environment for more advancement of Type 2 interval-valued fractional calculus.